第10章 波动习题解答
《大学物理》(下2010.12.9)习题课

第11章光的量子效应及光子理论一、 选择题1. 金属的光电效应的红限依赖于: 【 C 】(A)入射光的频率; (B)入射光的强度;(C)金属的逸出功; (D)入射光的频率和金属的逸出功。
2. 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U 0(使电子从金属逸出需做功eU 0),则此单色光的波长λ必须满足: 【 A 】hceU )D (;hceU )C (;eU hc )B (;eU hc)A (0≥≤≥≤λλλλ 3. 关于光电效应有下列说法:(1) 任何波长的可见光照射到任何金属表面都能产生光电效应;(2) 对同一金属如有光电子产生,则入射光的频率不同,光电子的初动能不同; (3) 对同一金属由于入射光的波长不同,单位时间内产生的光电子的数目不同; (4) 对同一金属,若入射光频率不变而强度增加一倍,则饱和光电流也增加一倍。
其中正确的是: 【 D 】(A) (1),(2),(3); (B) (2),(3),(4); (C) (2),(3); (D)(2),(4)二、填空题1. 当波长为300 nm 光照射在某金属表面时,光电子的能量范围从0到.J 100.419-⨯在作上述光电效应实验时遏止电压为V 5.2U a =;此金属的红限频率Hz 104140⨯=ν。
2. 频率为100MHz 的一个光子的能量是J 1063.626-⨯,动量的大小是s N 1021.234⋅⨯-。
3. 如果入射光的波长从400nm 变到300nm ,则从表面发射的光电子的遏止电势增大(增大、减小)V 03.1U =∆。
4. 某一波长的X 光经物质散射后,其散射光中包含波长大于X 光和波长等于X 光的两种成分,其中大于X 光波长的散射成分称为康普顿散射。
三、计算题1. 已知钾的红限波长为558 nm ,求它的逸出功。
如果用波长为400 nm 的入射光照射,试求光电子的最大动能和遏止电压。
由光电方程2m mv 21A h +=ν,逸出功0h A ν=,0chA λ=,eV 23.2A =用波长为400nm 的入射光照射,光电子的最大动能:A h mv 212m -=ν A chE km -=λ,将nm 400=λ和eV 23.2A =代入得到:eV 88.0E km =遏止电压:a 2m eU mv 21=,2m a mv e21U =,V 88.0U a = 2. 从铝中移出一个电子需要4.2 eV 的能量,今有波长为200 nm 的光投射至铝表面。
《大学物理》 第二版 课后习题答案 第十章

习题精解10-1 在平面简谐波的波射线上,A,B,C,D 各点离波源的距离分别是3,,,424λλλλ。
设振源的振动方程为cos 2y A t πω⎛⎫=+ ⎪⎝⎭ ,振动周期为T.(1)这4点与振源的振动相位差各为多少?(2)这4点的初相位各为多少?(3)这4点开始运动的时刻比振源落后多少? 解 (1) 122,2,2xxπϕπϕππλλ∆∆∆==∆==3432,222x x πϕπϕππλλ∆∆∆==∆== (2)112233440,,2223,222πππϕϕϕϕππϕϕπϕϕπ=-∆==-∆=-=-∆=-=-∆=-(3) 1212343411,,,24223,,,242t T T t T T t T T t T Tϕϕππϕϕππ∆∆∆==∆==∆∆∆==∆==10-2 波源做谐振动,周期为0.01s ,振幅为21.010m -⨯,经平衡位置向y 轴正方向运动时,作为计时起点,设此振动以1400u m s -=∙的速度沿x 轴的正方向传播,试写出波动方程。
解 根据题意可知,波源振动的相位为32ϕπ= 2122200, 1.010,4000.01A m u m s T ππωπ--====⨯=∙ 波动方程231.010cos 2004002x y t m ππ-⎡⎤⎛⎫=⨯-+ ⎪⎢⎥⎝⎭⎣⎦10-3 一平面简谐波的波动方程为()0.05cos 410y x t m ππ=-,求(1)此波的频率、周期、波长、波速和振幅;(2)求x 轴上各质元振动的最大速度和最大加速度。
解 (1)比较系数法 将波动方程改写成0.05cos10 2.5x y t m π⎛⎫=-⎪⎝⎭与cos x y A t u ω⎛⎫=-⎪⎝⎭比较得1120.05;10;0.21015; 2.5;0.5A m T s v s u m s u T m Tπωππλ--=======∙=∙=(2)各质元的速度为()10.0510sin 410v x t m s πππ-=⨯-∙ 所以1max 0.0510 1.57()v m s π-=⨯=∙ 各质元的加速度为()220.05(10)cos 410a x t m s πππ-=-⨯-∙ 所以22max 0.05(10)49.3()a m s π-=⨯=∙10-4 设在某一时刻的横波波形曲线的一部分如图10.1所示。
大学物理波动习题

y 0.10 cos165 (T / 4)
u=330 m/s
165 (T / 4) / 2 O 1 2 3 4 x (m)
-0.10
21、一驻波表达为 y Acos2x cos1。0位0t
于x1 = 1 /8 m的质元P1与位于x2 = 3 /8 m处的
质元P2的振动相位差为__________.
D 的动SS振方12P动程方为2.2程为,两y1列波((AAB在c))oyPys点2(22发t 生AA12相ccoo消)ss干((2,2涉则t,t若S2S12的1)振)
S2
(2
1 )
P
2
(C)
y2
A c os (2t
1)
2
(D) y2 2Acos(2t 0.1 )
r2 r1
9. 某时刻驻波波形曲线如图所示,则 a ,b两点的 为相差是
S 2连线上,S1外侧各点(例如P点)两波引起的
两谐振动的为相差是
(A) 0
(C) / 2
(B)
(D) 3 / 2
B
/4
P
S1
S2
(1
2)
2
r1
r2
动8 方. 如向图均所垂示直,于S1图和面S,2 发为出两波相长干为波源 ,的它简们谐的波振,
P点是两列波相遇区域中的一点,以知 S1P 2
的振动方程为y=Acos(t+),若波速为u,
求此波的波动方程。
解:波速沿负x方向,则波动方程为
y Acos[(t x 1) ]
u
u
x=-1
18、图为t = T / 4 时一平面简谐波的波形 曲线,则其波的表达式为.
y 0.10 cos165 (t x / 330) (SI)
10级大学物理复习题(第10章)

第10章 机械振动和波一、填空题易:1、质量为0.10kg 的物体,以振幅1cm 作简谐运动,其角频率为110s -,则物体的总能量为, 周期为 。
(4510J -⨯,0.628s )易:2、一平面简谐波的波动方程为y 0.01cos(20t 0.5x)ππ=-( SI 制),则它的振幅为 、角频率为 、周期为 、波速为 、波长为 。
(0.01m 、20π rad/s 、 0.1s 、 40m/s 、4m )易:3、一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的倔强系数为 ,振子的振动角频率为 。
(200N/m ,10rad/s )易:4、一横波的波动方程是y = 0.02cos2π(100t – 0.4X )( SI 制)则振幅是_________,波长是_ ,频率是 ,波的传播速度是 。
(0.02m ,2.5m ,100Hz ,250m.s -1)易:5、两个谐振动合成为一个简谐振动的条件是 。
(两个谐振动同方向、同频率)易:6、产生共振的条件是振动系统的固有频率与驱动力的频率 (填相同或不相同)。
(相同)易:7、干涉相长的条件是两列波的相位差为π的 (填奇数或偶数)倍。
(偶数)易:8、弹簧振子系统周期为T 。
现将弹簧截去一半,仍挂上原来的物体,作成一个新的弹簧振子,则其振动周期为 T 。
(T )易:9、作谐振动的小球,速度的最大值为,振幅为,则振动的周期为;加速度的最大值为。
(34π,2105.4-⨯)易:10、广播电台的发射频率为 。
则这种电磁波的波长为 。
(468.75m )易:11、已知平面简谐波的波动方程式为 则时,在X=0处相位为 ,在处相位为 。
(4.2s,4.199s)易:12、若弹簧振子作简谐振动的曲线如下图所示,则振幅;圆频率;初相。
(10m,1.2-s rad π,0)中:13、一简谐振动的运动方程为2x 0.03cos(10t )3ππ=+( SI 制),则频率ν为 、周期T 为 、振幅A 为 ,初相位ϕ为 。
基础物理学下册【韩可芳】第10章习题答案

第十章第十章第十章第十章 波动光学波动光学波动光学波动光学思考题思考题思考题思考题10-1 普通光源中原子发光有何特征?答答答:答:::因为普通光源是大量不同原子在不同时刻发的光,是自然光,因此不满足干涉条件,所以一 般普通光源观察不到干涉现象。
10-2 如何用实验检验一束光是线偏振光、部分偏振光还是自然光?答答答:答:::拿一块偏振片迎着这束光,转动偏振片,观察透射光。
(1)视场中光强有变化且有消光现象 的为线偏振光;(2)光强有变化但无消光现象的为部分偏振光;(3)光强无变化的为自然光。
10-3 自然光可以用两个独立的、相互垂直的、振幅相等的光振动表示。
那么线偏振光是否也可以用两个相互垂直的光振动表示?如果可以,则这两个相互垂直的光振动之间关系如 何?10-4 如何用实验测定不透明媒质的折射率?答答答:答:::光线入射到不透明的媒介上,改变入射角i ,并同时用偏振片测定反射光线的偏振化程度。
当反射光线为完全偏振光时,此时入射角i0 即为布儒斯特角,满足tan 可求得不透明介质的折射率n 。
10-5 如图(a)所示,一束自然光入射在方解石晶体的表面上,入射光线与光轴成一定角度;问将有几条光线从方解石透射 出来?如果把方解石切割成等厚的A 、B 两块,并平行地移 开很短一段距离,如图(b)所示,此时光线通过这两块方解石后有多少条光线射出来?如果把B 块沿沿沿沿光线转过一个角度, 此时将有几条光线从B 块射出来?为什么?i 0n ,测得 i0 即考思考思考思考题题题题10-5图图图图10-6 从普通光源获得两束相干光的一般方法是什么?在光的干涉中决定相遇点产生明纹或暗纹的因素是什么?答答答:答:::分波阵面法和分振幅法。
波源的相位差和波源到相遇点的光程差决定相遇点产生明纹或暗纹。
10-7 如图所示,设光线a 、b 从周相相同的A 、B 点传至P 点,试讨论:(1)在图中的三种情况下,光线a 、b 在相遇处P 是 否存在光程差?为什么?(2)若a 、b 为相干光,那么在相遇处的干涉情况怎 样?考题思考题思考题思考题 10-7 图图图图10-8 在杨氏双缝实验中,当作如下调节时,屏幕上的干涉条纹将如何变化?(要说明理由)(1)使两缝之间的距离逐渐减小;(2)保持双缝的间距不变,使双缝与屏幕的距离逐渐减小;(3)如图所示,把双缝中的一条狭缝遮住,并在两缝的垂直平分线上放置一块平面反射镜。
大学物理第10章 习题
r1
第十章 波动
16
物理学
第五版
第十章 习题
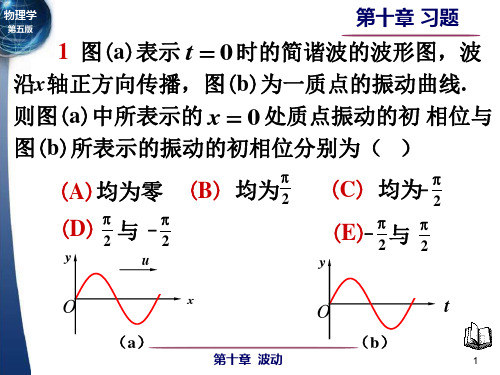
17 如图所示, 0 处有一运动方程为 x y A cos t 的平面波波源,产生的波沿x轴正、 负方向传播MN为波密介质的反射面,距波源 3λ / 4.求:(1)波源所发射的波沿波源O左右 传播的波动方程;(2)在MN处反射波的波动 方程;(3)在O~MN区域内形成的驻波方程, 以及波节和波腹的位置;(4)区域内合成波 M 的波动方程.
3 kg m ,求(1)该波的能流密度;(2)
1min内垂直通过4.0×10-4m2的总能量.
第十章 波动
13
物理学
第五版
第十章 习题
14 如图所示,两相干波源分别在P,Q 两点,它们发出频率为ν ,波长为 λ ,初 相相同的两列相干波,设PQ=3λ / 2 , R 为PQ连线上的一点.求:(1)自P、Q发 出的两列波在R处的相位差;(2)两波 在R处干涉时的合振幅.
3 一横波在沿绳子传播时的波动方程 为 y 0.20 cos 2.50t x) 式中y和x的单位 , ( 为 m , t的单位为s.(1) 求波的振幅、波速、 频率及波长;(2)求绳上的质点振动时的最 大速度;(3)分别画出t 1s 和 t 2s 时的波 形,并指出波峰和波谷.画出 x 1.0m 处质点的 振动曲线并讨论其与波形图的不同.
第十章 习题
5 已知一波动方程为 y 0.05 sin( 10t 2 x) 式中y的单位为 m ,t的单位为s. (1)求波长、频 率、波速和周期; (2)说明 x 0 时方程的意义, 并 作图表示.
第十章 波动
5
物理学
第五版
第十章 习题
6 有一平面简谐波在空间传播. 已知在波 线上某点B的运动规律为y A cos(t ) ,就 图(a)(b)(c)给出的三种坐标取法,分 别列出波动方程.并用这三个方程来描述与B相 距为b 的P点的运动规律.
第十章 波动 习题解答 (1)

(1)波动方程;
(2)求 x=0.5m 处质点的振动方程;画出该质点的振动图 ;
(3)求 t=1.0s 时各质点的位移分布,画出该时刻的波形图。
解:(1) 波函数 y = Acos[ω(t − x ) + ϕ] ,其中 T = 2s,ω = 2π / T = π , u = λ / T = 1m / s u
P
10.0m
x/m
x/m
y/m
u
O
t/s
O
x/m
A、振动 x-t 曲线
B、波动 y-x 曲线
(2)波源振动速度等于波速吗?振幅和周期呢?波动方程中波源的位置一定位于原点 O?
波源的初相?
波源振动速度不等于波速;波源的振幅和周期等于波动的振幅和周期
波函数为: y = 0.1cos[500π(t + x )+ π ](m) 5000 3
(C) A = A12 + A22 + 2 A1A2 cos ∆ϕ
(D) A1 − A2 ≤ A ≤ A1 + A2
∆ϕ
= ϕ2
− ϕ1
− 2π
r2 − r1 λ
拓展:B 选项改为“某时刻,在两列波相遇的区域中某质点若为静止,则这两列波必相干” 答案:错误
10.11 如图所示,S1、S2 为两平面简谐波相干波源,S2 的
=
4m , ∆ϕ
= ϕB0
− ϕ A0
−
2π λ
(rB
− rA )
=π
−
2π λ
(rB
− rA ) ,
干涉而静止的条件: ∆ϕ = ±(2k +1) π k = 0,1,2,
P 点为 AB 连线上任一点,rA 为 P 点到 A 点距离,rB 为 P 点到 B 点距离,
第10章 波 动习题
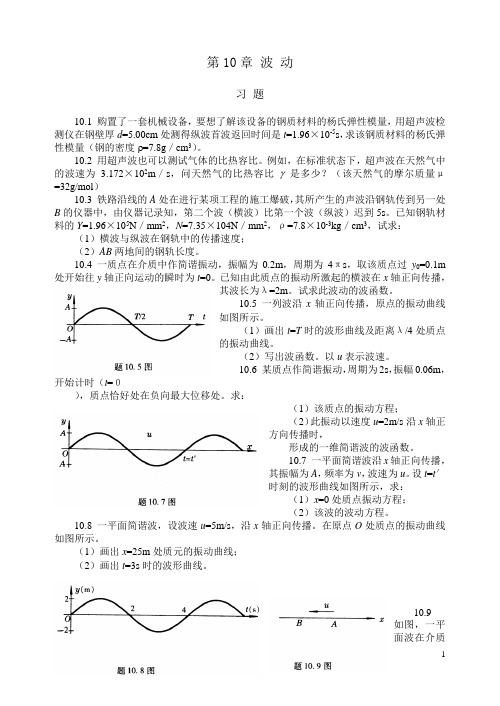
第10章波动习题10.1 购置了一套机械设备,要想了解该设备的钢质材料的杨氏弹性模量,用超声波检测仪在钢壁厚d=5.00cm处测得纵波首波返回时间是t=1.96×10-5s,求该钢质材料的杨氏弹性模量(钢的密度ρ=7.8g/cm3)。
10.2 用超声波也可以测试气体的比热容比。
例如,在标准状态下,超声波在天然气中的波速为 3.172×102m/s,问天然气的比热容比γ是多少?(该天然气的摩尔质量μ=32g/mol)10.3 铁路沿线的A处在进行某项工程的施工爆破,其所产生的声波沿钢轨传到另一处B的仪器中,由仪器记录知,第二个波(横波)比第一个波(纵波)迟到5s。
已知钢轨材料的Y=1.96×105N/mm2,N=7.35×104N/mm2,ρ=7.8×10-3kg/cm3,试求:(1)横波与纵波在钢轨中的传播速度;(2)AB两地间的钢轨长度。
10.4 一质点在介质中作简谐振动,振幅为0.2m,周期为4πs,取该质点过y0=0.1m 处开始往y轴正向运动的瞬时为t=0。
已知由此质点的振动所激起的横波在x轴正向传播,其波长为λ=2m。
试求此波动的波函数。
10.5 一列波沿x轴正向传播,原点的振动曲线如图所示。
(1)画出t=T时的波形曲线及距离λ/4处质点的振动曲线。
(2)写出波函数。
以u表示波速。
10.6 某质点作简谐振动,周期为2s,振幅0.06m,开始计时(t=0),质点恰好处在负向最大位移处。
求:(1)该质点的振动方程;(2)此振动以速度u=2m/s沿x轴正方向传播时,形成的一维简谐波的波函数。
10.7 一平面简谐波沿x轴正向传播,其振幅为A,频率为v,波速为u。
设t=t′时刻的波形曲线如图所示,求:(1)x=0处质点振动方程;(2)该波的波动方程。
10.8 一平面简谐波,设波速u=5m/s,沿x轴正向传播。
在原点O处质点的振动曲线如图所示。
(1)画出x=25m处质元的振动曲线;(2)画出t=3s时的波形曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2
15 15 . 5
5 5 . 5
(2)距波源为16.0m和17.0m的两质点间相位差
16 ,17 (100 t 16 or : 2
2
) (100 t 17
2
)
x,
x 17 16 1 m ,
则( C )
(A)波长为100m; (C)周期为 解:y
1 3 s
(B)波速为10m/s; (D)波沿x轴正方向传播
x u )]
;
A cos[ ( t
6
T 2
y 0 . 05 cos[ 6 ( t
x 100
)]
1 3
s
u 100 m / s
uT 33 . 3 m
第十章
波动
习题解答
1
第十章 习题
10-1 图(a)表示t=0 时的简谐波的波形图,波沿x轴正
方向传播,图(b)为一质点的振动曲线. 则图(a)中所
表示的x=0处质点振动的初相位与图(b)所表示的振动
的初相位分别为(D )
y A cos(t ) v A sin( t )
(A)均为零
(D) 2 与
y 0
y
2
(B) 均为 2
u
x
y 0
(C) 均为
(E) 2 与
y
2
2
v 0 2
O
(a)
v 0 2
O
(b)
t
2
10-2 机械波的表达式为
y 0 . 05 cos( 6 t 0 . 06 x )( m )
y /m
u
0.10 0.05 P 10.0m
x/m
O
-0.10
14
(1) 该波的波动方程
y W 0 . 1cos [ 500 ( t x / 5000 ) / 3 ]
(2) x=7.5m处质点的运动方程
y x 7 . 5 0 . 1cos [ 500 ( t 7 .5 5000
x (A)y A cos[ω(t ) ] u x (C)y A cos[ω(t ) ] u 2
x (B) y A cos[ω(t u) 2 ] x (D)y A cos[ω(t ) ] u
y
u
方法2: 可作出t=0时刻的波形图 由图可看出x=0的点在 t=0时刻y=-A, v>0
y
u
x 0,
t
T 4 2 T
A O -A
u: 速度大小
x
代入C式:
yo A cos[ω( T 0
图a
) ] 4 u 2
y 代入D式:o A cos[ω( yo A cos[
T 4
0 u
) ]
yo A cos 0 A
2
] 0
4
10- 3 一平面简谐波沿x轴负方向传播,角频率为ω, 波速为u.设t=T/4时刻的波形如图(a)所示,则该波 的表达式为( )D
10-10 波源作简谐运动,周期为0.02s,若该振动以 100m/s 的速度沿直线传播,设t=0时,波源处的质 点经平衡位置向正方向运动,求(1)距波源15.0m 和5.0m两点处质点的运动方程和初相;(2)距波源 分别为16.0m和17.0m的两质点间的相位差
解: 设波源为坐标原点(如图)
y o A cos( t )
3
)
y W 0 . 1cos [ 500 ( t x / u ) / 3 ]
由图: 2 10 20 m
u / T 20 250 5000 m / s
y W 0 . 1cos [ 500 ( t x / 5000 ) / 3 ]
(b)
(c)
11
y
u
u
y
y
u
B O
b
P (a)
x
P
b
B O
x
B O l
b
P
x
(b)
解: yB A cos(t ) (a) y
A cos[ ( t x u
x u
x0 l (c)
b u b u b u )] )]
)]
)]
x b:
y p A cos[ ( t
2 x
2 ( 0 .8 0 .3 ) 1
y A cos[ t
2 x
]
16
解:
y OV A cos( t )
y / m
t 0, yO
A 2
, v0 0
0.10 0.05
u
P 10.0m
x /m
O
3
-0.10
y OV 0 . 1 cos( 2 250 t
3
)
13
(1) 该波的波动方程
y OV 0 . 1 co轴负方向传播,角频率为ω, 波速为u.设t=T/4时刻的波形如图(a)所示,则该波 的表达式为( )D
x (A)y A cos[ω(t ) ] u x (C)y A cos[ω(t ) ] u 2
x (B) y A cos[ω(t u) 2 ] x (D)y A cos[ω(t ) ] u
y A cos[ ( t x u ) 0]
y 0 . 2 cos[ 2 . 5 ( t
x 2 .5
)]
2 . 5
u 2 .5 m / s
2
u
v=dy/dt
7
解:1)已知波动方程可表示为 y 与标准方程
y A cos[ ( t x u
x 100
)
2
) A cos( 100 t x
2
)
(1)距波源 15.0m 和 5.0m 两点处质 注意:波源为坐标原点 点的运动方程和初相;
y 15 A cos( 100 t 15 y 5 A cos( 100 t 5
) A cos( 100 t 15 . 5 ) ) A cos( 100 t 5 . 5 )
0 . 2 cos[ 2 . 5 ( t
x 2 .5
)]
) 0]
比较,可得:
A=0.20m
则
ω=2.5π/s
u=+2.5m/s
λ=u/ν=2.0m
φ0=0
ν=ω/2π =1.25Hz
2)v=dy/dt=-0.5πsin[2.5π(t-x/2.5)]
vmax=0.5π=1.57m/s
A O -A
x
t=T/4
图a
t=0
则x=0的点振动的初相位为
5
# 10-5 在驻波中,两个相邻波节间各质点的振动( B)
(A)、振幅相同,相位相同 (C)、振幅相同,相位不同 (B)、振幅不同,相位相同 (D)、振幅不同,相位不同
驻波特点: 两波节点间各点运动同相位,但振幅不同.
6
10-7 一横波在沿绳子传播时的波动方程 为 y 0.20 cos 2.50t x) 式中y和x的单位 , ( 为 m , t的单位为s.(1) 求波的振幅、波速、 频率及波长;(2)求绳上的质点振动时的最 大速度;(3)分别画出 t 1 s 和 t 2 s 时的波 形,并指出波峰和波谷.画出 x 1 . 0 m 处质点的 振动曲线并讨论其与波形图的不同.
uT
10
10-11 有一平面简谐波在空间传播. 已知在波 线上某点B的运动规律为y A cos(t ) ,就 图(a)(b)(c)给出的三种坐标取法,分 别列出波动方程.并用这三个方程来描述与B相 距为b 的P点的运动规律.
y
u
u
y
y
u
B
O
P
b
x
P
b
B O
x
B O l
b
P
x
(a)
y /m
) / 3 ] 0 . 1cos [ 500 t
13 12
]
t=0该点的振动速度.
v dy dt v t 0 50 sin ( 13 12 50 sin [ 500 t 13 12 ) 40 . 6 m s
1
u
2 / T 100 s
t 0, yo 0, v0 0
1
y
O
u
x
2 y OV A cos( 100 t ) 2 x y W A cos( 100 ( t ) ) 100 2
9
y W A cos( 100 ( t
3)t=1s和t=2s时的波形方程分别为:
y t 1 0 .2 cos ( 2 .5 π πx)
y x 1 0 . 2 cos[ 2 . 5 ( t 1 2 .5
8
y t 2 0 .2 cos ( 5 π πx)
)] 0 . 2 cos[ 2 . 5 t ] 0 . 2 cos 2 . 5 t
0.10 0.05 P
]
O
10.0m
x/m
-0.10
15
10-16 平面简谐波的波动方程为
