§27 极坐标系·径向速度与横向速度.ppt
极坐标的知识点总结PPT

极坐标的知识点总结极坐标是一种描述平面上点的坐标系统,与直角坐标系相对应。
在极坐标中,点的位置由极径和极角表示,极径代表点到原点的距离,极角代表点与正半轴的夹角。
极坐标具有一些独特的性质和应用,下面将逐步介绍极坐标的基本概念、转换公式以及在数学和物理等领域的应用。
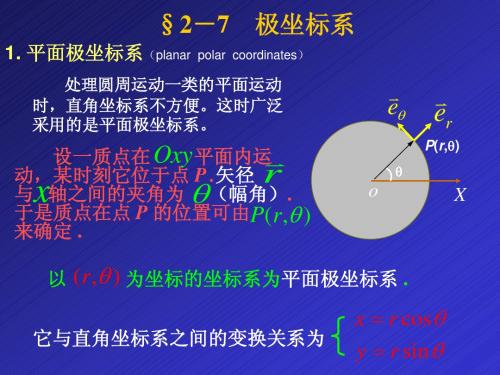
一、极坐标的基本概念 1. 极坐标系:极坐标系是由极轴和极角组成的坐标系,其中极轴是由原点O出发的射线,极角是由极轴和射线OP所夹的角度。
2. 极点和极径:极点是极坐标系的原点O,极径是点P到极点O的距离,用r表示。
3.极角:极角是由极轴和射线OP所夹的角度,通常用θ表示,取值范围为0到360度或0到2π弧度。
二、极坐标与直角坐标的转换公式 1. 极坐标到直角坐标的转换: - x = r * cosθ - y = r * sinθ 2. 直角坐标到极坐标的转换: - r = √(x^2 + y^2) - θ = arctan(y / x)三、极坐标的应用 1. 数学中的应用: - 极坐标方程:用极径和极角表示的方程,常用于描述曲线、圆和椭圆等几何图形。
- 极坐标下的微积分:在极坐标下,可以使用极坐标系的雅克比行列式来进行积分运算。
- 极坐标下的曲线积分:极坐标下的曲线积分可以简化对于弧长的计算,常用于求解环形路径上的物理量。
2. 物理中的应用: - 极坐标下的速度和加速度:利用极坐标转换公式,可以将速度和加速度从直角坐标系转换到极坐标系,从而更方便地描述物体的运动状态。
- 极坐标下的力和力矩:在某些情况下,使用极坐标可以更直观地描述物体受力和力矩的情况,尤其是涉及到旋转运动的问题。
总结:极坐标是一种用极径和极角表示点的坐标系统,可以简化某些数学和物理问题的描述和计算。
通过极坐标与直角坐标的转换公式,可以在不同坐标系之间进行转换。
在数学和物理等领域,极坐标具有广泛的应用,如曲线方程、微积分、曲线积分、运动学和动力学等。
了解和掌握极坐标的知识点有助于我们更好地理解和应用相关的数学和物理概念。
§2.7 极坐标系·径向速度与横向速度

∆θ
O
θ
r (t )
A
极轴
OA=OC
上页 下页 返回 结束
第二章 质点运动学 2. 速度
∆r ∆r ∆θ v = lim = lim er + lim r eθ ∆t → 0 ∆ t ∆t → 0 ∆ t ∆t → 0 ∆t dr dθ
= dt er + r dt eθ
v = v r e r + vθ eθ = v r + vθ
上页
下页
返回
结束
第二章 质点运动学
Байду номын сангаас
§2.7.2 径向速度与横向速度
1. 位移 若位矢的原点与极坐标的极点重合
r = rer 位移: 位移: ∆r = ∆r1 + ∆r2
横向位移 径向位移
eθ
∆r2
B
er
r
∆t很小时
∆r1 ≈ r∆θ eθ
C r ( t + ∆ t ) e ∆r ∆r1 θ e
∆r2 ≈ ∆rer
eθ
θ
r
P(r,θ)
er
x 是坐标不是位矢, 这里 r 是坐标不是位矢,当位矢的原点取在极点上 时,两者数字相同. 两者数字相同 径向单位矢量 e r 横向单位矢量 er eθ 不是常矢量 运动学方程 轨道方程
eθ
θ =常量 常量
r =常量 常量
r = r (t ) θ = θ (t )
r = r (θ )
径向速度 横向速度
dr vr = er dt
eθ
∆r2
B
er
r
dθ vθ = r eθ dt
O
上页
C r ( t + ∆ t ) e ∆r ∆r1 θ e
极坐标系 课件

2.若ρ>0,0≤θ<2π,则除极点外,点M(ρ,θ)与平面
内的点之间是否是一一对应的?
提示:如果我们规定ρ>0,0≤θ<2π,那么除极点外, 平面内的点可用唯一的极坐标(ρ,θ)来表示,这时,极坐标
的 极径 ,记为 ρ ;以极轴Ox为始边,射线OM为终边的角
xOM叫做点M的极角 ,记为 θ .有序数对 (ρ,θ) 叫做点
M的极坐标,记作 M(ρ,θ).
一般地,不作特殊说明时,我们认为 ρ≥0
,θ可
取 任意实数 .
2.极坐标与直角坐标的互化
(1)互化的前提条件
①极坐标系中的极点与直角坐标系中的原点重合;②
已知定点P4,π3 . (1)将极点移至O′ 2 3,π6 处极轴方向不变,求P点的 新坐标;
π (2)极点不变,将极轴顺时针转动 6 角,求P点的新坐 标.
[精讲详析] 本题考查极坐标系的建立及极坐标的求 法.解答本题需要根据题意要求建立正确的极坐标系,然 后求相应的点的极坐标.
(1)设P点新坐标为(ρ,θ),如图所示,由题意可知
|OO′|=2 3,|OP|=4,∠POx=π3 ,∠O′Ox=π6 , π
∴∠POO′= 6 .来自在△POO′中,ρ2=42+(2
3 )2-2·4·2
3 ·cos
π 6 =16
+12-24=4,∴ρ=2. 即|O′P|=2.
π ∴|OP|2=|OO′|2+|O′P|2,∠OO′P= 2 .
∴∠OPO′=π3 . ∴∠OP′P=π-π3 -π3 =π3 .
法一:由A(3,-
2-7极坐标系
& & v = ρe ρ + ρϕeϕ && && & && a = ( ρ − ρϕ )e ρ + ( ρϕ + 2 ρϕ )eϕ
2
径向速度 横向速度
dθ v v e 通常圆周运动时径向速度为0,这时: 通常圆周运动时径向速度为 ,这时: v(t) = r θ dt
这时常引入角速度矢量 定义: 定义:
ω
r
dθ 大 :ω = 小 v = rω dt v v v 方 :ω er e 满足右手定则 向 、 、θ
ω
v
质点的加速度为: 质点的加速度为: v v er e o v θ dθ v v dv d dr v a = = ( er +r e ) θ dt dt dt dt d2r dθ 2 v d2θ dr dθ v v v = 2 −r( ) er +r 2 +2 θ θ e = arer +aθ e dt dt dt dt dt 径向加速度 讨论: 讨论: 横向加速度
ρ
O
ϕ
A x
r (t ) = ρ e ρ
二、径向速度与横向速度
平面极坐标的径向单位矢量和横向单位矢量是随时间变化 是时间的函数,如果将它们用直角坐标来表示, 的,是时间的函数,如果将它们用直角坐标来表示,
e ρ = cos ϕ i + sin ϕ j e ϕ = − sin ϕ i + cos ϕ j
这两个单位矢量随时间的变化为: 这两个单位矢量随时间的变化为:
de ρ dt deϕ dt
& & = ( − sin ϕ i + cos ϕ j )ϕ = ϕ e ϕ & & = ( − cos ϕ i - sin ϕ j )ϕ = − ϕ e ρ
极坐标系的概念课件PPT学习教案

π B(2, )
4 D(1, 5π )
6
E(3.5, π) F (6, 4π )
3
G(5, 5π ) 3
5π
2π
6
•C 4
π
E • D•• •B •A
.O
x
G
4πF•
• 5π
3
3
第9页/共20页
2.边长为a的正六边形OABCDE在极坐标系中
的位置如图所示,求这个正六边形各顶点
的极坐标。
E
D
解:O(0, 0),A(a, B( 3a, 11π ) C(2a,
那么除极点外,平面内的点和极坐标就可以一一对应了. 特别强调:
一般情况下(若不作特别说明时),认为 ≥ 0.
第14页/共20页
Ex设点A(2, π ),直线l为过极点且垂直于极轴 6
的直线,分别求点A关于极轴、直线l、极点
的对称点的极坐标(限定 0, π π)
对极坐标平面中任意一点A(, )( 0, π π)
(1)点A关于极轴对称的点为__(__,____)_
(2)点A关于垂直于极轴的直线
对称的点为__(__,_π___ ) (3)点A关于极点对称的点为_(__,_____π_)_
第15页/共20页
变式:在极坐标系中,若等边三角形的两顶点
π
5π
是A(2, 4 ) ,B(2, 4 ) ,
那么顶点C的坐标可能是( )
第4页/共20页
在以上问题中,位置的确定是用
什么方法确定的? 距离与方向
在生活中人们经常用方向和距离来表 示一点的位置:如台风预报、地震预 报、测量、航空、航海等.
这种用方向和距离表示平面上一点的位 置的思想,就是极坐标的基本思想.
极坐标系

4.平面极坐标系在平面问题中,也常应用极坐标系,有些问题用极坐标系,比用直角坐标系来处理方便得多。
(1)质点的位置矢径在所研究的平面内取固定于参考系统的—点为原点,称为极点.又在上述平面内取一条通过极点的固定射线,称为极轴。
这就组成了极坐标系。
质点与极点的距离叫极径,记作 ρ;质点相对于极轴的方位角叫极角,记作 ϕ。
ρ与 ϕ即是质点的极坐标。
图1-6因为矢径的方向总是径向的。
所以 它只有径向分量 ρ,没有横向分量.即 ρ=r i (1. 36)i为沿径向的单位矢量,它的方向表明质点的方位角 ϕ。
虽然极坐标的极轴与极点固定于参考系不变,但不同的位置的径向单位矢量 i 却不同。
所以在极坐标中, i 不再是常矢量,也就是单位矢量 j 也是一样,不是常矢量这一点和直角坐标系大不一样,在求质点运动的速度和加速度时需要特别加以注意。
位置矢径()()()t t t ρ=r i 用极坐标表示可以写为()()t t ρρϕϕ=⎧⎨=⎩ (1. 37)这也就是轨道的参数方程,消去 t 可求得轨道方程 (,)0f ρϕ= (1. 38) (2)速度即(1. 39)可以证明v 可以表示为(1. 40)式中的 j 为横向的单位矢量。
速度的分量式为:v v ρϕ=+v i j。
这是很容易理解的,因就等于径向距离的时间变化率,横向速度就等于径向距离与角速度的乘积。
横向速度来源于极角 ϕ的变化,而矢径方向的单位矢量 i 的指向随着 ϕ的变化而变化。
3)加速度即(1. 41)可以证明所以2()(2)ρρϕρϕρϕ=-++ a i j , (1. 42)即2a ρρρϕ=- , 2a ϕρϕρϕ=+最终得 a a ρϕ=+a i j5.自然坐标系在不少情况下,如已知质点运动的轨道时,质点的位置常用从某个选定的点O 算起的曲线距离来表示。
(1)质点的位置设一个质点沿如图1-7所示轨道运动,在轨道上选一固定点O ,质点位于A 点时,它与O 点的曲线距离为 ()s s t =.(2) 速度质点沿轨道运动时,它的速度方向必沿轨道切线方向,速度的大小即速率为速度(1.43)图1-7上式中 τ 为切线方向的单位矢量。
极坐标系下的速度和加速度

活动坐标系以极坐标系下任意点P(r,θ)为原点,建立一个活动坐标系,该坐标系的两个主方向分别为径向(radial)和横向(transverse)。
径向与OP⃗⃗⃗⃗⃗ 的方向一致。
横向与径向垂直且朝向θ增加的方向。
该坐标系下的任一点或物理量可以通过主方向上的两个单位矢量(基)表示出来。
例如,假设P是一运动质点,则它的速度和加速度可以分解为v P=v r e r+vθeθ,a P=a r e r+aθeθ其中e r是径向单位矢量,eθ是横向单位矢量。
e r的直角坐标表示可以通过对OP⃗⃗⃗⃗⃗ 单位化获得。
e r=OP⃗⃗⃗⃗⃗|OP|=(cosθ,sinθ)而eθ的直角坐标表示可将e r逆时针旋转90°获得。
eθ=(−sinθ,cosθ)可以看出,{e r,eθ,P(r,θ)}刚好也是一个右手系。
并且该活动坐标系是与r的取值无关的(只要r≠0)。
所以当点P径向运动时,活动坐标系不发生改变;只有当点P有横向运动分量时活动坐标系才会发生改变。
e r,eθ关于θ的导数ddθe r=(−sinθ,cosθ)=eθddθeθ=−(cosθ,sinθ)=−e r极坐标系下的速度方法一设质点P(r,θ)的运动方程为{r=r(t)θ=θ(t)。
以时刻t为起点,建立活动坐标系{e r,eθ,P(r(t),θ(t))},则经过∆t时刻质点运动到P′=[r(t+∆t)−r(t)]e r+[θ(t+∆t)−θ(t)]r(t)eθ因此,在时刻t,质点速度在坐标系{e r,eθ,P(r(t),θ(t))}下可以表示为v P=lim∆t→0PP′∆t=ṙe r+rθeθ其中,径向速度为ṙ,横向速度为rθ。
方法二以r P代表质点P的坐标。
r P(t)就代表了质点P的运动方程。
由于r P(t)=(r(t)cosθ(t),r(t)sinθ(t))=r(t)e r(t)所以d dt r P(t)=ddt(r(t)e r(t))=(ddtr(t))e r(t)+r(t)(ddte r(t))其中d dte r=de rdθ·dθdt=θeθ这一项可以理解为由质点位置矢量的方向(e r)改变所引起的。
极坐标系ppt 优秀32页PPT

极坐标系ppt 优秀
11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时,两者数字相同.
径 向单 位矢量 er 横向单位矢量 e
er e 不是常矢量
运动学方程 r r(t)
=常量
r =常量
上页 下页 返回 结束
第二章 质点运动学
§2.7.2 径向速度与横向速度
1. 位移
若位矢的原点与极坐标的极点重合
r rer
位移:
Δt很 小
径向速度
vr
dr dt
er
横向速度
v
r d
dt
e
v
r(t
t
e
)Cr1 re2
B
er
r
er
O
r(t )
A
极轴
上页 下页 返回 结束
Δr Δr1
横向位移
时
r1 r e
Δr2 Δrer
Δr2
径向位移
r (t
O
t
e
r2
)C r1
e
B
er
r
er
r (t )
A
极轴
OA=OC
上页 下页 返回 结束
第二章 质点运动学
2.
速度
v lim
r
t0 t
lim
t 0
r t
er
lim r
t 0
t
e
dr dt
er
r
d
dt
e
v vr er v e vr
第二章 质点运动学
§2.7 极坐标系·径向速度与横向速度
§2.7.1 极坐标系 §2.7.2 径向速度与横向速度
上页 下页 返回 结束
第二章 质点运动学
§2.7.1 极坐标系
如图,极点O,极轴Ox,幅角,
规定自极轴逆时转为正,反之为负.
质点的极坐标(r,).
O
r
e
er
P(r,)
x
这里 r 是坐标不是位矢,当位矢的原点取在极点上
