初二四边形综合提高练习题(附详解)

合集下载

八年级四边形经典提高题(106题)

1 / 34八年级几何综合题（一）（2008学年静安区八下末）如图，在△ABC 中，点D 是边BC 的中点，点E 在△ABC ，AE 平分∠BAC ，CE ⊥AE ，点F 在边AB 上，EF ∥BC ．（1）求证：四边形BDEF 是平行四边形；（2）线段BF 、AB 、AC 的数量之间具有怎样的关系？证明你所得到的结论．（二）（2008学年静安区八下末）在梯形ABCD 中，AD ∥BC ，∠B=90°，∠C=45°，AB=8，BC=14，点E 、F 分别在边AB 、CD 上，EF ∥AD ，点P 与AD 在直线EF 的两侧，∠EPF=90°，PE=PF ，射线EP 、FP 与边BC 分别相交于点M 、N ，设AE=x ，MN=y ．（1）求边AD 的长；（2）如图，当点P 在梯形ABCD 部时，求y 关于x 的函数解析式，并写出定义域；（3）如果MN 的长为2，求梯形AEFD 的面积．（三）（2008学年徐汇区八下末）如图，平行四边形ABCD 中，点E 、F 、G 、H 分别在AB 、BC 、CD 、AD 边上且AE =CG ，AH =CF ．求证：四边形EFGH 是平行四边形；（四）（2008学年徐汇区八下末）如图，在△ABC 中，AB =BC ，BD 是中线，过点D 作DE ∥BC ，过点A 作AE ∥BD ，AE 与DE 交于点E ．求证：四边形ADBE 是矩形．F H D AEADBC2 / 34（五）（2008学年徐汇区八下末）如图，平行四边形ABCD 中，AB ⊥AC ，AB=1，BC =5．对角线AC 、BD 相交于点O ，将直线AC 绕点O 顺时针旋转，分别交BC 、AD 于点E 、F ．在旋转过程中，四边形BEDF 可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC 绕点O 顺时针旋转的最小度数．（六）（2008学年徐汇区八下末）如图，在平面直角坐标中，四边形OABC 是等腰梯形，CB ∥OA ，OC=AB=4，BC=6，∠COA=45°,动点P 从点O 出发，在梯形OABC 的边上运动，路径为O →A →B →C ，到达点C 时停止．作直线CP. （1）求梯形OABC 的面积；（2）当直线CP 把梯形OABC 的面积分成相等的两部分时，求直线CP 的解析式；（3）当∆OCP 是等腰三角形时，请写出点P 的坐标（不要求过程，只需写出结果）（七）（2008学年金山区八下末）如图，四边形A BC D ，AB∥DC，55B ∠=°，185∠=°， 240∠=° （1）求∠D 的度数；OF ED CBAOABCPxy3 / 34（2）求证：四边形A BC D 是平行四边形．（八）（2008学年金山区八下末）如图，已知四边形ABCD 是等腰梯形，AB=DC ，AD∥BC，AD=2，点P 为梯形部一点，若PB=PC ，且PA⊥PD．（1）求证：PA=PD ；（2）求PA 的长.（九）（2008学年金山区八下末）如图，已知在矩形ABCD 中，AB=3，点E 在BC 上且∠BAE =30°，延长BC 到点F 使CF ＝BE ，连结DF ．（1）判断四边形AEFD 的形状，并说明理由；（2）求DF 的长度；（3）若四边形AEFD 是菱形，求菱形AEFD 的面积．（十）（2008学年奉贤区八下末）如图，△ABC 中，点D 、E 分别是边BC 、AC 的中点，过点A 作AF//BC 交线段DE 的延长线相交于F 点，取AF 的中点G ，如果BC = 2 AB ．求证：（1）四边形ABDF 是菱形；（4分）（2）AC = 2DG ．（4分）A CBFDE G4 / 34（十一）（2008学年奉贤区八下末）边长为4的正方形ABCD 中，点O 是对角线AC 的中点， P 是对角线AC 上一动点，过点P 作PF ⊥CD 于点F ，作PE ⊥PB 交直线CD 于点E ，设PA=x ，S ⊿PCE =y ， ⑴ 求证：DF ＝EF ；（5分）⑵ 当点P 在线段AO 上时，求y 关于x 的函数关系式与自变量x 的取值围；（3分） ⑶ 在点P 的运动过程中，⊿PEC 能否为等腰三角形？如果能够，请直接写出PA 的长；如果不能，请简单说明理由。

初二数学经典四边形习题50道(附问题详解)

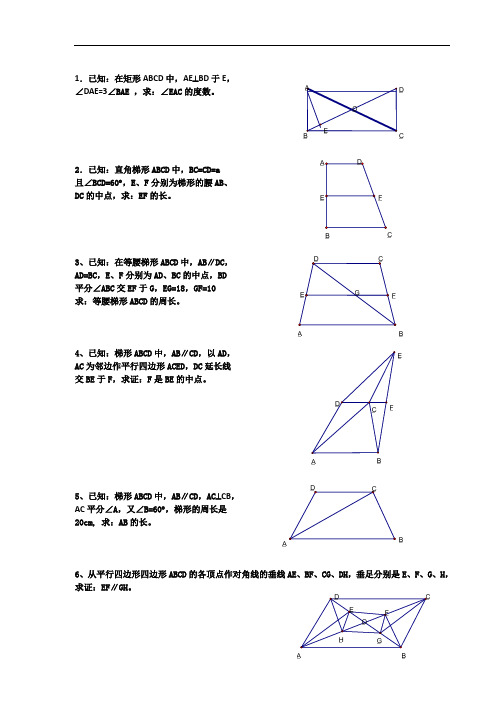
1．已知：在矩形ABCD 中，AE ⊥BD 于E ， ∠DAE=3∠BAE ，求：∠EAC 的度数。

2．已知：直角梯形ABCD 中，BC=CD=a 且∠BCD=60︒，E 、F 分别为梯形的腰AB 、 DC 的中点，求：EF 的长。

3、已知：在等腰梯形ABCD 中，AB ∥DC ， AD=BC ，E 、F 分别为AD 、BC 的中点，BD 平分∠ABC 交EF 于G ，EG=18，GF=10 求：等腰梯形ABCD 的周长。

4、已知：梯形ABCD 中，AB ∥CD ，以AD ， AC 为邻边作平行四边形ACED ，DC 延长线交BE 于F ，求证：F 是BE 的中点。

5、已知：梯形ABCD 中，AB ∥CD ，AC ⊥CB ， AC 平分∠A ，又∠B=60︒，梯形的周长是 20cm, 求：AB 的长。

6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ，垂足分别是E 、F 、G 、H ，求证：EF ∥GH 。

_ D_ C_ B _ C_ A _ B_ A _ B_ E _A_ B7、已知：梯形ABCD 的对角线的交点为E 若在平行边的一边BC 的延长线上取一点F ，使S ABC ∆=S EBF ∆，求证：DF ∥AC 。

8、在正方形ABCD 中，直线EF 平行于对角线AC ，与边AB 、BC 的交点为E 、F ，在DA 的延长线上取一点G ，使AG=AD ，若EG 与DF 的交点为H ，求证：AH 与正方形的边长相等。

9、若以直角三角形ABC 的边AB 为边，在三角形ABC 的外部作正方形ABDE ， AF 是BC 边的高，延长FA 使AG=BC ，求证：BG=CD 。

10、正方形ABCD ，E 、F 分别是AB 、AD 延长线上的一点，且AE=AF=AC ，EF 交BC 于G ，交AC 于K ，交CD 于H ，求证：EG=GC=CH=HF 。

11、在正方形ABCD 的对角线BD 上，取BE=AB ，若过E 作BD 的垂线EF 交CD 于F ，求证：CF=ED 。

初中八年级平行四边形拔高题综合题压轴题(含答案)

初中八年级平行四边形拔高题综合题压轴题(含答案)题目一已知平行四边形ABCD中，AB = 6cm，BC = 8cm，过点B作平行于AD的直线与AC交于点E，连接DE交BC的延长线于点F。

求EF的长度。

答案一连接DE并延长交BC于点G，根据平行四边形的性质，我们知道AG || DE。

所以AG || BF。

由此可得∆BFG与∆BCD为三角形对应边平行，则根据平行线截断比定理可知：$\frac{{BE}}{{BD}} = \frac{{FG}}{{GC}}$又已知$BE = BC + CE$，$CE = BD$，$BC = 8$，代入得：$\frac{{8+BD}}{{BD}} = \frac{{FG}}{{GC}}$整理可得：$\frac{{BD}}{{FG}} = \frac{{GC}}{{8+BD}}$ 由于$FG = GD$，所以：$\frac{{BD}}{{FG}} = \frac{{BD}}{{GD}} = 1$ 代入可得：$\frac{{1}}{{1}} = \frac{{GC}}{{8+BD}}$整理得：$BD = GC - 8$题目中已知BC=8，所以GC=16。

代入可得：$BD = 16 - 8 = 8$所以EF的长度等于BD，即EF=8cm。

题目二平行四边形PQRS中，已知PR = 5cm，PQ = 6cm，PS = 7cm。

点A在PS上，且PA的长度是PS的一半。

连接AQ并延长交QR 的延长线于点B，连接RP交QA的延长线于点C。

求BC的长度。

答案二设PS的长度为2x，则PA = x。

由平行四边形的性质可知AQ || RB，所以根据平行线截断比定理：$\frac{{RP}}{{PC}} = \frac{{AQ}}{{CQ}}$代入已知条件，得：$\frac{{2x + 6}}{{PC}} = \frac{{4}}{{2x - 6}}$ 整理可得：$(2x + 6)(2x - 6) = 4PC$解方程得：$x = 3$所以PA = 3cm。

2020年八年级数学下册四边形综合题重难点培优练习(含答案)

2020年八年级数学下册四边形综合题重难点培优练习1.如图，在矩形ABCDK AB=4cm BC=8cm点P从点D出发向点A运动，运动到点A即停止；同时点Q从点B出发向点C运动，运动到点C即停止.点P、Q的速度的速度都是1cm∕s ,连结PQ AQ CP设点P、Q运动的时间为t (S).(1)当t为何值时，四边形ABQP是矩形？(2)当t为何值时，四边形AQCP是菱形？(3)分别求出(2)中菱形AQCP的周长和面积.2.如图，在Rt△ ABC中，∠ ACB=90 ,过点C的直线m∕/ AB, D为AB边上一点，过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD BE(1)求证：CE=AD(2)当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)当∠ A的大小满足什么条件时，四边形BECD是正方形？(不需要证明)3.如图1 ,在矩形ABC中，动点P从点A出发，沿A→ D→ C→ B的路径运动.设点P运动的路程为X,△ PAB的面积为y.图2反映的是点P在A→D→C运动过程中，y与X的函数关系•请根据图象回答以下问题：(1) ______________________________ 矩形ABC啲边AD= , AB= ;(2)写出点P在C→B运动过程中y与X的函数关系式，并在图2中补全函数图象.4.在图1 , 2, 3中，已知？ABCD/ ABC=120 ,点E为线段BC上的动点，连接AE,以AE为边向上作菱形AEFG且∠ EAG=120 .⑴ 如图1,当点E与点B重合时，∠ CEF ___________ ° ;⑵如图2,连接AF.①填空：∠ FAD ________ ∠EAB填“>”，“<“，“=”);②求证：点F在∠ ABC的平分线上；⑶ 如图3,连接EG DG并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时, 求丄“的值.5∙如图，两个全等的△ ABC和^ DEF重叠在一起，固定△ ABC将厶DEF进行如下变换：(1)如图1, △ DEF沿直线CB向右平移(即点F在线段CB上移动)，连接AF、AD BD,请直接写出S△ABC与S四边形AFBD的关系(2)如图2,当点F平移到线段BC的中点时，若四边形AFBD为正方形，那么△ ABe应满足什么条件：请给出证明；(3)在(2)的条件下，将△ DEF沿DF折叠，点E落在FA的延长线上的点G处，连接CG请你画出图形，此时CG与CF有何数量关系.6.菱形ABCD中，点P为CD上一点，连接BP.(1)如图1,若BP⊥ CD菱形ABCD边长为10, PD=4,连接AP,求AP的长.(2)如图2,连接对角线AC BD相交于点Q点N为BP的中点，过P作PM⊥ AC于M连接ON MN.试判断△ MON勺形状，并说明理由.7∙如图，在Rt△ ABC中，∠ ACB=90 ,过点C的直线MN/ AB D为AB边上一点，过点D作DE⊥ BC交直线MN于E,垂足为F,连接CD BE.(1)求证：CE=AD(2)当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理3第4页共26页8.如图，在在四边形ABCD中，AD// BC, ∠ B=90°,且AD=12cm AB=8cm DC=IoCm 若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB 向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t 秒，回答下列问题：(1) ____________ BC= cm；(2)当t= _________ 秒时，四边形PQBA成为矩形•(3)当t为多少时，PQ=CD(4)是否存在t ,使得△ DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由.9∙如图1 ,已知正方形ABCD点E、F、G H分别在边AB BC CD DAh 若EGL FH则易证：EG=FH(1)如果把条件中的“正方形”改为“长方形”，并设AB=2, BC=3(如图2),试探究EG FH之间有怎样的数量关系，并证明你的结论；(2)如果把条件中的“ EGL FH'改为“ EG与FH的夹角为45°”，并假设正方形ABC啲边长为1,FH的长为(如图3),试求EG勺长度.10.如图，P为正方形ABC啲边BCh—动点(P与B C不重合)，连接AP,过点B乍BQLAP交CD于点0,将厶BQ(沿Bc所在的直线对折得到△ BQC ,延长QC交BA的延长线于点M(1)试探究AP与Be的数量关系，并证明你的结论；(2)当AB=3, BP=2PC 求QM勺长；(3)当BP=m PC=n寸，求AM勺长.第6 页共26 页11.如图，在矩形ABC中，点E为CE上一点，将△ BCE沿BE翻折后点C恰好落在AD⅛上的点F处，将线段EF绕点F旋转，使点E落在BE上的点G处，连接CG.⑴证明：四边形CEF是菱形；⑵ 若AB=8 BC=10,求四边形CEFG勺面积；⑶ 试探究当线段AB与BC满足什么数量关系时，BG=CG请写出你的探究过程.12.四边形ABCD是正方形，点E在边BC上（不与端点B C重合），点F在对角线AC上，且EF 丄AC,连接AE,点G是AE的中点，连接DF、FG2）求证： DF=（3）将图1中的△ CEF 绕点C 按顺时针旋转，使边CF 的顶点F 恰好在正方形 ABCD 勺边BC 上（如图2）,连接AE 、点G 仍是AE 的中点，猜想BF 与FG 之间的数量关系，并证明你的猜想.1）若 AB=7 BE= ,求FG 的长;FG ;13.△ ABC^n△ DEF都是边长为6cm的等边三角形，且A D B、F在同一直线上，连接CD BF.(1)求证：四边形BCDE是平行四边形；(2)若AD=2cm △ ABC沿着AF的方向以每秒Icm的速度运动，设△ ABC运动的时间为t 秒.(a)当t为何值时，平行四边形BCDE是菱形？说明理由；(b)平行四边形BCDE有可能是矩形吗？若有可能，求出t的值，并求出矩形的面积；若不可第10 页共26 页13.△ ABC^n△ DEF都是边长为6cm的等边三角形，且A D B、F在同一直线上，连接CD BF.能，说明理由.第11 页共26 页14.已知E,F分别为正方形ABCD勺边BC,CD上的点，AFQE相交于点G,当E,F分别为边BC,CD的中点时，有AF=DE,AF⊥ DE成立.试探究下列问题：(1)如图①，若点E不是边BC的中点,F不是边CD的中点，且CE=DF上述结论是否仍然成立?(请直接回答“成立”或“不成立”，不需要证明)(2)如图②，若点E,F分别在CB的延长线和DC的延长线上，且CE=DF此时，上述结论是否仍然成立?若成立，请写出证明过程，若不成立，请说明理由；⑶如图③，在⑵ 的基础上，连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点，请判断四边形MNPQl “矩形、菱形、正方形”中的哪一种，并证明你的结论.15.如图，在Rt△ ABCK∠ B=90°, AC=60cm ∠ A=60°,点D从点C出发沿CA方向以4cm∕s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm∕s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D E运动的时间是ts .过点D乍DF⊥ BC于点F,连接DE EF.(1)用t的代数式表示：AE= ____ ; DF= ______ ;(2)四边形AEFD^够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△ DE为直角三角形？请说明理由.1∙解:(1) 当四边形 ABQP 是矩形时，BQ=AP 即：t=8 - t ,解得t=4 .答：当t=4时，四边形 ABQR 是矩形；(2) 设t 秒后，四边形 AQCPl 菱形当AQ=CQ 即F =8- t 时，四边形AQCP 为菱形.解得:答：当t=3时，四边形 AQCPl 菱形;2∙ ( 1)证明：T 直线 m∕/ AB ∙∙∙ EC// AD又 τ∠ ACB=90 ,∙∙∙ BC⊥ AC 又 τ DEL BC, ∙ DE// AC.∙∙∙ EC / AD, DE// AC,：四边形 ADEC 是平行四边形.∙ CE=AD(2) 当点D 是AB 中点时，四边形 BECDl 菱形.证明：T D 是AB 中点，DE// AC (已证)，∙ F 为BC 中点，∙ BF=CF•••直线 m∕/ AB,∙∙∙∠ ECF=∠ DBF T ∠ BFDg CFE •△ BFD^△ CFE ∙ DF=EF V DEL BC, ∙ BC 和DE 垂直且互相平分.•••四边形 BECDl 菱形.(3) 当∠ A 的大小是45°时，四边形 BECD 是正方形.理由是：T ∠ ACB=90 , ∠ A=45°,∙∠ ABC 玄A=45°,∙ AC=BCT D 为 BA 中点，∙ CDL AB,∙∙∙∠ CDB=90 ,T 四边形BECD 是菱形，•四边形 BECDl 正方形，即当∠ A=45°时，四边形 BECDI 正方形.3.解：(1)根据题意得：矩形 ABC 啲边AD=2, AB=4;故答案为：2; 4;(2)当点P 在C →B 运动过程中，PB=8-x,∙∙∙ y=&× 4×( 8 — x ),即 y=-2x+16 (6≤ X ≤ 8), 正确作出图象，如图所示:参考答案t=3 .(3)当t=3时，CQ=5则周长为:4CQ=20cm 面积为: 4× 8 — 2×-- 2 × 3× 4=20 APB-4∙解: (1) V 四边形AEFG是菱形，∙∙∙∠AEF=180 - ∠ EAG=60 ,∙∙∙∠ CEF=Z AEC-∠ AEF=60 ,故答案为：60 ° ;⑵ ①V四边形ABCE是平行四边形，∙∠DAB=180 -∠ ABC=60 ,V四边形AEFG是菱形，∠ EAG=120 , ∙∠ FAE=60 ,∙∠FAD=Z EAB②作FM⊥ BC于M FN丄BA交BA的延长线于N,则∠ FNB=Z FMB=90 , ∙∠NFM=60 ,又∠ AFE=60 ,∙∠ AFN=Z EFMV EF=EA ∠ FAE=60 AEF为等边三角形，∙FA=FE[2ΛFN=ZEΨIB在△ AFN和△ EFM中，__ ji ∙. _. L ,•••△ AFN^△ EFM(AAS)IFA-FE•FN=FM 又FMI BC FN丄BA•点F在∠ ABC的平分线上；⑶ V四边形AEFG是菱形，∠ EAG=120 ,•∠ AGF=60 ,∙∠ FGE玄AGE=30 ,•四边形AEGH为平行四边形，•GE// AH•∠ GAH∠ AGE=30 , ∠ H=∠ FGE=30 ,∙∠ GAN=90 ,又∠ AGE=30 , ∙GN=2AN• ∠ DAB=60 , ∠ H=30° ,∙∠ ADH=30 , ∙AD=AH=GJE•四边形ABCD为平行四边形，∙BC=AD∙BC=GE•四边形ABEH为平行四边形，∠ HAE∠ EAB=30 , •平行四边形ABEN为菱形，∙AB=AN=NE ∙GE=3ABBCAB：■解：(1) S∆ABc=S 四边形AFBD)理由：由题意可得：AD// EQ则S^ ADF=S△ABD,故S^ ACF=SX ADl=S△ABD,贝S^ ABt=S 四边形AFBD(2)△ ABC为等腰直角三角形，即：AB=AC ∠ BAC=90 ,理由如下：∙∙∙ F 为BC的中点，∙∙∙CF=BF I CF=AD ∕∙ AD=BF又∙∙∙AD// BF, ∙四边形AFBD为平行四边形，∙∙∙ AB=AC F为BC的中点，∙AF⊥ BC, ∙平行四边形AFBD为矩形τ∠ BAC=90 , F 为BC的中点，∙AF=BC=BF∙四边形AFBD为正方形；(3)如图3所示：由(2)知，△ ABC为等腰直角三角形，AF⊥ BQ设CF=k,则GF=EF=CB=2K由勾股定理得：CG= k，∙∙∙ CG= CF.6.解：（1）如图1 中，•••四边形ABCD是菱形，∙∙∙AB=BC=CD=AD=10AB∕/ CD第17 页共26 页∙∙∙ PD=4,∙∙∙ PC=6 I PB 丄 CDPB⊥ AB ∕∙∠ CPB=∠ ABP=90 ,在 RT△ PCB 中，τ∠ CPB=90 P C=6, BC=IQ ∙ PB=J 昭？代唧］O J ? =8,在 RT △ ABP 中,∙∙∠ ABP=90 , AB=1Q PB=8,∙ PA ^^i ^P 2 =^Ll . (2)△ OMN 是等腰三角形•理由：如图2中，延长PM 交BC 于E.∙四边形 ABCD 是菱形，• AC ⊥ BD, CB=CD∙ CP=CE CML PE, ∙ PM=ME ∙ PN=NB7∙ ( 1)证明：∙ DEL Bq ∙∠ DFB=90 ,∙∠ ACB=90 , ∙∠ ACB ∠ DFB ∙ AC// DE∙ MIN/ AB 即CE// AD ∙四边形 ADEC 是平行四边形，∙ CE=AD(2) 解：四边形 BECD 是菱形，理由是：∙ D 为AB 中点，∙ AD=BD∙ CE=AD ∙ BD=CE ∙ BD// CE ∙四边形 BECD 是平行四边形, ∙∠ ACB=90 , D 为 AB 中点，∙ CD=BD ∙ ?四边形 BECD 是菱形；(3) 当∠ A=45时，四边形 BECD 是正方形，理由是：解：∙∠ ACB=90 , ∠ A=45°, ∙∠ ABC ∠ A=45°, ∙ AC=BC∙ D 为 BA 中点，∙ CDLAB ∙∠ CDB=90 ,∙四边形BECD 是菱形，∙菱形 BECD 是正方形，即当∠ A=45时，四边形 BECD 是正方形• 8∙ 解:抿据题胃得；P42lp c ς=3i,则FRAD PA=IS 儿CI)如虱过D 点、作DE 丄EC 于E,则四边形ABED 为拒册…-DE=AB=乱血，Jω=BE=12cκ,⅛ RtΔθE 中』', + ZCED=90-"・ DC=IQE it. DE=Scm 3 /-EC=Λ∕-D .∖0C=BE+EO18cm τ故答秦为 18;⑵IAD "DC, ZB=9C o 二当FEQ 时,四边形咖A 为矩形， PCCECD I CB∙ PE ⊥ AC, ∙ PE// BD ,∙ CP=CE ∙ PD=BE∙ BO=OD BN=NP ∙ ON=PD, ∙ ON=MN OMN 是等腰三角形^2t=lS-3t,解得t=^jb 故当伕晋秒时，四边形PQB 直为柜形』故答乘为普』C3)①当P"Q 3 "CD 时，如團,7AD //K J /.四边形CDrQ J ⅛∏亍四边形, 121'.P J Q J =CD, DP j=Cζ∖ .∖12-Ξt=3t, /.t=-⅛S⅛②如團」梯形PDCQ 是等腰梯形BL PQ6 易证」四边形PDEF 星矩形，/.EI ⅛I)P=12- 2t,易证，∆CDE ⅛≤∆QPF j .'.I TQ=CE=S J241∖(X=Fq ⅛Γ-KΓ=6+12- Ξt -⅛=3t j 二 t=千5〔4 4QC 杲等腰三角形时‘分三种情况讨论？① 3 QC=IIC 时，即 31=10, Λl=~f‰J ,St② 当 MJ=W? IFJ,专=G f .∙.i=Λjg o ς③ 当QD=QC 时「航■存 J 「■苦牛，丄罚 n9. ( 1)结论：EG FH=3: 2证明：过点A 作AM/ HF 交BC 于点M 作AN// EG 交CD 勺延长线于点N,如图1:∙∙∙ AM=HF AN=EG T 长方形 ABCD ∙∙∙∠ BAD 玄 ADN=90 ,∙∙∙ EG 丄 FH,∙∙∙∠ NAM=90 , ∙∠ BAM ∠ DAN •△ ABMhA ADN ∙ AM:AN=AB:AD T AB=2BC=AD=3 ∙ EG:FH=1.5;(2)解：过点A 作AM/ HF 交B(于点M 过点A 作AN// EG 交CDF 点N,如图2:,∙∙∙在 Rt △ ABM 中，BM=0.5将厶∙∙∙ AB=1, AM=FH=ANt绕点A旋转到△ APB∙∙∙ EG与FH的夹角为45°,∙∠ MAN=45 , ∙∠ DAN+∠ MAB=45即∠ PAM∠ MAN=45 ,从而△ APM^△ ANM ∙PM=NM设DN=X 贝U NC=I— x, NM=PM=0.5+在Rt△ CMN^, (0.5 +x) 2=0.25+(1 - x)2,解得x=1∕3 ,,答：EG的长为∙EG=AN=第20 页共26 页10.11.⑴ 证明：根据翻折的方法可得EF=EC ∠ FEG=/ CEG又V GE=GE EFG^△ ECG√∙ FG=GC.•••线段FG是由EF绕F旋转得到的，∙∙∙ EF=FG.∙∙∙ EF=EC=FG=GC t四边形FGC是菱形.(2)连接FC交GE于O点•根据折叠可得BF=BC=IO.：AB=8∙在Rt △ ABF中 ,根据勾股定理得AF=6. ∙FD=AD- AF=IO- 6=4.设EC=X 则DE=8- X, EF=x,在Rt△ FDE中, FD2+ DE=EF,即42+ (8-x) 2=X2.解得x=5.即CE=5.S菱形CEFG=CE∙ FD=5× 4=20.3）当时，BG=CG理由：由折叠可得BF=BC ∠ FBE=∠CBE，•••在Rt△ABF中,,∙∙∙BF=2AF.∙∙∙∠ ABF=30又τ∠ ABC=90 ,∙∠ FBE=Z CBE=30 , EC=0.5BE.∙∙∙∠ BCE=90 ,∙∠ BEC=60 .又'：GC=CE •△ GC为等边三角形. ∙GE=CG=CE=O∙5BE∙∙ G为BE的中点.∙CG=BG=Q.5BE.12.13.(1)证明：•••△ ABC和^ DEF是两个边长为6cm的等边三角形，∙∙∙ BC=DE ∠ ABC=/ FDE=60 ,二BC// DE 二四边形BCDE是平行四边形；(2)解：(a)当t=2秒时，?BCDE是菱形，此时A与D重合，∙CD=DE∙?ADEC是菱形;(b)若平行四边形BCDE是矩形，则∠ CDE=90 ,如图所示：∙∠CDB=90 - 60° =30° 同理∠ DCA=30 =∠ CDB ∙AC=AD 同理FB=EF, ∙ F 与B重合，∙t= (6+2)÷ 1=8秒，∙当t=8秒时，平行四边形BCDE是矩形.14.解：⑴成立.⑵成立•理由：I四边形ABCD为正方形，∙AD=DC∠ BCD∠ ADC=90 . 在△人。

八年级数学四边形之综合复习(四边形性质探索)基础练习(含答案)

八年级数学四边形之综合复习（四边形性质探索）基础练习试卷简介:<strong>全卷满分100分，测试时间60分钟，共四个大题：第一题选择，7个小题，每小题5分；第二题填空，4个小题，每小题5分；第三题计算，2个小题，每小题9分；第四题探究题，每小题9分。

</strong>学习建议:<strong>本讲内容是四边形之综合复习，本讲内容比较简单、也比较基础，但需要同学们对概念的掌握要准确，在计算过程中非常认真仔细，务必保证计算结果的正确性，同时也要提高做题速度。

</strong>一、单选题(共7道，每道5分)1.正方形具有而矩形不具有的性质是（）A.四个角都是直角B.对角线相等C.对角线互相平分D.对角线互相垂直答案：D解题思路：A、正方形，矩形四个角都是直角，故错误；B、矩形，正方形对角线都是相等的，故错误；C、平行四边形对角线都是互相平分的，故错误；D、正方形对角线互相垂直，但矩形对角线不一定垂直，故正确．故选D．易错点：对正方形和矩形的性质不熟悉试题难度：二颗星知识点：正方形的性质2.菱形具有而一般平行四边形不具有的性质是（）A.对角相等B.对边相等C.对角线互相垂直D.对角线相等答案：C解题思路：平行四边形的对角相等，对边相等，对角线相等，故A、B、D选项错误，对角线互相垂直的平行四边形为菱形，故C选项正确.易错点：对菱形和平行四边形的性质不熟悉试题难度：二颗星知识点：平行四边形的性质3.不能判定四边形ABCD是平行四边形的是（）A.AB= CD，AD= BCB. AB∥CD，AB= CDC.AD∥BC，AB= CDD. AB∥CD，AD∥BC答案：C解题思路：平行四边形的判定方法：①两组对边分别平行的四边形是平行四边形；②一组对边平行且相等的四边形是平行四边形；③两组对边分别相等的四边形是平行四边形；④两组对角分别相等的四边形是平行四边形；⑤对角线互相平分的四边形是平行四边形；⑥邻角互补的四边形是平行四边形。

八年级数学-四边形经典练习提高题含答案

梯形菱形正方形综合练习(含答案)1、如图，在矩形ABCD 中，AB = 3，AD = 4，P 是AD 上不与A 、D 重合的一动点，PE ⊥AC ，PF ⊥BD ，E 、F 为垂足，则PE + PF 的值为（）A 、2B 、2.4C 、2.5D 、2.62、下列命题正确的是（）A 、两邻边相等的四边形是菱形B 、一条对角线平分一个内角的平行四边形是菱形C 、对角线垂直且一组邻边相等的四边形是菱形D 、对角线垂直的四边形是菱形3、已知菱形的周长是高的8倍，则菱形较大的一个角是（）A 、100°B 、120°C 、135°D 、150°4.如图梯形ABCD 的两底长为AD =6，BC =10，中线为EF ，且∠B =90︒，若P 为AB 上的一点，且PE 将梯形ABCD 分成面积相同的两区域，则△EFP 与梯形ABCD 的面积比为何？(A) 1：6 (B) 1：10 (C) 1：12 (D) 1：16 。

5．如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，AD ＝4，BC ＝8，则AE ＋EF 等于（）A ．9B ．10C ．11D ．126.如图，在等腰梯形ABCD 中，AB ∥CD ，对角线AC ⊥BC ，∠B ＝60º，BC ＝2cm ，则梯形ABCD的面积为（）D C B AEF P ACB D (第3题图)60°30°D C B AA ．33cm 2B ．6 cm 2 C．36cm 2D ．12 cm 2 7．(1)梯形ABCD 中，AD ∥BC ，AB=CD=AD=2，∠B=60°，则下底BC 的长是( )A ．3B ．4C ． 2D ．5(2)已知等腰梯形的底角为45o ，高为2，上底为2，则其面积为（A ）2 （B ）6 （C ）8 （D ）128．如图，在等腰梯形ABCD 中，AC ⊥BD ，AC ＝6cm ，则等腰梯形ABCD 的面积为_____cm 2.9，在等腰梯形ABCD 中，AD ∥BC ，CD AD AB ==，若︒=∠60ABC ，12=BC ，则梯形ABCD 的周长为____________。

初二四边形综合提高测验题(附详解)-共9页

初二四边形综合提高练习题（附详解）1．如图，在Rt△ABC中，∠B=90°，C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．（1）求AB,AC的长；（2）求证：AE=DF；（3）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．（4）当t为何值时，△DEF为直角三角形？请说明理由.2．如图，已知菱形ABCD的对角线AC 、BD相交于点O，延长AB至点E，使BE=AB，连接CE．（1）求证：四边形BECD是平行四边形；（2）若∠E=60°，AC=求菱形ABCD的面积．3．在△ABC中，AB＝AC＝2，∠BAC＝45º.△AEF是由△ABC绕点A按逆时针方向旋转得到，连接BE，CF相交于点D.（1）求证：BE＝CF；（2）当四边形ABDF是菱形时，求CD的长.4．如图，四边形ABCD是正方形，点E，F分别在BC，AB上，点M在BA的延长线上，且CE=BF=AM，过点M，E分别作NM⊥DM，NE⊥DE交于N，连接NF．（1）求证：DE⊥DM；（2）猜想并写出四边形CENF是怎样的特殊四边形，并证明你的猜想．5．如图，正方形ABCD的面积为4，对角线交于点O，点O是正方形A1B1C1O的一个顶点，如果这两个正方形全等，正方形A1B1C1O绕点O旋转．（1）求两个正方形重叠部分的面积；（2）若正方形A1B1C1O旋转到B1在DB的延长线时，求A与C1的距离．6．在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．（备注：在直角三角形中30度角所对的边是斜边的一半）（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；（3）当t为何值时，△DEF为直角三角形？请说明理由．7．如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．（1）求证：AE=EF．（2）如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”其余条件不变，那么结论AE=EF是否成立呢？若成立，请你证明这一结论，若不成立，请你说明理由．8．已知□OABC的顶点A、C分别在直线x=2和x=4上，O为坐标原点，直线x=2分别与x轴和OC边交于D、E，直线x=4分别与x轴和AB边的交于点F、G．（1）如图，在点A、C移动的过程中，若点B在x轴上，①直线AC是否会经过一个定点，若是，请直接写出定点的坐标；若否，请说明理由．②□OABC是否可以形成矩形？如果可以，请求出矩形OABC的面积；若否，请说明理由．③四边形AECG是否可以形成菱形？如果可以，请求出菱形AECG的面积；若否，请说明理由．（2）在点A、C移动的过程中，若点B不在x轴上，且当□OABC为正方形时，直接写出点C的坐标．9．如图，矩形ABCD中，AB=9，AD=4．E为CD边上一点，CE=6．点P从点B出发，以每秒1个单位的速度沿着边BA向终点A运动，连接PE．设点P运动的时间为t秒．（1）求AE的长；（2）当t为何值时，△PAE为直角三角形？（3）是否存在这样的t，使EA恰好平分∠PED，若存在，求出t的值；若不存在，请说明理由．参考答案1．（1）AB=5，AC=10.（2）证明见解析；（3）能，当t=103时，四边形AEFD 为菱形．（4）当t=52秒或4秒时，△DEF 为直角三角形.【解析】（1）设AB=x,则AC=2x.由勾股定理得，(2x)2-x 2=(5)2,得x=5，故AB=5，AC=10.（2）证明：在△DFC 中，∠DFC=90°，∠C=30°，DC=2t ，∴DF=t．又∵AE=t，∴AE=DF．（3）能．理由如下：∵AB⊥BC，DF⊥BC，∴AE∥DF．又AE=DF ，∴四边形AEFD 为平行四边形．∵AB=5，∴AC=10．∴AD=AC -DC=10-2t ．若使□AEFD 为菱形，则需AE=AD ，即t=10-2t ，t=.即当t=时，四边形AEFD 为菱形．（4）①∠EDF=90°时，10-2t=2t ，t=．②∠DEF=90°时，10-2t=t ，t=4．③∠EFD=90°时，此种情况不存在．故当t=秒或4秒时，△DEF 为直角三角形.2．（1）证明见解析；（2）菱形ABCD 的面积为试题解析：（1）∵四边形ABCD 是菱形， ∴AB=CD，AB∥CD.；又∵BE=AB， ∴BE=CD.∵BE∥CD, ∴四边形BECD 是平行四边形.（2）∵四边形BECD 是平行四边形， ∴BD∥CE.∴∠ABO=∠E=60°. 又∵四边形ABCD 是菱形， ∴AC 丄BD,OA=OC. ∴∠BOA=90°，∴∠BAO=30°.∵AC= ∴OA=OC= ∴OB=OD=2. ∴BD=4.∴菱形ABCD 的面积=11422AC BD ⨯⨯=⨯=3．（1）证明见解析；（2）2试题解析：（1）∵△AEF 是由△ABC 绕点A 按逆时针方向旋转得到的，∴AE=AF=AB=AC=2，∠EAF=∠BAC=45°，∴∠BAC+∠3=∠EAF+∠3，即∠BAE=∠CAF，在△ABE 和△ACF 中{AB ACBAE CAF AE AF∠∠＝＝＝ ∴△ABE≌△ACF， ∴BE =CF ．（2）∵四边形ABDF 是菱形， ∴AB ∥DF ， ∴∠ACF ＝∠BAC ＝45°．∵AC =AF ， ∴∠CAF ＝90°，即△ACF 是以CF 为斜边的等腰直角三角形， ∴CF ＝又∵DF =AB ＝2， ∴CD ＝2．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了菱形的性质．4．【解析】（1）证明：∵四边形ABCD 是正方形，∴DC=DA，∠DCE=∠DAM=90°，在△DCE 和△MDA 中，， ∴△DCE≌△MDA（SAS ）， ∴DE=DM，∠EDC=∠MDA．又∵∠ADE+∠EDC=∠ADC=90°， ∴∠ADE+∠MDA=90°， ∴DE⊥DM；（2）解：四边形CENF 是平行四边形，理由如下：∵四边形ABCD 是正方形， ∴AB∥CD，AB=CD ．∵BF=AM， ∴MF=AF+AM=AF+BF=AB，即MF=CD ，又∵F 在AB 上，点M 在BA 的延长线上， ∴MF∥CD， ∴四边形CFMD 是平行四边形， ∴DM=CF，DM∥CF，∵NM⊥DM，NE⊥DE，DE⊥DM， ∴四边形DENM 都是矩形， ∴E N=DM ，EN∥DM，∴CF=EN，CF∥EN， ∴四边形CENF 为平行四边形．5．（1）1；（2解：解：（1）∵四边形ABCD 为正方形， ∴∠OAB =∠OBF =45°，OA =OB∵BO ⊥AC ， ∴∠AOE +∠EOB =90°，又∵四边形A 1B 1C 1O 为正方形， ∴∠A 1OC 1=90°，即∠BOF +∠EOB =90°， ∴∠AOE =∠BOF ，在△AOE 和△BOF 中，， ∴△AOE ≌△BOF （ASA ），∵S 两个正方形重叠部分=S △BOE +S △BOF ，又S △AOE =S △BOF∴S 两个正方形重叠部分=S ABO =S 正方形ABCD =×4=1；（2）如图，∵正方形的面积为4， ∴AD =AB =2，∵正方形A 1B 1C 1O 旋转到B 1在DB 的延长线时，∴C 1F =OC 1=1，AG =1 ∴C 1G =3，根据勾股定理，得AC 1=．6．（1）、证明见解析；（2）、t=10；（3）、t=152或12，理由见解析.试题解析：（1）、∵在Rt △ABC 中，∠C=90°﹣∠A=30°， ∴AB=12AC=12×60=30cm ∵CD=4t ，AE=2t ，又∵在Rt △CDF 中，∠C=30°， ∴DF=12CD=2t ∴DF=AE （2）、能。

八年级四边形综合拔高训练能力提升(含完整答案与解析)

1．如图，在四边形ABCD中，AB＝CD，点E在DC的延长线上，连接BE交AD于点F，BE平分∠ABC，BC＝EC，作FG⊥BA延长线于点G．（1）求证：四边形ABCD为平行四边形；（2）若F为AD中点，EF＝6，BC＝2，求GF的长．2．在四边形ABCD中，点E、F在对角线AC上，连接DE、BF，DE∥BF，DE＝BF，AF ＝CE．（1）如图1，求证：四边形ABCD是平行四边形；（2）如图2，∠ABC＝90°，DE⊥AC，连接BE、DF，请直接写出所有的全等的直角三角形．3．如图，在△ABC中，AB＝AC，AD是∠BAC的角平分线，点O是AB的中点，连接DO 并延长到点E，使OE＝OD，连接AE、BD．（1）求证：四边形AEBD是矩形；（2）当∠BAC＝90°时，判断四边形AEBD的形状，并证明你的结论．4．如图，四边形ABCD是正方形，点E，H分别在BC，AB上，点G在BA的延长线上，且CE＝AG，DE⊥CH于F．（1）求证：四边形GHCD为平行四边形．（2）在不添加任何辅助线的情况下，请直接写出图中所有与∠ECF互余的角．5．如图1，▱ABCD的对角线AC，BD相交于点O，且AE∥BD，BE∥AC，OE＝CD．（1）求证：四边形ABCD是菱形；（2）若∠ADC＝60°，BE＝2，求BD的长．6．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE＝AC，连接AE交OD于点F，连接CE、OE．（1）求证：四边形OCED为矩形；（2）若菱形ABCD的边长为6，∠ABC＝60°，求AE的长．7．如图，在四边形ABCD中，对角线AC、BD交于点O，AB∥DC，AB＝BC，BD平分∠ABC，过点C作CE⊥AB交AB的延长线于点E，连接OE．（1）求证：四边形ABCD是菱形；（2）若AB＝，OE＝2，求四边形ABCD的面积．8．如图，在△ABC中，AB＝AC，AD是BC边的中线，AG平分△ABC的外角∠BAF，BE ⊥AG，垂足为E．（1）求证：四边形ADBE是矩形；（2）连结DE，交AB于点O，若BC＝8，AO＝，则△ABC的面积是：．9．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作OE⊥BC交BC于点E．过点O作FG⊥AB交AB、CD于点F、G．（1）如图1，若BC＝5，OE＝3，求平行四边形ABCD的面积；（2）如图2，若∠ACB＝45°，求证：AF+FO＝EG．10．如图，点E为▱ABCD的边AD上的一点，连接EB并延长，使BF＝BE，连接EC并延长，使CG＝CE，连接FG．H为FG的中点，连接DH，AF．（1）若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；（2）求证：四边形AFHD为平行四边形；（3）连接EH，交BC于点O，若OC＝OH，求证：EF⊥EG．答案与解析1．如图，在四边形ABCD中，AB＝CD，点E在DC的延长线上，连接BE交AD于点F，BE平分∠ABC，BC＝EC，作FG⊥BA延长线于点G．（1）求证：四边形ABCD为平行四边形；（2）若F为AD中点，EF＝6，BC＝2，求GF的长．【解答】（1）证明：∵BE平分∠ABC，BC＝EC，∴∠ABF＝∠CBE，∠CBE＝∠E，∴∠ABF＝∠E，∴AB∥CD，又∵AB＝CD，∴四边形ABCD为平行四边形；（2）解：由（1）得：四边形ABCD为平行四边形，∴AD＝BC＝2，∵F为AD中点，∴AF＝DF＝，在△ABF和△DEF中，，∴△ABF≌△DEF（AAS），∴BF＝EF＝6，AB＝DE，∵AB＝CD，∴AB＝CD＝DE＝CE＝BC＝，∵FG⊥AB，∴∠G＝90°，∴GF2＝AF2﹣AG2＝BF2﹣BG2，即（）2﹣AG2＝62﹣（+AG）2，解得：AG＝，∴GF＝＝．【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、勾股定理等知识；熟练掌握平行四边形的判定与性质，证明三角形全等是解题的关键．2．在四边形ABCD中，点E、F在对角线AC上，连接DE、BF，DE∥BF，DE＝BF，AF ＝CE．（1）如图1，求证：四边形ABCD是平行四边形；（2）如图2，∠ABC＝90°，DE⊥AC，连接BE、DF，请直接写出所有的全等的直角三角形．【解答】（1）证明：∵DE∥BF，∴∠AFB＝∠CED，在△ABF和△CDE中，，∴△ABF≌△CDE（SAS），∴AB＝CD，∠BAF＝∠DCE，∴AB∥CD，∴四边形ABCD是平行四边形；（2）解：图中所有的全等的直角三角形为△ABC≌△CDA，△ABF≌△CDE，△BEF≌△DFE，△BCF≌△DAE，理由如下：∵DE⊥AC，∴∠AED＝∠CED＝90°，由（1）得：△ABF≌△CDE，AB＝CD，四边形ABCD是平行四边形，∴∠AFB＝∠CED＝90°，∴∠BFC＝90°，∵∠ABC＝90°，∴四边形ABCD是矩形，∴AD＝BC，∠CDA＝90°，在△ABC和△CDA中，，∴△ABC≌△CDA（SAS）；同理：△ABF≌△CDE（SAS），△BEF≌△DFE（SAS），△BCF≌△DAE（SAS）．【点评】本题考查了平行四边形的判定与性质、矩形的判定与性质、全等三角形的判定与性质等知识；熟练掌握平行四边形的判定与性质，证明三角形全等是解题的关键．3．如图，在△ABC中，AB＝AC，AD是∠BAC的角平分线，点O是AB的中点，连接DO 并延长到点E，使OE＝OD，连接AE、BD．（1）求证：四边形AEBD是矩形；（2）当∠BAC＝90°时，判断四边形AEBD的形状，并证明你的结论．【解答】（1）证明：∵点O为AB的中点，连接DO并延长到点E，使OE＝OD，∴四边形AEBD是平行四边形，∵AB＝AC，AD是∠BAC的角平分线，∴AD⊥BC，∴∠ADB＝90°，∴平行四边形AEBD是矩形；（2）∵∠BAC＝90°，AB＝AC，AD是∠BAC的角平分线，∴AD＝BD＝CD，∵由（1）得四边形AEBD是矩形，∴矩形AEBD是正方形．【点评】此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识，熟练掌握正方形和矩形的判定是解题关键．4．如图，四边形ABCD是正方形，点E，H分别在BC，AB上，点G在BA的延长线上，且CE＝AG，DE⊥CH于F．（1）求证：四边形GHCD为平行四边形．（2）在不添加任何辅助线的情况下，请直接写出图中所有与∠ECF互余的角．【解答】解：（1）证明：∵四边形ABCD是正方形，∴AD＝DC，∠GAD＝∠DCE＝90°，在△GAD和△ECD中，，∴△GAD≌△ECD（SAS），∴DE＝DG，∠GDA＝∠EDC，∴∠GDA+∠ADF＝∠EDC+∠ADF，即∠GDF＝∠ADC＝90°，∵DE⊥CH，∴∠DFH＝∠CDF＝90°，∴DG∥CH，∵∠HCB+∠HCD＝∠EDC+∠DCF＝90°，∴∠HCB＝∠EDC，在△HBC和△ECD中，，∴△HBC和△ECD（ASA）∴CH＝DE，∴DG＝CH，∵DG∥CH，∴四边形GHCD为平行四边形；（2）∵△HBC≌△ECD，∴∠BHC＝∠CED，∵∠ECF+∠FEC＝90°，∴∠FEC，∠BHC与∠ECF互余；∵AD∥BC，∴∠ADE＝∠DEC，∴∠ADE与∠ECF互余；∵∠DGA＝∠CHB，∴∠DGA与∠ECF互余；∵∠DCF+∠ECF＝90°，∴∠DCF与∠ECF互余；∴与∠ECF互余的角有：∠FEC、∠DCF、∠BHC、∠DGA、∠ADE．【点评】本题考查了全等三角形的性质和判定，平行线的性质和判定，正方形性质的应用，主要考查学生的推理能力．5．如图1，▱ABCD的对角线AC，BD相交于点O，且AE∥BD，BE∥AC，OE＝CD．（1）求证：四边形ABCD是菱形；（2）若∠ADC＝60°，BE＝2，求BD的长．【解答】（1）证明：∵AE∥BD，BE∥AC，∴四边形AEBO是平行四边形，∵四边形ABCD是平行四边形，∴DC＝AB．∵OE＝CD，∴OE＝AB．∴平行四边形AEBO是矩形，∴∠BOA＝90°．∴AC⊥BD．∴平行四边形ABCD是菱形；（2）解：由（1）得：四边形AEBO是矩形，四边形ABCD是菱形，∴OA＝BE＝2，AC⊥BD，BO＝DO，∠ADO＝30°，∴OD＝OA＝2，∴BD＝2OD＝4．【点评】本题考查了菱形的判定和性质，矩形的判定和性质，直角三角形的性质，平行四边形的判定与性质等知识；灵活运用有关性质是解题的关键．6．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE＝AC，连接AE交OD于点F，连接CE、OE．（1）求证：四边形OCED为矩形；（2）若菱形ABCD的边长为6，∠ABC＝60°，求AE的长．【解答】（1）证明：四边形ABCD是菱形，∴OA＝OC＝AC，AD＝CD，∵DE∥AC且DE＝AC，∴DE＝OA＝OC，∴四边形OADE、四边形OCED都是平行四边形，∵AC⊥BD，∴四边形OCED是矩形；（2）解：∵在菱形ABCD中，∠ABC＝60°，∴AC＝AB＝6，∴在矩形OCED中，CE＝OD＝＝3．∴在Rt△ACE中，AE＝＝3．【点评】本题考查了菱形的性质，矩形的判定与性质，勾股定理的应用．注意证得四边形OCED是平行四边形，四边形OCED是矩形是关键．7．如图，在四边形ABCD中，对角线AC、BD交于点O，AB∥DC，AB＝BC，BD平分∠ABC，过点C作CE⊥AB交AB的延长线于点E，连接OE．（1）求证：四边形ABCD是菱形；（2）若AB＝，OE＝2，求四边形ABCD的面积．【解答】（1）证明：∵AB∥DC，∴∠ABD＝∠CDB，∵BD平分∠ABC，∴∠ABD＝∠CBD，∴∠CDB＝∠CBD，∴BC＝CD，且AB＝BC，∴CD＝AB，且AB∥CD，∴四边形ABCD是平行四边形，∵AB＝BC，∴四边形ABCD是菱形；（2）解：由（1）得：四边形ABCD是菱形，∴OA＝OC，BD⊥AC，BO＝DO，∵CE⊥AB，∴AC＝2OE＝4，∴OA＝2，∴OB＝＝＝1，∴BD＝2OB＝2，∴菱形ABCD的面积＝AC×BD＝×4×2＝4．【点评】本题考查了菱形的判定和性质，角平分线的定义，勾股定理，直角三角形的性质等知识；证明四边形ABCD为菱形是解本题的关键．8．如图，在△ABC中，AB＝AC，AD是BC边的中线，AG平分△ABC的外角∠BAF，BE ⊥AG，垂足为E．（1）求证：四边形ADBE是矩形；（2）连结DE，交AB于点O，若BC＝8，AO＝，则△ABC的面积是：12．【解答】（1）证明：∵在△ABC中，AB＝AC，AD是BC边的中线，∴AD⊥BC，∠BAD＝∠CAD，∴∠ADB＝90°，∵AG为△ABC的外角∠BAF的平分线，∴∠BAE＝∠F AE，∴∠DAE＝90°，∵BE⊥AG，∴∠AEB＝90°，∴四边形ADBE为矩形；（2）解：∵AD是BC边的中线，BC＝8，∴BD＝CD＝4，由（1）得：四边形ADBE是矩形，∴AB＝DE＝2AO＝5，在Rt△ABD中，AD＝＝＝3，∴△ABC的面积＝BC×AD＝×8×3＝12；故答案为：12．【点评】此题考查了矩形的判定与性质、等腰三角形的性质、勾股定理等知识；熟练掌握矩形的判定与性质是解题的关键．9．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作OE⊥BC交BC于点E．过点O作FG⊥AB交AB、CD于点F、G．（1）如图1，若BC＝5，OE＝3，求平行四边形ABCD的面积；（2）如图2，若∠ACB＝45°，求证：AF+FO＝EG．【解答】解：（1）连接BD，∵平行四边形ABCD，∴BD过点O，∴S△OBC＝BC•OE＝×5×3＝∴平行四边形ABCD的面积＝4S△OBC＝30；（2）过点E作EH⊥EG，与GC的延长线交于点H，如图2，∵OE⊥BC，∴∠OEG+∠OEC＝∠GEC+∠CEH＝90°，∴∠OEG＝∠CEH，∵∠ACB＝45°，∴∠COE＝45°，∴OE＝CE，∵平行四边形ABCD中，AB∥CD，又FG⊥AB，∴FG⊥CD，∴∠EOG+∠ECG＝360°﹣90°﹣90°＝180°，∵∠ECH+∠ECG＝180°，∴∠EOG＝∠ECH，∴△OEG≌△CEH（ASA），∴OG＝CH，EG＝EH，∵四边形ABCD是平行四边形，∴OA＝OC，AB∥CD，∴∠OAF＝∠OCG，∵∠AOF＝∠COG，∴△OAF≌△OCG（ASA），∴AF＝CG，OF＝OG，∵CG+CH＝GH，∴AF+OF＝GH，∵∠GEH＝90°，EG＝EH，∴GH＝，∴AF+OF＝EG．【点评】本题主要考查了平行四边形的性质，全等三角形的性质与判定，勾股定理，三角形的面积公式，关键是证明全等三角形．10．如图，点E为▱ABCD的边AD上的一点，连接EB并延长，使BF＝BE，连接EC并延长，使CG＝CE，连接FG．H为FG的中点，连接DH，AF．（1）若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；（2）求证：四边形AFHD为平行四边形；（3）连接EH，交BC于点O，若OC＝OH，求证：EF⊥EG．【解答】（1）解：∵四边形ABCD是平行四边形，∴∠BAE＝∠BCD＝70°，AD∥BC，∵∠DCE＝20°，∵AB∥CD，∴∠CDE＝180°﹣∠BAE＝110°，∴∠DEC＝180°﹣∠DCE﹣∠CDE＝50°；（2）证明：∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∠BAE＝∠BCD，∵BF＝BE，CG＝CE，∴BC是△EFG的中位线，∴BC∥FG，BC＝FG，∵H为FG的中点，∴FH＝FG，∴BC∥FH，BC＝FH，∴AD∥FH，AD∥FH，∴四边形AFHD是平行四边形；（3）证明：连接EH，CH，∵CE＝CG，FH＝HG，∴CH＝EF，CH∥EF，∵EB＝BF＝EF，∴BE＝CH，∴四边形EBHC是平行四边形，∴OB＝OC，OE＝OH，∵OC＝OH，∴OE＝OB＝OC＝BC，∴△BCE是直角三角形，∴∠FEG＝90°，∴EF⊥EG．【点评】本题考查了平行四边形的判定与性质、三角形中位线定理、等腰三角形的性质以及三角形内角和定理；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．。

【精编版】数学中考专题训练——四边形的综合

中考专题训练——四边形的综合1．四边形ABCD为平行四边形，点P为平面内一点（1）若AP＝BC，连AP、DP；①如图1，点P在边BC上，求证：PD平分∠APC；②如图2，过P作PD的垂线交DC的延长线于点F，FP交AB于点E，求证：DF＝2AE．（2）如图3，∠ABC＝60°，点P在对角线DB上，点M在边AD上，MP＝CD且∠AMP ＝∠ABD，AB＝5，BP＝3，直接写出平行四边形ABCD的面积．2．在正方形ABCD中，AB＝6，E为直线AB上一点，EF⊥AB交对角线AC于F，点G为AF中点，连接CE，点M为CE中点，连接BM并延长交直线AC于点O．（1）如图1，E在边AB上时，＝，∠GBM＝；（2）将（1）中△AEF绕A逆时针旋转任意一锐角，其他条件不变，如图2，（1）中结论是否仍然成立？请加以证明．（3）若BE＝2，则CO长为．3．平面直角坐标系中，菱形ABCD．（1）若点A坐标是（0，2），点B坐标（﹣2，0），求∠ABC及菱形边长：（2）在（1）的条件下，连接OD，过C点向OD作垂线，垂足为E，求CE；（3）如图3所示，∠ABO＝60°，在y轴负半轴上取一点P，使得∠BPO＝15°，延长BD至Q，使得DQ＝CD，连接AQ，若AP＝BQ＝a，求线段AQ的长（用含a的式子表示）．4．矩形ACBD对角线AC、BD相交于点O，点P是对角线BD上的一个动点（不与B，D 重合），∠AOB＝α，过P点作PF∥AC，交AB于F，连接AP．将AP绕P点逆时针旋转α得到EP，连接BE．（1）若点P在BD上，∠AOB＝50°①求证：AF＝BE；②求∠ABE＝．（2）若点P在OD上，求∠ABE（用α表示）；（3）若BC＝8，将A绕点P顺时针方向旋转（180°﹣α）得到EP，连接DE，当DP＝3OP时，DE＝．5．如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N，连接CN．（1）如图1，求证：E，N、C三点在同一直线上；（2）如图1，若△CMN的面积与△CDN的面积比为3：1，求的值．（3）如图2，已知点P、Q、T分别是CM、CN、MN上的动点，若AN＝3，BM＝1，试直接写出PT+QT的最小值．6．已知平行四边形ABCD中，N是边BC上一点，延长DN、AB交于点Q，过A作AM⊥DN于点M，连接AN，则AD⊥AN．（1）如图①，若tan∠ADM＝，MN＝3，求BC的长；（2）如图②，过点B作BH∥DQ交AN于点H，若AM＝CN，求证：DM＝BH+NH．7．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2．动点P以每秒2个单位长度的速度从点A出发，沿A→C→B的方向向终点B运动（点P不与△ABC的顶点重合）．点P 关于点C的对称点为点D，过点P作PQ⊥AB于点Q，以PD、PQ为边作▱PDEQ．设▱PDEQ与△ABC．重叠部分的面积为S，点P的运动时间为t（s）（1）当点P在AC上运动时，用含t的代数式表示PD的长；（2）当点E落在△ABC的直角边上时，求t的值；（3）当▱PDEQ与△ABC重叠部分的图形是四边形时，求S与t之间的函数关系式．8．在菱形ABCD中，∠ABC＝60°（1）如图1，P是边BD延长线上一点，以AP为边向右作等边△APE，连接BE、CE．①求证：CE⊥AD；②若AB＝，BE＝，求AE的长；（2）如图2，P是边CD上一点，点D关于AP的对称点为E，连接BE并延长交AP的延长线于点F，连接DE、DF．若BE＝11，DE＝5，求△ADF的面积．9．如图，四边形ABCD中，AB＝AD，∠BAD＝60°，∠BCD＝30°，将AC绕着点A顺时针旋转60°得AE，连接BE，CE．（1）求证：△ADC≌△ABE；（2）求证：AC2＝DC2+BC2；（3）若AB＝2，点Q在四边形ABCD内部运动，且满足AQ2＝BQ2+DQ2，求点Q运动路径的长度．10．【阅读】如图1，四边形OABC中，OA＝a，OC＝8，BC＝6，∠AOC＝∠BCO＝90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC 的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．【理解】若点D与点A重合，则这个操作过程为FZ[45°，8]；【尝试】（1）若点D与OA的中点重合，则这个操作过程为FZ[，]；（2）若点D恰为AB的中点（如图2），求θ的值；【应用】经过FZ[45°，a]操作，点B落在点E处，若点E在四边形OABC的边AB上，直线l 与AB相交于点F，试画出图形并解决下列问题：①求出a的值；②若P为边OA上一动点，连接PE、PF，请直接写出PE+PF的最小值．（备注：等腰直角三角形的三边关系满足1：1：或：：2）11．如图，四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF＝90°，连接FC，G为FC的中点，连接GD，ED．（1）如图①，E在AB上，直接写出ED，GD的数量关系．（2）将图①中的△AEF绕点A逆时针旋转，其它条件不变，如图②，（1）中的结论是否成立？说明理由．（3）若AB＝5，AE＝1，将图①中的△AEF绕点A逆时针旋转一周，当E，F，C三点共线时，直接写出ED的长．12．如图，在平面直角坐标系中，已知A（﹣2，0），B（0，m）两点，且线段AB＝2，以AB为边在第二象限内作正方形ABCD．（1）求点B的坐标．（2）在x轴上是否存在点Q，使△QAB是以AB为腰的等腰三角形？若存在，请直接写出点Q的坐标，若不存在，请说明理由；（3）如果在坐标平面内有一点P（a，3），使得△ABP的面积与正方形ABCD的面积相等，求a的值．13．如图，矩形ABCD中，AB＝a，AD＝b，点P是对角线BD上的一个动点（点P不与B、D重合），连接AP并延长交射线BC于点Q，（1）当AP⊥BD时，求△ABQ的面积（用含a、b的代数式表示）；（2）若点M为AD边的中点，连接MP交射线BC于点N，证明：点N也为线段BQ的中点；（3）如图，当为何值时，△ADP与△BPQ的面积之和最小．14．如图1，AC⊥CH于点C，点B是射线CH上一动点，将△ABC绕点A逆时针旋转60°得到△ADE（点D对应点C）（1）延长ED交CH于点F，求证F A平分∠CFE；（2）如图2，当∠CAB＞60°时，点M为AB的中点，连接DM，请判断DM与DA、DE的数量关系，并证明；（3）如图3，作▱ABGE，连接DG，点N为DG的中点，连接EN．若AC＝EN＝3，直接写出四边形ADGE的面积．15．【操作】如图①，在矩形ABCD中，E为对角线AC上一点（不与点A重合）．将△ADE 沿射线AB方向平移到△BCF的位置，E的对应点为点F，易知△ADE≌△BCF（不需要证明）【探究】过图①的点E作BG∥BC交FB延长线于点G，连接AG，其它条件不变，如图②．求证：△EGA≌△BCF【拓展】将图②中的△BCF沿BC翻折得到△BCF′，连接GF′，其它条件不变，如图③当GF′最短时，若AB＝4，BC＝2，直接写出FF′的长和此时四边形BFCF′的周长．16．如1，在矩形ABCD中，AB＝6，AD＝10，E为AD上一点且AE＝6，连接BE．（1）将△ABE绕点B逆时针旋转90°至△ABF（如图2），且A、B、C三点共线，再将△ABF沿射线BC方向平移，平移速度为每秒1个单位长度，平移时间为t（s）（t≥0），当点A与点C重合时运动停止．①在平移过程中，当点F与点E重合时，t＝（s）．②在平移过程中，△ABF与四边形BCDE重叠部分面积记为S，求s与t的关系式．（2）如图3，点M为直线BE上一点，直线BC上有一个动点P，连接DM、PM、DP，且EM＝5，试问：是否存在点P，使得△DMP为等腰三角形？若存在，请直接写出此时线段BP的长；若不存在，请说明理由．17．如图1，△ABC和△CDE均为等边三角形，BC＝a，CD＝b（a＞b）．（1）当B、C、D共线时，BA、DE交于点M，①判断四边形ACEM的形状，并说明理由．②a、b为方程x2﹣（m﹣1）x+m2﹣2m﹣8＝0的两根，F为AE的中点，求CF的长．（2）将△CDE绕点C旋转（如图3所示），点E在△ABC内部，连接AE，∠BEC＝105°，若＝n，直接写出n的最小值．18．如图1，四边形ABCD中，对角线AC平分∠DCB，且AD＝AB，CD＜CB （1）求证：∠B+∠D＝180°；（2）如图2，在AC上取一点E，使得BE∥CD，且BE＝CE，点F在线段BC上，连接AF，且AB＝AF，求证：AE＝CF；（3）如图3，在（2）的条件下，若BE与AF交于点G，BF：AB＝2：7，求tan∠BGF 的值．19．已知四边形ABCD中，AD∥BC，∠D＝90°，AC平分∠BAD，∠ACD＝30°（1）如图1，求证：△ABC是等边三角形；（2）如图2，点E在边BA的延长线上，在边BC上取一点F，连接EC、EF且EC＝EF，求证：BF＝AE；（3）如图3，在（2）的条件下，连接AF，取AF的中点G，连接BG并延长交线段EC 于M，交线段AD于R，过点A作AN∥EC交线段BR于N，若GN＝2，EM＝5，求CM 的长．20．阅读材料题：浙教版九上作业本①第18页有这样一个题目：已知，如图一，P是正方形ABDC内一点，连接P A、PB、PC，若PC＝2，P A＝4，∠APC＝135°，求PB的长．小明看到题目后，思考了许久，仍没有思路，就去问数学老师，老师给出的提示是：将△P AC绕点A顺时针旋转90°得到△P'AB，再利用勾股定理即可求解本题．请根据数学老师的提示帮小明求出图一中线段PB的长为．【方法迁移】：已知：如图二，△ABC为正三角形，P为△ABC内部一点，若PC＝1，P A＝2，PB＝，求∠APB的大小．【能力拓展】：已知：如图三，等腰三角形ABC中∠ACB＝120°，D、E是底边AB上两点且∠DCE＝60°，若AD＝2，BE＝3，求DE的长．21．问题发现：（1）如图①，四边形ABCD中，∠DAB＝∠BCD＝90°，CB＝CD，对角线AC的长为6，则四边形ABCD的面积为．问题探究：（2）如图②，Rt△ABC中，∠CAB＝90°，AC＝5，AB＝12，点D和E都是边BC上的动点，且满足CD＝BE，连接AD、AE．求AD+AE的最小值；问题解决：（3）某校准备组织八年级同学开展一次去大明宫遗址公园的考古研学活动．小凯和小鹏在去之前先做了一个模拟“藏宝图”的游戏，为了使宝物隐藏得更神秘，小凯利用学过的数学知识，设计了如下方案，让小鹏破解．如图③，点B在点A的正东方向12m处，点P和Q都为平面内的动点，且满足P A＝8m，PB＝BQ，∠PBQ＝90°，当线段AQ长度最大时，点Q的位置即为藏宝地．请你帮助小鹏破解，藏宝地在点A的什么方向？距离点A多远？22．已知：如图，正方形ABCD，点E是DC边上的一动点，过点C作AE的垂线交AE延长线于点F，过D作DH⊥CF，垂足为H，点O是AC中点，连HO．（1）如图1，当∠CAE＝∠DAE时，证明：AE＝2CF；（2）如图2，当点E在DC上运动时，线段AF与线段HO之间是否存在确定的数量关系？若存在，证明你发现的结论：若不存在，请说明理由；（3）当E为DC中点时，AC＝2，直接写出AF的长．23．如图，在平面直角坐标系中，矩形ABCO的顶点O与坐标原点重合，顶点A、C在坐标轴上，B（18，6），将矩形沿EF折叠，使点A与点C重合．（1）求点E的坐标；（2）点P从O出发，沿折线O﹣A﹣E方向以每秒2个单位的速度匀速运动，到达终点E时停止运动，设P的运动时间为t，△PCE的面积为S，求S与t的关系式，直接写出t的取值范围；（3）在（2）的条件下，当P A＝PE时，在平面直角坐标系中是否存在点Q，使得以点P、E、G、Q为顶点的四边形为平行四边形？若不存在，请说明理由；若存在，请求出点Q的坐标．24．在▱ABCD中，∠ADC的平分线交直线BC于点E，交直线AB于点F．（1）如图①，证明：BE＝BF．（2）如图②，若∠ADC＝90°，O为AC的中点，G为EF的中点，试探究OG与AC的位置关系，并说明理由．（3）如图③，若∠ADC＝60°，过点E作DC的平行线，并在其上取一点K（与点F位于直线BC的同侧），使EK＝BF，连接CK，H为CK的中点，试探究线段OH与HA 之间的数量关系，并对结论给予证明．参考答案与试题解析1．四边形ABCD为平行四边形，点P为平面内一点（1）若AP＝BC，连AP、DP；①如图1，点P在边BC上，求证：PD平分∠APC；②如图2，过P作PD的垂线交DC的延长线于点F，FP交AB于点E，求证：DF＝2AE．（2）如图3，∠ABC＝60°，点P在对角线DB上，点M在边AD上，MP＝CD且∠AMP ＝∠ABD，AB＝5，BP＝3，直接写出平行四边形ABCD的面积．【分析】（1）①如图1中，由AP＝AD，推出∠ADP＝∠APD，再证明∠ADP＝∠DPC 即可解决问题．②如图2中，取DF的中点M，连接MA、MP．想办法证明四边形AEFM是平行四边形即可解决问题．（2）在BD上取点K，使AB＝AK，作DF⊥BA交BA的延长线于F．证明△ADK≌△PDM （AAS），推出DP＝DA，设DP＝DA＝x，则AF＝AD＝x．DF＝AF＝x，在Rt△BDF中，根据BD2＝BF2+DF2，构建方程求出x即可解决问题．【解答】解：（1）①如图1中，∵四边形ABCD是平行四边形，∴AD＝BC，∵AP＝BC，∴AP＝AD，∴∠APD＝∠ADP∵AD∥BC，∴∠ADP＝∠DPC，∴PD平分∠APC．②如图2中，取DF的中点M，连接MA、MP．∵PD⊥PF，∴∠DPF＝90°，∴PM＝DM＝MF，∵AP＝AD，∴AM为线段PD的垂直平分线，∴AM∥EF，∵EF⊥PD，∵AE∥FM，∴四边形AEFM为平行四边形，∴AE＝MF，∴DF＝2AE．（3）在BD上取点K，使AB＝AK，作DF⊥BA交BA的延长线于F．∵AB＝AK，∵∠AMP＝∠ABD，∴∠AMP＝∠AKB，∴∠DMP＝∠DKA，∵∠ADK＝∠PDM，PM＝CD＝AB＝AK，∴△ADK≌△PDM（AAS），∴DP＝DA，设DP＝DA＝x，∵AD∥BC，∴∠F AD＝∠ABC＝60°，∴AF＝AD＝x．DF＝AF＝x，在Rt△BDF中，∵BD2＝BF2+DF2，∴（3+x）2＝（5+x）2+（x）2，解得x＝16，∴S平行四边形ABCD＝AB•DF＝5××16＝．2．在正方形ABCD中，AB＝6，E为直线AB上一点，EF⊥AB交对角线AC于F，点G为AF中点，连接CE，点M为CE中点，连接BM并延长交直线AC于点O．（1）如图1，E在边AB上时，＝，∠GBM＝45°；（2）将（1）中△AEF绕A逆时针旋转任意一锐角，其他条件不变，如图2，（1）中结论是否仍然成立？请加以证明．（3）若BE＝2，则CO长为或3．【分析】（1）连接EG、GM．想办法证明△GBM是等腰直角三角形即可解决问题．（2）成立．延长GM到H，使得MH＝GM，连接BH，HC，延长HC交AF的延长线于I，设AI交CD于J．利用全等三角形的性质证明△GBM是等腰直角三角形即可解决问题．（3）分两种情形①点E在线段AB上．②点E在AB的延长线上，分别求解即可解决问题．【解答】解：（1）连接EG、GM．∵四边形ABCD是正方形，∴∠ABC＝90°，∠CAB＝∠ACB＝45°，∵EF⊥AB，∴∠AEF＝90°，∴∠EAF＝∠EF A＝45°，∵AG＝GF，∴EG⊥AF，∴∠EGC＝90°∵EM＝MC，∴GM＝BM＝CE，∴∠MCG＝∠MGC，∠MBC＝∠MCB，∴∠BMG＝∠BME+∠GME＝2∠BMC+2∠GCM＝2∠ACB＝90°．故△GMB为等腰直角三角形．∴＝．故答案为，45°．（2）成立．理由：延长GM到H，使得MH＝GM，连接BH，HC，延长HC交AF的延长线于I，设AI交CD于J．∵EM＝MC，GM＝MH，∠EMG＝∠HMC，∴△EMG≌△CMH（SAS），∴EG＝CH，∠EGM＝∠MHC，∴EC∥CH，∴∠AGE＝∠AIH＝90°，∵AG＝EG，∴AG＝CH，∵∠D＝∠I＝90°，∠AJD＝∠CJI，∴∠ICD＝∠IAD，∵∠BAG+∠IAD＝90°，∠BCH+∠ICF＝90°∴∠BCH＝∠BAG，∵BA＝BC∴△BAG≌△BCH（SAS），∴BG＝DH，∠ABG＝∠CBH，∴∠∠GBH＝∠ABC＝90°故△GBH是等腰直角三角形，∴＝，∠GBM＝45°．（3）当E在B上方时，如图3﹣1中，延长BO交CD于T．∴BE∥CT，∴∠MEB＝∠MCT，∵∠EMB＝∠CMT，EM＝CM，∴△EMB≌△CMT（ASA），∴BE＝CT＝2，∵CT∥AB，∴＝＝，∵AC＝6，∴OC＝×6∴CO＝当E在B下方时同法可得CO＝．综上所述，OC的长为或3．故答案为或3．3．平面直角坐标系中，菱形ABCD．（1）若点A坐标是（0，2），点B坐标（﹣2，0），求∠ABC及菱形边长：（2）在（1）的条件下，连接OD，过C点向OD作垂线，垂足为E，求CE；（3）如图3所示，∠ABO＝60°，在y轴负半轴上取一点P，使得∠BPO＝15°，延长BD至Q，使得DQ＝CD，连接AQ，若AP＝BQ＝a，求线段AQ的长（用含a的式子表示）．【分析】（1）在Rt△AOB中，解直角三角形求出AB，∠ABO即可．（2）根据S△ODC＝•OD•CE＝•OC•OA求解即可．（3）设菱形ABCD的边长为2x，过Q点作QM⊥AD交AD的延长线于M，过DN⊥x轴于N，根据AP＝BQ＝a，构建方程求解即可．【解答】解：（1）如图1中，∵A（0，2），B（﹣2，0），∴OA＝2，OB＝2，∴tan∠ABO＝＝，∴∠ABC＝60°，∴∠OAB＝90°﹣60°＝30°，∴AB＝2OB＝4，∴菱形的边长为4．（2）如图2中，∵四边形ABCD是菱形，AB＝AD＝CD＝BC＝4，∴C（2，0），D（4，2），∴OD＝＝2，∵CE⊥OD，∴S△ODC＝•OD•CE＝•OC•OA，∴EC＝＝．（3）设菱形ABCD的边长为2x，过Q点作QM⊥AD交AD的延长线于M，过DN⊥x 轴于N，在△QDM中，∠QDM＝30°，DQ＝2x，∴QM＝DQ＝x，DM＝x，AM＝2x+x＝（2+）x，又QM⊥AM，利用勾股定理可求AQ＝（+）x，BD＝2x，∵AP＝BQ＝a，∴2x+2x＝a，得x＝，继而得AQ＝（+）x＝a．4．矩形ACBD对角线AC、BD相交于点O，点P是对角线BD上的一个动点（不与B，D 重合），∠AOB＝α，过P点作PF∥AC，交AB于F，连接AP．将AP绕P点逆时针旋转α得到EP，连接BE．（1）若点P在BD上，∠AOB＝50°①求证：AF＝BE；②求∠ABE＝50°．（2）若点P在OD上，求∠ABE（用α表示）；（3）若BC＝8，将A绕点P顺时针方向旋转（180°﹣α）得到EP，连接DE，当DP＝3OP时，DE＝2或4．【分析】（1）①证明△APF≌△EPB（SAS）可得结论．②利用全等三角形的性质以及三角形内角和定理解决问题即可．（2）如图2中，证明△FP A≌△BPE（SAS），推出∠F AP＝∠PEB，由∠F AP+∠P AB＝180°，推出∠P AB+∠PEB＝180°，推出∠ABE+∠APE＝180°可得结论．（3）分两种情形：如图3中，当点P在OD上时，如图3所示，过点P作PF∥OA，交AD于点F，如图4所示，当点P在OB上时，过点P作PF∥OA，交DA的延长线于点F，分别求解即可解决问题．【解答】（1）①证明：∵四边形ABCD是矩形，∴OA＝OC＝OB＝OD，∵PF∥OA，∴＝，∠FPB＝∠AOB＝α，∴PF＝PB，∠EPB＝∠FPB﹣∠FPE＝α﹣∠FPE，∵AP＝EP，∠APE＝α，∴∠APF＝α﹣∠FPE，∴∠APF＝∠EPB，∴△APF≌△EPB（SAS），∴AF＝BE．②∵△APF≌△EPB，∴∠AFP＝∠EBP，∵∠AFP＝∠FPB+∠OBA，∠EBP＝∠ABE+∠OBA，∴∠ABE＝∠FPB，∴∠ABE＝α＝50°．故答案为50°．（2）如图2中，∵P A＝PE，∠APE＝α，同法可证PF＝PB，∠FPB＝α，∴∠FPB＝∠APE，∴∠FP A＝∠BPE，∴△FP A≌△BPE（SAS），∴∠F AP＝∠PEB，∵∠F AP+∠P AB＝180°，∴∠P AB+∠PEB＝180°，∴∠ABE+∠APE＝180°，∴∠ABE＝180°﹣α．（3）如图3中，当点P在OD上时，如图3所示，过点P作PF∥OA，交AD于点F，∵DP＝3OP，即OD＝4OP，∴＝＝＝，∴AF＝AD＝BC＝2．类比（1）①得：△APF≌△EPD，∴DE＝AF＝2．如图4所示，当点P在OB上时，过点P作PF∥OA，交DA的延长线于点F，∵DP＝3OP，即OD＝2OP，∴＝＝＝，∴AF＝AD＝BC＝4．类比（1）①得：△APF≌△EPD，∴DE＝AF＝4．综上所述，DE的长为2或4．故答案为2或4．5．如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N，连接CN．（1）如图1，求证：E，N、C三点在同一直线上；（2）如图1，若△CMN的面积与△CDN的面积比为3：1，求的值．（3）如图2，已知点P、Q、T分别是CM、CN、MN上的动点，若AN＝3，BM＝1，试直接写出PT+QT的最小值2．【分析】（1）证明∠ENM+∠CNM＝∠DNM+∠ANM＝180°，可得结论．（2）如图1中，首先过点N作NH⊥BC于点H，由△CMN的面积与△CDN的面积比为3：1，易得MC＝3ND＝3HC，然后设DN＝x，由勾股定理，可求得MN的长，继而求得答案，（3）如图2中，由（1）得出△CMN是等腰三角形，而TQ+TA最小就是点T到等腰三角形的两腰的距离之和最小就是等腰三角形腰上的高．【解答】（1）证明：如图1中，由折叠的性质可得：∠ENM＝∠DNM，即∠ENM＝∠ENA+∠ANM，∠DNM＝∠DNC+∠CNM，∵∠ENA＝∠DNC，∴∠ANM＝∠CNM，∴∠ENM+∠CNM＝∠DNM+∠ANM＝180°，∴E，N、C三点在同一直线上．（2）解：如图1中，过点N作NH⊥BC于点H，则四边形NHCD是矩形，∴HC＝DN，NH＝DC，∵△CMN的面积与△CDN的面积比为3：1，∴＝＝＝3，∴MC＝3ND＝3HC，∴MH＝2HC，设DN＝x，则HC＝x，MH＝2x，∴CM＝3x＝CN，在Rt△CDN中，DC＝＝2x，∴HN＝2x，在Rt△MNH中，MN＝＝2x，∴＝＝2．（3）如图2中，∵CM＝CN∴△CMN是等腰三角形，要使PT+QT的最小值，也就是等腰三角形的底边上一点到两腰上距离之和最短，即：TQ⊥CN，TP⊥CM，而等腰三角形的底边上一点到两腰的距离之和等于腰上的高，过点N作NH⊥BC，∴PT+QT的最小值就是NH＝AB，由折叠得，AM＝CM＝AN＝3，∴BM＝AN＝1在Rt△ABM中，根据勾股定理得，AB＝＝2．∴NH＝2，即：PT+QT的最小值为2．故答案为2．6．已知平行四边形ABCD中，N是边BC上一点，延长DN、AB交于点Q，过A作AM⊥DN于点M，连接AN，则AD⊥AN．（1）如图①，若tan∠ADM＝，MN＝3，求BC的长；（2）如图②，过点B作BH∥DQ交AN于点H，若AM＝CN，求证：DM＝BH+NH．【分析】（1）如图①中，设AM＝3k，DM＝4k，则AD＝5k，由△ADM∽△NDA，可得AD2＝DM•AN，由此构建方程即可解决问题．（2）如图②中，连接CH，在DM上取一点K，使得DK＝BH．证明△ADK≌△CBH （SAS），推出AK＝CH，再证明Rt△AMK≌Rt△CNH（HL），推出MK＝HN即可解决问题．【解答】（1）解：如图①中，∵AM⊥DN，∴∠AMD＝90°，∵tan∠ADM＝＝，∴可以假设AM＝3k，DM＝4k，则AD＝5k，∵AD⊥AN，∴∠DAN＝90°＝∠AMD，∵∠ADM＝∠ADN，∴△ADM∽△NDA，∴AD2＝DM•AN，∴（5k）2＝4k（4k+3），解得k＝，∴AD＝，∵四边形ABCD是平行四边形，∴BC＝AD＝．（2）证明：如图②中，连接CH，在DM上取一点K，使得DK＝BH．∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠ADK＝∠BNQ，∵BH∥DQ，∴∠CBH＝∠BNQ，∴∠ADK＝∠CBH，∵DK＝BH，DA＝BC，∴△ADK≌△CBH（SAS），∴AK＝CH，∵AM⊥DQ，AN⊥AD，AD∥BC，∴AN⊥BC，∴∠AMK＝∠CNH＝90°，∵AM＝CN，∴Rt△AMK≌Rt△CNH（HL），∴MK＝NH，∴DM＝DK+MK＝BH+HN．7．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2．动点P以每秒2个单位长度的速度从点A出发，沿A→C→B的方向向终点B运动（点P不与△ABC的顶点重合）．点P 关于点C的对称点为点D，过点P作PQ⊥AB于点Q，以PD、PQ为边作▱PDEQ．设▱PDEQ与△ABC．重叠部分的面积为S，点P的运动时间为t（s）（1）当点P在AC上运动时，用含t的代数式表示PD的长；（2）当点E落在△ABC的直角边上时，求t的值；（3）当▱PDEQ与△ABC重叠部分的图形是四边形时，求S与t之间的函数关系式．【分析】（1）由题意，可先写出AP的长，再写出CP的长，由对称的性质即可写出PD 的长；（2）①如图2﹣1，当点E落在BC边上时，过点Q作QH⊥AD于H，证明CE＝HQ＝AP＝CD，即可列出关于t方程，求出t的值；②如图2﹣2，当点E落在AC边上时，过点Q作QG⊥BC于G，证明CE＝GQ＝BP＝CD，即可列出关于t的方程，求出t的值即可；（3）如图3﹣1，当0＜t≤时，求出梯形PQMC的面积即可；如图3﹣2，当≤t≤2时，求出梯形PQCN的面积即可．【解答】解：（1）由题意，得AP＝2t，CP＝2﹣2t，∴PD＝2CP＝4﹣4t；（2）①如图2﹣1，当点E落在BC边上时，过点Q作QH⊥AD于H，由题意知，△AQP和△CED为等腰直角三角形，∴CE＝HQ＝AP，CE＝CD，∵HQ＝AP＝t，CD＝PC＝2﹣2t，∴t＝2﹣2t，∴t＝；②如图2﹣2，当点E落在AC边上时，过点Q作QG⊥BC于G，由题意知，△BQP和△CED为等腰直角三角形，∴CE＝GQ＝BP，CE＝CD，∵GQ＝BP＝（4﹣2t）＝2﹣t，CD＝PC＝2t﹣2，∴2﹣t＝2t﹣2，∴t＝，综上所述，点E落在△ABC的直角边上时，t的值为或；（3）如图3﹣1，当0＜t≤时，S＝S梯形PQMC＝t（2﹣2t+2﹣t）＝﹣t2+2t；如图3﹣2，当≤t≤2时，S＝S梯形PQNC＝（2﹣t）（2t﹣2+t）＝﹣t2+4t﹣2，综上所述，S＝．8．在菱形ABCD中，∠ABC＝60°（1）如图1，P是边BD延长线上一点，以AP为边向右作等边△APE，连接BE、CE．①求证：CE⊥AD；②若AB＝，BE＝，求AE的长；（2）如图2，P是边CD上一点，点D关于AP的对称点为E，连接BE并延长交AP的延长线于点F，连接DE、DF．若BE＝11，DE＝5，求△ADF的面积．【分析】（1）①证△ADC和△ABC是等边三角形，再证△BAP≌△CAE，推出∠ACE＝30°，由∠ACE+∠CAD＝90°即可证明结论；②如图1，设AC与BD交于点O，证∠BCE＝90°，由勾股定理求出CE，BP的长，由锐角三角函数等分别求出OA，OP的长，由勾股定理即可求出AP的长，即AE的长；（2）如图2，连接AE，过点A作AH⊥BF于点H，证∠HAF＝∠BAD＝60°，再证△DEF为等边三角形，即可求出HF，AH的长，进一步求出△AEF的面积，证△ADF≌△AEF即可．【解答】（1）①证明：在菱形ABCD中，∠ABC＝60°，∴∠ADC＝60°，且AB＝BC＝DA＝DC，∴△ADC和△ABC是等边三角形，∴AB＝AC，∠BAC＝∠CAD＝60°，又∵△APE是等边三角形，∴AE＝AP，∠EAP＝60°，∴∠BAC+∠CAP＝∠P AE+∠CAP，即∠BAP＝∠CAE，∴△BAP≌△CAE（SAS），∴∠ACE＝∠ABP＝∠ABC＝30°，∵∠CAD＝60°，∴∠ACE+∠CAD＝90°，∴CE⊥AD；②解：如图1，设AC与BD交于点O，由①知，∠ACE＝30°，且∠ACB＝60°，∴∠ACE+∠ACB＝∠BCE＝90°，∵在Rt△BCE中，BC＝AB＝，BE＝，∴CE＝＝4，由①知，△BAP≌△CAE，∴BP＝CE＝4，在Rt△BOC中，∠ACB＝60°，∴BO＝BC＝，CO＝AO＝BC＝，∴OP＝BP﹣BO＝，∴在Rt△AOP中，AP＝＝＝，∴AE＝AP＝；（2）解：如图2，连接AE，过点A作AH⊥BF于点H，∵点D关于AP的对称点为E，∴AP垂直平分DE，∴AD＝AE，FD＝FE，∴∠EAF＝∠DAF＝∠EAD，∠DF A＝∠EF A＝∠DFE，又∵在菱形ABCD中，AB＝AD，∴AB＝AE，∴AH垂直平分BE，∴EH＝BH＝BE＝，∠BAH＝∠EAH＝∠BAE，∴∠HAF＝∠EAH+∠EAF＝∠BAD，∵∠ABC＝60°，∴∠BAD＝180°﹣∠ABC＝120°，∴∠HAF＝60°，∴∠AFH＝90°﹣∠HAF＝30°，∴∠DFE＝60°，∴△DEF为等边三角形，∴EF＝DE＝5，∴HF＝HE+EF＝+5＝，在Rt△AHF中，∠AFH＝30°，∴AH＝HF＝，∴S△AEF＝EF•AH＝×5×＝，∵AD＝AE，FD＝FE，AF＝AF，∴△ADF≌△AEF（SSS），∴△ADF的面积为．9．如图，四边形ABCD中，AB＝AD，∠BAD＝60°，∠BCD＝30°，将AC绕着点A顺时针旋转60°得AE，连接BE，CE．（1）求证：△ADC≌△ABE；（2）求证：AC2＝DC2+BC2；（3）若AB＝2，点Q在四边形ABCD内部运动，且满足AQ2＝BQ2+DQ2，求点Q运动路径的长度．【分析】（1）推出∠DAC＝∠BAE，则可直接由SAS证明△ADC≌△ABE；（2）证明△BCE是直角三角形，再证DC＝BE，AC＝CE即可推出结论；（3）如图2，设Q为满足条件的点，将AQ绕着点A顺时针旋转60度得AF，连接QF，BF，QB，DQ，AF，证△ADQ≌△ABF，由勾股定理的逆定理证∠FBQ＝90°，求出∠DQB＝150°，确定点Q的路径为过B，D，C三点的圆上，求出的长即可．【解答】（1）证明：∵∠CAE＝∠DAB＝60°，∴∠CAE﹣∠CAB＝∠DAB﹣∠CAB，∴∠DAC＝∠BAE，又∵AD＝AB，AC＝AE，∴△ADC≌△ABE（SAS）；（2）证明：在四边形ABCD中，∠ADC+∠ABC＝360°﹣∠DAB﹣∠DCB＝270°，∵△ADC≌△ABE，∴∠ADC＝∠ABE，CD＝BE，∴∠ABC+ABE＝∠ABC+∠ADC＝270°，∴∠CBE＝360°﹣（∠ABC+ABE）＝90°，∴CE2＝BE2+BC2，又∵AC＝AE，∠CAE＝60°，∴△ACE是等边三角形，∴CE＝AC＝AE，∴AC2＝DC2+BC2；（3）解：如图2，设Q为满足条件的点，将AQ绕着点A顺时针旋转60度得AF，连接QF，BF，QB，DQ，AF，则∠DAQ＝∠BAF，AQ＝QF，△AQF为等边三角形，又∵AD＝AB，∴△ADQ≌△ABF（SAS），∴AQ＝FQ，BF＝DQ，∵AQ2＝BQ2+DQ2，∴FQ2＝BQ2+BF2，∴∠FBQ＝90°，∴∠AFB+∠AQB＝360°﹣（∠QAF+∠FBQ）＝210°，∴∠AQD+∠AQB＝210°，∴∠DQB＝360°﹣（∠AQD+∠AQB）＝150°，∴点Q的路径为过B，D，C三点的圆上，如图2，设圆心为O，则∠BOD＝2∠DCB＝60°，连接DB，则△ODB与△ADB为等边三角形，∴DO＝DB＝AB＝2，∴点Q运动的路径长为：＝π．10．【阅读】如图1，四边形OABC中，OA＝a，OC＝8，BC＝6，∠AOC＝∠BCO＝90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC 的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．【理解】若点D与点A重合，则这个操作过程为FZ[45°，8]；【尝试】（1）若点D与OA的中点重合，则这个操作过程为FZ[45°，16]；（2）若点D恰为AB的中点（如图2），求θ的值；【应用】经过FZ[45°，a]操作，点B落在点E处，若点E在四边形OABC的边AB上，直线l 与AB相交于点F，试画出图形并解决下列问题：①求出a的值；②若P为边OA上一动点，连接PE、PF，请直接写出PE+PF的最小值．（备注：等腰直角三角形的三边关系满足1：1：或：：2）【分析】【尝试】（1）如图1所示，若点D恰为AO的中点，证明Rt△OCP≌Rt△ODP，进而得到OD＝OC＝AD＝8，a＝16，可得结论；则θ＝30°；（2）如图2所示，若点D恰为AB的中点，作辅助线，证明△BDM≌△ADN（ASA），得DM＝DN，根据线段垂直平分线的性质可得OM＝ON，根据等腰三角形的性质可得∠MOD＝∠NOD，所以∠MOD＝∠MOC＝θ，可得结论；【应用】①如图3，作辅助线，根据点B与点E关于直线l对称，知∠OF A＝∠OFB＝90°，证明四边形BCOH是平行四边形，得BH＝CO＝8，OH＝CB＝6，可得OA的值，即a的值；②作辅助线，如图4，则有∠QAO＝∠F AO＝45°，QA＝F A，从而可得∠QAF＝90°．然后根据勾股定理可求出AB、AF、AQ、OF、OB、BF，由折叠可求出EF，从而可求出AE长，在Rt△QAE中，运用勾股定理可求出EQ2长，然后根据两点之间线段最短可得：当点E、P、Q三点共线时，PE+PF＝PE+PQ最短，最小值为线段EQ长，问题得以解决．【解答】解：（1）点D与OA的中点重合，如图1，由折叠得：∠COP＝∠DOP＝45°，∠C＝∠ODP＝90°，∴CP＝PD，∵OP＝OP，∴Rt△OCP≌Rt△ODP（HL），∴OC＝OD＝8，∵D为OA的中点，∴OA＝a＝16，则这个操作过程为FZ[45°，16]；故答案为：45°，16；（2）延长MD、OA，交于点N，如图2．∵∠AOC＝∠BCO＝90°，∴∠AOC+∠BCO＝180°，∴BC∥OA，∴∠B＝∠DAN．在△BDM和△ADN中，，∴△BDM≌△ADN（ASA），∴DM＝DN．∵∠ODM＝∠OCM＝90°，∴根据线段垂直平分线的性质可得OM＝ON，∴根据等腰三角形的性质可得∠MOD＝∠NOD．由折叠可得∠MOD＝∠MOC＝θ，∴∠COA＝3θ＝90°，∴θ＝30°；【应用】①过点B作BH⊥OA于点H，如图3．∵∠COA＝90°，∠COF＝45°，∴∠FOA＝45°．∵点B与点E关于直线l对称，∴∠OF A＝∠OFB＝90°，∴∠OAB＝45°，∴∠HBA＝90°﹣45°＝45°＝∠HAB，∴BH＝AH．∵CO⊥OA，BH⊥OA，∴CO∥BH．∵BC∥OA，∴四边形BCOH是平行四边形，∴BH＝CO＝8，OH＝CB＝6，∴OA＝OH+AH＝OH+BH＝6+8＝14．∴a的值为14．②过点B作BH⊥OA于点H，过点F作OA的对称点Q，连接AQ、EQ，OB，如图4，则有∠QAO＝∠F AO＝45°，QA＝F A，∴∠QAF＝90°．在Rt△BHA中，AB＝＝8．在Rt△OF A中，∠AFO＝90°，∠AOF＝∠OAF＝45°∴AF＝OF＝＝7，∴AQ＝AF＝7．在Rt△OCB中，OB＝＝＝10．在Rt△OFB中，BF＝AB﹣AF＝8﹣7＝．由折叠可得EF＝BF＝，∴AE＝AF﹣EF＝7﹣＝6．在Rt△QAE中，EQ2＝AE2+AQ2＝（6）2+（7）2＝170．根据两点之间线段最短可得：当点E、P、Q三点共线时，PE+PF＝PE+PQ最短，最小值为线段EQ长．∴PE+PF的最小值的是．11．如图，四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF＝90°，连接FC，G为FC的中点，连接GD，ED．（1）如图①，E在AB上，直接写出ED，GD的数量关系．（2）将图①中的△AEF绕点A逆时针旋转，其它条件不变，如图②，（1）中的结论是否成立？说明理由．（3）若AB＝5，AE＝1，将图①中的△AEF绕点A逆时针旋转一周，当E，F，C三点共线时，直接写出ED的长．【分析】（1）结论：DE＝DG．如图1中，连接EG，延长EG交BC的延长线于M，连接DM．证明△CMG≌△FEG（AAS），推出EF＝CM，GM＝GE，再证明△DCM≌△DAE（SAS）即可解决问题．（2）如图2中，结论成立．连接EG，延长EG到M，使得GM＝GE，连接CM，DM，延长EF交CD于R．证明方法类似．（3）分两种情形：①如图3﹣1中，当E，F，C共线时．②如图3﹣2中，当E，F，C 共线时，分别求解即可．【解答】解：（1）结论：DE＝DG．理由：如图1中，连接EG，延长EG交BC的延长线于M，连接DM．∵四边形ABCD是正方形，∴AD＝CD，∠B＝∠ADC＝∠DAE＝∠DCB＝∠DCM＝90°，∵∠AEF＝∠B＝90°，∴EF∥CM，∴∠CMG＝∠FEG，∵∠CGM＝∠EGF，GC＝GF，∴△CMG≌△FEG（AAS），∴EF＝CM，GM＝GE，∵AE＝EF，∴AE＝CM，∴△DCM≌△DAE（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∴DG⊥EM，DG＝GE＝GM，∴△EGD是等腰直角三角形，∴DE＝DG．（2）如图2中，结论成立．理由：连接EG，延长EG到M，使得GM＝GE，连接CM，DM，延长EF交CD于R．∵EG＝GM，FG＝GC，∠EGF＝∠CGM，∴△CGM≌△FGE（SAS），∴CM＝EF，∠CMG＝∠GEF，∴CM∥ER，∴∠DCM＝∠ERC，∵∠AER+∠ADR＝180°，∴∠EAD+∠ERD＝180°，∵∠ERD+∠ERC＝180°，∴∠DCM＝∠EAD，∵AE＝EF，∴AE＝CM，∴△DAE≌△DCM（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∵EG＝GM，∴DG＝EG＝GM，∴△EDG是等腰直角三角形，∴DE＝DG．（3）①如图3﹣1中，当E，F，C共线时，在Rt△ADC中，AC＝＝＝5，在Rt△AEC中，EC＝＝＝7，∴CF＝CE﹣EF＝6，∴CG＝CF＝3，∵∠DGC＝90°，∴DG＝＝＝4．∴DE＝DG＝4．②如图3﹣2中，当E，F，C共线时，同法可得DE＝3．综上所述，DE的长为4或3．12．如图，在平面直角坐标系中，已知A（﹣2，0），B（0，m）两点，且线段AB＝2，以AB为边在第二象限内作正方形ABCD．（1）求点B的坐标．（2）在x轴上是否存在点Q，使△QAB是以AB为腰的等腰三角形？若存在，请直接写出点Q的坐标，若不存在，请说明理由；（3）如果在坐标平面内有一点P（a，3），使得△ABP的面积与正方形ABCD的面积相等，求a的值．【分析】（1）在直角三角形AOB中，由OA与AB的长，利用勾股定理求出OB的长即可；（2）存在，以AB为腰，有两种情况：分别以A、B为顶点作等腰三角形的顶角，根据AB＝2，结合图形可得Q的坐标；（3）作辅助线，构建高线PG，分两种情况：P在y轴的左侧和右侧，根据三角函数可得PH的长，从而得a的值．【解答】解：（1）∵A（﹣2，0），∴OA＝2，∵AB＝2，由勾股定理得：OB＝＝4，∴B（0，4）；（2）分两种情况：①以AB为腰，∠BAQ为顶角时，如图1，AB＝AQ＝2，∴Q1（﹣2﹣2，0），Q2（2﹣2，0），②以AB为腰，∠ABQ为顶角时，如图1，A与Q3关于y轴对称，∴Q3（2，0）；综上，点Q的坐标是（﹣2﹣2，0）或（2﹣2，0）或（2，0），（3）分两种情况：①当P在y轴的右边时，如图2，作直线l：y＝3，直线l交AB于H，交y轴于E，∵P（a，3），∴点P在直线l上，过P作PG⊥AB于G，∵S△ABP＝S正方形ABCD，∴•AB•PG＝AB2，PG＝2AB＝4，∵l∥x轴，∴∠PHG＝∠OAB，∴sin∠PHG＝sin∠OAB，即，∴，PH＝10，∵EH∥OA，∴，即，∴EH＝，∴PE＝10﹣0.5＝9.5，∴P（9.5，3）即a＝9.5；②当点P在y轴的左侧时，如图3，同理可得PH＝10，∴P（﹣10.5，3），∴a＝﹣10.5，综上，a的值是9.5或﹣10.5．13．如图，矩形ABCD中，AB＝a，AD＝b，点P是对角线BD上的一个动点（点P不与B、D重合），连接AP并延长交射线BC于点Q，（1）当AP⊥BD时，求△ABQ的面积（用含a、b的代数式表示）；（2）若点M为AD边的中点，连接MP交射线BC于点N，证明：点N也为线段BQ的中点；（3）如图，当为何值时，△ADP与△BPQ的面积之和最小．【分析】（1）利用相似三角形的性质求出BQ即可解决问题．（2）证明△AMP∽△QNP，△DMP∽△BNP推出，可得，因为点M是AD的中点，所以AM＝DM．（3）如图②，过点P作EF⊥AD交AD、BC于E、F．构建一元二次方程，利用根的判别式解决最值问题即可．【解答】（1）解：如图①：。

中考数学总复习《四边形的综合题》练习题附带答案

中考数学总复习《四边形的综合题》练习题附带答案一、单选题1．如图，两个平行四边形的面积分别为18、12，两阴影部分的面积分别为a、b （a＞b），则(a−b)等于（）A．3B．4C．5D．6 2．如图，在矩形ABCD中，对角线AC、BD相交于点O，∠ABD＝60°，则∠BOC的大小为（）A．30°B．60°C．90°D．120°3．若一个多边形的内角和是外角和的2.5倍，则该多边形为（）A．五边形B．六边形C．七边形D．八边形4．如图，矩形ABCD对角线相交于点O，∠AOB=60°，AB=4，则矩形的对角线AC 为（）A．4 B．8 C．4√3D．10 5．一个长方形的周长为28厘米，长的2倍比宽的3倍多3厘米，则这个长方形的面积是（）A．45平方厘米B．35平方厘米C．25平方厘米D．20平方厘米6．如图，在矩形ABCD中，对角线AC，BD相交于点O，AE垂直平分BO，AE=√3cm，则OD=（）A．1cm B．1.5cm C．2cm D．3cm 7．如图，矩形纸片ABCD中，AB=4，AD=8 ，将纸片沿EF折叠使点B与点D 重合，折痕EF与BD相交于点O，则DF的长为()A．3B．4C．5D．6 8．如图，⊙O的半径为4，点P是⊙O外的一点PO=10，点A是⊙O上的一个动点，连接PA，直线l垂直平分PA，当直线l与⊙O相切时PA的长度为（）A．10B．212C．11D．434 9．已知平行四边形一边长为8，一条对角线长为6，则另一条对角线α满足（）A．10＜α＜22B．4＜α＜20C．4＜α＜28D．2＜α＜1410．如图，两张等宽的纸条交又重叠在一起，重叠的部分为四边形ABCD，若测得A，C之间的距离为6cm，点B，D之间的距离为8cm，则线段AB的长为（）A．a2B．5cm C．2√7cm D．6cm 11．如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF，将∠BCE绕着正方形的中心O按逆时针方向旋转到∠CDF的位置，则旋转角是（）A ．45°B ．60°C ．90°D ．120°12．Rt∠ABC 两直角边的长分别为6cm 和8cm ，则连接这两条直角边中点的线段长为( ) A ．10cmB ．3cmC ．4cmD ．5cm二、填空题13．如图，点E 在边长为2的正方形ABCD 内，满足∠AEB ＝90°，若∠DAE ＝30°，则图中阴影部分的面积为．14．把一把直尺和一块三角板如图放置，若∠1=42°，则∠2的度数为 °.15．已知 ▱ABCD 中一条对角线分 ∠A 为35°和45°，则 ∠B = 度. 16．如图，在一块长AB =26m ，宽BC =18m 的长方形草地上，修建三条宽均为3m 的长方形小路，则这块草地的绿地面积（图中空白部分）为 m 217．如图，在∠ABC 中，∠ABC ＝90°，E 为AC 的中点，AD∠BE 交BC 于D ，若AD＝152，BE ＝5，则BD ＝ .18．如图，在四边形ABCD中，∠A＝90°，AB＝12，AD＝5．点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的最大值是．三、综合题19．如果抛物线C1：y=ax2+bx+c与抛物线C2：y=−ax2+dx+e的开口方向相反，顶点相同，我们称抛物线C2是C1的“对顶”抛物线.（1）求抛物线y=x2−4x+7的“对顶”抛物线的表达式；（2）将抛物线y=x2−4x+7的“对顶”抛物线沿其对称轴平移，使所得抛物线与原抛物线y=x2−4x+7形成两个交点M、N，记平移前后两抛物线的顶点分别为A、B，当四边形AMBN是正方形时求正方形AMBN的面积.（3）某同学在探究“对顶”抛物线时发现：如果抛物线C1与C2的顶点位于x轴上，那么系数b与d，c与e之间的关系是确定的，请写出它们之间的关系.20．解答题（1）如图1，在平行四边形ABCD 中，已知点E 在AB 上，点F 在CD 上，且AE=CF ．求证：DE=BF ；（2）如图2，AB 是∠O 的直径，点C 在AB 的延长线上，CD 与∠O 相切于点D ，若∠C=20°，求∠CDA 的度数．21．如图，▱ABCD 放置在平面直角坐标系申，已知点A （-2，0）、B （-6，0）、D（0，3）．点C 在反比例函数y=k x的图象上。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初二四边形综合提高练习题（附详解）1．如图，在Rt△ABC中，∠B=90°，BC=53，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．（1）求AB,AC的长；（2）求证：AE=DF；（3）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．（4）当t为何值时，△DEF为直角三角形？请说明理由.2．如图，已知菱形ABCD的对角线AC 、BD相交于点O，延长AB至点E，使BE=AB，连接CE．（1）求证：四边形BECD是平行四边形；（2）若∠E=60°，AC=43,求菱形ABCD的面积．3．在△ABC中，AB＝AC＝2，∠BAC＝45º.△AEF是由△ABC绕点A按逆时针方向旋转得到，连接BE，CF相交于点D.（1）求证：BE＝CF；（2）当四边形ABDF是菱形时，求CD的长.4．如图，四边形ABCD是正方形，点E，F分别在BC，AB上，点M在BA的延长线上，且CE=BF=AM，过点M，E分别作NM⊥DM，NE⊥DE交于N，连接NF．（1）求证：DE⊥DM；（2）猜想并写出四边形CENF是怎样的特殊四边形，并证明你的猜想．5．如图，正方形ABCD的面积为4，对角线交于点O，点O是正方形A1B1C1O的一个顶点，如果这两个正方形全等，正方形A1B1C1O绕点O旋转．（1）求两个正方形重叠部分的面积；（2）若正方形A1B1C1O旋转到B1在DB的延长线时，求A与C1的距离．6．在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．（备注：在直角三角形中30度角所对的边是斜边的一半）（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；（3）当t为何值时，△DEF为直角三角形？请说明理由．7．如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．（1）求证：AE=EF．（2）如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”其余条件不变，那么结论AE=EF是否成立呢？若成立，请你证明这一结论，若不成立，请你说明理由．8．已知□OABC的顶点A、C分别在直线x=2和x=4上，O为坐标原点，直线x=2分别与x轴和OC边交于D、E，直线x=4分别与x轴和AB边的交于点F、G．（1）如图，在点A、C移动的过程中，若点B在x轴上，①直线AC是否会经过一个定点，若是，请直接写出定点的坐标；若否，请说明理由．②□OABC是否可以形成矩形？如果可以，请求出矩形OABC的面积；若否，请说明理由．③四边形AECG是否可以形成菱形？如果可以，请求出菱形AECG的面积；若否，请说明理由．（2）在点A、C移动的过程中，若点B不在x轴上，且当□OABC为正方形时，直接写出点C的坐标．9．如图，矩形ABCD中，AB=9，AD=4．E为CD边上一点，CE=6．点P从点B出发，以每秒1个单位的速度沿着边BA向终点A运动，连接PE．设点P运动的时间为t秒．（1）求AE的长；（2）当t为何值时，△PAE为直角三角形？（3）是否存在这样的t，使EA恰好平分∠PED，若存在，求出t的值；若不存在，请说明理由．参考答案1．（1）AB=5，AC=10.（2）证明见解析；（3）能，当t=103时，四边形AEFD为菱形．（4）当t=52秒或4秒时，△DEF为直角三角形.【解析】（1）设AB=x,则AC=2x.由勾股定理得，(2x)2-x2=(5)2,得x=5，故AB=5，AC=10.（2）证明：在△DFC中，∠DFC=90°，∠C=30°，DC=2t，∴DF=t．又∵AE=t，∴AE=DF．（3）能．理由如下：∵AB⊥BC，DF⊥BC，∴AE∥DF．又AE=DF，∴四边形AEFD为平行四边形．∵AB=5，∴AC=10．∴AD=AC-DC=10-2t．若使□AEFD为菱形，则需AE=AD，即t=10-2t，t=.即当t=时，四边形AEFD为菱形．（4）①∠EDF=90°时，10-2t=2t，t=．②∠DEF=90°时，10-2t=t，t=4．③∠EFD=90°时，此种情况不存在．故当t=秒或4秒时，△DEF为直角三角形.2．（1）证明见解析；（2）菱形ABCD的面积为83试题解析：（1）∵四边形ABCD是菱形，∴AB=CD，AB∥CD.；又∵BE=AB，∴BE=CD.∵BE∥CD,∴四边形BECD是平行四边形.（2）∵四边形BECD是平行四边形，∴BD∥CE.∴∠ABO=∠E=60°.又∵四边形ABCD是菱形，∴AC丄BD,OA=OC. ∴∠BOA=90°，∴∠BAO=30°.∵AC=3∴OA=OC=23∴OB=OD=2. ∴BD=4.∴菱形ABCD的面积=1143483 22AC BD⨯⨯=⨯=3．（1）证明见解析；（2）222试题解析：（1）∵△AEF是由△ABC绕点A按逆时针方向旋转得到的，∴AE=AF=AB=AC=2，∠EAF=∠BAC=45°，∴∠BAC+∠3=∠EAF+∠3，即∠BAE=∠CAF，在△ABE和△ACF中{AB ACBAE CAF AE AF∠∠＝＝＝ ∴△ABE≌△ACF， ∴BE =CF ．（2）∵四边形ABDF 是菱形， ∴AB ∥DF ， ∴∠ACF ＝∠BAC ＝45°．∵AC =AF ， ∴∠CAF ＝90°，即△ACF 是以CF 为斜边的等腰直角三角形， ∴CF ＝22．又∵DF =AB ＝2， ∴CD ＝22－2．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了菱形的性质． 4．【解析】（1）证明：∵四边形ABCD 是正方形， ∴DC=DA，∠DCE=∠DAM=90°，在△DCE 和△MDA 中，， ∴△DCE≌△MDA（SAS ）， ∴DE=DM，∠EDC=∠MDA．又∵∠ADE+∠EDC=∠ADC=90°， ∴∠ADE+∠MDA=90°， ∴DE⊥DM；（2）解：四边形CENF 是平行四边形，理由如下： ∵四边形ABCD 是正方形， ∴AB∥CD，AB=CD ． ∵BF=AM， ∴MF=AF+AM=AF+BF=AB，即MF=CD ，又∵F 在AB 上，点M 在BA 的延长线上， ∴MF∥CD， ∴四边形CFMD 是平行四边形， ∴DM=CF，DM∥CF，∵NM⊥DM，NE⊥DE，DE⊥DM， ∴四边形DENM 都是矩形， ∴EN=DM，EN∥DM， ∴CF=EN，CF∥EN， ∴四边形CENF 为平行四边形． 5．（1）1；（2）10解：解：（1）∵四边形ABCD 为正方形， ∴∠OAB =∠OBF =45°，OA =OB ∵BO ⊥AC ， ∴∠AOE +∠EOB =90°，又∵四边形A 1B 1C 1O 为正方形， ∴∠A 1OC 1=90°，即∠BOF +∠EOB =90°， ∴∠AOE =∠BOF ，在△AOE 和△BOF 中，， ∴△AOE ≌△BOF （ASA ），∵S 两个正方形重叠部分=S △BOE +S △BOF ，又S △AOE =S △BOF ∴S 两个正方形重叠部分=S ABO =S 正方形ABCD =×4=1；（2）如图，∵正方形的面积为4， ∴AD =AB =2，∵正方形A 1B 1C 1O 旋转到B 1在DB 的延长线时， ∴C 1F =OC 1=1，AG =1 ∴C 1G =3，根据勾股定理，得AC 1=．6．（1）、证明见解析；（2）、t=10；（3）、t=152或12，理由见解析.试题解析：（1）、∵在Rt△ABC中，∠C=90°﹣∠A=30°，∴AB=12AC=12×60=30cm∵CD=4t，AE=2t，又∵在Rt△CDF中，∠C=30°，∴DF=12CD=2t ∴DF=AE（2）、能。

∵DF∥AB，DF=AE，∴四边形AEFD是平行四边形当AD=AE时，四边形AEFD是菱形，即60﹣4t=2t，解得：t=10 ∴当t=10时，AEFD是菱形（3）、若△DEF为直角三角形，有两种情况：①如图1，∠EDF=90°，DE∥BC，则AD=2AE，即60﹣4t=2×2t，解得：t=152。

②如图2，∠DEF=90°，DE⊥AC，则AE=2AD，即2t=2（60-4t），解得：t=12。

综上所述，当t=152或12时，△DEF为直角三角形试题解析：（1）证明：取AB的中点G，连接EG∵四边形ABCD是正方形∴AB=BC，∠B=∠BCD=∠DCG=90°∵点E是边BC的中点∴AM=EC=BE ∴∠BGE=∠BEG=45°∴∠AGE=135°，∵CF平分∠DCG，∴∠DCF=∠FCG=45°，∴∠ECF=180°－∠FCG=135°，∴∠AGE=∠ECF∵∠AEF=90°∴∠AEB+∠CEF=90°，又∵∠AEB+∠GAE=90°，∴∠GAE=∠CEF，在△AGE和△ECF中，∠GAE=∠CEF，AG=CE，∠AGE=∠ECF∴△AGE≌△ECF（ASA），∴AE=EF （2）证明：在AB上取一点M，使AM=EC，连结ME，∴BM=BE∴∠BME=45°∴∠AME=135°.∵CF是外角平分线，∴∠DCF= 45°.∴∠ECF= 135°.∴∠AME= ∠ECF .∵∠AEB+∠BAE=90°，∠AEB+ ∠CEF= 90°,∴∠BAE= ∠CEF.∴△AME≌ △ECF（ASA). ∴AE=EF.8．（1）①是，定点（3，0），②可以，12，③可以，3；（2）（4，2）或（4，-2）试题解析：（1）①根据题意得：∠ADO=∠CFB=90°，∵四边形ABCD 是平行四边形， ∴OA∥BC，OA=BC ， ∴∠AOD=∠CBF，在△AOD 和△CBF 中，∴△AOD≌△CBE（AAS ）， ∴OD=BE=2∴OB 的中点坐标为（3，0） ∴直线 AC 是经过一个定点（3，0） ②可以易证∠OCF=∠CBF ，得∠OCB=90°，由OABC 是平行四边形得OABC 是矩形，在Rt ΔOCB 中，CF 2=BF ×OF=2×4=8 ∴CF=∴S ΔOCB =×6×= ∴S 矩形OABC =③可以，3（2）（4，2）或（4，-2）9．(1)5；(2)6或23；(3)296. 试题解析：（1）∵矩形ABCD 中，AB=9，AD=4， ∴CD=AB=9，∠D=90°， ∴DE=9﹣6=3， ∴222234DE AD +=+；（2）①若∠EPA=90°，t=6；②若∠PEA=90°，()()22226t 459t ++=﹣﹣，解得t=23．综上所述，当t=6或t=23时，△PAE 为直角三角形；（3）假设存在．∵EA 平分∠PED ， ∴∠PEA=∠DEA ．∵CD ∥AB ， ∴∠DEA=∠EAP ， ∴∠PEA=∠EAP ， ∴PE=PA ， ∴()()2226t 49t +=﹣﹣，解得t=296． ∴满足条件的t 存在，此时t=296. 考点：四边形综合题．。