五年级寒假第3讲-应用题一(教师版)
【寒假讲义】温故知新篇03《倍数与因数》—2020-2021学年五年级数学上册寒假学习精编讲义

2020-2021学年北师大版五年级数学上册寒假学习精编讲义温故知新篇03 倍数与因数一.选择题1.(2020秋•南丹县期中)一个数是9的倍数,这个数一定是( )的倍数.A .3B .5C .62.(2018秋•深圳期末)一个数,它既是12的倍数,又是12的因数,这个数是( )A .6B .12C .24D .1443.(2019•连江县)和奇数K 相邻的两个奇数是( )A .1K -和1K +B .1K -和3K +C .2K -和2K +D .3K -和3K +4.自然数按是不是2的倍数来分,可以分为( )A .奇数和偶数B .素数和合数C .素数、合数、0和15.(2018春•漳平市校级期末)从0、1、4、5这四个数字中选择三个不同的数字,组成既是3的倍数,又是2的倍数的三位教,有( )种不同的组法.A .2B .3C .4D .5 6.(2015春•昭通月考)自然数(0除外)按因数的个数分,可以分为( )A .奇数和偶数B .质数和合数C .质数、合数和1二.填空题7.(2020秋•临漳县期中)一个数的最大因数是56,这个数是 ;一个数的最小倍数是18,这个数是 。
8.(2020•石阡县)用1,0,8三个数字组成三位数,其中能被2整除的最大数是 ;能被3整除的最小数是 ;能被2,3,5整除的数是 .9.(2019•长沙)一个分数,分子是最小的质数,分母是20以内的最大的奇数,这个分数是 .10.(2020•长沙)我是一个两位数,十位数字是最小的合数,个位数字是最小的质数,我是 .11.(2016•长沙模拟)自然数1~9中,最小的质数、最小的合数、最大的质数、最大的合数这四个数的和是.12.(2014秋•温江区期中)两个质数相加的和为49,这两个数的积是.13.(2015春•东胜区期中)猜猜我是谁.(1)我是6的倍数,又是4的倍数,别忘了我还是12的因数.(2)我们两个的和是6,积是8,质数是,合数是.(3)我们两个的和是18,积是77,这两个质数分别是和.(4)我们两个的和是20,差是6,这两个质数分别是和.14.(2013秋•射洪县校级期中)在乘法运算中积是100,如果一个因数扩大20倍,另一个因数缩小10倍,积是.三.判断题15.(2019秋•高平市期末)自然数中,最小的质数与最小的合数相差2..(判断对错)16.(2020秋•高台县期中)偶数都是合数,奇数都是质数(判断对错)17.(2020•洛阳)两个质数相乘的积一定是偶数.(判断对错)18.(2016春•未央区期末)相邻的两个自然数的积一定是偶数..(判断对错)19.一个数既是12的因数,又是12的倍数,那么这个数一定是12.(判断对错)四.计算题20.写出下面各数的因数.25 12 49 36.五.应用题21.(2020秋•新丰县期中)幼儿园大班有一些小朋友(多于10人,且少于40人),李老师拿了48颗糖平均分给他们,正好分完,小朋友的人数可能是多少?22.龙一鸣和壮壮玩抽数字卡片游戏,有意思的是,一次两人抽出卡片上的数都是质数,且两个数的和是奇数,还是小于50的7的倍数.这两个质数的积可能是多少?23.某电影院的座位号码是单号与单号相邻,双号与双号相邻.(1)一个人拿了三张座位相邻的电影票,这三个座位号码相加之和等于15,这三个座位分别是多少号?(2)若三张座位相邻的电影票的座位号码相加之和等于36,这三个座位分别是多少号?六.解答题24.(2020秋•成都期中)小明、小红、小刚三人的年龄正好是三个连续的偶数,他们的年龄总和是48岁,他们中最小的是多少岁?最大的是多少岁?25.(2019春•罗平县校级期中)两个质数的和是18,积是65,这两个质数分别是多少?26.(2019春•兴仁市月考)五(1)班6名同学去给小树苗浇水,小树苗不到30棵,他们发现每人浇水棵数相同,这批小树苗可能有多少棵?27.(2019春•洪泽区校级期中)三个连续偶数的和是72,这三个数分别是多少?28.(2019秋•惠城区校级期中)按要求写数.24的因数有:50以内6的倍数有:29.(2016秋•惠济区校级期中)三个相邻偶数的和是84,这三个偶数分别是多少?30.(2019秋•定西期中)小明家有三种塑料桶,分别是5千克装,10千克装,2千克装.小明妈妈买回75千克豆油,选哪种塑料桶装能正好把豆油装完?需这样的桶多少个?31.(2016春•克州校级期中)一个人说大于2的偶数,另一个人说两个质数,这两个质数的和等于第一个人说的偶数,你能写这样的三组吗?如:偶数10;两个质数3和7;3710+=写三组:参考答案与试题解析一.选择题1.【解答】解:因为9是3倍数,所以一个数是9的倍数,这个数一定是3的倍数。
第3讲 图形的运动(教师版)(知识梳理+典例分析+举一反三+巩固提升)北师大版

第3讲图形的运动知识点一:图形的旋转1. 图形旋转的含义及三要素旋转中心、旋转方向、旋转角度2. 在方格纸上画简单图形绕其顶点旋转90°后的图形图形绕某一点旋转一定的度数,图形中的对应点、对应线段都旋转了相同的度数,对应点到旋转点的距离相等,对应线段相等,对应角相等。
3.旋转的特点旋转不改变图形的形状和大小,只改变图形的位置。
知识点二:图形的运动1.在方格纸上图形的平移、旋转(1)图形平移时,先确定移动的方向,再确定移动的格数;(2)旋转应找准旋转中心、旋转方向以及旋转角度;(3)作轴对称图形要先确定对称轴。
图形经过平移、旋转、轴对称变换后,图形大小不变。
2. 记录图形位置的“还原”过程用平移或旋转进行图形运动时,要先观察变化前后各部分的位置,再确定如何通过平移或旋转得到。
知识点三:欣赏与设计利用平移、旋转和轴对称设计美丽的图案一个图形通过平移、旋转或轴对称变换可以得到不同的图案。
复杂的图案是由一个或几个简单的基本图形变换而来的。
考点一:图形的旋转例1.(2020春•綦江区期末)画一画,填一填.(1)画出把长方形绕0点顺时针方向旋转90°后的图形.(2)旋转前A点的位置是(4,3),旋转后A点的位置是(2,5).(3)画出把三角形向下平移4格后的图形.(4)画出三角形的各边缩小为原来的后的图形.【分析】(1)根据旋转的特征,长方形绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,及长方形旋转前、后A所在的列与行即可分别用数对表示出来。
(3)根据平移的特征,把三角形的各顶点分别向下平移4格,依次连结即可得到平移后的图形。
(4)图中三角形是两直角边分别为4格、2格的直角三角形,根据图形放大与缩小的意义,缩小后的图形是两直角分别为(4×)格、(2×)格的直角三角形。
第3讲 1~5的认识和加减法(教师版)(知识梳理+典例分析+举一反三+巩固提升)人教版
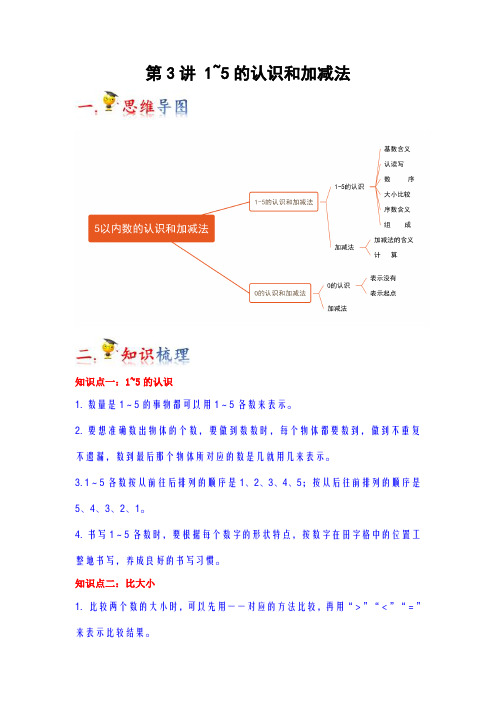
第3讲 1~5的认识和加减法知识点一:1~5的认识1.数量是1~5的事物都可以用1~5各数来表示。
2.要想准确数出物体的个数,要做到数数时,每个物体都要数到,做到不重复不遗漏,数到最后那个物体所对应的数是几就用几来表示。
3.1~5各数按从前往后排列的顺序是1、2、3、4、5;按从后往前排列的顺序是5、4、3、2、1。
4.书写1~5各数时,要根据每个数字的形状特点,按数字在田字格中的位置工整地书写,养成良好的书写习惯。
知识点二:比大小1.比较两个数的大小时,可以先用一一对应的方法比较,再用“>”“<”“=”来表示比较结果。
2.“>”和“<”的相同点和不同点:(1) 相同点:大于号和小于号的开口都对着大数。
(2) 不同点:大于号开口向左,小于号开口向右。
知识点三:第几1.“几”表示物体的数量,可以有一个或多个;2.“第几”表示物体所在的位置或次序,只表示其中的一个物体;3.确定物体的排列顺序时,先确定数数的方向,然后从1开始数,数到几,它的顺序就是“第几”。
知识点四:分与合1. 4能分成1和3、2和2、3和1,相应地1和3、2和2、3和1都能合成4。
2. 5能分成1和4、2和3、3和2、4和1,相应地1和4、2和3、3和2、4和1都能合成5。
知识点五:加法1.把两部分合并在一起,求一共是多少,用加法计算。
用这种方法可以解决生活中简单的数学问题。
2.5以内加法的计算方法:计算5以内的加法时,可以用点数法,接着数、想数的组成等方法来计算出结果。
知识点六:减法1.从总数里面去掉一部分,求另一部分是多少,用减法计算。
2.计算5以内的减法时,可以用倒着数、想数的分成、想加法算减法等方法来计算出结果。
知识点七:0的认识1.0 的含义:0 可以表示一个物体也没有,还可以表示起点。
从0 开始,右边的数依次是1、2、3、4、5……2. 一个数减去它本身,结果是0。
3. 一个数加上0或减去0,结果仍是原数。
考点一:1~5的认识和比大小【例1】按顺序填数。
五年级 第3讲 因数与倍数(教师版)【修订版1.0】

第3讲因数与倍数一、教学目标1.掌握因数与倍数的概念.2.掌握求一个数因数与倍数的方法.3.学会用因数与倍数解决实际应用题.二、知识要点1.因数与倍数:在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数(约数).例如:12÷2=6,我们说12是2的倍数,2是12的因数;同时12÷6=2,所以12也是6的倍数,同样的,6也是12的因数.综上所述,12是6和2的倍数,6和2是12的因数.注意:①倍数、因数存在的前提是“整除”,整除必须符合三个必备条件,整除不同于除尽.②倍数和因数相互依存,不可能独立存在和出现.2.求任一整数的因数:方法一:找一个数的因数,就用1开始去除这个数,一直除到除数和商交换位置或除数和商相同.然后找出等号左右两边的数,这些数就是要找的这个数的因数,因数重复时,只写一次.例如:我们来找64的因数,直接用64去除以1、2、3、4、5……,因为64不是3、5、6、7的倍数,3、5、6、7就不需要计算.现在看,64÷1=64、64÷2=32、64÷4=16,接着,64÷8=8,在这些算式中就可以找出64的所有因数,64的因数有1,64,2,32,4,16,8.(也就是等号左右两边的数)方法二:先将所给的数分解质因数,将质因数进行组合求积,所得到的不重复的数再加上1和它本身,就是该数的因数.例如:90=2×5×3×3,有:1、2、3、5、2×3=6、3×3=9、2×5=10、5×3=15、2×3×3=18、2×5×3=30、5×3×3=45、2×5×3×3=90.所以90的因数有:1、2、3、5、6、9、10、15、18、30、45、90.3.求任一整数因数的个数:一个整数因数的个数是先对其严格分解质因数,再将每个质因数的指数(次数)加1后,相乘所得的积.如:1400严格分解质因数之后为32⨯⨯,所以它的因数有(3+1)×(2+1)257×(1+1)=4×3×2=24个.(包括1和1400本身)4.求任一整数的所有因数的和:一个整数的所有因数的和是在对其严格分解质因数后,将它的每个质因数依次从1加至这个质因数的最高次幂求和,然后再将这些得到的和相乘,乘积便是这个合数的所有因数的和.如:33=⨯⨯⨯,所以21000所有因数的和为2100023572323++++++++=(1222)(13)(1555)(17)74880三、例题精选【例1】120的因数有多少个?这些因数分别是多少?【★★★★★】【解析】16个.将120分解质因数:360=2×2×2×3×5=3235⨯⨯.因数个数应为:(3+1)×(1+1)×(1+1)=16(个)因数分别是:1、120、2、60、3、40、4、30、5、24、6、20、8、15、10、12.【巩固1】60的因数有多少个?它们分别是多少?【★★★★★】【解析】12个.将60分解质因数:60=2×2×3×5=2235⨯⨯.因数个数应为:(2+1)×(1+1)×(1+1)=12(个)因数分别是:1、60、2、30、3、20、4、15、5、12、6、10.【例2】12345678987654321第二大的因数是多少?【★★★★★】【解析】4115226329218107.因为这是奇数,不能被2整除;一个数的各位上的数的和能被3整除,这个数就能被3整除.这个数各位上的数全部相加等于81,这个数能被3整除,所以3是这个数除了1以外的最小因数,那么除了这个数本身的最大因数就是这个数除以3的商.即这个数是:12345678987654321÷3=4115226329218107.【巩固2】20182018第二大的因数是多少?【★★★★★】【解析】10091009.20182018=2×73×137×100920182018第一大的因数是:20182018.20182018第二大的因数是:10091009.【例3】把一个自然数的所有因数都写出来,然后将这些因数两两相加,就可以得到若干个不同的和.其中最小的和是4,最大的和是140.那么,这个自然数是多少?【★★★★★】【解析】105.自然数的最小因数都是1,最大因数是它本身,故可知第二小的因数为:4-1=3.相应地,A的第二大因数应为A÷3,再由两个因数最大的和是140得:140÷(1+3)×3=105.【巩固3】一个两位数有6个因数,且这个数最小的3个因数之和为11.那么此数是多少?【★★★★★】【解析】63.自然数的最小因数都是1,则另两个因数和应为:11-1=10,又10=2+8=3+7=4+6=5+5,因为因数个数为偶数,排除5+5;如果是2和8的倍数,则一定还有因数4,排除;如果是4、6的倍数一定也是2的倍数,排除;故只剩1、3、7作为最小的三个因数.6=2×3=(1+1)×(2+1),则可知有质因数3和7,其中一个次数为1,另一个次数为2,得:3×72=147(舍去),32×7=63.故此数为63.【例4】如图,A、B、C是三个顺次咬合的齿轮,当A转4圈时,B恰好转3圈:当B转4圈时,C恰好转5圈,则A、B、C的齿数的最小数分别是多少?【★★★★★】【解析】15、20、16.当A转4圈时B转3圈,可知A的齿轮数乘4等于B的齿轮数乘3,假设A有的齿轮数为3份,则B的齿轮数为4份.同理,假设B的齿轮数5份时,C的齿轮数为4份,因为B的齿轮数可以分成4份也可以分成5份,所以B的齿轮数一定是4和5的公倍数,可想到4×5=20,并且验证得20是4和5最小的公倍数.而当B的齿轮数为20时,A的齿轮数为15,C的齿轮数为16.故A、B、C齿轮数最小分别是:15、20、16.【巩固4】如例4图,A、B、C是三个顺次咬合的齿轮,当A转3圈时,B恰好转2圈;当B转3圈时,C恰好转4圈.则A、B、C的齿数的最小数分别是多少?【★★★★★】【解析】8、12、9.当A转3圈时B转2圈,可知A的齿轮数乘3等于B的齿轮数乘2,假设A有的齿轮数为2份,则B的齿轮数为3份.同理,假设B的齿轮数4份时,C的齿轮数为3份,因为B的齿轮数可以分成3份也可以分成4份,所以B的齿轮数一定是3和4的公倍数,可想到3×4=12,并且验证得12是3和4最小的公倍数.而当B的齿轮数为12时,A的齿轮数为8,C的齿轮数为9.故A、B、C齿轮数最小分别是:8、12、9.【例5】已知偶数A不是4的整数倍,它的因数的个数为12,4A的因数有几个?【★★★★★】【解析】24个.由于A是偶数但不是4的倍数,所以A只含有一个因子2,可将A分解成1=⨯,其中B是奇数,根据因数个数公式,它的因数个数为:(1+1)A B2×N=12,解得N=6。
冀教版五年级数学下册 6.3 应用问题(一) 习题课件【新版】

第3课时 应用问题(一)
五年级下册
作业习题
作业提升方向
(1)具体数量是分数的分数除法问题 (2)运用推理法解决分数除法问题 (3)运用对应法解决分数除法问题
作业提升练
6.一根不锈钢钢管截去全长的 2 ,正好截去了 8
3
9
米,这根钢管还剩下多少米?
8 2 - 8= 4 (米) 939 9
Hale Waihona Puke 7.同学们参加野炊活动,如果一人一个饭碗,两 人一个菜碗,三人一个汤碗,一共用了55个碗, 那么有多少名同学参加野炊活动?
解:设一共有x名同学。 x x x =55
23 x=30
8.张师傅三天做完一批零件,第一天做了这批零件 的 1 ,已知第一天和第二天共做了57个,第一 3 天和第三天共做了63个。这批零件一共有多少个?
1 5
,四年前父亲
比儿子大40岁,今年父子各多少岁?
解:设今年父亲x岁。
(x-4)-40=
x 5
-4
x= 50
50×
1 5
=10(岁)
今年父亲50岁,儿子10岁。
解:设一共有x个。 57 63 1 x=x
3 x=90
作业拓展练
9.(1)今年儿子的年龄是父亲年龄的
1 5
,四年前父
子年龄的和是46岁,今年父子各多少岁?
解:设今年父亲x岁。
(x-4)+(
1 5
x-4)=46
x= 45
45×
1 5
=9(岁)
今年父亲45岁,儿子9岁。
(2)今年儿子的年龄是父亲年龄的
冀教版小学数学五年级下册第三课 应用问题(一)(教案)

对本课的知识点加以总结,使学生更能掌握本课的重点和难点。
板书
教学反思
应用问题(一)
解:设一共用了x个气球。
答:一共用了63个气球。
通过学生熟悉的生活场景引入课题,让学生亲自感受应用题中数量之间的联系,想方设法让学生在学习过程中发现规律。从而让学生真切地体会并归纳出:解答分数乘法应用题的关键是从题目的关键句找出数量之间的相等关系。在教学中努力体现“自主、合作、探究”的学习方式。教学中我把分数除法应用题与引入的分数乘法应用题结合起来教学,让学生通过讨论交流对比,亲自感受它们之间的异同,挖掘它们之间的内在联系与区别,从而增强学生分析问题、解决问题的能力。在计算应用题的时候,充分让学生亲身实践体验,让学生在探究中加深对这类应用题数量关系及解法的理解,提高能力,为学生进入更深层次的学习做好充分的准备。
爷爷的年龄是单位“1”。爷爷的年龄× -3
=小明的年龄。
通过巩固练习,使学生对本节课的知识掌握得更加牢固。
对所学知识加以巩固练习,以便学生更牢固地掌握本课所学。
拓展练习,使学生更好地掌握本课知识点。
课堂小结
这节课你学会了什么?
(1)可以借助线段图来理解分数除法的应用问题。
(2)根据“求一个数的几分之几是多少用乘法计算”来列方程解答。
学生回答。
联系生活中学生熟悉的场景引入课题,激发学习数学的兴趣,为这节课做好铺垫。1:同学们开联欢会布置会场,用的红气球占气球总数的 ,一共用了多少个气球?
你知道了哪些数学信息?
这个问题可以怎样解决?
2、小组讨论:说说你是怎样想的。
气球总数× =红气球的个数。
解:设一共用了x个气球。
寒假数学第3讲《比例应用题》

甲 班 共 有 5x 人 , 乙 班 共 有 9y 人 , 总 人 数 之 比 为 5x:9y=5× 3:9× 2=5:6.
例7
-------------------------------------------------------------------------------------------
(2)艾迪、大宽的糖数之比为 3:2,大宽、薇儿的糖数之比 为 3:4,并且知道艾迪比薇儿多 10 块糖,那么三人共有 块糖. (3)艾迪、大宽、薇儿一共有 45 块糖,艾迪吃掉 1 块, 大宽吃掉 2 块,薇儿吃掉 3 块后,三个人剩下的糖数之比 是 4:3:6,那么艾迪原有 块糖。 [按比分配]★ ★ 【分析】 (1)1份是45÷ (4+5+6)=3块糖, 艾迪有3× 4=12 块糖,大宽有3× 5=15块糖,薇儿有3× 6=18块糖; (2)统一比为9:6以及6:8,艾迪比薇儿多9-8=1份,对应10块 糖,所以共有(9+6+8)× 10=230块糖; (3)1 份是 (45-1-2-3)÷ (4+3+6)=3 块糖,艾迪原有 3× 4+1=13 块糖。
例5
1 1 : 7 :10 . 10 7
-------------------------------------------------------------------------------------------
(1) 艾迪和薇儿身上的钱数之比为 3:2,妈妈又给艾迪 4 元钱后,艾迪与薇儿的钱数之比变成 8:5,则薇儿身上有
2
1 1 1 : : 6 : 4 : 3 ,时间相 2 3 4
五年级 第 3 讲 比例应用题 (C 版)
08春小学五年级 第03讲 典型应用题(一) 系统复习班 教师版

关于植树的路线,有封闭与不封闭两种路线.1.不封闭路线例:如图① 若题目中要求在植树的线路两端都植树,则棵数比段数多1.如上图把总长平均分成5段,但植树棵数是6棵.全长、棵数、株距三者之间的关系是:棵数=段数+1=全长÷株距+1全长=株距×(棵数-1)株距=全长÷(棵数-1)② 如果题目中要求在路线的一端植树,则棵数就比在两端植树时的棵数少1,即棵数与段数相等.全长、棵数、株距之间的关系就为:全长=株距×棵数;棵数=全长÷株距;株距=全长÷棵数.③ 如果植树路线的两端都不植树,则棵数就比②中还少1棵.棵数=段数-1=全长÷株距-1.如右图所示.段数为5段,植树棵数为4棵.株距=全长÷(棵数+1).2.封闭的植树路线例如:在圆、正方形、长方形、闭合曲线等上面植树,因为头尾两端重合在一起,所以种树的棵数等于分成的段数.如右图所示.棵数=段数=周长÷株距.有些植树问题,从表面上看并没有出现“植树”情节,但题意反映的是植树问题的基本数量关系.我们要认真读题,分析.【例1】晶晶上楼,从第一层走到第三层需要走36级台阶.如果从第一层走到第六层需要走多少级台阶?(各层楼之间的台阶数相同)【分析】题意的实质反映的是一线段上的点数与间隔数之间的关系.线段示意图如下:解:①每相邻两层楼之间有多少级台阶?36÷(3-1)=18(级)②从第一层走到第六层共多少级台阶?18×(6-1)=90(级)答:从第一层走到第六层需要走90级台阶.【例2】有三根木料,打算把每根锯成3段,每锯开一处需用3分钟,全部锯完需要多少分钟?【分析】求锯的次数属植树问题思路.一根木料锯成了3段,只要锯3-1=2次,锯3根木料要2×3=6次,问题随之可求.解:①一根木料要锯成3段,共要锯多少次?3-1=2(次)②锯开三根木料要多少次?2×3=6(次)③锯三根木料要多少时间?3×6=18(分钟)综合算式:3×[(3-1)×3]=18(分钟)或3×(3-1)×3=18(分钟)答:全部锯完要18分钟.【例3】从甲地到乙地每隔45米安装一根电线杆,加上两端共53根;现在改成每隔60米安装一根电线杆.求可余下多少根电线杆?【分析】该题含植树问题、相差关系两组数量关系.解:①从甲地到乙地距离多少米?45×(53-1)=2340(米)②间隔距离变化后,甲乙两地之间安装多少根电线杆?2340÷60+1=40(根)③可余下多少根电线杆?53-40=13(根)综合算式:53-[45×(53-1)÷60+1]=13(根)答:可余下13根电线杆.【拓展】在某校周长400米的环形跑道上,每隔8米插一面红旗,然后在相邻两面红旗之间每隔2米插一面黄旗,应准备红旗______面,黄旗______面.【分析】40O ÷8=50 (红旗)8÷2-1=3 3×50=150 (黄旗)【例4】 园林工人要在周长300米的圆形花坛边等距离地栽上树.他们先沿着花坛的边每隔3米挖一个坑,当挖完30个坑时,突然接到通知:改为每隔5米栽一颗树.这样,他们还要挖多少个坑才能完成任务?【分析】这道题的关键就在之间每3米一个,已经挖的坑,和后来改成5米挖一个坑,有多少个是重复不需要挖的,那么一步一步分析如下:(1)从第1个坑到第30个坑,共有多长?(30-1)×3=87(米)(2)改为“每5米栽一棵树”,有多少坑仍然有用?87÷15=5 (12)5+1=6(个)(3)改为“每5米栽一棵树”,一共应挖多少个坑?300÷5=60(个)(4)还要挖多少个?60-6=54(个)答:还要挖54个才能完成任务.解题要点:对于鸡兔同笼问题,应先假设,然后把假设情形与事实情形作比较,得出两种情形下总数的差.然后找到出现这个“差”的原因是经过假设,每份数增加了.最后根据这个因果关系列式,求出份数.【例5】 (1)在一个笼子里有鸡和兔共8只,鸡兔共22只脚.问鸡和兔各有多少只?【分析】鸡和兔共8只,就是说鸡、兔一共有8个头,每只鸡有2只脚,每只兔有4只脚.这是一道古代的“鸡兔同笼问题”.根据题意画出图,可用图示法解答.解:(1)先画出8个头,用“〇”表示:(2)每个头的下面画出两只脚:把8只全看做是鸡,共画了16只脚,比题中给出的脚少了22-16=6只脚.(3)再给每只鸡添上两只脚使鸡变成兔,边画边数,画够22只脚:答:笼子里有5只鸡,3只兔.(2)今有鸡兔共居一笼,已知鸡头与兔头共35个,鸡脚与兔脚共94只,问鸡兔各几只?【分析】方法一:从已知的35个头,可知鸡兔共35只;又知鸡一只有2只脚,兔一只有’4只脚,假设笼中全是鸡,那么笼中共有(2×35)=70只脚,实际上笼中有94只脚,多出(94—70)=24只脚,什么原因?因为我们把笼中的兔都当作了鸡,每只兔少算了2只脚,所以笼中兔应有(24÷2)=12只,那么鸡有(35—12)=23只.综合算式:(94—2×35)÷(4—2)=12(只),35—12=23(只)方法二:还可假设笼中都是兔,则35只兔有(4×35)=140只脚,这比笼中实际脚的只数多(140—94)=46只,原因是把鸡都算作了兔,每只鸡多算了2只脚,总共多算了46只脚,所以鸡应该有(46÷2)=23只,兔有(35—23)=12只.综合算式:(4×35—94)÷(4—2)=23(只),35—23=12(只)方法三:还可以这样假设;假设笼中每个动物砍掉2只脚,则鸡无脚,每只兔只剩下2只脚,笼还剩的脚共有(94—2×35)=24只,所以有24÷(4—2)=12只兔,所以鸡有35—12=23只.答:笼中有12只兔,23只鸡.【例6】鸡、兔共100只,鸡脚比兔脚多20只.问:鸡、兔各多少只?【分析】假设100只都是鸡,没有兔,那么就有鸡脚200只,而兔的脚数为零.这样鸡脚比兔脚多200只,而实际上只多20只,这说明假设的鸡脚比兔脚多的数比实际上多200—20=180(只).现在以兔换鸡,每换一只,鸡脚减少2只,兔脚增加4只,即鸡脚比兔脚多的脚数中就会减少4+2=6(只),而180÷6=30,因此有兔子30只,鸡100—30=70(只).【例7】(1)某次数学竞赛,共有20道题,每道题做对得5分,没做或做错都要扣3分,小聪得了60分,他做对了_______道题.【分析】20道题全对应该得20×5=100分,还有100+60=40(分)没有得.做错(5×20-60 ) ÷(5+3)=5(道)因此,做对的20-5=15(道).(2)春风小学3名云参加数学竞赛,共10道题,答对一道题得10分,答错一道题扣3分,这3名同学都回答了所有的题,小明得了87分,小红得了74分,小华得了9分,他们三人一共答对了_____道题.【分析】三人共得87+74+9=170(分),比满分10×10×3=300(分)少300-170=130(分)因此三个人共做错:130÷(10+3)=10(道)题,共答对了30-10=20(道)题【例8】 有蜘蛛、蜻蜓、蝉三种动物共18只,共有腿118条,翅膀20对(蜘蛛8条腿;蜻蜓6条腿,两对翅膀;蝉6条腿,一对翅膀),求蜻蜓有多少只?【分析】这是在鸡兔同笼基础上发展变化的问题.观察数字特点,蜻蜓、蝉都是6条腿,只有蜘蛛8条腿.因此,可先从腿数入手,求出蜘蛛的只数.我们假设三种动物都是6条腿,则总腿数为 6×18=108(条),所差 118-108=10(条),必然是由于少算了蜘蛛的腿数而造成的.所以,应有(118-108)÷(8-6)=5(只)蜘蛛.这样剩下的18-5=13(只)便是蜻蜓和蝉的只数.再从翅膀数入手,假设13只都是蝉,则总翅膀数1×13=13(对),比实际数少 20-13=7(对),这是由于蜻蜓有两对翅膀,而我们只按一对翅膀计算所差,这样蜻蜓只数可求7÷(2-1)=7(只).盈亏问题的特点是问题中每一同类量都要出现两种不同的情况.分配不足时,称之为“亏”,分配有余称之为“盈”;还有些实际问题,是把一定数量的物品平均分给一定数量的人时,如果每人少分,则物品就有余(也就是盈),如果每人多分,则物品就不足(也就是亏),凡研究这一类算法的应用题叫做“盈亏问题”.盈亏问题的一般思维方法是比较法.一般解法是:(盈+亏)÷两次分配数的差=人数物品数可由其中一种分法和人数求出.也有的问题两次都有余或两次都不足,不管哪种情况,都是属于按两个数的差求未知数的“盈亏问题”.【例9】 王老师去买儿童小提琴,若买7把,则所带的钱差110元;若买5把,则所带的钱还差30元.则儿童小提琴多少钱一把?王老师带了多少钱?【分析】本题在购物的两个方案中,每一个方案都出现钱不足的情况,买7把小提琴差110元,买5把小提琴差30元.从买7把变成买5把,少买了7—5=2(把)提琴,而钱的差额减少了110—30=80(元),即80元钱可以买2把小提琴,可见小提琴的单价为每把40元.王老师带了40×7-110=170元钱.【例10】某校安排学生宿舍,如果每间住5人则有14人没有床位;如果每间住7人,则多出4个床位,问宿舍几间?住宿生几人?【分析】由已知条件每间5人少14个床位每间7人多4个床位比较两次分配的方案,可以看出,由于第二种方案比第一种每间多住(7—5)=2人,一共要多出(14+4)=18个床位,根据两种方案每间住的人数的差和床位差,可以求出宿舍间数,然后根据已知条件可求出住宿生人数.解:(4+14)÷(7—5)=9(间)5×9+14=59(人),或7×9—4=59(人)答:有宿舍9间,住宿生59人.【例11】有一批笔记本奖给三好生,如果每人发5本就多12本;如果每人发8本就多3本.问有多少本笔记本?【分析】由题意可知,第一次每人发5本,多出12本;第二次每人发8本就多出3本,这两次分配结果相差(12—3)=9本,这是因为两次分配中每人所发本数相差(8—5)=3本,多少人就相差9本呢?9÷3=3(人),再求出一共有多少本笔记本.解:(12—3)÷(8—5)=9÷3=3(人)5×3+12=27(本)答:有27本笔记本.【例12】有若干个苹果和若干个梨.如果按每1个苹果配2个梨分堆,那么梨分完时还剩2个苹果;如果按每3个苹果配5个梨分堆,那么苹果分完时还剩1个梨.苹果和梨各有多少个?【分析】容易看出这是一道盈亏应用题,但是盈亏总额与两次分配数之差很难找到.原因在于第一种方案是1个苹果“搭配”2个梨,第二种方案是3个苹果“搭配”5个梨.如果将这两种方案统一为1个苹果“搭配”若干个梨,那么问题就好解决了.将原题条件变为“1个苹果搭配2个梨,缺4个梨;1个苹果搭配5/3个梨,多1个梨”,此时盈亏总额为4+1=5(个)梨,两次分配数之差为2-5/3=1/3(个)梨.所以有苹果(4+1)÷(2-5/3)=15(个),有梨15×2—4=26(个).【附1】一个圆形花坛,周长是180米.每隔6米种一棵芍药花,每相邻的两棵芍药花之间均匀地栽两棵月季花.问可栽多少棵芍药?多少棵月季?两棵月季之间的株距是多少米?【分析】 ①在圆形花坛上栽花,是封闭路线问题,其株数=段数.② 由于相邻的两棵芍药花之间等距的栽有两棵月季,则每6米之中共有3棵花,且月季花棵数是芍药的2倍.解:共可栽芍药花:180÷6=30(棵)共种月季花:2×30=60(棵)两种花共:30+60=90(棵)两棵花之间距离:180÷90=2(米)相邻的花或者都是月季花或者一棵是月季花另一棵是芍药花,所以月季花的株距是2米或4米. 答:种芍药花30棵,月季花60棵,两棵月季花之间距离为2米或4米.【附2】马路的一边每相隔9米栽有一棵柳树.张军乘汽车5分钟共看到501棵树.问汽车每小时走多少千米?【分析】 张军5分钟看到501棵树意味着在马路的两端都植树了;只要求出这段路的长度就容易求出汽车速度.解:5分钟汽车共走了:9×(501-1)=4500(米),汽车每分钟走:4500÷5=900(米),汽车每小时走:900×60=54000(米)=54(千米)列综合式:9×(501-1)÷5×60÷1000=54(千米)答:汽车每小时行54千米.【附3】现有大小油桶50个,每个大桶可装油4千克,每个小桶可装油2千克,大桶比小桶共多装油20千克,问大小桶各多少个?分析与解答一:假设50个油桶都是大桶,则共装油(4×50)=200千克,而这小桶所装油则为0.这样大桶比小桶多装200千克,比条件所给的差数多了(200—80)=180千克,若在50个大桶中把一部分大桶换成小桶,则每拿一个大桶换成小桶,大桶装的油就减少4千克,而小桶共装的油就增加2千克,那么大桶比小桶多装的数量就减少(4+2)=6千克,那么该把多少个大桶换成小桶才符合题意呢?解: (4×50—20)÷(4+2)=180÷6=30(个)(小桶)50—30=20(个) (大桶)分析与解答二:这道题也可以用另外一种假设;每个大桶比每个小桶多装2千克,如果大小桶同样多,大桶要比小桶共多装20千克,则应该大小桶各20÷(4—2)=10个,现在共有50个桶,在剩下的(50—10×2)=30个桶中,大小桶应装同样多的油,而每个大桶装的油是每个小桶装的(4÷2)=2倍,那么在这30个桶中,应该有[30÷(1+2)]=10个大桶,(30—10)=20个小桶;所以可求出50个桶中,有大小桶各多少个.解:20÷(4—2)=10(个)(50—10×2)÷(1+2)=10(个) (大桶)10+10=20(个) (大桶共有)50一20=30(个) (小桶共有)答:有大桶20个,小桶30个.【附4】100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人?【分析】本题由中国古算名题“百僧分馍问题”演变而得.如果将大和尚、小和尚分别看作鸡和兔,馍看作腿,那么就成了鸡兔同笼问题,可以用假设法来解.假设100人全是大和尚,那么共需馍300个,比实际多300-140=160(个).现在以小和尚去换大和尚,每换一个总人数不变,而馍就要减少3——1=2(个),因为160÷2=80,故小和尚有80 人,大和尚有100-80=20(人).【附5】东东从家去学校,如果每分走80米,结果比上课提前6分到校,如果每分走50米,则要迟到3分,那么东东家到学校的路程是______米.【分析】这道题看似行程问题,实质却可以用盈亏问题来解.先求出东东从家到学校路上要用多长时间,根据已知,(80×6+50×3)÷(80—50)=630÷30=21(分钟),然后可求东东家离校的路程为:80×(21—6)=1200(米).【附6】有两次自然测验,第一次24道题,答对1题得5分,答错(包含不答)1题倒扣1分;第二次15道题,答对1题8分,答错或不答1题倒扣2分,小明两次测验共答对30道题,但第一次测验得分比第二次测验得分多10分,问小明两次测验各得多少分?【分析】法一:如果小明第一次测验24题全对,得5×24=120(分).那么第二次只做对30-24=6(题)得分是8×6-2×(15-6)=30(分).两次相差120-30=90(分).比题目中条件相差10分,多了80分.说明假设的第一次答对题数多了,要减少.第一次答对减少一题,少得5+1=6(分),而第二次答对增加一题不但不倒扣2分,还可得8分,因此增加8+2=10分.两者两差数就可减少6+10=16(分).(90-10)÷(6+10)=5(题).因此,第一次答对题数要比假设(全对)减少5题,也就是第一次答对19题,第二次答对30-19=11(题).第一次得分5×19-1×(24- 9)=90.第二次得分8×11-2×(15-11)=80.法二:答对30题,也就是两次共答错24+15-30=9(题).第一次答错一题,要从满分中扣去5+1=6(分),第二次答错一题,要从满分中扣去8+2=10(分).答错题互换一下,两次得分要相差6+10=16 (分).如果答错9题都是第一次,要从满分中扣去6×9.但两次满分都是120分.比题目中条件“第一次得分多10分”,要少了6×9+10.因此,第二次答错题数是(6×9+10)÷(6+10)=4(题).第一次答错 9-4=5(题).第一次得分 5×(24-5)-1×5=90(分).第二次得分 8×(15-4)-2×4=80(分).1. 有一条公路长900米,在公路的一侧从头到尾每隔10米栽一根电线杆,可栽多少根电线杆?【分析】 要以两棵电线杆之间的距离作为分段标准.公路全长可分成若干段.由于公路的两端都要求栽杆,所以电线杆的根数比分成的段数多1.解:以10米为一段,公路全长可以分成900÷10=90(段)共需电线杆根数:90+1=91(根)答:可栽电线杆91根.2. 小梅数她家的鸡与兔,数头有16个,数脚有44只.问:小梅家的鸡与兔各有多少只?【分析】假设16只都是鸡,那么就应该有2×16=32(只)脚,但实际上有44只脚,比假设的情况多了44-32=12(只)脚,出现这种情况的原因是把兔当作鸡了.如果我们以同样数量的兔去换同样数量的鸡,那么每换一只,头的数目不变,脚数增加了2只.因此只要算出12里面有几个2,就可以求出兔的只数.解:有兔(44-2×16)÷(4-2)=6(只),有鸡16-6=10(只).答:有6只兔,10只鸡.3. 小明妈妈养鸡兔若干只,已知鸡比兔多13只,鸡的脚比兔的脚多16只,问妈妈养鸡兔各几只?【分析】如果每只兔砍去2只脚,则鸡比兔要多出(2×13)=26只脚,实际上只多出16只脚,相差(26—16)=10只脚,这就是砍去的兔脚,每只兔砍去2只脚,从而可求出兔的只数.解: (2×13—16)÷2’=10÷2=5(只) (兔)5+13=18(只) (鸡)答:小明妈妈养兔5只,养鸡18只.4. 小朋友分糖果,若每人分3粒则剩2粒;若每人分5粒则少6粒.问:有多少个小朋友?多少粒糖果?【分析】 (6+2)÷(4-2)=4(人),3×4+2=14(粒).答:有4个小朋友,14粒糖果.5. 一张数学试卷,只有25道选择题,做对一题得4分,做错一题倒扣1分,如不做,不得分也不扣分,若某同学得了78分,那么他做对______题,做错______题,不做______题.【分析】78÷4=19.5>19,就是说小明至少做对20道题,假设他做对21题,即使其余4题全做错了,也应得21×4-4×1=80(分) >78(分),所以小明做对20题,从而易知小明3题不做 ,做错2道题.答案为20,2,3.断 箭不相信自己的意志,永远也做不成将军.春秋战国时代,一位父亲和他的儿子出征打战.父亲已做了将军,儿子还只是马前卒.又一阵号角吹响,战鼓雷鸣了,父亲庄严地托起一个箭囊,其中插着一只箭.父亲郑重对儿子说:"这是家袭宝箭,配带身边,力量无穷,但千万不可抽出来.那是一个极其精美的箭囊,厚牛皮打制,镶着幽幽泛光的铜边儿,再看露出的箭尾.一眼便能认定用上等的孔雀羽毛制作.儿子喜上眉梢,贪婪地推想箭杆、箭头的模样,耳旁仿佛嗖嗖地箭声掠过,敌方的主帅应声折马而毙.果然,配带宝箭的儿子英勇非凡,所向披靡.当鸣金收兵的号角吹响时,儿子再也禁不住得胜的豪气,完全背弃了父亲的叮嘱,强烈的欲望驱赶着他呼一声就拔出宝箭,试图看个究竟.骤然间他惊呆了.一只断箭,箭囊里装着一只折断的箭.我一直刳着只断箭打仗呢!儿子吓出了一身冷汗,仿佛顷刻间失去支柱的房子,轰然意志坍塌了.结果不言自明,儿子惨死于乱军之中.拂开蒙蒙的硝烟,父亲拣起那柄断箭,沉重地啐一口道:"不相信自己的意志,永远也做不成将军."把胜败寄托在一只宝箭上,多么愚蠢,而当一个人把生命的核心与把柄交给别人,又多么危险!比如把希望寄托在儿女身上;把幸福寄托在丈夫身上;把生活保障寄托在单位身上…… 温馨提示:自己才是一只箭,若要它坚韧,若要它锋利,若要它百步穿杨,百发百中,磨砺它,拯救它的都只能是自己.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲应用题一一、植树问题植树问题又称间隔问题,主要是研究间隔数(段数)、棵数、每段长度、路长之间的关系,从而解决诸如爬楼梯、锯木头等这一类实际问题.1. 直线型植树问题分为以下三类:1)两端植树:在植树的线路两端都植树,则棵数比段数多1,即:棵树=段数+1.2)一端植树:在植树的线路两端都植树,则棵数等于段数,即:棵树=段数.3)两端都不植树:在植树的线路两端都不植树,则棵树比段数少1,即:棵树=段数−1.2. 封闭型植树问题:在圆、正方形、长方形、闭合曲线等上面植树,棵树等于段数,即:棵树=段数.3. 基本关系:段数=总长每段长度;总长=每段长度段数.二、方阵行数和列数相等的正方形方队叫做方阵,例如学生排队,士兵列队时横排、竖排相等.1. 实心方阵:总人(或物)数= 最外层每边人(或物)数最外层每边人(或物)数.2. 实心方阵和空心方阵:1)方阵无论在哪一层,每边上的人(或物)数量都相同,每向里一层,每边上的人数就少2,每层总数少;2)每层总数= [每边人(或物)数] ;每边人(或物)数=每层总数.3、空心方阵:总人(或物)数= (最外层每边人(或物)数−层数)层数;总人(或物)数= (最外层人(或物)数最内层人(或物)数)层数三、盈亏问题盈亏问题的特点是问题中每一同类量都要出现两种不同的情况.分配不足时,称之为“亏”,分配有余称之为“盈”;还有些实际问题,是把一定数量的物品平均分给一定数量的人时,如果每人少分,则物品就有余(也就是盈),如果每人多分,则物品就不足(也就是亏),凡研究这一类算法的应用题叫做“盈亏问题”.可以得出盈亏问题的基本关系式:(盈+亏)÷两次分得之差=人数或单位数(盈-盈)÷两次分得之差=人数或单位数(亏-亏)÷两次分得之差=人数或单位数按两个数的差求未知数的“盈亏问题”.注意:1.条件转换;2.关系互换.四、年龄问题计算有关年龄一类的问题叫做年龄问题,它一般以和差、和倍以及差倍应用题的形式出现.年龄变化基本规律:1.两人年龄差不变2.两人年龄倍数关系不是一成不变的,它会随时间改变3.随着时间推移,两人年龄的增加量相等注意:上面的规律适用于两个人之间的年龄关系,但若涉及到一人年龄与另几人年龄和之间的关系则另当别论.计算年龄问题的基本方法:几年后的年龄=大小年龄差÷倍数差-小年龄几年前的年龄=小年龄-大小年龄差÷倍数差五、鸡兔同笼鸡兔同笼问题的基本公式:1.如果假设全是兔,那么则有鸡数=(每只兔子脚数×鸡兔总数−实际脚数)÷(每只兔子脚数−每只鸡的脚数)兔数=鸡兔总数−鸡数2.如果假设全是鸡,那么则有兔数=(实际脚数−每只鸡的脚数×鸡兔总数)÷(每只兔子脚数−每只鸡的脚数)鸡数=鸡兔总数−兔数六、平均数问题1.平均数问题是把若干个大小不等的数,在总量不变的条件下,通过移多补少,使它们成为相等的几份,求其中的一份是多少.2.平均数不是一个真实的数,它反映一组数据的总体情况,不能反映某一个具体的数据.3.解平均数问题,关键是要找准总数量及对应的总份数.4.平均数问题的数量关系式:“总数量÷总份数=平均数”,“总数量÷平均数=总份数”,“总份数⨯平均数=总数量”5.平均速度=总路程÷总时间例题1从甲地到乙地原来每隔45米要装一根电线杆,加上两端的两根一共有53根电线杆,现在改为每隔60米安装一根电线杆,除两端的两根不需要移动外,中间还有几根不需移动?【分析】(53−1)×45=2340m45、60 的公倍数:180、3602340÷180=13不需要移动的杆:13+1=14,除了两端的:14−2=12例题2【一】有一群学生排成三层空心方阵,多9人,如空心部分增加两层,又少15人,问有学生多少人?【分析】增加的两层人数为:9 +15=24(人),这两层人数之差是8人,因此最里层有(24 −8)÷2 = 8(人),现在的方阵共5层,那么最外层有8 + 8×4=40(人),知道最外层人数及层数就不难求出总人数是105 人.【二】仪仗队员组成两个实心方阵,甲方阵每边16人,后来两队合在一起排成一个中空方阵的丙方阵,丙方阵最外层一边人数比乙方阵最外层一边人数多8人,又原来甲方阵的人正好填满丙方阵空心.求原乙方阵每边的人数(指最外层一边人数)是多少?【分析】根据题意可知在乙方阵外再增加8 ÷2 = 4层的话乙方阵与丙方阵最外层人数相等,此时若将丙方阵的空心填满,那么增加4 层后的乙方阵与填满空心的丙方阵总人数也相等,,由此可得:乙方阵总人数+ 新加4 层的人数= 丙方阵总人数+ 甲方阵总人数= 甲方阵总人数+ 乙方阵总人数+甲方阵总人数,可见乙方阵新加4 层所需人数等于甲方阵总人数的两倍.那么乙方阵新增加4 层所需人数为16×16× 2 = 512(人),那么原乙方阵最外层每边人数为512 ÷ 4 ÷ 4 + 4 −2×4 = 28(人)例题3夏令营营员们到一招待所住宿.若每间宿舍住6人,那么就多14人;若每间宿舍住7人,那么就多1间宿舍.有多少个营员?有多少间宿舍?【分析】每间6 人多14 人每间7 人多1 间说明少7 人(7+14)/(7−6)=21 间21*6+14=140 人例题4一人从家出发到会所参加会议,先用每分钟走50米的速度走了2分钟,如果这样走下去,他就要迟到8分钟;后来他改用每分钟60米的速度前进,结果早到5分钟.这个人从家到会所的距离是多少?【分析】设从家到会所还有X分钟开会(X+8)*50=(X−7)*60+2*50 X=72 分钟50*(72+8)=4000 米例题5小飞家是个四口之家.今年爸爸妈妈和小飞的年龄和是125岁,爷爷比小飞大57岁,爸爸比妈妈大2岁.5年前这个家庭成员的年龄和为107岁.这个家庭成员现在各几岁?【分析】今年爸爸妈妈和小飞的年龄和是125 岁,5 年前年龄和是105岁,说明小飞现在3 岁,爷爷60 岁;爸爸妈妈的年龄和62 岁,爸爸比妈妈大2 岁;有和差问题得妈妈30 岁,爸爸32 岁.例题6箱子里红、白两种玻璃球,红球数是白球数的3倍多2只,每次从箱子里取出7只白球、15只红球.如果经过若干次以后,箱子里剩下3只白球、53只红球.那么箱子里原有红球多少只?【分析】假设每次一起取7 只白球和21 只红球,由于每次拿得红球都是白球的3倍,所以最后剩下的红球数应该刚好是白球数的3倍多2 .由于每次取的白球和原定的一样多,所以最后剩下的白球应该不变,仍然是3个.按照我们的假设,剩下的红球应该是白球的3倍多2,即3×3 + 2 =11(只).但是实际上最后剩了53 只红球,比假设多剩42 只,因为每一次实际取得与假设相比少6 只,所以可以知道一共取了42 ÷6 = 7 (次).所以可以知道原来有红球7×15 + 53 =158 (只).例题7在一次考试中有选择题、填空题和解答题三类题共22道.选择题和填空题每题4分,解答题每题10分.这次考试总分是100分,其中选择题和解答题的分值比填空题多4分,这次考试有多少道选择题?多少道填空题?多少道解答题?【分析】选择题和填空题的分值一样,可以归为一类.如果这次考试的22 道题全是解答题,则总分应是:22×10 = 220 (分),但实际总分是100分,所以选择题和填空题共有:(220 −100)÷(10 −4)= 20(道),解答题有:22 −20 = 2 (道).选择题比填空题少:2×10 −4 =16 (分),选择题有:(100 −2×10 −16)÷2 ÷ 4 = 8 (道),填空题有:20 −8 =12 (道).例题8某次数学竞赛原定一等奖10人,二等奖20人,现在将一等奖中最后4人调整为二等奖,那么二等奖学生的平均分提高了1分,一等奖学生的平均分提高了3分.那么原来一等奖平均分比二等奖平均分多多少分?【分析】(方法一)调整后得一等奖的有10 − 4 = 6(人),平均分提高了3分,说明原来求一等奖的平均分时,这6个人给所调整的4人一共添了6 ×3 = 18(分);调整后得二等奖的平均分提高了1分,一共用了1×(20 + 4) = 24(分),说明计算新的平均分时所调整的4人一共拿出了24分平分给得二等奖的每个人;上面两部分合在一起,就可以求出原来一等奖的平均分比二等奖的平均分多的分数为[3× (10 −4) +1×(20 + 4)] ÷4 =10.5(分).(方法二)矩形图,其中横向代表获奖人数,纵向代表平均分.相比较前后两次,减少了矩形1,增加了矩形2 和矩形3 .前后两次总分不变,所以矩形的总面积不变.所以,矩形1的面积等于矩形2 和矩形3 的面积之和.这样可以求出原来一等奖的平均分和现在二等奖的平均分的差;从而就能求出原来一等奖的平均分和二等奖的平均分的差.原来一等奖平均分比二等奖平均分多[3× (10 −4) +1×20] ÷4 +1 =10.5(分).练习1在800米的环岛上,每隔50米插一面彩旗,后来又增加了一些彩旗,就把彩旗的间隔缩短了,起点的彩旗不动,重新插完后发现,一共有4根彩旗没动,问现在的彩旗间隔多少米?【分析】800÷4=200200=50×4=40×5所以间隔是40练习2有一个用方形瓷砖拼成的正方形,要在横、竖方向分别增加三排瓷砖,拼成一个大正方形,一共需要增加159块瓷砖,问原来的正方形是由几块瓷砖拼成的?【分析】原来的正方形最外层的瓷砖块数为(159 −1−3−5) ÷3÷2 = 25(块),那么原来的正方形中瓷砖的块数为25×25 = 625(块).练习3用绳子测量井深,把绳子三折来量,井外余2米;把绳子四折来量,绳子距井口1米,求井深和绳子长?【分析】3折4 段4 折5 段(2+1)/(5−4)=3 米/段3*5−1=14 米(绳长) (14−2)/4+2=5 米深练习4小雪和小芳各买了一本《奥林匹克读物》,约定在相同的时间内完成.小雪计划前两周做30题,以后每周做25题;小芳计划前两周做35题,以后每周做30题,还剩2周复习.问《奥林匹克读物》有几题?他们约定几周完成?【分析】约定X周完成2*30+(X−2)*25=2*35+(X−4)*30 X=12 2*30+(12−2)*25=310题练习5一家三口,妈妈和爸爸同岁,妈妈的年龄是儿子的3倍,三人4年前的年龄和是72岁,三人现在各几岁?【分析】设现在儿子x岁,妈妈爸爸各为3x岁;7x−12 = 72 ;得x =12;现在儿子12 岁,妈妈36 岁,爸爸36 岁.练习6买一些4分和8分的邮票,共花6元8角.已知8分的邮票比4分的邮票多40张,那么两种邮票各买了多少张【分析】解一:如果拿出40 张8 分的邮票,余下的邮票中8 分与 4 分的张数就一样多. (680−8×40)÷(8+4)=30(张),这就知道,余下的邮票中,8 分和 4 分的各有30 张. 因此8 分邮票有40+30=70(张).解二:譬如,假设有20 张4 分,根据条件"8 分比4 分多40 张",那么应有60 张8 分.以"分"作为计算单位,此时邮票总值是4×20+8×60=560(分). 比680少,因此还要增加邮票.为了保持"差"是40,每增加1 张4 分,就要增加1 张8分,每种要增加的张数是(680−4×20−8×60)÷(4+8)=10(张).因此4 分有20+10=30(张),8 分有60+10=70(张).练习7犀牛、羚羊、孔雀三种动物共有头26个,脚80只,犄角20只.已知犀牛有4只脚、1只犄角,羚羊有4只脚,2只犄角,孔雀有2只脚,没有犄角.那么,犀牛、羚羊、孔雀各有几只呢?【分析】这道题有三种不同的动物混合在一起,这样假设起来会比较麻烦,像前面的题一样,我们可以观察一下:虽然有三种不同的动物,但是犀牛和羚羊都是4 只脚,这样,只看脚数,就可以把孔雀与这两种动物分开,转化成我们熟悉的“鸡兔同笼”问题,然后再通过犄角的不同,把犀牛和羚羊分开,也就是说我们需要做两次“鸡兔同笼”.假设26只都是孔雀,那么就有脚:26× 2 = 52(只),比实际的少:80 −52 = 28(只),这说明孔雀多了,需要增加犀牛和羚羊.每增加一只犀牛或羚羊,减少一只孔雀,就会增加脚数:4 −2 = 2(只).所以,孔雀有26 −28 ÷2 =12(只),犀牛和羚羊总共有26 −12 =14(只).假设14 只都是犀牛,那么就有犄角:14×1 =14(只),比实际的少:20 −14 = 6(只),这说明犀牛多了羚羊少了,需要减少犀牛增加羚羊.每增加一只羚羊,减少一只犀牛,犄角数就会增加:2 −1 =1(只),所以,羚羊的只数:6 ÷1 = 6(只),犀牛的只数:14 − 6 = 8(只).练习8小华期末考试时,语文、数学和音乐三科成绩平均分是96分,英语成绩公布后,四科平均分下降了2分,小华英语成绩是多少分?【分析】方法一:已知三科成绩平均分是96 分,可以求出三科成绩总分数,英语成绩公布后,四科平均成绩是:96 −2 = 94 (分),就可以求出四科的总分数,用四科的总分数减去三科的总分数就是英语的分数.⑴语文、数学和音乐三科总分数:96×3 = 288 (分)⑵四科总分数:(96 −2)×4 = 376 (分)⑶英语的分数:376 −288 = 88 (分)综合列式:(96 −2)×4 −96×3 = 88(分)方法二:根据平均分自身特点,可以用“移多补少”的方法.英语成绩公布后,平均分下降了2 分,即四科平均的成绩是96 −2 = 94 (分),根据题意,可以知道英语成绩低于94分,而英语成绩必须加上其他三科补给的分数,才能达到94 分.由于三科平均成绩下降了2 分,这样三科共低了2×3 = 6 (分),这6分补给英语成绩,才达到94分,这样就可以求出英语的考试分数.⑴四科平均分是:96 −2 = 94 (分)⑵原三科共下降了:2×3 = 6 (分)⑶英语成绩是:94 −6 = 88 (分)综合列式:(96 −2)−2× 3 = 88(分)。
