八年级数学三角形中位线培优专题训练

合集下载

(完整版)初二中位线专题训练

B三角形的中位线专题训练22，梯形ABCD 中，AB CD ∥，点F 在BC 上，连DF 与AB 的延长线交于点G ．（1）求证：CDF BGF △∽△；（2）当点F 是BC 的中点时，过F 作EF CD ∥交AD 于点E ，若6cm 4cm AB EF ==，，求CD 的长．三角形中位线的性质例1、求证:三角形的一条中位线与第三边上的中线互相平分.例2、如图，三角形三条中位线组成的图形与原三角形的形状、大小（面积和周长）有怎样的关系？四边形ADEF 的周长与AB+AC 的关系如何？例3、已知在四边形ABCD 中，AB=CD ，E 、F 、G 分别是BD 、AC 、BC 的中点，H 是EF的中点.求证：EF ⊥GH.例4、已知：如图，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点.求证：四边形EFGH 是平行四边形.一、梯形中位线的性质1、已知等腰梯形的中位线和腰长相等，都等于8cm ，这个等腰梯形的周长为（） A 、16 cm B 、32 cm C 、24 cm D 、40 cm2、已知四边形ABCD 是高为10的等腰梯形，AB=DC ，AD ∥BC ，又AC ⊥BD，求中位线ABCFBBB1、在梯形ABCD 中，AD ∥BC ，E 、F 分别是AB 、CD 的中点，E 、F 分别交BD 、AC 于点G 、H ，求证：GH=21(BC-AD).变式一：在梯形ABCD 中，AD ∥BC ，E 、F 分别是AB 、CD 的中点，E 、F 分别交BD 、AC 于点G 、H ，AD=a ，BC=b ，求EF 、FH 、GH 的长。

变式二：在梯形ABCD 中，AD ∥BC ，G 、H 分别是BF 、AC 的中点，求证：EF 是梯形ABCD 的中位线。

4、在梯形ABCD 中，AD ∥BC ，∠BAD 与∠ABC 的平分线交于CDB5、直线l 过口ABCD 的顶点B ，AA ’⊥l ，CC ’⊥l ，DD ’⊥l,试证明AA ’+ CC ’= DD ’二、直角三角形和中位线1、在Rt △ABC 中，∠BAC=90°，延长BA 到D ，使AD=21AB ，E 、F 分别是BC 、AC 的中点。

八年级数学中心对称和三角形中位线最新最全练习巩固含答案-初中数学培优

中心对称班级：___________姓名：___________得分：__________一、选择题1、下面的图形是天气预报中的图标，其中既是轴对称图形又是中心对称图形的是（）.A. B. C. D.2、下列图形中，既是轴对称图形又是中心对称图形的有（）A ．4个B ．3个C ．2个D ．1个A ．B ．C ．D ．4．有五张卡片（形状、大小、质地都相同），上面分别画有下列图形：①线段；②正三角形；③平行四边形；④等腰梯形；⑤圆。

将卡片背面朝上洗匀，从中抽取一张，正面图形一定满足既是轴对称图形，又是中心对称图形的概率是（）A.51 B. 52 C. 53D. 545. 下列图形中，中心对称图形的个数是（）A ． 1个B ． 2个C ． 3个D ． 4个6、下列说法错误的是 ( )A．中心对称图形一定是旋转对称图形B．轴对称图形不一定是中心对称图形C．在成中心对称的两个图形中，连接对称点的线段都被对称中心平分。

D．旋转对称图形一定是中心对称图形。

7、关于中心对称的两个图形,对应线段的关系是( )．(A) 平行 (B) 相等 (C) 平行且相等 (D) 相等且平行或在同一直线上二、填空题1、请写出一个是中心对称图形的几何图形的名称：．2、把汉字“目”绕其中心旋转90°后，所得图形与汉字相似．3、已知点O是 ABCD对角线的交点,则图中关于点O对称的三角形有对,它们分别是 .4、如图, ΔOAB绕点O旋转180°得到ΔOCD,连结AD、BC,得到四边形ABCD,则AB CD(填位置关系),与ΔAOD成中心对称的是，由此可得AD BC(填位置关系)．三、解答题1、在艺术字中，有些汉字或字母是中心对称图形．下面的汉字或字母，是中心对称图形吗？如果是，请标出它们的对称中心．2、请你写出5个成中心对称的汉字，填在下面的方框内．3、如图，在正方形网格上有一个△ABC．（1）作出△ABC关于点O的中心对称图形△A′B′C′（不写作法，但要标出字母）；（2）若网格上的最小正方形边长为1，求出△ABC的面积．4．在ABCD 中，已知∠B=30°，将△ABC 沿AC 翻折至△AB ′C ，连结B ′D.（1）如图1，若0AB D B ,5A 73'==∠ ，则∠ACB= °，BC= ；（2）如图2，AB 23=，BC=1，AB ′与边CD 相交于点E ，求△AEC 的面积；（3）已知AB 23=，当BC 长为多少时，是△AB ′D 直角三角形？参考答案一、选择题1、A【解析】轴对称图形与中心对称图形的特征。

2022-2023学年第二学期初二数学名校优选培优训练专题09 三角形中位线定理

2022-2023学年第二学期初二数学名校优选培优训练专题测试专题09 三角形中位线定理姓名：___________班级：___________考号：___________题号一二三总分得分评卷人得分一．选择题（共10小题，满分20分，每小题2分）1．（2022春•雨花区校级月考）如图，四边形ABCD中，R、P分别是BC、CD上的点，E、F分别是AP、RP的中点，当点P在CB上从C向D移动而点R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不变D．线段EF的长与点P的位置有关2．（2022秋•二道区校级期末）如图，在△ABC中，AB＝BC＝13，BD平分∠ABC交AC于点D，点F在BC上，且BF＝5，连接AF，E为AF的中点，连接DE，则DE的长为（）A．3 B．4 C．5 D．63．（2022春•横县期中）如图，△ABC中，M是BC的中点，AD平分∠BAC，BD⊥AD于点D，若AC＝9，DM＝2，则AB等于（）A．4 B．5 C．6 D．84．（2022春•新城区校级期末）如图，在△ABC中，∠ABC＝90°，AB＝4，BC＝3，若DE是△ABC的中位线，延长DE，交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）A．4 B．C．D．55．（2022春•乐陵市期末）数学课上，大家一起研究三角形中位线定理的证明，小丽和小亮在学习思考后各自尝试作了一种辅助线，如图1，2．其中辅助线作法能够用来证明三角形中位线定理的是（）图1为小丽的辅助线作法：延长DE到F，使EF＝DE，连接DC、AF、FC．图2为小亮的辅助线作法：过点E作GE∥AB，过点A作AF∥BC，GE与AF交于点F．A．小丽和小亮的辅助线作法都可以B．小丽和小亮的辅助线作法都不可以C．小丽的辅助线作法可以，小亮的不可以D．小亮的辅助线作法可以，小丽的不可以6．（2022春•通川区期末）如图，在△ABC中，M是BC边的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC的长为（）A．8 B．10 C．12 D．147．（2022春•禅城区期末）已知：△ABC中，D、E、F分别是边BC、CA、AB的中点，则四边形AFDE的周长等于（）A．AB+AC B．BA+BC C．CA+CB D．△ABC的周长8．（2022春•青山区期中）如图，在Rt△ABC中∠ACB＝90°，∠A＝30°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF＝BC，若EF＝4，则DE的长为（）A．4 B．C．2 D．9．（2021春•金坛区期中）如图，已知四边形ABCD中，AC⊥BD，AC＝6，BD＝8，点E、F分别是边AD、BC的中点，连接EF，则EF的长是（）A．B．5 C．D．1010．（2022春•高唐县期末）如图，△ABC中，∠BAD＝∠CAD，BE＝CE，AD⊥BD，DE＝，AB＝4，则AC的值为（）A．6 B．C．7 D．8评卷人得分二．填空题（共10小题，满分20分，每小题2分）11．（2020春•凯里市期末）如图，CD是△ABC的中线，点E、F分别是AC、DC的中点，若，则AB＝．12．（2022春•南岗区校级期中）如图，△ABE中，∠B＝60°，D为AB上一点，C为BE延长线上一点，连接CD、AE，取AE中点F，取CD中点G，连接FG，若AD＝8，CE＝10，则FG＝．13．（2022春•兴城市期末）如图，△ABC中，D、F分别是AC、BC的中点，E在DF上，且BE⊥CE，若AB＝8，BC＝6，则DE＝．14．（2022•华蓥市模拟）如图，在边长为a的等边△ABC中，分别取△ABC三边的中点A1，B1，C1，得△A1B1C1；再分别取△A1B1C1三边的中点A2，B2，C2，得△A2B2C2；这样依次下去…，经过第2022次操作后得△A2022B2022C2022，则△A2022B2022C2022的面积为．15．（2022春•府谷县期末）如图，在▱ABCD中，点E、F分别为AD、DC的中点，过点C作CM⊥AB交AB延长线于M，连接EF，若CD＝4，BM＝2，CM＝6，则EF的长为．16．（2022春•宝应县期末）如图，四边形ABCD中，AB＝CD＝6，且AB与CD不平行，P、M、N分别是AD、BD、AC的中点，设△PMN的面积为S，则S的范围是．17．（2022春•黄陵县期末）如图，点D，E，F分别是△ABC各边的中点，AH是△ABC的高，如果HF＝5，则ED的长为．18．（2022春•涟水县期末）在Rt△ABC中，∠C＝90°，AC＝5，BC＝12，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN、MN的中点，则DE的最小值是．19．（2021秋•北碚区校级期末）已知在△ABC中，AC＝6cm，点D、E分别是AC、BC的中点，连接DE，在DE上有一点F，EF＝1cm，连接AF，CF，若AF⊥CF，则AB＝．20．（2022•上蔡县模拟）若将三个如图1所示的直角三角形拼成如图2所示的图形，在图2中标记字母，并连接AE，CD，G，H分别为AE，CD的中点，连接GH，如图3所示．若AC＝2，则GH的长为．评卷人得分三．解答题（共8小题，满分60分）21．（2022春•宁都县期末）如图，AC、BD是四边形ABCD的对角线，E、F分别为AD、BC的中点，G、H分别为BD、AC的中点．请你判断EF与GH的关系，并证明你的结论．22．（2022春•海淀区校级期中）如图，在△ABC中，∠ABC＝90°，在边AC上截取AD＝AB，连接BD，过点A作AE⊥BD于点E，F是边BC的中点，连接EF．若AB＝5，BC＝12，求EF的长度．23．（2021秋•桓台县期末）如图，在四边形ABCD中，E，F分别是AD，BC的中点．（1）若AB＝6，CD＝8，∠ABD＝30°，∠BDC＝120°，求EF的长；（2）若∠BDC﹣∠ABD＝90°，求证：AB2+CD2＝4EF2．24．（2022春•西城区校级期中）如图，在△ABC中，AE平分∠BAC，BE⊥AE于点E，点F是BC的中点．（1）如图1，BE的延长线与AC边相交于点D，求证：EF＝（AC﹣AB）；（2）如图2，写出线段AB、AC、EF的数量关系，并证明你的结论．25．（2022春•抚远市期末）如图，在△ABC中，已知AB＝6，AC＝10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE的长．26．（2022春•西峰区校级月考）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：AF＝DC；（2）若AB＝AC，试判断四边形ADCF的形状，并证明你的结论．27．（2022•开福区校级一模）在Rt△ABC中，∠BAC＝90°，E、F分别是BC、AC的中点，延长BA到点D，使AB＝2AD，连接DE、DF、AE、EF，AF与DE交于点O．（1）试说明AF与DE互相平分；（2）若AB＝8，BC＝12，求DO的长．28．（2017春•西城区期中）如图，在四边形ABCD中，M、N分别是对角线AC、BD的中点，又AD、BC 的延长线交于P，求证：S△PMN＝S四边形ABCD．答案与解析一．选择题（共10小题，满分20分，每小题2分）1．（2022春•雨花区校级月考）如图，四边形ABCD中，R、P分别是BC、CD上的点，E、F分别是AP、RP的中点，当点P在CB上从C向D移动而点R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不变D．线段EF的长与点P的位置有关解：如图，连接AR，∵E、F分别是AP、RP的中点，∴EF是△APR的中位线，∴EF＝AR，∵点R不动，∴AR大小不变，∴线段EF的长不变，故选：C．2．（2022秋•二道区校级期末）如图，在△ABC中，AB＝BC＝13，BD平分∠ABC交AC于点D，点F在BC上，且BF＝5，连接AF，E为AF的中点，连接DE，则DE的长为（）A．3 B．4 C．5 D．6解：∵BC＝13，BF＝5，∴FC＝BC﹣BF＝13﹣5＝8，∵AB＝BC，BD平分∠ABC，∴AD＝DC，∵AE＝EF，∴DE是△AFC的中位线，∴DE＝FC＝×8＝4．故选：B．3．（2022春•横县期中）如图，△ABC中，M是BC的中点，AD平分∠BAC，BD⊥AD于点D，若AC＝9，DM＝2，则AB等于（）A．4 B．5 C．6 D．8解：如图，延长BD与AC相交于点F，∵M为BC中点，∴DM是△BCF的中位线，∴DM＝CF＝2．∴CF＝4．∵AD平分∠BAC，BD⊥AD，∴AF＝AB，BD＝DF，∵AC＝9，∴CF＝AC﹣AF＝AC﹣AB＝9﹣AB＝4，∴AB＝5．故选：B．4．（2022春•新城区校级期末）如图，在△ABC中，∠ABC＝90°，AB＝4，BC＝3，若DE是△ABC的中位线，延长DE，交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）A．4 B．C．D．5解：在Rt△ABC中，AC＝＝＝5，∵DE是△ABC的中位线，∴DE＝BC＝1.5，DE∥BC，EC＝AC＝2.5，∴∠EFC＝∠FCM，∵CF是∠ACM的平分线，∴∠ECF＝∠FCM，∴∠EFC＝∠ECF，∴EF＝EC＝2.5，∴DF＝DE+EF＝1.5+2.5＝4，故选：A．5．（2022春•乐陵市期末）数学课上，大家一起研究三角形中位线定理的证明，小丽和小亮在学习思考后各自尝试作了一种辅助线，如图1，2．其中辅助线作法能够用来证明三角形中位线定理的是（）图1为小丽的辅助线作法：延长DE到F，使EF＝DE，连接DC、AF、FC．图2为小亮的辅助线作法：过点E作GE∥AB，过点A作AF∥BC，GE与AF交于点F．A．小丽和小亮的辅助线作法都可以B．小丽和小亮的辅助线作法都不可以C．小丽的辅助线作法可以，小亮的不可以D．小亮的辅助线作法可以，小丽的不可以解：小丽的作法：∵AE＝EC，DE＝EF，∴四边形ADCF为平行四边形，∴CF＝AD，CF∥AD，∵AD＝DB，∴DB＝CF，∴四边形DBCF为平行四边形，∴DE＝BC，DE∥BC，能够用来证明三角形中位线定理；小亮的作法：∵GE∥AB，AF∥BC，∴四边形ABGF为平行四边形，∴AB＝FG，AF＝BG，∵DB＝AB，EG＝FG，∴BD＝EG，∴四边形DBGE为平行四边形，∴DE＝BG，DE∥BG，∵AF∥BC，∴∠AFE＝∠CGE，在△AEF和△CEG中，，∴△AEF≌△CEG（AAS），∴AF＝GC，∴BG＝GC，∴DE＝BC，能够用来证明三角形中位线定理，故选：A．6．（2022春•通川区期末）如图，在△ABC中，M是BC边的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC的长为（）A．8 B．10 C．12 D．14 解：如图，延长BN交AC于点D，∵AN平分∠BAC，∴∠BAN＝∠DAN，∵BN⊥AN，∴∠ANB＝∠AND＝90°，在△ANB与△AND中，，∴△ANB≌△AND（ASA），∴AB＝AD＝8，BN＝DN，又∵M是BC边的中点，∴MN是△BCD的中位线，∴MN＝CD，∵MN＝2，∴CD＝4，∴AC＝AD+CD＝8+4＝12，故选：C．7．（2022春•禅城区期末）已知：△ABC中，D、E、F分别是边BC、CA、AB的中点，则四边形AFDE的周长等于（）A．AB+AC B．BA+BC C．CA+CB D．△ABC的周长解：如图1，∵D、E、F分别是边BC、CA、AB的中点，∴DF＝AC，DE＝AB，AF＝AB，AE＝AC，∴四边形AFDE的周长为AF+DF+CE+AE＝AB+AC+AB+AC＝AB+AC，故选：A．8．（2022春•青山区期中）如图，在Rt△ABC中∠ACB＝90°，∠A＝30°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF＝BC，若EF＝4，则DE的长为（）A．4 B．C．2 D．解：如图，连接DC，在Rt△ABC中∠ACB＝90°，∠A＝30°，点D是边AB的中点，∴DC＝AB，BC＝AB，∴BC＝DC，∵点D，E分别是边AB，AC的中点，∴DE∥CF，DE＝BC，∵CF＝BC，∴DE＝CF，∴四边形DEFC是平行四边形，∴DC＝EF＝4，∴BC＝4，∴DE＝×4＝2．故选：C．9．（2021春•金坛区期中）如图，已知四边形ABCD中，AC⊥BD，AC＝6，BD＝8，点E、F分别是边AD、BC的中点，连接EF，则EF的长是（）A．B．5 C．D．10解：如图，取AB的中点G，连接EG、FG，∵E、F分别是边AD、CB的中点，∴EG∥BD且EG＝BD＝×8＝4，FG∥AC且FG＝AC＝×6＝3，∵AC⊥BD，∴EG⊥FG，∴EF＝＝＝5．故选：B．10．（2022春•高唐县期末）如图，△ABC中，∠BAD＝∠CAD，BE＝CE，AD⊥BD，DE＝，AB＝4，则AC的值为（）A．6 B．C．7 D．8解：如图，延长BD，交AC于F，∵AD⊥BD，∴∠ADB＝∠ADF＝90°，在△ABD和△AFD中，，∴△ABD≌△AFD（ASA），∴BD＝DF，AF＝AB＝4，∵BE＝CE，∴CF＝2DE＝3，∴AC＝AF+CF＝4+3＝7，故答案为：C．二．填空题（共10小题，满分20分，每小题2分）11．（2020春•凯里市期末）如图，CD是△ABC的中线，点E、F分别是AC、DC的中点，若，则AB＝6．解：∵点E、F分别是AC、DC的中点，∴EF是△ACD的中位线，∴AD＝2EF＝3，∵CD是△ABC的中线，∴AB＝2AD＝6，故答案为：6．12．（2022春•南岗区校级期中）如图，△ABE中，∠B＝60°，D为AB上一点，C为BE延长线上一点，连接CD、AE，取AE中点F，取CD中点G，连接FG，若AD＝8，CE＝10，则FG＝．解：连接AC，取AC中点M，连接MF、MG，作GN⊥MF于N．∵G为CD的中点，∴MG∥AD，MF∥BC，MF＝，MG＝＝＝4，∵∠B＝60°，∴∠FMG＝60°，∴∠MGN＝30°，∴MN＝＝＝2，NG＝＝2，∴NF＝MF﹣MN＝5﹣2＝3，∴FG＝＝＝．13．（2022春•兴城市期末）如图，△ABC中，D、F分别是AC、BC的中点，E在DF上，且BE⊥CE，若AB＝8，BC＝6，则DE＝1．解：∵D、F分别是AC、BC的中点，∴DF是△ABC的中位线，∴DF＝AB＝×8＝4，∵BE⊥CE，∴∠BEC＝90°，在Rt△BEC中，∠BEC＝90°，F是BC的中点，∴EF＝BC＝3，∴DE＝DF﹣EF＝4﹣3＝1，故答案为：1．14．（2022•华蓥市模拟）如图，在边长为a的等边△ABC中，分别取△ABC三边的中点A1，B1，C1，得△A1B1C1；再分别取△A1B1C1三边的中点A2，B2，C2，得△A2B2C2；这样依次下去…，经过第2022次操作后得△A2022B2022C2022，则△A2022B2022C2022的面积为a2．解：∵点A1、B1分别是CA、CB的中点，∴点A1B1是△ABC的中位线，∴A1B1＝AB＝a，同理可得：A2B2＝A1B1＝a，……则A2022B2022＝a，∴S＝（a）2＝a2，故答案为：a2．15．（2022春•府谷县期末）如图，在▱ABCD中，点E、F分别为AD、DC的中点，过点C作CM⊥AB交AB延长线于M，连接EF，若CD＝4，BM＝2，CM＝6，则EF的长为3．解：连接AC，∵四边形ABCD为平行四边形，∴AB＝CD＝4，∴AM＝AB+BM＝4+2＝6，∴AC＝＝＝6，∵点E、F分别为AD、DC的中点，∴EF是△ADC的中位线，∴EF＝AC＝3，故答案为：3．16．（2022春•宝应县期末）如图，四边形ABCD中，AB＝CD＝6，且AB与CD不平行，P、M、N分别是AD、BD、AC的中点，设△PMN的面积为S，则S的范围是0＜S≤4.5．解：作ME⊥PN，如图所示，∵P，M，N分别是AD，BD，AC中点，∴PM＝AB＝3，PN＝CD＝3，∴S△PMN＝PN•ME＝1.5ME，∵AB与CD不平行，∴M，N不能重合，∴ME＞0．∵ME≤MP＝3．∴0＜S△≤4.5．故答案是：0＜S≤4.5．17．（2022春•黄陵县期末）如图，点D，E，F分别是△ABC各边的中点，AH是△ABC的高，如果HF＝5，则ED的长为5．解：∵AH是△ABC的高，∴∠AHC＝90°，∵∠AHC＝90°，F是边AC的中点，∴AC＝2HF＝10，∵D、E分别是△ABC各边的中点，∴DE是△ABC的中位线，∴DE＝AC＝5．故答案为：5．18．（2022春•涟水县期末）在Rt△ABC中，∠C＝90°，AC＝5，BC＝12，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN、MN的中点，则DE的最小值是．解：如图，连接CM，∵点D、E分别为CN，MN的中点，∴DE＝CM．当CM⊥AB时，CM的值最小，此时DE的值也最小．由勾股定理得：AB＝＝＝13．∵S△ABC＝•AB•CM＝•AC•BC，∴CM＝．∴DE＝CM＝．故答案是：．19．（2021秋•北碚区校级期末）已知在△ABC中，AC＝6cm，点D、E分别是AC、BC的中点，连接DE，在DE上有一点F，EF＝1cm，连接AF，CF，若AF⊥CF，则AB＝8cm．解：在Rt△AFC中，点D是AC的中点，AC＝6cm，∴DF＝AC＝×6＝3（cm），∵EF＝1cm，∴DE＝DF+EF＝3+1＝4（cm），∵点D，E分别是AC，BC的中点，∴DE是△ABC的中位线，∴AB＝2DE＝2×4＝8（cm），故答案为：8cm．20．（2022•上蔡县模拟）若将三个如图1所示的直角三角形拼成如图2所示的图形，在图2中标记字母，并连接AE，CD，G，H分别为AE，CD的中点，连接GH，如图3所示．若AC＝2，则GH的长为．解：根据题意可知：Rt△ABC≌Rt△DEB≌Rt△FCE，∴BC＝BC＝CE，∴△BCE是等边三角形，∴∠BCE＝60°，如图，取CE的中点Q，连接GQ，HQ，过点G作GN⊥HQ于点N，∵G，H分别为AE，CD的中点，∴GQ∥AC，GQ＝AC＝2＝1，∴∠GQC+∠ACQ＝180°，∴∠GQC＝180°﹣90°﹣60°＝30°，∵△ADF是等边三角形，∴∠BAC＝60°，∴AB＝DE＝2AC＝4，∵H是CD中点，Q是CE中点，∴HQ∥DE，HQ＝DE＝4＝2，∴∠HQC＝∠CEF＝90°，∴∠GQH＝90°﹣30°＝60°，∵GN⊥HQ，GQ＝1，∴NQ＝GQ＝，∴GN＝，∴NH＝HQ﹣NQ＝2﹣＝，∴GH＝＝＝．故答案为：．三．解答题（共8小题，满分60分）21．（2022春•宁都县期末）如图，AC、BD是四边形ABCD的对角线，E、F分别为AD、BC的中点，G、H分别为BD、AC的中点．请你判断EF与GH的关系，并证明你的结论．解：EF与GH互相平分，理由如下：连接EG、GF、FH、EH，∵E、F分别为AD、BC的中点，G、H分别为BD、AC的中点，∴EG是△ADB的中位线，FH是△ACB的中位线，∴EG＝AB，EG∥AB，FH＝AB，FH∥AB，∴EG＝FH，EG∥FH，∴四边形EGFH为平行四边形，∴EF与GH互相平分．22．（2022春•海淀区校级期中）如图，在△ABC中，∠ABC＝90°，在边AC上截取AD＝AB，连接BD，过点A作AE⊥BD于点E，F是边BC的中点，连接EF．若AB＝5，BC＝12，求EF的长度．解：在△ABC中，∠ABC＝90°，AB＝5，BC＝12，则AC＝＝＝13，∵AD＝AB＝5，∴DC＝AC﹣AD＝13﹣5＝8，∵AD＝AB，AE⊥BD，∴BE＝ED，∵BF＝FC，∴EF＝DC＝4．23．（2021秋•桓台县期末）如图，在四边形ABCD中，E，F分别是AD，BC的中点．（1）若AB＝6，CD＝8，∠ABD＝30°，∠BDC＝120°，求EF的长；（2）若∠BDC﹣∠ABD＝90°，求证：AB2+CD2＝4EF2．（1）解：如图，取BD的中点P，连接EP、FP．∵E，F分别是AD、BC的中点，AB＝6，CD＝8，∴PE∥AB，且PE＝AB＝3，PF∥CD且PF＝CD＝4．又∵∠ABD＝30°，∠BDC＝120°，∴∠EPD＝∠ABD＝30°，∠DPF＝180°﹣∠BDC＝60°，∴∠EPF＝∠EPD+∠DPF＝90°，在直角△EPF中，由勾股定理得到：EF＝＝＝5，即EF＝5；（2）证明：如图，取BD的中点P，连接EP、FP．∵E，F分别是AD、BC的中点，∴PE∥AB，且PE＝AB，PF∥CD且PF＝CD．∴∠EPD＝∠ABD，∠BPF＝∠BDC，∴∠DPF＝180°﹣∠BPF＝180°﹣∠BDC，∵∠BDC﹣∠ABD＝90°，∴∠BDC＝90°+∠ABD，∴∠EPF＝∠EPD+∠DPF＝∠ABD+180°﹣∠BDC＝∠ABD+180°﹣（90°+∠ABD）＝90°，∴PE2+PF2＝（AB）2+（CD）2＝EF2，∴AB2+CD2＝4EF2．24．（2022春•西城区校级期中）如图，在△ABC中，AE平分∠BAC，BE⊥AE于点E，点F是BC的中点．（1）如图1，BE的延长线与AC边相交于点D，求证：EF＝（AC﹣AB）；（2）如图2，写出线段AB、AC、EF的数量关系，并证明你的结论．（1）证明：如图1中，∵AE⊥BE，∴∠AED＝∠AEB＝90°，∴∠BAE+∠ABE＝90°，∠DAE+∠ADE＝90°，∵∠BAE＝∠DAE，∴∠ABE＝∠ADE，∴AB＝AD，∵AE⊥BE，∴BE＝DE，∵BF＝FC，∴EF＝DC＝＝（AC﹣AB）．（2）结论：EF＝（AB﹣AC），理由：如图2中，延长AC交BE的延长线于点P．∵AE⊥BP，∴∠AEP＝∠AEB＝90°，∴∠BAE+∠ABE＝90°，∠P AE+∠APE＝90°，∵∠BAE＝∠P AE，∴∠ABE＝∠APE，∴AB＝AP，∵AE⊥BD，∴BE＝PE，∵BF＝FC，∴EF＝PC＝（AP﹣AC）＝（AB﹣AC）．25．（2022春•抚远市期末）如图，在△ABC中，已知AB＝6，AC＝10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE的长．解：如图，延长BD与AC相交于点F，∵AD平分∠BAC，BD⊥AD，∴∠DAB＝∠DAF，AD＝AD，∠ADB＝∠ADF，∴△ADB≌△ADF，∴AF＝AB，BD＝DF，∵AB＝6，AC＝10，∴CF＝AC﹣AF＝AC﹣AB＝10﹣6＝4，∵E为BC中点，∴DE是△BCF的中位线，∴DE＝CF＝×4＝2．26．（2022春•西峰区校级月考）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：AF＝DC；（2）若AB＝AC，试判断四边形ADCF的形状，并证明你的结论．（1）证明：∵E是AD的中点，∴AE＝DE，∵AF∥BC，∴∠AFE＝∠DBE．在△AFE和△DBE中，，∴△AFE≌△DBE（AAS），∴AF＝DB．∵AD是BC边上的中线，∴DC＝DB，∴AF＝DC；（2）解：四边形ADCF是矩形．证明：连接DF，由（1）得AF＝DB，AF∥DB，∴四边形ABDF是平行四边形，∴AB＝DF，∵AB＝AC，∴AC＝DF，由（1）得AF＝DC，AF∥DC，∴四边形ADCF是平行四边形，∴四边形ADCF是矩形．27．（2022•开福区校级一模）在Rt△ABC中，∠BAC＝90°，E、F分别是BC、AC的中点，延长BA到点D，使AB＝2AD，连接DE、DF、AE、EF，AF与DE交于点O．（1）试说明AF与DE互相平分；（2）若AB＝8，BC＝12，求DO的长．解：（1）∵E、F分别是BC、AC的中点，∴EF是△ABC的中位线，∴EF∥AB且EF＝AB．又AB＝2AD，即AD＝AB，∴AD∥EF，AD＝EF，∴四边形AEFD是平行四边形，∴AF与DE互相平分；（2）∵在Rt△ABC中，∠BAC＝90°，AB＝8，BC＝12，∴由勾股定理得AC＝＝＝4又由（1）知，OA＝OF，且AF＝CF，∴OA＝AC＝．∴在△AOD中，∠DAO＝90°，AD＝AB＝4，OA＝，∴由勾股定理得DO＝＝＝．28．（2017春•西城区期中）如图，在四边形ABCD中，M、N分别是对角线AC、BD的中点，又AD、BC 的延长线交于P，求证：S△PMN＝S四边形ABCD．解：如图所示，连接DM，BM，∵M是AC的中点，∴△ADM的面积＝×△ACD的面积，△ABM的面积＝×△ACB的面积，∴△ADM的面积+△ABM的面积＝（△ACD的面积+△ACB的面积）＝×四边形ABCD的面积，∵M是AC的中点，∴△BPM的面积＝△MPC的面积+△MBC的面积＝×△ACP的面积+×△ABC的面积＝×△ABP的面积，∵N是BD的中点，∴△BPN的面积＝×△BDP的面积，△BMN的面积＝×△BDM的面积，∴S△PMN＝△BPM的面积﹣△BPN的面积﹣△BMN的面积＝×△ABP的面积﹣×△BDP的面积﹣×△BDM的面积＝（△ABP的面积﹣△BDP的面积﹣△BDM的面积）＝（△ADM的面积+△ABM的面积）＝××S四边形ABCD＝S四边形ABCD。

八下9.5三角形的中位线难题训练（有答案）

八下9.5三角形的中位线难题训练（有答案）八下9.5三角形的中位线难题训练姓名：___________班级：___________考号：___________一、选择题1.若顺次连结四边形四条边的中点，所得的四边形是菱形，则原四边形一定是()A. 平行四边形B. 矩形C. 对角线相等的四边形D. 对角线互相垂直的四边形2.如图，△ABC中，AB=15，AC=13，点D为BC上一点，且AD=12，BD=9，点E，F分别为AB，AC的中点，则△DEF的周长为()A. 25B. 24C. 26D. 213.如图，正方形ABCD和正方形DEFG的边长分别为5和3，点E，G分别为AD，CD边上的点，H为BF的中点，连接HG，则HG的长为A. 2√2B. 4C. √15D. √174.如图，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.过点D作DG//BE，交BC于点G，连接FG交BD于点O.若AB=3，AD=4，则FG的长为()A. 258B. 158C. 254D. 1545.如图，三角形ABC中，∠B，∠C的平分线BF，CE相交于O，AG⊥BF于G，AH⊥CE于H.其中AB=9cm，AC=14cm，BC=18cm，则GH的长为()A. 2cmB. 52cm C. 3cm D. 72cm6.如图，在平行四边形ABCD中，AD=2AB，CE⊥AB于点E，点F、G分别是AD、BC的中点，连接CF、EF、FG，下列结论：①CE⊥FG；②四边形ABGF是菱形；③EF=CF；④∠EFC=2∠CFD.其中正确的个数是()A. 1个B. 2个C. 3个D. 4个7.如图，AC，BD是四边形ABCD的对角线，点E，F分别是AD，BC的中点，点M，N分别是AC，BD的中点，连接EM，MF，FN，NE，要使四边形EMFN为正方形，则需添加的条件是()A. AB=CD，AB⊥CDB. AB=CD，AD=BCC. AB=CD，AC⊥BDD. AB=CD，AD//BC8.如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边中点得到第二个矩形，依次类推若第一格矩形的面积为1，则第n个矩形的面积为()A. 12n B. 14nC. 12n?1D. 14n?1二、填空题9.如图所示，?ABCD的对角线AC，BD相交于点O，AE=EB，OE=3，AB=5，?ABCD的周长________.10.如图，在梯形ABCD中，AD//BC，∠BCD=90°，BC=2AD，F、E分别是BA、BC的中点，现有四个结论：①△ABC 是等腰三角形②四边形EFAM是菱形③S△BEF=12S△ACD④DE平分∠CDF.则下列结论正确的是_______________ 11.如图，E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，当四边形ABCD的边至少满足________时，四边形EFGH是菱形．12.如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=13，AC=8，则DF的长为___________13.如图，△ABC中，BD平分∠ABC，AD⊥BD于D，F为AC中点，AB=5，BC=7，则DF=_________．14.如图，已知矩形ABCD的长和宽分别为16cm和12cm，连接其对边中点，得到四个矩形，顺次连接矩形AEFG各边中点，得到菱形l1；连接矩形FMCH对边中点，又得到四个矩形，顺次连接矩形FNPQ各边中点，得到菱形l2；…如此操作下去，则l4的面积是______cm2．三、解答题15.类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)概念理解：如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件，你添加的条件是．(2)问题探究：如图2，在“等邻边四边形”ABCD中，∠DAB=60°，∠ABC=∠ADC=90°，AB=AD=6，求对角线AC的长．(3)拓展应用：如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD=60°，∠BCD=30°，AC为对角线，试探究AC，BC，DC的数量关系，并证明你的结论．16.在△ABC中，借助作图工具可以作出中位线EF，沿着中位线EF 一刀剪切后，用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP，剪切线与拼图如图示1，仿上述的方法，按要求完成下列操作设计，并在规定位置画出图示，(1)在△ABC中，增加条件______ ，沿着______ 一刀剪切后可以拼成矩形，剪切线与拼图画在图示2的位置；(2)在△ABC中，增加条件______ ，沿着______ 一刀剪切后可以拼成菱形，剪切线与拼图画在图示3的位置；(3)在△ABC中，增加条件______ ，沿着______ 一刀剪切后可以拼成正方形，剪切线与拼图画在图示4的位置．17.阅读下面材料：子薇遇到这样一个问题：如图1，在正方形ABCD中，点E、F分别为DC、BC边上的点，∠EAF=45°，连接EF，求证：DE+BF=EF．子薇是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段集中到同一条线段上．她先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．她的方法是将△ADE绕点A顺时针旋转90°得到△ABG(如图2)，此时GF即是DE+BF．请回答：在图2中，∠GAF的度数是_______．参考子薇得到的结论和思考问题的方法，解决下列问题：(1)如图3，在直角梯形ABCD中，AD//BC(AD>BC)，∠D=90°，AD=CD=10，E是CD上一点，若∠BAE=45°，DE=4，求BE的长度．(2)如图4，在平面直角坐标系xOy中，点B是x轴上一动点，且点A(?3,2)，连接AB和AO，并以AB为边向上作正方形ABCD，若C(x,y)，求用含x的代数式表示y。

湘教版数学八年级下册_《三角形的中位线》提高训练

《三角形的中位线》提高训练一、选择题1．如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=16，E为AC中点，DE∥BC，D为AB上的点，则DE的长度为（）A．2B．4C．6D．82．如图，△ABC中，BE平分∠ABC，AE⊥BE于点E，M为AB的中点，连接ME 并延长交AC于点N．若AB=6，BC=12，则线段EN的长为（）A．2B．3C．4D．53．如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠PEF=25°，则∠EPF的度数是（）A．100°B．120°C．130°D．150°4．如图，点D、E、F分别是△ABC的边AB、BC、CA的中点，连接DE、EF、FD 得△DEF，如果△ABC的周长是24cm，那么△DEF的周长是（）A．6cm B．12cm C．18cm D．48cm5．如图，△ABC中，D、E分别是AB、AC边的中点，延长DE至F，使EF=DF，若BC=8，则DF的长为（）A．6B．8C．4D．二、填空题6．如图，△ABC中，AB=7cm，BC=6cm，AC=5cm，D，E，F分别是AB，BC，AC 的中点，则四边形ADEF的周长等于cm．7．如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=5，BC=7，则EF的长为．8．如图，已知等边三角形ABC边长为1，△ABC的三条中位线组成△A1B1C1，△A1B1C1的三条中位线组成△A2B2C2，依此进行下去得到△A5B5C5的周长为．9．如图，已知△ABC中，∠ABC的角平分线BE交AC于点E，DE∥BC，如果点D是边AB的中点，AB=8，那么DE的长是．10．如图所示，在△ABC中，AB=AC，D，E分别是AB，AC的中点，G，H为BC 上的点连接DH，EG．若AB=5cm，BC=6cm，GH=3cm，则图中阴影部分的面积为．三、解答题11．在△ABC中，AB=AC=6，点D为BC的中点，点E为AC的中点，连接DE，求DE的长．12．如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．（1）求证：EF垂直平分AD．（2）若四边形AEDF的周长为24，AB=15，求AC的长；13．如图、在△ABC中，AB=AC，M，N分别为AC，BC的中点，以AC为斜边在△ABC的外侧作Rt△ACD，且∠CAD=30°，连接MN，DM，DN．（1）求证：△DMN是等腰三角形；（2）若AC平分∠BAD，AB=6，求DN的长．14．如图，△ABC中，过点A分别作∠ABC，∠ACB的外角的平分线的垂线AD，AE．D，E为垂足，求证：（1）ED∥BC；（2）ED=（AB+AC+BC）．15．（1）如图1，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别是F、G，连接FG．求证：FG=（AB+BC+AC）．[提示：分别延长AF、AG与直线BC相交]（2）如图2，若BD、CE分别是△ABC的内角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别是F、G，连接FG．线段FG与△ABC的三边又有怎样的数量关系？写出你的猜想，并给予证明．《三角形的中位线》提高训练参考答案与试题解析一、选择题1．如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=16，E为AC中点，DE∥BC，D为AB上的点，则DE的长度为（）A．2B．4C．6D．8【分析】先根据直角三角形的性质求出BC的长，再由三角形中位线定理即可得出结论．【解答】解：∵在Rt△ABC中，∠C=90°，∠A=30°，AB=16，∴BC=AB=8．∵D为AB的中点，E为AC的中点，∴DE是△ABC的中位线，∴DE=BC=4．故选：B．【点评】本题考查的是三角形中位线定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．2．如图，△ABC中，BE平分∠ABC，AE⊥BE于点E，M为AB的中点，连接ME 并延长交AC于点N．若AB=6，BC=12，则线段EN的长为（）A．2B．3C．4D．5【分析】延长AE交BC于H，根据等腰三角形的判定和性质得到AE=EH，BH=AB，求出HC，根据三角形中位线定理计算．【解答】解：延长AE交BC于H，∵BE平分∠ABC，AE⊥BE，∴AE=EH，BH=AB=6，∴HC=BC﹣BH=6，∵AE=EH，AN=NC，∴EN=HC=3，故选：B．【点评】本题考查的是三角形中位线定理、等腰三角形的判定和性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．3．如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠PEF=25°，则∠EPF的度数是（）A．100°B．120°C．130°D．150°【分析】根据三角形中位线定理得到PE=AD，PF=BC，根据等腰三角形的性质、三角形内角和定理计算即可．【解答】解：∵P是对角线BD的中点，E，F分别是AB，CD的中点，∴PE=AD，PF=BC，∵AD=BC，∴PE=PF，∴∠PFE=∠PEF=25°，∴∠EPF=130°，故选：C．【点评】本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．4．如图，点D、E、F分别是△ABC的边AB、BC、CA的中点，连接DE、EF、FD 得△DEF，如果△ABC的周长是24cm，那么△DEF的周长是（）A．6cm B．12cm C．18cm D．48cm【分析】利用三角形的中位线定理可以得到：DE=AC，EF=AB，DF=BC，则△DEF的周长是△ABC的周长的一半，据此即可求解．【解答】解：∵D、E分别是△ABC的边AB、BC的中点，∴DE=AC，同理，EF=AB，DF=BC，=DE+EF+DF=AC+BC+AB=（AC+BC+AC）=×24=12cm．∴C△DEF故选：B．【点评】本题考查了三角形的中位线定理，正确根据三角形中位线定理证得：△DEF的周长是△ABC的周长的一半是关键．5．如图，△ABC中，D、E分别是AB、AC边的中点，延长DE至F，使EF=DF，若BC=8，则DF的长为（）A．6B．8C．4D．【分析】根据三角形中位线定理求出DE，根据题意计算即可．【解答】解：∵D、E分别是AB、AC边的中点，∴DE=BC=4，∵EF=DF，∴EF=2，∴DF=6，故选：A．【点评】本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．二、填空题6．如图，△ABC中，AB=7cm，BC=6cm，AC=5cm，D，E，F分别是AB，BC，AC 的中点，则四边形ADEF的周长等于12cm．【分析】根据三角形中位线定理得到DE∥AC，DE=AC，EF∥AB，EF=AB，得到四边形ADEF是平行四边形，计算即可．【解答】解：∵D，E分别是AB，BC的中点，∴DE∥AC，DE=AC=2.5cm，同理，EF∥AB，EF=AB=3.5cm，∴四边形ADEF是平行四边形，∴四边形ADEF的周长=2×（2.5+3.5）=12（cm），故答案为：12．【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．7．如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=5，BC=7，则EF的长为1．【分析】根据三角形中位线定理得到DE=BC=3.5，根据直角三角形的性质得到DF=AB=2.5，计算即可．【解答】解：∵DE是△ABC的中位线，∴DE=BC=3.5，DE∥BC，∵∠AFB=90°，D为AB的中点，∴DF=AB=2.5，∴EF=DE﹣DF=1，故答案为：1．【点评】本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半和在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．8．如图，已知等边三角形ABC边长为1，△ABC的三条中位线组成△A1B1C1，△A1B1C1的三条中位线组成△A2B2C2，依此进行下去得到△A5B5C5的周长为．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出A1B1=AC，B1C1=AB，A1C1=BC，从而得到△A1B1C1是△ABC周长的一半，依此类推，下一个三角形是上一个三角形的周长的一半，根据此规律求解即可．【解答】解：∵△ABC的三条中位线组成△A1B1C1，∴A1B1=AC，B1C1=AB，A1C1=BC，∴△A1B1C1的周长=△ABC的周长=×3=，依此类推，△A2B2C2的周长=△A1B1C1的周长=×=，故答案为：．【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半的性质，求出后一个三角形的周长等于前一个三角形的周长的一半是解题的关键．9．如图，已知△ABC中，∠ABC的角平分线BE交AC于点E，DE∥BC，如果点D是边AB的中点，AB=8，那么DE的长是4．【分析】根据三角形的中位线定理即可求出答案．【解答】解：连接BE，∵BE平分∠ABC，∴∠ABE=∠CBE，∵DE∥BC，∴∠DEB=∠ABE，∴∠ABE=∠DEB，∴BD=DE，∵D是AB的中点，∴AB=BD，∴DE=AB=4，故答案为：4【点评】本题考查三角形的综合问题，涉及角平分线的性质，平行线的性质等性质，需要学生灵活运用所学知识．10．如图所示，在△ABC中，AB=AC，D，E分别是AB，AC的中点，G，H为BC 上的点连接DH，EG．若AB=5cm，BC=6cm，GH=3cm，则图中阴影部分的面积为6cm2．【分析】连接DE，作AF⊥BC于F，根据三角形中位线定理求出DE，根据勾股定理求出AF，根据相似三角形的判定定理和性质定理计算即可．【解答】解：连接DE，作AF⊥BC于F，∵D，E分别是AB，AC的中点，∴DE=BC=3，DE∥BC，∵AB=AC，AF⊥BC，∴BF=BC=3，在Rt△ABF中，AF==4，∴△ABC的面积=×6×4=12，∵DE∥BC，∴△ADE∽△ABC，∴△ADE的面积=12×=3，∴四边形DBCE的面积=12﹣3=9，△DOE的面积+△HOG的面积=×3×2=3，∴图中阴影部分的面积=9﹣3=6（cm2），故答案为：6cm2．【点评】本题考查的是三角形中位线定理、相似三角形的判定和性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．三、解答题11．在△ABC中，AB=AC=6，点D为BC的中点，点E为AC的中点，连接DE，求DE的长．【分析】利用三角形中位线定理可以直接求得DE的长度．【解答】解：∵点D为BC的中点，点E为AC的中点，∴DE是△ABC的中位线，∴DE=AB．又AB=AC=6，∴DE=3．【点评】本题考查了三角形的中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半．12．如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．（1）求证：EF垂直平分AD．（2）若四边形AEDF的周长为24，AB=15，求AC的长；【分析】（1）根据直角三角形的性质得到DE=AE，DF=AF，根据线段垂直平分线的判定定理证明；（2）根据直角三角形的性质得到DE=AE=AB=，DF=AF=AC，根据四边形的周长公式计算．【解答】（1）证明：∵AD是高，∴∠ADB=∠ADC=90°，又E、F分别是AB、AC的中点，∴DE=AB=AE，DF=AC=AF，∴EF垂直平分AD；（2）解：由（1）得，DE=AE=AB=，DF=AF=AC，∵四边形AEDF的周长为24，∴AE+ED+DF+FA=24，∴DF+FA=24﹣15=9，∴AC=9．【点评】本题考查的是线段垂直平分线的判定，直角三角形的性质，掌握直角三角形中，斜边上的中线等于斜边的一半是解题的关键．13．如图、在△ABC中，AB=AC，M，N分别为AC，BC的中点，以AC为斜边在△ABC的外侧作Rt△ACD，且∠CAD=30°，连接MN，DM，DN．（1）求证：△DMN是等腰三角形；（2）若AC平分∠BAD，AB=6，求DN的长．【分析】（1）依据三角形的中位线定理可得到MN=AB，由直角三角形斜边上中线的性质可得到DM=AM=AC，然后结合已知条件可得到DM=MN；（2）由AM=DM可得到∠CAD=∠ADM=30°，从而可得到∠DMC=60°，然后再证明∠CMN=30°，从而可得到∠DMN=90°，最后，依据勾股定理求解即可．【解答】解：（1）∵在△ABC中，M、N分别是AC、BC的中点，∴MN∥AB，MN=AB，AM=MC=AC．∵∠ADC=90°，DM为斜边上的中线，∴MD=AC．∵AC=AB，∴MN=DM．∴△DMN是等腰三角形．（2）∵∠CAD=30°，AC平分∠BAD，∴∠BAC=∠CAD=30°．∵MN∥AB，∴∠NMC=∠BAC=30°．由（1）DM=AM，∴∠DMC=60°．∴∠DMN=∠DMC+∠NMC=30°+60°=90°．在Rt△ABC中，DN2=DM2+MN2，DM=MN=AB=3，∴DN=3．【点评】本题主要考查的是三角形的中位线定理、勾股定理、等腰三角形的判断，熟练掌握相关知识是解题的关键．14．如图，△ABC中，过点A分别作∠ABC，∠ACB的外角的平分线的垂线AD，AE．D，E为垂足，求证：（1）ED∥BC；（2）ED=（AB+AC+BC）．【分析】（1）分别延长AD、AE与直线BC交于点F、G，根据AD⊥BD，得到∠ADB=∠FDB=90°，再根据BD=BD，∠ABD=∠FBD，证得△ABD≌△FBD，进而得到AD=FD、AE=EG，证得DE∥BC．（2）根据上题证得的△ABD≌△FBD，AB=BF，同理AC=CG，证得GF=FB+BC+GC=AB+BC+AC，从而证得结论．【解答】证明：（1）分别延长AD、AE与直线BC交于点F、G，∵AD⊥BD，∴∠ADB=∠FDB=90°，∵BD=BD，∠ABD=∠FBD，∴△ABD≌△FBD∴AD=FD，同理可得AE=EG，∴DE∥BC；（2）由（1）知△ABD≌△FBD，∴AB=BF，同理AC=CG，∵DE=FG∴GF=FB+BC+GC=AB+BC+AC，∴DE=（AB+BC+AC）【点评】本题考查了三角形的中位线定理及三角形的有关知识，解题的关键是正确的利用中位线定理得到中位线与第三边的位置或数量关系．15．（1）如图1，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别是F、G，连接FG．求证：FG=（AB+BC+AC）．[提示：分别延长AF、AG与直线BC相交]（2）如图2，若BD、CE分别是△ABC的内角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别是F、G，连接FG．线段FG与△ABC的三边又有怎样的数量关系？写出你的猜想，并给予证明．【分析】（1）利用全等三角形的判定定理ASA证得△ABF≌△MBF，然后由全等三角形的对应边相等进一步推出MB=AB，AF=MF，同理CN=AC，AG=NG，由此可以证明FG为△AMN的中位线，然后利用中位线定理求得FG=（AB+BC+AC）；（2）延长AF、AG，与直线BC相交于M、N，与（1）类似可以证出答案．【解答】解：（1）如图1，∵AF⊥BD，∠ABF=∠MBF，∴∠BAF=∠BMF，在△ABF和△MBF中，，∴△ABF≌△MBF（ASA），∴MB=AB，∴AF=MF，同理：CN=AC，AG=NG，∴FG是△AMN的中位线，∴FG=MN，=（MB+BC+CN），=（AB+BC+AC）．（2）猜想：FG=（AB+AC﹣BC），证明：如图2，延长AG、AF，与直线BC相交于M、N，∵由（1）中证明过程类似证△ABF≌△NBF，∴NB=AB，AF=NF，同理CM=AC，AG=MG，∴FG=MN，∴MN=2FG，∴BC=BN+CM﹣MN=AB+AC﹣2FG，∴FG=（AB+AC﹣BC）．【点评】本题主要考查了三角形的中位线定理，三角形的内角和定理，等腰三角形的性质和判定等知识点，解此题的关键是作辅助线转化成三角形的中位线．。

2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线

2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线结合【例题讲解】（1）如图1，已知△ABC中，F是BC上一点，AB＝BF，BE⊥AF，垂足是E，D是AC的中点，请说明FC和DE有怎样的关系？（请写出详细的推理过程）（2）如图2，在△ABC中，M、D分别是边AB、AC的中点，E是线段MD上的一点．连接AE、BE，∠AEB ＝90°，且AB＝8，BC＝14，则DE的长是______．解：（1）12DE FC DE FC=∥，，理由如下：∵AB=BF，BE⊥AF，∴AE=EF，即点E是AF的中点，又∵D是AC的中点，∴DE是△ACF的中位线，∴12DE FC DE FC=∥，；（2）∵M、D分别是AB、AC的中点，∴MD是△ABC的中位线，∴172MD BC==，∵∠AEB=90°，AB=8，M是AB的中点，∴142ME AB==，∴DE=MD-ME=3．【综合演练】1．如图，在Rt△ABC中，∠ABC＝90°，BF是AC边上的中线，DE是△ABC的中位线，若DE＝10，则BF的长为（）A ．10B ．5C ．8D ．62．如图，在ABC 中，BF 平分ABC ∠，AF BF ⊥于点F ，D 为AB 的中点，连接DF 延长交AC 于点.E 若10AB =，=16BC ，则线段EF 的长为（）A ．2B ．3C ．4D ．53．如图，在RtΔABC 中，∠ACB =90，AC =6、BC =4，点F 为射线CB 上一动点，过点C 作CM ⊥AF 于M 交AB 于E ， D 是AB 的中点，则DM 长度的最小值是( )A ．3B ．2C ．1D ．6-24．如图，在正方形ABCD 中，对角线AC 与BD 相交于点O ，E 为BC 上一点，CE ＝5，F 为DE 的中点．若△CEF 的周长为18，则OF 的长为( )A ．3B ．4C ．52D ．72第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题(共0分)5．已知，如图，在△ABC 中，D 、E 、F 分别是各边的中点，AH 是高，已知AB ＝6cm ，AC ＝8cm ，7cm 3CH BH -=，则△DHE 的周长为________cm ．6．如图，在Rt ABC 中，90ACB ∠=︒，30A ∠=︒，D ，E ，F 分别为AB ，AC ，AD 的中点，若6BC =，则EF 的长度为 _____．7．如图，菱形ABCD 中，DE AB ⊥，垂足为E ，点F 、G 分别为边AD 、DC 的中点，5,8EF FG ==，则ABCD S =菱形___________．8．如图，在ABC 和ABD △中，90ACB ADB ∠=∠=︒，E 、F 、G 分别为AB 、AC 、BC 的中点，若1DE =，则FG =_________．9．如图，在正方形ABCD 中，F 在AB 上，E 在BC 的延长线上，AF ＝CE ，连接DF 、DE 、EF ，EF 交对角线BD 于点N ，M 为EF 的中点，连接MC ，下列结论：①△DEF 为等腰直角三角形；②∠FDB ＝∠FEC ；③直线MC 是BD 的垂直平分线；④若BF ＝2，则MC ＝2；其中正确结论的有_______．10．如图，ABC ∆中，90ACB ∠=，D 为AC 边上的中点，E 为AB 边上一点，4AB BE =，连接CE DE 、，延长DE 交CB 延长线于F ，若3BF =，10AB =，则CE =________．11．如图，在Rt ABC 中，90,8,6ACB AC BC ∠=︒==，点P 是平面内一个动点，且4AP =，Q 为BP 的中点，在P 点运动过程中，设线段CQ 的长度为m ，则m 的取值范围是_______．三、解答题(共0分)12．如图，在四边形ABCD 中，∠ABC =90°，AC=AD ，M ，N 分别是AC ，CD 的中点，连接BM ，MN ，BN ．(1)求证：BM=MN；(2)若∠BAD=60°，AC平分∠BAD，AC=2．①求∠BMN的度数；②求BN的长．13．如图，D、E、F分别是△ABC三边中点，AH⊥BC于H．求证：（1）∠BDF＝∠BAC；（2）DF＝EH．14．在平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AB，点E、F分别是OA、BC的中点，连接BE、EF．BC；(1)求证：EF=12(2)在上述条件下，若AC=BD，G是BD上一点，且BG:GD=3:1，连接EG、FG，试判断四边形EBFG的形状，并证明你的结论．15．如图，在平面直角坐标系中，A（0，4），B（4，0），C（6，2），连接AB，BC，平移BC至AD（点B 与点A对应，点C与点D对应），连接CD．(1)①直接写出点D的坐标为．②判断四边形ABCD的形状，并证明你的结论；(2)如图1，点E为AB边上一点，连接DE，DF平分∠EDC交BC于F，连接EF，若∠DFE＝45°，求BE 的长；(3)如图2，N为BC边的中点，若∠AMC＝90°，连接MN，请直接写出MN的取值范围．16．已知，在△ABC中，以△ABC的两边BC，AC为斜边向外测作Rt△BCD和Rt△ACE，使∠CAE=∠CBD，取△ABC边AB的中点M，连接ME，MD．特例感知：（1）如图1，若AC=BC，∠ACB=60°，∠CAE=∠CBD=45°，取AC，BC的中点F，G，连接MF，MG，EF，DG，则ME与MD的数量关系为______，∠EMD=______；（2）如图2，若∠ACB=90°，∠CAE=∠CBD=60°，取AC，BC的中点F，G，连接MF，MG，EF，DG，请猜想ME与MD的数量关系以及∠EMD的度数，并给出证明；类比探究：（3）如图3，当△ABC是任意三角形，∠CAE=∠CBD=α时，连接DE，请猜想△DEM的形状以及∠EMD 与α的数量关系，并说明理由．中，D为BC中点，BE、CF与射线AE分别相交于点E、F（射线AE不经过点D）．17．在ABC(2)如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND．求证：AM=AN(3)如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND．求证：∠EMD=∠FND．18．（1）如图1，已知△ABC中，F是BC上一点，AB＝BF，BE⊥AF，垂足是E，D是AC的中点，请说明FC和DE有怎样的关系？（请写出详细的推理过程）（2）如图2，在△ABC中，M、D分别是边AB、AC的中点，E是线段MD上的一点．连接AE、BE，∠AEB ＝90°，且AB＝8，BC＝14，则DE的长是______．答案与解析【例题讲解】（1）如图1，已知△ABC中，F是BC上一点，AB＝BF，BE⊥AF，垂足是E，D是AC的中点，请说明FC和DE有怎样的关系？（请写出详细的推理过程）（2）如图2，在△ABC中，M、D分别是边AB、AC的中点，E是线段MD上的一点．连接AE、BE，∠AEB ＝90°，且AB＝8，BC＝14，则DE的长是______．解：（1）12DE FC DE FC=∥，，理由如下：∵AB=BF，BE⊥AF，∴AE=EF，即点E是AF的中点，又∵D是AC的中点，∴DE是△ACF的中位线，∴12DE FC DE FC=∥，；（2）∵M、D分别是AB、AC的中点，∴MD是△ABC的中位线，∴172MD BC==，∵∠AEB=90°，AB=8，M是AB的中点，∴142ME AB==，∴DE=MD-ME=3．【综合演练】1．如图，在Rt△ABC中，∠ABC＝90°，BF是AC边上的中线，DE是△ABC的中位线，若DE＝10，则BF的长为（）A．10 B．5 C．8 D．6【分析】根据三角形中位线定理求出AC ，根据直角三角形的斜边上的中线等于斜边的一半计算，得到答案．【解答】解：∵DE 是△ABC 的中位线，若DE =10，∴AC =2DE =20，在Rt △ABC 中，∠ABC =90°，BF 是AC 边上的中线，∴BF =12AC =10，故选：A ．【点评】本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．2．如图，在ABC 中，BF 平分ABC ∠，AF BF ⊥于点F ，D 为AB 的中点，连接DF 延长交AC 于点.E 若10AB =，=16BC ，则线段EF 的长为（）A ．2B ．3C ．4D ．5 【答案】B【分析】先求出152DF AB AD BD ====，然后证明DE BC ∥，根据平行线分线段成比例可得=AE EC ，再根据三角形中位线定理求出DE 即可．【解答】解：AF BF ⊥，90AFB ∴∠=︒，10AB =，D 为AB 中点，152DF AB AD BD ∴====， ABF BFD ∠∠∴=，又BF 平分ABC ∠，ABF CBF ∠∠∴=，CBF DFB ∠∠∴=，∴DE BC ∥，∴=AD AE DB EC，182DE BC ∴==， 853EF DE DF ∴=-=-=，故选：B ．【点评】本题考查了直角三角形斜边中线的性质，等腰三角形的判定和性质，平行线的判定，平行线分线段成比例定理以及三角形中位线定理等知识，证明DE BC ∥是解答本题的关键．3．如图，在RtΔABC 中，∠ACB =90，AC =6、BC =4，点F 为射线CB 上一动点，过点C 作CM ⊥AF 于M 交AB 于E ， D 是AB 的中点，则DM 长度的最小值是( )A ．3B ．2C ．1D ．6-2【答案】C【分析】取AC 的中点T ，连接DT ，MT ．利用三角形的中位线定理求出DT ，利用直角三角形的中线的性质求出MT ，再根据DM MT DT ≥-，可得结论．【解答】解：如图，取AC 的中点T ，连接DT ，MT ．∵AD DB =，AT TC =，∴122DT BC ==． ∵CE AF ⊥，∴90AMC ∠=︒，∴132TM AC ==， ∴点M 的运动轨迹是以T 为圆心，TM 为半径的圆，∴321DM TM DT ≥-=-=，∴DM 的最小值为1，故选：C ．【点评】本题考查点与圆的位置关系，三角形中位线定理，直角三角形斜边中线的性质等知识，解题的关键是学会添加常用辅助线，构造三角形中位线，直角三角形斜边中线解决问题．4．如图，在正方形ABCD 中，对角线AC 与BD 相交于点O ，E 为BC 上一点，CE ＝5，F 为DE 的中点．若△CEF 的周长为18，则OF 的长为( )A ．3B ．4C ．52D ．72 【答案】D【分析】先根据直角三角形的性质求出DE 的长，再由勾股定理得出CD 的长，进而可得出BE 的长，由三角形中位线定理即可得出结论．【解答】∵CE=5，△CEF 的周长为18，∴CF+EF=18-5=13．∵F 为DE 的中点，∴DF=EF ．∵∠BCD=90°，∴CF=12DE ，∴EF=CF=12DE=6.5，∴DE=2EF=13，∴CD=2212DE CE -=，∵四边形ABCD是正方形，∴BC=CD=12，O为BD的中点，∴OF是△BDE的中位线，∴OF=12(BC－CE)=12(12－5)=3.5，故选D．【点评】本题考查的是正方形的性质，涉及到直角三角形的性质、三角形中位线定理等知识，难度适中．使用勾股定理是解决这个问题的关键．5．已知，如图，在△ABC中，D、E、F分别是各边的中点，AH是高，已知AB＝6cm，AC＝8cm，7 cm 3CH BH-=，则△DHE的周长为________cm．【答案】496##186【分析】根据直角三角形斜边上的中线的性质求出DH，根据三角形中位线定理求出DE，根据三角形的周长公式计算，得到答案．【解答】解：∵AH是△ABC的高，∴∠AHB=90°，∵点D是AB的中点，∴DH=12AB=12×6=3cm，∵D、E分别是BA、BC的中点，∴DE是△ABC的中位线，∴DE=12AC=12×8=4cm，∵BE=EC，CH-BH=73 cm，∴HE=76 cm，∴△DHE的周长=DH+DE+HE=496cm，故答案为：496．【点评】本题考查的是三角形中位线定理、直角三角形斜边上的中线的性质，掌握三角形中位线等于第三边的一半是解题的关键．6．如图，在Rt ABC 中，90ACB ∠=︒，30A ∠=︒，D ，E ，F 分别为AB ，AC ，AD 的中点，若6BC =，则EF 的长度为 _____．【答案】3【分析】根据含30°的直角三角形的性质求出CD ，根据直角三角形的性质求出CD ，根据三角形中位线定理计算，得到答案．【解答】解：∵∠ACB ＝90°，∠A ＝30°，∴AB ＝2BC ＝12．∵∠ACB ＝90°，D 为AB 的中点，∴CD ＝12AB ＝6，∵E ，F 分别为AC ，AD 的中点，∴EF 为△ACD 的中位线，∴EF ＝12CD ＝3．故答案为：3．【点评】本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．7．如图，菱形ABCD 中，DE AB ⊥，垂足为E ，点F 、G 分别为边AD 、DC 的中点，5,8EF FG ==，则ABCD S =菱形___________．【答案】96【分析】连接,AC BD ，交于点O ，先根据直角三角形斜边上的中线等于斜边的一半可得10AD =，再根据三角形的中位线定理可得16AC =，然后根据菱形的性质和勾股定理可得12BD =，最后利用菱形的面积公式即可得．【解答】解：如图，连接,AC BD ，交于点O ，,5DE AB EF ⊥=，且点F 为边AD 的中点，210AD EF ∴==，点,F G 分别为边,AD DC 的中点，8FG =，216AC FG ∴==，四边形ABCD 是菱形，1,8,22AC BD OA AC BD OD ∴⊥===， 226OD AD OA ∴=-=，12BD ∴=，1116129622ABCD S AC BD ∴=⋅=⨯⨯=菱形，故答案为：96．【点评】本题考查了直角三角形斜边上的中线等于斜边的一半、三角形的中位线定理、勾股定理、菱形的性质，熟练掌握菱形的性质是解题关键．8．如图，在ABC 和ABD △中，90ACB ADB ∠=∠=︒，E 、F 、G 分别为AB 、AC 、BC 的中点，若1DE =，则FG =_________．【答案】1【分析】由直角三角形斜边中线的性质得出AB =2DE ，再由三角形中位线的性质可得FG 的长；【解答】解：∵Rt △ABC 中，点E 是AB 的中点，DE =1，∴AB =2DE =2，∵点F 、G 分别是AC 、BC 中点，∴112FG AB ==，故答案为：1【点评】本题考查了直角三角形的性质及三角形中位线的性质等知识；熟练掌握中位线定理是解题的关键． 9．如图，在正方形ABCD 中，F 在AB 上，E 在BC 的延长线上，AF ＝CE ，连接DF 、DE 、EF ，EF 交对角线BD 于点N ，M 为EF 的中点，连接MC ，下列结论：①△DEF 为等腰直角三角形；②∠FDB ＝∠FEC ；③直线MC 是BD 的垂直平分线；④若BF ＝2，则MC ＝2；其中正确结论的有_______．【答案】①②③④【分析】先根据SAS 定理证出ADF CDE ≅，再根据全等三角形的性质可得,DF DE ADF CDE =∠=∠，然后根据等腰直角三角形的判定即可判断①；先根据等腰直角三角形的性质可得45DEF DFE ∠=∠=︒，再根据对顶角相等可得DNF BNE ∠=∠，然后根据三角形的内角和定理即可得判断②；连接BM DM ,，先根据直角三角形斜边上的中线等于斜边的一半可得12BM DM EF ==，再根据线段垂直平分线的判定即可判断③；取BE 的中点O ，连接MO ，先根据三角形中位线定理可得11,2MO BF MO BF ==∥，再根据等腰三角形的三线合一可得1452BCM BCD ∠=∠=︒，然后在Rt MOC 中，利用勾股定理即可得．【解答】解：四边形ABCD 是正方形，,90,45AB AD CD BC A ABC BCD ADC CBD ∴===∠=∠=∠=∠=︒∠=︒，在ADF △和CDE 中，90AD CD A DCE AF CE =⎧⎪∠=∠=︒⎨⎪=⎩，()SAS ADF CDE ∴≅，,DF DE ADF CDE ∴=∠=∠，90EDF CDE CDF ADF CDF ADC ∴∠=∠+∠=∠+∠=∠=︒，DEF ∴为等腰直角三角形，结论①正确；45DEF DFE ∴∠=∠=︒，又45,CBD DNF BNE ∠=︒∠=∠，180180DNF CBD BN E E DF ∴︒-∠=︒-∠-∠∠-，即FDB FEC ∠=∠，结论②正确；如图，连接BM DM ,，M 为Rt DEF △和Rt BEF △斜边EF 上的中点，12BM DM EF ∴==，又BC CD =，∴直线MC 是BD 的垂直平分线，结论③正确；如图，取BE 的中点O ，连接MO ，1121,22MO BF MO BF ∴==⨯=∥，90MOC ABC ∴∠=∠=︒，直线MC 是BD 的垂直平分线，BC CD =，1452BCM BCD ∴∠=∠=︒（等腰三角形的三线合一）， Rt COM ∴是等腰直角三角形，且1OC MO ==，222MC MO OC ∴=+=，结论④正确；综上，正确结论的有①②③④，故答案为：①②③④．【点评】本题考查了正方形的性质、三角形全等的判定与性质、等腰直角三角形的判定与性质、勾股定理、线段垂直平分线的判定、三角形中位线定理等知识点，熟练掌握各判定与性质是解题关键．10．如图，ABC ∆中，90ACB ∠=，D 为AC 边上的中点，E 为AB 边上一点，4AB BE =，连接CE DE 、，延长DE 交CB 延长线于F ，若3BF =，10AB =，则CE =________．【答案】972【分析】取AB 的中点G ，连接DG ，则AB ＝2BG ，可得BE ＝EG ，再利用三角形中位线定理得BC ＝2DG ，DG BF ∥，利用ASA 证明△GDE ≌△BFE ，得DG ＝BF ＝3，DE ＝EF ，从而解决问题．【解答】解：取AB 的中点G ，连接DG ，则AB ＝2BG ，∵AB ＝4BE ，∴BE ＝EG ，∵D 为AC 边上的中点，G 为AB 的中点，∴DG 为△ABC 的中位线，∴BC ＝2DG ，DG BF ∥， ∴∠GDE ＝∠F ，在△GDE 和△BFE 中，GDE F DEG FEB GE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△GDE ≌△BFE （ASA ），∴DG ＝BF ＝3，DE ＝EF ，∴BC ＝6，∴CF ＝9，由勾股定理得，AC ＝8，∴CD ＝4，在Rt △CDF 中，由勾股定理得，DF ＝22224997CD CF +=+=，∵∠ACB ＝90°，EF ＝DE ，∴CE ＝12DF ＝972，故答案为：972．【点评】本题主要考查了勾股定理，三角形中位线定理，全等三角形的判定与性质，直角三角形斜边上中线的性质等知识，证明点E 是DF 的中点是解题的关键．11．如图，在Rt ABC 中，90,8,6ACB AC BC ∠=︒==，点P 是平面内一个动点，且4AP =，Q 为BP 的中点，在P 点运动过程中，设线段CQ 的长度为m ，则m 的取值范围是_______．【答案】3m 7≤≤【分析】取AB 的中点M ，连接QM 、CM ，得到QM 是△APB 的中位线，CM 是Rt ABC 斜边上的中线，求得QM 、CM 的长，在△QMC 中利用三角形三边关系得到CQ 的范围即可．【解答】取AB 的中点M ，连接QM 、CM ，∴QM 是△APB 的中位线，CM 是Rt ABC 斜边上的中线，∴122QM AP ==，12CM AB =，在Rt ABC 中，90,8,6ACB AC BC ∠=︒==，∴226810AB =+=，∴CM =5，∵点P 是平面内一个动点，∴点Q 是动点，且点Q 以点M 为圆心，QM 长为半径的圆上运动，∴C 、Q 、M 可以三点共线，∴CM -MQ ≤CQ ≤CM +MQ ，∴3m 7≤≤，故答案为：3m 7≤≤．【点评】本题考查勾股定理、直角三角形斜边中线的性质，中位线定理、三角形三边关系等知识，分析点Q 的运动是解题的关键．12．如图，在四边形ABCD 中，∠ABC =90°，AC=AD ，M ，N 分别是AC ，CD 的中点，连接BM ，MN ，BN ．(1)求证：BM=MN ；(2)若∠BAD =60°，AC 平分∠BAD ，AC =2．①求∠BMN 的度数；②求BN 的长．题的关键是灵活应用三角形的中位线平行于第三边，并且等于第三边的一半．13．如图，D、E、F分别是△ABC三边中点，AH⊥BC于H．求证：（1）∠BDF＝∠BAC；（2）DF＝EH．【答案】（1）见解析；（2）见解析．【分析】（1）根据三角形中位线定理得到DF//AC，根据平行线的性质证明结论；AC，等量代换证明结论．（2）根据直角三角形的性质得到EH＝12【解答】（1）∵D、F分别是△ABC两边中点，∴DF是△ABC的中位线，AC，∴DF//AC，DF＝12∴∠BDF＝∠BAC；（2）∵AH⊥BC于H，E是AC的中点，AC，∴EH＝12由（1）得，DF＝12 AC，∴DF＝EH．【点评】本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．14．在平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AB，点E、F分别是OA、BC的中点，连接BE、EF．BC；(1)求证：EF=12(2)在上述条件下，若AC=BD，G是BD上一点，且BG:GD=3:1，连接EG、FG，试判断四边形EBFG的形状，并证明你的结论．∴EBFG是平行四边形，连接CG，∵G是OD的中点，而CO=12AC=12BD=AB=CD，∴CG⊥OD，而F是BC的中点，∴GF=12BC=BF，∴平行四边形EBFG是菱形．【点评】本题考查了平行四边形的性质和判定，矩形性质，菱形性质，三角形的中位线，直角三角形斜边上中线性质，等腰三角形的性质等知识点，主要考查学生综合运用定理进行推理的能力，注意：直角三角形斜边上中线等于斜边的一半．15．如图，在平面直角坐标系中，A（0，4），B（4，0），C（6，2），连接AB，BC，平移BC至AD（点B 与点A对应，点C与点D对应），连接CD．(1)①直接写出点D的坐标为．②判断四边形ABCD的形状，并证明你的结论；(2)如图1，点E为AB边上一点，连接DE，DF平分∠EDC交BC于F，连接EF，若∠DFE＝45°，求BE 的长；(3)如图2，N为BC边的中点，若∠AMC＝90°，连接MN，请直接写出MN的取值范围．段CD上取一点G，使DG=DE，∵∠FDE=∠FDG，DF=DF，∴△DFE≌△DFG（SAS），∴∠DFE=∠DFG=45°，EF=GF，∴∠EFG=90°，∵∠EFB+∠GFC=90°，∠GFC+∠FGC=90°，∴∠EFB=∠FGC，∵∠EBF=∠FCG=90°，EF=GF，∴△EBF≌△FCG（AAS），∴EB=FC，BF=CG，设EB=FC=x，则22BF CG BC x x==-=-，∴222222(42)(22)DE AE AD x DG=+=-+=，∵222()(4222)DG CD GC x=-=-+，∴222 (4222)(42)(22)x x-+=-+，解得：423x，即423BE=；（3）解：如图，连接AC，取AC的中点H，连接MH，NH，∵点A（0，4），B（4，0），D（2，6），∴42,210AB AC==，∵H为AC的中点，N为BC边的中点，∴1122,1022NH AB HM AC====，∵HM-NH≤MN≤HM+NH，∴MN的取值范围为10222210MN-≤≤+．【点评】本题是四边形综合题，主要考查了平行四边形和矩形的性质、三角形全等、勾股定理的运用，直角三角形的性质，三角形中位线定理等，综合性强，难度较大，熟练掌握相关知识点是解题的关键．16．已知，在△ABC中，以△ABC的两边BC，AC为斜边向外测作Rt△BCD和Rt△ACE，使∠CAE=∠CBD，取△ABC 边AB 的中点M ，连接ME ，MD ．特例感知：（1）如图1，若AC =BC ，∠ACB =60°，∠CAE =∠CBD =45°，取AC ，BC 的中点F ，G ，连接MF ，MG ，EF ，DG ，则ME 与MD 的数量关系为______，∠EMD =______；（2）如图2，若∠ACB =90°，∠CAE =∠CBD =60°，取AC ，BC 的中点F ，G ，连接MF ，MG ，EF ，DG ，请猜想ME 与MD 的数量关系以及∠EMD 的度数，并给出证明；类比探究：（3）如图3，当△ABC 是任意三角形，∠CAE =∠CBD =α时，连接DE ，请猜想△DEM 的形状以及∠EMD 与α的数量关系，并说明理由．【答案】（1）ME=MD ，∠EMD=90°；（2）ME=MD ，∠EMD=120°；（3）△DEM 是等腰三角形，∠EMD=2α．【分析】（1）如图1，证明△EAM ≌△DBM ，可得EM=DM ，先根据三角形的中位线得：11FM AC MG BC 22===，由直角三角形斜边中线等于斜边一半可得12EF AC =，得EF=FM ，且顶角∠EFM=150°，得∠FEM=∠FME=15°，同理∠DMG=15°，相加可得结论；（2）如图2，证明△MEF ≌△DMG ，可得EM=DM ，∠EMF=∠MDG=15°，相加可得∠EMD=120°；（3）如图，作辅助线，取AC ，BC 的中点F ，G ，连接MF ，MG ，EF ，DG ，同理可证出EF=MG ，DG=FM ，∠3=2∠2，∠4=2∠1，证明△MEF ≌△DMG ．则EM=DM ，∠EMF=∠MDG ．表示∠EMD=∠MDG+∠DMG+∠ACB ，代入可得结论．【解答】解：（1）ME=MD ，∠EMD=90°；理由是：如图1，∵AC=BC ，∠ACB=60°，∴△ABC 是等边三角形，∴∠CAB=∠CBA=60°，在 Rt △BCD 和Rt △ACE 中，∠CAE=∠CBD=45°，∴AC=2AE，BC=2BD，∴AE=BD，∵M是AB的中点，∴AM=BM，∵∠EAM=45°+60°=105°，∠DBM=45°+60°=105°，∴∠EAM=∠DBM，∴△EAM≌△DBM，∴EM=DM，∵F、G分别是AC、BC的中点，∴FM=MG=12AC=CF=CG，∴四边形CFMG是菱形，∴∠FMG=∠BCA=60°，Rt△ACE中，∵F是斜边AC的中点，∴EF=12AC=FM，∵∠EFM=90°+60°=150°，∴∠FEM=∠FME=15°，同理∠DMG=15°，∴∠EMD=60°+15°+15°=90°，故答案为EM=DM，90°；（2）ME=MD，∠EMD=120°；证明：∵F，G，M是△ABC的三边AC，BC，AB的中点，∴FM=12BC=CG，FM∥BC，MG=12AC=CF，MG∥AC．∴四边形CFMG是平行四边形，∴∠AFM=∠FMG=∠ACB=∠MGD=90°．∵∠AEC=∠BDC=90°，F，G是AC，BC的中点，∴EF=AF=FC=12AC，CG=BG=DG=12BC．∴∠2=∠CEF，∠1=∠CDG，EF=MG，DG=FM．∴∠3=∠2+∠CEF=2∠2，∠4=∠1+∠CDG=2∠1.∵∠2+∠EAC=90°，∠1+∠CBD=90°，∠CAE=∠CBD=60°，∴∠1=∠2=30°．∴∠3=∠4=60°．∴∠EFM=∠3+∠AFM=150°，∠DGM=∠4+∠CGM=150°∴∠EFM=∠DGM．又∵EF=MG，FM=DG，∴△MEF≌△DMG．∴EM=DM，∠EMF=∠MDG=15°．∴∠EMD=90°+2×15°=90°30°=120°；（3）△DEM是等腰三角形，∠EMD=2α．证明：取AC，BC的中点F，G，连接MF，MG，EF，DG，同（2）证法相同，可证出EF=MG，DG=FM，∠3=2∠2，∠4=2∠1．∵∠2+∠EAC=90°，∠1+∠CBD=90°，∠CAE=∠CBD=α，∴∠1=∠2=90°-α．∴∠3=∠4=2（90°-α）．∴∠EFM=∠3+∠AFM=∠3+∠ACB，∠DGM=∠4+∠BGM=∠4+∠ACB．∴∠EFM=∠DGM．又∵EF=MG，FM=DG，∴△MEF≌△DMG．∴EM=DM，∠EMF=∠MDG．∴△DEM是等腰三角形；∵∠EMD=∠FME+∠FMG+∠DMG，由（2）知∠FMG=∠ACB，∴∠EMD=∠MDG+∠DMG+∠ACB．∵∠MDG+∠DMG=180°-∠DGM=180°-（∠4+∠ACB ）=180°-2（90°-α）-∠ACB=2α-∠ACB．∴∠EMD=2α-∠ACB+∠ACB=2α．【点评】本题是三角形的综合题，考查了三角形全等的性质和判定、三角形中位线定理、直角三角形斜边中线的性质、平行四边形的性质、等边三角形的性质等知识，并运用了类比的思想依次解决问题．∆中，D为BC中点，BE、CF与射线AE分别相交于点E、F（射线AE不经过点D）．17．在ABC(1)如图①，当BE∥CF时，连接ED并延长交CF于点H. 求证：四边形BECH是平行四形；(2)如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND．求证：AM=AN(3)如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND．求证：∠EMD=∠FND．【答案】(1)证明见解析(2)证明见解析(3)证明见解析【分析】（1）根据两直线平行内错角相等求得∠DBE=∠DCH，然后依据ASA求得BDE≅CDH得出ED=HD，最后根据有一组对边平行且相等的四边形是平行四边形求得．（2）连接FD、ED，延长ED交CF于点H，根据直角三角形斜边的中线定理和三角形的中位线定理求得ME=DN，MD=NF，从而证得AM=AN；（3）在（2）的条件下根据SSS 即可证明MED ≅NDF ，最后根据全等三角形的对应角相等求得∠EMD =∠FND ．（1）如图①，∵D 为BC 的中点，∴BD =CD ，∵BE ∥CF ，∴∠DBE =∠DCH ，在BDE 与CDH 中，DBE DCH BD CD BDE CDH ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴BDE ≅CDH (AAS )，∴ED =HD ，∴四边形BECH 是平行四边形；（2）如图②连接FD 、ED ，延长ED 交CF 于点H ，∵BE ⊥AE ，CF ⊥AE ，）可知BDE≅CDHRt EHFRt AEBRt ACF在MED与NDF∴MED≅NDF。

人教版八年级数学下册三角形的中位线练习题(含答案)

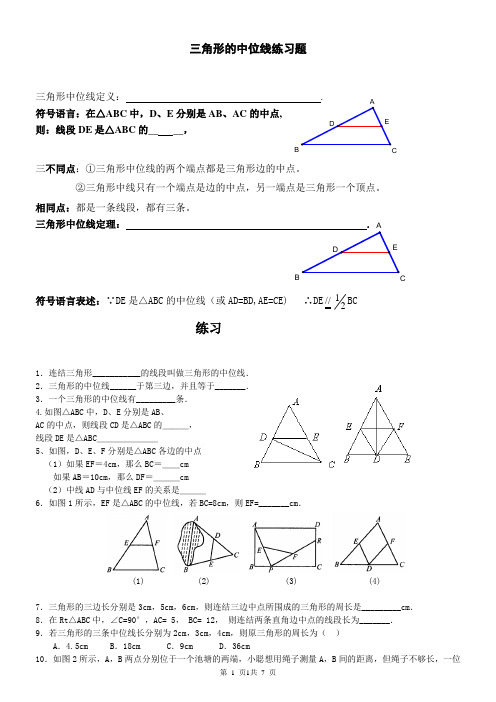
三角形的中位线练习题三角形中位线定义： . 符号语言：在△ABC 中，D 、E 分别是AB 、AC 的中点, 则：线段DE 是△ABC 的__ __，三不同点：①三角形中位线的两个端点都是三角形边的中点。

②三角形中线只有一个端点是边的中点，另一端点是三角形一个顶点。

相同点：都是一条线段，都有三条。

三角形中位线定理： .符号语言表述：∵DE 是△ABC 的中位线（或AD=BD,AE=CE) ∴DE //21BC练习1．连结三角形___________的线段叫做三角形的中位线． 2．三角形的中位线______于第三边，并且等于_______． 3．一个三角形的中位线有_________条． 4.如图△ABC 中，D 、E 分别是AB 、AC 的中点，则线段CD 是△ABC 的＿＿＿，线段DE 是△ABC ＿＿＿＿＿＿＿5、如图，D 、E 、F 分别是△ABC 各边的中点（1）如果EF ＝4cm ，那么BC ＝＿＿cm 如果AB ＝10cm ，那么DF ＝＿＿＿cm （2）中线AD 与中位线EF 的关系是＿＿＿6．如图1所示，EF 是△ABC 的中位线，若BC=8cm ，则EF=_______cm ．(1) (2) (3) (4)7．三角形的三边长分别是3cm ，5cm ，6cm ，则连结三边中点所围成的三角形的周长是_________cm ． 8．在Rt △ABC 中，∠C=90°，AC=•5，•BC=•12，•则连结两条直角边中点的线段长为_______． 9．若三角形的三条中位线长分别为2cm ，3cm ，4cm ，则原三角形的周长为（） A ．4.5cm B ．18cm C ．9cm D ．36cm10．如图2所示，A ，B 两点分别位于一个池塘的两端，小聪想用绳子测量A ，B 间的距离，但绳子不够长，一位E DBEDA同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点D ，E ，并且测出DE 的长为10m ，则A ，B 间的距离为（）A ．15mB ．25mC ．30mD ．20m11．已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形，•再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（） A 、20081 B 、20091 C 、220081 D 、22009112．如图3所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点，E ，F 分别是AP ，RP 的中点，当点P 在BC 上从点B 向点C 移动而点R 不动时，那么下列结论成立的是（） A ．线段EF 的长逐渐增大 B ．线段EF 的长逐渐减少 C ．线段EF 的长不变 D ．线段EF 的长不能确定13．如图4,在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6，AC=4，则四边形AEDF•的周长是（） A ．10 B ．20 C ．30 D ．4014．如图所示，□ ABCD 的对角线AC ，BD 相交于点O ，AE=EB ，求证：OE ∥BC ．15.已知矩形ABCD 中，AB =4cm ，AD =10cm ，点P 在边BC 上移动，点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点.求证：EF +GH =5cm ；16．如图所示，在△ABC 中，点D 在BC 上且CD=CA ，CF 平分∠ACB ，AE=EB ，求证：EF=12BD ．17．如图所示，已知在□ABCD 中，E ，F 分别是AD ，BC 的中点，求证：MN ∥BC ．BG A E FH D C 图518．已知：如图，四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．19.如图，点E ，F ，G ，H 分别是CD ，BC ，AB ，DA 的中点。

三角形的中位线练习题(8年级)

三角形的中位线练习题（8年级）1、如图。

D 、E 、F 分别是△ABC 各边的中点，(1)如果EF=4cm ，那么BC= ------，如果AB=10.那么DF=----； (2)中线AD 与中位线EF 的关系是-------1.BC=8cm DF=5cm2.AD 与EF 互相平分6\（2010•河源）如图，在△ABC 中，BC=6cm ，E 、F 分别是AB 、AC 的中点，则EF= 4cm ．考点：三角形中位线定理．分析：根据三角形的中位线等于第三边的一半进行计算．解答：解：∵E 、F 分别是AB 、AC 的中点，∴EF 是△ABC 的中位线，∴EF=21BC=21×8=4cm ．点评：此题考查了三角形的中位线定理的数量关系，熟练掌握定理是解题的关键．2、、三角形各边分别是3cm 、5cm 、6cm ，则连接各边中点所围成的三角形的周长是 7cm ．考点：三角形中位线定理．分析：根据三角形的中位线等于第三边的一半，分别求得连接各边中点所围成的三角形的三边，从而求得周长．解答：解：根据三角形的中位线定理，得连接各边中点所围成的三角形的三边分别是1.5cm ，2.5cm ，3cm ，则其周长是7cm ．故答案为7．点评：此题考查了三角形的中位线定理，即三角形的中位线平行于第三边，且等于第三边的一半．3、若三角形的三条中位线长分别为2cm ，3cm ，4cm ，则原三角形的周长为（）A ．4.5cmB ．18cmC ．9cmD ．36cm 考点：三角形中位线定理．分析：根据三角形中位线定理可以求得三条边的长度，然后由三角形的周长公式可知原三角形的周长．解答：解：∵三角形的三条中位线长分别为2cm ，3cm ，4cm ，∴原三角形的三条边长分别为2cm×2=4cm ，3cm×2=6cm ，4cm×2=8cm ，∴原三角形的周长为：4cm+6cm+8cm=18cm ；故选C ．点评：本题考查了三角形中位线定理，即三角形的中位线平行于第三边且等于第三边的一半．4、如图，A ，B 两点分别位于一个池塘的两端，小聪想用绳子测量A ，B 间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点M ，N ，并且测出MN 的长为10m ，则A ，B 间的距离为 20m 考点：三角形中位线定理．分析：M 、N 是AC 和BC 的中点，则MN 是△ABC 的中位线，则依据三角形的中位线定理即可求解．解答：解：∵M 、N 是AC 和BC 的中点，∴AB=2MN=2×10=20m ．故答案是：20m ．点评：本题考查了三角形的中位线定理，正确理解定理是关键．5、已知△ABC 周长为1，连接△ABC 三边中点构成第二个三角形，再连接第二个三角形三边中点构成第三个三角形，以此类推，第2010个三角形的周长为 220091．考点：三角形中位线定理．专题：规律型．分析：根据已知条件，首先可知各三角形都相似，然后根据题意可得规律：第n 个三角形与原三角形的相似比为1：2n-1，又由△ABC 周长为1，即可求得第2010个三角形的周长．解答：解：∵连接△ABC 三边中点构成第二个三角形，∴新三角形的三边与原三角形的三边的比值为1：2，∴它们相似，且相似比为1：2，同理：第三个三角形与第二个三角形的相似比为1：2，即第三个三角形与第一个三角形的相似比为：1：22，以此类推：第2010个三角形与原三角形的相似比为1：22009，∵△ABC 周长为1，∴第2010个三角形的周长为220091．．点评：此题考查了相似三角形的性质与三角形中位线的性质．此题难度较大，解题的关键是找到规律：第n 个三角形与原三角形的相似比为1：2n-1．6、（2003•桂林）如图，已知矩形ABCD 中，R 、P 分别是DC 、BC 上的点，E 、F 分别是AP 、RP 的中点，当P 在BC 上从B 向C 移动而R 不动时，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减小C ．线段EF 的长不改变D ．线段EF 的长不能确定考点：三角形中位线定理．分析：因为R 不动，所以AR 不变．根据中位线定理，EF 不变．解答：解：连接AR ．因为E 、F 分别是AP 、RP 的中点，则EF 为△APR 的中位线，所以EF=21AR ，为定值．所以线段EF 的长不改变．故选C ．点评：本题考查了三角形的中位线定理，只要三角形的边AR 不变，则对应的中位线的长度就不变．7、平行四边形ABCD 的对角线AC,BD 相交于点O,AE=EB,求证:OE//BC∵AE＝BE∴E是AB的中点∵四边形ABCD是平行四边形∴AO＝OC∴EO是△ABC的中位线∴OE‖BC8、如图,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF=1/2BD因为CD=CA,CF平分∠ACB,CF为公共边，所以三角形ACF与三角形DCF全等所以F为AD边的中点又因为AE=BE所以E为AB的中点所以EF为三角形ABD的中位线所以EF=1/2BD9、如图，已知在平行四边形ABCD中E、F分别是ad.bc的中点，求证MN∥BC在△MBF和△MEA中：∵AD∥BC∴∠MBF = ∠MEA , ∠MFB = ∠MAE又E、F分别是AD、BC的中点∴BF = EA∴△MBF≌△MEA∴BM = ME同理：CN = NE∴MN是△EBC的中位线∴MN∥BC10、在空间四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．求证：四边形EFGH 是平行四边形．考点：平面的基本性质及推论；空间中直线与直线之间的位置关系．专题：证明题．分析：只需证明FG ∥EH ，且FG=EH 即可．依据是平行公理四：和同一条直线平行的直线平行．解答：证明：如图，连接BD ．因为FG 是△CBD 的中位线，所以FG ∥BD ，FG=21BD ．又因为EH 是△ABD 的中位线，所以EH ∥BD ，EH=21BD ．根据公理4，FG ∥EH ，且FG=EH ．所以四边形EFGH 是平行四边形．点评：主要考查知识点：简单几何体和公理四，证明平行四边形常用方法：对边平行且相等；或对边分别平行；或对角线相交且平分．要注意：对边相等的四边形不一定是平行四边形．11、已知：△ABC 的中线BD 、CE 交于点O ，F 、G 分别是OB 、OC 的中点．求证：四边形DEFG 是平行四边形．考点：平行四边形的判定；三角形中位线定理．专题：证明题．分析：利用三角形中线的性质、中位线的定义和性质证得四边形EFGD 的对边DE ∥GF ，且DE=GF=21BC ；然后由平行四边形的判定--对边平行且相等的四边形是平行四边形，证得结论．解答：证明：∵BD 、CE 是△ABC 的两条中线，∴点D 、E 分别是边AC 、AB 的中点，∴DE ∥CB ，DE=21CB ；又∵F 、G 分别是OB 、OC 的中点， ∴GF ∥CB ，GF=21CB ； ∴DE ∥GF ，且DE=GF ，∴四边形DEFG 是平行四边形（对边平行且相等的四边形是平行四边形）．点评：本题考查了三角形中位线定理、平行四边形的判定．平行四边形的判定：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；一组对边平行，一组对角相等的四边形是平行四边形．12、（2004•哈尔滨）如图，已知E 为平行四边形ABCD 中DC 边的延长线的一点，且CE=DC ，连接AE ，分别交BC 、BD 于点F 、G ，连接AC 交BD 于O ，连接OF ．求证：AB=2OF ．考点：平行四边形的性质；全等三角形的判定与性质．专题：证明题．分析：此题的根据平行四边形的性质可以证明△ABF ≌△ECF ，然后利用全等三角形的性质可以解决问题．解答：证明：∵四边形ABCD 是平行四边形，∴AB=CD ，OA=OC ．∴∠BAF=∠CEF ，∠ABF=∠ECF ．∵CE=DC ，在平行四边形ABCD 中，CD=AB ，∴AB=CE ．∴在△ABF 和△ECF 中，∠BAF=∠CEFAB=CE∠ABF=∠ECF∴△ABF ≌△ECF ，∴BF=CF ．∵OA=OC ，∴OF 是△ABC 的中位线，∴AB=2OF ．点评：此题主要考查了平行四边形的性质，全等三角形的性质与判定．此题还可以利用三角形的中位线解题．。

八年级数学三角形中位线培优专题训练

八年级数学三角形中位线培优专题训练一、内容提要1. 三角形中位线平行于第三边，并且等于第三边的一半。

梯形中位线平行于两底，并且等于两底和的一半。

2. 中位线性质定理的结论，兼有位置和大小关系，可以用它判定平行，计算线段的长度，确定线段的和、差、倍关系。

3. 运用中位线性质的关键是从出现的线段中点，找到三角形或梯形，包括作出辅助线。

4. 中位线性质定理，常与它的逆定理结合起来用。

它的逆定理就是平行线截比例线段定理及推论，①一组平行线在一直线上截得相等线段，在其他直线上截得的线段也相等 ②经过三角形一边中点而平行于另一边的直线，必平分第三边 ③经过梯形一腰中点而平行于两底的直线，必平分另一腰 5. 有关线段中点的其他定理还有： ①直角三角形斜边中线等于斜边的一半②等腰三角形底边中线和底上的高，顶角平分线互相重合 ③对角线互相平分的四边形是平行四边形 ④线段中垂线上的点到线段两端的距离相等因此如何发挥中点作用必须全面考虑。

二、例题例1. 已知：△ABC 中，分别以AB 、AC 为斜边作等腰直角三角形ABM 和CAN ，P 是BC 的中点。

求证：PM ＝PN证明：作ME ⊥AB ，NF ⊥AC ，垂足E ，F ∵△ABM 、△CAN 是等腰直角三角形∴AE ＝EB＝ME ，AF ＝FC ＝NF ，根据三角形中位线性质 PE ＝21AC ＝NF ，PF ＝21AB ＝MEPE ∥AC ，PF ∥AB∴∠PEB ＝∠BAC ＝∠PFC 即∠PEM ＝∠PFN∴△PEM ≌△PFN ∴PM ＝PN例2.已知△ABC 中，AB ＝10，AC ＝7，AD 是角平分线，CM ⊥AD 于M ，且N 是BC 的中点。

求MN 的长。

分析：N 是BC 的中点，若M 是另一边中点，则可运用中位线的性质求MN 的长，根据轴称性质作出△AMC 的全等三角形即可。

辅助线是：延长CM 交AB 于E （证明略例3.如图已知：△ABC 中，AD 是角平分线，BE ＝CF ，M 、N 分别是BC 和EF 的中点求证：MN ∥AD 证明一：连结EC ，取EC 的中点P ，连结PM 、PNP NMP ∥AB ，MP ＝21AB ，NP ∥AC ，NP ＝21AC ∵BE ＝CF ，∴MP ＝NP∴∠3=∠4=2MPN-180∠∠MPN ＋∠BAC ＝180（两边分平行的两个角相等或互补）∴∠1=∠2=2MPN-180∠ ， ∠2=∠3∴NP ∥AC ∴MN ∥AD证明二：连结并延长EM 到G ，使MG ＝ME 连结CG ，FG则MN ∥FG ，△MCG ≌△MBE ∴CG ＝BE ＝CF ∠B ＝∠BCG∴AB ∥CG ，∠BAC ＋∠FCG ＝180∠CAD ＝21（180－∠FCG ） ∠CFG ＝21（180－∠FCG ）=∠CAD ∴ MN ∥AD 例4. 已知：△ABC 中，AB ＝AC ，AD 是高，CE 是角平分线，EF ⊥BC 于F ，GE ⊥CE交CB 的延长线于G 求证：FD ＝41CG 证明要点是：延长GE 交AC 于H ，可证E 是GH 的中点过点E 作EM ∥GC 交HC 于M ，则M 是HC 的中点，EM ∥GC ，EM ＝21GC由矩形EFDO 可得FD ＝EO ＝21EM ＝41GC三、练习1. 如图11，M 、P 分别为△ABC 的AB 、AC 上的点，且AM=BM ，AP=2CP ，BP 与CM 相交于N ，已知PN=1，则PB 的长为 ( ) A. 2 B. 3 C .4 D. 52. 如图12，△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点，AB=10，则MD 的长为 ( )A. 10B. 8 C .6 D. 53. 如图13，△ABC 是等边三角形，D 、E 、F 分别是AB 、BC 、AC 的中点，P 为不同于B 、E 、C 的BC 上的任意一点，△DPH 为等边三角形.连接FH ，则EP 与FH 的大小关系是 ( ) A. E P>FH B. EP=FH C. EP<FH D.不确定4. 如图14，在△ABC 中，AD 平分∠BAC ，BD ⊥AD ，DE ∥AC ，交AB 于E ,若AB=5，则DE 的长为 .C5. 如图15，△ABC中，AB=4，AC=7，M为BC的中点，AD平分∠BAC，过M作MF∥AD，交AC于F，则FC的长等于.6. 如图25，P为△ABC内一点，∠P AC=∠PBC，PM⊥AC于M，PN⊥BC于N.D是AB的中点.求证：DM=DN7. 如图16，在△ABC中，D、E是AB、AC上的点，且BD=CE，M、N分别是BE、CD的中点，直线MN分别交AB、AC于P、Q.求证：AP=AQ8. 如图17，BE、CF是△ABC的角平分线，AN⊥BE于N，AM⊥CF于M.求证：MN∥BC.9. 如图18，在△ABC中，AD平分∠BAC，AD=AB，CM⊥AD于M.求证：AB+AC=2AM10.如图19，四边形ABCD中，G、H分别是AD、BC的中点，AB=CD.BA、CD的延长线交HG的延长线于E、F.求证：∠BEH=∠CFH.1. 如图20，在△ABC中，∠ABC=2∠C，AD平分∠BAC，过BC的中点M作ME⊥AD，交BA的延长线于E，交AD的延长线于F.求证：12BE BD.2. 如图21，在△ABC中，AB<AC，P为AC上的点，CP=AB，K为AP的中点，M为BC的中点，MK的延长线交BA的长线于N.求证：AN=AK.3. 如图22，分别以△ABC的边AC、BC为腰，A、B为直角顶点，作等腰直角△ACE和等腰直角△BCD，M为ED的中点.求证：AM⊥BM.4. 如图23，点O是四边形ABCD内一点，∠AOB=∠COD=1200，AO=BO，CO=DO，E、F、G分别为AB、CD、BC的中点.求证：△EFG为等边三角形.5. 如图24，△ABC中，M是AB的中点，P是AC的中点，D是MB的中点，N是CD的中点，Q是MN的中点，直线PQ交MB于K.求证：K是DB的中点.6. 如图25，P为△ABC内一点，∠P AC=∠PBC，PM⊥AC于M，PN⊥BC于N.D是AB的中点.求证：DM=DN图21 图22 图23 图24 图257. 如图26，AP是△ABC的角平分线，D、E分别是AB、AC上的点，且BD=CE.又G、H分别为BC、DE的中点.求证：HG∥AP.8. 如图27，已知△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=900，如图(a)，连接DE，设M为DE的中点.(1)求证：MB=MC;(2)设∠BAD=∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图(b)的位置，试问MB=MC是否成立?并证明其结论.9. 已知△ABC面积为S，作直线l∥BC，交AB于D，交AC于E，若△BED的积为K.求证：S≥4K.10.如图28，在△ABC中，AB=AC，D是BC边上的一点，E是线段AD上的一点．且∠BED=2∠CED=∠BAC.求证：BD=2CD.图26 图27。

2020-2021学年北师大版八年级数学下册《6.3三角形的中位线》同步优生辅导训练(附答案)

2021年北师大版八年级数学下册《6.3三角形的中位线》同步优生辅导训练（附答案）1．已知三角形的3条中位线分别为3cm、4cm、6cm，则这个三角形的周长是（）A．3cm B．26cm C．24cm D．65cm2．如图所示，▱ABCD中，对角线AC，BD交于点O，E是CD中点，连接OE，若OE＝3cm，则AD的长为（）A．3cm B．6cm C．9cm D．12cm3．如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若AB ＝10，BC＝8，则EF的长是（）A．B．1C．D．1.54．已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD＝BE＝4，则AC 的长等于（）A．7B．C．D．6.55．如图，平地上A、B两点被池塘隔开，测量员在岸边选一点C，并分别找到AC和BC的中点M、N，测量得MN＝16米，则A、B两点间的距离为（）A．30米B．32米C．36米D．48米6．如图，在△ABC中，点D、E分别是AB、AC的中点，∠C＝105°，将△ABC沿DE折叠，点A的对应点是点A′，则∠AEA′的度数为（）A．145°B．150°C．155°D．160°7．如图，四边形ABCD中，点E、F、G分别为边AB、BC、CD的中点，若△EFG的面积为4，则四边形ABCD的面积为（）A．8B．12C．16D．188．如图，在△ABC中，点D在BC上，BD＝AB，BM⊥AD于点M，N是AC的中点．连接MN，若AB＝5，BC＝8，则MN的长为（）A．6B．3C．1.5D．19．直角三角形两条边长分别是6和8，则连接两条直角边中点的线段长是（）A．3B．5C．4或5D．5或310．如图，在△ABC中，E、D、F分别是AB、BC、CA的中点，AB＝6，AC＝4，则四边形AEDF的周长是（）A．10B．20C．30D．4011．如图，Rt△ABC中，D、E分别是边AB，AC的中点，DE＝3，AB＝10，则AC＝．12．如图，D、E分别是△ABC的边AB、AC的中点，且BE平分∠ABC，DE＝2cm，AE＝1.5cm，则△ABC的周长是．13．如图，△ABC中，AE平分∠BAC，CD⊥AE于D，BE⊥AE，F为BC中点，连接DF、EF，若AB＝10，AC＝6，∠DFE＝135°，则△DEF的面积是．14．如图，在▱ABCD中AC、BD相交于点O，点E是AB的中点，OE＝6cm，则BC的长是cm．15．如图，在四边形ABCD中，对角线AC、BD相交于点O，且AC＝BD，E、F分别是AB、CD的中点，EF分别交BD、AC于点G、H，若∠OBC＝55°，∠OCB＝45°，则∠OGH ＝°．16．如图，△ABC边长分别为AB＝14，BC＝16，AC＝26，P为∠A的平分线AD上一点，且BP⊥AD，M为BC的中点，则PM的值是．17．如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝6，BC＝8，则EF的长为．18．如图，已知△ABC的周长为1，连接△ABC三边的中点构成第二个三角形，再连接第二个三角形三边的中点构成第三个三角形，…依此类推，则第n个三角形的周长为．19．如图所示，四边形ABCD中，AB＝CD，E、F、P分别是BD、AC、BC边的中点，若∠EPF＝50°，则∠PEF＝．20．如图，BD平分∠ABC，DE∥BC，过E作BD的垂线交BD于O，交BC于F，P是ED 的中点．若OP＝15，BF的长为．21．如图，在△ABC中，AB＝10，∠BAC的平分线AD交BD于点D，且BD⊥AD，DE∥AC交AB于E，则DE的长是．22．如图，△ABC中，AD平分∠BAC，AD⊥BD，E为BC的中点．（1）求证：DE∥AC；（2）若AB＝4，AC＝6，求DE的长．23．已知：△ABC中，D是BC上的一点，E、F、G、H分别是BD、BC、AC、AD的中点，求证：EG、HF互相平分．24．如图，在四边形ABCD中，AC⊥BD，BD＝12，AC＝16，E，F分别为AB，CD的中点，求EF的长．25．如图，AD是△ABC的中线，E是AD的中点，F是BE延长线与AC的交点，求证：AF ＝CF．26．如图，在四边形ABCD中，AC、BD相交于点O，E、F是AD、BC的中点，EF分别交AC、BD于M、N，且OM＝ON．求证：AC＝BD．27．【教材呈现】如图是华师版九年级上册数学教材第80页的第3题，请完成这道题的证明．【结论应用】（1）如图②，在上边题目的条件下，延长图①中的线段AD交NM的延长线于点E，延长线段BC交NM的延长线于点F．求证：∠AEN＝∠F．（2）若（1）中的∠A+∠ABC＝122°，则∠F的大小为．28．如图，点D、E是Rt△ABC两直角边AB、AC上的一点，连接BE，已知点F、G、H 分别是DE、BE、BC的中点．（1）求∠FGH度数；（2）连CD，取CD中点M，连接GM，若BD＝8，CE＝6，求GM的长．参考答案1．解：∵D，E，F分别是△ABC的三边的中点，∴DE＝AC，DF＝BC，EF＝AB，∴AC+BC+AB＝2（DE+DF+EF）＝2×（3+4+6）＝26（cm）．故选：B．2．解：根据平行四边形基本性质：平行四边形的对角线互相平分．可知点O是BD中点，所以OE是△BCD的中位线．根据中位线定理可知AD＝2OE＝2×3＝6（cm）．故选：B．3．解：∵D、E分别是BC、AC的中点，∴DE∥AB，DE＝AB＝5，BD＝BC＝4，∴∠ABF＝∠BFD，∵BF平分∠ABC，∴∠ABF＝∠DBF，∴∠DBF＝∠BFD，∴DF＝DB＝4，∴EF＝DE﹣DF＝1，故选：B．4．解：过D点作DF∥BE，∵AD是△ABC的中线，AD⊥BE，∴F为EC中点，AD⊥DF，∵AD＝BE＝4，则DF＝2，AF＝＝2，∵BE是△ABC的角平分线，AD⊥BE，∴△ABG≌△DBG，∴G为AD中点，∴E为AF中点，∴AC＝AF＝3．故选：C．5．解：∵点M、N是分别是AC和BC的中点，∴MN是△ABC的中位线，MN＝16米，∴MN＝AB＝16米，∴AB＝32米．故选：B．6．解：∵点D、E分别是AB、AC的中点，∴DE∥BC，∴∠AED＝∠C＝105°，由折叠的性质可知，∠DEA′＝∠AED＝105°，∴∠AEA′＝360°﹣105°﹣105°＝150°，故选：B．7．解：记△BEF，△DGH，△CFG，△AEH的面积分别为S1，S2，S3，S4，四边形ABCD 的面积为S．连接AC．∵BF＝CF，BE＝AE，CG＝DG，AH＝DH，∴EF∥AC，EF＝AC，GH∥AC，GH＝AC，∴EF∥GH，EF＝GH，∴四边形EFGH是平行四边形，∴S平行四边形EFGH＝2S△EFG＝8，∵△BEF∽△BAC，∴S1＝S△ABC，同理可得S2＝S△ACD，∴S1+S2＝（S△ABC+S△ACD）＝S，同法可得S3+S4＝S，∴S1+S2+S3+S4＝S，∴S四边形EFGH＝S，∴S＝2S四边形EFGH＝16．故选：C．8．解：∵BD＝AB，BM⊥AD于点M，∴AM＝DM，∵N是AC的中点，∴AN＝CN，∴MN是三角形ADC的中位线，∴MN＝DC，∵AB＝5，BC＝8，∴DC＝3，∴MN＝1.5，故选：C．9．解：分两种情况：①8是直角边，如图：点E、F分别是直角边AC、BC的中点，∴EF是Rt△ABC的中位线，∴EF＝AB；在Rt△ABC中，根据勾股定理知，AB＝＝10，∴EF＝5；②8是斜边，如图：点D、E分别是直角边BC、AC的中点，∴EF是Rt△ABC的中位线，∴EF＝AB＝4．综上可知连接两条直角边中点的线段长是5或4．故选：C．10．解：∵在△ABC中，E、D、F分别是AB、BC、CA的中点，∴DE＝AF＝AC＝2，DF＝AE＝AB＝3，∴四边形AEDF的周长是（2+3）×2＝10．故选：A．11．解：∵D、E分别是边AB，AC的中点，DE＝3，∴DE是△ABC的中位线，∴BC＝2DE＝6．∵AB＝10，∴AC＝＝＝8．故答案为：8．12．解：∵D、E分别是△ABC的边AB、AC的中点，∴DE∥BC，DE＝BC，AB＝2AD，AC＝2AE．∴∠DEB＝∠EBC，∵BE平分∠ABC，∴∠ABE＝∠EBC，∴∠ABE＝∠DEB，∴BD＝DE，∴AB＝2DE＝4cm，又AC＝2AE＝3cm，BC＝2DE＝4cm，∴△ABC的周长＝AB+BC+AC＝11cm．故答案为11cm．13．解：延长CD交AB于M，延长AC、BE交于点N，作EH⊥DF交DF的延长线于H．∵AD⊥CM，∴∠ADC＝∠ADM＝90°，∵∠DAM＝∠DAC，∠DAM+∠AMC＝90°，∠DAC+∠ACM＝90°，∴∠AMC＝∠ACM，∴AM＝AC＝6，同理可以证明：AB＝AN＝10，∴BM＝CN＝4，∵AD⊥CM，AM＝AC，∴DM＝DC，同理BE＝EN，∵BF＝CF，∴FD＝BM＝2，EF＝CN＝2，∵∠DFE＝135°，∴∠EFH＝45°，EH＝EF＝，∴S△DEF＝•DF•HE＝，故答案为．14．解：∵四边形ABCD为平行四边形，∴BO＝DO，∵点E是AB的中点，∴OE为△ABC的中位线，∴BC＝2OE，∵OE＝6cm，∴BC＝12cm．故答案为：12．15．解：取BC中点M，连接ME、FM，∵E、F分别是AB、CD的中点，∴EM＝AC，MF＝DB，EM∥AC，MF∥BD，∵AC＝BD，∴EM＝MF，∴∠MEF＝∠MFE，∵EM∥AC，MF∥BD，∴∠OHG＝∠MEF，∠OGH＝∠MFE，∴∠OHG＝∠OGH，∵∠OBC＝55°，∠OCB＝45°，∴∠BOC＝180°﹣55°﹣45°＝80°，∴∠HOG＝80°，∴∠OGH＝（180°﹣80°）÷2＝50°，故答案为：50．16．解：延长BP交AC于点E，∵AD为∠BAC的平分线，∴∠BAP＝∠EAP，∵BP⊥AD于D，∴∠APB＝∠APE＝90°，在△APB和△APE中，，∴△APB≌△APE（ASA），∴AB＝AE＝14，∵AC＝26，∴EC＝26﹣14＝12，∵△APB≌△APE，∴BP＝EP，∵M是BC的中点，∴PM＝EC＝×12＝6．故答案为6．17．解：∵DE为△ABC的中位线，∠AFB＝90°，∴DE＝BC，DF＝AB，∵AB＝6，BC＝8，∴DE＝×8＝4，DF＝×6＝3，∴EF＝DE﹣DF＝4﹣3＝1．故答案为：1．18．解：△ABC周长为1，因为每条中位线均为其对应边的长度的，所以：第2个三角形对应周长为；第3个三角形对应的周长为×＝；第4个三角形对应的周长为××＝；…以此类推，第n个三角形对应的周长为；故答案为：．19．解：∵F、P分别是AC、BC边的中点，∴PF＝AB，同理可证PE＝CD，∵AB＝CD，∴PE＝PF，∴∠PEF＝（180°﹣∠EPF）＝（180°﹣50°）＝65°，故答案为：65°．20．解：∵DE∥BC，∴∠D＝∠CBD，∵BD平分∠ABC，∴∠EBD＝∠CBD，∴∠D＝∠EBD，∴EB＝ED，∵EF⊥BD，∴BO＝DO，∠DOE＝∠BOF＝90°，∴△DOE≌△BOF，∴BF＝DE，∵P是ED的中点，OP＝15，∴BE＝30，∴BF＝30．故答案为30．21．解：∵AD是∠BAC的平分线，∴∠CAD＝∠BAD，∵DE∥AC，∴∠CAD＝∠ADE，∴∠ADE＝∠BAD，∴AE＝DE，∵BD⊥AD，∴∠ADE+∠BDE＝∠BAD+∠ABD＝90°，∴∠ABD＝∠BDE，∴DE＝BE，∴DE＝AB，∵AB＝10，∴DE＝×10＝5．故答案为：5．22．（1）证明：延长BD交AC于H，在△ADB和△ADH中，，∴△ADB≌△ADH，∴BD＝HD，又E为BC的中点．∴DE∥AC；（2）解：∵△ADB≌△ADH，∴AH＝AB＝4，∴CH＝AC﹣AH＝2，∵BD＝HD，又E为BC的中点，∴DE＝CH＝1．23．证明：连接EH，GH，GF，∵E、F、G、H分别是BD、BC、AC、AD的中点，∴AB∥EH∥GF，GH∥BC，∴GH∥BF．∴四边形EHGF为平行四边形．∵GE，HF分别为其对角线，∴EG、HF互相平分．24．解：如图，取BC边的中点G，连接EG、FG．∵E，F分别为AB，CD的中点，∴EG是△ABC的中位线，FG是△BCD的中位线，∴EG AC，FG BD．又BD＝12，AC＝16，AC⊥BD，∴EG＝8，FG＝6，EG⊥FG，∴在直角△EGF中，由用勾股定理，得EF＝＝＝10，即EF的长度是10．25．证明：如图，过D作DG∥AC，则∠EAF＝∠EDG，∵AD是△ABC的中线，∴D为BC中点，∴G为BF中点，∴DG＝CF，∵E为AD中点，∴AE＝DE，在△AEF和△DEG中，，∴△AEF≌△DEG（ASA），∴DG＝AF，∴AF＝CF．26．证明：取AB和CD的中点分别为G、H，连接EG、GF、FH、EH，则EH∥AC，EH＝AC，HF∥BD，FH＝BD，∴∠3＝∠2，∠1＝∠4，∵OM＝ON，∴∠1＝∠2，∴∠4＝∠3＝∠1＝∠2，同理∠EFH＝∠GFE＝∠1＝∠2，∴∠4＝∠EFH，∴EH＝HF，∵EH＝AC，FH＝BD，∴AC＝BD．27．【教材呈现】证明：∵P是BD的中点，M是DC的中点，∴PM＝BC，同理，PN＝AD，∵AD＝BC，∴PM＝PN，∴∠PMN＝∠PNM，【结论应用】（1）证明：∵P是BD的中点，M是DC的中点，∴PM∥BC，∴∠PMN＝∠F，同理，∠PNM＝∠AEN，∵∠PMN＝∠PNM，∴∠AEN＝∠F；（2）解：∵PN∥AD，∴∠PNB＝∠A，∵∠DPN是△PNB的一个外角，∴∠DPN＝∠PNB+∠ABD＝∠A+∠ABD，∵PM∥BC，∴∠MPD＝∠DBC，∴∠MPN＝∠DPN+∠MPD＝∠A+∠ABD+∠DBC＝∠A+∠ABC＝122°，∵PM＝PN，∴∠PMN＝×（180°﹣122°）＝29°，∴∠F＝∠PMN＝29°，故答案为：29°．28．解：（1）∵F、G、H分别是DE、BE、BC的中点，∴FG∥DB，GH∥EC．∴∠DBE＝∠FGE，∠EGH＝∠AEG．∠FGH＝∠FGE+∠EGH＝∠ABE+∠BEA＝180°﹣∠A＝180°﹣90°＝90°．（2）如图所示：连接FM、HM．∵M、H分别是BC和DC的中点，∴MH∥BD，MH＝．同理：GF∥BD，GF＝．∴四边形FGHM为平行四边形．∵G、H、M分别是BE、BC、DC的中点，∴GH＝＝3，，由（1）可知：∠FGH＝90°，∴四边形FGHM为矩形．∴∠GHM＝90°．∴GM＝＝5。

初二数学三角形中位线练习题(含答案)

初二数学三角形中位线练习题一．选择题（共5小题）1．如图，为了测量池塘边A、B两地之间的距离，在线段AB的同侧取一点C，连结CA并延长至点D，连结CB并延长至点E，使得A、B分别是CD、CE的中点，若18DE m=，则线段AB的长度是()A．9m B．12m C．8m D．10m2．已知三角形的周长是16，它的三条中位线围成的三角形的周长是()A．16B．12C．8D．43．如图，在四边形ABCD中，点P是边CD上的动点，点Q是边BC上的定点，连接AP，PQ，E，F分别是AP，PQ的中点，连接EF．点P在由C到D运动过程中，线段EF的长度() A．保持不变B．逐渐变小C．先变大，再变小D．逐渐变大4．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD BC=，∠的度数是()∠=︒，则EFPEPF136A．68︒B．34︒C．22︒D．44︒5．如图，D是ABC⊥，E、F、G、H分别是边AB、BD、CD、AC的中点．若∆内一点，BD CDCD=，则四边形EFGH的周长是()BD=，6AD=，810A．24B．20C．12D．10第3题图第4题图第5题图二．填空题（共5小题）6．某直角三角形的两条边长分别是10和24，则连接两条直角边中点的线段的长是．7．如图，在Rt ABCABC∠=︒，点D、E、F分别是AB、AC，∆中，90BE=，则DF=．BC边上的中点，连结BE，DF，已知58．如图，在四边形ABCD中，220∠+∠=︒，E、F分别是AC、ADC BCDBD 的中点，P 是AB 边上的中点，则EPF ∠= ︒．9．如图，在四边形ABCD 中，//AB CD ，E ，F 分别是AC ，BD 的中点，已知12AB =，6CD =，则EF = ．10．如图，在ABC ∆中，8AB =，6AC =，AM 平分BAC ∠，CM AM ⊥于点M ，N 为BC 的中点，连结MN ，则MN 的长为．第8题图第9题图第10题图三．解答题（共3小题）11．如图所示，在ABC ∆中，点D 在BC 上且CD CA =，CF 平分ACB ∠，AE EB =，求证：12EF BD =．12．如图：D 、E 是ABC ∆边AB ，AC 的中点，O 是ABC ∆内一动点，F 、G 是OB ，OC 的中点．判断四边形DEGF 的形状，并证明．13．已知：如图，在四边形ABCD 中，对角线AC 、BD 相交于O ，且AC BD =，E 、F 分别是AB 、CD 的中点，E 、F 分别交BD 、AC 于点G 、H ．求证：OG OH =．答案与解析一．选择题（共5小题）1．如图，为了测量池塘边A 、B 两地之间的距离，在线段AB 的同侧取一点C ，连结CA 并延长至点D ，连结CB 并延长至点E ，使得A 、B 分别是CD 、CE 的中点，若18DE m =，则线段AB 的长度是( )A ．9mB ．12mC ．8mD ．10m【分析】根据三角形的中位线定理解答即可．【解答】解：A 、B 分别是CD 、CE 的中点， ∴AB 是△CDE 的中位线，192AB DE m ∴==，故选：A ．2．已知三角形的周长是16，它的三条中位线围成的三角形的周长是( ) A ．16 B ．12 C ．8 D ．4【分析】由中位线定义可得新三角形的各边长为原三角形各边长的一半，即可得出其周长等于原三角形周长的一半．【解答】解：三角形的周长是16，∴它的三条中位线围成的三角形的周长是11682⨯=．故选：C ．3．如图，在四边形ABCD 中，点P 是边CD 上的动点，点Q 是边BC 上的定点，连接AP ，PQ ，E ，F 分别是AP ，PQ 的中点，连接EF ．点P 在由C 到D 运动过程中，线段EF 的长度( )A ．保持不变B ．逐渐变小C ．先变大，再变小D ．逐渐变大【分析】连接AQ ，根据三角形中位线定理解答即可．【解答】解：如图所示，连接AQ ，点Q 是边BC 上的定点， AQ ∴的大小不变，E ，F 分别是AP ，PQ 的中点， ∴EF 是△APQ 的中位线， 12EF AQ ∴=， ∴线段EF 的长度保持不变，故选：A ．4．如图，在四边形ABCD 中，P 是对角线BD 的中点，E 、F 分别是AB 、CD 的中点，AD BC =，136EPF ∠=︒，则EFP ∠的度数是( )A ．68︒B ．34︒C ．22︒D ．44︒【分析】根据三角形中位线定理得到12PE AD =，12PF BC =，根据等腰三角形的性质、三角形内角和定理计算即可．【解答】解：P 是BD 的中点，E 是AB 的中点， ∴EP 是△BCD 的中位线， 12PE AD ∴=，同理，12PF BC =， AD BC =， PE PF ∴=，1(180)222EFP EPF ∴∠=⨯︒-∠=︒，故选：C ． 5．如图，D 是ABC ∆内一点，BD CD ⊥，E 、F 、G 、H 分别是边AB 、BD 、CD 、AC 的中点．若10AD =，8BD =，6CD =，则四边形EFGH 的周长是( )A ．24B ．20C ．12D ．10【分析】利用勾股定理列式求出BC 的长，再根据三角形的中位线平行于第三边并且等于第三边的一半求出12EH FG BC ==，12EF GH AD ==，然后代入数据进行计算即可得解．【解答】解：BD CD ⊥，8BD =，6CD =，22228610BC BD CD ∴=+=+，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，12EH FG BC ∴==，12EF GH AD ==，∴四边形EFGH 的周长EH GH FG EF AD BC =+++=+，又10AD =，∴四边形EFGH 的周长101020=+=，故选：B ．二．填空题（共5小题）6．某直角三角形的两条边长分别是10和24，则连接两条直角边中点的线段的长是 13或12 ．【分析】根据勾股定理求出AB ，根据三角形中位线定理计算，得到答案．【解答】解：分两种情况讨论：①当24是直角边时，由勾股定理得，斜边2222241026AB AC BC =+=+=，M 、N 分别为CA 、CB 的中点， ∴MN 是△ABC 的中位线，1132MN AB ∴==，②当24是斜边时，1122MN AB ==，故答案为：13或12．7．如图，在Rt ABC ∆中，90ABC ∠=︒，点D 、E 、F 分别是AB 、AC ，BC 边上的中点，连结BE ，DF ，已知5BE =，则DF = 5 ．【分析】已知BE 是Rt ABC ∆斜边AC 的中线，那么12BE AC =；DF 是ABC ∆的中位线，则12DF AC =，则5DF BE ==．【解答】解：ABC ∆是直角三角形，BE 是斜边的中线， 12BE AC ∴=，又DF 是ABC ∆的中位线，12DF AC ∴=， 5DF BE ∴==．故答案为5．8．如图，在四边形ABCD 中，220ADC BCD ∠+∠=︒，E 、F 分别是AC 、BD 的中点，P 是AB 边上的中点，则EPF ∠= 40 ︒．【分析】依据四边形内角和即可得到140BAD ABC ∠+∠=︒，再根据三角形中位线定理即可得到BPF BAD ∠=∠，APE ABC ∠=∠，进而得出140APE BPF ∠+∠=︒，即可得到EPF ∠的度数．【解答】解：四边形ABCD 中，220ADC BCD ∠+∠=︒， 360220140BAD ABC ∴∠+∠=︒-︒=︒，E 、F 分别是AC 、BD 的中点，P 是AB 边上的中点， PE ∴是ABC ∆的中位线，PF 是ABD ∆的中位线， //PE BC ∴，//PF AD ，BPF BAD ∴∠=∠，APE ABC ∠=∠，140APE BPF BAD ABC ∴∠+∠=∠+∠=︒， 18014040EPF ∴∠=︒-︒=︒，故答案为：40．9．如图，在四边形ABCD 中，//AB CD ，E ，F 分别是AC ，BD 的中点，已知12AB =，6CD =，则EF = 3 ．【分析】连接CF 并延长交AB 于G ，证明FDC FBG ∆≅∆，根据全等三角形的性质得到6BG DC ==，CF FG =，求出AG ，根据三角形中位线定理计算，得到答案．【解答】解：连接CF 并延长交AB 于G ， //AB CD ，FDC FBG ∴∠=∠，在FDC ∆和FBG ∆中， FDC FBG FD FBDFC BFG ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()FDC FBG ASA ∴∆≅∆ 6BG DC ∴==，CF FG =， 1266AG AB BG ∴=-=-=， CE EA =，CF FG =， ∴EF 是△ACG 的中位线， 132EF AG ∴==，故答案为：3． 10．如图，在ABC ∆中，8AB =，6AC =，AM 平分BAC ∠，CM AM ⊥于点M ，N 为BC 的中点，连结MN ，则MN 的长为 1 ．【分析】延长CM 交AB 于H ，证明AMH AMC ∆≅∆，根据全等三角形的性质得到6AH AC ==，CM MH =，根据三角形中位线定理解答．【解答】解：延长CM 交AB 于H ，在AMH ∆和AMC ∆中， 90MAH MAC AM AMAMH AMC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ()AMH AMC ASA ∴∆≅∆6AH AC ∴==，CM MH =， 2BH AB AH ∴=-=， CM MH =，CN BN =， ∴MN 是△BCH 的中位线， 112MN BH ∴==，故答案为：1．三．解答题（共3小题）11．如图所示，在ABC ∆中，点D 在BC 上且CD CA =，CF 平分ACB ∠，AE EB =，求证：12EF BD =．【分析】首先根据等腰三角形的性质可得F 是AD 中点，再根据三角形的中位线定理可得12EF BD =．【解答】证明：CD CA =，CF 平分ACB ∠， F ∴是AD 中点， AE EB =， E ∴是AB 中点，EF ∴是ABD ∆的中位线， 12EF BD ∴=． 12．如图：D 、E 是ABC ∆边AB ，AC 的中点，O 是ABC ∆内一动点，F 、G 是OB ，OC 的中点．判断四边形DEGF 的形状，并证明．【分析】根据三角形中位线定理得到12DE BC =，//DE BC ，12FGT BC =，//FG BC ，得到DE FG =，//DE FG ，根据平行四边形的判定定理证明结论．【解答】解：四边形DEGF 是平行四边形，理由：D 、E 是ABC ∆边AB ，AC 的中点， ∴DE 是△ABC 的中位线，12DE BC ∴=，//DE BC ， F 、G 是OB ，OC 的中点， ∴FG 是△BCO 的中位线，12FG BC ∴=，//FG BC ，DE FG ∴=，//DE FG∴四边形DEGF 是平行四边形．13．已知：如图，在四边形ABCD中，对角线AC、BD相交于O，且AC BD=，E、F分别是AB、CD的中点，E、F分别交BD、AC于点G、H．求证：OG OH=．【分析】取BC边的中点M，连接EM，FM，则根据三角形的中位线定理，即可证得EMF∆是等腰三角形，根据等边对等角，即可证得MEF MFE∠=∠，然后根据平行线的性质证得OGH OHG∠=∠，根据等角对等边即可证得．【解答】解：取BC边的中点M，连接EM，FM，M、F分别是BC、CD的中点，∴MF是△BCD的中位线，//MF BD ∴，12MF BD=，同理：//ME AC，12ME AC=，AC BD=ME MF∴=MEF MFE∴∠=∠，//MF BD，MFE OGH∴∠=∠，同理，MEF OHG∠=∠，OGH OHG∴∠=∠OG OH∴=．。

北师大版八年级数学下册三角形的中位线巩固练习含答案解析

【巩固练习】一.选择题1.已知△ABC 的各边长度分别为3cm ，4cm ，5cm ，则连结各边中点的三角形的周长为（）A ．2cmB ．7cmC ．5cmD ．6cm2. 如图，点D 、E 、F 分别为△ABC 三边的中点，若△DEF 的周长为10，则△ABC 的周长为（）A ．5B ．10C ．20D ．403. （2016•梧州）在△ABC 中，AB=3，BC=4，AC=2，D 、E 、F 分别为AB 、BC 、AC 中点，连接DF 、FE ，则四边形DBEF 的周长是（）A ．5B ．7C ．9D ．114．（2015•莆田模拟）如图，△ABC 的中线BD 、CE 交于点O ，连接OA ，点G 、F 分别为OC 、OB 的中点，BC=8，AO=6，则四边形DEFG 的周长为（）A ．12B ．14C ．16D ．185. 如图所示，在△ABC 中，AB ＝AC ，M ，N 分别是AB ，AC 的中点，D ，E 为BC 上的点，连接DN 、EM ，若AB ＝5cm ，BC ＝8cm ，DE ＝4cm ，则图中阴影部分的面积为（）A ．12cmB ．1.52cmC ．22cmD ．32cm6. 如图，在四边形ABCD 中，AB ∥CD ，点E 、F 、G 分别是BD 、AC 、DC 的中点.已知两底的差是6，两腰的和是12，则△EFG 的周长是（）A.8B.9C.10D.12二.填空题7. 顺次连接一个四边形各边中点得到的四边形是_________________.8. 如图, E、F分别是口ABCD 的两边AB、CD的中点, AF交DE于P, BF交CE于Q,则PQ与AB的关系是 .9. 如图，E、F、G、H分别是四边形ABCD各边的中点，对角线AC、BD的长分别为7和9，则四边形EFGH的周长是______.10.（2015•广州）如图，四边形ABCD中，∠A=90°，AB=3，AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为．11.（2016秋•东营区校级期末）如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ 的长．12.如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列三个结论：①∠BOC＝90°＋12∠A；②设OD ＝m ，AE ＋AF ＝n ，则AEF S mn △；③EF 不能成为△ABC 的中位线．其中正确的结论是_______.三.解答题13.如图，四边形ABCD 中，AD∥BC，M 、N 、P 、Q 分别为AD 、BC 、BD 、AC 的中点．求证：MN 和PQ 互相平分．14.已知：在△ABC 中，BC ＞AC ，动点D 绕△ABC 的顶点A 逆时针旋转，且AD ＝BC ，连接DC ．过AB 、DC 的中点E 、F 作直线，直线EF 与直线AD 、BC 分别相交于点M 、N ．（1）如图1，当点D 旋转到BC 的延长线上时，点N 恰好与点F 重合，取AC 的中点H ，连接HE 、HF ，根据三角形中位线定理和平行线的性质，可得结论∠AMF＝∠BNE（不需证明）；（2）当点D 旋转到图2或图3中的位置时，∠AMF 与∠BNE 有何数量关系？请分别写出猜想，并任选一种情况证明．15.（万州区校级模拟）已知，如图，在Rt△ABC 中，∠ACB=90°，点D 为AB 中点，连接CD ．点E 为边AC 上一点，过点E 作EF∥AB，交CD 于点F ，连接EB ，取EB 的中点G ，连接DG 、FG ．（1）求证：EF=CF ；（2）求证：FG⊥DG．【答案与解析】一.选择题1.【答案】D ；【解析】由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半，即可求其周长．2.【答案】C ；【解析】根据中位线定理可得BC ＝2DF ，AC ＝2DE ，AB ＝2EF ，继而结合△DEF 的周长为10，可得出△ABC 的周长．3.【答案】B ；【解析】∵D 、E 、F 分别为AB 、BC 、AC 中点，∴DF=12BC=2，DF ∥BC ，EF=12AB=32，EF ∥AB ， ∴四边形DBEF 为平行四边形， ∴四边形DBEF 的周长=2（DF+EF ）=2×（2+32）=7．故选B ．4.【答案】B ；【解析】解：∵BD，CE 是△ABC 的中线，∴ED∥BC 且ED=BC ，∵F 是BO 的中点，G 是CO 的中点，∴FG∥BC 且FG=BC ，∴ED=FG=BC=4，同理GD=EF=AO=3，∴四边形DEFG 的周长为3+4+3+4=14．故选B ．5.【答案】B ；【解析】连接MN ，作AF⊥BC 于F ．∵AB＝AC ，∴BF＝CF ＝12BC ＝12×8＝4，在Rt△ABF 中，AF 22AB BF -2254-3，∵M、N 分别是AB ，AC 的中点，∴MN 是中位线，即平分三角形的高且MN ＝8÷2＝4，∴NM＝12BC ＝DE ，∴△MNO≌△EDO，O也是ME，ND的中点，∴阴影三角形的高是12AF÷2＝1.5÷2＝0.75，∴S阴影＝4×0.75÷2＝1.5．6.【答案】B；【解析】连接AE，延长交CD于H，可证AB＝DH，CH＝两底的差，EF是△AHC的中位线，EF＝12两底的差，EG＋FG＝12两腰的和，故△EFG的周长是9.二.填空题7.【答案】平行四边形；8.【答案】PQ∥AB，PQ＝12 AB；【解析】P，Q分别是AF，BF的中点.9.【答案】16；【解析】根据三角形中位线的性质得出HG 12AC，EF12AC，HE12DB，GF12BD，进而得出HE＝GF＝12BD，HG＝FE＝12AC，即可得出答案．10.【答案】3；【解析】解：∵ED=EM，MF=FN，∴EF=DN，∴DN最大时，EF最大，∵N与B重合时DN最大，此时DN=DB==6，∴EF的最大值为3．故答案为3．11.【答案】3；【解析】∵△ABC的周长是26，BC=10，∴AB+AC=26﹣10=16，∵∠ABC的平分线垂直于AE，∴在△ABQ和△EBQ中，，∴△ABQ≌△EBQ，∴AQ=EQ，AB=BE，同理，AP=DP，AC=CD，∴DE=BE+CD﹣BC=AB+AC﹣BC=16﹣10=6，∵AQ=DP，AP=DP，∴PQ是△ADE的中位线，∴PQ=12DE=3．故答案是：3．12.【答案】①，③；【解析】①根据三角形内角和定理求解；②根据△AEF的面积＝△AOE的面积＋△AOF的面积求解；③若此三角形为等边三角形，则EF即为中位线．三.解答题13.【解析】证明：连接MP，PN，NQ，QM，∵AM＝MD，BP＝PD，∴PM是△ABD的中位线，∴PM∥AB，PM＝12 AB；同理NQ＝12AB，NQ∥AB，∴PM＝NQ，且PM∥NQ．∴四边形MPNQ是平行四边形．∴MN与PQ互相平分．14.【解析】解：图1：∠AMF＝∠ENB；图2：∠AMF＝∠ENB；图3：∠AMF＋∠ENB＝180°．证明：如图2，取AC的中点H，连接HE、HF．∵F是DC的中点，H是AC的中点，∴HF∥AD，HF＝12 AD，∴∠AMF＝∠HFE，同理，HE∥CB，HE＝12 CB，∴∠E NB＝∠HEF．∵AD＝BC，∴HF＝HE，∴∠HEF＝∠HFE，∴∠ENB＝∠AMF．如图3：取AC的中点H，连接HE、HF．∵F是DC的中点，H是AC的中点，∴HF∥AD，HF＝12 AD，∴∠AMF＋∠HFE＝180°，同理，HE∥CB，HE＝12 CB，∴∠ENB＝∠HEF．∵AD＝BC，∴HF＝HE，∴∠HEF＝∠HFE，∴∠AMF＋∠ENB＝180°．15.【解析】证明：（1）如图，∵在Rt△ABC中，∠ACB=90°，点D为AB中点，∴CD是斜边AB上的中线，∴C D=AD=BD=AB．又EF∥AB，∴=，∴==1，∴EF=CF；（2）如图，延长EF交BC于点M，连接GM．∵EF∥AB，∴∠CMF=∠CBD．又∵AD=BD=AB，∴∠DCM=∠CBD，即∠FCM=∠CBD，∴∠CMF=∠FCM，∴CF=MF．又由（1）知，EF=CF，∴EF=FM，即点F是EM的中点，又∵EF∥AB，则FM∥AB∴EM是△ABC的中位线，则点M是BC的中点，∵点G是BE的中点，∴DG是△AEB的中位线，GM是△BEC的中位线，∴GD∥AE，GM∥EC，∴点D、G、M三点共线，∴FG是△CDM的中位线，∴FG∥CM．又∵MC⊥EC，∴FG⊥DG．。

初二数学三角形中位线练习题（含答案）

初二数学三角形中位线练习题一．选择题（共5小题）1．如图，为了测量池塘边A 、B 两地之间的距离，在线段AB 的同侧取一点C ，连结CA 并延长至点D ，连结CB 并延长至点E ，使得A 、B 分别是CD 、CE 的中点，若18DE m =，则线段AB 的长度是( ) A ．9mB ．12mC ．8mD ．10m2．已知三角形的周长是16，它的三条中位线围成的三角形的周长是( ) A ．16B ．12C ．8D ．43．如图，在四边形ABCD 中，点P 是边CD 上的动点，点Q 是边BC 上的定点，连接AP ，PQ ，E ，F 分别是AP ，PQ 的中点，连接EF ．点P 在由C 到D 运动过程中，线段EF 的长度( )A ．保持不变B ．逐渐变小C ．先变大，再变小D ．逐渐变大4．如图，在四边形ABCD 中，P 是对角线BD 的中点，E 、F 分别是AB 、CD 的中点，AD BC =，136EPF ∠=︒，则EFP ∠的度数是( )A ．68︒B ．34︒C ．22︒D ．44︒5．如图，D 是ABC ∆内一点，BD CD ⊥，E 、F 、G 、H 分别是边AB 、BD 、CD 、AC 的中点．若10AD =，8BD =，6CD =，则四边形EFGH 的周长是( )A ．24B ．20C ．12D ．10第3题图题图第4题图题图第5题图题图二．填空题（共5小题）6．某直角三角形的两条边长分别是10和24，则连接两条直角边中点的线段的长是． 7．如图，在Rt ABC ∆中，90ABC ∠=︒，点D 、E 、F 分别是AB 、AC ，BC 边上的中点，连结BE ，DF ，已知5BE =，则DF = ． 8．如图，在四边形ABCD 中，220ADC BCD ∠+∠=︒，E 、F 分别是AC 、BD 的中点，P 是AB 边上的中点，则EPF ∠= ︒．9．如图，在四边形ABCD 中，//AB CD ，E ，F 分别是AC ，BD 的中点，已知12AB =，6CD =，则EF = ．10．如图，在ABC ∆中，8AB =，6AC =，AM 平分BAC ∠，CM AM ⊥于点M ，N 为BC 的中点，连结MN ，则MN 的长为．第8题图题图第9题图题图第10题图题图三．解答题（共3小题）11．如图所示，在ABC ∆中，点D 在BC 上且CD CA =，CF 平分ACB ∠，AE EB =，求证：12EF BD =．12．如图：D 、E 是ABC ∆边AB ，AC 的中点，O 是ABC ∆内一动点，F 、G 是OB ，OC 的中点．判断四边形DEGF 的形状，并证明．13．已知：如图，在四边形ABCD 中，对角线AC 、BD 相交于O ，且AC BD =，E 、F 分别是AB 、CD 的中点，E 、F 分别交BD 、AC 于点G 、H ．求证：OG OH =．答案与解析一．选择题（共5小题）1．如图，为了测量池塘边A 、B 两地之间的距离，在线段AB 的同侧取一点C ，连结CA 并延长至点D ，连结CB 并延长至点E ，使得A 、B 分别是CD 、CE 的中点，若18DE m =，则线段AB 的长度是( )A ．9mB ．12mC ．8mD ．10m【分析】根据三角形的中位线定理解答即可．【解答】解：A Q 、B 分别是CD 、CE 的中点， ∴AB 是△CDE 的中位线， 192AB DE m ∴==，故选：A ．2．已知三角形的周长是16，它的三条中位线围成的三角形的周长是( )A ．16B ．12C ．8D ．4【分析】由中位线定义可得新三角形的各边长为原三角形各边长的一半，即可得出其周长等于原三角形周长的一半．【解答】解：Q 三角形的周长是16，∴它的三条中位线围成的三角形的周长是11682⨯=．故选：C ．3．如图，在四边形ABCD 中，点P 是边CD 上的动点，点Q 是边BC 上的定点，连接AP ，PQ ，E ，F 分别是AP ，PQ 的中点，连接EF ．点P 在由C 到D 运动过程中，线段EF 的长度( )A ．保持不变B ．逐渐变小C ．先变大，再变小D ．逐渐变大【分析】连接AQ ，根据三角形中位线定理解答即可．【解答】解：如图所示，连接AQ ， Q 点Q 是边BC 上的定点， AQ ∴的大小不变，E Q ，F 分别是AP ，PQ 的中点， ∴EF 是△APQ 的中位线， 12EF AQ ∴=，∴线段EF 的长度保持不变，故选：A ．4．如图，在四边形ABCD 中，P 是对角线BD 的中点，E 、F 分别是AB 、CD 的中点，AD BC =，136EPF ∠=︒，则EFP ∠的度数是( )A ．68︒B ．34︒C ．22︒D ．44︒【分析】根据三角形中位线定理得到12PE AD =，12PF BC =，根据等腰三角形的性质、三角形内角和定理计算即可．【解答】解：P Q 是BD 的中点，E 是AB 的中点， ∴EP 是△BCD 的中位线， 12PE AD ∴=，同理，12PF BC =， AD BC =Q ， PE PF ∴=，1(180)222EFP EPF ∴∠=⨯︒-∠=︒，故选：C ． 5．如图，D 是ABC ∆内一点，BD CD ⊥，E 、F 、G 、H 分别是边AB 、BD 、CD 、AC 的中点．若10AD =，8BD =，6CD =，则四边形EFGH 的周长是( )A ．24B ．20C ．12D ．10【分析】利用勾股定理列式求出BC 的长，再根据三角形的中位线平行于第三边并且等于第三边的一半求出12EH FG BC ==，12EF GH AD ==，然后代入数据进行计算即可得解．【解答】解：BD CD ⊥Q ，8BD =，6CD =，22228610BC BD CD ∴=+=+=，E Q 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，12EH FG BC ∴==，12EF GH AD ==，∴四边形EFGH 的周长EH GH FG EF AD BC =+++=+，又10AD =Q ，∴四边形EFGH 的周长101020=+=，故选：B ．二．填空题（共5小题）6．某直角三角形的两条边长分别是10和24，则连接两条直角边中点的线段的长是 13或12 ．【分析】根据勾股定理求出AB ，根据三角形中位线定理计算，得到答案．【解答】解：分两种情况讨论：①当24是直角边时，由勾股定理得，斜边2222241026AB AC BC =+=+=，M Q 、N 分别为CA 、CB 的中点，∴MN 是△ABC 的中位线， 1132MN AB∴==， ②当24是斜边时，1122MN AB ==，故答案为：13或12．7．如图，在Rt ABC ∆中，90ABC ∠=︒，点D 、E 、F 分别是AB 、AC ，BC 边上的中点，连结BE ，DF ，已知5BE =，则DF = 5 ．【分析】已知BE 是Rt ABC ∆斜边AC 的中线，那么12BE AC =；DF 是ABC ∆的中位线，则12DF AC =，则5DF BE ==．【解答】解：ABC ∆Q 是直角三角形，BE 是斜边的中线， 12BE AC∴=，又DF Q 是ABC ∆的中位线，12DF AC ∴=，5DF BE ∴==．故答案为5．8．如图，如图，在四边形在四边形ABCD 中，220ADC BCD ∠+∠=︒，E 、F 分别是AC 、BD 的中点，P 是AB 边上的中点，则EPF ∠= 40 ︒．【分析】依据四边形内角和即可得到140BAD ABC ∠+∠=︒，再根据三角形中位线定理即可得到BPF BAD ∠=∠，APE ABC ∠=∠，进而得出140APE BPF ∠+∠=︒，即可得到EPF ∠的度数．【解答】解：Q 四边形ABCD 中，220ADC BCD ∠+∠=︒， 360220140BAD ABC ∴∠+∠=︒-︒=︒，E Q 、F 分别是AC 、BD 的中点，P 是AB 边上的中点， PE ∴是ABC ∆的中位线，PF 是ABD ∆的中位线， //PE BC ∴，//PF AD ，BPF BAD ∴∠=∠，APE ABC ∠=∠，140APE BPF BAD ABC ∴∠+∠=∠+∠=︒， 18014040EPF ∴∠=︒-︒=︒，故答案为：40．9．如图，在四边形ABCD 中，//AB CD ，E ，F 分别是AC ，BD 的中点，已知12AB =，6CD =，则EF = 3 ．【分析】连接CF 并延长交AB 于G ，证明FDC FBG ∆≅∆，根据全等三角形的性质得到6BG DC ==，CF FG =，求出AG ，根据三角形中位线定理计算，得到答案．【解答】解：连接CF 并延长交AB 于G ， //AB CD Q ，FDC FBG ∴∠=∠，在FDC ∆和FBG ∆中， FDC FBG FD FB DFC BFG∠=∠⎧⎪=⎨⎪∠=∠⎩， ()FDC FBG ASA ∴∆≅∆6BG DC ∴==，CF FG =， 1266AG AB BG ∴=-=-=， CE EA =Q ，CF FG =， ∴EF 是△ACG 的中位线， 132EF AG ∴==，故答案为：3．10．如图，在ABC ∆中，8AB =，6AC =，AM 平分BAC ∠，CM AM ⊥于点M ，N 为BC 的中点，连结MN ，则MN 的长为 1 ．【分析】延长CM 交AB 于H ，证明AMH AMC ∆≅∆，根据全等三角形的性质得到6AH AC ==，CM MH =，根据三角形中位线定理解答．【解答】解：延长CM 交AB 于H ，在AMH ∆和AMC ∆中， 90MAH MAC AM AM AMH AMC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ()AMH AMC ASA ∴∆≅∆6AH AC ∴==，CM MH =， 2BH AB AH ∴=-=， CM MH =Q ，CN BN =， ∴MN 是△BCH 的中位线， 112MN BH∴==，故答案为：1．三．解答题（共3小题） 11．如图所示，在ABC ∆中，点D 在BC 上且CD CA =，CF 平分ACB ∠，AE EB =，求证：12EF BD =．【分析】首先根据等腰三角形的性质可得F 是AD 中点，再根据三角形的中位线定理可得12EF BD =．【解答】证明：CD CA =Q ，CF 平分ACB ∠，F ∴是AD 中点， AE EB =Q ， E ∴是AB 中点，EF ∴是ABD ∆的中位线，12EF BD∴=．12．如图：D 、E 是ABC ∆边AB ，AC 的中点，O 是ABC ∆内一动点，F 、G 是OB ，OC 的中点．判断四边形DEGF 的形状，并证明．【分析】根据三角形中位线定理得到12DE BC =，//DE BC ，12FGT BC =，//FG BC ，得到DE FG =，//DE FG ，根据平行四边形的判定定理证明结论．【解答】解：四边形DEGF 是平行四边形，理由：D Q 、E 是ABC ∆边AB ，AC 的中点， ∴DE 是△ABC 的中位线， 12DE BC ∴=，//DE BC， F Q 、G 是OB ，OC 的中点， ∴FG 是△BCO 的中位线，12FG BC ∴=，//FG BC， DE FG ∴=，//DE FG∴四边形DEGF 是平行四边形．13．已知：如图，在四边形ABCD 中，对角线AC 、BD 相交于O ，且AC BD =，E 、F 分别是AB 、CD 的中点，E 、F 分别交BD 、AC 于点G 、H ．求证：OG OH =．【分析】取BC 边的中点M ，连接EM ，FM ，则根据三角形的中位线定理，即可证得EMF ∆是等腰三角形，根据等边对等角，即可证得MEF MFE ∠=∠，然后根据平行线的性质证得OGH OHG ∠=∠，根据等角对等边即可证得．【解答】解：取BC 边的中点M ，连接EM ，FM ，M Q 、F 分别是BC 、CD 的中点， ∴MF 是△BCD 的中位线，//MF BD ∴，12MF BD=，同理：//ME AC ，12ME AC =，AC BD =Q ME MF ∴=MEF MFE ∴∠=∠， //MF BD Q ，MFE OGH ∴∠=∠，同理，MEF OHG ∠=∠， OGH OHG ∴∠=∠ OG OH ∴=．。

北师大版数学八年级下册：6.3 三角形的中位线同步练习(附答案)

3 三角形的中位线知识点1 三角形中位线定理1．如图，点D ，E 分别是△ABC 边BA ，BC 的中点，AC ＝3，则DE 的长为（） A ．2B.43C ．3D.32第1题图第2题图2．如图，M ，N 分别是△ABC 的边AB ，AC 的中点．若∠A ＝65°，∠ANM ＝45°，则∠B ＝（）A ．20°B ．45°C ．65°D ．70°3．已知△ABC 的周长为16，点D ，E ，F 分别为△ABC 三条边的中点，则△DEF 的周长为（）A ．8B ．2 2C ．16D ．44．如图，在△ABC 中，D ，E 分别是AB ，BC 的中点，点F 在DE 延长线上，添加一个条件使四边形ADFC 为平行四边形，则这个条件是（）A ．∠B ＝∠F B ．∠B ＝∠BCFC ．AC ＝CFD ．AD ＝CF第4题图第5题图5．如图，在▱ABCD 中，点M 为边AD 上一点，AM ＝2MD ，点E ，F 分别是BM ，CM 的中点．若EF ＝6，则AM 的长为．6．如图，在△ABC 中，点D ，E ，F 分别为边AB ，BC ，CA 的中点．求证：四边形DECF 是平行四边形．7．如图，在等腰△ABC中，AB＝AC＝8，AD是∠BAC的平分线，交BC于点D，点E是AB的中点，连接DE.求线段DE的长．知识点2三角形中位线定理的应用8．如图，要测量池塘两岸相对的A，B两点间的距离，可以在池塘外选一点C，连接AC，BC，分别取AC，BC的中点D，E，测得DE＝50 m，则AB的长是m.第8题图第9题图9．如图，吴伯伯家有一块等边三角形的空地ABC，已知点E，F分别是边AB，AC的中点，量得EF＝5米，他想把四边形BCFE用篱笆围成一圈放养小鸡，则需用篱笆的长是（）A．15米B．20米C．25米D．30米10．如图，在△ABC中，∠ABC＝90°，AB＝8，BC＝6.若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）A．7B．8C．9D ．1011．如图，D 是△ABC 内一点，BD ⊥CD ，AD ＝7，BD ＝4，CD ＝3，E ，F ，G ，H 分别是AB ，BD ，CD ，AC 的中点，则四边形EFGH 的周长为（）A ．12B ．14C ．24D ．21第11题图第12题图12．如图，在四边形ABCD 中，点P 是对角线BD 的中点，点E ，F 分别是AB ，CD 的中点，AD ＝BC ，∠PEF ＝35°，则∠PFE 的度数是．13．如图，在△ABC 中，∠BAC ＝90°，延长BA 到点D ，使AD ＝12AB ，E ，F 分别是边BC ，AC 的中点．求证：DF ＝BE.14．如图，在△ABC 中，AB ＝4，AC ＝3，AD ，AE 分别是△ABC 的角平分线和中线，过点C 作CG ⊥AD 于点F ，交AB 于点G ，连接EF ，求线段EF 的长．15．如图，在四边形ABCD中，已知AB＝CD，点E，F分别为AD，BC的中点，延长BA，CD，分别交射线FE于P，Q两点．求证：∠P＝∠CQF.参考答案：3 三角形的中位线知识点1 三角形中位线定理1．如图，点D ，E 分别是△ABC 边BA ，BC 的中点，AC ＝3，则DE 的长为（D ） A ．2B.43C ．3D.32第1题图第2题图2．如图，M ，N 分别是△ABC 的边AB ，AC 的中点．若∠A ＝65°，∠ANM ＝45°，则∠B ＝（D ）A ．20°B ．45°C ．65°D ．70°3．已知△ABC 的周长为16，点D ，E ，F 分别为△ABC 三条边的中点，则△DEF 的周长为（A ）A ．8B ．2 2C ．16D ．44．如图，在△ABC 中，D ，E 分别是AB ，BC 的中点，点F 在DE 延长线上，添加一个条件使四边形ADFC 为平行四边形，则这个条件是（B ）A ．∠B ＝∠F B ．∠B ＝∠BCFC ．AC ＝CFD ．AD ＝CF第4题图第5题图5．如图，在▱ABCD 中，点M 为边AD 上一点，AM ＝2MD ，点E ，F 分别是BM ，CM 的中点．若EF ＝6，则AM 的长为8．6．如图，在△ABC 中，点D ，E ，F 分别为边AB ，BC ，CA 的中点．求证：四边形DECF 是平行四边形．证明：∵D ，F 分别是边AB ，AC 的中点， ∴DF ∥BC.同理：DE ∥AC.∴四边形DECF 是平行四边形．7．如图，在等腰△ABC 中，AB ＝AC ＝8，AD 是∠BAC 的平分线，交BC 于点D ，点E 是AB 的中点，连接DE.求线段DE 的长．解：∵AB ＝AC ，AD 平分∠BAC ， ∴AD 是等腰△ABC 底边BC 上的中线． ∴点D 是BC 的中点．又∵点E 是AB 的中点， ∴DE 是△ABC 的中位线． ∴DE ＝12AC ＝4.知识点2 三角形中位线定理的应用8．如图，要测量池塘两岸相对的A ，B 两点间的距离，可以在池塘外选一点C ，连接AC ，BC ，分别取AC ，BC 的中点D ，E ，测得DE ＝50 m ，则AB 的长是100m.第8题图第9题图9．如图，吴伯伯家有一块等边三角形的空地ABC ，已知点E ，F 分别是边AB ，AC 的中点，量得EF ＝5米，他想把四边形BCFE 用篱笆围成一圈放养小鸡，则需用篱笆的长是（C ）A ．15米B ．20米C ．25米D ．30米10．如图，在△ABC 中，∠ABC ＝90°，AB ＝8，BC ＝6.若DE 是△ABC 的中位线，延长DE 交△ABC 的外角∠ACM 的平分线于点F ，则线段DF 的长为（B ）A ．7B ．8C ．9D ．1011．如图，D 是△ABC 内一点，BD ⊥CD ，AD ＝7，BD ＝4，CD ＝3，E ，F ，G ，H 分别是AB ，BD ，CD ，AC 的中点，则四边形EFGH 的周长为（A ）A ．12B ．14C ．24D ．21第11题图第12题图12．如图，在四边形ABCD 中，点P 是对角线BD 的中点，点E ，F 分别是AB ，CD 的中点，AD ＝BC ，∠PEF ＝35°，则∠PFE 的度数是35°．13．如图，在△ABC 中，∠BAC ＝90°，延长BA 到点D ，使AD ＝12AB ，E ，F 分别是边BC ，AC 的中点．求证：DF ＝BE.证明：∵E ，F 分别是边BC ，AC 的中点， ∴EF ＝12AB ，EF ∥AB ，AF ＝FC ，BE ＝EC.∵AD ＝12AB ，∴EF ＝AD.∵∠BAC ＝90°，EF ∥AB ， ∴∠DAF ＝∠EFC ＝90°. 又∵AF ＝FC ，AD ＝FE ， ∴△DAF ≌△EFC （SAS ）． ∴DF ＝EC.又∵BE ＝EC ，∴DF ＝BE.14．如图，在△ABC 中，AB ＝4，AC ＝3，AD ，AE 分别是△ABC 的角平分线和中线，过点C 作CG ⊥AD 于点F ，交AB 于点G ，连接EF ，求线段EF 的长．解：∵AF 是△ABC 的角平分线，∴∠GAF ＝∠CAF. 又∵CG ⊥AD ，∴∠AFC ＝∠AFG ＝90°. 在△AGF 和△ACF 中，⎩⎨⎧∠GAF ＝∠CAF ，AF ＝AF ，∠AFG ＝∠AFC ，∴△AGF ≌△ACF （ASA ）． ∴AG ＝AC ＝3，GF ＝CF. ∴BG ＝AB －AG ＝4－3＝1.又∵BE ＝CE ，∴EF 是△BCG 的中位线． ∴EF ＝12BG ＝12.15．如图，在四边形ABCD 中，已知AB ＝CD ，点E ，F 分别为AD ，BC 的中点，延长BA ，CD ，分别交射线FE 于P ，Q 两点．求证：∠P ＝∠CQF.证明：连接BD ，取BD 的中点M ，连接EM ，FM. ∵点E 是AD 的中点， ∴EM ∥AB ，EM ＝12AB.∴∠MEF ＝∠P.同理可证：FM ∥CD ，FM ＝12CD.∴∠MFE ＝∠CQF. 又∵AB ＝CD ，∴EM ＝FM. ∴∠MEF ＝∠MFE.∴∠P ＝∠CQF.。

浙教版八年级数学下册 4.5 《中位线》提优训练(含答案)

八年级数学提优训练——中位线1．如图，在四边形ABCD中，AD＝BC，E，F，G分别是AB，CD，AC的中点，若∠DAC＝20°，∠ACB＝84°，则∠FEG等于（）A．32°B．38°C．64°D．30°2．如图，△ABC的周长为32，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝12，则PQ的长为（）A．2 B．3 C．4 D．53．如图，△ABC中，AB＞AC，AD，AE分别是其角平分线和中线，过点C作CG⊥AD于点F，交AB于点G，连接EF，则①EF∥AB；②∠BCG＝（∠ACB﹣∠ABC）；③EF＝（AB﹣AC）；④（AB﹣AC）＜AE＜（AB+AC）．其中正确的是（）A．①②③④B．①②C．②③④D．①③④4．已知△ABC的周长为1，连接其三边中点构成第二个三角形，再连接第二个三角形的中点构成第三个三角形，以此类推，则第2012个三角形的周长为（）A．B．C．D．5．如图，在△ABC中，D，E分别是AB，AC的中点，AC＝10，F是DE上一点，连接AF，CF，DF＝1．若∠AFC ＝90°，则BC的长度为（）A．10 B．12 C．14 D．166．已知：四边形ABCD中，AB＝2，CD＝3，M、N分别是AD，BC的中点，则线段MN的取值范围是（）A．1＜MN＜5 B．1＜MN≤5 C．＜MN＜D．＜MN≤7．如图，在△ABC中，BF平分∠ABC，AG⊥BF，垂足为点D，交BC于点G，E为AC的中点，连结DE，DE＝2.5cm，AB＝4cm，则BC的长为cm．8．如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于G，AB＝6，则AG＝．9．如图，顺次连结△ABC三边的中点D，E，F得到的三角形面积为S1，顺次连结△CEF三边的中点M，G，H得到的三角形面积为S2，顺次连结△CGH三边的中点得到的三角形面积为S3．设△ABC的面积为S，则S1+S2+S3＝．10．如图，在R△ABC中，∠ACB＝90°，BC＝3，AC＝4，点M为边AC的中点，点N为边BC上任意一点，若点C关于直线MN的对称点C′恰好落在△ABC的中位线上，则CN的长为．11．如图，在△ABC中，D，E分别是AB，AC的中点，F是线段DE上一点，连接AF，BF，若AB＝16，EF＝1，∠AFB＝90°，则BC的长为．12．如图，在△ABC中，AE平分∠BAC，BE⊥AE于点E，点F是BC的中点．（1）如图1，BE的延长线与AC边相交于点D，求证：EF＝（AC﹣AB）；（2）如图2，请直接写出线段AB、AC、EF的数量关系．13．如图所示，在△ABC中，AD是BC边的中线，F是AD的中点，连接BF并延长交AC于E，求证：EC＝2AE．14．探索与证明如图，在△ABC中，BD、CE分别是边AC、AB上的中线，BD与CE相交于点O，M、N分别是BO、CO的中点，顺次连接E、M、N、D四点．（1）求证：EMND是平行四边形；（2）探索：BC边上的中线是否过点O？为什么？15．已知△ABC（如图所示）．（1）在图中找出重心O；（2）设BC，AC，AB边的中点为M，N，G，度量OM和OA，ON与OB，OG与OC，根据度量的结果，猜想三角形的重心到三角形顶点的距离与到对边中点的距离之间的距离，并给予证明．16．如图，AD为△ABC的中线，BE为△ABD的中线．（1）在△BED中作BD边上的高，垂足为F；（2）若△ABC的面积为20，BD＝5．①△ABD的面积为，②求△BDE中BD边上的高EF的长；（3）过点E作EG∥BC，交AC于点G，连接EC、DG且相交于点O，若S△ABC＝2m，又S△COD＝n，求S△GOC．（用含m、n的代数式表示）17．如图，四边形ABCD中，已知AB＝CD，点E、F分别为AD、BC的中点，延长BA、CD，分别交射线FE于P、Q两点．求证：∠BPF＝∠CQF．参考答案1． A．2． C．3． A．4． C．5． B．6． D．7．9 8． 2 9．S．10．或． 11． 1812．（1）证明：如图1中，∵AE⊥BD，∴∠AED＝∠AEB＝90°，∴∠BAE+∠ABE＝90°，∠DAE+∠ADE＝90°，∵∠BAE＝∠DAE，∴∠ABE＝∠ADE，∴AB＝AD，∵AE⊥BD，∴BE＝DE，∵BF＝FC，∴EF＝DC＝＝（AC﹣AB）．（2）结论：EF＝（AB﹣AC），理由：如图2中，延长AC交BE的延长线于P．∵AE⊥BP，∴∠AEP＝∠AEB＝90°，∴∠BAE+∠ABE＝90°，∠PAE+∠APE＝90°，∵∠BAE＝∠PAE，∴∠ABE＝∠ADE，∴AB＝AP，∵AE⊥BD，∴BE＝PE，∵BF＝FC，∴EF＝PC＝（AP﹣AC）＝（AB﹣AC）．13．证明：∵AD是BC边的中线，F是AD的中点，∴点D是BC的中点，DF＝AF．如图，过E作DG∥AC交BE于点G．∵DG∥AC，且AD是BC边的中线．∴DG是△BEC的中位线，△DGF∽△AEF，∴DG＝EC，＝＝1∴DG＝AE，∴AE＝EC．即EC＝2AE．14．（1）证明：△ABC的边AC、AB上的中线BD、CE相交于点O，M、N分别是BO、CO的中点，∴ED∥BC且ED＝BC，MN∥BC且MN＝BC，∴ED∥MN且ED＝MN，∴四边形MNDE是平行四边形．（2）BC边上的中线过点O，理由如下：作BC边上的中线AF，交BD于M，连接DF，∵BD、AF是边AC、BC上的中线，∴DF∥BA，DF＝BA．∴△MDF∽△MBA，∴＝，即BD＝3DM，∵BO＝BD，∴O和M重合，即BC边上的中线一定过点O．15．证明：如图所示，取BO，CO的中点K，H，连接KH，HN，NG，KG，∵G，N分别是AB，AC的中点，∴GN平行且等于BC．又∵K，H分别是OB，OC边的中点，∴KH平行且等于BC．∴GN平行且等于KH．∴四边形KHNG是平行四边形．∴GO＝OH，NO＝KO．而BK＝KO，CH＝HO，∴BO＝2ON，CO＝2OG．若取AO的中点R，同理，可证AO＝2OM．∴AO＝2OM，BO＝2ON，CO＝2OG．16．解：（1）作EF⊥BD垂足为F，（2）①∵AD为△ABC的中线，∴S△ABD＝S△ABC，∵△ABC的面积为20，∴△ABD的面积为10；②∵BE为△ABD的中线，∴S△BDE＝S△ABD＝5，∵BD＝5，∴EF的长＝2；③∵EG∥BC，BE为△ABD的中线，∴EG是△ACD的中位线，∴DG是△ACD的中线，∴S△BDE＝S△CDG，S△BDE＝S△CDG＝S△ABD＝S△ABC＝，∴S△GDC＝，又∵S△COD＝n，∴S△GOC＝S△GDC﹣S△COD＝．17．证明：如图，连接BD，作BD的中点M，连接EM、FM．∵点E是AD的中点，∴在△ABD中，EM∥AB，EM＝AB，∴∠MEF＝∠P同理可证：FM∥CD，FM＝CD．∴∠MFQ＝∠CQF，又∵AB＝CD，∴EM＝FM，∴∠MEF＝∠MFE，∴∠P＝∠CQF．．。

中考数学复习三角形的中位线【培优讲练】

9.5 三角形的中位线同步培优讲练综合三角形的中位线1．连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于第三边，并且等于第三边的一半.顺次连接特殊的平行四边形各边中点得到的四边形的形状（1）顺次连接平行四边形各边中点得到的四边形是平行四边形.（2）顺次连接矩形各边中点得到的四边形是菱形.（3）顺次连接菱形各边中点得到的四边形是矩形.（4）顺次连接正方形各边中点得到的四边形是正方形.一、三角形中位线有关的求解问题【例1】如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得10=，则A，B之间的距离是()CD mA.5m B．10mC．20m D．40m【例2】如图，在ABC∆中，点D、E分别是边AB、AC的中点，连接DE，ABC∠的平分线BF交DE于点F，若4AB=，6BC=，则EF的长为．【例3】如图，在四边形ABCD 中，点P 是对角线BD 的中点，点E 、F 分别是AB 、CD 的中点，AD BC =，30PEF ∠=︒，则EPF ∠的度数是．【例4】在ABC 中，120AB AC BAC =∠=︒，，D 为ABC 形内一点，以AD 为腰作等腰DAE ，使DAE BAC ∠=∠，连接BE CD 、，若M N 、分别是DE BC 、的中点，1MN =，则CD 的长为_______．【例5】有一块梯形形状的土地，现要平均分给两个农户种植（即将梯形面积两等分），试设计两种方案，并说明理由．（平分图案画在备用图上，保留作图痕迹）【例6】如图，在ABC ∆中，点D ，E ，F 分别是边AB ，BC ，CA 上的中点，且10AB cm =，16AC cm =，则四边形ADEF 的周长等于 cm ．【例7】如图，四边形ABCD 中，1AB =，4CD =，M 、N 分别是AD 、BC 的中点，则线段MN 的取值范围是( )A ．35MN <<B ．35MN <C ．3522MN <<D ．3522MN <【例8】如图，Rt ABC △中，90BAC ∠=︒，6AB =，10BC =，AD 、AE 分别是其角平分线和中线，过点B 作BG AD ⊥于G ，交AC 于F ，连接EG ，则线段EG 的长为（）A ．12 B ．1 C ．32 D ．2二、三角形中位线相关的面积问题【例1】如图，在ABC ∆中，D 、E 、F 分别是BC 、AC 、AD 的中点，若ABC ∆的面积是40，则四边形BDEF 的面积是( )A ．10B ．12.5C ．15D ．20【例2】E 、F 是线段AB 上的两点，且16AB =，2AE =，4BF =，点G 是线段EF 上的一动点，分别以AG 、BG 为斜边在AB 同侧作两个等腰直角三角形，直角顶点分别为D 、C ，如图所示，连接CD 并取中点P ，连接PG ，点G 从E 点出发运动到F 点，则线段PG 扫过的图形面积为______．【例3】如图，在ABC 中，D ，E ，F 分别是BC AD CE ，，的中点，22cm BCF S =，则ABC S =_____2cm【例4】如图，ABC 三边的中线AD ，BE ，CF 的公共点为G ，且:2:1AG GD =，若12ABC S =△，则图中阴影部分的面积是_____．【例5】如图，在Rt ABC △中，90BAC ∠=︒，,E F 分别是,BC AB 的中点，延长CA 到点D ，使得2AC AD =，连接,,,,DE DF AE EF AF 与DE 交于点O ．5,13AB BC ==，求四边形AEFD 的面积．三、与三角形中位线有关的应用和证明【例1】在ABC ∆中，点M 是边BC 的中点，AD 平分BAC ∠，BD AD ⊥，BD 的延长线交AC 于点E ，12AB =，20AC =．（1）求证：BD DE =；（2）求DM 的长．【例2】如图，ABC ∆中，AH BC ⊥于点H ，点D ，E 分别是AB ，AC 的中点，连接DH ，EH ，DE ．（1）求证：AD DH =；（2）若四边形ADHE 的周长是30，ADE ∆的周长是21，求BC 的长．【例3】如图，在四边形ABCD 中，P 是对角线BD 的中点，E 、F 分别是AB 、CD 的中点，AD BC =，20PEF ∠=︒，求PFE ∠的度数．【例4】在Rt ABC 中，90BAC ∠=︒，E 、F 分别是BC 、AC 的中点，延长BA 到点D ，使2AB AD =，连接DE 、DF 、AE 、EF ，AF 与DE 交于点O ．(1)试说明AF 与DE 互相平分；(2)若8AB =，12BC =，求DO 的长．四、梯形中位线【例1】已知一个梯形的中位线长为5cm ，其中一条底边的长为6cm ，那么该梯形的另一条底边的长是 cm ．【例2】如图，已知直角梯形ABCD 的一条对角线把梯形分为一个直角三角形和一个边长为8cm 的等边三角形，则梯形ABCD 的中位线长为( )A. 4cm B ．6cmC ．8cmD ．10cm【例3】如图，梯形ABCD 的两底长为6AD =，10BC =，中位线为EF ，且90B ∠=︒，若P 为AB 上的一点，且PE 将梯形ABCD 分成面积相同的两区域，则EFP ∆与梯形ABCD 的面积比为．五、中点四边形【例1】顺次连接四边形四条边的中点，所得的四边形是菱形，则原四边形一定是( )A ．平行四边形B ．对角线相等的四边形C ．矩形D ．对角线互相垂直的四边【例2】若顺次连接四边形ABCD 各边的中点所得到的四边形是矩形，则原四边形必定是（）A ．正方形B ．对角线相等的四边形C ．菱形D ．对角线互相垂直的四边形【例3】依次连接下列四边形四条边的中点得到四边形不是菱形的是（）A ．矩形B ．菱形C ．正方形D ．等腰梯形【例4】如图，四边形ABCD 中，AC a =，BD b =．且AC BD ⊥，顺次连接四边形ABCD 各边中点，得到四边形1111D C B A ，再顺次连接四边形1111D C B A 各边中点，得到四边形2222,A B C D ⋅⋅⋅，如此进行下去，得到四边形n n n n A B C D ．下列结论正确的是（）①四边形2222A B C D 是矩形；②四边形4444A B C D 是菱形；③四边形5555A B C D 的周长是4a b+，④四边形n n n n A B C D 的面积是12n ab+．A ．①②③B ．②③④C ．①②D ．②③1、如图，在Rt ABC ∆中，90C ∠=︒，5AC =，12BC =．若D ，E 分别为边AC ，BC 的中点，则DE 的长为( )A ．5B ．5.5C ．6D ．6.52、如图是屋架设计图的一部分，其中30A ∠=︒，点D 是斜梁AB 的中点，BC 、DE 垂直于横梁AC ，16AB m =，则DE 的长为( )A. 8mB ．4mC ．2mD ．6m3、如图，点D 、E 、F 分别是AC 、BC 、AB 中点，且BD 是ABC ∆的角平分线．求证：BE AF =．4．如图，平行四边形ABCD 中，对角线AC ，BD 相交于O ，2BD AD =，E ， F ， G 分别是OC ， OD ，AB 的中点，下列结论中：①BE AC ⊥；②四边形BEFG 是平行四边形；③EG GF =；④EA 平分GEF ∠，正确的是（）A ．①②B ．①②④C ．①②③D ．②③④5．如图，四边形ABCD 中，对角线AC BD ⊥，且8AC =，4BD =，各边中点分别为1A ，1B ，1C ，1D ，顺次连接得到四边形1111D C B A ；再取各边中点2A ，2B ，2C ，2D ，顺次连接得到四边形2222A B C D ；依此类推，这样得到四边形n n n n A B C D ，则四边形n n n n A B C D 的面积为____．6．已知一个对角线长分别为12cm 和16cm 的菱形，顺次连接它的四边中点得到的四边形的面积是______．7．如图，在ABC 和ABD △中，90ACB ADB ∠=∠=︒，E 、F 、G 分别为AB 、AC 、BC 的中点，若1DE =，则FG =________．8、如图，在ABC ∆中，90ACB ∠=︒，M 、N 分别是AB 、AC 的中点，延长BC 至点D ，使13CD BD =．连接DM 、DN 、MN ．若6AB =，求DN 的长．9．如图，在四边形ABCD 中，E ，F 分别是AD BC ，的中点．(1)若102430120AB CD ABD BDC ==∠=︒∠=︒，，，，求EF 的长．(2)若90BDC ABD ∠-∠=︒，求证：2224AB CD EF +=．10．已知：如图，四边形ABCD 四条边上的中点分别为E 、F 、G 、H ，顺次连接EF 、FG 、GH 、HE ，得到四边形(EFGH 即四边形ABCD 的中点四边形)．(1)四边形EFGH 的形状是______，请证明你的结论；(2)当四边形ABCD 的对角线满足______条件时，四边形EFGH 是菱形；(3)你学过的哪种特殊的平行四边形的中点四边形是菱形？请写出一种．11．定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在Rt ABC △中，90A ∠=︒，AB AC =，点D 、E 分别在边AB 、AC 上，AD AE =，连接DE 、DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点，且连接PM 、PN ．(1)观察猜想线段PM 与PN ______填（“是”或“不是”）“等垂线段”．(2)ADE 绕点A 按逆时针方向旋转到图2所示的位置，连接BD ，CE ，试判断PM 与PN 是否为“等垂线段”，并说明理由．(3)拓展延伸把ADE 绕点A 在平面内自由旋转，若2DE =，4BC =，请直接写出PM 与PN 的积的最大值．9.5 三角形的中位线同步培优讲练综合三角形的中位线1．连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于第三边，并且等于第三边的一半.顺次连接特殊的平行四边形各边中点得到的四边形的形状（1）顺次连接平行四边形各边中点得到的四边形是平行四边形.（2）顺次连接矩形各边中点得到的四边形是菱形.（3）顺次连接菱形各边中点得到的四边形是矩形.（4）顺次连接正方形各边中点得到的四边形是正方形.一、三角形中位线有关的求解问题【例1】如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点CD m，则A，B之间的距离是()C，D，量得10B.5m B．10mC．20m D．40m【答案】C【解析】解：点C，D分别是OA，OB的中点，220()AB CD m ∴==，故选：C ．【例2】如图，在ABC ∆中，点D 、E 分别是边AB 、AC 的中点，连接DE ，ABC ∠的平分线BF 交DE 于点F ，若4AB =，6BC =，则EF 的长为．【答案】1【解析】解：连接AF 并延长交BC 于H ，点D 、E 分别为边AB 、AC 的中点，//DE BC ∴，132DE BC ==，FH =，在BFA ∆和BFH ∆中，ABF HBF AFB HFB FA FH ∠=∠⎧⎪∠=∠⎨⎪=⎩，()BFA BFH AAS ∴∆≅∆，4BH AB ∴==，AD DB =，AF FH =，122DF BH ∴==， 1EF DE DF ∴=-=，故答案为：1．【例3】如图，在四边形ABCD 中，点P 是对角线BD 的中点，点E 、F 分别是AB 、CD 的中点，AD BC =，30PEF ∠=︒，则EPF ∠的度数是．【答案】120【解析】解：点P 是对角线BD 的中点，点E 、F 分别是AB 、CD 的中点，12PF BC ∴=，12PE AD =，又AD BC =， PE PF ∴=，30PFE PEF ∴∠=∠=︒，120EPF ∴∠=︒，故答案为：120︒．【例4】在ABC 中，120AB AC BAC =∠=︒，，D 为ABC 形内一点，以AD 为腰作等腰DAE ，使DAE BAC ∠=∠，连接BE CD 、，若M N 、分别是DE BC 、的中点，1MN =，则CD 的长为_______．【答案】2【解析】解：如图，连接BD ，取BD 的中点F ，连接FM FN ，，∵BAC EAD ∠=∠，BAC EAD ∠=∠， ∴BAC BAD EAD BAD ∠-∠=∠-∠，即BAE CAD ∠=∠，在AEB △和ADC △中，AE AD BAE CADAB AC =⎧⎪∠=∠⎨⎪=⎩，∴AEB ADC SAS ≌（），∴BE CD =，∵M 是ED 的中点，F 是BD 的中点，∴FM 是BED 的中位线， ∴12FM BE =，FM BE ∥，∴DFM EBD ∠=∠，同理得，1 2FN CD =，FN CD ，FM FN FNB DCB ∴=∠=∠，，∵DFN DBC FNB DBC DCB ∠=∠+∠=∠+∠，∴18012060MFN DFM DFN EBD DBC DCB ∠=∠+∠=∠+∠+∠=︒-︒=︒，∴FMN 是等边三角形，∴1MN FN ==，∴2CD =．故答案为：2．【例5】有一块梯形形状的土地，现要平均分给两个农户种植（即将梯形面积两等分），试设计两种方案，并说明理由．（平分图案画在备用图上，保留作图痕迹）【答案】见解析【解析】解：设梯形上、下底分别为a 、b ，高为h ．方案一：如图1，连接梯形上、下底的中点E 、F ，则()4ABFE EFCD a b h S S +==四边形四边形；方案二：如图2，连接AC ，取AC 的中点E ，连接BE ED 、，则图中的四边形ABED 的面积=梯形ABCD 的面积的一半，∵AE EC =，∴ABE BEC S S =，AED ECD S S =， ∴ABE AED BEC ECD S S S S +=+，∴四边形ABED 的面积=梯形ABCD 的面积的一半．方案三：如图3，分别量出梯形上、下底a 、b 的长，在下底BC 上截取2a b BE +=，连接AE ， ∴()1•24ABE a b h S BE h +==，()()()244ABE AECD ABCD a b h a b h a b h S S S +++=-=-=四边形梯形，则()4ABE AECD a b h S S +==四边形．【例6】如图，在ABC ∆中，点D ，E ，F 分别是边AB ，BC ，CA 上的中点，且10AB cm =，16AC cm =，则四边形ADEF 的周长等于 cm ．【答案】26【解析】解：点D ，E ，F 分别是边AB ，BC ，CA 上的中点，DE ∴，EF 都是ABC ∆的中位线，182DE AC cm ∴==，//DE AC ，152EF AB cm ==，//EF AB ， ∴四边形ADEF 是平行四边形，∴四边形ADEF 的周长2()21326()DE EF cm =+=⨯=．故答案为：26．【例7】如图，四边形ABCD 中，1AB =，4CD =，M 、N 分别是AD 、BC 的中点，则线段MN 的取值范围是( )A ．35MN <<B ．35MN <C ．3522MN <<D ．3522MN < 【答案】D【解析】解：连接AC ，取AC 的中点H ，连接MH 、NH ，M 、H 分别是AD 、AC 的中点，122MH CD ∴==，同理可得，1122NH AB ==，在MHN ∆中，MH NH MN MH NH -<<+，即3522MN <<，当H 在MN 上时，52MN MH NH =+=，∴3522MN <，故选：D ．【例8】如图，Rt ABC △中，90BAC ∠=︒，6AB =，10BC =，AD 、AE 分别是其角平分线和中线，过点B 作BG AD ⊥于G ，交AC 于F ，连接EG ，则线段EG 的长为（）A ．12 B ．1 C ．32 D ．2【答案】B【解析】解：Rt ABC △中，6AB =，10BC =，∴8AC ==，∵BG AD ⊥，∴AGB AGF ∠=∠．∵AD 平分BAC ∠，∴BAG FAG ∠=∠，在AGB 和AGF 中BAG FAG AG AGAGB AGF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴AGB AGF ≌∴6,AB AF BG FG ===，∴2CF =，∵AE 是ABC 的中线，∴BE CE =，∴EG 是BCF △的中位线，∴112EG CF ==，故选：B ．二、三角形中位线相关的面积问题【例1】如图，在ABC ∆中，D 、E 、F 分别是BC 、AC 、AD 的中点，若ABC ∆的面积是40，则四边形BDEF 的面积是( )A ．10B ．12.5C ．15D ．20 【答案】C【解析】解：D 、E 、F 分别是BC 、AC 、AD 的中点，12ADE ADC S S ∆∆∴=，12ADC ABC S S ∆∆=，12DEF ADE S S ∆∆=， 1140588DEF ABC S S ∆∆∴==⨯=， D 、E 、F 分别是BC 、AC 、AD 的中点，11402022ABD ABC S S ∆∆∴==⨯=， 11201022BDF ADB S S ∆∆∴==⨯=， ∴四边形BDEF 的面积15BDF DEF S S ∆∆=+=，故选：C ．【例2】E 、F 是线段AB 上的两点，且16AB =，2AE =，4BF =，点G 是线段EF 上的一动点，分别以AG 、BG 为斜边在AB 同侧作两个等腰直角三角形，直角顶点分别为D 、C ，如图所示，连接CD 并取中点P ，连接PG ，点G 从E 点出发运动到F 点，则线段PG 扫过的图形面积为______．【答案】30【解析】解：分别延长AD 、BC 相交于点H ，连接PH ，EH ，FH ，∵ADG △、GCB △为等腰直角三角形，∴45DGA CGB A B ∠=∠=∠=∠=︒，∴90DGC ∠=︒，∴AH GC ∥，又∵90HCG ∠=︒，∴90HCG DGC ∠=∠=︒，∴DG HB ∥，∴四边形DGCH 为矩形，∵点P 为DC 中点，∴点G 、P 、H 三点共线，且P 为HG 的中点，过P 作MN AB ∥分别交EH 、FH 与M 、N ，∴MN 为HEF 的中位线，且MN 即为点P 的运动轨迹， ∴GP 扫过的图形即为梯形MEFN ，∵16AB =，2AE =，4BF =，∴162410EF =--=， ∴152MN EF ==，过点H 作HO 垂直AB 于O ，∵45A B ∠=∠=︒，∴AH BH =，180454590AHB ∠=︒-︒-︒=︒， ∴182HO AO BO AB ====，∵MN 为HEF 的中位线， ∴118422PO HO ==⨯=，即梯形的高为4， ∴()14105302MEFN S =⨯⨯+=梯形，即线段PG 扫过的图形面积为30．故答案为：30．【例3】如图，在ABC 中，D ，E ，F 分别是BC AD CE ，，的中点，22cm BCF S =，则ABC S =_____2cm【答案】8【解析】解：如图，连接BE ，∵E 是AD 的中点， ∴12ABE ABD S S =△△，12ACE ACD S S =， ∴()11112222ABE ACE ABD ACD ABD ACD ABC S S S S S S S +++===， ∴12CBE ABC S S =，∵F 是CE 的中点， ∴1124FBC EBC ABC S S S ==，而22cm BCF S =， ∴28cm ABC S =．故答案为：8．【例4】如图，ABC 三边的中线AD ，BE ，CF 的公共点为G ，且:2:1AG GD =，若12ABC S =△，则图中阴影部分的面积是_____．【答案】4【解析】解：∵ABC 的三条中线AD ，BE ，CF 交于点G ，:2:1AG GD =，∴AE CE =， ∴13CGE AGE ACF S S S ==△△△，13BGF BGD BCF S S S ==，∵1112622ACF BCF ABC S S S ===⨯=△△△，∴231316CGE ACF S S ==⨯=，231316BGF BCF S S ==⨯=， ∴4CGE BGF S S S +==阴影．故答案为：4．【例5】如图，在Rt ABC △中，90BAC ∠=︒，,E F 分别是,BC AB 的中点，延长CA 到点D ，使得2AC AD =，连接,,,,DE DF AE EF AF 与DE 交于点O ．5,13AB BC ==，求四边形AEFD 的面积．【答案】15【解析】解：∵,E F 分别是,BC AB 的中点，∴EF 是ABC 的中位线，∴EF AC ∥，2AC EF =，∵2AC AD =，∴AD EF =，又∵AD EF ∥，∴四边形ADFE 是平行四边形，在Rt ABC △中，90BAC ∠=︒，5,13AB BC ==，∴12AC =，162EF AC AD ===， ∴1522AF AB ==， ∴56152ADFE S AD AF ==⨯=⨯平行四边形．与三角形中位线有关的应用和证明【例1】在ABC ∆中，点M 是边BC 的中点，AD 平分BAC ∠，BD AD ⊥，BD 的延长线交AC 于点E ，12AB =，20AC =．（1）求证：BD DE =；（2）求DM 的长．【答案】见解析【解析】（1）证明：AD 平分BAC ∠，BAD DAE ∴∠=∠．AD BD ⊥，90ADB ADE ∴∠=∠=︒．在ADB ∆与ADE ∆中，BAD EAD AD ADADB ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩ADB ADE ∴∆≅∆，BD DE ∴=．（2）ADB ADE ∆≅∆，12AE AB ∴==，8EC AC AE ∴=-=． M 是BC 的中点，BD DE =，142DM EC ∴==．【例2】如图，ABC ∆中，AH BC ⊥于点H ，点D ，E 分别是AB ，AC 的中点，连接DH ，EH ，DE ．（1）求证：AD DH =；（2）若四边形ADHE 的周长是30，ADE ∆的周长是21，求BC 的长．【答案】见解析【解析】解：（1）AH BC ⊥，90AHB ∴∠=︒，点D 是AB 的中点，12AD DH AB ∴==；（2）AH BC ⊥，90AHB AHC ∴∠=∠=︒，点D ，E 分别是AB ，AC 的中点，12AD DH AB ∴==，12AE HE AC ==，四边形ADHE 的周长是30，130152AD AE ∴+=⨯=， ADE ∆的周长是21，21156DE ∴=-=，点D ，E 分别是AB ，AC 的中点，DE ∴是ABC ∆的中位线，212BC DE ∴==．【例3】如图，在四边形ABCD 中，P 是对角线BD 的中点，E 、F 分别是AB 、CD 的中点，AD BC =，20PEF ∠=︒，求PFE ∠的度数．【答案】20【解析】解：P 是BD 的中点，E 是AB 的中点，PE ∴是ABD ∆的中位线，12PE AD ∴=，同理，12PF BC =， AD BC =，PE PF ∴=，20PFE PEF ∴∠=∠=︒．【例4】在Rt ABC 中，90BAC ∠=︒，E 、F 分别是BC 、AC 的中点，延长BA 到点D ，使2AB AD =，连接DE 、DF 、AE 、EF ，AF 与DE 交于点O ．(1)试说明AF 与DE 互相平分；(2)若8AB =，12BC =，求DO 的长．【答案】(1)见解析【解析】（1）∵E 、F 分别是BC 、AC 的中点，∴EF 是ABC 的中位线，∴EF AB ∥且12EF AB =．又2AB AD =，即12AD AB =， ∴AD EF ，AD EF =，∴四边形AEFD 是平行四边形，∴AF 与DE 互相平分；（2）∵在Rt ABC 中，90BAC ∠=︒，8AB =，12BC =，∴由勾股定理得AC又由（1）知，OA OF =，且AF CF =，∴14OA AC =∴在AOD △中，90DAO ∠=︒，142AD AB ==，OA∴由勾股定理得 DO ==三、梯形中位线【例1】已知一个梯形的中位线长为5cm ，其中一条底边的长为6cm ，那么该梯形的另一条底边的长是 cm ．【答案】4【解析】解：设梯形的另一条底边为xcm ，由题意得：625x +=⨯，解得4x =．即梯形的另一条底边的长为4cm ．故答案为：4．【例2】如图，已知直角梯形ABCD 的一条对角线把梯形分为一个直角三角形和一个边长为8cm 的等边三角形，则梯形ABCD 的中位线长为( )B. 4cmB ．6cmC ．8cmD ．10cm【答案】B【解析】解：DBC ∆是等边三角形，8DB DC BC cm ∴===，60DBC ∠=︒，90ABC ∠=︒，30ABD ∴∠=︒，90A ∠=︒，142AD BD cm ∴==，∴梯形ABCD 的中位线是11()(48)622AD BC cm cm cm +=⨯+=，故选：B ．【例3】如图，梯形ABCD 的两底长为6AD =，10BC =，中位线为EF ，且90B ∠=︒，若P 为AB 上的一点，且PE 将梯形ABCD 分成面积相同的两区域，则EFP ∆与梯形ABCD 的面积比为．【答案】1：16【解析】解：梯形ABCD 的两底长为6AD =，10BC =，11()(610)822EF AD BC ∴=+=⨯+=，()()11610822ABCD S AD BC AB AB AB ∴=+⨯=⨯+⨯=梯形．()()1117682242AFED S AD EF AB AB AB =+⨯=+⨯=梯形，1714222EFP ABCD AFED S S S AB AB AB ∆∴=-=-=梯形梯形，1::81:162EFP ABCD S S ∆∴==梯形．故答案为：1:16．四、中点四边形【例1】顺次连接四边形四条边的中点，所得的四边形是菱形，则原四边形一定是() A ．平行四边形 B ．对角线相等的四边形C ．矩形D ．对角线互相垂直的四边【答案】B【解析】解：四边形EFGH 是菱形，1122EH FG EF HG BD AC ∴=====，故AC BD =．故选：B ．【例2】若顺次连接四边形ABCD 各边的中点所得到的四边形是矩形，则原四边形必定是（）A ．正方形B ．对角线相等的四边形C ．菱形D ．对角线互相垂直的四边形【答案】D【解析】解：如图，四边形EFGH 是矩形90FEH ∴∠=︒点E 、F 的分别是AD 、AB 的中点EF ∴是ABD ∆的中位线EF BD ∴∥90FEH OMH ∴∠=∠=︒点E 、H 的分别是AD 、CD 的中点EH ∴是ACD ∆的中位线EH AC ∴90OMH COB ∴∠=∠=︒AC BD ∴⊥．故选：D【例3】依次连接下列四边形四条边的中点得到四边形不是菱形的是（）A ．矩形B ．菱形C ．正方形D ．等腰梯形【答案】B【解析】解：如图所示，依次连接四边形四条边的中点，∵矩形ABCD ，∴AB CD ，AD BC ∥，AB CD =，AD BC =，且点E ，F ，G ，H 分别为四边的中点，∴AEF BGF CGH DEH △≌△≌△≌△， ∴EF GF GH EH ===，∴EFGH 是菱形；∴A 选项不符合题意；如上图所示，由A 选项结论得菱形EFGH ，点O ，P ，Q ，R 分别为四边的中点，∴EO OF FP PG QG QH HR ER =======，且菱形的对角相等，∴(SAS)EOR GPQ △≌△，(SAS)OFP HQR △≌△，∴OR PQ =，OP QR =，∴四边形OPRQ 是平行四边形，不一定是菱形；∴B 选项符合题意；如下图所示，正方形ABCD ，点E ，F ，G ，H 分别为四边的中点，∴AE AF FB BG GC CH HD DE =======，且90A B C D ∠=∠=∠=∠=︒，∴AEF BGF CGH DEH △≌△≌△≌△， ∴EF GF GH EH ===，∴EFGH 是菱形；∴C 选项不符合题意；如下图所示，等腰梯形ABCD ，点E ，F ，G ，H 分别为四边的中点，∴AE DE =，AF DH =，A D ∠=∠，∴(SAS)AEF DEH △≌△，∴EF EH =，同理可得，FG GH =，连接AC ，在ACD ，ACB △中，点E ，F ，G ，H 分别为四边的中点，根据三角形的中位线的性质可知，FG AC ，12FG AC =，EH AC ，12EH AC =，∴FG EH =，FG EH ∥，∴四边形EFGH 是平行四边形，又∵EF EH =，FG GH =，∴EFGH 是菱形；∴D 选项不符合题意．故选：B ．【例4】如图，四边形ABCD 中，AC a =，BD b =．且AC BD ⊥，顺次连接四边形ABCD 各边中点，得到四边形1111D C B A ，再顺次连接四边形1111D C B A 各边中点，得到四边形2222,A B C D ⋅⋅⋅，如此进行下去，得到四边形n n n n A B C D ．下列结论正确的是（）①四边形2222A B C D 是矩形；②四边形4444A B C D 是菱形；③四边形5555A B C D 的周长是4a b+，④四边形n n n n A B C D 的面积是12n ab+．A ．①②③B ．②③④C ．①②D ．②③【答案】B【解析】解：①连接A 1C 1，B 1D 1．∵在四边形ABCD 中，顺次连接四边形ABCD 各边中点，得到四边形A 1B 1C 1D 1，∴A 1D 1∥BD ，B 1C 1∥BD ，C 1D 1∥AC ，A 1B 1∥AC ；∴A 1D 1∥B 1C 1，A 1B 1∥C 1D 1，∴四边形A 1B 1C 1D 1是平行四边形；∵AC ⊥BD ，∴四边形A 1B 1C 1D 1是矩形，∴B 1D 1=A 1C 1（矩形的两条对角线相等）；∴A 2D 2=C 2D 2=C 2B 2=B 2A 2（中位线定理），∴四边形A 2B 2C 2D 2是菱形；故①错误；②由①知，四边形A2B2C2D2是菱形；∴根据中位线定理知，四边形A4B4C4D4是菱形；故②正确；③根据中位线的性质易知，A 5B 5=12A 3B 3=1122⨯A 1B 1=111222⨯⨯AC ， B 5C 5=12B 3C 3=1122⨯B 1C 1=111222⨯⨯BD ， ∴四边形A 5B 5C 5D 5的周长是()1284a b a b +⨯+=故③正确；④∵四边形ABCD 中，AC=a ，BD=b ，且AC ⊥BD ，∴S 四边形ABCD=12ab ；由三角形的中位线的性质可以推知，每得到一次四边形，它的面积变为原来的一半，四边形AnBnCnDn 的面积是12n ab+故④正确；综上所述，②③④正确．故选：B ．1、如图，在Rt ABC ∆中，90C ∠=︒，5AC =，12BC =．若D ，E 分别为边AC ，BC 的中点，则DE 的长为( )A ．5B ．5.5C ．6D ．6.5【答案】D【解析】解：90C ∠=︒，5AC =，12BC =，13AB ∴=，AD DC =，CE EB =，1 6.52DE AB ∴==，故选：D ．2、如图是屋架设计图的一部分，其中30A ∠=︒，点D 是斜梁AB 的中点，BC 、DE 垂直于横梁AC ，16AB m =，则DE 的长为( )B. 8mB ．4mC ．2mD ．6m 【答案】B【解答】解：30A ∠=︒，16AB m =，1116822BC AB m ∴==⨯=， BC 、DE 垂直于横梁AC ，//BC DE ∴，点D 是斜梁AB 的中点，118422DE BC m ∴==⨯=．故选：B ．3、如图，点D 、E 、F 分别是AC 、BC 、AB 中点，且BD 是ABC ∆的角平分线．求证：BE AF =．【答案】见解析【解析】【解答】证明：连接DE ，点D 、E 、F 分别是AC 、BC 、AB 中点．//DE AB ∴，//EF AC ，∴四边形ADEF 是平行四边形，AF DE ∴=， BD 是ABC ∆的角平分线，ABD DBE ∴∠=∠，DBE BDE ∴∠=∠，BE DE ∴=，BE AF ∴=．4．如图，平行四边形ABCD 中，对角线AC ，BD 相交于O ，2BD AD =，E ， F ， G 分别是OC ，OD ，AB 的中点，下列结论中：①BE AC ⊥；②四边形BEFG 是平行四边形；③EG GF =；④EA 平分GEF ∠，正确的是（）A ．①②B ．①②④C ．①②③D ．②③④【答案】B【解析】解：如图，四边形ABCD 是平行四边形BO DO ∴==12BD ，AD BC =，AB CD =，又2BD AD =，OB BC OD DA ∴===，且点E 是OC 中点，BE AC ∴⊥，故①正确，E 、F 分别是OC 、OD 的中点，∴EF CD ∥，EF =12CD ，点G 是Rt ABE △斜边AB 上的中点，GE ∴=12AB AG BG ==EG EF AG BG ∴===，无法证明GE GF =，故③错误，BG EF =，BG EF CD ∥∥∴四边形BEFG 是平行四边形故②正确，EF CD AB ∥∥，BAC ACD AEF ∠∠∠∴==，AG GE =，GAE AEG ∠∠∴=，EF CD ∥AEF ACD ∴∠=∠,AB CD ∥，GAE ACD ∴∠=∠，AEG AEF ∠∠∴=，AE ∴平分GEF ∠，故④正确；故选：B ．5．如图，四边形ABCD 中，对角线AC BD ⊥，且8AC =，4BD =，各边中点分别为1A ，1B ，1C ，1D ，顺次连接得到四边形1111D C B A ；再取各边中点2A ，2B ，2C ，2D ，顺次连接得到四边形2222A B C D ；依此类推，这样得到四边形n n n n A B C D ，则四边形n n n n A B C D 的面积为____．【答案】162n【解析】∵四边形ABCD 中，对角线AC BD ⊥，且8AC =，4BD = ∴11841622=⨯⨯=⨯⨯=ABCD S AC BD∵中点四边形的面积是原四边形面积的一半 ∴11111162==⨯A B C D ABCD S S222221162==⨯A B C D ABCD S S 以此类推，1161622==⨯=n n n n A B C D ABCD n n S S6．已知一个对角线长分别为12cm 和16cm 的菱形，顺次连接它的四边中点得到的四边形的面积是______．【答案】48【解析】解：E 、F 、G 、H 分别为各边中点，EF GH AC ∴∥∥，2EF GH AC ==，12EH FG BD ==，EH FG BD ∥∥，DB AC ⊥， EF EH ∴⊥，∴四边形EFGH 是矩形， 16cm 2EH BD ==，18cm 2EF AC ==，∴矩形EFGH 的面积26848cm EH EF =⨯=⨯=，故答案为：248cm ．7．如图，在ABC 和ABD △中，90ACB ADB ∠=∠=︒，E 、F 、G 分别为AB 、AC 、BC 的中点，若1DE =，则FG =________．【答案】1【解析】解：Rt ABC 中，点E 是AB 的中点，1DE =，22AB DE ∴==，点F 、G 分别是AC 、BC 中点， ∴112FG AB ==，故答案为：18、如图，在ABC ∆中，90ACB ∠=︒，M 、N 分别是AB 、AC 的中点，延长BC 至点D ，使13CD BD =．连接DM 、DN 、MN ．若6AB =，求DN 的长．【答案】3【解析】解：连接CM ，90ACB ∠=︒，M 是AB 的中点，132CM AB ∴==， M 、N 分别是AB 、AC 的中点，12MN BC ∴=，//MN BC ， 13CD BD =，MN CD ∴=，又//MN BC ，∴四边形NDCM 是平行四边形，3DN CM ∴==．9．如图，在四边形ABCD 中，E ，F 分别是AD BC ，的中点．(1)若102430120AB CD ABD BDC ==∠=︒∠=︒，，，，求EF 的长．(2)若90BDC ABD ∠-∠=︒，求证：2224AB CD EF +=．【答案】（1）13 （2）见解析【解析】（1）如图，取BD 的中点P ，连接EP FP 、，∵E ，F 分别是AD BC 、的中点，1024AB CD ==，，∴PE AB ∥，且152PE AB ==，PF CD ∥，且1122PF CD ==．又∵30120ABD BDC ∠=︒∠=︒，，∴3018060EPD ABD DPF BDC ∠=∠=︒∠=︒-∠=︒，，∴90EPF EPD DPF ∠=∠+∠=︒．在Rt EPF中，13EF ===．（2）证明：如图，取BD 的中点P ，连接EP FP 、．∵E ，F 分别是AD BC 、的中点，∴PE AB ，且12PE AB =，PF CD ∥，且12PF CD =．∴180EPD ABD DPF BDC ∠=∠∠=︒-∠，．∵90BDC ABD ∠-∠=︒，∴90∠=︒+∠BDC ABD ，∴180EPF EPD DPF ABD BDC ∠=∠+∠=∠+︒-∠180(90)90ABD ABD =∠+︒-︒+∠=︒， ∴222221122PE PF AB CD EF ⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭， ∴2224AB CD EF +=．10．已知：如图，四边形ABCD 四条边上的中点分别为E 、F 、G 、H ，顺次连接EF 、FG 、GH 、HE ，得到四边形(EFGH 即四边形ABCD 的中点四边形)．(1)四边形EFGH 的形状是______，请证明你的结论；(2)当四边形ABCD 的对角线满足______条件时，四边形EFGH 是菱形；(3)你学过的哪种特殊的平行四边形的中点四边形是菱形？请写出一种．【答案】(1)平行四边形．证明见解析(2)AC BD =；(3)矩形的中点四边形是菱形．【解析】（1）四边形EFGH 的形状是平行四边形．理由如下：如图1，连接BD ．E 、H 分别是AB 、AD 中点，EH BD ∴∥，12EH BD =，同理FG BD ∥，12FG BD =，EH FG ∴∥，EH FG =，∴四边形EFGH 是平行四边形；故答案为：平行四边形；（2）当四边形ABCD 的对角线满足AC BD =的条件时，四边形EFGH 是菱形．理由如下：如图2，连接AC 、BD ．E 、F 、G 、H 分别为四边形ABCD 四条边上的中点，EH BD ∴∥，HG AC ∥，1=2EH BD ，12HG AC =，AC BD =，EH HG ∴=，又四边形EFGH 是平行四边形∴平行四边形EFGH 是菱形；故答案为：AC BD =；（3）矩形的中点四边形是菱形．理由如下：连接AC 、BD ．E 、F 、G 、H 分别为四边形ABCD 四条边上的中点，EH BD ∴∥，HG AC ∥，FG BD ∥，EF AC ∥，12FG EH BD ==，12EF HG AC ==，四边形ABCD 是矩形，AC BD ∴=，EH BD HG AC ===，∴四边形EFGH 是菱形．11．定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在Rt ABC △中，90A ∠=︒，AB AC =，点D 、E 分别在边AB 、AC 上，AD AE =，连接DE 、DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点，且连接PM 、PN ．(1)观察猜想线段PM 与PN ______填（“是”或“不是”）“等垂线段”．(2)ADE 绕点A 按逆时针方向旋转到图2所示的位置，连接BD ，CE ，试判断PM 与PN 是否为“等垂线段”，并说明理由．(3)拓展延伸把ADE 绕点A 在平面内自由旋转，若2DE =，4BC =，请直接写出PM 与PN 的积的最大值．【答案】】(1)是(2)是，答案见解析(3)92【解析】（1）解：线段PM 与PN 是“等垂线段”．理由如下：∴12MP EC =，12PN BD =，∵AB AC =，AD AE =，∴AB AD AC AE -=-，即BD CE =，∴MP PN =．∵点M 、P 、N 分别为DE 、DC 、BC 的中点，∴MP EC ∥，PN BD ∥，∵在Rt ABC △中，90A ∠=，AB AC =，∴45B ACB ∠=∠=︒，∴45ACD DCB ∠=︒-∠，180135BDC B DCB DCB ∠=︒-∠-∠=︒-∠，∵MP EC ∥，PN BD ∥，∴45MPD ACD DCB ∠=∠=︒-∠，()180********DPN BDC DCB DCB ∠=︒-∠=︒-︒-∠=︒+∠， ∴454590MPD DPN DCB DCB ∠+∠=︒-∠+︒+∠=︒，∴MP PN ⊥，即线段PM 与PN 是“等垂线段”，故答案为：是．（2）解：线段PM 与PN 是“等垂线段”，理由如下：∵ADE 绕点A 按逆时针方向旋转到图2所示的位置，∴AD AE =，=90DAE ∠︒，∵90BAC ∠=︒，∴BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠，在ABD △与ACE △中，∵AB AC BAD CAE DA EA =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ABD ACE △≌△， ∴BD CE =，∴12MP EC =，12PN BD =，∵BD CE =，∴MP PN =．∵点M 、P 、N 分别为DE 、DC 、BC 的中点，∴MP EC ∥，PN BD ∥，∵在Rt ABC △中，90BAC ∠=，AB AC =，∴45ABC ACB ∠=∠=︒，∴45ACD DCB ∠=︒-∠，45DBC ABD ∠=︒-∠，()180********BDC DBC DCB ABD DCB ABD DCB ∠=︒-∠-∠=︒-︒-∠-∠=︒+∠-∠ ∵MP EC ∥，PN BD ∥，∴MPD ECD ECA ACD ∠=∠=∠+∠，∵()SAS ABD ACE △≌△，∴ABD ACE ∠=∠，即MPD ECD ABD ACD ∠=∠=∠+∠()18018045DPN BDC ABD DCB ABD DCB ∠=︒-∠=︒-︒+∠-∠=︒-∠+∠， ∴45454590MPD DPN ABD ACD ABD DCB ∠+∠=∠+∠+︒-∠+∠=︒+︒=︒， ∴MP PN ⊥．∵MP PN =，MP PN ⊥．故线段PM 与PN 是“等垂线段”．（3）解：由（2）可知，MP PN =，MP PN ⊥，故222MN PM PN PM ⨯==，当MN 取最大值时，PM 与PN 的积有最大值．∵把ADE 绕点A 在平面内自由旋转，∴当N 、A 、M 三点共线，且点A 在NM 之间时，MN 取最大值．∴此时MN NA AM =+．∵在Rt ABC △中，90BAC ∠=，AB AC =，4BC =，N 为BC 的中点， ∴122NA BC ==，同理可得，112MA DE ==， ∴MN 的最大值为3，PM 与PN 的积有最大值92．。

三角形的中位线培优练习精品

精品∙三角形的中位线培优练习知识点：1、三角形的中位线定义：连结三角形两边中点的线段.2、三角形中位线定理： ①三角形的中位线于第三边（位置关系）②三角形的中位线等于（数量关系）3、三角形中位线特点：①三角形中位线所截的小三角形的周长等于原三角形周长的1/2,面积等于原三角形的1/4②线过三角形一边的中点的直线如平行第三边，则它必经过另一边的中点一、基础练习1. 如图，DE 是△ABC 的中位线，则△ABC 与△ADE 的周长的比是 ( )A ．1:2B ．2:1C ．1:3D ．3:12. 如图，在Rt △ABC 中，∠A=30°，BC=1，点D ，E 分别是直角边BC ，AC 的中点，则DE 的长为（）A ．1B ．2C．D ．1+3. 如图，DE 是△ABC 的中位线，过点C 作CF ∥BD 交DE 的延长线于点F ，则下列结论正确的是（）A ．EF=CFB ．EF=DEC ．CF ＜BD D ．EF ＞DE4. 一个三角形的周长是36 cm ，则以这个三角形各边中点为顶点的三角形的周长是 ( )A ．6 cmB ．12 cmC ．18 cmD ．36 cm5. 如图，在△ABC 中，∠ABC=90°，AB=8，BC=6．若DE 是△ABC 的中位线，延长DE 交△ABC 的外角∠ACM 的平分线于点F ，则线段DF 的长为（） A ．7B ．8C ．9D ．106. 如图，在△ABC 中，∠ACB=90°，AC=8，于点E ，则DE 的长为（） A ．6B ．5C ．4D ．37. 如图，在△ABC 中，点D ，E 分别是边AB ，AC 的中点，AF ⊥BC ，垂足为点F ，∠ADE=30°，DF=4，则BF 的长为（）A ．4B ．8C ．2D ．48. 在△ABC 中，AB=3，BC=4，AC=2，D 、E 、F 分别为AB 、BC 、AC 中点，连接DF 、FE ，则四边形DBEF 的周长是（）A ．5B ．7C ．9D ．119. 如图，在△ABC 中，D 、E 分别是边AB 、AC 的中点，BC=8，则DE= ．(9) (10) (11) (12) (13) (14)10. 如图，小明为了测量学校里一池塘的宽度AB ，选取可以直达A 、B 两点的点O处，再分别取OA 、OB 的中点M 、N ，量得MN=20m ，则池塘的宽度AB 为 m11. 如图，在Rt △ABC 中，∠ACB=90°，D 、E 、F 分别是AB 、BC 、CA 的中点，若CD=5cm ，则EF= cm ．12. 如图，在△ABC 中，∠ACB=90°，M 、N 分别是AB 、AC 的中点，延长BC 至点D ，FMECB APFEDCBFNMECBANMDCBA使CD=BD，连接DM、DN、MN．若AB=6，则DN= ．13. 如图，M是△ABC的边BC的中点，AN平分∠BAC，且BN⊥AN，垂足为N，且AB ＝6，BC＝10，MN＝1.5，则△ABC的周长是．14. 如图，在△ABC中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于cm．二、提高练习【利用角平分线+垂直、必有等腰三角形】例题1：如图，△ABC中，CD平分∠ACB，AD⊥CD，垂足为D点，点E为AB 的中点.（1）求证：DE∥BC；（2）求证：DM=（BC-AC）/2练习：如图，△ABC中，点M为△ABC的边BC的中点，AD为∠BAC的外角平分线，且DB⊥AD,连接DM.（1）求证：MD∥AC；（2）求证：DM=（AB+AC）/2练习：如图，在∆ABC中，AB=BC，∠ABC=90°，F为BC上一点，M为AF的中点，BE平分∠ABC，且EF⊥BE，求证：CF=2ME。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级数学三角形中位线培优专题训练
一、内容提要
1. 三角形中位线平行于第三边，并且等于第三边的一半。

梯形中位线平行于两底，并且等于两底和的一半。

2. 中位线性质定理的结论，兼有位置和大小关系，可以用它判定平行，计算线段的长度，
确定线段的和、差、倍关系。

3. 运用中位线性质的关键是从出现的线段中点，找到三角形或梯形，包括作出辅助线。

4. 中位线性质定理，常与它的逆定理结合起来用。

它的逆定理就是平行线截比例线段定理
及推论，
①一组平行线在一直线上截得相等线段，在其他直线上截得的线段也相等 ②经过三角形一边中点而平行于另一边的直线，必平分第三边 ③经过梯形一腰中点而平行于两底的直线，必平分另一腰 5. 有关线段中点的其他定理还有： ①直角三角形斜边中线等于斜边的一半
②等腰三角形底边中线和底上的高，顶角平分线互相重合 ③对角线互相平分的四边形是平行四边形 ④线段中垂线上的点到线段两端的距离相等因此如何发挥中点作用必须全面考虑。

二、例题
例1. 已知：△ABC 中，分别以AB 、AC 为斜边作等腰直角三角形ABM 和CAN ，P 是
BC 的中点。

求证：PM ＝PN
证明：作ME ⊥AB ，NF ⊥AC ，垂足E ，F ∵△ABM 、△CAN 是等腰直角三角形
∴AE ＝EB
＝ME ，AF ＝FC ＝NF ，
根据三角形中位线性质 PE ＝
21AC ＝NF ，PF ＝2
1
AB ＝ME
PE ∥AC ，PF ∥AB
∴∠PEB ＝∠BAC ＝∠PFC 即∠PEM ＝∠PFN
∴△PEM ≌△PFN ∴PM ＝PN
例2.已知△ABC 中，AB ＝10，AC ＝7，AD 是角平分线，CM ⊥AD 于M ，且N 是BC 的中点。

求MN 的长。

分析：N 是BC 的中点，若M 是另一边中点，则可运用中位线的性质求MN 的长，根据轴称性质作出△AMC 的全等三角形即可。

辅助线是：延长CM 交AB 于E （证明略例3.如图已知：△ABC 中，AD 是角平分线，BE ＝CF ，M 、N 分别是BC 和EF 的中点求证：MN ∥AD 证明一：连结EC ，取EC 的中点P ，连结PM 、PN
P N
MP ∥AB ，MP ＝
21AB ，NP ∥AC ，NP ＝2
1AC ∵BE ＝CF ，∴MP ＝NP
∴∠3=∠4=2
MPN
-180∠
∠MPN ＋∠BAC ＝180
（两边分平行的两个角相等或互补）
∴∠1=∠2=2
MPN
-180∠ ， ∠2=∠3
∴NP ∥AC ∴MN ∥AD
证明二：连结并延长EM 到G ，使MG ＝ME 连结CG ，FG
则MN ∥FG ，△MCG ≌△MBE ∴CG ＝BE ＝CF ∠B ＝∠BCG
∴AB ∥CG ，∠BAC ＋∠FCG ＝180 ∠CAD ＝
2
1（180
－∠FCG ） ∠CFG ＝
2
1（180
－∠FCG ）=∠CAD ∴ MN ∥AD 例4. 已知：△ABC 中，AB ＝AC ，AD 是高，CE 是角平分线，EF ⊥BC 于F ，GE ⊥CE
交CB 的延长线于G 求证：FD ＝
4
1
CG 证明要点是：延长GE 交AC 于H ，可证E 是GH 的中点
过点E 作EM ∥GC 交HC 于M ，
则M 是HC 的中点，EM ∥GC ，EM ＝2
1
GC
由矩形EFDO 可得FD ＝EO ＝21EM ＝4
1
GC
三、练习
1. 如图11，M 、P 分别为△ABC 的AB 、AC 上的点，且AM=BM ，AP=2CP ，BP 与CM 相交于N ，已知PN=1，则PB 的长为 ( ) A. 2 B. 3 C .4 D. 5
2. 如图12，△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点，AB=10，则MD 的长为 ( )
A. 10
B. 8 C .6 D. 5
3. 如图13，△ABC 是等边三角形，D 、E 、F 分别是AB 、BC 、AC 的中点，P 为不同于B 、E 、C 的BC 上的任意一点，△DPH 为等边三角形.连接FH ，则EP 与FH 的大小关系是 ( ) A. E P>FH B. EP=FH C. EP<FH D.不确定
4. 如图14，在△ABC 中，AD 平分∠BAC ，BD ⊥AD ，DE ∥AC ，交AB 于E ,若AB=5，则DE 的长为 .
C
5. 如图15，△ABC中，AB=4，AC=7，M为BC的中点，AD平分∠BAC，过M作MF∥AD，
交AC于F，则FC的长等于.
6. 如图25，P为△ABC内一点，∠P AC=∠PBC，PM⊥AC于M，PN⊥BC于N.D是AB的
中点.
求证：DM=DN
7. 如图16，在△ABC中，D、E是AB、AC上的点，且BD=CE，M、N分别是BE、CD的中点，直线MN分别交AB、AC于P、Q.
求证：AP=AQ
8. 如图17，BE、CF是△ABC的角平分线，AN⊥BE于N，AM⊥CF于M.
求证：MN∥BC.
9. 如图18，在△ABC中，AD平分∠BAC，AD=AB，CM⊥AD于M.
求证：AB+AC=2AM
10.如图19，四边形ABCD中，G、H分别是AD、BC的中点，AB=CD.BA、CD的延长线交
HG的延长线于E、F.
求证：∠BEH=∠CFH.
1. 如图20，在△ABC中，∠ABC=2∠C，AD平分∠BAC，过BC的中点M作ME⊥AD，交
BA的延长线于E，交AD的延长线于F.
求证：
1
2
BE BD
.
2. 如图21，在△ABC中，AB<AC，P为AC上的点，CP=AB，K为AP的中点，M为BC
的中点，MK的延长线交BA的长线于N.
求证：AN=AK.
3. 如图22，分别以△ABC的边AC、BC为腰，A、B为直角顶点，作等腰直角△ACE和等
腰直角△BCD，M为ED的中点.
求证：AM⊥BM.
4. 如图23，点O是四边形ABCD内一点，∠AOB=∠COD=1200，AO=BO，CO=DO，E、
F、G分别为AB、CD、BC的中点.
求证：△EFG为等边三角形.
5. 如图24，△ABC中，M是AB的中点，P是AC的中点，D是MB的中点，N是CD的中
点，Q是MN的中点，直线PQ交MB于K.
求证：K是DB的中点.
6. 如图25，P为△ABC内一点，∠P AC=∠PBC，PM⊥AC于M，PN⊥BC于N.D是AB的
中点.
求证：DM=DN
图21 图22 图23 图24 图25
7. 如图26，AP是△ABC的角平分线，D、E分别是AB、AC上的点，且BD=CE.又G、H
分别为BC、DE的中点.
求证：HG∥AP.
8. 如图27，已知△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=900，如图(a)，连接
DE，设M为DE的中点.
(1)求证：MB=MC;
(2)设∠BAD=∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图(b)的位置，
试问MB=MC是否成立?并证明其结论.
9. 已知△ABC面积为S，作直线l∥BC，交AB于D，交AC于E，若△BED的积为K.
求证：S≥4K.
10.如图28，在△ABC中，AB=AC，D是BC边上的一点，E是线段AD上的一点．且∠BED=2
∠CED=∠BAC.
求证：BD=2CD.
图26 图27。

八年级数学三角形中位线培优专题训练

(完整版)初二中位线专题训练

八年级数学中心对称和三角形中位线最新最全练习巩固含答案-初中数学培优

2022-2023学年第二学期初二数学名校优选培优训练专题09 三角形中位线定理

八下9.5三角形的中位线难题训练（有答案）

湘教版数学八年级下册_《三角形的中位线》提高训练

2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线

人教版八年级数学下册三角形的中位线练习题(含答案)

三角形的中位线练习题(8年级)

八年级数学三角形中位线培优专题训练

2020-2021学年北师大版八年级数学下册《6.3三角形的中位线》同步优生辅导训练(附答案)

初二数学三角形中位线练习题(含答案)

北师大版八年级数学下册 三角形的中位线 巩固练习 含答案解析

初二数学三角形中位线练习题（含答案）

北师大版数学八年级下册：6.3 三角形的中位线 同步练习(附答案)

浙教版八年级数学下册 4.5 《中位线》提优训练(含答案)

中考数学复习三角形的中位线【培优讲练】

三角形的中位线培优练习精品

北师大版八年级数学下册三角形的中位线巩固练习含答案解析

北师大版数学八年级下册：6.3 三角形的中位线同步练习(附答案)