第二章恒定电场09
合集下载
第二章静电场恒定电场和恒定磁场

图2.1电介质的极化
介质中的高斯定理表示为 式中电位移矢量为
在线性的各向同性的电介质中
例2.1在空气中放入一个带电量为Q、半径为a的球体,该球体的 相对介电常数为εr。求该球体内、外任意一点的电场强度。
解(1) 球内任意一点,设到球心距离为r,做高斯面为以r为半径的球面, 如图2.2所示。
由电场的对称性可知,E和D的方向为er,所以
大小、它们之间的距离和周围的电介质,即可以不用电容器。
例2.10同心金属球与球壳系统如图2.12所示,内导体球半径为a,外导体 球壳的内外半径分别为b和c,导体球与导体球壳带有等量异号电荷,它
们之间充满相对介电常数为 r 的电介质,球外为空气。求该导体系统
的电容。
解:根据高斯定理不难求出空间各点的电场强度,设导体球和导体球壳的 带电量分别是q和-q,则导体和导体球壳之间的电场强度的大小为
电场能为
WeΒιβλιοθήκη 1 2dVv
(2) 对于多导体系统
We
1 2
dV
v
例2.12半径分别为a和b的同轴线,外加电压为U,内圆柱体电荷量为正,外圆柱 面单位长度上的电荷量与内圆柱体等值异号。如图2.16(a)所示,两电极间在θ1的 角度内填充介电常数为ε的电介质,其余部分为空气,求同轴线单位长度上储存 的电场能量。
示,求在l长度上的外电感。
图2.25例2.20用图
例2.21一个半径为a的无限长直导线,在导线均匀流过的电流为I,求这个导线
在单位长度上的内电感,如图2.26所示(设导体内部的磁导率近似为μ0)。 解:截面上的磁通并没有与全部电流I交链,而只是与一部分电流交链,交链的总 磁链为
图2.26
2. 互 有两感个回路l1和l2,如图2.27所示。
介质中的高斯定理表示为 式中电位移矢量为
在线性的各向同性的电介质中
例2.1在空气中放入一个带电量为Q、半径为a的球体,该球体的 相对介电常数为εr。求该球体内、外任意一点的电场强度。
解(1) 球内任意一点,设到球心距离为r,做高斯面为以r为半径的球面, 如图2.2所示。
由电场的对称性可知,E和D的方向为er,所以
大小、它们之间的距离和周围的电介质,即可以不用电容器。
例2.10同心金属球与球壳系统如图2.12所示,内导体球半径为a,外导体 球壳的内外半径分别为b和c,导体球与导体球壳带有等量异号电荷,它
们之间充满相对介电常数为 r 的电介质,球外为空气。求该导体系统
的电容。
解:根据高斯定理不难求出空间各点的电场强度,设导体球和导体球壳的 带电量分别是q和-q,则导体和导体球壳之间的电场强度的大小为
电场能为
WeΒιβλιοθήκη 1 2dVv
(2) 对于多导体系统
We
1 2
dV
v
例2.12半径分别为a和b的同轴线,外加电压为U,内圆柱体电荷量为正,外圆柱 面单位长度上的电荷量与内圆柱体等值异号。如图2.16(a)所示,两电极间在θ1的 角度内填充介电常数为ε的电介质,其余部分为空气,求同轴线单位长度上储存 的电场能量。
示,求在l长度上的外电感。
图2.25例2.20用图
例2.21一个半径为a的无限长直导线,在导线均匀流过的电流为I,求这个导线
在单位长度上的内电感,如图2.26所示(设导体内部的磁导率近似为μ0)。 解:截面上的磁通并没有与全部电流I交链,而只是与一部分电流交链,交链的总 磁链为
图2.26
2. 互 有两感个回路l1和l2,如图2.27所示。
恒定电场_new
恒定电场是无源无旋场。
四.分界面上的衔接条件
1
S
2
2
1
J2
1
l1
1
2 由 E dl 0 l E2
2
J1
l 0
E1
l2 0 由
(1)
J dS 0
S
E1t E2t
(2)
在各向同性媒质中, J E ,二者方向一致 tan 1 1 ——折射定律 tan 2 2
§2-3恒定电场基本方程· 分界面 上的衔接条件
一.电流连续性方程
电荷守恒定律,
高斯散度公式
q J dS S t
——积分形式
J dS J dV S V q dV t t V
J dV dV V t V
S
在导体内任一闭合面内包含的净电荷q=0, 所以在均匀导体内部虽然有恒定电流,但没有 电荷,电荷只能分布在导体表面上。
二.电场强度的环路线积分
( E Ee ) dl E dl Ee dl
l l l
设积分路径经过电源,
若积分路径不经过电源,则
q 在恒定电场中, 0 t
J t
——微分形式
J dS 0
S
, J 0
恒定电场是一个无源场,电流线是连续的(无 头无尾的闭合线)。
对于均匀导电媒质,电导率 是常量,
J 0
J E
或,
E E 0 E 0 E dS 0
R1
R2
E
内外导体间电压:
第二章-静电场恒定电场磁场-汪

D
介质中微分形式的高斯定律表明,某点电位移的散度等于该点 自由电荷的体密度。 电位移也可用一系列曲线表示。曲线上某点的切线方向等于该
点电位移的方向,这些曲线称为电位移线。若规定电位移线组成的
相邻的通量管中电位移的通量相等,那么电位移线的疏密程度即可 表示电位移的大小。值得注意的是,电位移线起始于正的自由电荷,
极化产生的面分布及体分布的束缚电荷又称为极化电荷。可以证明
极化电荷可表示为
(r ) P(r ) en S
(r ) P (r )
右式又可写为积分形式
q P dS
S
由此可见,任一块介质内部体分布的束缚电荷与介质块的表 面束缚电荷是等值异性的。
4. 介质中的静电场方程
q r r 4π 0 r r
若观察距离远大于两电荷的间距 l ,则可认为 e r ,er 与 er 平行,则
r r l cos
l l r r r cos r cos r 2 2 2
若B点为电位参考点 ,即 B 0 ,则A点电位为
B
A
B E dl A
若电荷以一定的密度分布在一个有限的体积内,电位与电荷体密 度的关系为:
1 将 R | r r | 带入上式 (r ) 4π 0
电场强度与电荷体密度的关系为
1 (r ) 4π 0
V R dV
在介质内部,穿过任一闭合面 S 的电通应为
S
E dS
1
0
(q q)
式中 q 为闭合面 S 中的自由电荷,q为闭合面S 中的束缚电荷。那么
令 D 0 E P,求得
介质中微分形式的高斯定律表明,某点电位移的散度等于该点 自由电荷的体密度。 电位移也可用一系列曲线表示。曲线上某点的切线方向等于该
点电位移的方向,这些曲线称为电位移线。若规定电位移线组成的
相邻的通量管中电位移的通量相等,那么电位移线的疏密程度即可 表示电位移的大小。值得注意的是,电位移线起始于正的自由电荷,
极化产生的面分布及体分布的束缚电荷又称为极化电荷。可以证明
极化电荷可表示为
(r ) P(r ) en S
(r ) P (r )
右式又可写为积分形式
q P dS
S
由此可见,任一块介质内部体分布的束缚电荷与介质块的表 面束缚电荷是等值异性的。
4. 介质中的静电场方程
q r r 4π 0 r r
若观察距离远大于两电荷的间距 l ,则可认为 e r ,er 与 er 平行,则
r r l cos
l l r r r cos r cos r 2 2 2
若B点为电位参考点 ,即 B 0 ,则A点电位为
B
A
B E dl A
若电荷以一定的密度分布在一个有限的体积内,电位与电荷体密 度的关系为:
1 将 R | r r | 带入上式 (r ) 4π 0
电场强度与电荷体密度的关系为
1 (r ) 4π 0
V R dV
在介质内部,穿过任一闭合面 S 的电通应为
S
E dS
1
0
(q q)
式中 q 为闭合面 S 中的自由电荷,q为闭合面S 中的束缚电荷。那么
令 D 0 E P,求得
恒定电场
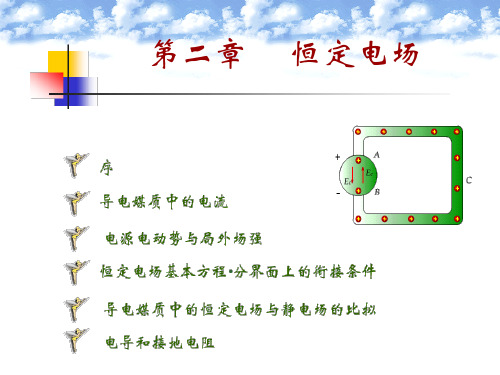
E J I 2l R2 I I R U E dl d ln 2 R1 2l 2 l R1 2l G I 电导 U R2 ln R1 I I J 设 2l
图2.5.1
同轴电缆横截面
绝缘电阻
1 1 ln R2 R G 2l R1
I dI J lim n n S 0 S dS
单位: 安培/米2 (A/m2)
电流密度
可以从电流密度J求出流过任意面积S的电流强度。一
般情况下,电流密度J和面积元dS的方向并不相同。
此时,通过面积S的电流就等于电流密度J在S上的通
量,即
I J dS JdScosθ
R2
1
U 0 e
电流 电导
I J dS
U 0 U h R (e ) hd (e ) 0 ln 2 S R R1 I h R2 G ln ( S m) U 0 R1
2.5.2
接地电阻
安全接地与工作接地的概念
接地器电阻
接地电阻 接地器与土壤之间的接触电阻 土壤电阻(接地电阻以此电阻为主) 1. 深埋球形接地器
•
• •
两种场的电极形状、尺寸与相对位置相同(相拟);
相应电极的电压相同; 若两种场中媒质分片均匀,只要分界面具有相似
r1 1 r2 2
的几何形状,且满足条件
时,则这两种场
在分界面处折射情况仍然一样,相拟关系仍成立。
2.4.3
静电比拟的应用
1. 静电场便于计算—— 用静电比拟方法计算 恒定电场
2 0
D1n D2n
I J dS
S
2 0
S
q D dS
E1t E2t
图2.5.1
同轴电缆横截面
绝缘电阻
1 1 ln R2 R G 2l R1
I dI J lim n n S 0 S dS
单位: 安培/米2 (A/m2)
电流密度
可以从电流密度J求出流过任意面积S的电流强度。一
般情况下,电流密度J和面积元dS的方向并不相同。
此时,通过面积S的电流就等于电流密度J在S上的通
量,即
I J dS JdScosθ
R2
1
U 0 e
电流 电导
I J dS
U 0 U h R (e ) hd (e ) 0 ln 2 S R R1 I h R2 G ln ( S m) U 0 R1
2.5.2
接地电阻
安全接地与工作接地的概念
接地器电阻
接地电阻 接地器与土壤之间的接触电阻 土壤电阻(接地电阻以此电阻为主) 1. 深埋球形接地器
•
• •
两种场的电极形状、尺寸与相对位置相同(相拟);
相应电极的电压相同; 若两种场中媒质分片均匀,只要分界面具有相似
r1 1 r2 2
的几何形状,且满足条件
时,则这两种场
在分界面处折射情况仍然一样,相拟关系仍成立。
2.4.3
静电比拟的应用
1. 静电场便于计算—— 用静电比拟方法计算 恒定电场
2 0
D1n D2n
I J dS
S
2 0
S
q D dS
E1t E2t
(电磁场PPT)第二章 恒定电场

第二章
由电路理论
恒定电场
2.1.3 欧姆定律的微分形式
U RI
R l
S
电导率与电阻率的关系: 1 ,
(r 电阻率), (电导率)。 r
图2.1.5 J 与 E 之关系
在场论中 dI J dS
dU dI R J dS dl
dS
E dl
J E 欧姆定律 微分形式。
第二章
恒定电场
U RI 欧姆定律 积分形式。
本章要求:
理解各种电流密度的概念,通过欧姆定律和焦耳 定律深刻理解场量之间的关系。
掌握导电媒质中的恒定电场基本方程和分界面衔 接条件。
熟练掌握静电比拟法和电导的计算。
第二章
恒定电场知识结构
基本物理量 J、 E
欧姆定律
恒定电场
J 的散度
基本方程
E 的旋度
边界条件
边值问题
电位
一般解法 电导与接地电阻 特殊解(静电比拟)
第二章
第二章 恒定电场
Steady Electric Field
导电媒质中的电流 电源电动势与局外场强 基本方程 • 分界面衔接条件 • 边值问题 导电媒质中恒定电场与静电场的比拟 电导和接地电阻
恒定电场
第二章
恒定电场
通有直流电流的导电媒质中同时存在着电流场和 恒定电场。恒定电场是动态平衡下的电荷产生的,电 荷作宏观运动,电荷的分布不随时间变化(即:恒定 ),它与静电场有相似之处。
—焦耳定律积分形式
第二章
2.2 电源电动势与局外场强
2.2.1 电源 (Source)
恒定电场
提供非静电力将其它形式的 能转为电能的装置称为电源。
图2.2.1 恒定电流的形成
恒定电场基本方程课件.ppt
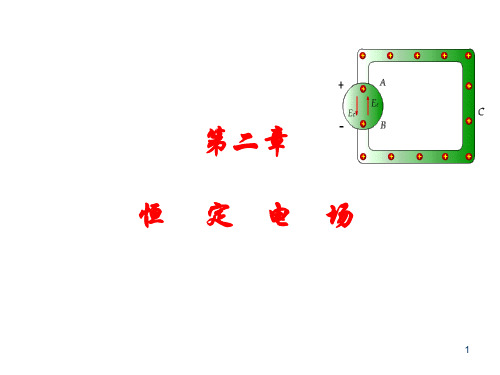
答:( C )
24
2、同轴电缆的内导体半径R1=1mm,外导体内表 面半径R2=5mm,长为20m,导体间充满非理想绝 缘材料,材料的电导率为=10-18S/m,求同轴电 缆的内外导体间电阻。1.281×1016
25
作业
P81:2-4-2 P88:2-5-2 P91:习题2-12
26
2
U0
45º 2
0 R1 R2 x
d
2( ) =C + D
由边界条件、分界条件求出A、B、C、D
1( ) 、 2( ) 12
解: 求出1( ) 、 2( ) E
I
G
E=
=
e
1 r
d d
J = E
I = SJ • dS
G= I U
Jy
1 1J
▽
22 =
1
2
2 2 2
=0
1 |( =/2) = U0 边界条件
2 |( =0) =0 1 |( =/4) = 2 |( =/4)
分界条件
1
d1 d
= / 4
=
2
d 2 d
= / 4
解微分方程,得通解: 1( ) =A + B
y
1 1J
要减小电阻:
五、深埋电极的接地电阻: 则增大接地体的面积;
或在接地体附近掺入高的媒质。
假设I J E U R
距离圆心r处的电流密度为:
J=
I
4r 2
er
电场强度为:
E=
J
=
I
4 r 2
er
I
电压为:U =
24
2、同轴电缆的内导体半径R1=1mm,外导体内表 面半径R2=5mm,长为20m,导体间充满非理想绝 缘材料,材料的电导率为=10-18S/m,求同轴电 缆的内外导体间电阻。1.281×1016
25
作业
P81:2-4-2 P88:2-5-2 P91:习题2-12
26
2
U0
45º 2
0 R1 R2 x
d
2( ) =C + D
由边界条件、分界条件求出A、B、C、D
1( ) 、 2( ) 12
解: 求出1( ) 、 2( ) E
I
G
E=
=
e
1 r
d d
J = E
I = SJ • dS
G= I U
Jy
1 1J
▽
22 =
1
2
2 2 2
=0
1 |( =/2) = U0 边界条件
2 |( =0) =0 1 |( =/4) = 2 |( =/4)
分界条件
1
d1 d
= / 4
=
2
d 2 d
= / 4
解微分方程,得通解: 1( ) =A + B
y
1 1J
要减小电阻:
五、深埋电极的接地电阻: 则增大接地体的面积;
或在接地体附近掺入高的媒质。
假设I J E U R
距离圆心r处的电流密度为:
J=
I
4r 2
er
电场强度为:
E=
J
=
I
4 r 2
er
I
电压为:U =
电磁场课件 第2章 恒定电场

I
a 4r 2 4a
R 1/( 4a )
深埋球形接地器
(2) 非深埋(浅) 的球形接地器
考虑地面的影响,用镜像法处理。
C G
实际电阻与计算电阻:
√ R实际=2 R计算?
R实际=
1 2
R计算?
理由: R实际 || R实际 R计算
浅埋半球形接地器
2.5.3 跨步电压 (Step Voltage)
J dS
l
S
dl
dS
(2) E dl (J dS)(
dl
)
γdS
意义: • 电场是维持恒定电 流的必要条件。
J γE
微分形式 • 恒定电流场与恒定
电场相互依存。一一
对应
2.1.3 焦尔定律的微分形式
导电媒质中有电流时,必伴随功率损耗。
P p
IU dP
d ( IU
)
(J
dS)( E
2.1.1 电流密度和元电流段
电荷密度的定向移动形成电流密度。
(1) 电流面密度
分布的体电荷以速度v作匀速运动形成的电流。
J
ρv
(A/m 2 )
电流 I SJ dS
(2) 电流线密度
分布的面电荷在曲面上以速度v运动形成的电流。
K σv (A m)
电流
I l(K en )dl
(3) 线电流
折射定律: tg1 1 tg2 2
若1为导体,2为介质:
结导论体:表只面要穿出1,良2导,体电表流面线近垂似直为于等良
位面。
2.3.5 恒定电场的边值问题
2 0 —— 拉普拉斯方程
分界面衔接条件: 1 2
1
2
n
第二章恒定电场-工程电磁场导论-冯慈章课件
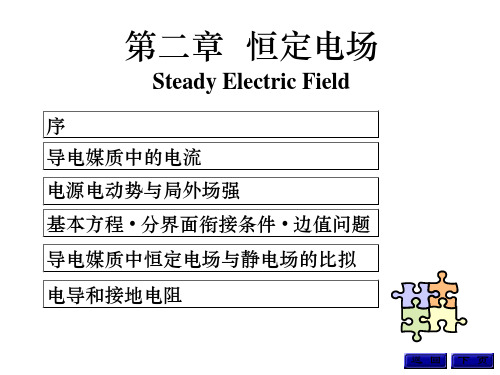
一、电源电动势与局外场强
电源是一种将其它能量转换成电能的装置; 局外力: f e
局外场强:Ee
方向由电源负极指向正 极
电源电动势: Ee dl
l
库仑场强:E
方向由电源正极指向负 极
Engineering electrical magnetic field
二、恒定电场
导电媒质中的恒定电场; 通有恒定电流的导体周围电介质或空气中的 恒定电场。
J1 J 2 J I / S E1 E2 J / p1 p2 P p1Sd , P2 p2 S 2d 1 P2 2 P 1
图2-4 平行板电容器的电场 功率的一个计算例子
2.2电源电动势与局外场强
Engineering electrical magnetic field
。 返 回 上 页 下 页
4. 元电流段的概念 元电流是元电荷dq以速度 v 运动形成的电流
C m s A m
νdV (体电流元) JdV
dq
νdS (面电流元) KdS νdl (线电流元) Idl
2.1.3 欧姆定律的微分形式 (Differential Form of Ohm’s Law)
dq I dt
2.1.2 电流密度(Current Density)
1. 电流面密度 J 体电荷 以速度 v 作匀速运动形成的电流。 电流密度 电流
J v
I J dS
S
J的大小 垂直于电流方向的平面 里,单位面积上通过 的电流强度。
A m2 J的方向与电流方向相同 ;
J2
en 2
2
1
1 J1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R2
(R1 r R2 )
E
J
I 2l
I
R1
R2 d ln 2l 2 l 34 R1
I
电导
绝缘电阻
解法二
I 2l G R2 U ln R1 1 1 R2 R ln G 2l R1
静电比拟法
I
R1
由静电场解得
C 关系式得 则根据 G 2l 同轴电缆电导 G R2 ln R1
电路中的焦耳定律,可由它的积分而得,即
P UI I R
2
(W)—— 焦耳定律的积分形式
10
小结:
I
S
J dS
欧姆定律的微分形式
J
J E
I
S 面:用与I 流动的 方向垂直的平面去 切导电媒质得到的 截面。
焦耳定律的微分形式
p E
(W/m3 )
11
体分布dV JdV ( dV )v 面分布 s dS KdS ( s dS )v 线分布 l dl Idl ( dl )v ( v )dl
定义:流经导体的电流与导体两端的电压之比称为电导,用 G表示 G I U 其单位为S或(西门子)。
R U I 1 G
电导的倒数称为电阻 单位为(欧姆)。
导体的电导或电阻的大小与导体的电导率、形状、几何尺 寸以及电极的位置等因素相关。一般情况下导体的形状并 不规则,难于用解析的方法计算其电导或电阻,此时,可 采用图解法或数值计算方法。
J E
J 0
E 0
18
e E dl 0
• 恒定电场是无源无旋场。
恒定电场积分
形式基本方程:
静电场积分
形式基本方程:
E d l 0 J d S 0 J E
S l
E d l 0 0 D d S q D E
0
0 ,
U0
方程通解为
界条件,可得
C1 C2 ,代入边
电位函数
(
U0
图2.5.2 弧形导电片
U0 E e e 36
) ,
电流密度
电流
U 0 J E e
R2
I J dS
S
不含场源
19
l
2.3.2
分界面的衔接条件
分界面上的衔接条件
E dl 0
L
S
E1t E 2t J1n J 2 n
J dS 0
说明分界面上电场强度的切向分 量是连续的,电流密度法向分量是连 续的。
折射定律为
tan 1 1 tan 2 2
图2.3.1 20 电流线的折射
2l C , R2 ln R1
绝缘电阻
R2
,
R2 R ln 2 l R 35 1
1
例2.5.2 求图示电导片的电导,已知给定
0 时, 0; 时 , U0
解:取圆柱坐标系,
( ) ,边值问题
2 1 2 2 2 0
第二章
恒定电场
1
基本概念: •
通有恒定电流的导电媒质中的恒定电场 (电流场)
• 通有恒定电流的导电媒质周围电介质中 的静态电场
• 注意:本章只研究导电媒质内部的区域
• 本章研究的对象是导电媒质,其 与静电场中所说的导体是什么关 2 系?
§2-1
导电媒质中的电流
在外电场的作用下,自由电荷定向运动形成电流 导电媒质中的运动电荷的定向运动形成的电流叫传导电流 单位时间内通过某一横截面的电量, 简称为电流。
12
元电荷dq
元电流dqv
2.2 电源电势与局外场强
2.2.1 电源 要想在导线中维持恒定电 流,必须依靠非静电力将B极 板的正电荷抵抗电场力搬到A 极板。这种提供非静电力将其
它形式的能量转为电能装置称
为电源。
图2.2.2 恒定电流的形成
13
2.2.2 电源电动势与局外场强
fe 设局外场强为 E e ,则电源电动势为: q
2 1 2 2 2 2 0 2
( 2 区域)
场域边界条件
0
0,
2
, 2
U0
衔接条件
1 2
图2.3.3 不同媒质弧形导电片
1
1 2 2 , ( ) 4
24
电位
4 2U 0 ( 1 2 )U 0 1 , ( 1 2 ) 1 2
31
例2.5.1 求同轴电缆的绝缘电 阻。设内外的半径分别为R1、R2,长 度为 ,中间媒质的电导率为 ,介
l
电常数为
。
图2.5.1
同轴电缆横截面
32
I
S
J dS
33
解法一
直接用电流场的计算方法
解:设同轴电缆长为 L, 假设漏电流为 I.
I
J
I 2l
R1 R2
U E dl
dq I dt
A
I 是通量,并不反映电流在 每一点的流动情况。
3
2.1.1 电流强度
1.电流体密度
分布的体电荷以速度v 作匀速运动形成的电流。
J v
亦称电流面密度
电流
Am
2
I
S
J dS
4
2. 电流面密度
分布的面电荷在曲面上以速度v运动形成的电流。
K v
电流
Am
线电流密度矢量
l
E e dl
(V )
电源电动势与有无外电路无关,它是表示电源本身的特征量。
考虑局外场强
J ( E Ee )
因此
Ee
( E E ) dl E dl E
l e l l
e
dl
0
局外场 Ee 是非保守场。
图2.2.3 电源电动势与局外场强
I ( K en )dl
l
I
l:用与I 流动的方向垂直的平
面去切导电媒质得到的截线。
en 是垂直于dl,且通过dl与
曲面相切的单位矢量
5 图2.1.3 电流线密度及其通量
工程意义:
• 同轴电缆的外导体视为电流面密度分布;
• 媒质的磁化,其表面产生磁化电流可用电流面密度表示, 如图示;
• 交变电场的集肤效应,即高频情况下,电流趋於表面分 布,可用电流面密度表示。 3、线电流
那么,通过对一个场的求解或实验研究,利用对应量关系便可
得到另一个场的解。
27
静电场
1 2 2 2 ( , ) 1 2 1 2
28
图示恒定电流场对应什么样的静电场?比拟条件?
图2.4.2
静电场平行板造型 29
2.5 电导与接地电阻
J E
2 0
q D D dS
S
2 0
I
E1t E2t D1n D2n
E1t E2t J1n J 2n
26
J dS
S
表2 两种场对应物理量 静电场 ( 0) 导电媒质中恒定电场(电源外) E
D
q
E
J
I
两种场各物理量所满足的方程一样,若边界条件也相同,
S
R1
U 0 U 0 h R2 (e ) hd (e ) ln R1
电导
I h R2 G ln U 0 R1
( S m)
图2.5.2 弧形导电片
37
2.5.2 接地电阻
为了保证电气设备正常工作和操作人员人身安全,应使用接 地装置将用电设备的某一部分接地。 接地装置包括接地体和接地线。接地体是埋入地下的金属导 体(如圆钢、扁钢、钢管等),接地导线将设备连接到接地 体上。 工作电流、短路电流或雷电电流通过接地线流向接地体,再 分散流入大地。 接地电阻等于设备接地点对地电压与通过接地线、接地体流 入大地的电流之比,它包括接地线、接地体的电阻,接地体 与土壤之间的接触电阻,以用电设备大地接地体及电流所流 经土壤的电阻。其中土壤的电阻占主要部分,通常我们把这 一电阻近似作为接地电阻。
14
2.3 恒定电场的基本方程 2.3.1
分界面上的衔接条件 边值问题
恒定电场的基本方程
1. J 的散度 电流的连续性定律
q J d S S t
• 定义:由电荷守恒定律,从
任一闭合面流出的传导电流, 应等于该面所围体积内电荷 的减少率:
15
q J dS t S q I J dS dV t t V S
元电荷dq
元电流dqv
面分布KdS KdS (dS )v 线分布Idl Idl (dl )v
(v)dl
7
2.1.3 欧姆定律的微分形式
U 欧姆定律: I R
电场是维持恒定电流的必要 条件。可以证明
J E
式中 为电导率,单位s/m( 西门子/米)。
例2.3.1 特殊情况分界面上的电场分布。
解:媒质1是良导体,
1 5 10 s / m
7
媒质2是不良导体, 由折射定理得
2 102 s / m
t an 1 1 ,则 2 0 t an 2 2
表明,只要
1
,电流
2
线垂直于良导体表面穿出,良 导体表面近似为等位面。
(R1 r R2 )
E
J
I 2l
I
R1
R2 d ln 2l 2 l 34 R1
I
电导
绝缘电阻
解法二
I 2l G R2 U ln R1 1 1 R2 R ln G 2l R1
静电比拟法
I
R1
由静电场解得
C 关系式得 则根据 G 2l 同轴电缆电导 G R2 ln R1
电路中的焦耳定律,可由它的积分而得,即
P UI I R
2
(W)—— 焦耳定律的积分形式
10
小结:
I
S
J dS
欧姆定律的微分形式
J
J E
I
S 面:用与I 流动的 方向垂直的平面去 切导电媒质得到的 截面。
焦耳定律的微分形式
p E
(W/m3 )
11
体分布dV JdV ( dV )v 面分布 s dS KdS ( s dS )v 线分布 l dl Idl ( dl )v ( v )dl
定义:流经导体的电流与导体两端的电压之比称为电导,用 G表示 G I U 其单位为S或(西门子)。
R U I 1 G
电导的倒数称为电阻 单位为(欧姆)。
导体的电导或电阻的大小与导体的电导率、形状、几何尺 寸以及电极的位置等因素相关。一般情况下导体的形状并 不规则,难于用解析的方法计算其电导或电阻,此时,可 采用图解法或数值计算方法。
J E
J 0
E 0
18
e E dl 0
• 恒定电场是无源无旋场。
恒定电场积分
形式基本方程:
静电场积分
形式基本方程:
E d l 0 J d S 0 J E
S l
E d l 0 0 D d S q D E
0
0 ,
U0
方程通解为
界条件,可得
C1 C2 ,代入边
电位函数
(
U0
图2.5.2 弧形导电片
U0 E e e 36
) ,
电流密度
电流
U 0 J E e
R2
I J dS
S
不含场源
19
l
2.3.2
分界面的衔接条件
分界面上的衔接条件
E dl 0
L
S
E1t E 2t J1n J 2 n
J dS 0
说明分界面上电场强度的切向分 量是连续的,电流密度法向分量是连 续的。
折射定律为
tan 1 1 tan 2 2
图2.3.1 20 电流线的折射
2l C , R2 ln R1
绝缘电阻
R2
,
R2 R ln 2 l R 35 1
1
例2.5.2 求图示电导片的电导,已知给定
0 时, 0; 时 , U0
解:取圆柱坐标系,
( ) ,边值问题
2 1 2 2 2 0
第二章
恒定电场
1
基本概念: •
通有恒定电流的导电媒质中的恒定电场 (电流场)
• 通有恒定电流的导电媒质周围电介质中 的静态电场
• 注意:本章只研究导电媒质内部的区域
• 本章研究的对象是导电媒质,其 与静电场中所说的导体是什么关 2 系?
§2-1
导电媒质中的电流
在外电场的作用下,自由电荷定向运动形成电流 导电媒质中的运动电荷的定向运动形成的电流叫传导电流 单位时间内通过某一横截面的电量, 简称为电流。
12
元电荷dq
元电流dqv
2.2 电源电势与局外场强
2.2.1 电源 要想在导线中维持恒定电 流,必须依靠非静电力将B极 板的正电荷抵抗电场力搬到A 极板。这种提供非静电力将其
它形式的能量转为电能装置称
为电源。
图2.2.2 恒定电流的形成
13
2.2.2 电源电动势与局外场强
fe 设局外场强为 E e ,则电源电动势为: q
2 1 2 2 2 2 0 2
( 2 区域)
场域边界条件
0
0,
2
, 2
U0
衔接条件
1 2
图2.3.3 不同媒质弧形导电片
1
1 2 2 , ( ) 4
24
电位
4 2U 0 ( 1 2 )U 0 1 , ( 1 2 ) 1 2
31
例2.5.1 求同轴电缆的绝缘电 阻。设内外的半径分别为R1、R2,长 度为 ,中间媒质的电导率为 ,介
l
电常数为
。
图2.5.1
同轴电缆横截面
32
I
S
J dS
33
解法一
直接用电流场的计算方法
解:设同轴电缆长为 L, 假设漏电流为 I.
I
J
I 2l
R1 R2
U E dl
dq I dt
A
I 是通量,并不反映电流在 每一点的流动情况。
3
2.1.1 电流强度
1.电流体密度
分布的体电荷以速度v 作匀速运动形成的电流。
J v
亦称电流面密度
电流
Am
2
I
S
J dS
4
2. 电流面密度
分布的面电荷在曲面上以速度v运动形成的电流。
K v
电流
Am
线电流密度矢量
l
E e dl
(V )
电源电动势与有无外电路无关,它是表示电源本身的特征量。
考虑局外场强
J ( E Ee )
因此
Ee
( E E ) dl E dl E
l e l l
e
dl
0
局外场 Ee 是非保守场。
图2.2.3 电源电动势与局外场强
I ( K en )dl
l
I
l:用与I 流动的方向垂直的平
面去切导电媒质得到的截线。
en 是垂直于dl,且通过dl与
曲面相切的单位矢量
5 图2.1.3 电流线密度及其通量
工程意义:
• 同轴电缆的外导体视为电流面密度分布;
• 媒质的磁化,其表面产生磁化电流可用电流面密度表示, 如图示;
• 交变电场的集肤效应,即高频情况下,电流趋於表面分 布,可用电流面密度表示。 3、线电流
那么,通过对一个场的求解或实验研究,利用对应量关系便可
得到另一个场的解。
27
静电场
1 2 2 2 ( , ) 1 2 1 2
28
图示恒定电流场对应什么样的静电场?比拟条件?
图2.4.2
静电场平行板造型 29
2.5 电导与接地电阻
J E
2 0
q D D dS
S
2 0
I
E1t E2t D1n D2n
E1t E2t J1n J 2n
26
J dS
S
表2 两种场对应物理量 静电场 ( 0) 导电媒质中恒定电场(电源外) E
D
q
E
J
I
两种场各物理量所满足的方程一样,若边界条件也相同,
S
R1
U 0 U 0 h R2 (e ) hd (e ) ln R1
电导
I h R2 G ln U 0 R1
( S m)
图2.5.2 弧形导电片
37
2.5.2 接地电阻
为了保证电气设备正常工作和操作人员人身安全,应使用接 地装置将用电设备的某一部分接地。 接地装置包括接地体和接地线。接地体是埋入地下的金属导 体(如圆钢、扁钢、钢管等),接地导线将设备连接到接地 体上。 工作电流、短路电流或雷电电流通过接地线流向接地体,再 分散流入大地。 接地电阻等于设备接地点对地电压与通过接地线、接地体流 入大地的电流之比,它包括接地线、接地体的电阻,接地体 与土壤之间的接触电阻,以用电设备大地接地体及电流所流 经土壤的电阻。其中土壤的电阻占主要部分,通常我们把这 一电阻近似作为接地电阻。
14
2.3 恒定电场的基本方程 2.3.1
分界面上的衔接条件 边值问题
恒定电场的基本方程
1. J 的散度 电流的连续性定律
q J d S S t
• 定义:由电荷守恒定律,从
任一闭合面流出的传导电流, 应等于该面所围体积内电荷 的减少率:
15
q J dS t S q I J dS dV t t V S
元电荷dq
元电流dqv
面分布KdS KdS (dS )v 线分布Idl Idl (dl )v
(v)dl
7
2.1.3 欧姆定律的微分形式
U 欧姆定律: I R
电场是维持恒定电流的必要 条件。可以证明
J E
式中 为电导率,单位s/m( 西门子/米)。
例2.3.1 特殊情况分界面上的电场分布。
解:媒质1是良导体,
1 5 10 s / m
7
媒质2是不良导体, 由折射定理得
2 102 s / m
t an 1 1 ,则 2 0 t an 2 2
表明,只要
1
,电流
2
线垂直于良导体表面穿出,良 导体表面近似为等位面。
