哈工大 电磁场第二章恒定电场
合集下载
电磁场教案恒定电场公开课一等奖优质课大赛微课获奖课件
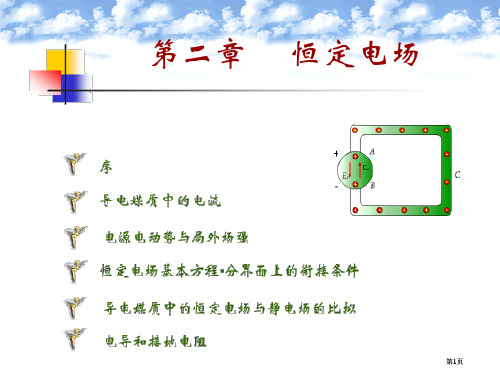
电导率为 ,介电 常数为 。
解法一 直接用电流场计算办法
设
IJ I E J I
2l
2l
图2.5.1 同轴电缆横截面
解法二 静电比拟法
U E dl R2 I d I ln R2
R1 2l
2 l R1
电导 绝缘电阻
G I 2l
U ln R2 R1
R 1 1 ln R2
G 2l R1
(W)
—— 焦耳定律积分形式
2.2 电源电势与局外场强
2.2.1 电源
要想在导线中维持恒定电流,必须依托非 静电力将B极板正电荷抵抗电场力搬到A极板。 这种提供非静电力将其它形式能量转为电能装 置称为电源。
图2.2.2 恒定电流形成
第6页
2.2.2 电源电动势与局外场强
设局外场强为
Ee
fe q
,则电源电动势为 l Ee dl
s J dS 0 e E dl 0
• 恒定电场是无源无旋场。
J 0 E 0
J E
第8页
2.3.2 分界面衔接条件
分界面上衔接条件
LE dl 0 SJ dS 0
E1t E2t J1n J 2n
阐明分界面上电场强度切向分量是连续,电流 密度法向分量是连续。
折射定律为
tan1 1 tan2 2
第9页
b) 媒质1是导体,( 1 0) 媒质2是抱负介质 ( 2 0) 情况。
2 0 J2 0 J2n J1n 0
表明 1 导体表面是一条电流线。
E2n
J 2n
2
0
E1n
J1n 1
D2n D1n 2 E 2n
表明 2 导体与抱负介质分界面上必有恒定(动态
解法一 直接用电流场计算办法
设
IJ I E J I
2l
2l
图2.5.1 同轴电缆横截面
解法二 静电比拟法
U E dl R2 I d I ln R2
R1 2l
2 l R1
电导 绝缘电阻
G I 2l
U ln R2 R1
R 1 1 ln R2
G 2l R1
(W)
—— 焦耳定律积分形式
2.2 电源电势与局外场强
2.2.1 电源
要想在导线中维持恒定电流,必须依托非 静电力将B极板正电荷抵抗电场力搬到A极板。 这种提供非静电力将其它形式能量转为电能装 置称为电源。
图2.2.2 恒定电流形成
第6页
2.2.2 电源电动势与局外场强
设局外场强为
Ee
fe q
,则电源电动势为 l Ee dl
s J dS 0 e E dl 0
• 恒定电场是无源无旋场。
J 0 E 0
J E
第8页
2.3.2 分界面衔接条件
分界面上衔接条件
LE dl 0 SJ dS 0
E1t E2t J1n J 2n
阐明分界面上电场强度切向分量是连续,电流 密度法向分量是连续。
折射定律为
tan1 1 tan2 2
第9页
b) 媒质1是导体,( 1 0) 媒质2是抱负介质 ( 2 0) 情况。
2 0 J2 0 J2n J1n 0
表明 1 导体表面是一条电流线。
E2n
J 2n
2
0
E1n
J1n 1
D2n D1n 2 E 2n
表明 2 导体与抱负介质分界面上必有恒定(动态
电磁场与电磁波(第2章静电场与恒定电场)

V
1 4 0
V
(r ') RdV ' 3 R
面电荷和线电荷产生的电场只需在上式中将电荷体密度、体积元 和积分区域作相应替换即可,如
4 0 1 E r 4 0
E r
1
s r ' R
3
V
R l r ' R
3泊松方程拉普拉斯方程由0?e?称为静电场的标量位函数又称电位函数xyzexeyez?????????????????????lel????由此可求得电位的微分d??ddlel??el在任意方向上的分量e空间ab两点的电位差dbebala?????l若选取为电位参即则任意点的电位为ppppxyz0p?axyzxyzdpppxyzapl?????el1电位函数za?ya?xa?ezyx??????????对于点电荷的电位体电荷面电荷和线电荷分布的电位函数表达式为
R r r '
式中0 为真空介电常数。
0 8.854187817 10 12 (F / m) 1 10 9 (F/m) 36π
库仑定律分析: 作用力的性质:电荷 q1 在空间激发电场,电场力
q1 ( r r ' ) F12 4 | r r ' |3 q2 0
结 果 分 析
(1)当 z→0,此时 P点移到圆心,圆环上各点产生的电场抵消, E=0 (2)当 z→∞, R 与 z 平行且相等,r<<z ,带电圆环相当于一个点 电荷,有
E z
q 4 0 R
e 2 z
例:求真空中半径为a,带电量为Q的导体球在球外空间 中产生E。 由球体的对称性分析可知: 电场方向沿半径方向: 电场大小只与场点距离球心的距离相关。 解:在球面上取面元ds,该面元在P点处 产生的电场径向分量为:
1 4 0
V
(r ') RdV ' 3 R
面电荷和线电荷产生的电场只需在上式中将电荷体密度、体积元 和积分区域作相应替换即可,如
4 0 1 E r 4 0
E r
1
s r ' R
3
V
R l r ' R
3泊松方程拉普拉斯方程由0?e?称为静电场的标量位函数又称电位函数xyzexeyez?????????????????????lel????由此可求得电位的微分d??ddlel??el在任意方向上的分量e空间ab两点的电位差dbebala?????l若选取为电位参即则任意点的电位为ppppxyz0p?axyzxyzdpppxyzapl?????el1电位函数za?ya?xa?ezyx??????????对于点电荷的电位体电荷面电荷和线电荷分布的电位函数表达式为
R r r '
式中0 为真空介电常数。
0 8.854187817 10 12 (F / m) 1 10 9 (F/m) 36π
库仑定律分析: 作用力的性质:电荷 q1 在空间激发电场,电场力
q1 ( r r ' ) F12 4 | r r ' |3 q2 0
结 果 分 析
(1)当 z→0,此时 P点移到圆心,圆环上各点产生的电场抵消, E=0 (2)当 z→∞, R 与 z 平行且相等,r<<z ,带电圆环相当于一个点 电荷,有
E z
q 4 0 R
e 2 z
例:求真空中半径为a,带电量为Q的导体球在球外空间 中产生E。 由球体的对称性分析可知: 电场方向沿半径方向: 电场大小只与场点距离球心的距离相关。 解:在球面上取面元ds,该面元在P点处 产生的电场径向分量为:
2恒定电场

V
─ 焦耳定律积分形式
导体有电流时,必有功率损耗,其功率密度为
p dP dV J E
W/m3 ─ 焦耳定律微分形式
9
2.2
电源电动势与局外场强
2.2.1 电源电动势与局外场强 提供非静电力将其它形式的
能量转为电能的装置称为电源。
恒定电流的形成
要产生恒定电场,形成恒定电流,需要连接 直流电源。直流电源能将电源内的原子或分子的 正、负电荷分开,使正电荷移向正极,负电荷移 向负极。显然,这种移动电荷的作用力不是电场 的库仑力,称之为局外力,用 f e 表示。
第二章
序 导电媒质中的电流
恒定电场
电源电动势与局外场强
恒定电场基本方程、分界面上的衔接条件 导电媒质中恒定电场与静电场的比拟
电导和部分电导
1
2.0 序
静电场中,导体内没有电场,没有电荷的运 动,导体是等位体,导体表面是等位面。 维持导体中具有恒定电流的电场称为恒定电 场。它与静电场有相似之处。 本章要求: 理解各种电流密度的概念,通过欧姆定律和焦 耳定律理解场量之间的关系。 掌握恒定电场的基本方程和分界面上的衔接条 件。 掌握静电比拟法和电导的计算。
E1n J1n / 1 0
理想介质
导体中
导体与理想介质分界面
E1t E2t J1t / 1 J1 / 1 0
D2 n D1n 2 E 2 n 1 E1n 2 E 2 n
结论1 分界面导体侧的电流一定与导体表面平行。 结论2 导体与理想介质分界面上必有面电荷。
l
( E ) dS 0
S
得 E 0
恒定电场是无旋场。
14
3. 恒定电场(电源外)的基本方程
─ 焦耳定律积分形式
导体有电流时,必有功率损耗,其功率密度为
p dP dV J E
W/m3 ─ 焦耳定律微分形式
9
2.2
电源电动势与局外场强
2.2.1 电源电动势与局外场强 提供非静电力将其它形式的
能量转为电能的装置称为电源。
恒定电流的形成
要产生恒定电场,形成恒定电流,需要连接 直流电源。直流电源能将电源内的原子或分子的 正、负电荷分开,使正电荷移向正极,负电荷移 向负极。显然,这种移动电荷的作用力不是电场 的库仑力,称之为局外力,用 f e 表示。
第二章
序 导电媒质中的电流
恒定电场
电源电动势与局外场强
恒定电场基本方程、分界面上的衔接条件 导电媒质中恒定电场与静电场的比拟
电导和部分电导
1
2.0 序
静电场中,导体内没有电场,没有电荷的运 动,导体是等位体,导体表面是等位面。 维持导体中具有恒定电流的电场称为恒定电 场。它与静电场有相似之处。 本章要求: 理解各种电流密度的概念,通过欧姆定律和焦 耳定律理解场量之间的关系。 掌握恒定电场的基本方程和分界面上的衔接条 件。 掌握静电比拟法和电导的计算。
E1n J1n / 1 0
理想介质
导体中
导体与理想介质分界面
E1t E2t J1t / 1 J1 / 1 0
D2 n D1n 2 E 2 n 1 E1n 2 E 2 n
结论1 分界面导体侧的电流一定与导体表面平行。 结论2 导体与理想介质分界面上必有面电荷。
l
( E ) dS 0
S
得 E 0
恒定电场是无旋场。
14
3. 恒定电场(电源外)的基本方程
哈工程第二章-静态电磁场I静电场剖析
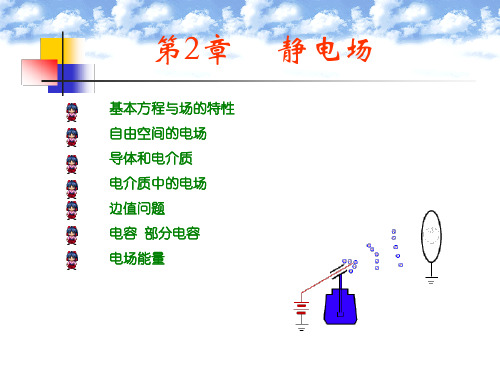
对右图闭合曲线作曲线积分, 并应用斯托克斯定理,得:
E • d l E • d l E • d l E • d S 0
AmBA nm AB BnAS
即
E •dlE •dlE •dl
Am B BnA AnB
图 电场力作功与路径无关
表明在静电场中,电场力作功与路径无关,仅取 决于起点和终点的位置。
静电场知识结构框图
静电场是本课程的基础。由此建立的物理概念、分析方法在一 定条件下可类比推广到恒定电场,恒定磁场及时变场。
第2章 静态电磁场I:静电场
• 演绎法(补充): 演绎法是与归纳法相反的一种研究方法,是从既有的普遍性结论或一般性 事理,推导出个别性结论的一种方法,即由较大范围,逐步缩小到所需的特定范 围。它是从一般到特殊,由定义、根本规律等出发一步步递推,逻辑严密结论可 靠,且能体现事物的特性。 演绎法的基本形式是三段论式,它包括: (1)大前提,是已知的一般原理或一般性假设; (2)小前提,是关于所研究的特殊场合或个别事实的判断,小前提应与大 前提有关; (3)结论,是从一般已知的原理(或假设)推出的,对于特殊场合或个别 事实作出的新判断。由相对于观察者为静止的、且量值不随时间变化的电荷所激 发的电场。
例2-2 已知真空中在半径为a的球形空间内分布有呈球对称形态的电
荷,它在其球形分布区域内外产生的空间电场分别为
E(r) 1
20
er(0ra)
和
试求该给定静电场的旋度。
E(r)
a2
20r2
er(r
a)
解:
2.2 自由空间的电场
2.2.1 自由空间中的E和
1. 电位函数的引入
•亥姆霍兹定理(回顾)
显然,静电场是有散(有源)、无旋场。
E • d l E • d l E • d l E • d S 0
AmBA nm AB BnAS
即
E •dlE •dlE •dl
Am B BnA AnB
图 电场力作功与路径无关
表明在静电场中,电场力作功与路径无关,仅取 决于起点和终点的位置。
静电场知识结构框图
静电场是本课程的基础。由此建立的物理概念、分析方法在一 定条件下可类比推广到恒定电场,恒定磁场及时变场。
第2章 静态电磁场I:静电场
• 演绎法(补充): 演绎法是与归纳法相反的一种研究方法,是从既有的普遍性结论或一般性 事理,推导出个别性结论的一种方法,即由较大范围,逐步缩小到所需的特定范 围。它是从一般到特殊,由定义、根本规律等出发一步步递推,逻辑严密结论可 靠,且能体现事物的特性。 演绎法的基本形式是三段论式,它包括: (1)大前提,是已知的一般原理或一般性假设; (2)小前提,是关于所研究的特殊场合或个别事实的判断,小前提应与大 前提有关; (3)结论,是从一般已知的原理(或假设)推出的,对于特殊场合或个别 事实作出的新判断。由相对于观察者为静止的、且量值不随时间变化的电荷所激 发的电场。
例2-2 已知真空中在半径为a的球形空间内分布有呈球对称形态的电
荷,它在其球形分布区域内外产生的空间电场分别为
E(r) 1
20
er(0ra)
和
试求该给定静电场的旋度。
E(r)
a2
20r2
er(r
a)
解:
2.2 自由空间的电场
2.2.1 自由空间中的E和
1. 电位函数的引入
•亥姆霍兹定理(回顾)
显然,静电场是有散(有源)、无旋场。
(电磁场PPT)第二章 恒定电场

第二章
由电路理论
恒定电场
2.1.3 欧姆定律的微分形式
U RI
R l
S
电导率与电阻率的关系: 1 ,
(r 电阻率), (电导率)。 r
图2.1.5 J 与 E 之关系
在场论中 dI J dS
dU dI R J dS dl
dS
E dl
J E 欧姆定律 微分形式。
第二章
恒定电场
U RI 欧姆定律 积分形式。
本章要求:
理解各种电流密度的概念,通过欧姆定律和焦耳 定律深刻理解场量之间的关系。
掌握导电媒质中的恒定电场基本方程和分界面衔 接条件。
熟练掌握静电比拟法和电导的计算。
第二章
恒定电场知识结构
基本物理量 J、 E
欧姆定律
恒定电场
J 的散度
基本方程
E 的旋度
边界条件
边值问题
电位
一般解法 电导与接地电阻 特殊解(静电比拟)
第二章
第二章 恒定电场
Steady Electric Field
导电媒质中的电流 电源电动势与局外场强 基本方程 • 分界面衔接条件 • 边值问题 导电媒质中恒定电场与静电场的比拟 电导和接地电阻
恒定电场
第二章
恒定电场
通有直流电流的导电媒质中同时存在着电流场和 恒定电场。恒定电场是动态平衡下的电荷产生的,电 荷作宏观运动,电荷的分布不随时间变化(即:恒定 ),它与静电场有相似之处。
—焦耳定律积分形式
第二章
2.2 电源电动势与局外场强
2.2.1 电源 (Source)
恒定电场
提供非静电力将其它形式的 能转为电能的装置称为电源。
图2.2.1 恒定电流的形成
电磁场课件 第2章 恒定电场

I
a 4r 2 4a
R 1/( 4a )
深埋球形接地器
(2) 非深埋(浅) 的球形接地器
考虑地面的影响,用镜像法处理。
C G
实际电阻与计算电阻:
√ R实际=2 R计算?
R实际=
1 2
R计算?
理由: R实际 || R实际 R计算
浅埋半球形接地器
2.5.3 跨步电压 (Step Voltage)
J dS
l
S
dl
dS
(2) E dl (J dS)(
dl
)
γdS
意义: • 电场是维持恒定电 流的必要条件。
J γE
微分形式 • 恒定电流场与恒定
电场相互依存。一一
对应
2.1.3 焦尔定律的微分形式
导电媒质中有电流时,必伴随功率损耗。
P p
IU dP
d ( IU
)
(J
dS)( E
2.1.1 电流密度和元电流段
电荷密度的定向移动形成电流密度。
(1) 电流面密度
分布的体电荷以速度v作匀速运动形成的电流。
J
ρv
(A/m 2 )
电流 I SJ dS
(2) 电流线密度
分布的面电荷在曲面上以速度v运动形成的电流。
K σv (A m)
电流
I l(K en )dl
(3) 线电流
折射定律: tg1 1 tg2 2
若1为导体,2为介质:
结导论体:表只面要穿出1,良2导,体电表流面线近垂似直为于等良
位面。
2.3.5 恒定电场的边值问题
2 0 —— 拉普拉斯方程
分界面衔接条件: 1 2
1
2
n
第二章恒定电场-工程电磁场导论-冯慈章课件
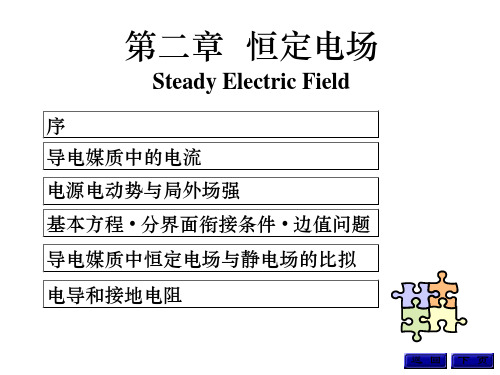
一、电源电动势与局外场强
电源是一种将其它能量转换成电能的装置; 局外力: f e
局外场强:Ee
方向由电源负极指向正 极
电源电动势: Ee dl
l
库仑场强:E
方向由电源正极指向负 极
Engineering electrical magnetic field
二、恒定电场
导电媒质中的恒定电场; 通有恒定电流的导体周围电介质或空气中的 恒定电场。
J1 J 2 J I / S E1 E2 J / p1 p2 P p1Sd , P2 p2 S 2d 1 P2 2 P 1
图2-4 平行板电容器的电场 功率的一个计算例子
2.2电源电动势与局外场强
Engineering electrical magnetic field
。 返 回 上 页 下 页
4. 元电流段的概念 元电流是元电荷dq以速度 v 运动形成的电流
C m s A m
νdV (体电流元) JdV
dq
νdS (面电流元) KdS νdl (线电流元) Idl
2.1.3 欧姆定律的微分形式 (Differential Form of Ohm’s Law)
dq I dt
2.1.2 电流密度(Current Density)
1. 电流面密度 J 体电荷 以速度 v 作匀速运动形成的电流。 电流密度 电流
J v
I J dS
S
J的大小 垂直于电流方向的平面 里,单位面积上通过 的电流强度。
A m2 J的方向与电流方向相同 ;
J2
en 2
2
1
1 J1
(电磁场PPT)第二章+恒定电场

第二章
由电路理论
2.1.3 欧姆定律的微分形式
恒定电场
U RI
R l
S
电导率与电阻率的关系: 1 ,
(r 电阻率), (电导率)。 r
图2.1.5 J 与 E 之关系
在场论中 dI J dS
dU dI R J dS dl
dS
E dl
J E 欧姆定律 微分形式。
常数
J 0 ( E) E 0
得
2 0
分界面衔接条件
E1t E2t
由
J1n J2n
拉普拉斯方程
1 2
得
1
1
n
2
2
n
思考 恒定电场中是否存在泊松方程?
第二章
恒定电场
例2.3.2 试用边值问题求解电弧片中电位、电场及
E dl
l总
l (E Ee ) dl
图2.2.2 电源电动势与局外场强
E dl
l
l Ee dl
局外场 Ee 是非保守场。
0ee
恒定电场的研究:导体周围介质中的恒定电场(同静电场 的求解方法);以及导电媒质中的电场(本章所讨论的内容).
第二章
恒定电场
第二章
2.2.2 电源电动势 (Source EMF)
恒定电场
电源电动势是电源本身的特征量,与外电路无关。
1、局外力 fe :电源中使正、负电极之间的电压维持恒 定,而使得正、负电荷分离开来的力,称为局外力 fe (
注意:“分开的力”的方向)。
2、局外场强 Ee :电源中单位正电荷所受的局外力假设 为一个等效场强,这个场强称为局外场强 。区别于库 仑场强 E 。Ee 的方向由电源的负极指向正极,与库仑场 强 E 方向相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5cm ,外半径 R2 10cm ,内外导体间的非理性电介质 的电导率 109 S/m ,若内外导体间电压 U 0 1000V ,求内外导体间的 、 E 、 J 和绝缘电阻 R 。
R1 R2
6. 同轴电缆内导体半径为 R1 ,外导体半径为 R3 ,内外导体之间有两层媒质。内 层从 R1 到 R2 ,媒质的参数为 r1 和 1 ;外层从 R2 到 R3 ,媒质的参数为 r2 和 2 , r2 2 如图所示。求
7. 图示平行平板电容器,两极板间距为 d ,极板之间有两种电介质,第一种电 介质厚度为 a ,介电常数为 1 ,电导率为 1 ;第二种电介质厚度为 d a ,介电 常数为 2 ,电导率为 2 。若两极板间加电压 U ,求电介质中的电场强度、漏电 流密度和电介质分界面上的自由电荷面密度。
1 r1 (1) 每层单位长度的电容; R1 R2 (2) 每层单位长度的电导; (3) 单位长度的总电容; R3 (4) 单位长度的总电导; (5) 当同轴电缆长度为 L ,内外导体之间的电压为 U ,忽略边缘效应,利用 边界上的衔接条件分别求界面 R1 、 R2 和 R3 上的电荷面密度。
第二章 恒定电场
1. 直径为 3mm 的导线,如果流过它的电流是 10A,且电流密度均匀,导线的电 导率为 5.8107S/m,导线内电荷的密度为 9109C/m3。求导线内部的电场强度以 及电子的漂移速率。 (提示:电子的漂移速率即为导线内电子的运动速率。 )
2 2 2. 已知 J (10 y2 zex 2 x2 ye y 2 x ze z )A/m 。求穿过 x 3m 处, 2m y 3m , 3.8m z 5.2m 面积上在 ex 方向的总电流 I 。
3. 平行板电容器极板间距离为 d ,其中媒质的电导率为 ,两板接有电流为 I 的 电流源,测得媒质的功率损耗为 P 。如将板间距离扩为 2d ,其间仍充满电导率 为 的媒质,则此电容器的功率损耗是多少? 4. 在无界非均匀导电媒质(电导率和介电常数均是坐标函数)中, 若有恒定电流存
在,证明媒质中的自由电荷密度为 E ( )
a d a
1 1
U
2 2
8. 在不良导体的恒定电流场中放入一小块良导体,从不良导体一侧看,电流密 度是趋向垂直于分界面还是平行于分界面? 9. 在良导体的恒定电流场中放入一小块不良导体,从良导体一侧看,电流密度 是趋向垂直于分界面还是平行于分界面? 10. 假设大地为均匀导电媒质,浅埋于地下的不规则形状接地体电流流入大地。 在远离接地体的大地内,电流如何分布? 11. 在恒定电场的电源中,总的电场强度闭合线积分为零吗?局外电场强度的闭 合线积分为零吗?库仑电场强度的闭合线积分为零吗?在电源之外, 上述 3 个闭 合线积分是否为零? 12. 导体和理想电介质的分界面上,导体一侧没有法线方向的电流密度,因此也 没有法线方向的电场强度和电通密度矢量。 但在电介质一侧却可能有法线方向的 电场强度和电通密度矢量。为什么?
R1 R2
6. 同轴电缆内导体半径为 R1 ,外导体半径为 R3 ,内外导体之间有两层媒质。内 层从 R1 到 R2 ,媒质的参数为 r1 和 1 ;外层从 R2 到 R3 ,媒质的参数为 r2 和 2 , r2 2 如图所示。求
7. 图示平行平板电容器,两极板间距为 d ,极板之间有两种电介质,第一种电 介质厚度为 a ,介电常数为 1 ,电导率为 1 ;第二种电介质厚度为 d a ,介电 常数为 2 ,电导率为 2 。若两极板间加电压 U ,求电介质中的电场强度、漏电 流密度和电介质分界面上的自由电荷面密度。
1 r1 (1) 每层单位长度的电容; R1 R2 (2) 每层单位长度的电导; (3) 单位长度的总电容; R3 (4) 单位长度的总电导; (5) 当同轴电缆长度为 L ,内外导体之间的电压为 U ,忽略边缘效应,利用 边界上的衔接条件分别求界面 R1 、 R2 和 R3 上的电荷面密度。
第二章 恒定电场
1. 直径为 3mm 的导线,如果流过它的电流是 10A,且电流密度均匀,导线的电 导率为 5.8107S/m,导线内电荷的密度为 9109C/m3。求导线内部的电场强度以 及电子的漂移速率。 (提示:电子的漂移速率即为导线内电子的运动速率。 )
2 2 2. 已知 J (10 y2 zex 2 x2 ye y 2 x ze z )A/m 。求穿过 x 3m 处, 2m y 3m , 3.8m z 5.2m 面积上在 ex 方向的总电流 I 。
3. 平行板电容器极板间距离为 d ,其中媒质的电导率为 ,两板接有电流为 I 的 电流源,测得媒质的功率损耗为 P 。如将板间距离扩为 2d ,其间仍充满电导率 为 的媒质,则此电容器的功率损耗是多少? 4. 在无界非均匀导电媒质(电导率和介电常数均是坐标函数)中, 若有恒定电流存
在,证明媒质中的自由电荷密度为 E ( )
a d a
1 1
U
2 2
8. 在不良导体的恒定电流场中放入一小块良导体,从不良导体一侧看,电流密 度是趋向垂直于分界面还是平行于分界面? 9. 在良导体的恒定电流场中放入一小块不良导体,从良导体一侧看,电流密度 是趋向垂直于分界面还是平行于分界面? 10. 假设大地为均匀导电媒质,浅埋于地下的不规则形状接地体电流流入大地。 在远离接地体的大地内,电流如何分布? 11. 在恒定电场的电源中,总的电场强度闭合线积分为零吗?局外电场强度的闭 合线积分为零吗?库仑电场强度的闭合线积分为零吗?在电源之外, 上述 3 个闭 合线积分是否为零? 12. 导体和理想电介质的分界面上,导体一侧没有法线方向的电流密度,因此也 没有法线方向的电场强度和电通密度矢量。 但在电介质一侧却可能有法线方向的 电场强度和电通密度矢量。为什么?
