课题∶圆锥曲线的切线方程和切点弦方程
圆锥曲线的切线与切点弦方程
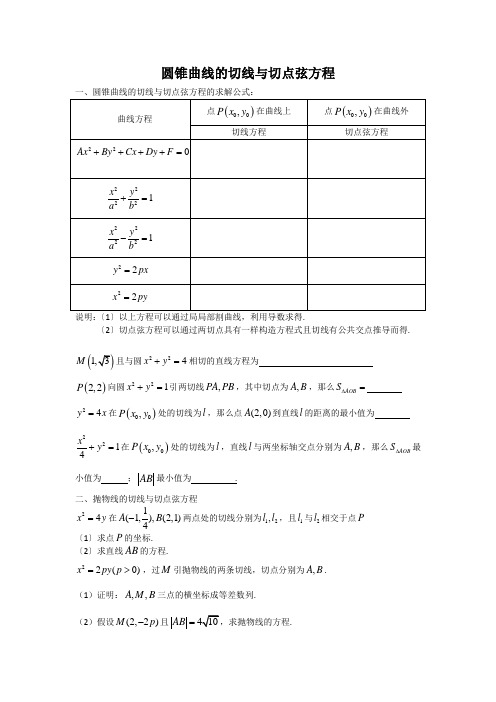
圆锥曲线的切线与切点弦方程说明:〔1〕以上方程可以通过局局部割曲线,利用导数求得.〔2〕切点弦方程可以通过两切点具有一样构造方程式且切线有公共交点推导而得.(M 且与圆224x y +=相切的直线方程为 ()2,2P 向圆221x y +=引两切线,PA PB ,其中切点为,A B ,那么AOB S ∆=24y x =在()00,P x y 处的切线为l ,那么点(2,0)A 到直线l 的距离的最小值为 2214x y +=在()00,P x y 处的切线为l ,直线l 与两坐标轴交点分别为,A B ,那么AOB S ∆最小值为 ;AB 最小值为 .二、抛物线的切线与切点弦方程24x y =在1(1,),(2,1)4A B -两点处的切线分别为12,l l ,且1l 与2l 相交于点P 〔1〕求点P 的坐标.〔2〕求直线AB 的方程.22(0)x py p =>,过M 引抛物线的两条切线,切点分别为,A B .(1)证明:,,A M B 三点的横坐标成等差数列.(2)假设(2,2)M p -且AB =.24x y =,过点P 的直线l 交抛物线于,A B 两点,分别以,A B 为切点的两切线12,l l . 〔1〕假设(2,2)P ,求1l 与2l 交点M 的轨迹方程.〔2〕假设点P 为抛物线的焦点F ,证明:〔i 〕MF AB ⊥; 〔ii 〕MA MB ⊥.C :22x py =的焦点(0,)F c (0)c >到直线l :20x y --=的距离为322,设P 为直线l 上点,过点P 作抛物线的两条切线12,l l ,求切点分别为,A B .〔1〕求抛物线C 的方程;〔2〕当00(,)P x y 为定点时,求直线AB 的方程;〔3〕当P 在直线上运动时,求FA FB ⋅的最小值. 1C :22221x y a b+=的两个焦点1(2,0)F -,2(2,0)F ,点(2,3)A 在椭圆上,过点A 的直线l 与抛物线2C :24x y =交于,B C 两点,抛物线2C 在,B C 两点处的切线分别为12,l l 且1l 与2l 相交于点P .〔1〕求椭圆1C 的方程;〔2〕是否存在满足1212PF PF AF AF +=+的点P ,假设存在,请指出个数?假设不存在说明理由.。
第10讲:圆锥曲线的切线

第12讲:圆锥曲线的切线不管是哪一种圆锥曲线的切线,其本质都是圆锥曲线与直线只有一个交点,即联立圆锥曲线方程与直线方程所得到的一元二次方程有且仅有一个根,即0=∆,相信这对于大家来说都不是问题,在这里我们对圆锥曲线的切线做一些总结,以方便大家在最短的时间内解决题目。
(一)椭圆的切线:①12222=+b y a x 在点P(00,y x )处的切线方程为12020=+by y a x x ②过椭圆外一点Q (11,y x )可以做椭圆的两条切线,两切点所在的直线方程为12121=+by y a x x ③直线m kx y +=与椭圆12222=+by a x 相切时,满足2222m b k a =+例:已知P 为椭圆13422=+y x 上一动点,求点P 到直线062=--y x 的最小值与最大值。
(二)双曲线的切线:①1-2222=by a x 在点P(00,y x )处的切线方程为1-2020=b y y a x x②过椭圆外一点Q (11,y x )可以做椭圆的两条切线,两切点所在的直线方程为1-2121=byy a x x ③直线m kx y +=与椭圆12222=+by a x 相切时,满足2222-m b k a =(三)抛物线的切线:①py x 22=上某点P (00,y x )的切线斜率为p x k 0=,点P(px x 2,20),则切线方程为p x x x p x y 2)(2000+-= ,即pxp x x y 2200-=,通过观察我们知道: 与x 轴的交点为)0,2(x ,切线与x 轴的截距为切点处横坐标的一半, 与y 轴的交点为)2-,0(20px ,在y 轴上的截距为切点纵坐标的相反数。
②A (11,y x ),B (22,y x )均在抛物线py x 22=上,请推证A 、B 处两切线及其两切线的交点坐标。
A 点处切线p x p x x y 2211-=B 点处切线pxp x x y 2222-=两条切线的焦点坐标(1212,22x x x x p+) 我们发现:i 、两切线的交点横坐标为两个切点的中点M 的横坐标 ii 、根据前面弦长知识点可知,直线与抛物线的两个交点满足:122x x pb =-(b 为直线与对称轴的截距),那么我们得到:两切线的交点纵坐标(12222x x pbb p p-==-)与直线与对称轴的截距互为相反数 延伸一:过抛物线对称轴上一点(0,b)做直线与抛物线相交于A 、B 两点,过A 、B 分别做抛物线的切线,两切线相交于点Q ,通过几何画板作图我们发现:不论直线绕P(0,b)如何旋转,两切线的交点的纵坐标恒为-b证明:令过P 的直线为y kx b =+,221212(,),(,)22x x A x B x p p联立22x pyy kx b ⎧=⎨=+⎩得122x x pb =-设A 点处切线pxp x x y 2211-=, B 点处切线p x p x x y 2222-=则两条切线的焦点坐标Q (1212,22x x x x p+) ∴12222Q x x pby b p p -===- 证 毕延伸二、过点Q (,)a b (22b pa <)做抛物线的两条切线分别切抛物线于点A 、B , 直线AB 与y 轴的截距为-b斜率22121212222ABx x x x a p p k x x p p-+===- ∴切点弦方程为:ay x b p=-③对于焦点在x 轴上的抛物线,求切线一般联立方程,利用0=∆求解。
圆锥曲线的切线方程

圆锥曲线的切线方程点击此处添加副标题作者:鲜海东微信:xhd143848832211),(1),()0(13))(())((),())(())((),(),()()(2),(),(1202022220020200022222000020000002222000020000222=+=+=+=+=--+--=--+--=-+-=+=+=+by y a x x M b y a x y x M by y a x x y x M b a b y a x r b y b y a x a x M y x M rb y b y a x a x y x M y x M r b y a x r y y x x M y x M r y y x x y x M r y x 弦所在直线方程为:点的引切线有两条,过两切的外部时,过在椭圆当切线方程为:上一点>>:过椭圆结论所在直线方程:点切线有两条:切点弦在圆外,过若切线方程:则过一点为圆上,若的方程::若圆心不在原点,圆结论。
弦所在直线方程为,过两切点的点引切线有且只有两条在圆外时,过当。
的切线方程为上一点:经过圆结论。
两点的直线方程为、所以过两切点,满足直线现观察以上两个等式,发、以有是两条切线的交点,所。
又因、:两点的切线方程分别为、可知过由为引两条切线,切点分别外一点>>()设过椭圆(即由点斜式得切线方程为,得求导,得的两边对)大学隐函数求导)(证明:11),(),,(.11),(11)1().,(),,(),()0121),(,02211(20202020221120220220120100222221212211002222202000202002020222222=+=+=+=+=+=+=+=+--==--==='='+=+b y y a x x B A b y y a x x y x B y x A b y y a x x b y y a x x y x M b y y a x x b y y a x x B A y x B y x A y x M b a by a x by y a x x x x y a x b y y y a x b x x y b y y a x x b y a x)(),()0(2);(),()0(2)2()(),()0(2);(),()0(2)1(511),(1),()00(140000200002000020000220202222002020002222y y p x x y x M p py x y y p x x y x M p py x x x p y y y x M p px y x x p y y y x M p px y by y a x x M b y a x y x M by y a x x y x M b a b y a x +==+==+==+===-=-=-=-弦所在直线方程为的引两条切线,过两切点的外部一点>过抛物线切线方程为上一点>过抛物线弦所在直线方程为的引两条切线,过两切点的外部一点>过抛物线切线方程为上一点>过抛物线:结论。
圆锥曲线中的切线问题

圆锥曲线中的切线问题过曲线上一点P(x o ,y o )的切线方程(焦点在x 轴上):圆:200r b)-b)(y -(y a)-a)(x -(x =+;椭圆:12020=+b y y a x x ;双曲线:12020=-b y y a x x ;抛物线:)(00x x p y y +=.证明:以双曲线为例.442222020220220420222022022020242022202222202022222020)(4)1)(b a x (4)2(,012)b a x (x .11.11b a b a a y x b x a x b y b y a x b y y y b y b y ax b y y a x x b y a x b y y a x x ---=---=∆=-+--⎪⎪⎩⎪⎪⎨⎧+=+=⇒⎪⎪⎩⎪⎪⎨⎧=-=-得消去①式平方后除以②式,,,.0012222202202220220,即证,所以,得又=∆=--=-b a b a y a x b b y a x 过曲线外一点P(x o ,y o )作曲线的切线,切点A 、B ,过切点A 、B 的直线方程(焦点在x 轴上):圆:200r b)-b)(y -(y a)-a)(x -(x =+;椭圆:12020=+b y y a x x ;双曲线:12020=-b y y a x x ;抛物线:)(00x x p y y +=.证明:以椭圆为例.设切点),(),,(2211y x B y x A ,以A ,B 为切点的直线方程分别为.1122222121=+=+b y y a x x b y y a x x ,若两切线均是P(x o ,y o )点引出的,即两切线均过点P ,则有.112022********=+=+by y ax x by y ax x ,可知点),(),,(2211y x B y x A 均在直线12020=+b y y a x x 上,所以过切点A ,B 的直线方程为12020=+by y a x x .即证.思考1.(2021全国乙卷)已知抛物线C :x 2=2py(y>0)的焦点为F ,且点F 与圆M :x 2+(y+4)2=1上的点最小值为4.(1)求p ;(2)若点P 在M 上,PA ,PB 是C 的两条切线,A ,B 是切点,求PAB ∆面积的最大值.).520;2(最大值为=p 解:(1)焦点坐标为(0,2p ),于4142p=-+是得到p=2;(2)设P(x 0,y 0),切点为),(),,(2211y x B y x A ,设过点),(11y x A 的方程为x 1x=2(y+y 1),联立x 2=4y ,化为关于x 的一元二次方程X 2-2x 1x+4y 1=0,得0=∆,所以x 1x=2(y+y 1)是抛物线上过A 的切线方程,同理可得x 2x=2(y+y 2)是抛物线上过B 点的切线方程.于是过P(x 0,y 0)作抛物线的切线,则过切点A ,B 的方程为x 0x=2(y+y 0),联立抛物线方程消去y 得X 2-2x 0x+4y 0=0,4|4|d AB P 16441||200200202+-=-+=x y x y x x AB 的距离到,点.520S -5)35(151221S 4-114)4(214|4|1644121d ||21S PAB 00020PAB 2020202030202002002020PAB取最小值为时,当,)(,于是)(而所以∆∆∆=-≤≤----=+==++-=+--+=⋅=y y y y y x y x y x x y x y x x AB 2.已知椭圆)0(12222>>=+b a b y a x 的左右焦点分别为F 1,F 2,且|F 1F 2|=2,点M 在直线x=-2上运动,线段MF 2与椭圆相交于N ,当NF 1⊥x 轴时,直线MF 2的斜率的绝对值为42.(1)求椭圆方程;(2)设P 是椭圆上一点,直线PF 1的斜率与直线MF 2的斜率之积为31-,证明直线MP 始终与椭圆相切.(1222=+y x )解:(1).12.2,0122,,22,22,422222222221=+==--=-====y x a a a c b a a b c c a b k NF MF 所以得所以又得为通径的一半,所以(2)设P(x 0,y 0),M(-2,y 1),设过P 的直线方程为1200=+y y xx ,联立椭圆方程消去x 得,.0,12,884024)2(20202020204020022020=∆=+-+=∆=-+-+所以而,y x x y x x x y y y x y .3131,31.121000021-=-⋅+-=⋅=+y x y k k y y x x MF PF 即由是椭圆的切线方程所以.MP .12M )1,2(M ,10000001与椭圆相切即证明直线满足椭圆的切线切线,点于是点=++-+=y y xx y x y x y。
圆锥曲线的切点弦方程及其应用

圆锥曲线的切点弦方程及其应用摘要:切点弦的问题是圆锥曲线中的重要内容之一,是近几年高考的热点考题,切点弦涉及到的问题,难度较大,技巧性强,计算繁琐,学生遇到此类问题较为棘手,束手无策,这里通过类比推理,探究其规律,掌握其性质,触类旁通,化繁就简,降低难度,进一步提高学习效率。
关键词:圆锥曲线;弦方程;应用1.内容解析1.切点弦的概念:过曲线C(圆,椭圆,双曲线,抛物线)外一点(对非封闭曲线是开口外一点)引两条切线,可以得到两个切点,连接切点即为切点弦。
2.微专题概述:圆锥曲线的切点弦方程是平面解析几何中的一类难点问题,围绕切点弦命制的解析几何试题具有内涵深刻、灵活多变的特点。
本专题在讲解一道课本习题即“过圆上一点圆的切线问题”的求解方法的基础上,立足学生思维的“最近发展区”,通过设置环环紧扣的问题串,最后得出椭圆、双曲线、抛物线的切点弦的一般性结论。
本微专题坚持“以小见大、微中知著”,最终达到启迪学生思维、开阔数学视野、培养类比归纳能力的目的;另一方面,客观题中熟练掌握切点弦方程结论,可以帮助学生有效简化解题过程、提高解题速度。
1.本专题所蕴含的数学思想方法及教学策略分析思想方法:数形结合思想、化归与转化思想、特殊与一般的思想教学策略:讲授法、分组讨论法、引导启示法立足高三年级学生实际、对基本概念和知识点采取讲授的方法;通过设置环环相扣的问题串,让学生分组讨论,教师引导实现同类知识的的迁移和整合归纳;注重问题串的整体性,在问题串的引领下,引导启示学生进行系列、连续的思维活动,使学生思维达到新高度。
1.教学目标1.知识与技能(1)掌握圆锥曲线在某点处的切点弦方程;(2)会用切点弦方程解决一些实际问题;(3)通过复习渗透数形结合、类比的思想,逐步培养学生分析问题和解决问题的能力。
2.过程与方法首先,通过对过圆上一点的圆的切线的求法的研究,进而设置一些列有较强逻辑关系的问题串,采取学生小组讨论法、教师启发引导法从而完成教学目标。
专题14 圆锥曲线的切线问题

专题14 圆锥曲线的切线问题一、结论圆锥曲线的切线问题常用方法有几何法,代数法:比如求圆的切线,常用圆心到直线的距离等于半径来解决切线问题,也可以联立直线与圆的方程根据0∆=来求解;比如涉及到椭圆的切线问题,也常常联立直线与椭圆的方程根据0∆=来求解; 对于抛物线的切线问题,可以联立,有时也可以通过求导来求解. 而对于这些圆锥曲线也常常存在一些特殊的求切线公式:1.过圆C :222()()x a y b R −+−=上一点00(,)P x y 的切线方程为200()()()()x a x a y b y b R −−+−−=.2.过椭圆22221x y a b+=上一点00(,)P x y 的切线方程为00221x x y ya b +=.3.已知点00(,)M x y ,抛物线C :22(0)y px p =≠和直线l :00()y y p x x =+.(1)当点00(,)M x y 在抛物线C 上时,直线l 与抛物线C 相切,其中M 为切点,l 为切线. (2)当点00(,)M x y 在抛物线C 外时,直线l 与抛物线C 相交,其中两交点与点M 的连线分别是抛物线的切线,即直线l 为切点弦所在的直线.(3)当点00(,)M x y 在抛物线C 内时,直线l 与抛物线C 相离.二、典型例题1.(2021·安徽·六安一中高二期末(文))已知椭圆具有如下性质:若椭圆的方程为()222210x y a b a b +=>>,则椭圆在其上一点()00,A x y 处的切线方程为00221x x y y a b +=,试运用该性质解决以下问题;椭圆221:12x C y +=,点B 为1C 在第一象限中的任意一点,过B 作1C 的切线l ,l 分别与x 轴和y 轴的正半轴交于,C D 两点,则OCD 面积的最小值为( )A .1 BCD .2【答案】C 【详解】设1111(,),(0,0)B x y x y >>,由题意得,过点B 的切线l 的方程为:1112x xy y +=, 令0y =,可得12(,0)C x ,令0x =,可得11(0,)D y ,所以OCD 面积111112112S x y x y =⨯⨯=,又点B 在椭圆上,所以221112x y +=,所以121111121111122x y S x y x y x x y y +===+≥=当且仅当11112x yy x =,即111,x y = 所以OCD故选:C【反思】过椭圆()222210x y a b a b+=>>上一点()00,A x y 作切线,切线方程为:00221x x y ya b+=,该结论可以在小题中直接使用,但是在解答题中,需先证后用,所以在解答题中不建议直接使用该公式.2.(2020·江西吉安·高二期末(文))已知过圆锥曲线221x y m n+=上一点()00,P x y 的切线方程为001x x y y m n +=.过椭圆221124x y +=上的点()3,1A −作椭圆的切线l ,则过A 点且与直线l 垂直的直线方程为( ) A .30x y −−= B .-20x y += C .2330x y +−= D .3100x y −−=【答案】B 【详解】过椭圆221124x y +=上的点()3, 1A −的切线l 的方程为()31124y x −+=,即40x y −−=,切线l的斜率为1.与直线l 垂直的直线的斜率为-1,过A 点且与直线l 垂直的直线方程为()13y x +=−−,即20x y +−=. 故选:B【反思】根据题中信息,直接代入公式,但是在代入切线方程为001x x y ym n+=注意不要带错,通过对比本题信息,12m =,4n =,03x =,01y =−,将这些数字代入公式,可求出切线l ,再利用直线垂直的性质求解.3.(2022·江苏南通·一模)过点()1,1P 作圆22:2C x y +=的切线交坐标轴于点A 、B ,则PA PB ⋅=_________.【答案】2− 【详解】圆C 的圆心为()0,0C ,10110CP k −==−, 因为22112+=,则点P 在圆C 上,所以,PC AB ⊥,所以,直线AB 的斜率为1AB k =−,故直线AB 的方程为()11y x −=−−,即20x y +−=, 直线20x y +−=交x 轴于点()2,0A ,交y 轴于点()0,2B , 所以,()1,1PA =−,()1,1PB =−,因此,112PA PB ⋅=−−=−. 故答案为:2−.另解:过圆C :222()()x a y b R −+−=上一点00(,)P x y 的切线方程为200()()()()x a x a y b y b R −−+−−=.可知01x =,01y =;0a b ==,22R =,代入计算得到过点()1,1P 作圆22:2C x y +=的切线为:(10)(0)(10)(0)2x y −−+−−=,整理得:20x y +−=,直线20x y +−=交x 轴于点()2,0A ,交y 轴于点()0,2B , 所以,()1,1PA =−,()1,1PB =−,因此,112PA PB ⋅=−−=−. 故答案为:2−.【反思】本题中提供了常规方法和使用二级结论的解法,特别提醒同学们,二级结论的公式代入数字时,最忌讳代入错误,所以需要特别仔细。
圆锥曲线中的切线方程与切点弦方程(高阶拓展、竞赛适用)(学生版)-2025版高中数学一轮复习考点帮

第16讲圆锥曲线中的切线方程与切点弦方程(高阶拓展、竞赛适用)(4类核心考点精讲精练)1.5年真题考点分布【命题规律】本节内容是新高考卷的选考内容,设题不定,难度中等或偏难,分值为5-17分【备考策略】1.理解、掌握圆锥曲线切线的定义2.理解、掌握圆锥曲线的切线问题及其相关计算【命题预测】本节内容是新高考卷的常考内容,小题和大题都会作为载体命题,同学们要会结合公式运算,需强化训练复习1过圆2+2=2上一点0,0的切线方程:B 0+B 0=22.设0,0为椭圆22+22=1上的点,则过该点的切线方程为:B 02+B 02=13.设0,0为双曲线22−22=1上的点,则过该点的切线方程为:B 02−B 02=14.设0,0为抛物线y 2=2B 上的点,则过该点的切线方程为B 0=+05.设0,0为圆2+2=2外一点,则切点弦的方程为:B 0+B 0=26.设0,0为椭圆22+22=1外一点,过该点作椭圆的两条切线,切点为A ,B 则弦B 的方程为:B 02+B 02=17.过0,0为双曲线22−22=的两支作两条切线,则切点弦方程为B 02−B 02=18.设0,0为抛物线2=2B 开口外一点,则切点弦的方程为:001.(2022高三·全国·专题练习)椭圆223144x y +=上点P (1,1)处的切线方程是.2.(22-23高三下·河南·阶段练习)已知椭圆222:1y C x t+=,离心率为2,过()1,2P 的直线分别与C 相切于A ,B 两点,则直线AB 方程为()A .10x y +-=或410x y +-=B .410x y +-=C .10x y +-=D .10x y ++=或410x y +-=3.(22-23高二上·江西吉安·期末)已知过圆锥曲线221x y m n +=上一点(),o o P x y 的切线方程为001x x y y m n+=.过椭圆221124x y +=上的点()3,1A -作椭圆的切线l ,则过A 点且与直线l 垂直的直线方程为()A .30x y --=B .-20x y +=C .2330x y +-=D .3100x y --=1.(2022·全国·高三专题练习)求过椭圆221169x y +=上一点3222,2M ⎛⎫⎪⎝⎭的切线l 方程.2.(22-23高三全国·课后作业)曲线194+=上点到直线280x y -+=距离的最小值为.3.(2022·全国·高三专题练习)已知直线62260x y +-=经过椭圆()222210x y a b a b+=>>的一个顶点E 和一个焦点F .(1)求椭圆的标准方程;(2)求过()5,3P与椭圆相切的直线方程.4.(24-25高三上·湖南·开学考试)已知椭圆22:1(0)y x M a b a b+=>>过点(6和(3.(1)求M 的离心率;(2)若直线:l y x m =+与M 有且仅有一个交点,求l 的一般式方程.5.(23-24高二下·河南开封·期末)已知椭圆C 的两个焦点坐标分别是()12,0F -,()22,0F ,且经过点53,22P ⎛⎫⎪⎝⎭.(1)求C 的标准方程;(2)已知直线l 与2PF 平行,且与C 有且只有一个公共点,求l 的方程.考点二、双曲线中的切线方程和切点弦方程1.(2024高三·全国·专题练习)求双曲线2214x y -=在点(3P 处的切线方程.2.(2023高二·全国·专题练习)过点(3,3)P 作双曲线C :221x y -=的两条切线,切点分别为,A B ,求直线AB 的方程.3.(2022高三·全国·专题练习)已知双曲线22153x y -=的一条切线的斜率为2,求这条切线方程.1.(2024高三·全国·专题练习)(1)求双曲线2212y x -=在点处的切线方程;(2)已知()1,1P 是双曲线外一点,过P 引双曲线2212y x -=的两条切线,PA PB ,A ,B 为切点,求直线AB的方程.2.(2020高三·江苏·专题练习)在双曲线22925225x y =-上求一点,使到直线30x y --=的距离最短.1.(2022高三·全国·专题练习)抛物线214y x =过点(0,2)-的切线方程为()A .0x =B .22y x =±-C .2y x =±-D .2y =-2.(2022高三·全国·专题练习)过点()2,1P -作抛物线C :22x y =的两条切线,切点分别为A ,B ,求直线AB 的方程.3.(2024·全国·模拟预测)已知抛物线2:4C y x =,过点()1,1P -作抛物线C 的两条切线,PM PN ,切点分别为,M N ,则MN =.4.(2024高三·全国·专题练习)已知M 是直线:220l x y --=上的动点,过点M 作抛物线21:4C y x =的两条切线,切点分别为A ,B (与坐标原点O 不重合),当0OA OB ⋅=时,直线AB 的方程为.1.(2023高三·全国·专题练习)过抛物线24x y =上一点()4,4的抛物线的切线方程为.2.(21-22高二下·河南新乡·期末)过点()30A -,作抛物线24y x =的切线,则切点的横坐标为.3.(2023·山东·模拟预测)已知抛物线C :24x y =,过直线l :24x y +=上的动点P 可作C 的两条切线,记切点为,A B ,则直线AB ()A .斜率为2B .斜率为2±C .恒过点()0,2-D .恒过点()1,2--4.(24-25高三上·贵州遵义·阶段练习)已知抛物线2:2(0)C x py p =>的焦点为F ,且F 与圆22:(2)1M x y ++=上点的距离的最小值为2.(1)求p ;(2)已知点(1,2)P --,PA ,PB 是抛物线C 的两条切线,A ,B 是切点,求AB .1.(2021·天津·高考真题)已知椭圆()222210+=>>x y a b a b 的右焦点为F ,上顶点为B BF =(1)求椭圆的方程;(2)直线l 与椭圆有唯一的公共点M ,与y 轴的正半轴交于点N ,过N 与BF 垂直的直线交x 轴于点P .若//MP BF ,求直线l 的方程.2.(2021·全国·高考真题)已知抛物线()2:20C x py p =>的焦点为F ,且F 与圆22:(4)1M x y ++=上点的距离的最小值为4.(1)求p ;(2)若点P 在M 上,,PA PB 是C 的两条切线,,A B 是切点,求PAB 面积的最大值.1.(2024·四川德阳·三模)已知F 为抛物线C :24x y =的焦点,过点F 且倾斜角为60o 的直线l 与抛物线C 相交于不同的两点A B 、,若抛物线C 在A B 、两点处的切线相交于点P ,则PF =.2.(2024·河南洛阳·模拟预测)(多选)过点4)向抛物线28x y =作两条切线,切点分别为()()1122,,,A x y B x y F 、为抛物线的焦点,则()A.12x x +=-B .1232x x =C .||||49AF BF ⋅=D .||||18AF BF +=3.(2024高三·全国·专题练习)在直角坐标系xoy 中,曲线C :24x y =与直线(),0y kx a a =+>交与M ,N 两点,(1)当0k =时,分别求C 在点M 和N 处的切线方程;(2)y 轴上是否存在点P ,使得当k 变动时,总有OPM OPN ∠=∠?说明理由.4.(2024高三·全国·专题练习)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2e =,椭圆上的点P 与两个焦点12F F 、构成的三角形的最大面积为1.(1)求椭圆C 的方程;(2)若点Q 为直线20x y +-=上的任意一点,过点Q 作椭圆C 的两条切线QD QE 、(切点分别为D E 、),试证明动直线DE 恒过一定点,并求出该定点的坐标.5.(2024·全国·模拟预测)设抛物线2:2(0)C x py p =>,直线10x y -+=与C 交于A ,B 两点,且8AB =.(1)求抛物线C 的方程;(2)已知点P 为()2211x y ++=上一点,过点P 作抛物线C 的两条切线PD ,PE ,设切点分别为D ,E ,试求直线PD ,PE 斜率之积的最小值.6.(2024·全国·模拟预测)已知椭圆2222:1(0)x y E a b a b +=>>的长轴为双曲线2212x y -=的实轴,且经过点2P ⎛⎫⎪ ⎪⎝⎭.(1)求椭圆E 的标准方程.(2)已知椭圆22221(0)x y a b a b+=>>在其上一点()00,Q x y 处的切线方程为00221xx yy a b +=.过椭圆E 的左焦点1F 作直线l 与椭圆E 相交于,A B 两点,过点,A B 分别作椭圆的切线,两切线交于点M .求证:1MF AB ⊥.1.(2022高三·全国·专题练习)求过椭圆221169x y +=上一点M ⎛ ⎝⎭的切线l 方程.2.(2022高三·全国·专题练习)设双曲线C :2221x y -=上点P .求双曲线C 在点P 处的切线l 的方程.3.(2021高三·全国·专题练习)求与双曲线221164x y -=有共同的渐近线,且与直线5680x y --=相切的标准双曲线方程.4.(22-23高三上·广东佛山·阶段练习)已知圆的方程为221x y +=,抛物线的方程为283y x =,则两曲线的公共切线的其中一条方程为.5.(2023·全国·模拟预测)已知拋物线2:2(0),C x py p C =>的一条切线方程为10x y --=,则C 的准线方程为.6.(24-25高三上·浙江·开学考试)已知抛物线22(0)y px p =>与斜率为32p 的直线恰有一个公共点P ,则点P 的纵坐标为()A .164B .132C .116D .187.(2024高三·全国·专题练习)已知()1,1P 是双曲线外一点,过P 引双曲线2212yx -=的两条切线,PA PB ,,A B 为切点,求直线AB 的方程.8.(2020·陕西西安·一模)在平面直角坐标系中,动点P 在椭圆22:1169x y C +=上运动,则点P 到直线50x y --=的距离的最大值为.9.(24-25高三上·北京·阶段练习)已知抛物线24x y =,P 为直线1y =-上一点,过P 作抛物线的两条切线,切点分别为,A B ,则PA PB ⋅的值为()A .0B .1C .-2D .-110.(2023高三·全国·专题练习)已知点P (x ,y )是椭圆22194x y +=上任意一点,则点P 到直线l :y x =+的最大距离为.1.(2022高三·全国·专题练习)已知椭圆221259x y +=与双曲线()2222:10,0x y C m n m n -=>>有公共焦点12,F F ,点94,5P ⎛⎫⎪⎝⎭在双曲线C 上,则该双曲线在点P 处的切线的斜率为.2.(2024·广东茂名·模拟预测)已知抛物线C :24x y =,定点()1,0T ,M 为直线112y x =-上一点,过M 作抛物线C 的两条切线MA ,MB ,A ,B 是切点,则TAB △面积的最小值为.3.(2024高三·全国·专题练习)(多选)已知O 为坐标原点,抛物线2=2B >0上有异于原点的()11,A x y ,()22,B x y 两点,F 为抛物线的焦点,以A ,B 为切点的抛物线的切线分别记为PA ,PB ,则()A .若2124p x x =,则A ,F ,B 三点共线B .若212y y p =-,则A ,F ,B 三点共线C .若π2APB ∠=,则A ,F ,B 三点共线D .若112FA FB p +=,则A ,F ,B 三点共线4.(24-25高三上·河北邢台·开学考试)已知()0,2,A P 是抛物线21:4C x y =上任一点,Q 为PA 的中点,记动点Q 的轨迹为2C .(1)求2C 的方程;(2)过点P 作曲线2C 的两条切线,切点分别为,M N ,求点P 到直线MN 的距离的最小值.5.(24-25高三上·甘肃白银·阶段练习)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为()()12,0,,0F c F c -,上顶点为A ,抛物线2:2(0)T y px p =>的焦点为2F .(1)记椭圆C 与抛物线T 在第一象限的交点为B ,若13BF =T 的方程;(2)过点1F 的直线l 与抛物线T 相切于第一象限,切点为P ,证明:直线l 经过点A ,且A 为线段1PF 的中点.6.(23-24高三下·山东济宁·开学考试)已知双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12,F F ,渐近线方程为3y x =±,且经过点P ⎛- ⎝⎭.(1)求双曲线C 的方程;(2)过点P 作双曲线C 的切线,l l 与x 轴交于点Q ,试判断1F PQ ∠与2F PQ ∠的大小关系,并给予证明.7.(2024·陕西安康·模拟预测)已知双曲线2222Γ:1(0,0)x y a b a b-=>>的右焦点为1F ,过1F 与x 轴垂直的直线交Γ于,A B 两点,且1AB =,离心率为2.(1)求Γ的方程;(2)已知圆222(0)x y r r +=>上点()00,x y 处的切线方程是200x x y y r +=,利用类比思想可知双曲线22221(0,0)x y a b a b-=>>上点()00,x y 处的切线方程为00221x x y y a b -=.过点(),1(22)C m m -<<分别作双曲线2222Γ:1(0,0)x y a b a b-=>>的左、右两支的切线,切点分别为,P Q ,连接PQ ,并过线段PQ 的中点F 分别再作双曲线左、右两支的切线,切点分别为,D E ,证明:点,,C D E 在同一条直线上.8.(23-24高三下·河南·阶段练习)已知椭圆22122:1x y C b a+=与双曲线()222122:10,x y C a b C a b -=>>的焦点与2C的焦点间的距离为1b =.(1)求1C 与2C 的方程;(2)过坐标轴上的点P 可以作两条1C 与2C 的公切线.(i )求点P 的坐标.(ii )当点P 在y 轴上时,是否存在过点P 的直线l ,使l 与12,C C 均有两个交点?若存在,请求出l 的方程;若不存在,请说明理由.9.(23-24高二上·湖南衡阳·期末)已知曲线C 上的动点M 满足12||||||2MF MF -=,且()()122,0,2,0F F -.(1)求C 的方程;(2)已知直线l 与C 交于,P Q 两点,过,P Q 分别作C 的切线,若两切线交于点R ,且点R 在直线14x =上,证明:l 经过定点.10.(2024·全国·模拟预测)已知椭圆()2222:10x y E a b a b+=>>的左、右焦点分别为1F 、2F ,O 为坐标原点,在椭圆E 上仅存在6个点()1,2,3,4,5,6i M i =,使得12i M F F △为直角三角形,且12i M F F △面积的最大值为2.(1)求椭圆E 的标准方程;(2)已知点P 是椭圆E 上一动点,且点P 在y 轴的左侧,过点P 作24y x =的两条切线,切点分别为A 、B .求22OF A OF B S S +△△的取值范围.(1)求实数b 的值;(2)求以点A 为圆心,且与抛物线2.(安徽·高考真题)设F (Ⅰ)过点()0,4P -作抛物线,A B 到直线的距离为(1)求抛物线E的方程;(2)设动直线l与抛物线点7.(湖南·高考真题)已知抛物线的焦点也是椭圆C的公共弦的长为26.2)过点的直线相交于,两点,与相交于,两点,且在点处的切线与绕点旋转时,(1)求点A,B的坐标;(2)求PAB∆的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公共点为切点.。
圆锥曲线的切点弦、中点弦、切线

圆锥曲线的切点弦、中点弦、切线
圆锥曲线中点弦公式:py-αx=pβ-α^2。
立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。
旋转轴叫做圆锥的轴。
垂直于轴的边旋转而成的曲面叫做圆锥的底面。
不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。
曲线,是微分几何学研究的主要对象之一。
直观上,曲线可看成空间质点运动的轨迹。
微分几何就是利用微积分来研究几何的学科。
为了能够应用微积分的知识,我们不能考虑一切曲线,甚至不能考虑连续曲线,因为连续不一定可微。
这就要我们考虑可微曲线。
第1页共1页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:圆锥曲线的切线方程和切点弦方程
主讲人: 安庆一中 李治国 教学目标:
(1).掌握圆锥曲线在某点处的切线方程及切点弦方程。
(2).会用切线方程及切点弦方程解决一些问题。
(3)通过复习渗透数形结合、类比的思想,逐步培养学生分析问题和解决问题的能力。
(4) 掌握曲线与方程的关系。
教学重点:
切线方程及切点弦方程的应用
教学难点:
如何恰当使用切线方程及切点弦方程
教学过程:
1. 引入:
通过09年安徽省高考题及近几年各省考察圆锥曲线的实例引出本节课。
2. 知识点回顾:
1.
2. 3.
4. 圆锥曲线切线的几个性质:
性质1 过椭圆的准线与其长轴所在直线的交点作椭圆的两条切线,则切点弦长等于该椭圆的通径.同理:双曲线,抛物线也有类似的性质
性质2 过椭圆的焦点F 1的直线交椭圆于A ,B 两点,过A ,B 两点作椭圆的切线交
于点P ,则P 点的轨迹是焦点 的对应的准线,并且
同理:双曲线,抛物线也有类似的性质
3. 例题精讲:
练习1:
抛物线 与直线 围成的封闭的图形的面积为 ,若直线l 与抛物线相
切,且平行于直线 ,则直线l 的方程为
例1: 设抛物线 的焦点为F ,动点P 在直线
22200
(,)x y r M x y +=过圆 上一点 的切线方程:200xx yy r +=00221xx yy a b +=22
0022(,)1x y P x y a b +=设为椭圆上的点,则过该点的切线方程为:22
0022
(,)1x y P x y a b -=设为双曲线上的点,则过该点的切线方程为:00221xx yy a b -=00(,)2P x y px =2设为抛物线y 上的点,则过该点的切线方程为:00()
yy p x x =+1PF AB ⊥1F :20
l x y --=2:C y x =2(0)y ax a =>1x =43260x y -+=
上运动,过P 作抛物线C 的两条切线PA 、PB ,且与抛物线C 分别相切于A 、B 两点.求△APB 的重心G 的轨迹方程.
4. 圆锥曲线的切点弦方程:
1.
2.
3.
4. 练习2:
例题3:
5.小结: 1.判断直线与圆锥曲线的位置关系时,注意数形结合;
2. 掌握求曲线方程的方法:
3. 两种方程两种思想
作业: 6. 反思
22
0022(,)1x y P x y a b +=设为椭圆外一点,过该点作椭圆的两条切线,切点为A ,B 则弦AB 的方程为:22200(,)P x y x y r +=设为圆外一点,则切点弦的方程为:
2
00xx yy r +=220022(,)1x y P x y a b -=过为双曲线的两支作两条切线,则切点弦方程为:00221xx yy a b -=00(,)2P x y px =2设为抛物线y 开口外一点,则切点弦的方程为:
00()yy p x x =+22
221(,0). x y P m a b
A B AB ±=≠对于圆锥曲线,过点,(m 0)作两条切线,切点为,则直线恒过定点22x 21,4312A,B AB OMN y P x y +=+=已知椭圆是在直线位于第一象限上一点,由P 向已知椭圆作两切线,切点分别为,问当直线与两坐标
轴围成的三角形面积最小,最小值为多少?
2l y x+3P y 2A,B.PAB P x ==∆已知是直线:上一点,过点作抛物线
的两条切线,切点分别为求面积
的最小值。
00221
xx yy a b +=。
