初中相似图形-练习题
初三图形的相似练习题

初三图形的相似练习题在初三的数学学习中,相似形是一个非常基础且重要的概念。
了解并掌握相似形的性质和运用方法,对于解决各种几何问题起到至关重要的作用。
为了帮助同学们更好地理解和掌握相似形的知识,下面将提供一些相似形的练习题供大家练习。
练习题1:已知图形ABCD与图形EFGH是相似形,已知AB=4cm,EF=6cm,BC=5cm,FG=10cm。
求图形EFGH的其他边长。
解答:由相似形的性质可知,相似形的对应边长之间的比例相等。
设ED为图形ABCD与图形EFGH对应的边长。
根据比例关系可以得到:AB/EF = BC/FG = CD/GH = AD/EH代入已知条件,得到:4/6 = 5/10 = CD/10解方程可得:CD = 20/3 cm由此可知,图形EFGH的其他边长为:EF = 6cm,FG = 10cm,GH = 2*(20/3) = 40/3 cm,EH = 2*4 = 8cm。
练习题2:已知图形PQRS与图形IJKL是相似形,已知PQ=8cm,IJ=12cm,PR=10cm,KL=15cm。
求图形PQRS的其他边长。
解答:同样地,根据相似形的性质可得到:PQ/IJ = PR/KL = PS/JL = QS/KI代入已知条件,得到:8/12 = 10/15 = PS/15解方程可得:PS = 20/3 cm由此可知,图形PQRS的其他边长为:PQ = 8cm,PR = 10cm,RS = 2*(20/3) = 40/3 cm,QS = 2*8 = 16cm。
练习题3:已知图形WXYZ与图形ABCD是相似形,已知WX=12cm,AB=8cm,YZ=16cm。
求图形WXYZ的其他边长。
解答:同样地,根据相似形的性质可得到:WX/AB = WY/AD =XZ/BC = YZ/CD代入已知条件,得到:12/8 = WY/AD = XZ/BC = 16/CD解方程可得:CD = 32/3 cm由此可知,图形WXYZ的其他边长为:WX = 12cm,XY = 2*(32/3) = 64/3 cm,YZ = 16cm,ZW = 2*12 = 24cm。
初三相似图形练习题

初三相似图形练习题1.已知x?1,则x?y的值为 y2x?y1 ?1 -332.在比例尺为1∶20的图纸上画出的某个零件的长是32mm,这个零件的实际长是64m 640cm 64cm 64mm3.已知C是线段AB的黄金分割点∶∶∶∶24.如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形1对 2对 3对 4对5.ΔABC中,DE∥BC,且AD∶DB=2∶1,那么DE∶BC 等于2∶1 1∶ 2∶ 3∶26.如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,则梯子的长为3.85m .00m .40m .50m7. 如图,∠ACB=∠ADC=90°,BC=a, AC=b, AB=c, 要使△ABC∽△CAD,只要CD等于b2b2a2ab ccac8、已知△ABC的三边长分别为,,2, △A′B′C′的两边长分别是1和3, 如果△ABC与△A′B′C′相似,那么△A′B′C′的第三边长应该是239、下列命题中正确的是.所有等腰三角形都相似所有的直角三角形都相似所有等边三角形都相似所有的矩形都相似10、我们做物理实验时,如图所示,火焰上光线穿过小孔O,在暗箱里形成倒立的像,蜡烛的长度AB为9cm,OB=24cm,OD=8cm,则蜡烛的像的长度CD为3cm4cm cm 1.5cm二、填空题11. 已知x?3, 则x?y?_____. y4y12、已知1,,x ,5四个数成比例,则x的值应该是 .13、若a?c?e?3,则a?c?e?______; bdf4b?d?f14、如图, △ABC中, D, E分别是AB,AC上的点,当时, △ADE与△ABC相似.15、已知△ABC∽△DEF,且它们的面积之比为1:9,那么它们的周长之比为。
三、解答题16.在方格纸中,每个小格的顶点叫做格点.以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A1B1C1,使ΔA1B1C1与格点三角形ABC相似.17.已知线段a、b、c、d是成比例线段,其中a = ,b =,d =,求线段c的长.18.已知x?y?z,求x?2y?3z的值. 1089y?5z19、小颖测得2m高的标杆在太阳下的影长为1.2m,同时又测得一棵树的影长为3.6m, 请你帮助小颖计算出这棵树的高度.23.如图,在梯形ABCD中,AB⊥BC,∠BAD=90°,对角线BD⊥DC.ΔABD与ΔDCB相似吗?请说明理由.如果AD=4,BC=9,求BD的长.25、如图,点C、D在线段AB上,且ΔPCD是等边三角形.当AC,CD,DB满足怎样的关系时,ΔACP∽ΔPDB;当ΔACP∽ΔPDB时,试求∠APB的度数.。
九年级的相似图形练习题

一、选择题1. 下列图形中,属于相似图形的是()A. 两个等腰三角形B. 两个等边三角形C. 两个等腰梯形D. 两个等腰直角三角形2. 已知两个相似三角形的对应边长之比为2:3,那么它们的面积比为()A. 4:9B. 2:3C. 1:2D. 1:33. 下列哪个图形不是相似图形()A. 两个正方形B. 两个等腰三角形C. 两个等腰梯形D. 两个等边三角形4. 若两个相似三角形的面积比为4:9,则它们的对应边长之比为()A. 2:3B. 3:2C. 4:3D. 3:45. 下列哪个图形不是相似图形()A. 两个正方形B. 两个等腰三角形C. 两个等腰梯形D. 两个等边三角形二、填空题1. 若两个相似三角形的面积比为9:16,则它们的对应边长之比为______。
2. 两个相似三角形的周长比为2:3,那么它们的面积比为______。
3. 若两个相似三角形的对应边长之比为1:2,那么它们的周长比为______。
4. 两个相似三角形的面积比为4:9,则它们的对应边长之比为______。
5. 若两个相似三角形的周长比为3:4,那么它们的面积比为______。
三、解答题1. 已知两个相似三角形的对应边长之比为2:3,求它们的面积比。
2. 两个相似三角形的周长比为2:3,求它们的面积比。
3. 若两个相似三角形的对应边长之比为1:2,求它们的周长比。
4. 两个相似三角形的面积比为4:9,求它们的对应边长之比。
5. 若两个相似三角形的周长比为3:4,求它们的面积比。
四、应用题1. 一个等腰三角形的底边长为8cm,高为6cm,求与它相似的三角形,底边长为12cm时的高。
2. 一个长方形的长为10cm,宽为5cm,求与它相似的矩形,长为15cm时的宽。
3. 一个圆的半径为3cm,求与它相似的圆,半径为4.5cm时的面积。
4. 一个正方形的边长为6cm,求与它相似的正方形,边长为8cm时的周长。
5. 一个三角形的边长分别为3cm、4cm、5cm,求与它相似的三角形,边长分别为6cm、8cm、10cm时的面积。
27.1图形的相似同步练习
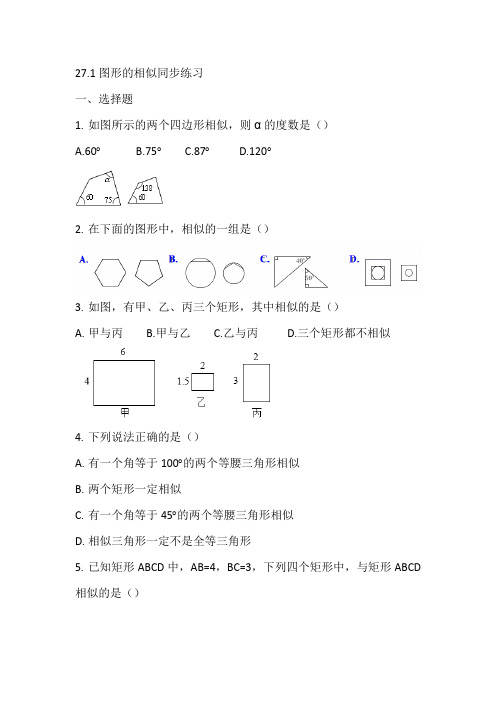
27.1图形的相似同步练习一、选择题1.如图所示的两个四边形相似,则α的度数是()A.60°B.75°C.87°D.120°2.在下面的图形中,相似的一组是()3.如图,有甲、乙、丙三个矩形,其中相似的是()A.甲与丙B.甲与乙C.乙与丙D.三个矩形都不相似4.下列说法正确的是()A.有一个角等于100°的两个等腰三角形相似B.两个矩形一定相似C.有一个角等于45°的两个等腰三角形相似D.相似三角形一定不是全等三角形5.已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD 相似的是()6.如图所示,在长为8cm,宽为6cm的条形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是()A.28cm2B.27cm2C.21cm2D.20cm27.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为()A.23B.32C.94D.498.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形最大边长为18,则最短边长为()A.6B. 8C. 12D. 109.下列说法正确的个数有()①同一底片印出来的不同尺寸的照片是相似的②放电影时胶片上的图象和它映射到屏幕上的图象是相似的③放大镜放大后的图形与原来的图形是相似的④水平观看装在带有水的透明玻璃杯中的金鱼所组成的像与金鱼本身的像是相似的A.1个B.2个C.3个D.4个10.用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:甲说:三角形的每个内角都扩大到原来的5倍;乙说:三角形的每条边都扩大到原来的5倍;丙说:三角形的面积扩大到原来的5倍;丁说:三角形的周长扩大到原来的5倍,上述说法中正确的是()A.甲和乙B.乙和丙C. 丙和丁D.乙和丁二、填空题1.一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是_______.2.两个相似多边形的周长的比为2:3,较大多边形的面积为45cm2,则较小多边形的面积为_________cm23.如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD 与矩形EABF相似,则相似比等于________.4.秋天红透的枫叶,总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”如图是两片形状完全相同,大小不同的枫叶,则x的值为_______cm。
最新初中数学图形的相似技巧及练习题附答案解析

最新初中数学图形的相似技巧及练习题附答案解析一、选择题1.要做甲、乙两个形状相同(相似)的三角形框架,已知甲三角形框架三边的长分别为50 cm、60 cm、80 cm,乙三角形框架的一边长为20 cm,则符合条件的乙三角形框架共有().A.1种B.2种C.3种D.4种【答案】C【解析】试题分析:根据相似图形的定义,可由三角形相似,那么它们边长的比相同,均为5:6:8,乙那个20cm的边可以当最短边,最长边和中间大小的边.故选:C.点睛:本题考查的是相似形的定义,相似图形的形状相同,但大小不一定相同.2.如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数1yx=-、2yx=的图象交于B、A两点,则∠OAB大小的变化趋势为()A.逐渐变小B.逐渐变大C.时大时小D.保持不变【答案】D【解析】【分析】如图,作辅助线;首先证明△BEO∽△OFA,,得到BE OEOF AF=;设B为(a,1a-),A为(b,2b),得到OE=-a,EB=1a-,OF=b,AF=2b,进而得到222a b=,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB=22为定值,即可解决问题.【详解】解:分别过B和A作BE⊥x轴于点E,AF⊥x轴于点F,则△BEO∽△OFA,∴BE OE OF AF=,设点B 为(a ,1a -),A 为(b ,2b ), 则OE=-a,EB=1a-,OF=b ,AF=2b , 可代入比例式求得222a b =,即222a b =, 根据勾股定理可得:OB=22221OE EB a a +=+,OA=22224OF AF b b +=+, ∴tan ∠OAB=2222222212244b a OB a b OA b b b b++==++=222214()24b b b b ++=22 ∴∠OAB 大小是一个定值,因此∠OAB 的大小保持不变.故选D【点睛】该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答.3.如图,在平面直角坐标中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为13,点A ,B ,E 在x 轴上.若正方形ABCD 的边长为2,则点F 坐标为( )A .(8,6)B .(9,6)C .19,62⎛⎫ ⎪⎝⎭ D .(10,6)【答案】B【解析】【分析】直接利用位似图形的性质结合相似比得出EF的长,进而得出△OBC∽△OEF,进而得出EO 的长,即可得出答案.【详解】解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,∴13 BC OBEF EO==,∵BC=2,∴EF=BE=6,∵BC∥EF,∴△OBC∽△OEF,∴136BOBO=+,解得:OB=3,∴EO=9,∴F点坐标为:(9,6),故选:B.【点睛】此题主要考查了位似变换以及相似三角形的判定与性质,正确得出OB的长是解题关键.4.如图,正方形OABC的边长为6,D为AB中点,OB交CD于点Q,Q是y=kx上一点,k的值是()A.4 B.8 C.16 D.24【答案】C【解析】【分析】延长根据相似三角形得到:1:2BQ OQ=,再过点Q作垂线,利用相似三角形的性质求出QF、OF,进而确定点Q的坐标,确定k的值.【详解】解:过点Q 作QF OA ⊥,垂足为F ,OABC Q 是正方形,6OA AB BC OC ∴====,90ABC OAB DAE ∠=∠=︒=∠,D Q 是AB 的中点,12BD AB ∴=, //BD OC Q ,OCQ BDQ ∴∆∆∽, ∴12BQ BD OQ OC ==, 又//QF AB Q ,OFQ OAB ∴∆∆∽, ∴22213QF OF OQ AB OA OB ====+, 6AB =Q , 2643QF ∴=⨯=,2643OF =⨯=, (4,4)Q ∴,Q 点Q 在反比例函数的图象上,4416k ∴=⨯=,故选:C .【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定,利用相似三角形性质求出点Q 的坐标是解决问题的关键.5.如图1,在Rt △ABC 中,∠ACB=90°,点P 以每秒1cm 的速度从点A 出发,沿折线AC -CB 运动,到点B 停止.过点P 作PD ⊥AB ,垂足为D ,PD 的长y (cm )与点P 的运动时间x (秒)的函数图象如图2所示.当点P 运动5秒时,PD 的长是( )A .1.5cmB .1.2cmC .1.8cmD .2cm【答案】B【解析】【分析】【详解】 由图2知,点P 在AC 、CB 上的运动时间时间分别是3秒和4秒,∵点P 的运动速度是每秒1cm ,∴AC=3,BC=4.∵在Rt △ABC 中,∠ACB=90°,∴根据勾股定理得:AB=5.如图,过点C 作CH ⊥AB 于点H ,则易得△ABC ∽△ACH . ∴CH AC BC AB =,即AC BC 3412CH CH AB 55⋅⨯=⇒==. ∴如图,点E (3,125),F (7,0). 设直线EF 的解析式为y kx b =+,则 123k b {507k b=+=+, 解得:3k 5{21b 5=-=. ∴直线EF 的解析式为321y x 55=-+. ∴当x 5=时,()3216PD y 5 1.2cm 555==-⨯+==.6.矩形ABCO如图摆放,点B在y轴上,点C在反比例函数ykx=(x>0)上,OA=2,AB=4,则k的值为()A.4 B.6 C.325D.425【答案】C【解析】【分析】根据矩形的性质得到∠A=∠AOC=90°,OC=AB,根据勾股定理得到OB22OA AB=+=5C作CD⊥x轴于D,根据相似三角形的性质得到CD85=,OD45=求得8545,)于是得到结论.【详解】解:∵四边形ABCO是矩形,∴∠A=∠AOC=90°,OC=AB,∵OA=2,AB=4,∴过C作CD⊥x轴于D,∴∠CDO=∠A=90°,∠COD+∠COB=∠COB+∠AOB=90°,∴∠COD=∠AOB,∴△AOB∽△DOC,∴OB AB OA OC CD OD==,2542CD OD==,∴CD855=,OD45=,∴C(455,855),∴k325 =,【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,矩形的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.7.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为12米,若小明的眼晴与地面的距离为1.5米,则旗杆的高度为()A.9 B.12 C.14 D.18【答案】A【解析】【分析】如图,BC=2m,CE=12m,AB=1.5m,利用题意得∠ACB=∠DCE,则可判断△ACB∽△DCE,然后利用相似比计算出DE的长.【详解】解:如图,BC=2m,CE=12m,AB=1.5m,由题意得∠ACB=∠DCE,∵∠ABC=∠DEC,∴△ACB∽△DCE,∴AB BCDE CE=,即1.5212DE=,∴DE=9.即旗杆的高度为9m.故选A.【点睛】本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,用相似三角形对应边的比相等的性质求物体的高度.8.在相同时刻,物高与影长成正比,如果高为1米的标杆影长为2米,那么影长为30米的旗杆的高为( )A .20米B .18米C .16米D .15米【答案】D【解析】【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似,利用标杆的高:标杆影长=旗杆的高:旗杆的影长,列出方程,求解即可得出旗杆的高度.【详解】解:根据题意解:标杆的高:标杆影长=旗杆的高:旗杆的影长,即1:2=旗杆高:30, ∴旗杆的高=130=152⨯米. 故选:D .【点睛】 本题主要考察的是相似三角形的应用,正确列出方程是解决本题的关键.9.如图,四边形ABCD 内接于O e ,AB 为直径,AD CD =,过点D 作DE AB ⊥于点E ,连接AC 交DE 于点F .若3sin 5CAB ∠=,5DF =,则AB 的长为( )A .10B .12C .16D .20【答案】D【解析】【分析】连接BD ,如图,先利用圆周角定理证明ADE DAC ∠=∠得到5FD FA ==,再根据正弦的定义计算出3EF =,则4AE =,8DE =,接着证明ADE DBE ∆∆∽,利用相似比得到16BE =,所以20AB =.【详解】解:连接BD ,如图,AB Q 为直径,90ADB ACB ∴∠=∠=︒,AD CD =Q ,DAC DCA ∴∠=∠,而DCA ABD ∠=∠,DAC ABD ∴∠=∠,DE AB ∵⊥,90ABD BDE ∴∠+∠=︒,而90ADE BDE ∠+∠=︒,ABD ADE ∴∠=∠,ADE DAC ∴∠=∠,5FD FA ∴==,在Rt AEF ∆中,3sin 5EF CAB AF ∠==Q , 3EF ∴=, 22534AE ∴-=,538DE =+=,ADE DBE ∠=∠Q ,AED BED ∠=∠,ADE DBE ∴∆∆∽,::DE BE AE DE ∴=,即8:4:8BE =,16BE ∴=,41620AB ∴=+=.故选:D .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90︒的圆周角所对的弦是直径.也考查了解直角三角形.10.如图,三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2∶3,若三角尺的一边长为8 cm ,则这条边在投影中的对应边长为( )A .8 cmB .12 cmC .16 cmD .24 cm【答案】B【解析】试题分析:利用相似比为2:3,可得出其对应边的比值为2:3,进而求出即可.解:∵三角尺与其灯光照射下的中心投影组成了位似图形,它们的相似比为2:3,三角尺的一边长为8cm ,∴设这条边在投影中的对应边长为:x ,则=,解得:x=12.故选B .考点:位似变换.11.如图,点D 是ABC V 的边BC 上一点,,2BAD C AC AD ∠=∠= ,如果ACD V 的面积为15,那么ABC V 的面积为( )A .20B .22.5C .25D .30 【答案】A【解析】【分析】先证明C ABD BA ∽△△,再根据相似比求出ABC V 的面积即可.【详解】∵,BAD C B B ∠=∠=∠∠∴C ABD BA ∽△△∵2AC AD =∴4S ABD S CBA =V V ∴43S ACD S CBA =V V ∵ACD V 的面积为15 ∴44152033S CBA S ACD ==⨯=V V故答案为:A .【点睛】本题考查了相似三角形的问题,掌握相似三角形的性质以及判定定理是解题的关键.12.如图,在ABC V 中,//,,30DE BC AF BC ADE ⊥∠=︒,2,33,DE BC BF ==则DF 的长为()A .4B .23C .33D .3【答案】D【解析】【分析】先利用相似三角形的相似比证明点D 是AB 的中点,再解直角三角形求得AB ,最后利用直角三角形斜边中线性质求出DF .【详解】解:∵//DE BC ,∴ADE ~ABC V V ,∵2DE BC =,∴点D 是AB 的中点,∵,30AF BC ADE ⊥∠=︒,33BF =∴∠B =30°,∴AB 6cos30BF ==︒, ∴DF=3,故选:D .【点睛】 此题主要考查相似三角形的判定与性质、解直角三角形和直角三角形斜边中线性质,熟练掌握性质的运用是解题关键.13.如图,△ABC 中,∠BAC =45°,∠ACB =30°,将△ABC 绕点A 顺时针旋转得到△AB 1C 1,当点C 1、B 1、C 三点共线时,旋转角为α,连接BB 1,交AC 于点D .下列结论:①△AC 1C 为等腰三角形;②△AB 1D ∽△BCD ;③α=75°;④CA =CB 1,其中正确的是( )A.①③④B.①②④C.②③④D.①②③④【答案】B【解析】【分析】将△ABC绕点A顺时针旋转得到△AB1C1,得到△ABC≌△AB1C1,根据全等三角形的性质得到AC1=AC,于是得到△AC1C为等腰三角形;故①正确;根据等腰三角形的性质得到∠C1=∠ACC1=30°,由三角形的内角和得到∠C1AC=120°,得到∠B1AB=120°,根据等腰三角形的性质得到∠AB1B=30°=∠ACB,于是得到△AB1D∽△BCD;故②正确;由旋转角α=120°,故③错误;根据旋转的性质得到∠C1AB1=∠BAC=45°,推出∠B1AC=∠AB1C,于是得到CA=CB1;故④正确.【详解】解:∵将△ABC绕点A顺时针旋转得到△AB1C1,∴△ABC≌△AB1C1,∴AC1=AC,∴△AC1C为等腰三角形;故①正确;∴AC1=AC,∴∠C1=∠ACC1=30°,∴∠C1AC=120°,∴∠B1AB=120°,∵AB1=AB,∴∠AB1B=30°=∠ACB,∵∠ADB1=∠BDC,∴△AB1D∽△BCD;故②正确;∵旋转角为α,∴α=120°,故③错误;∵∠C1AB1=∠BAC=45°,∴∠B1AC=75°,∵∠AB1C1=∠BAC=105°,∴∠AB1C=75°,∴∠B1AC=∠AB1C,∴CA=CB1;故④正确.故选:B.【点睛】本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,旋转的性质,正确的识别图形是解题的关键.14.如图,Rt ABO ∆中,90AOB ∠=︒,3AO BO =,点B 在反比例函数2yx =的图象上,OA 交反比例函数()0k y k x=≠的图象于点C ,且2OC CA =,则k 的值为( )A .2-B .4-C .6-D .8-【答案】D【解析】 【分析】 过点A 作AD ⊥x 轴,过点C 作CE ⊥x 轴,过点B 作BF ⊥x 轴,利用AA 定理和平行证得△COE ∽△OBF ∽△AOD ,然后根据相似三角形的性质求得21()9BOF OAD S OB S OA ==V V ,24()9COE AOD S OC S OA ==V V ,根据反比例函数比例系数的几何意义求得212BOF S ==V ,从而求得4COE S =V ,从而求得k 的值.【详解】解:过点A 作AD ⊥x 轴,过点C 作CE ⊥x 轴,过点B 作BF ⊥x 轴∴CE ∥AD ,∠CEO=∠BFO=90°∵90AOB ∠=︒∴∠COE+∠FOB=90°,∠ECO+∠COE=90°∴∠ECO=∠FOB∴△COE ∽△OBF ∽△AOD 又∵3AO BO =,2OC CA =∴13OB OA =,23OC OA = ∴21()9BOF OAD S OB S OA ==V V ,24()9COE AOD S OC S OA ==V V ∴4COE BOFS S =V V∵点B 在反比例函数2y x =的图象上 ∴212BOF S ==V ∴4COE S =V∴42k =,解得k=±8 又∵反比例函数位于第二象限,∴k=-8故选:D .【点睛】本题考查反比例函数的性质和相似三角形的判定和性质,正确添加辅助线证明三角形相似,利用数形结合思想解题是关键.15.如图,顶角为36o 的等腰三角形,其底边与腰之比等k ,这样的三角形称为黄金三角形,已知腰AB=1,ABC ∆为第一个黄金三角形,BCD ∆为第二个黄金三角形,CDE ∆为第三个黄金三角形以此类推,第2020个黄金三角形的周长()A .2018kB .2019kC .20182k k + D .2019(2)k k +【答案】D【解析】【分析】根据相似三角形对应角相等,对应边成比例,求出前几个三角形的周长,进而找出规律:第n 个黄金三角形的周长为k n-1(2+k ),从而得出答案.【详解】解:∵AB=AC=1,∴△ABC 的周长为2+k ;△BCD 的周长为k+k+k 2=k (2+k );△CDE 的周长为k 2+k 2+k 3=k 2(2+k );依此类推,第2020个黄金三角形的周长为k 2019(2+k ).故选:D .【点睛】此题考查黄金分割,相似三角形的性质,找出各个三角形周长之间的关系,得出规律是解题的关键.16.如图,在□ABCD 中,E 、F 分别是边BC 、CD 的中点,AE 、AF 分别交BD 于点G 、H ,则图中阴影部分图形的面积与□ABCD 的面积之比为( )A .7 : 12B .7 : 24C .13 : 36D .13 : 72【答案】B【解析】【分析】 根据已知条件想办法证明BG=GH=DH ,即可解决问题;【详解】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC ,AB=CD ,AD=BC ,∵DF=CF ,BE=CE , ∴12DH DF HB AB ==,12BG BE DG AD ==, ∴13DH BG BD BD ==, ∴BG=GH=DH ,∴S △ABG =S △AGH =S △ADH ,∴S 平行四边形ABCD =6 S △AGH ,∴S △AGH :ABCD S 平行四边形=1:6,∵E 、F 分别是边BC 、CD 的中点, ∴12EF BD =,∴14EFCBCDDSS=VV,∴18EFCABCDSS=V四边形,∴1176824AGH EFCABCDS SS+=+=V V四边形=7∶24,故选B.【点睛】本题考查了平行四边形的性质、平行线分线段成比例定理、等底同高的三角形面积性质,题目的综合性很强,难度中等.17.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为()A.1 B.1.2 C.2 D.2.5【答案】B【解析】【分析】由AB∥GH∥CD可得:△CGH∽△CAB、△BGH∽△BDC,进而得:GH CHAB BC=、GH BHCD BC=,然后两式相加即可.【详解】解:∵AB∥GH,∴△CGH∽△CAB,∴GH CHAB BC=,即2GH CHBC=①,∵CD∥GH,∴△BGH∽△BDC,∴GH BHCD BC=,即3GH BHBC=②,①+②,得:123GH GH CH BHBC BC+=+=,解得:61.25GH==.故选:B.【点睛】本题考查了相似三角形的判定和性质,属于基本题型,熟练掌握相似三角形的判定和性质是解题的关键.18.如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是()A.∠ABD=∠C B.∠ADB=∠ABC C.AB CB BDCD=D.AD ABAB AC=【答案】C【解析】【分析】由∠A是公共角,利用有两角对应相等的三角形相似,即可得A与B正确;又由两组对应边的比相等且夹角对应相等的两个三角形相似,即可得D正确,继而求得答案,注意排除法在解选择题中的应用.【详解】∵∠A是公共角,∴当∠ABD=∠C或∠ADB=∠ABC时,△ADB∽△ABC(有两角对应相等的三角形相似),故A与B正确,不符合题意要求;当AB:AD=AC:AB时,△ADB∽△ABC(两组对应边的比相等且夹角对应相等的两个三角形相似),故D正确,不符合题意要求;AB:BD=CB:AC时,∠A不是夹角,故不能判定△ADB与△ABC相似,故C错误,符合题意要求,故选C.19.如图,在ABC∆中,,D E分别是边,AB AC的中点,ADE∆和四边形BCED的面积分别记为12,S S,那么12SS的值为()A.12B.14C.13D.23【答案】C【解析】【分析】根据已知可得到△ADE∽△ABC,从而可求得其面积比,则不难求得12SS的值.【详解】∵,D E分别是边,AB AC的中点,∴DE∥BC,∴△ADE∽△ABC,∴DE:BC=1:2,所以它们的面积比是1:4,所以1211 =413S S= -,故选C.【点睛】本题考查了三角形的中位线定理和相似三角形的性质:(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.20.两个相似多边形的面积比是9∶16,其中小多边形的周长为36 cm,则较大多边形的周长为 )A.48 cm B.54 cm C.56 cm D.64 cm【答案】A【解析】试题分析:根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.解:两个相似多边形的面积比是9:16,面积比是周长比的平方,则大多边形与小多边形的相似比是4:3.相似多边形周长的比等于相似比,因而设大多边形的周长为x,则有=,解得:x=48.大多边形的周长为48cm.故选A.考点:相似多边形的性质.。
初中数学图形的相似练习题及参考答案

初中数学图形的相似练习题及参考答案相似是初中数学中的一个重要概念,它描述了两个图形在形状上的相似程度。
相似的图形具有相同的形状但不一定相等的大小。
在这篇文章中,我们将介绍几道关于相似图形的练习题,并提供参考答案供大家参考。
题目一:已知三角形ABC和三角形DEF相似,且比例系数为3:4。
若AB=6cm,BC=8cm,DE=12cm,求EF的长度。
解答一:根据相似三角形的定义,相似三角形的对应边长之比相等。
即AB/DE=BC/EF。
代入已知条件,得到以下等式:6/12=8/EF通过交叉乘法可以求解EF的长度:6*EF=12*8EF=16cm所以,EF的长度为16cm。
题目二:如果一个正方形的边长为6cm,那么和它相似的另一个正方形的边长是多少?解答二:由于两个正方形相似,所以它们的对应边长之比相等。
设另一个正方形的边长为x,则根据相似三角形的性质得到以下等式:x/6=6/6通过交叉乘法可以求解x的长度:x=6cm所以,和给定正方形相似的另一个正方形的边长也是6cm。
题目三:已知一个矩形的长为10cm,宽为5cm。
如果和它相似的另一个矩形的长为15cm,求这个矩形的宽。
解答三:根据相似矩形的性质,两个矩形的边长比相等。
设相似矩形的宽为x,则根据已知条件可以得到以下等式:10/x=15/5通过交叉乘法可以求解x的长度:10*5=15*x50=15*xx=50/15x=10/3 cm所以,这个矩形的宽为10/3 cm。
题目四:如果一个三角形的三边分别为3cm,4cm和5cm,那么和它相似的另一个三角形的三边分别是多少?解答四:根据相似三角形的性质,两个三角形的边长比相等。
设相似三角形的三边分别为x、y、z,则根据已知条件可以得到以下等式:x/3=y/4=z/5通过交叉乘法可以求解x、y、z的长度:x=3*(4/5)=12/5 cmy=4*(4/5)=16/5 cmz=5*(4/5)=20/5 cm所以,和给定三角形相似的另一个三角形的三边分别是:12/5 cm、16/5 cm和20/5 cm。
人教版九年级数学下册图形的相似)同步练习题

第二十七章 相似27.1 图形的相似基础题1.下列各组图形相似的是( )2.将左图中的箭头缩小到原来的12,得到的图形是( )3.将一个直角三角形三边扩大3倍,得到的三角形一定是( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .以上三种情况都有可能 4.下列各线段的长度成比例的是( ) A .2 cm ,5 cm ,6 cm ,8 cm B .1 cm ,2 cm ,3 cm ,4 cm C .3 cm ,6 cm ,7 cm ,9 cm D .3 cm ,6 cm ,9 cm ,18 cm5.两个相似多边形一组对应边分别为3 cm ,4.5 cm ,那么它们的相似比为( ) A.23B.32C.49D.946.(莆田中考)下列四组图形中,一定相似的是( ) A .正方形与矩形 B .正方形与菱形 C .菱形与菱形 D .正五边形与正五边形7.在比例尺为1∶200的地图上,测得A ,B 两地间的图上距离为4.5 cm ,则A ,B 两地间的实际距离为______m.8.在一张复印出来的纸上,一个多边形的一条边由原图中的2 cm 变成了6 cm ,这次复印的放缩比例是________.9.如图所示是两个相似四边形,求边x 、y 的长和∠α的大小.中档题10.下列说法:①放大(或缩小)的图片与原图片是相似图形;②比例尺不同的中国地图是相似形;③放大镜下的五角星与原来的五角星是相似图形;④放电影时胶片上的图象和它映射到屏幕上的图象是相似图形;⑤平面镜中,你的形象与你本人是相似的.其中正确的说法有()A.2个B.3个C.4个D.5个11.(重庆中考)如图,△ABC与△DE F相似,相似比为1∶2,BC的对应边是EF,若BC =1,则EF的长是()A.1 B.2C.3 D.412.某机器零件在图纸上的长度是21 mm,它的实际长度是630 mm,则图纸的比例尺是()A.1∶20 B.1∶30C.1∶40 D.1∶5013.如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是()A.2DE=3MNB.3DE=2MNC.3∠A=2∠FD.2∠A=3∠F14.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是()15.如图所示,它们是两个相似的平行四边形,根据条件可知,∠α=________,m=________.16.如图,左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形,要求大小与左边四边形不同.17.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:(1)每块地砖的长与宽分别为多少?(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.综合题18.如图:矩形ABCD的长AB=30,宽BC=20.(1)如图1,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD 与A′B′C′D′相似吗?请说明理由;(2)如图2,x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?参考答案1.B 2.A 3.A 4.D 5.A 6.D 7.9 8.1∶3 9.∵两个四边形相似,∴AD A′D′=BC B′C′=AB A′B′,即416=6x =7y. ∴x =24,y =28.∵∠B =∠B′=73°,∴∠α=360°-∠A -∠D -∠B =83°.10.D 11.B 12.B 13.B 14.B 15.125° 12 16.图略. 17.(1)设矩形地砖的长为a cm ,宽为b cm , 由题图可知4b =60,即b =15.因为a +b =60,所以a =60-b =45,所以矩形地砖的长为45 cm ,宽为15 cm.(2)不相似.理由:因为所铺成矩形地面的长为2a =2×45=90(cm),宽为60 cm , 所以长宽=9060=32,而a b =4515=31,32≠31,即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.所以它们不相似.18.(1)不相似,AB =30,A ′B ′=28,BC =20,B ′C ′=18,而2830≠1820,故矩形ABCD与矩形A′B′C′D′不相似.(2)矩形ABCD 与A′B′C′D′相似,则A′B′AB =B′C′BC 或A′B′BC =B′C′AB .则:30-2x 30=20-220,或30-2x 20=20-230,解得x =1.5或9,故当x =1.5或9时,矩形ABCD 与A′B′C′D′相似.高频考点强化训练:三视图的有关判断及计算时间:30分钟 分数:50分 得分:________ 一、选择题(每小题4分,共24分)1.(2016·杭州中考)下列选项中,如图所示的圆柱的三视图画法正确的是( )乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..2.(2016·贵阳中考)如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是【易错6】( )3.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )4.如图所示的几何体的主视图、左视图、俯视图中有两个视图是相同的,则不同的视图是( )5.一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )A .36cm 2B .40cm 2C .90cm 2D .36cm 2或40cm 2第5题图 第6题图6.(2016·承德模拟)由一些大小相同的小正方体组成的几何体乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..的俯视图和左视图如图所示,那么组成这个几何体的小正方体个数可能有( )A .8个B .6个C .4个D .12个二、填空题(每小题4分,共16分)7.下列几何体中:①正方体;②长方体;③圆柱;④球.其中,三个视图形状相同的几何体有________个,分别是________(填几何体的序号).8.如图,水平放置的长方体的底面是边长为3和5的长方形,它的左视图的面积为12,则长方体的体积等于________.9.如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是________.第8题图 第9题图 第10题图10.(2016·秦皇岛卢龙县模拟)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则x 的值为________,y 的乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..值为________.三、解答题(10分)11.如图所示的是某个几何体的三视图. (1)说出这个几何体的名称;(2)根据图中的有关数据,求这个几何体的表面积.中考必考点强化训练专题:简单三视图的识别◆类型一 简单几何体的三视图1.(2016·杭州中考)下列选项中,如图所示的圆柱的三视图画法正确的是( )乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ……………………密………………………………….封……………………….线…………………………………………………………………………..第1 题图第2题图第3题图2.(2016·抚顺中考)如图所示几何体的主视图是( )3.(2016·南陵县模拟)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )4.(2016·肥城市一模)如图所示的四个几何体中,它们各自的主视图与俯视图不相同的几何体的个数是( )A.1个 B.2个 C.3个 D.4个5.(2016·宁波中考)如图所示的几何体的主视图为( )6.(2016·鄂州中考)一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是( )7.(2016·菏泽中考)如图所示,该几何体的俯视图是( )◆类型二 简单组合体的三视图8.(2016·黔西南州中考)如图,是由几个完全相同的小正方体搭建的几何体,它的左视图是( )9.(2016·营口中考)如图所示的物体是由两个紧靠在一起的圆柱体组成,小明准备画出它的三视图,那么他所画的三视图中的主视图应该是( )10.(2016·日照中考)如图,小明同学将一个圆锥和一个三棱柱组成组合图形,观察其三视图,其俯视图是( )11.(2016·烟台中考)如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )乡镇__________________ 学校_____________________ 班级____________ 姓名____________ 座号__________ ………………………………密………………………………….封……………………….线…………………………………………………………………………..。
八年级下数学第四章相似图形练习题

D B C A第9题图第5题图 第7题图 第14题图 八年级下数学第四章相似图形练习题 姓名1.如果ad=bc,那么下列比例式中错误的是()2.若则下列各式中能成立的是( )3.下列说法中一定正确的是( )(A)有一个锐角相等的两个等腰三角形相似 (B)底角为45˚的两个等腰梯形相似(C)任意两个菱形相似 (D)有一个钝角相等的两个等腰三角形相似 4.延长线段AB 到C,使得BC= AB,则AC:AB=( ) (A)2:1 (B)3:1 (C)3:2 (D)4:35.如图△ABC 中,DE ∥BC ,BE 、CD 交于O ,S △DOE :S △BOC = 4:25,则AD :DB= ( )A 2:5B 2:3C 4:9D 3 :56.三角形三边之比为3:4:5,与它相似的另一个三角形的最短边为6cm,则这个三角形的周长为( )A 12B 18C 24D 307.如图,根据下列条件中( )可得AB ∥EF 。
(A) OA:AE=OB:BF (B) AC:AE=BD:DF(C) OA:OE=OB:DF (D)AE:BF=OA:DB8.在梯形ABCD 中,AD ∥BC.AC,BD 相交于O ,如果AD :BC=1:3, 那么下列结论正确的是( ) A. B. C. D.9.如图,在平行四边形ABCD 中,E 为CD 中点.AE 交BD 于O ,S △DOE =12.则S △AOB 等于( ) A 24 B 36 C 48 D 6010.如果mn= ab,(a,b,m,n 都不等于0)则下列比列式中错误的是( )A. B. C. D. 11.若45=-b b a ,则=ba . 12.△ABC ∽△DEF,且△ABC 的三边长分别为,2,14,2△DEF 的两边长分别为1,7,则第三边长为 .13.如果两个相似多边形的周长之比为2:3,则它们的面积之比为 .14.如图,△ABC 中AB>AC,过AC 上一点D 作直线DE ,交AB 于E ,使△ADF 与△ABC 相似,这样的直线最多可作 条。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四 相似图形一、填空题: 1、已知线段a=4、b=9,则线段a 、b 的比例中项c 是 ,线段c 、a 、b 的第四比例项d 是 。
2、电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB 长为12m ,试计算主持人应走到离A 点至少 m 处 3.已知a 、b 、c 是非零实数,且k cb a dd a b c d c a b d c b a =++=++=++=++,k = 。
4. 已知△ABC ∽△DEF ,S △ABC :S △DEF =1:16,△ABC 的周长为15厘米,则△DEF 的周长为 厘米。
5.如图,M 是AC 的中点,AB =9,AC =12,当AN = 时,△ABC ∽△AMN .)6、在比例尺为1∶5000的地图上,一块多边形地区的面积是320cm 2,这个地区的实际面积是___________________m 2.7.雨后初晴,一学生在运动场上玩耍,从他前面2m 远一块小积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为40m ,该生的眼部高度是,那么旗杆的高度是___________m.8、如图,AD=DF=FB ,DE ∥FG ∥BC ,则S Ⅰ∶S Ⅱ∶S Ⅲ= . 9.如图,若CD 是RtΔABC 斜边上的高,AD=3,CD=4,则BD=________ .10.已知43=y x ,则._____=-yyx11.已知点C 是线段AB 的黄金分割点,且AC>BC,则AC ∶AB= .12.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为 【13.已知两数4和8,试写出第三个数,使这三个数中,其中一个数是其余两数的比例中项,第三个数是 (只需写出一个即可).14.已知D 、E 分别是ΔABC 的边AB 、AC 上的点,请你添加一个条件,使ΔABC 与ΔAED 相似.你添加的条件是 (只需添加一个你认为适当的条件即可).15.如图,锐角三角形ABC 的边AB 、AC 上的高线CE 和BF 相交于点D ,请写出图中的两对相似三角形: (用相似符号连接).16.下列说法:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有等腰直角三角形都相似;④所有的直角三角形都相似.其中正确的是 (把你认为正确的说法的序号都填上).17.如图,已知∠1=∠2,若再增加一个条件就能使结论“AB •ED=AD •BC ”成立,则这个条件可以是 .第2题图 第5题图 A B CM N , 第8题图 (第9题图】&(第16题图) (第18题图) (第19题图) (第20题图)18.在方格纸中,每个小格的顶点叫做格点.以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A 1B 1C 1,使ΔA 1B 1C 1与格点三角形ABC 相似(相似比不为1).19.请设计三种不同的分法,将如图所示的直角三角形分割成四个小三角形,使得每个小三角形与原三角形都相似(要求画出分割线段,标出能够说明分法的必要记号,不要求写出画法,不要求说明理由).20、如图,在平行四边形ABCD 中,M 、N 为AB 的三等分点,DM 、DN 分别交AC 于P 、Q 两点,则AP :PQ :QC= .】21、如图,将①∠BAD = ∠C ;②∠ADB = ∠CAB ;二.选择题(每空3分,共 21分) 22、如果y y x + = 47,那么y x 的值是( ) A 、43 B 、32 C 、34 D 、23 23、下列说法正确的是( )A .所有的矩形都是相似形B . 有一个角等于1000的两个等腰三角形相似C .对应角相等的两个多边形相似D .对应边成比例的两个多边形相似 —24.已知:如图所示,在△ABC 中,∠ADE=∠B ,则下列等式成立的是( )A ..AD AEAE AD B AB ACBC BD == C ..DE AEDE ADD BC ABBC AC==25.点E 是平行四边形ABCD 的边BC 延长线上的一点,AE 与CD 相交于G ,则图中相似三角形共有( )A 、2对B 、3对C 、4对D 、5对26.若a 、b 、c 、d 是互不相等的正数,且dcb a = ,则下列式子错误..的是( ) A 、d d c b b a -=- B 、d c d c b a b a +-=+- C 、2222d c b a = D 、1111++=++d c b a—27.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC 相似的是 ( )?28.如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ =2,则此三角形移动的距离PP′是()A.12B.22C.1 D.21-29.在比例尺为1:5000的地图上,量得甲,乙两地的距离为25cm,则甲,乙两地的实际距离是( )已知0432≠==cba,则cba+的值为( )A.54 B.45D.2131. 一个钢筋三角架三长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( ) A.一种 B.两种 C.三种 D.四种32. 如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形()"(A)1对(B)2对(C)3对(D)4对33.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC∽⊿CAD,只要CD等于( )A.cb2B.ab2C.cab D.ca2(第32题图) (第33题图) (第34题图) (第35题图)"34.如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P做直线截ΔABC,使截得的三角形与ΔABC相似,满足这样条件的直线共有()(A)1条(B)2条(C)3条(D)4条35.如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是()(A)ACAEABAD=(B)FBEACFCE=(C)BDADBCDE=(D)CBCFABEF=36.如图,ΔABC中,P为AB上一点,在下列四个条件中:①∠APC=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足ΔAPC与ΔACB相似的条件是()(A)①②③(B)①③④(C)②③④(D)①②④37.如图,ΔADE绕正方形ABCD的顶点A顺时针旋转90°,得ΔABF,连结EF交AB于H,P P'QR R'Q'则下列结论错误的是()(A)AE⊥AF (B)EF ∶AF=2∶1 (C)AF 2=FH •FE (D)FB ∶FC=HB ∶EC。
(第36题图) (第37题图) (第38题图)38.如图,在正方形网格上有6个斜三角形:①ΔABC ,②ΔBCD ,③ΔBDE ,④ΔBFG ,⑤ΔFGH ,⑥ΔEFK.其中②~⑥中,与三角形①相似的是( ) (A)②③④ (B)③④⑤ (C)④⑤⑥ (D)②③⑥;39. 如图,在Rt ABC △内有边长分别为a ,b ,c 的三个正方形.则a ,b ,c 满足的关系式是( )A .b a c =+B .b ac =C .222b ac =+ D .22b a c ==40、如图,五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形,且PA 1=32PA ,则AB ׃A 1B 1等于( ) A.32. B. 23. C. 53. D. 35.41、下列说法“①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1∶2;④两个相似多边形的面积比为4∶9,则周长的比为16∶81.”中,正确的有( ) A 、1个 B 、2个 C 、3个 D 、4个。
三、解答下列各题42.如图已知:点D 在△ABC 的边AB 上,连结CD ,∠1=∠B ,AD=4,AC=5,求 AB 的长.(本题7分)!43.如图,四边形EFGH 是ABC 内接正方形,BC=21cm ,AD 是ABC 的高且AD=15cm ,求:内接正方形HEFG 的边长。
(本题9分)ABCD1A 第E 1D1C 1B 1A 1BDACPA B C— x·44.如图,⊿ABC 是等边三角形,点D,E 分别在BC,AC 上,且BD=CE,AD 与BE 相交于点F. (1)试说明⊿ABD ≌⊿BCE.(2)⊿AEF 与⊿ABE 相似吗说说你的理由. (3)BD 2=AD ·DF 吗请说明理由.!45.等腰△ABC ,AB=AC ,∠BAC=120°,P 为BC 上的中点,小慧拿着含 30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 旋转到图2情形时,三角板的两边分别交BA 的延长线与点E 、交边AC 于点F,连结EF ,△BPE 与△PFE 是否相似请说明理由;(本题10分)-46.某老师上完“探索三角形相似的条件”后,出了如下一道思考题:(本题9分) 如图所示,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于O ,试问:△AOB 和△DOC 是否相似某学生对上题作如下解答:答:△AOB ∽△DOC .理由如下:在△AOB 和△DOC 中,∵AD ∥BC , ∴∠OAD=∠OCB ∠ODA=∠OBC ∴△AOD ∽△COB $∴AO DOOC OB又∵∠AOB=∠DOC ∴△AOB ∽△DOC请你回答,该学生的解答是否正确如果正确,请在每一步后面写出根据;如果不正确,请简要说明理由.47、在右面的网格图中按要求画出图形. (本题9分)○1画出△ABC 关于X 轴对称的△A 1B 1C 1; ○2画出△ABC 关于Y 轴对称的△A 2B 2C 2;; ○3画出以点O 为位似中心,与△ABC 位似且 位似比为的△A 3B 3C 3;(2)A B CEF P(说明:必须用铅笔画图)!48.如图,已知矩形ABCD 的边长3cm 6cm AB BC ==,.某一时刻,动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动;同时,动点N 从D 点出发沿DA 方向以2cm /s 的速度向A 点匀速运动,问:是否存在时刻t ,使以A M N ,,为顶点的三角形与ACD △相似若存在,求t 的值;若不存在,请说明理由.(本题12分)49、(5分)阳光通过窗口照射到室内,在地面上留下宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=,窗口高AB=,求窗口底边离地面的高BC.50、(8分)如图,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=x, CE=y.(l )如果∠BAC=300,∠DAE=l050,试确定y 与x 之间的函数关系式;(2)如果∠BAC=α,∠DAE=β,当α, β满足怎样的关系时,(l )中y 与x 之间的函数关系式还成立试说明理由.《51.如图,一条河的两岸有一段是平行的.在河的南岸每相距5米栽一棵树,在河的北岸每相距50米栽一根电线杆.在南岸离开岸边25米处看北岸,看到北岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽。
