9-第九讲-有限元四边形单元
有限元入门ppt课件

有限体积法 (Finite Volume Method)
其基本思路是:将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有一个控制体积;将待解的微分方程对每一个控制体积积分,便得出一组离散方程。其中的未知数是网格点上的因变量的数值。为了求出控制体积的积分,必须假定值在网格点之间的变化规律,即假设值的分段的分布的分布剖面。
1-2 应力的概念
作用于弹性体的外力(或称荷载)可能有两种: 表面力,是分布于物体表面的力,如静水压力,一物体与另一物体之间的接触压力等。单位面积上的表面力通常分解为平行于座标轴的三个成分,用记号 来表示。 体力,是分布于物体体积内的外力,如重力、磁力、惯性力等。单位体积内的体力亦可分解为三个成分,用记号X、Y、Z表示。 弹性体受外力以后,其内部将产生应力。
边界元法 (Boundary Element Method)
边界元法是一种继有限元法之后发展起来的一种新的数值方法,与有限元法不同,边界元法仅在定义域的边界划分单元,用满足控制方程的函数去逼近边界条件。所以边界元与有限元相比具有单元和未知数少、数据准备简单等优点,但边界元法解非线性问题时,遇到同非线性项相对应的区域积分,这种积分奇异点处的强烈的奇异性,使求解遇到困难。边界元法在塑性问题中应用还比较少。
弹性力学 — 区别与联系 — 材料力学 弹性力学与材料力学既有联系又有区别。它们都同属于固体力学领域,但弹性力学研究的对象更普遍,分析的方法更严密,研究的结果更精确,因而应用的范围更广泛。 弹性力学 固有弱点: 由于研究对象的变形状态较复杂,处理的方法又较严谨,因而解算问题时,往往需要冗长的数学运算。但为了简化计算,便于数学处理,它仍然保留了材料力学中关于材料性质的假定:
塑性有限元常用软件
有限元分析中常用单元类型与单位制

SOLID453-D结构实体单元产品:MP ME ST <> <> PR <> <> <> PP EDSOLID45单元说明solid45单元用于构造三维实体结构.单元通过8个节点来定义,每个节点有3个沿着xyz方向平移的自由度.单元具有塑性,蠕变,膨胀,应力强化,大变形和大应变能力。
有用于沙漏控制的缩减积分选项。
有关该单元的细节参看ANSYS, 理论参考中的SOLID45部分。
类似的单元有适用于各向异性材料的solid64单元。
Solid45单元的更高阶单元是solid95。
图 45.1 SOLID45几何描述SOLID45输入数据该单元的几何形状、结点位置、坐标系如图45.1: "SOLID45 几何描述"所示。
该单元可定义8个结点和正交各向异性材料。
正交各向异性材料方向对应于单元坐标方向。
单元坐标系方向参见坐标系部分。
单元荷载参见结点和单元荷载部分。
压力可以作为表面荷载施加在单元各个表面上,如图45.1: "SOLID45 几何描述"所示。
正压力指向单元内部。
可以输入温度和流量作为单元节点处的体载荷。
节点 I 处的温度 T(I) 默认为 TUNIF。
如果不给出其它节点处的温度,则默认等于 T(I)。
对于任何其它的输入方式,未给定的温度默认为 TUNIF。
对于流量的输入与此类似,只是默认值用零代替了TUNIF。
KEYOPT(1)用于指定包括或不包括附加的位移形函数。
KEYOPT(5)和KEYOPT(6)提供不同的单元输出选项(参见单元输出部分)。
当KEYOPT(2)=1时,该单元也支持用于沙漏控制的均匀缩减(1点)积分。
均匀缩减积分在进行非线性分析时有如下好处:∙相对于完全积分选项而言,单元刚度集成和应力(应变)计算需要更少的CPU时间,而仍能获得足够精确的结果。
∙当单元数量相同时,单元历史存储记录(.ESAV 和 .OSAV)的长度约为完全积分(2×2×2)的1/7。
有限元分析中常用单元类型与单位制

SOLID453-D结构实体单元产品:MP ME ST <> <> PR <> <> <> PP EDSOLID45单元说明solid45单元用于构造三维实体结构.单元通过8个节点来定义,每个节点有3个沿着xyz方向平移的自由度.单元具有塑性,蠕变,膨胀,应力强化,大变形和大应变能力。
有用于沙漏控制的缩减积分选项。
有关该单元的细节参看ANSYS, 理论参考中的SOLID45部分。
类似的单元有适用于各向异性材料的solid64单元。
Solid45单元的更高阶单元是solid95。
图 45.1 SOLID45几何描述SOLID45输入数据该单元的几何形状、结点位置、坐标系如图45.1: "SOLID45 几何描述"所示。
该单元可定义8个结点和正交各向异性材料。
正交各向异性材料方向对应于单元坐标方向。
单元坐标系方向参见坐标系部分。
单元荷载参见结点和单元荷载部分。
压力可以作为表面荷载施加在单元各个表面上,如图45.1: "SOLID45 几何描述"所示。
正压力指向单元内部。
可以输入温度和流量作为单元节点处的体载荷。
节点 I 处的温度 T(I) 默认为 TUNIF。
如果不给出其它节点处的温度,则默认等于 T(I)。
对于任何其它的输入方式,未给定的温度默认为 TUNIF。
对于流量的输入与此类似,只是默认值用零代替了TUNIF。
KEYOPT(1)用于指定包括或不包括附加的位移形函数。
KEYOPT(5)和KEYOPT(6)提供不同的单元输出选项(参见单元输出部分)。
当KEYOPT(2)=1时,该单元也支持用于沙漏控制的均匀缩减(1点)积分。
均匀缩减积分在进行非线性分析时有如下好处:∙相对于完全积分选项而言,单元刚度集成和应力(应变)计算需要更少的CPU时间,而仍能获得足够精确的结果。
∙当单元数量相同时,单元历史存储记录(.ESAV 和 .OSAV)的长度约为完全积分(2×2×2)的1/7。
有限元讲义弹性力学平面问题有限单元法(四结点四边形等参元,八结点曲线四边形等参元,问题补充)分析

2.6 四结点四边形单元(The four-node quadrilateral element)前面介绍了四结点的矩形单元其位移函数:xy y x U 4321αααα+++=xy y x V8765αααα+++=为双线性函数,应力,应变在单元内呈线性变化,比常应力三角形单元精度高。
但它对边界要求严格。
本节介绍的四结点四边形等参元,它不但具有较高的精度,而且其网格划分也不受边界的影响。
对任意四边形单元(图见下面)若仍直接采用前面矩形单元的位移函数,在边界上它便不再是线性的(因边界不与x,y 轴一致),这样会使得相邻两单元在公共边界上的位移可能会出现不连续现象(非协调元),而使收敛性受到影响。
可以验证,利用坐标变换就能解决这个问题,即可以通过坐标变换将整体坐标中的四边形(图a )变换成在局部坐标系中与四边形方向无关的边长为2的正方形。
正方形四个结点i,j,m,p 按反时钟顺序对应四边形的四个结点i j m p 。
正方形的 1-=η 和 1=η 二条边界,分别对应四边形的i ,j 边界和p,m 边界;ξ=-1和ξ=+1分别对应四边形的i ,p 边界和j ,m 边界。
如果用二组直线等分四边形的四个边界线段,使四边形绘成一个非正交网格,那么该非正交网格在正方形上对应着一个等距离的规则网格(见图a, b )。
当然, 局部坐标上的A 点与整体坐标的A 点对应。
一、四结点四边形等参单元的形函数及坐标变换由于可以将整体坐标下的四边形单元变换成局部坐标下的正方形单元,对于这种正方形单元,自然仍取形函数为: ξηαηαξαα2321+++=U ξηαηαξαα8765+++=V引入边界条件,即可得位移函数:∑=ijmpi i U N Ui ijmpi V N V ∑==写成矩阵形式:{}{}[]{}ee p i p i ed N d N N N N V U f =⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=000 式中形函数: ()()()ηηξξηξi i i N ++=1141, ()p m j i ,,, 按照等参元的定义,我们将坐标变换式亦取为: p p m m j j i i i ijmpi x N x N x N x N x N x +++==∑p p m m j j i i i ijmpi y N y N y N y N y N y +++==∑ ()162-- 式中形函数N 与位移函数中的完全一致。
第九讲 有限元
x 0 y 1 2 xy 2(1 )
平面应变问题弹性矩阵D
6. 单元刚度矩阵
[ K e ] [ B]T [ D][B]d (vol)
V
a b
a b
[ B]T [ D][B]tdxdy t——厚度
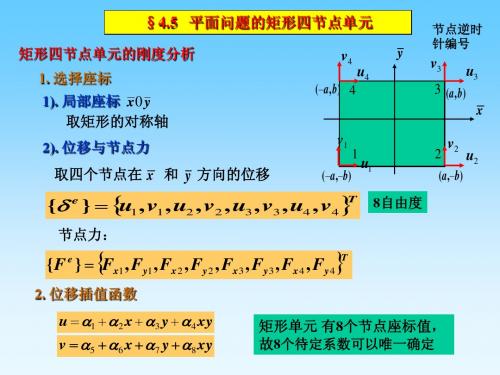
§4.5 平面问题的矩形四节点单元
矩形四节点单元的刚度分析 1. 选择座标 1). 局部座标 x0 y 取矩形的对称轴 2). 位移与节点力
v4
( a , b ) 4
y
节点逆时 针编号
u4
v3
3 (a , b)
u3
x
v1
(a,b)
1
T
取四个节点在 x 和 y 方向的位移
e
u1
8自由度
2
v2
u2
v 5 6 x 7 y 8 xy
矩形单元 有8个节点座标值, 故8个待定系数可以唯一确定
u 1 2 x 3 y 4 xy
v 5 6 x 7 y 8 xy
1 2 3 u 1 x y xy 0 0 0 0 4 0 0 0 0 1 x y xy 5 v 6 7 8
e E T T A
Fx1 N1 F 0 y1 N Fx 2 2 F t 0 y2 N3 Fx 3 0 F y3
E
0 0 N1q y N1 0 0 0 dxdy t N q dxdy N 2 q y 2 y 0 0 N 3q y N3
[B]——矩形4节点单元几何矩阵 简写成:
有限元单元介绍

第二章单元在显式动态分析中可以使用下列单元:·LINK160杆·BEAM161梁·PLANE162平面·SHELL163壳·SOLID164实体·COMBI165弹簧阻尼·MASS166质量·LINK167仅拉伸杆本章将概括介绍各种单元特性,并列出各种单元能够使用的材料类型。
除了PLANE162之外,以上讲述的显式动态单元都是三维的,缺省时为缩减积分(注意:对于质量单元或杆单元缩减积分不是缺省值)缩减积分意味着单元计算过程中积分点数比精确积分所要求的积分点数少。
因此,实体单元和壳体单元的缺省算法采用单点积分。
当然,这两种单元也可以采用全积分算法。
详细信息参见第九章沙漏,也可参见《LS-DYNA Theoretical Manual》。
这些单元采用线性位移函数;不能使用二次位移函数的高阶单元。
因此,显式动态单元中不能使用附加形状函数,中节点或P-单元。
线位移函数和单积分点的显式动态单元能很好地用于大变形和材料失效等非线性问题。
值得注意的是,显单元不直接和材料性能相联系。
例如,SOLID164单元可支持20多种材料模型,其中包括弹性,塑性,橡胶,泡沫模型等。
如果没有特别指出的话(参见第六章,接触表面),所有单元所需的最少材料参数为密度,泊松比,弹性模量。
参看第七章材料模型,可以得到显式动态分析中所用材料特性的详细资料。
也可参看《ANSYS Element Reference》,它对每种单元作了详细的描述,包括单元的输入输出特性。
2.1实体单元和壳单元2.1.1 SOLID164SOLID164单元是一种8节点实体单元。
缺省时,它应用缩减(单点)积分和粘性沙漏控制以得到较快的单元算法。
单点积分的优点是省时,并且适用于大变形的情况下。
当然,也可以用多点积分实体单元算法(KEYOPT(1)=2);关于SOLID164的详细描述,请参见《ANSYS Element Reference》和《LS-DYNA Theoretical Manual》中的§3.3节。
有限元讲稿四面体单元PPT课件
p x
解上述线性方程组,求出系数(a1,a2,a3,a4) 代入上式可得:
u Niui N ju j Nmum N pu p
同理可得v,w得位移关系为:
v Nivi N jv j Nmvm N pvp w Ni wi N j wj Nmwm N pwp
October 9, 2004
(u, v, w)
或表示为矩阵形式:
u1
1
N1 2 ,
1
N2 2
对二次单元有3个节点1= -1、2=1、3=0,形函数为:
N1
1
2
,
N2
1
2
,
N3 1 2
October 9, 2004
1=-1 =0 2=+1
1
o
2
一次单元
1=-1 1
3=0 o
3
2=+1 2
二次单元
第四章-13
第13页/共35页
(1)单元形函数
如图示,二维基本单元是平面内的正方形。局部坐标系原点位于正方形的中 心处,单元边界是4条直线。对平面线性单元有4个节点,形函数为:
u a1 a2 x a3 y a4 z v a5 a6 x a7 y a8z w a9 a10 x a11 y a12 z
October 9, 2004
第四章-1
第1页/共35页
(1)位移模式
将节点节点坐标和位移分量代入上式可得:
y j
o z
i m
ui a1 a2 xi a3 yi a4 zi u j a1 a2 x j a3 y j a4 z j um a1 a2 xm a3 ym a4 zm u p a1 a2 xp a3 y p a4 z p
有限元四边单元网格模型的参数化重建
有限元四边单元网格模型的参数化重建I. 引言- 研究背景- 研究目的- 四边单元网格模型的重要性II. 相关技术介绍- 有限元方法及其应用- 四边单元网格模型的特点与应用- 数字化建模技术及其应用- 参数化建模技术及其应用III. 四边单元网格模型的参数化重建- 模型构建流程与步骤- 空间特征的提取与处理- 模型网格化与优化- 参数化建模与自动化设计- 实现案例与分析IV. 实验结果与讨论- 模型重建的可行性与可靠性- 模型参数化建模的效率与精度- 模型自动化设计的优越性与局限性- 不同参数化方式的比较与分析V. 结论与展望- 本文研究的主要结论- 对未来相关研究的展望- 研究成果的应用前景I. 引言随着计算机技术不断发展和完善,数字化建模技术得到了广泛应用,为工程设计、制造和生产等领域提供了强有力的支持和保障。
其中,有限元方法在应用中得到了广泛的认可和应用,成为了解决工程问题的主流方法之一。
而四边单元网格模型作为有限元分析中最常用的一类模型,在各个领域也得到了广泛的应用。
本文旨在研究四边单元网格模型的参数化重建方法,探索如何通过数字化建模技术将三维空间中的物体转化为离散的网格模型,并通过参数化建模的方式实现自动化设计。
本文主要分为以下几个部分。
第二章,介绍了有限元方法及其应用,四边单元网格模型的特点与应用,数字化建模技术及其应用,参数化建模技术及其应用等相关技术。
第三章,重点介绍了四边单元网格模型的参数化重建方法。
通过模型构建流程和步骤,对空间特征的提取与处理、模型网格化与优化、参数化建模与自动化设计等方面进行了详细的介绍和分析,最终实现了参数化建模与自动化设计的目标。
第四章,介绍了实验结果和讨论。
主要关注模型重建的可行性和可靠性,模型参数化建模的效率和精度,以及不同参数化方式的比较和分析。
第五章,总结了本文的研究结论和成果,并对未来进一步研究的方向和展望进行了讨论。
同时,也探讨了本文研究成果的应用前景和展望。
9-有限元四面体及六面体单元
8 节 点 正 六 面 体
与平面4节点四边形单元类似,由单元的位移表达式(4117)可知,该单元的位移在x,y,z方向呈线性变化,所以称
为线性位移模式,正因为在单元的边界上,位移是按线性变
化的,且相邻单元公共节点上有共同的节点位移值,可保证 两个相邻单元在其公共边界上的位移是连续的,这种单元的 位移模式是完备(completeness)和协调(compatibility)的,它 的应变和应力为一次线性变化,因而比4节点四面体常应变单
基本概念 空间问题有限元分析
1. 4节点四面体单元几何和节点描述
4 节 点 四 面 体
(4-102) (4-103)
基本概念 空间问题有限元分析
2.单元位移场的表达
4 节 点 四 面 体
该单元有4个节点,单元的节点位移有12个自由度(DOF)。因此每个方向的 位移场可以设定4个待定系数,根据节点个数以及确定位移模式的基本原则 (从低阶到高阶的完备性、唯一确定性),选取该单元的位移模式为
4 节 点 四 面 体
(4-108)
基本概念 空间问题有限元分析
3.单元应变场的表达Fra bibliotek4 节 点 四 面 体
(4-109)
(4-110)
基本概念 空间问题有限元分析
4.单元应力场的表达
4 节 点 四 面 体
(4-111)
基本概念 空间问题有限元分析
5.单元的刚度矩阵及节点等效载荷矩阵
4 节 点 四 面 体
元精度高。
基本概念 空间问题有限元分析
1.空间4节点四面体单元分析的算例
空 间 问 题 分 析 的 算 例
基本概念 空间问题有限元分析
1.空间4节点四面体单元分析的算例
有限元课件ppt
将所有单元的刚度矩阵依照一定的方式组合起来,形成整体的刚度 矩阵。
载荷向量与束缚条件
载荷向量
表示作用在结构上的外力,包括集中力和散布力。
束缚条件
表示结构在某些结点上的位移受到限制,常见的束缚有固定束缚、 弹性束缚等。
载荷向量和束缚条件的引入
在建立整体刚度矩阵后,需要将载荷向量和束缚条件引入到整体刚 度矩阵中,形成完全的线性方程组。
并行计算
采取并行计算技术,提高计算效率。
算法改进
优化算法,提高计算精度和效率。
06 有限元分析软件 介绍
ANSYS
01
功能特点
ANSYS是一款功能强大的有限元分析软件,广泛应用于结构、流体、
电磁等多种工程领域。它提供了丰富的建模工具和求解器,能够处理复
杂的工程问题。
02
优点
ANSYS具有友好的用户界面和强大的前后处理功能,使得建模和网格
有限元法的应用领域
结构分析
有限元法在结构分析中应用最 为广泛,可以用于分析各种类 型的结构,如桥梁、建筑、机
械零件等。
热传导
有限元法可以用于求解温度场 的问题,如热传导、热对流和 热辐射等问题。
流体动力学
有限元法在流体动力学领域也 有广泛应用,可以用于求解流 体流动和流体传热等问题。
其他领域
除了上述领域外,有限元法还 广泛应用于电磁场、声场、化
学反应等领域。
02 有限元的数学基 础
线性代数基础
向量与矩阵
01
介绍向量的基本概念、向量的运算、矩阵的表示和运算规则等
。
线性方程组
02
论述线性方程组的解法,包括高斯消元法、LU分解等。
特征值与特征向量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面
问
题
的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
(2) 建模方案2的有限元分析列式
平 面 问 题 的
4 节 点 矩 形 单 元
(4-77)
连续体结构有基本限概念元分析
9.三角形单元与矩形单元计算精度的比较
平
面
从以上计算可以看出,用三角形单元计算时,由于形函数是
问
完全一次式,因而其应变场和应力场在单元内均为常数;而四边
元 变单元精度高。
连续体结构有基本限概念元分析
7.采用无量纲坐标 (自然坐标)
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
7.采用无量纲坐标 (自然坐标)
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
7.采用无量纲坐标 (自然坐标)
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
8.基于4节点四边形单元的矩形薄板分析
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
9.三角形单元与矩形单元计算精度的比较
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
9.三角形单元与矩形单元计算精度的比较
连续体结构有基本限概念元分析
1.单元的几何和节点描述
平 面 问 题 的
4 节 点 矩 形 单 元
(4-50) (4-51)
连续体结构有基本限概念元分析
单元的所有力学参量用节点位移列阵及相关的插值函数来表示
平 2. 单元位移场的表达
面
从图可以看出,节点条件共有8个,即x方向4个,y方向4个,因
问
此,x和y方向的位移场可以各有4个待定单
元
题
作为单元的位移场模式
的
4
(4-52)
节
点
矩
形
单
元
连续体结构有基本限概念元分析
单元的所有力学参量用节点位移列阵及相关的插值函数来表示
平 2. 单元位移场的表达 面 问 题 的
4 节 点 矩 形 单 元
(4-53) (4-54)
连续体结构有基本限概念元分析
单元的所有力学参量用节点位移列阵及相关的插值函数来表示
平 2. 单元位移场的表达 面 问 题 的
4 节 点 矩 形 单 元
(4-55)
连续体结构有基本限概念元分析
单元的所有力学参量用节点位移列阵及相关的插值函数来表示
平 2. 单元位移场的表达
面
将式(4-54)写成矩阵形式,有
问
题
的
4 节 点 矩 形 单 元
(4-57)
连续体结构有基本限概念元分析
单元的所有力学参量用节点位移列阵及相关的插值函数来表示
面
问
(4-61)
题
的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
5.单元势能的表达
平 面 问 题 的
4 节 点 矩 形 单 元
(4-62) (4-63)
连续体结构有基本限概念元分析
6. 4节点矩形单元的线性应变和应力
平 面
由单元的位移表达式可知,4节点矩形单元的位移在
问 x,y方向呈线性变化,所以称为双线性位移模式,正因
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
(1) 建模方案1的有限元分析列式
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
(1) 建模方案1的有限元分析列式
平
位移场、应变场及应力场的分布如图所示
面
问
题
的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
平 3.单元应变场的表达 面 问 题 的
4 节 点 矩 形 单 元
(4-58) (4-59)
连续体结构有基本限概念元分析
3.单元应变场的表达
平
将式(4-59)写成子矩阵形式,有
面
问
题
的
4 节 点 矩 形 单 元
(4-60) (4-61)
连续体结构有基本限概念元分析
4.单元应力场的表达
平
由弹性力学中平面问题的物理方程,可得到单元的应力表达式
题 的
为在单元的边界x=±a和y=±b上,位移是按线性变化的,
4 且相邻单元公共节点上有共同的节点位移值,可保证两
节 点
个相邻单元在其公共边界上的位移是连续的,这种单元
矩 的位移模式是完备(completeness)和协调(compatibility)
形 单
的,它的应变和应力为一次线性变化,因而比3节点常应
(1) 建模方案1的有限元分析列式
平 面 问 题 的
4 节 点 矩 形 单 元
(4-72)
连续体结构有基本限概念元分析
(2) 建模方案2的有限元分析列式
平 面 问 题 的
4 节 点 矩 形 单 元
连续体结构有基本限概念元分析
(2) 建模方案2的有限元分析列式
平
位移场、应变场及应力场的分布如图所示
题
形单元其形函数带有二次式,计算得到的应变场和应力场都是坐
的
标的一次函数,但不是完全的一次函数,对提高计算精度有一定
4
作用;根据最小势能原理,势能越小,则整体计算精度越高,从
节 点
式(4-72) 与式(4-77) 比较两种单元计算得到的系统势能,可以看
矩
出,在相同的节点自由度情况下,矩形单元的计算精度要比三角
