12-4 衍射光栅及光栅光谱解析
合集下载
光栅衍射
例7、 一平面光栅的光栅常数为d=6.0×10-3mm, 缝宽a=1.2 ×10-3mm.平行单色光垂直射到光栅 上，求单缝衍射中央明纹范围内有几条谱线？
解：由单缝衍射暗纹公式
a sinθ ′ = m′λ m′ = ±1,±2,L
m′ = 1时，得中央明纹一半宽度的条件是：
sin
θ
′
=
λ
a
由光栅方程 d sinθ = mλ
dθ dλ
=
m
d cos θ
中心角距离
dθ
=
m dλ d cos θ
δθ
半角宽
δθ
=
λ Nd cos θ
dθ
瑞利判据
λ + dλ
m
λ
dθ > δθ dθ =δθ dθ < δθ
可分辨 恰好可分辨 不可分辨
mdλ
=
λ
N
R
≡
λ dλ
=
mN
分辨 本领
恰能分辨的两条谱线的平均波长与这两条谱线的波长差之比----色分辨本领
级
2.光栅光谱的应用
(a) 测光波波长——分光计
d sin θ = ±mλ 平行光管
望远镜
(b)得光谱进行光谱分析 分析物质成分
θ d一定： λ
要求 1、谱线窄而明—读数准 2、能区分不同波长的谱线
出现哪些谱线——判定元素的存在
谱线的强度——判断含量
3、半角宽度
m, λ
d sinθm = mλ
δθ
sin θ
=
mλ
d
依题意，取 sinθ = sinθ ′
则
m
=
d a
=
6.0 ×10−3 1.2 ×10−5
大学物理：衍射光栅 光栅光谱
主要内容：
1. 线偏振光 2. 圆偏振光和椭圆偏振光 3. 自然光
15.11.1 线偏振光
振动面
y
O
z
E
x
y
15.11.2 圆偏振光和椭圆偏振光
1.圆偏振光
O
右旋圆偏振光
理学院 物理系 陈强
线偏振光的表示法
•••••
(光矢量垂直板面)
(光矢量平行板面)
(光矢量与板面斜交)
x
c
z
截面图
叠加图
左旋圆偏振光
理学院 物理系 陈强
§15.9 衍射光栅 光栅光谱
主要内容：
1.衍射光栅 2.光栅光谱
15.9.1 衍射光栅
理学院 物理系 陈强
衍射光栅: 利用多缝衍射原理使光发生色散的元件.
1. 衍射光栅参数
a
光栅常数
d ab
总缝数
b
光栅宽度为 l mm, 每毫米缝
数为 m , 总缝数 N ml
2. 光栅衍射现象 λ
偏振片是一种光学器件. 利用偏振片可以从自然光中获得线偏振光或者改变入射光 的偏振态.
2.起偏和检偏
起起偏偏器器 起偏器 检 检偏 偏器 器 检偏器
自 自••然然光光•• II00自•• •然光• I0•
偏振化方向
线线偏 偏振 振光 光线II 偏振光I α
II
11 22
II
00
I
1 2
I
0
I
I10I 2
主要内容：
1. X射线 2. 布拉格公式
1. X射线
理学院 物理系 陈强
X射线是波长很短的电磁波，波长范围在10-11m~10-8m .
2. 晶体
1. 线偏振光 2. 圆偏振光和椭圆偏振光 3. 自然光
15.11.1 线偏振光
振动面
y
O
z
E
x
y
15.11.2 圆偏振光和椭圆偏振光
1.圆偏振光
O
右旋圆偏振光
理学院 物理系 陈强
线偏振光的表示法
•••••
(光矢量垂直板面)
(光矢量平行板面)
(光矢量与板面斜交)
x
c
z
截面图
叠加图
左旋圆偏振光
理学院 物理系 陈强
§15.9 衍射光栅 光栅光谱
主要内容：
1.衍射光栅 2.光栅光谱
15.9.1 衍射光栅
理学院 物理系 陈强
衍射光栅: 利用多缝衍射原理使光发生色散的元件.
1. 衍射光栅参数
a
光栅常数
d ab
总缝数
b
光栅宽度为 l mm, 每毫米缝
数为 m , 总缝数 N ml
2. 光栅衍射现象 λ
偏振片是一种光学器件. 利用偏振片可以从自然光中获得线偏振光或者改变入射光 的偏振态.
2.起偏和检偏
起起偏偏器器 起偏器 检 检偏 偏器 器 检偏器
自 自••然然光光•• II00自•• •然光• I0•
偏振化方向
线线偏 偏振 振光 光线II 偏振光I α
II
11 22
II
00
I
1 2
I
0
I
I10I 2
主要内容：
1. X射线 2. 布拉格公式
1. X射线
理学院 物理系 陈强
X射线是波长很短的电磁波，波长范围在10-11m~10-8m .
2. 晶体
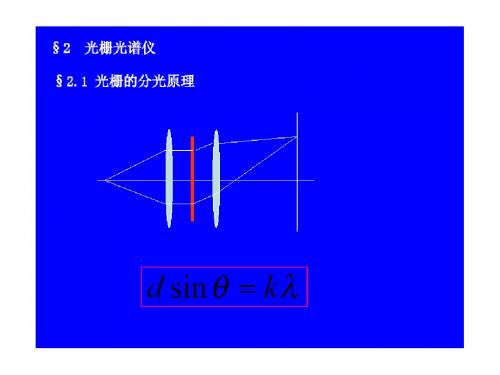
光栅光谱仪
单缝衍射中央主极大方向 光栅衍射中央主极大方向
q b -q b D
qb
d
图4.4-10 闪耀光栅的衍射（垂直槽面照射）
② 平行光垂直光栅平面入射 由于刻槽表面相对于光栅面法线方向夹角为qb，单槽衍射的0级极大值 不再沿刻槽面法线方向，而是沿与光栅面夹角 q0=2qb的反射方向。相邻刻
槽表面反射的光束间的光程差变为：D=dsin(2qb)。因此，闪耀条件变为 ， j= 1, 2, 3, · · ·
4、光栅的色分辨本领
色散本领只反映谱线（主极强）中心分离的程度，它 不能说明两条谱线是否重迭，要分辨波长很接近的谱线需
要每条谱线都很细。
λ λ+δλ 角间隔：δθ 谱线半角宽度:Δθ 无法分辨:Δθ＞δθ 刚好分辨:Δθ =δθ 较好分辨:Δθห้องสมุดไป่ตู้δθ （见图2-2）
瑞利判据： Δθ=δθ 两条谱线刚好分辨的极限 谱线的半角宽度：△θ=λ/(N d cosθk ) δλ=δθ /Dθ= △θ/Dθ = (λ/N d cosθk ) / [k /(d cosθk) ] =λ/(N k) δλ越小，色分辨本领越大。 分光仪器的色分辨本领定义为：R=λ/δλ 光栅的色分辨本领公式为：R=N k 只与k、N有关，与d无关。
( j 0,1,2,3, ) 布喇格方程
即当满足上式时，各层面上的众多粒子的无穷次波（即反射光）相干加 强，形成细锐的亮点，称为 j 级衍射主极大。
因为晶体中粒子排列的空间性，所以，劳厄斑是由空间分布的亮斑组成。
X射线衍射现象
晶体
X 射线
劳厄斑
诺贝尔奖颁奖现场
X 射线的应用不仅开创了研究晶体结构的新领域， 而且用它可以作光谱分析，在科学研究和工程技 术上有着广泛的应用。 在医学和分子生物学领域也不断有新的突破。 1953年英国的威尔金斯、沃森和克里克利用 X 射线的结构分析得到了遗传基因脱氧核糖 核酸（DNA) 的双螺旋结构，荣获了1962 年 度诺贝尔生物和医学奖。
q b -q b D
qb
d
图4.4-10 闪耀光栅的衍射（垂直槽面照射）
② 平行光垂直光栅平面入射 由于刻槽表面相对于光栅面法线方向夹角为qb，单槽衍射的0级极大值 不再沿刻槽面法线方向，而是沿与光栅面夹角 q0=2qb的反射方向。相邻刻
槽表面反射的光束间的光程差变为：D=dsin(2qb)。因此，闪耀条件变为 ， j= 1, 2, 3, · · ·
4、光栅的色分辨本领
色散本领只反映谱线（主极强）中心分离的程度，它 不能说明两条谱线是否重迭，要分辨波长很接近的谱线需
要每条谱线都很细。
λ λ+δλ 角间隔：δθ 谱线半角宽度:Δθ 无法分辨:Δθ＞δθ 刚好分辨:Δθ =δθ 较好分辨:Δθห้องสมุดไป่ตู้δθ （见图2-2）
瑞利判据： Δθ=δθ 两条谱线刚好分辨的极限 谱线的半角宽度：△θ=λ/(N d cosθk ) δλ=δθ /Dθ= △θ/Dθ = (λ/N d cosθk ) / [k /(d cosθk) ] =λ/(N k) δλ越小，色分辨本领越大。 分光仪器的色分辨本领定义为：R=λ/δλ 光栅的色分辨本领公式为：R=N k 只与k、N有关，与d无关。
( j 0,1,2,3, ) 布喇格方程
即当满足上式时，各层面上的众多粒子的无穷次波（即反射光）相干加 强，形成细锐的亮点，称为 j 级衍射主极大。
因为晶体中粒子排列的空间性，所以，劳厄斑是由空间分布的亮斑组成。
X射线衍射现象
晶体
X 射线
劳厄斑
诺贝尔奖颁奖现场
X 射线的应用不仅开创了研究晶体结构的新领域， 而且用它可以作光谱分析，在科学研究和工程技 术上有着广泛的应用。 在医学和分子生物学领域也不断有新的突破。 1953年英国的威尔金斯、沃森和克里克利用 X 射线的结构分析得到了遗传基因脱氧核糖 核酸（DNA) 的双螺旋结构，荣获了1962 年 度诺贝尔生物和医学奖。
衍射光栅及光栅光谱
k = 0, 1, 2, 3,…
例 一束波长为 480 nm 的单色平行光，照射在每毫米内有600 条刻痕的平面透射光栅上。
求 (1) 光线垂直入射时，最多能看到第几级光谱？
(2) 光线以 30°入射角入射时，最多能看到第几级光谱？
解 (1)
d
1 600 103
1 6
105
m
d sin k
k
d
则缺级 k 2, 4, 6,
则缺级 k 3, 6, 9,
P
o f
单缝衍射振幅曲线
缺级
3. 斜入射的光栅方程
相邻两束光的光程差
d (sin sin )
p
若 和 在法线的异侧
相邻两束光的光程差
d(sin sin )
主极大条件
d sin θ
d sin
k
d(sin sin ) k
例（练习册59页）波长λ= 600nm的单色光垂直入射在光栅上，
测得第二级主极大的衍射角为300，且第三级缺级。求：
（1）光栅常数 ( a b )为多少？ （2）透光缝可能的最小宽度 a
等于多少？ （3）在选定了上述 ( a b ) 和 a 之后，求在衍射
角 1 1 范围内可能观察到的全部主极大的级次。
因此 k =3，6，9，........缺级．
又因为
kmax
ab
sin90 0
4
所以实际呈现 k =0，±1，±2级明纹 (k =±4在 2
处看不到。)
例（练习册59页）一衍射光栅，每厘米200条透光缝，每条透光 缝宽为a=2×10-3cm,在光栅后放一焦距f=1m的凸透镜，现一 λ=600nm的单色平行光垂直照射光栅，求：（1）透光缝a的单缝
12-4 光栅衍射和偏振
结论： 光栅有N条狭缝 结论： 光栅有 条狭缝 相邻两主极大明纹之间有N-1条暗纹。 条暗纹。 相邻两主极大明纹之间有 条暗纹 相邻两主极大明纹之间有N-2条次级明纹 。 条次级明纹 相邻两主极大明纹之间有 由于N非常大，次级明纹很弱， 由于 非常大，次级明纹很弱， 非常大 实际上只能看到主极大明纹
作业： 作业：12-22
12§12-5 光的偏振
12-5-1 自然光与偏振光
光是一种电磁波（横波）。电矢量 E 与磁矢量 H 相 光是一种电磁波（横波）。电矢量 ）。 互垂直，它们分别又与电磁波的传播方向垂直。 互垂直，它们分别又与电磁波的传播方向垂直。 光振动： 振动。 光振动：电磁波的 E 振动。 光矢量： 矢量。 光矢量：电磁波的 E 矢量。
v
2、自然光：在垂直于光传播方向上的所有可能方 、自然光： 向上， 振动的振幅都相等。 向上， 振动的振幅都相等。
E
Ey
v
自然光是横波，但它不具有偏振性。 自然光是横波，但它不具有偏振性。
Ex
自然光可分解成任意两个振动面垂直的偏振 光，且这两个偏振光的强度相同。 且这两个偏振光的强度相同。 3、部分偏振光：各个方向都有振动，但某一方向的光振动 、部分偏振光：各个方向都有振动， 最强，与之相垂直的另一方向的光振动最弱。 最强，与之相垂直的另一方向的光振动最弱。
E
vБайду номын сангаас
一、光的偏振性：振动方向相对传播方向的不对称性。 光的偏振性：振动方向相对传播方向的不对称性。 只有横波能产生偏振，纵波不具有偏振性。） （只有横波能产生偏振，纵波不具有偏振性。）
二、三种偏振态 1、线偏振光：某一光束只含有一个方向的光振动。（平面偏振光） 。（平面偏振光 、线偏振光：某一光束只含有一个方向的光振动。（平面偏振光） 振动面：光振动方向与传播方向所确定的那平面。 振动面：光振动方向与传播方向所确定的那平面。
光学中的光栅与光谱分析
光学中的光栅与光谱分析光栅是一种常见的光学元件，广泛应用于光学测量、光谱分析、光学通信等领域。
本文将从理论原理、光栅结构、光栅的工作原理以及光谱分析等方面对光栅进行介绍和分析。
一、光栅的理论原理光栅的理论基础可以追溯到著名的杨氏实验，即杨氏双缝干涉实验。
杨氏实验中，光经过两个狭缝后形成干涉条纹，其间距与入射光的波长、狭缝间距有关。
而如果将这两个狭缝换成许多等距离的狭缝，则可以得到一个光栅。
光栅的理论原理基于光的衍射现象。
当光通过光栅时，光栅会将入射光分成多个次级光波，并在特定方向上形成明暗相间的衍射图案。
这些次级光波的干涉效应造成了光栅上出现的多重条纹，称为光栅的衍射光谱。
二、光栅的结构光栅主要由一系列平行的透明或不透明条纹组成，这些条纹可以是等宽的，也可以是非等宽的。
光栅的条纹间距是光栅常数，通常用d表示。
光栅常数决定了光栅的分辨率和光谱的光谱范围。
光栅的常见结构包括平行光栅、棱柱光栅以及体积光栅。
平行光栅是最常见的光栅类型，由等宽平行条纹组成。
棱柱光栅的条纹是由棱面组成的，可以用于更复杂的光学系统中。
体积光栅是一种将条纹刻在介质内部的光栅，具有更高的分辨率和光谱纯度。
三、光栅的工作原理光栅通过衍射现象实现光的分光，可以将入射光按照波长分解成不同的光束。
当入射光通过光栅时，每个波长的光经过衍射后会形成不同的衍射角。
这些衍射角和光的波长之间有着特定的关系，通过测量衍射角可以使用光栅来进行光谱分析。
光栅的工作原理可以用衍射公式来描述。
对于光栅上的第n级次发生衍射，光栅衍射公式为：sinθ = nλ / d其中，θ为衍射角，n为衍射级次，λ为入射光的波长，d为光栅常数。
通过测量衍射角θ，可以计算出入射光的波长，从而实现光谱分析。
四、光谱分析光谱分析是光栅应用的重要领域之一。
光栅可以用于实现高分辨率的光谱测量和光谱分析。
通过测量光栅上的衍射光谱，并分析其中的条纹或峰值，可以获取样品的成分、浓度以及其他光学性质。
6甲型光学第六章衍射光栅-2012解析
的光程差为
d
0 d sin(0 B )
d sin(0 B )
0 0 B 0
0 0 0
d[sin(0 B ) sin(0 B )] 0
衍射主极大的方向不是缝间干涉零级的方向
相邻闪耀面入射光之间的光程差
入射光与AD垂直，
A
0 法线与闪耀面垂直
d
B 0 D
BAD B 0 BD AB sin(B 0)
10
0
j0
6.1.4 双缝衍射，N=2
I
(
)
4I0
sin 2 u2
u
cos2
• 而杨氏干涉为
I
2 I 0 [1
cos( )]
2 I 0 [1
cos(2 d
sin )]
2I0 (1 cos 2 ) 4I0 cos2
当a 时，a sin 0
sin u 1 u
两者相等
杨氏干涉中，狭缝足够细，每一缝只
sin
N ( ) sin(N ) sin
N元干涉因子
光栅衍射的复振幅与强度
U~(P) U~( )N~( )
eikr0 KU (Q)
ei( N 1)
sin u
sin
N
f
u sin
I
(P)
I0
(
sin u
u
)2
(
sin N sin
)2
I0
a
KU~0 f
(Q)
2
满足近轴条件时，单个狭缝在像方焦点处的光强
• 闪耀光栅具有这种能力。
j=0 j=1 j=2
N=6,d=5a
• 光栅的衍射包括单元衍射和缝间干涉两部分。
光栅衍射和光谱
1.2 光栅衍射
• 平行单色光垂直照射在光栅G上，光栅后面的衍射光束通 过透镜L2后会聚在透镜焦平面处的屏E上，并在屏上产生 一组明暗相间的衍射条纹。
1.2 光栅衍射
一般说来，这些衍射条纹与单缝衍射条纹相比有明显的差 别，其主要特点是：明纹很亮很细，明纹之间有较暗的背 景，并且随着缝数的增加，屏上明纹越来越细，也越来越 亮，相应地，这些又细又亮的条纹之间的暗背景也越来越 暗。 如果入射光有波长不同的成分组成，则每一波长都将产生 和它对应的又细又亮的明纹，即光栅有色散分光作用。 正是由于光栅衍射条纹这一特点，促使近几十年来光栅刻 制技术飞速发展，迄今已能在1mm内刻制数千条平行狭缝。
(a b)sin k (k 0,1, 2, ...)
对应于 k=0 的条纹叫中央明纹， k=1,2,……的明纹分别叫第 一级、第二级、…明纹，亦称为各级主极大。正、负号表 示各级明纹对称分布在中央明纹两侧。
1.4 光栅光谱
• 对于一个确定的光栅，光栅常数 确定。 • 由光栅方程式知，同一级谱线的衍射角θ 的大小与入射光
大学物理
光栅衍射和光谱
• 1.1 • 1.2 • 1.3 • 1.4 • 1.5 • 1.6
光栅 光栅衍射 明纹条件 光栅方程 光栅光谱 缺级问题 光栅的衍射光强分布
1.1 光栅
在单缝衍射中，若缝较宽，明纹亮度虽较强，但相邻明条纹的 间隔很窄而不易分辨；若缝很窄，间隔虽可加宽，但明纹的亮 度却显著减小。 在这两种情况下，都很难精确地测定条纹宽度，所以用单缝衍 射并不能精确地测定光波波长。 那么，我们是否可以使获得的明纹本身既亮又窄，且相邻明纹 分得很开呢？利用光栅可以获得这样的衍射条纹。 广义地说，具有周期性空间结构或光学性能（透射率，反射率 和折射率等）的衍射屏，统称为光栅。 光栅的种类很多，有透射光栅、平面反射光栅和凹面光栅等。 构造光栅有许多方法。 光栅是光谱仪、单色仪及许多光学精密测量仪器的重要元件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
I/16I0
光栅衍射 光强曲线 单缝衍射 轮廓线
0
sin
Hale Waihona Puke 单缝衍射对缝间干涉调制的特例：缺级
若衍射角θ同时满足条件
1， 2，（缝间干涉主极大） d sin k ， k 0， 2， 3，（单缝衍射暗纹） a sin k ， k 1，
则每缝出射的光线因各缝自身的单缝衍射而相消， 因而尽管各缝间的干涉是加强，但仍为暗纹。 ——这一现象叫缺级
7
6
l
二. 光栅衍射图样的形成
光栅平面 透镜L S 观察屏 透镜L p · 0 f f
*
那么光栅的衍射条纹是不是把N个缝的衍射 条纹直接叠加就可以了呢？下面我们看一些在 实验室拍的单缝和光栅衍射的照片。
单缝和不同缝数光栅的衍射条纹
N 1
N 5
N 2
N 6
N 3
N 20
单缝衍射与光栅衍射条纹光强分布的比较
d km a
N、a、d和λ对条纹的影响 光栅方程
Flash
d sin k , (k 0,1,2,)
主极大半角宽度
半
主极大间隔
Nd
d
k 1, sin k 1 sin k
三 衍射光谱
入射光为白光时， k不同，按波长分开形成光谱. 不同，
缺级满足的关系 从
d sin k 和 a sin k
得
d k a k
d k k (k 1,2,3) a
则 2,4,6 缺级
缺级满足关系
如果
d 2 a
问：缺级是否一定从存在？ 光栅条纹的特点四：可能缺级
例：双缝衍射的结果讨论
讨 论 观察屏上条纹最高级次
返回
1. 缝间干涉
明纹（主极大）条件
衍射角
a
d sin k (k 0,1, 2, )
b
d
d sin
2
设每个缝自身衍射后的光线 的光矢量振幅为A1(θ)，则明纹主 极大处总振幅
A( ) NA 1 ( )
I ( ) N I1 ( )
光栅条纹的特点一：明亮
暗纹条件 以与0级主极大相邻的暗纹为例 当 Nd sin 时， 可以把整个光栅分为两 个光线不连续的“半波 带”，对应的缝间的光 线干涉相消，P处形成 暗纹。 可得0级主极大的半角宽度
解
例：用波长λ=600nm的单色光垂直入射到一衍射光栅上，
测得第二级主极大的衍射角为30°，且第三级是缺级，求 （1）光栅常数（a+b）等于多少； （2）透光缝可能的最小宽度a等于多少； （3）在确定了的上述（a+b）和a之后，在屏上呈现出的全 部主极大的级次。
解
单缝位置对衍射图的影响
返回
N、a、d的变化对条纹的影响
有600条刻痕的平面透射光栅上。 求 (1) 光线垂直入射时，最多能看到第几级光谱？ (2) 光线以 30o入射角入射时，最多能看到第几级光谱？
1 1 5 解 (1) d sin k d 10 m 3 600 10 6 105 kmax d 3 7 6 4.8 10
例如，当N=5时（暂没有考虑各缝自身衍射的影响）
I I0
2 d
d
0
d
2 d
sin
由于次极大的光强太小了以至于人眼看不 到，所以在相邻的两个主极大之间是一片暗区 光栅条纹的特点三：分散
2.单缝衍射对光栅多光束干涉结果的调制
I / I0
sin
单缝衍射 光强曲线
I/I0
sin
d sin k
k sin k d
(k 0,1,2,)
π , 2 d k k max
单缝衍射中央明纹区条纹最高级次
1， 2， （干涉主极大） 由 d sin k， k 0， a sin 1 ，（单缝衍射一级暗纹）
k sin sin 1 d a
P
Nd
0半 sin
Nd
0
光栅条纹的特 点二：细窄
同理，可得其它级次的暗纹条件
Nd sin k ， k 1 ， 2， 3， 且k kN
由以上分析可得，相邻的两个主极大之间有 N-1条暗纹，相邻暗纹之间的光强也不为0，但是 要远小于又光栅方程决定的明纹主极大的强度， 称之为次极大，故相邻的两个明纹主极大之间还 有N-2条次极大。
(2) d (sin sin30o ) k 由θ < 90o 得 k max 5
30
由θ > -90o 得 k max 1
例：一块每毫米刻痕为500条的光栅，用钠黄光正入射，
钠黄光中含有两条谱线，其波长分别为589.6nm和589.0nm。 求分别在第2级和第3级光谱中这两条谱线分开的角度。
d sin k
(k 0,1,2,)
I
sin
d
0
一级光谱
三级光谱 二级光谱
光谱分析
由于不同元素（或化合物）各有自己特定的光谱， 所以由谱线的成分，可分析出发光物质所含的元素或 化合物；还可从谱线的强度定量分析出元素的含量．
例 题 一束波长为 480 nm 的单色平行光，照射在每毫米内
透射光栅
反射光栅
2 . 光栅常数d
d ab
光栅常数d是描述光栅性质的最 重要的物理量之一，它反映了光 栅的空间周期性。
b 不透光宽度
a 透光宽度
设光栅宽度为 l ，每毫米缝数为 m ，则总缝数
且光栅宽度 l 与总缝数N和光栅常数d存在如下关系
l Nd
在实验室中用的光栅，一般有
a(或d )： 10 ~ 10 m
单缝衍射 光强曲线
o
I
sin
I
0
光栅衍射 光强曲线
sin
由照片和光强分布曲线的对比可以看出： 光栅衍射条纹并不是N个单缝的衍射条纹 的直接叠加，为什么呢？
原因在于光栅衍射中不同缝发出的 光线之间也会发生相干叠加。
光栅衍射条纹的分析
光栅
透镜L
光栅衍
射条纹是每
P
个缝自身的
衍射和缝之
间的干涉的
综合效果。
单缝的夫郎和费衍射
缝宽a减小 缝宽a增大 衍射效果明显 （要求a～λ）； 条纹亮度大 （一般a～10-3m）；
如何解决矛盾？
单缝沿垂直透镜主光轴方向的微小移动不会影响衍 射图样。
Flash
单缝衍射的上述特点对我们解决这个矛盾又能给我 们什么启发呢？
Ch12-4 衍射光栅及光栅光谱
一. 衍射光栅
1. 光栅 — 大量等宽等间距的平行狭缝(或反射面)构成的光学元件
光栅衍射 光强曲线 单缝衍射 轮廓线
0
sin
Hale Waihona Puke 单缝衍射对缝间干涉调制的特例：缺级
若衍射角θ同时满足条件
1， 2，（缝间干涉主极大） d sin k ， k 0， 2， 3，（单缝衍射暗纹） a sin k ， k 1，
则每缝出射的光线因各缝自身的单缝衍射而相消， 因而尽管各缝间的干涉是加强，但仍为暗纹。 ——这一现象叫缺级
7
6
l
二. 光栅衍射图样的形成
光栅平面 透镜L S 观察屏 透镜L p · 0 f f
*
那么光栅的衍射条纹是不是把N个缝的衍射 条纹直接叠加就可以了呢？下面我们看一些在 实验室拍的单缝和光栅衍射的照片。
单缝和不同缝数光栅的衍射条纹
N 1
N 5
N 2
N 6
N 3
N 20
单缝衍射与光栅衍射条纹光强分布的比较
d km a
N、a、d和λ对条纹的影响 光栅方程
Flash
d sin k , (k 0,1,2,)
主极大半角宽度
半
主极大间隔
Nd
d
k 1, sin k 1 sin k
三 衍射光谱
入射光为白光时， k不同，按波长分开形成光谱. 不同，
缺级满足的关系 从
d sin k 和 a sin k
得
d k a k
d k k (k 1,2,3) a
则 2,4,6 缺级
缺级满足关系
如果
d 2 a
问：缺级是否一定从存在？ 光栅条纹的特点四：可能缺级
例：双缝衍射的结果讨论
讨 论 观察屏上条纹最高级次
返回
1. 缝间干涉
明纹（主极大）条件
衍射角
a
d sin k (k 0,1, 2, )
b
d
d sin
2
设每个缝自身衍射后的光线 的光矢量振幅为A1(θ)，则明纹主 极大处总振幅
A( ) NA 1 ( )
I ( ) N I1 ( )
光栅条纹的特点一：明亮
暗纹条件 以与0级主极大相邻的暗纹为例 当 Nd sin 时， 可以把整个光栅分为两 个光线不连续的“半波 带”，对应的缝间的光 线干涉相消，P处形成 暗纹。 可得0级主极大的半角宽度
解
例：用波长λ=600nm的单色光垂直入射到一衍射光栅上，
测得第二级主极大的衍射角为30°，且第三级是缺级，求 （1）光栅常数（a+b）等于多少； （2）透光缝可能的最小宽度a等于多少； （3）在确定了的上述（a+b）和a之后，在屏上呈现出的全 部主极大的级次。
解
单缝位置对衍射图的影响
返回
N、a、d的变化对条纹的影响
有600条刻痕的平面透射光栅上。 求 (1) 光线垂直入射时，最多能看到第几级光谱？ (2) 光线以 30o入射角入射时，最多能看到第几级光谱？
1 1 5 解 (1) d sin k d 10 m 3 600 10 6 105 kmax d 3 7 6 4.8 10
例如，当N=5时（暂没有考虑各缝自身衍射的影响）
I I0
2 d
d
0
d
2 d
sin
由于次极大的光强太小了以至于人眼看不 到，所以在相邻的两个主极大之间是一片暗区 光栅条纹的特点三：分散
2.单缝衍射对光栅多光束干涉结果的调制
I / I0
sin
单缝衍射 光强曲线
I/I0
sin
d sin k
k sin k d
(k 0,1,2,)
π , 2 d k k max
单缝衍射中央明纹区条纹最高级次
1， 2， （干涉主极大） 由 d sin k， k 0， a sin 1 ，（单缝衍射一级暗纹）
k sin sin 1 d a
P
Nd
0半 sin
Nd
0
光栅条纹的特 点二：细窄
同理，可得其它级次的暗纹条件
Nd sin k ， k 1 ， 2， 3， 且k kN
由以上分析可得，相邻的两个主极大之间有 N-1条暗纹，相邻暗纹之间的光强也不为0，但是 要远小于又光栅方程决定的明纹主极大的强度， 称之为次极大，故相邻的两个明纹主极大之间还 有N-2条次极大。
(2) d (sin sin30o ) k 由θ < 90o 得 k max 5
30
由θ > -90o 得 k max 1
例：一块每毫米刻痕为500条的光栅，用钠黄光正入射，
钠黄光中含有两条谱线，其波长分别为589.6nm和589.0nm。 求分别在第2级和第3级光谱中这两条谱线分开的角度。
d sin k
(k 0,1,2,)
I
sin
d
0
一级光谱
三级光谱 二级光谱
光谱分析
由于不同元素（或化合物）各有自己特定的光谱， 所以由谱线的成分，可分析出发光物质所含的元素或 化合物；还可从谱线的强度定量分析出元素的含量．
例 题 一束波长为 480 nm 的单色平行光，照射在每毫米内
透射光栅
反射光栅
2 . 光栅常数d
d ab
光栅常数d是描述光栅性质的最 重要的物理量之一，它反映了光 栅的空间周期性。
b 不透光宽度
a 透光宽度
设光栅宽度为 l ，每毫米缝数为 m ，则总缝数
且光栅宽度 l 与总缝数N和光栅常数d存在如下关系
l Nd
在实验室中用的光栅，一般有
a(或d )： 10 ~ 10 m
单缝衍射 光强曲线
o
I
sin
I
0
光栅衍射 光强曲线
sin
由照片和光强分布曲线的对比可以看出： 光栅衍射条纹并不是N个单缝的衍射条纹 的直接叠加，为什么呢？
原因在于光栅衍射中不同缝发出的 光线之间也会发生相干叠加。
光栅衍射条纹的分析
光栅
透镜L
光栅衍
射条纹是每
P
个缝自身的
衍射和缝之
间的干涉的
综合效果。
单缝的夫郎和费衍射
缝宽a减小 缝宽a增大 衍射效果明显 （要求a～λ）； 条纹亮度大 （一般a～10-3m）；
如何解决矛盾？
单缝沿垂直透镜主光轴方向的微小移动不会影响衍 射图样。
Flash
单缝衍射的上述特点对我们解决这个矛盾又能给我 们什么启发呢？
Ch12-4 衍射光栅及光栅光谱
一. 衍射光栅
1. 光栅 — 大量等宽等间距的平行狭缝(或反射面)构成的光学元件