二次函数的图像专项练习题集
二次函数的图像与性质经典练习题(11套)附带详细答案

练习一21.二次函数的图像开口向____,对称轴是____,顶点坐标是___yax_,图像有最___点,x___时,y随x的增大而增大,x___时,y随x的增大而减小。
12222.关于,yx,y3x的图像,下列说法中不正确的是()yx3A.顶点相同B.对称轴相同C.图像形状相同D.最低点相同223.两条抛物线yx与在同一坐标系内,下列说法中不正确的是()yxA.顶点相同B.对称轴相同C.开口方向相反D.都有最小值24.在抛物线上,当y<0时,x的取值范围应为()yxA.x>0B.x<0C.x≠0D.x≥0225.对于抛物线yx与yx下列命题中错误的是()xA.两条抛物线关于轴对称B.两条抛物线关于原点对称C.两条抛物线各自关于y轴对称D.两条抛物线没有公共点26.抛物线y=-bx+3的对称轴是___,顶点是___。
127.抛物线y=-(x2)-4的开口向___,顶点坐标___,对称轴___,x_2__时,y随x的增大而增大,x___时,y随x的增大而减小。
28.抛物线y2(x1)3的顶点坐标是()A.(1,3)B.(1,3)C.(1,3)D.(1,3)为()9.已知抛物线的顶点为(1,2),且通过达式(1,10),则这条抛物线的表22A.y=3(x1)-2B.y=3(x1)+222C.y=3-2D.y=-3-2(x1)(x1)210.二次函数的图像向左平移2个单位,向下平移3个单位,所得新函数表达yax式为()22A.y=a+3B.y=a-3(x2)(x2)22C.y=a(x2)+3D.y=a(x2)-324411.抛物线的顶点坐标是()yxxA.(2,0)B.(2,-2)C.(2,-8)D.(-2,-8)2212.对抛物线y=2(x2)-3与y=-2(x2)+4的说法不正确的是()A.抛物线的形状相同B.抛物线的顶点相同C.抛物线对称轴相同D.抛物线的开口方向相反213.函数y=a+c与y=ax+c(a≠0)在同一坐标系内的图像是图中的()x243243214.化yxx为y=xx为ya(x h)k的形式是____,图像的开口向____,顶点是____,对称轴是____。
二次函数的图像专项练习题

九年级第十三周材料二次函数基础定义知识点一:二次函数的定义形如yax2bxc(a0)【注意:二次项的系数a0;x的最高次幂为2】a1x例题:若ya1x3二次函数,则a的值为.2m1【变式训练】若ym1x2x1二次函数,则m的值为.知识点二:“一般式”化“顶点式”例题:yx24x52xx2x22x2x22x2 方法一:4522225(222)25(2)1yx22b4acbb4acb2x22方法二:1,(2)12,yx4x5(x)2a4a2a4a【变式训练】把下列二次函数化成顶点式2x2x2x①23yx;②yx121;③y2x47知识点三:开口方向,对称轴,顶点坐标,最大(小)值,增减性【温馨提示】形状相同,则二次项的系数a相等yax 2开口bxc方向对称轴顶点坐标最大(小)值y随x增大y随x增大而增大而减小a>0 a<0 向上最小值b2b4acbx24)a(,2aa向下最大值4ac4a4ac4a2b2bxxbbx2a2abbx2a2a【变式训练】完成下列表格函数开口方向对称轴顶点坐标y随x增大而增大时,x的取值范围最大(小)值y 2xx642y5(x1)1知识点四:二次函数与x轴交点的个数及交点的坐标,与y轴的交点坐标2,当△=b24ac>0,图像与x轴有两个交点;当△【温馨提示】1.对于二次函数yaxbxc2 =b4ac2=0,图像与x轴有一个交点;当△=b4ac <0,图像与x轴没有交点。
2.求二次函数y2ax bx c 与x轴的交点坐标就是令y=0,求出x1,x2,则交点坐标为(x1,0),2(x2,0);二次函数yaxbxc与y轴的交点坐标就是令x=0,求出y,则交点坐标为(0,y);【变式训练】完成下列表格1九年级第十三周材料函数与x轴交点个数与x轴交点坐标与y轴交点坐标5y 2xx61y 2xx2知识点五:二次函数图像的平移【温馨提示】二次函数图像的平移其实就是顶点的平移2x2x例题:二次函数yx61的图像经过怎样平移能够变成yx452x2x【分析】yx61的顶点坐标为(-3,-8),yx45的顶点坐标为(2,1).点(-3,2x-8)向右平移5个单位,再向上平移9个单位变成(2,1),所以yx61向右平移5个单位,再2x向上平移9个单位变成yx45【变式训练】完成下列表格平移前函数平移方式平移后函数22y(x3)4先向平移个单位,再向平移单位y(x2)32x2xyx21先向平移个单位,再向平移单位yx45知识点六:待定系数法求二次函数的解析式【温馨提示】一般知道三个点的坐标,设二次函数的解析式为yax2bxc,然后将三个点的坐标代2,得到一个三元一次方程组;如果知道两个点的坐标,其中一个点为顶点(m,n),则入yaxbxc22设二次函数的解析式为ya(xm)n,再把另一个点的坐标代入ya(xm)n 求出a的值;若知道三个点的坐标,其中有两个点(x1,0),(x2,0)在x轴上,则可设()()yaxx1xx,再把另2一个点的坐标代入()()yaxx1xx,求出a的值。
二次函数图像与性质运用练习题

二次函数图像与性质运用练习题1、二次函数y =ax 2+bx +c (a ≠0)的图象如图,给出下列四个结论:①4ac ﹣b 2<0;②4a +c <2b ;③3b +2c <0;④m (am +b )+b <a (m ≠﹣1),其中正确结论的是 。
2、已知一元二次方程230x bx +-=的一根为3-,在二次函数23y x bx =+-的图象上有三点14 5,y ⎛⎫- ⎪⎝⎭、25 4,y ⎛⎫- ⎪⎝⎭、31 6,y ⎛⎫⎪⎝⎭,1y 、2y 、3y 的大小关系是 。
3、若是方程(x -a )(x -b )= 1(a <b )的两个根,则实数x 1,x 2,a ,b 的大小关系为( ) A .x 1<x 2<a <b B .x 1<a <x 2<b C .x 1<a <b <x 2 D .a <x 1<b <x 2 4、若二次函数c x x y +-=62的图象经过A (-1,y 1)、B (2,y 2)、C (23+,y 3)三点,则关于y 1、y 2、y 3大小关系是 。
4、已知二次函数y =ax 2+bx +c (a ≠0)的图象如图,且关于x 的一元二次方程ax 2+bx +c ﹣m =0没有实数根,有下列结论:①b 2﹣4ac >0;②abc <0;③m >2.其中,正确结论的是 。
5、抛物线y =ax 2+bx +c 的顶点为D (﹣1,2),与x 轴的一个交点A 在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b 2﹣4ac <0;②a +b +c <0;③c ﹣a =2;④方程ax 2+bx +c ﹣2=0有两个相等的实数根.其中正确结论的个数为 。
6、“如果二次函数y =ax 2+bx +c 的图象与x 轴有两个公共点,那么一元二次方程ax 2+bx +c =0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m 、n (m <n )是关于x 的方程1﹣(x ﹣a )(x ﹣b )=0的两根,且a <b ,则a 、b 、m 、n 的大小关系是( ) A . m <a <b <nB . a <m <n <bC . a <m <b <nD . m <a <n <b7、二次函数的图象如图,对称轴为1=x .若关于x 的一元二次方程02=-+t bx x (为实数)在41<<-x 的范围内有解,则t 的取值范围是 。
二次函数图像性质练习题(附答案)

二次函数图像性质练习题1、函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,y 随x 的增大而减小, 函数有最 值 。
2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标。
(1)右移2个单位;(2)左移32个单位;(3)先左移1个单位,再右移4个单位。
3、请你写出函数()21+=x y 和12+=x y 具有的共同性质(至少2个)。
4、二次函数()2h x a y -=的图象如图:已知21=a ,OA=OC ,试求该抛物线的解析式。
5、抛物线2)3(3-=x y 与x 轴交点为A ,与y 轴交点为B ,求A 、B 两点坐标及⊿AOB 的面积。
6、二次函数2)4(-=x a y ,当自变量x 由0增加到2时,函数值增加6。
求:(1)求出此函数关系式。
(2)说明函数值y 随x 值的变化情况。
7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值。
1、请写出一个以(2, 3)为顶点,且开口向上的二次函数: 。
2、二次函数 y =(x -1)2+2,当 x = 时,y 有最小值。
3、函数 y =12 (x -1)2+3,当 x 时,函数值 y 随 x 的增大而增大。
4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向 平移3个单位,再向 平移2个单位得到。
5、已知抛物线的顶点坐标为()2,1,且抛物线过点()3,0,则抛物线的关系式是6、如图所示,抛物线顶点坐标是P (1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( )A 、x>3B 、x<3C 、x>1D 、x<17、已知函数()9232+--=x y 。
(1)确定下列抛物线的开口方向、对称轴和顶点坐标;(2)当x= 时,抛物线有最 值,是 。
(3)当x 时,y 随x 的增大而增大;当x 时,y 随x 的增大而减小。
二次函数的图像和性质练习题

二次函数的图像和性质练习题1. 画出二次函数 \(y = 2x^2 - 4x + 3\) 的图像,并标出顶点坐标。
2. 给定二次函数 \(y = -3x^2 + 6x - 2\),求出它的顶点坐标和对称轴。
3. 判断下列函数是否为二次函数,并说明理由:- \(y = x^2 + 2x + 1\)- \(y = x^3 - 4x\)- \(y = 5\)4. 已知二次函数 \(y = ax^2 + bx + c\) 的图像经过点 (1, 2) 和(2, 5),求 a、b、c 的值。
5. 给定二次函数 \(y = 4x^2 - 12x + 9\),求出它的开口方向、顶点坐标、对称轴以及与x轴的交点坐标。
6. 已知二次函数 \(y = 2x^2 - 4x + 1\) 的图像与x轴相交于点 A和 B,求 A 和 B 的坐标。
7. 判断二次函数 \(y = -x^2 + 4x - 3\) 的图像是否在x轴上方,解释原因。
8. 给定二次函数 \(y = 3x^2 - 6x + 2\),求出它在x轴下方的区间。
9. 已知二次函数 \(y = x^2 - 6x + 8\) 的图像与y轴相交于点 C,求 C 的坐标。
10. 给定二次函数 \(y = -2x^2 + 4x + 1\),求出它的顶点坐标和对称轴,并判断其开口方向。
11. 判断二次函数 \(y = x^2 - 2x - 3\) 的图像是否经过原点,说明理由。
12. 给定二次函数 \(y = 5x^2 - 10x + 1\),求出它的图像与x轴的交点坐标。
13. 已知二次函数 \(y = -3x^2 + 12x - 8\) 的图像与x轴相交于点D 和 E,求 D 和E 的坐标。
14. 给定二次函数 \(y = 2x^2 + 4x + 1\),求出它的图像与y轴的交点坐标。
15. 判断二次函数 \(y = -x^2 + 6x - 8\) 的图像是否经过第一象限,解释原因。
二次函数--图像专题及答案解析

二次函数经典题一、选择题61.二次函数y=ax 2+bx+c (a≠0)的图象如图所示,其对称轴为x=1,则正确的结论是( )A .abc>0B .3a +c <0C .4a+2b+c <0D .b 2 -4ac <062.如图是二次函数y=ax 2+bx+c 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc <0;②2a ﹣b=0;③4a+2b+c <0;④若(﹣5,y 1),(,y 2)是抛物线上两点,则y 1>y 2.其中说法正确的是( )~A .①②B .②③C .①②④D .②③④63.如图,半圆D 的直径AB=4,与半圆O 内切的动圆O 1与AB 切于点M ,设⊙O 1的半径为y ,AM=x ,则y 关于x 的函数关系式是 ( )A .21y x x 4B .2y x xC .21y x x 4D .21y x x 4 64.如右图,已知二次函数y=ax 2+bx +c 的图象过A (-3,0),对称轴为直线x=-1,下列结论:①b 2>4ac ;②2a +b=0;③a -b +c=0;④5a<b ;⑤a -b>m(am +b)(m ≠-1)其中正确的结论有( )A .1个B .2个C .3个D .4个?65.如图,二次函数y=ax 2+bx+c 的图象经过点(0,﹣2),与x 轴交点的横坐标分别为x 1,x 2,且﹣1<x 1<0,1<x 2<2,下列结论正确的是( )A .a <0B .a ﹣b+c <0C .2b a>1 D .4ac ﹣b 2<﹣8a 66.如图,已知二次函数y=ax 2+bx+c 的图象与y 轴正半轴的交点在(0,2)的下方,与x 轴的交点为(x 1,0)和(2,0),且-2<x 1<-1,则下列结论正确的是( )A 、0abc >B 、0a b c -+<C 、210a b ++>D 、0a b +>67.给出下列命题及函数y x =,2y x =和1y x =的图象 :①如果21a a a>>,那么0a 1<<; ②如果21a a a>>,那么a 1>; ③如果21a a a>>,那么1a 0-<<; ④如果21a a a>>时,那么a 1<-. 则( )A. 正确的命题是①④B. 错误..的命题是②③④ C. 正确的命题是①② D. 错误..的命题只有③ -68.二次函数y=ax 2+bx+c 的图象如图所示,有下列结论:①a<0,②b<0,③c<0,④4a-2b+c<0,⑤b+2a=0其中正确的个数有( )A .1个B .2个C .3个D .4个69.二次函数)0(2≠++=a c bx x a y 图像如图所示,下列结论:①0abc >,②20a b +=,③930a b c ++>,④方程20ax bx c ++=的解是-2和4,⑤不等式20ax bx c ++>的解集是24x -<<,其中正确的结论有( )A .2个B .3个C .4个D .5个<70.小明从如图所示的二次函数y=ax 2+bx+c (a≠0)的图象中,观察得出了下面五条信息:①ab >0;②a+b+c <0;③b+2c >0;④a ﹣2b+4c >0;⑤32ab . 你认为其中正确信息的个数有( )A. 2个B. 3个C. 4个D. 5个71.已知二次函数2y ax bx c =++(0)a ≠的图象如图所示,下列说法错误的是( )A .图象关于直线1x =对称B .函数2y ax bx c =++(0)a ≠的最小值是-4C .当1x <时,y 随x 的增大而增大…D .-1和3是方程20ax bx c ++=(0)a ≠的两个根72.给出下列四个命题:(1)将一个n (n≥4)边形的纸片剪去一个角,则剩下的纸片是n+1或n-1边形;(2)若31x x --=,则x=1或x=3;(3)若函数32(23)k y k x x-=-+是关于x 的反比例函数,则32k =;(4)已知二次函数2y ax bx c =++,且a >0,a-b+c <0,则240b ac -≤。
二次函数图像题-专题练习

类型一二次函数系数与图像的关系1、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a >0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的序号数是()2、如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(),下列2A.1B.2C.3D.4(1题图)(2题图)(3题图)(4题图)3.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是()4已知二次函数y=ax2+bx+c的图象如图所示,给出以下结论:①a+b+c<0;②b2﹣4ac>0;③b>0;④4a﹣2b+c<0;⑤c﹣a>1,其中正确的结论有_________.类型二:二次函数与一次函数、反比例函数在同一图像问题1、在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为()2 二次函数y=ax2+bx+c的图像如图所示,反比列函数与正比列函数在同一坐标系内的大致图像是()3.已知二次函数y=(x-a)(x-b)(其中a>b)的图象如下面右图所示,则函数y=ax+b的图象可能正确的是ayx=y bx=xA B第3题图类型三:用图像解决二次函数与一元二次方程关系的有关问题二次函数y=ax 2+bx+c 的图像如图 根据图像解答下列问题:(1) 写出方程02=++c bx ax 的两根 (2)写出不等式02>++c bx ax 的解集 (2) 写出y 随x 的增大而增大的自变量x 的取值范围(3) 如方程k c bx ax =++2有两个不相等的实数根,求k 的取值范围(5)如方程无实数根,求k 的取值范围自我检测:1.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,下列结论:①b <0;②4a+2b+c <0;③a ﹣b+c >0;④(a+c )2<b 2.其中正确的结论是( )2.如图,二次函数y=ax 2+bx+c (a≠0)的图象的顶点在第一象限且过点(0,1) 和(﹣1,0)下列结论:①ab <0,②b 2>4a ,③0<a+b+c <2,④0<b <1,⑤当x >﹣1时,y >0,其中正确结论是( )(1题图) (2题图) (4题图)4.如图是二次函数y=ax 2+bx+c (a ≠0)的图象的一部分,给出下列命题:①abc <0②b >2a ;③a+b+c=0④ax 2+bx+c=0的两根分别为﹣3和1;⑤8a+c >0.其中正确的命题是 _______________5.二次函数y=ax 2+bx+c 的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;③abc <0;④4ac ﹣b 2<0;⑤当x ≠2时,总有4a+2b >ax 2+bx 其中正确的有 _________ (填写正确结论的序号).(5题图) (6题图) (7题图)6 如图所示,二次函数y=ax 2+bx+c (a ≠0)的图象经过点(﹣1,2),且与x 轴交点的横坐标为x 1、x 2,其中﹣2<x 1<﹣1,0<x 2<1,下列结论:①abc >0;②4a ﹣2b+c <0;③2a ﹣b >0;④b 2+8a >4ac ,正确的结论是 _________ .7.如图是二次函数y=ax 2+bx+c 图象的一部分,图象过点A (x 1,0),﹣3<x 1<﹣2,对称轴为x=﹣1.给出四个结论:①abc >0;②2a+b=0;③b 2>4ac ;④a ﹣b >m (ma+b )(m ≠﹣1的实数);⑤3b+2c >0.其中正确的结论有( )8设a、b为常数,并且b<0,抛物线的图象为图中的四个图象之一.则a=_________.课后延伸:1.(2013•鄂州)小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤.你认为其中正确信息有()2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a>0,b>0;②c <0,△<0;③c﹣4b>0;④4a﹣2b+c=16a+4b+c.其中正确结论的是()3已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列四个结论:①abc>0;②3a+b>0;③>﹣3;④2c>3b,其中结论正确的为()4.(2013•德州)函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为()(4题图)(5题图)(6题图)5.如图,开口向下的抛物线y=ax2+hx+c交y轴的正半轴于点A,对称轴是直线x=1,则abc>0;(3)8a+c>0;(4)6a+3b+c>0,其中正确的结论的个数是()7.已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①4a﹣2b+c=0;②a﹣b+c<0;③2a+c >0;④2a﹣b+1>0.其中正确结论的是().。
九年级数学二次函数的图像解答题10道题专题训练.docx
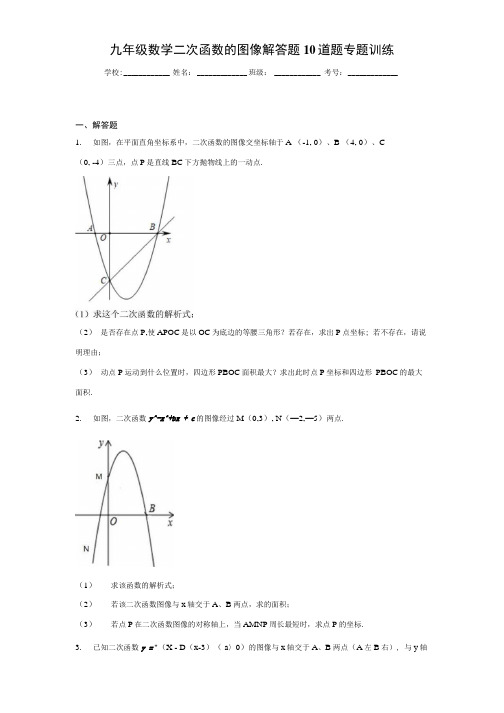
九年级数学二次函数的图像解答题10道题专题训练学校: ____________ 姓名:_____________ 班级: ____________ 考号:_____________一、解答题1.如图,在平面直角坐标系中,二次函数的图像交坐标轴于A (-1, 0)、B (4, 0)、C(0, -4)三点,点P是直线BC下方抛物线上的一动点.(2)是否存在点P,使APOC是以OC为底边的等腰三角形?若存在,求出P点坐标; 若不存在,请说明理由;(3)动点P运动到什么位置时,四边形PBOC面积最大?求出此时点P坐标和四边形PBOC的最大面积.2.如图,二次函数y^-x^+bx + c的图像经过M(0,3), N(—2,—5)两点.(1)求该函数的解析式;(2)若该二次函数图像与x轴交于A、B两点,求的面积;(3)若点P在二次函数图像的对称轴上,当AMNP周长最短时,求点P的坐标.3.已知二次函数y = "(X - D(x-3)( a〉0)的图像与x轴交于A、B两点(A左B右), 与y轴交于C点(0, 3) .P为x轴下方二次函数y = a(x - 1)(尢-3) (a > 0)图像上一点,P点横坐标为加.(1)求a的值;(2)若P为二次函数y = a(x —l)(x —3) (a > 0)图像的顶点,求证:ZAC0=ZPCB;(3)Q ("7 + ",)'o)为二次函数歹=a(x - 1)0-3) (a > 0)图像上一点,且ZAC0 = ZQCB,求n的取值范围.4.如图,已知二次函数yi=ax2+bx + c的图像经过点4(—1,0), C(0,3),且对称轴为直线x = -2, 一次函数y2 =mx + n的图像经过4』两点.(2)若点5C关于抛物线的对称轴对称,根据图像直接写出满足^>y2时x的取值范围.5.已知如图,二次函数y="ax2"+bx+c的图像过A、B、C三点观察图像写出A、B、C三点的坐标求出二次函数的解析式6.已知二次函数y = -x2 +(m-2)x + 3(m + l)的图像如图所示.(1)当mM -4时,说明这个二次函数的图像与x轴必有两个交点;(2)如图情况下,若OAOB = 6,求点C的坐标.(1)求这个二次函数的解析式;(2)观察图像,直接写出:何时y随x的增大而增大?何时y<0?&已知二次函数的图像如图所示.(1)求这个二次函数的表达式;(2)观察图像,当-2<x< 1时,写出y的取值范围.9.如图,已知二次函数y=ax2+bx+3的图像经过点A (1, 0) , B (—2, 3).(1)求该二次函数的表达式;(2)求该二次函数的最大值;(3)结合图像,解答问题:当y>3时,x的取值范围是___________ .与y轴交于C点.(1)求A、8两点的坐标:(2)若P(m,-2)为二次函数y = x2-x-2图像上一点,求加的值.参考答案1. (1) y1=x2-3x-4; (2)存在满足条件的P点,其坐标为(3上価、_2); (3) 16.2【解析】【分析】(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由题意可知点P在线段OC的垂直平分线上,则可求得P点纵坐标,代入抛物线解析式可求得P点坐标;(3)过P作PE丄x轴,交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长, 则可表示出四边形PBOC的面积,利用二次函数的性质可求得四边形PBOC面积的最大值及P点的坐标【详解】解:(1)设抛物线解析式为y=ax2+bx+c,把A、B、C三点坐标代入可得a-b+c=O< 16a + 4b + c = 0 ,c = —4a = 1解得b = —3,c =-4抛物线解析式为y=x2-3x-4;(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图2,,-.PO=PC,此时P点即为满足条件的点,VC (0, -4),.•.D (0,-2),•°.P点纵坐标为-2,代入抛物线解析式可得x2-3x-4=-2,解得x上也(小于0,舍去)或x= 土位,2 2•••存在满足条件的P点,其坐标为(土戸,-2).2(3)•.•点P在抛物线上,可设P (t, t2-3t-4),过P作PE丄x轴于点E,交直线BC于点F,如图1,VB (4, 0), C (0, -4),直线BC解析式为y=x-4,.•.F (t, t-4),.•.PF= (t-4) - (t2-3t-4) =-t2+4t,• • S四边形PBOC = BCO = S pre + S PFB + S BCO=—PF«OE+ — PF«BE+ — xOC«BO= — PF(OE+BE)+ — x4x42 2 2 2 2 =丄PF9B+8 =丄(屮+盘)x4+8=-2 (t-2) 2+16,2 2.•.当t=2时,S㈣边形FBOC最大值为16,此时t2-3t-4=-6,.•.当P点坐标为(2,-6)时,四边形PBOC的最大面积为16.【点睛】本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、三角形的面积、方程思想等知识.在(1)中注意待定系数法的应用,在(2)中确定出P点的位置是解题的关键,在(3)中用P点坐标表示出四边形PBOC的面积是解题的关键.2. (1) y = -x2 +2x + 3 ; (2) 6; (3) P(l,l)【解析】【分析】(1)将M,N两点代入y = -.X2 + bx + c求出be值,即可确定表达式;(2)令y=0求x的值,即可确定A、B两点的坐标,求线段AB长,由三角形面积公式求解.(3)求出抛物线的对称轴,确定M关于对称轴的对称点G的坐标,直线NG与对称轴的交点即为所求P点,利用一次函数求出P点坐标.【详解】解:将点M(0,3)> N(-2,-5)代入y--x2+bx+c中得,1 = 3_4 - 2b + c = -5,b = 2解得,°,c = 3Ay与x之间的函数关系式为y = -x2 + 2x + 3;(2)如图,当y=0时,一干+2兀+ 3 = 0,.*.X1=3,X2= -1,・・・A(・l,0),B(3,0),・・・AB=4,1 o AS A ABM=— X4X3 = 6 .2即AAW 的面积是6.答案第3页,总11页(3)如图,抛物线的对称轴为直线% = - —= = 1 ,2a -2点M(0,3)关于直线x=l的对称点坐标为G(2, 3),.•.PM=PG,连MG交抛物线对称轴于点P,此时NP+PM=NP+PG最小,即AMNP周长最短.设直线NG的表达式为y=mx+n,将N(-2,-5),G(2,3)代入得,—2m+n = —52m+n=3m = 2解得,\ ° ,n = -ly=2m-l,・・・P点坐标为(1,1).【点睛】本题考查抛物线与图形的综合题,涉及待定系数法求解析式,图象的交点问题,利用对称性解决线段和的最小值问题,利用函数观点解决图形问题是解答此题的关键.如图,二次函数y=-x2 +bx+c的图像经过M(0,3), N(-2,-5炳点.3.(1) 1; (2)证明见解析;(3) -1<77<1 ^|<n< |【解析】试题分析:⑴把点C (0, 3)代Ay = a(x - l)(x - 3) (a > 0)即可求出a=l;(2)求出点P的坐标,再求出CP=2苗,BP=<2, CB=3近,判断出ABCP为直角三角形, 通过解直角三角形,得出tanZACO=tanZPCB,从而证出:ZACO=,PCB;(3)通过分类讨论,即可得出-l<n<l< n < |试题解析:(1)把点C (0, 3)代Ay = a(x - 1)(% - 3) (a > 0)得:3=3a•I a= 1即a的值为1(2) V a=l抛物线的解析式为:y = (% - 1)(% - 3) = %2 - 4x + 3 = (x — 2尸—1:.P (2, -1)•:B (3, 0) , C (0, 3):.CP=2 忑,BP^y/2, CB=3 近:.BP2 + BC2 = 20, CP? = (2A/5)2 = 20:.BP2 + BC2 = CP2.\ZCBP=90otanZPCB辔= ^ = | 连接AC•/tanZAOC=—=-OC 3tan ZPCB= tanZAOC・•・ ZAOC=ZPCB(3) ( i )当点0在BC左侧的抛物线上时由(2)可知Q (2, -1)m+n=2P为兀轴下方二次函数尸1 )(兀-3)(°>0)图像上一点l<m<3l<2-n<3 /.-l<n<l(ii)当点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数基础定义知识点一:二次函数得定义形如)0(2≠++=a c bx ax y 【注意:二次项得系数0≠a ;x 得最高次幂为2】例题:若()311+++=-x xa y a 二次函数,则a 得值为 、【变式训练】若()12112+-+=+x x m y m二次函数,则m 得值为 、知识点二:“一般式”化“顶点式”例题:542++=x x y方法一:1)2(52)222(522225422222222++=+-+⋅⋅+=+-+⋅⋅+=++=x x x x x x x y方法二:144,222=--=-a b ac a b ,1)2(44)2(542222++=-++=++=x ab ac a b x x x y 【变式训练】把下列二次函数化成顶点式①322+-=x x y ; ②1122+-=x x y ; ③7422++=x x y知识点三:开口方向,对称轴,顶点坐标,最大(小)值,增减性 【温馨提示】形状相同,则二次项得系数a 相等【温馨提示】1、对于二次函数c bx ax y ++=2,当△=ac b 42->0,图像与x 轴有两个交点;当△=ac b 42-=0,图像与x 轴有一个交点;当△=ac b 42-<0,图像与x 轴没有交点。
2、求二次函数c bx ax y ++=2与x 轴得交点坐标就就是令y =0,求出x 1,x 2,则交点坐标为(x 1,0),(x 2,0);二次函数c bx ax y ++=2与y 轴得交点坐标就就是令x =0,求出y ,则交点坐标为(0,y );【变式训练】完成下列表格知识点五:二次函数图像得平移【温馨提示】二次函数图像得平移其实就就是顶点得平移例题:二次函数162++=x x y 得图像经过怎样平移能够变成542+-=x x y【分析】162++=x x y 得顶点坐标为(-3,-8),542+-=x x y 得顶点坐标为(2,1)、点(-3,-8)向右平移5个单位,再向上平移9个单位变成(2,1),所以162++=x x y 向右平移5个单位,再向上平移9个单位变成542+-=x x y【变式训练】完成下列表格 知识点六:待定系数法求二次函数得解析式【温馨提示】一般知道三个点得坐标,设二次函数得解析式为c bx ax y ++=2,然后将三个点得坐标代入c bx ax y ++=2,得到一个三元一次方程组;如果知道两个点得坐标,其中一个点为顶点),(n m ,则设二次函数得解析式为n m x a y +-=2)(,再把另一个点得坐标代入n m x a y +-=2)(求出a 得值;若知道三个点得坐标,其中有两个点(x 1,0),(x 2,0)在x 轴上,则可设))((21x x x x a y --=,再把另一个点得坐标代入))((21x x x x a y --=,求出a 得值。
【变式训练】1、已知抛物线c bx ax y ++=2经过(-1,2)、(1,-1)、(0,3)三点,求抛物线得函数关系式。
2、已知二次函数得顶点坐标就是(1,-2),且图像经过(3,5)三点,求二次函数得解析式。
二次函数图像基础练习题1、二次函数c bx x y ++=2得图象上有两点(3,-8)与(-5,-8),此拋物线得对称轴就是( )A.x =4 B 、 x =3 C 、 x =-5 D 、 x =-12、已知a -b +c=0 ,9a +3b +c=0,则二次函数y=ax 2+bx +c 得图像得顶点可能在( )A 、第一或第二象限B 、第三或第四象限C 、第一或第四象限D 、第二或第三象限3、已知M,N 两点关于y 轴对称,且点M 在双曲线y x=12上,点N 在直线y x =+3上,设点M 得坐标为(a ,b ),则二次函数y abx a b x =-++2()( )。
A 、 有最小值92 B 、 有最大值-92 C 、 有最大值92 D 、 有最小值-924、抛物线1822-+-=x x y 得顶点坐标为( ) (A)(-2,7) (B)(-2,-25) (C)(2,7) (D)(2,-9)5.在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得得抛物线关于y 轴作轴对称变换,那么经两次变换后所得得新抛物线得解析式为( )A.22y x x =--+B.22y x x =-+-C.22y x x =-++D.22y x x =++ 6.二次函数2365y x x =--+得图象得顶点坐标就是( ) A.(18)-, B.(18),C.(12)-,D.(14)-,7、抛物线y=x 2一3x+2与y 轴交点得坐标就是( ) A.(0,2) B.(1,O) C.(0,一3) D.(0,O) 8、如图所示就是二次函数2y ax bx c =++图象得一部分, 图象过A 点(3,0),二次函数图象对称轴为1x =,给出四个结论:①24b ac >;②0bc <;③20a b +=;④0a b c ++=,其中正确结论就是( ) A.②④B.①③C.②③D.①④9、二次函数2(1)2y x =--得图象上最低点得坐标就是Oyx1x =(30)A ,第8题图A.(-1,-2)B.(1,-2)C.(-1,2)D.(1,2)10、已知=次函数y =ax 2+bx+c 得图象如图.则下列5个代数式:ac, a+b+c,4a -2b+c, 2a+b,2a -b 中,其值大于0得个数为( ) A.2B 3C 、4D 、511、二次函数y=(x+1)2 +2得最小值就是( )A B C D 2、 2 、1 、-3 、 312、已知二次函数y=ax 2+bx+c(a ≠0)得图象如图3所示,下列结论:①abc >0 ②2a+b <0 ③4a -2b+c <0 ,其中正确结论得个数为( ) A 、0个 B 、3个 C 、2个 D 、112题13题 15题13、小强从如图所示得二次函数2y ax bx c =++得图象中,观察得出了下面五条信息:(1)0a <;(2)1c >;(3)0b >;(4)0a b c ++>;(5)0a b c -+>. 您认为其中正确信息得个数有( )A.2个B.3个C.4个D.5个14、已知0≠a ,在同一直角坐标系中,函数ax y =与2ax y =得图象有可能就是( ) 15、二次函数c bx ax y ++=得图象如图6所示,则下列关系式不正确得就是a abc >0 C 、cb a ++>0 D 、ac b 416、在平面直角坐标系中,将二次函数22x y =得图象向上平移2个单位,所得图象得解析式为( )A.222-=x yB.222+=x yC.2)2(2-=x yD.2)2(2+=x yx1y 2 -11O-1Oyx1-1A. xyO 1-1B. xy O1-1xyO1-11O y17、抛物线(1)(3)(0)y a x x a =+-≠得对称轴就是直线( ) A.1x =B.1x =-C.3x =-D.3x =18、已知二次函数2y ax bx c =++(0a ≠)得图象如图所示, 有下列四个结论:20040b c b ac <>->①②③④0a b c -+<, 其中正确得个数有( ) A.1个B.2个C.3个D.4个19、二次函数2(0)y ax bx c a =++≠得图象如图所示, 对称轴就是直线1x =,则下列四个结论错误..得就是( ) A.0c > B.20a b += C.240b ac -> D.0a b c -+>20、将抛物线y =2x 2向上平移3个单位得到得抛物线得解析式就是( ) A.y =2x 2+3 B.y =2x 2-3 C.y =2(x +3)2D.y =2(x -3)221、将抛物线22y x =向左平移1个单位,得到得抛物线就是( ) A.22(1)y x =+B.22(1)y x =-C.221y x =+D.221y x =-22、图6(1)就是一个横断面为抛物线形状得拱桥,当水面在l 时,拱顶(拱桥洞得最高点)离水面2m,水面宽4m.如图6(2)建立平面直角坐标系,则抛物线得关系式就是( ) A.22y x =- B.22y x =C.212y x =-D.212y x =23、如图9, 已知抛物线212y x bx c =++与x 轴交于A (-4,0) 与B (1,0)两点,与y 轴交于C 点. (1)求此抛物线得解析式;(2)设E 就是线段AB 上得动点,作EF //AC 交BC 于F ,连接CE ,当△CEF 得面积就是△BEF 面积得2倍时,求E 点得坐标;1O xy3111-O xy(19题图)图6(1) 图6(2)xyOC A24、已知:如图,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E .(1)写出直线BC 得解析式. (2)求ABC △得面积.(3)若点M 在线段AB 上以每秒1个单位长度得速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 以每秒2个单位长度得速度从B 向C 运动.设运动时间为t 秒,请写出MNB △得面积S 与t 得函数关系式,并求出点M 运动多少时间时,MNB △得面积最大,最大面积就是多少?2(2010湖南常德)如图9, 已知抛物线212y x bx c =++与x 轴交于A (-4,0) 与B (1,0)两点,与y轴交于C 点. (1)求此抛物线得解析式;(2)设E 就是线段AB 上得动点,作EF //AC 交BC 于F ,连接CE ,当△CEF 得面积就是△BEF 面积得2倍时,求E 点得坐标;3(2010广东东莞)已知二次函数c bx x y ++-=2得图象如图所示,它与x 轴得一个交点坐标为(-1,0),与y 轴得交点坐标为(0,3)⑴求出b ,c 得值,并写出此时二次函数得解析式;⑵根据图象,写出函数值y 为正数时,自变量x 得取值范围.6、如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它得顶点为A ,连接AB,把AB 所得直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 就是直线l 上一动点、(1) 求点A 得坐标;(2) 以点A 、B 、O 、P 为顶点得四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形得顶点P 得坐标;xy 3-1 O xyO BC A例2、已知抛物线y=x 2+(1-2a)x+a 2 (a ≠0)与x 轴交于两点A(x 1,0),B(x 2,0) , (x 1≠x 2)(1)求a 得取值范围,并证明A 、B 两点都在原点得左侧; (2)若抛物线与y 轴交于点C,且OA+OB=OC-2,求a得值。
