维特比译码简介
viterbi译码算法详解

viterbi译码算法详解Viterbi译码算法是一种常用的序列解码算法,广泛应用于语音识别、自然语言处理、通信等领域。
本文将详细介绍Viterbi译码算法的原理和步骤,以及它的应用。
Viterbi译码算法是一种动态规划算法,用于在给定观测序列的情况下,求解最可能的隐藏状态序列。
在这个过程中,算法会基于概率模型和观测数据,通过计算每个可能的状态路径的概率,选择概率最大的路径作为输出。
Viterbi译码算法的基本原理是利用动态规划的思想,将问题分解为一系列子问题,并利用子问题的最优解来求解整体问题的最优解。
在Viterbi译码算法中,我们假设隐藏状态的转移概率和观测数据的发射概率已知,然后通过计算每个时刻的最优路径来递推地求解整个序列的最优路径。
具体而言,Viterbi译码算法包括以下步骤:1. 初始化:对于初始时刻t=0,计算每个隐藏状态的初始概率,即P(x0=s)。
2. 递推计算:对于时刻t>0,计算每个隐藏状态的最大概率路径。
假设在时刻t-1,每个隐藏状态的最大概率路径已知,则在时刻t,可以通过以下公式计算:P(xt=s) = max(P(xt-1=i) * P(xi=s) * P(ot=s|xi=s))其中,P(xt=s)表示在时刻t,隐藏状态为s的最大概率路径;P(xt-1=i)表示在时刻t-1,隐藏状态为i的最大概率路径;P(xi=s)表示从隐藏状态i转移到隐藏状态s的转移概率;P(ot=s|xi=s)表示在隐藏状态s的情况下,观测到观测值为s的发射概率。
3. 回溯路径:在最后一个时刻T,选择概率最大的隐藏状态作为最终的输出,并通过回溯的方式找到整个序列的最优路径。
通过上述步骤,Viterbi译码算法可以求解出给定观测序列下的最可能的隐藏状态序列。
这个算法的时间复杂度为O(N^2T),其中N 是隐藏状态的个数,T是观测序列的长度。
Viterbi译码算法在实际应用中有着广泛的应用。
维特比译码算法

维特比(Viterbi)译码算法是一种常用于纠错码解码的动态规划算法,它用于找到给定接收信号中最有可能的发送序列,从而纠正错误。
维特比算法在通信领域和编码理论中广泛应用,特别是在卷积码和循环码等纠错码的解码过程中。
维特比译码算法的基本思想是,在接收到一串含有噪声的数据后,找到最有可能的原始数据序列,以最小化解码错误。
这个算法利用了动态规划的思想,通过逐步迭代地考虑所有可能的状态转移路径,选择最有可能的路径,从而找到最佳的发送序列。
下面是维特比译码算法的基本步骤:
1. **初始化:** 初始化第一个时间步的状态,通常为接收到的第一个数据。
将各个状态的初始路径度量设为接收到的数据与可能发送数据之间的距离(如汉明距离等)。
2. **递归计算:** 对每个时间步,计算到达每个状态的路径度量,考虑从前一个时间步到当前状态的所有可能路径。
选择最小路径度量作为当前状态的路径度量,并记录最佳路径。
3. **回溯:** 在最后一个时间步结束后,通过回溯最小路径度量,找到最佳路径,即最可能的发送序列。
维特比算法适用于许多不同类型的纠错码,包括卷积码、循环码等。
在实际应用中,它可以帮助恢复传输中的错误,提高通信系统的可靠性。
需要注意的是,维特比算法的复杂性会随着状态数和时间步数的增加而增加,因此在实际应用中,可能会通过一些优化策略来减少计
算复杂性,例如利用部分距离计算、并行计算等。
维特比译码算法在通信系统和编码理论中是一个重要的概念,如果你希望了解更多关于维特比算法的详细内容和数学推导,可以参考相关的通信和编码领域的教材和研究论文。
卷积码及维特比译码 notes
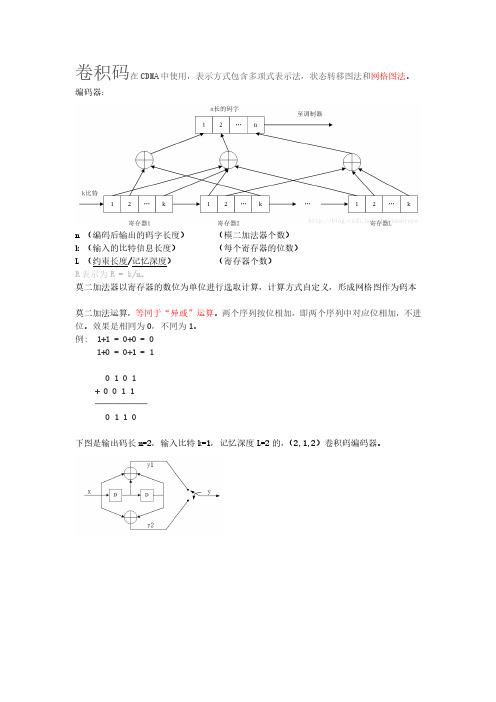
卷积码在CDMA中使用,表示方式包含多项式表示法,状态转移图法和网格图法。
编码器:n (编码后输出的码字长度)(模二加法器个数)k (输入的比特信息长度)(每个寄存器的位数)L (约束长度/记忆深度)(寄存器个数)R表示为R = k/n。
莫二加法器以寄存器的数位为单位进行选取计算,计算方式自定义,形成网格图作为码本莫二加法运算,等同于“异或”运算。
两个序列按位相加,即两个序列中对应位相加,不进位。
效果是相同为0,不同为1。
例: 1+1 = 0+0 = 01+0 = 0+1 = 10 1 0 1+ 0 0 1 1──────0 1 1 0下图是输出码长n=2,输入比特k=1,记忆深度L=2的,(2,1,2)卷积码编码器。
如编码序列“0 1 1 0 0”在图中的序列如下:汉明距离两个二进制数之间进行逐位对比,得到不同的个数如1000,与1100为1,与1110为2,与1111为3维特比算法综合状态之间的转移概率和前一层各状态的概率情况计算出概率最大的状态转换路径,从而推断出隐含状态的序列的情况。
的分支度量(汉明距离)。
其中有两条路径的分支量度为0。
3.寻找最大似然路径 - 译码过程维特比算法的关键点在于,接收机可以使用分支度量和先前计算的路径度量递推地计算当前状态的路径度量。
初始时,状态00代价为0,其它状态代价为正无穷(∞)。
算法的主循环由两个主要步骤组成:首先计算下一时刻监督比特序列的分支度量,然后计算该时刻各状态的路径度量。
路径度量的计算可以认为是一个“加-比-选”的过程1)将分支度量与上一时刻状态的路径度量相加。
2)每一状态比较来自前一时刻状态可达到的所有路径(只有两条这样的路径进行比较)3)每一状态删除其余到达路径,选择最小度量的路径保留(称为幸存路径/存活路径)若进入某个状态的部分路径中,有两条路径的度量值相等,则可以任选其一作为幸存路径。
下图显示了维特比译码的过程。
此例接收到的位序列为11 10 11 00 01 10(偷偷告诉你:这是有误码的信息)此时,产生了具有相同路径度量的四个不同路径,通向这四个状态的任一路径都是可能发送的比特序列(它们都具有度量为2的汉明距离)。
viterbi译码算法详解

viterbi译码算法详解Viterbi译码算法详解Viterbi译码算法是一种在序列估计问题中广泛应用的动态规划算法。
它被用于恢复在一个已知的输出序列中最有可能的输入序列。
该算法最初由Andrew Viterbi在1967年提出,并被广泛应用于各种领域,如语音识别、自然语言处理、无线通信等。
Viterbi译码算法的基本思想是在一个已知的输出序列中寻找最有可能的输入序列。
它通过计算每个可能的输入序列的概率,并选择概率最大的输入序列作为最终的估计结果。
该算法的关键是定义一个状态转移模型和一个观测模型。
状态转移模型描述了输入序列的转移规律,即从一个输入状态转移到另一个输入状态的概率。
观测模型描述了输入序列和输出序列之间的关系,即给定一个输入状态,产生一个输出状态的概率。
在Viterbi译码算法中,首先需要进行初始化。
假设有n个可能的输入状态和m个可能的输出状态,我们需要初始化两个矩阵:状态概率矩阵和路径矩阵。
状态概率矩阵记录了每个时刻每个状态的最大概率,路径矩阵记录了每个时刻每个状态的最大概率对应的前一个状态。
接下来,我们通过递归的方式计算状态概率和路径矩阵。
对于每个时刻t和每个可能的输入状态i,我们计算当前状态的最大概率和对应的前一个状态。
具体的计算方式是通过上一个时刻的状态概率、状态转移概率和观测概率来计算当前时刻的状态概率,并选择其中最大的概率作为当前状态的最大概率。
我们通过回溯的方式找到最有可能的输入序列。
从最后一个时刻开始,选择具有最大概率的状态作为最终的估计结果,并通过路径矩阵一直回溯到第一个时刻,得到整个输入序列的最有可能的估计结果。
Viterbi译码算法的优势在于它能够处理大规模的状态空间和观测空间。
由于使用动态规划的思想,该算法的时间复杂度为O(nmT),其中n和m分别为可能的输入状态和输出状态的数量,T为输出序列的长度。
因此,在实际应用中,Viterbi译码算法能够高效地处理各种序列估计问题。
维特比译码算法

维特比译码算法
维特比译码算法是一种卷积码的译码算法,其基本原理是利用动态规划的方法,通过计算每个状态转移的路径度量值,找到最小路径度量的路径作为幸存路径,从而得到译码输出。
维特比译码算法的复杂度与信道质量无关,其计算量和存储量都随约束长度N和信息元分组k呈指数增长,因此当约束长度和信息元分组较大时并不适用。
为了充分利用信道信息,提高卷积码译码的可靠性,可以采用软判决维特比译码算法。
此时解调器不进行判决而是直接输出模拟量,或是将解调器输出波形进行多电平量化,而不是简单的0、1两电平量化,然后送往译码器。
即编码信道的输出是没有经过判决的“软信息”。
维特比译码原理

维特比译码原理
维特比译码是一种序列鉴别算法,用于解码已被编码的序列。
它主要用于纠错编码和通信领域。
维特比译码基于动态规划的思想,通过计算每个时刻的最大可能性路径来找到最优解码结果。
维特比译码的基本原理如下:
1. 建立状态图:首先根据编码方案的特点,建立一个有向无环状态图,其中每个节点表示一个状态,每个边表示从一个状态转移到另一个状态的转移。
2. 计算到达每个状态的最大概率:从起始状态开始,根据编码的输入序列逐步计算每个状态的到达概率。
对于每个状态,可以通过考虑前一个时刻的所有状态的概率和转移概率来计算到达该状态的最大概率。
3. 选择最大概率路径:在到达最后一个状态时,根据计算得到的最大概率路径,可以通过回溯的方式找到整个序列的最优解码结果。
维特比译码的核心思想是利用动态规划的方法,在计算过程中保存中间结果,以避免重复计算。
通过逐步计算每个状态的最大概率,可以在最后找到最优解码结果。
维特比译码在纠错编码和通信系统中广泛应用,可以有效地解
码受到噪声、干扰和丢失的编码序列,提高通信的可靠性和性能。
卷积码的维特比译码原理及仿真

卷积码的维特比译码原理及仿真摘 要 本课程设计主要解决对一个卷积码序列进行维特比(Viterbi)译码输出,并通过Matlab 软件进行设计与仿真,并进行误码率分析。
实验原理QPSK :QPSK 是英文QuadraturePhaseShiftKeying 的缩略语简称,意为正交相移键控,是一种数字调制方式。
四相相移键控信号简称“QPSK ”。
它分为绝对相移和相对相移两种。
卷积码:又称连环码,是由伊莱亚斯(P.elias)于1955年提出来的一种非分组码。
积码将k 个信息比特编成n 个比特,但k 和n 通常很小,特别适合以串行形式进行传输,时延小。
卷积码是在一个滑动的数据比特序列上进行模2和操作,从而生成一个比特码流。
卷积码和分组码的根本区别在于,它不是把信息序列分组后再进行单独编码,而是由连续输入的信息序列得到连续输出的已编码序列。
卷积码具有误码纠错的能力,首先被引入卫星和太空的通信中。
NASA 标准(2,1,6)卷积码生成多项式为: 346134562()1()1g D D D D D g D D D D D=++++=++++其卷积编码器为:图1.1 K=7,码率为1/2的卷积码编码器维特比译码:采用概率译码的基本思想是:把已接收序列与所有可能的发送序列做比较,选择其中码距最小的一个序列作为发送序列。
如果接收到L 组信息比特,每个符号包括v 个比特。
接收到的Lv 比特序列与2L 条路径进行比较,汉明距离最近的那一条路径被选择为最有可能被传输的路劲。
当L 较大时,使得译码器难以实现。
维特比算法则对上述概率译码做了简化,以至成为了一种实用化的概率算法。
它并不是在网格图上一次比较所有可能的2kL 条路径(序列),而是接收一段,计算和比较一段,选择一段最大似然可能的码段,从而达到整个码序列是一个最大似然值得序列。
下面以图2.1的(2,1,3)卷积码编码器所编出的码为例,来说明维特比解码的方法和运作过程。
卷积码编码和维特比译码的原理、性能与仿真分析

卷积码编码和维特比译码的原理、性能与仿真分析1.引言卷积码的编码器是由一个有k位输入、n位输出,且具有m位移位寄存器构成的有限状态的有记忆系统,通常称它为时序网络。
编码器的整体约束长度为v,是所有k个移位寄存器的长度之和。
具有这样的编码器的卷积码称作[n,k,v]卷积码。
对于一个(n,1,v)编码器,约束长度v等于存储级数m.卷积码是由k个信息比特编码成n(n>k)比特的码组,编码出的n比特码组值不仅与当前码字中的k个信息比特值有关,而且与其前面v个码组中的v*k个信息比特值有关。
卷积码有三种译码方式:序列译码、门限译码和概率译码。
其中,概率译码根据最大似然译码原理在所有可能路径中求取与接收路径最相似的一条路径,具有最佳的纠错性能,维特比译码是概率译码中极重要的一种方式。
序列译码和门限译码则不一定能找出与接收路径最相似的一条路径。
不同于维特比译码,门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于(m+1)个接收分组,而不是基于整个接收序列。
与维特比译码所使用的对数似然量度不同,序列译码所使用的量度为Fano量度。
在接收序列受扰严重的情况下,序列译码的计算量大于维特比译码所需的固定计算量,虽然序列译码要求的平均计算次数通常小于维特比译码。
在采用并行处理的情况下,维特比译码的速度会优于序列译码。
在同样码率和存储级数的条件下,门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式,本文选取生成多项式为561,753的(2,1,8)卷积码对硬判决的性能进行分析,并依据维特比译码的原理以及卷积码的特性,对卷积码编码和维特比译码过程在加性高斯白噪声(AWGN)信道下进行仿真,并且根据仿真结果对维特比译码(硬判决)的结果进行分析。
由于卷积码的生成可以看做一个马尔科夫过程,因此,不同状态间的转移概率对描述这个过程有极关键的作用。
本文则基于MATLAB对不同状态间的转移概率进行求解,从而更准确地分析维特比译码的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在上例中卷积码的约束长度为N = 3,需要 存储和计算8条路径的参量。由此可见,维 特比算法的复杂度随约束长度N按指数形式 2N增长。故维特比算法适合约束长度较小 (N 10)的编码。
所以,维特比译码的过程可以简单的理解 为:接收端使用相同的网格图,从同一状 态开始猜测发送端可能的编码序列,然后 与接收到的码组比较,其中与接收到的码 组最近的猜测序列即使为译码序列,也就 是码距最小的序列。
设卷积码为(n, k, m) = (3,沿路径每一级有4种状态a, b, c和d。每种状态只有两条路径可以到达。故 4种状态共有8条到达路径。 比较网格图中的这8条路径和接收序列之间 的汉明距离。 比较到达每个状态的两条路径的汉明距离, 将距离小的一条路径保留,也就是幸存路径。 这样,就剩下4条路径了。 继续考察接收序列中的后继的比特,最后得 出总的汉明距离最小的路径,也就是发送序 列。
维特比算法简介
维特比译码是将接收到的序列和所有可能 的发送序列作比较,选择其中汉明距离最 小的序列当作是现在的发送序列的一种算 法。译码器从某个状态出发,每次向右延伸 一个分支,并与接收数字相应分支进行比较, 计算它们之间的距离,然后将计算所得距 离加到被延伸路径的累积距离值中。
对到达每个状态的各条路径的距离累积值 进行比较,保留距离值最小的一条路径, 称为幸存路径,当有两条以上取最小值时, 可任取其中之一。这种算法所保留的路径 与接收序列之间的似然概率为最大,所以 又称为最大似然译码。
假设现在的发送信息位为1101 编码后的发送序列:111 110 010 100 001 011 000 接收序列:111 010 010 110 001 011 000 (红色为 错码) 发送序列的约束长度为N = m + 1 = 3 最后的幸存路径画出的网格图示于下图中,图中粗 线路径是距汉明离最小(等于2)的路径。
