The interaction of internal and external information in a problem solving task
关于矛盾的英语作文

Contradiction is a fundamental concept in philosophy and everyday life, representing the opposition and conflict between two opposing sides of a matter.It is an essential driving force for the development and change of things.In this essay,we will explore the nature of contradictions and their role in various contexts.The Essence of ContradictionsContradictions are inherent in all aspects of life and are the source of movement,change, and development.They exist within every entity and are the basis for the interconnection and interaction between different elements.The essence of a contradiction lies in the unity of opposites,where opposing forces are both in conflict and interdependent.Types of Contradictions1.Primary and Secondary Contradictions:In any situation,there is often a primary contradiction that determines the nature and direction of development,along with secondary contradictions that are subordinate to the primary one.2.Internal and External Contradictions:These refer to the conflicts within an entity and those arising from interactions with external factors.3.Universality and Particularity of Contradictions:Every entity has its unique set of contradictions,yet they also share common characteristics with other entities. Contradictions in Social LifeIn society,contradictions are manifested in various forms,such as class struggle,social conflicts,and ideological differences.They are the driving force behind social progress and transformation.Recognizing and resolving these contradictions is crucial for maintaining social harmony and stability.Contradictions in Personal DevelopmentIndividuals also experience contradictions in their personal growth and development. These can be between desires and reality,between personal goals and societal expectations,or between ones values and the actions of others.Navigating these contradictions is essential for personal maturity and selfimprovement.Resolving ContradictionsResolving contradictions requires a dialectical approach that acknowledges the complexity and interconnectedness of opposing forces.It involves understanding the root causes of the conflict,finding common ground,and seeking compromise or solutions that can lead to progress.ConclusionContradictions are an inevitable part of existence,and they play a vital role in shaping the world around us.By understanding and addressing them effectively,we can foster growth, innovation,and positive change in both our personal lives and society at large. Embracing the concept of contradictions allows us to appreciate the dynamic and evolving nature of life,encouraging us to seek balance and harmony amidst the complexities of existence.。
团队内隐异质性:内涵拓展及其效能机制

心理科学进展 2014, Vol. 22, No. 2, 323–333 Advances in Psychological ScienceDOI: 10.3724/SP.J.1042.2014.00323323团队内隐异质性:内涵拓展及其效能机制*姚春序 项小霞 倪旭东(浙江理工大学经济管理学院, 杭州 310018)摘 要 从内隐异质性的内涵维度及其效能机制, 包括内隐异质性作用于绩效的中间过程和情境因素、内隐异质性和外显异质性的交互作用、团队断裂带和内隐异质性的跨层次研究方面阐述了团队内隐异质性研究的最新成果和进展, 并在此基础上提出了未来研究的一个整合框架。
未来的研究需要在内隐异质性内涵维度及其前因变量、内隐异质性的跨层次研究、团队断裂带及其与团队结果变量之间关系、社会网络背景下内隐异质性与团队绩效之间的关系等方面进一步探索。
关键词 内隐异质性; 跨层次; 交互作用; 团队断裂带 分类号B849:C931 引言团队已经成为组织开展活动的基本单位, 有关于团队运作和团队管理的研究层出不穷, 而异质性研究是其中的关键部分。
团队异质性(或者说团队多样化)包括外显异质性(如年龄、种族、性别等看得见的异质性)和内隐异质性(如专长和职业背景等看不见的异质性)两种类型(Harrison, Price, & Bell, 1998)。
传统团队异质性的研究主要基于社会分类视角和信息加工视角(Williams & O’Reilly, 1998)两大视角。
社会分类视角(social categoriza- tion perspective)认为通常个体将同质性和异质性作为对自己和团队内其他成员进行归类的标准, 进而区分其自身的“圈内人”和“圈外人” (Williams & O’Reilly, 1998), 从而降低团队凝聚力, 影响沟通和绩效; 它强调的是同质性团队的价值, 关注焦点在于成员关系。
Abstract

Strict Polynomial-time in Simulation and Extraction∗Boaz Barak Department of Computer Science Weizmann Institute of Science Rehovot76403,Israel. boaz@wisdom.weizmann.ac.ilYehuda Lindell†IBM T.J.Watson Research 19Skyline Drive,Hawthorne New York,10532,USA.lindell@February2,2004AbstractThe notion of efficient computation is usually identified in cryptography and complexity with (strict)probabilistic polynomial time.However,until recently,in order to obtain constant-roundzero-knowledge proofs and proofs of knowledge,one had to allow simulators and knowledge-extractors to run in time that is only polynomial on the average(i.e.,expected polynomialtime).Recently Barak gave thefirst constant-round zero-knowledge argument with a strict(incontrast to expected)polynomial-time simulator.The simulator in his protocol is a non-black-box simulator(i.e.,it makes inherent use of the description of the code of the verifier).In this paper,we further address the question of strict polynomial-time in constant-round zero-knowledge proofs and arguments of knowledge.First,we show that there exists a constant-round zero-knowledge argument of knowledge with a strict polynomial-time knowledge extractor.As in the simulator of Barak’s zero-knowledge protocol,the extractor for our argument of know-ledge is not black-box and makes inherent use of the code of the prover.On the negative side,we show that non-black-box techniques are essential for both strict polynomial-time simulationand extraction.That is,we show that no(non-trivial)constant-round zero-knowledge proof orargument can have a strict polynomial-time black-box simulator.Similarly,we show that no(non-trivial)constant-round zero-knowledge proof or argument of knowledge can have a strictpolynomial-time black-box knowledge extractor.Keywords:Zero-knowledge proof systems,proofs of knowledge,expected vs.strict polynomial-time,black-box vs.non-black-box algorithms.∗An extended abstract of this paper appeared in the34th STOC,2002.†Much of this work was carried out while at the Weizmann Institute of Science,Israel.1IntroductionThis paper deals with the issue of expected versus strict polynomial-time with respect to simulators and extractors for zero-knowledge proofs and arguments and zero-knowledge proofs and arguments of knowledge.11.1Expected Polynomial-Time in Zero KnowledgeThe principle behind the definition of(computational)zero-knowledge proofs,as introduced by Goldwasser,Micali and Rackoff[29],is the following:Anything that an efficient verifier can learn as a result of interacting with the prover,can be learned without interaction by applying an efficient procedure(i.e.,simulator)tothe public input.Note that there are two occurrences of the word“efficient”in this sentence.When providing a formal definition of zero knowledge,the issue of what is actually meant by“efficient computation”must be addressed.The standard interpretation in cryptography and complexity is that of probabilistic polynomial-time.However,in the context of zero knowledge,efficiency has also been taken to mean polynomial on the average(a.k.a.expected polynomial-time).That is,if wefix the input, and look at the running time of the machine in question as a random variable(depending on the machine’s coins),then we only require that the expectation of this random variable is polynomial. Three versions of the formal definition of zero knowledge appear in the literature,differing in their interpretations of efficient computation:1.Definition1–strict/strict:According to this definition both the verifier and simulatorrun in strict polynomial-time.This is the definition adopted by Goldreich[22,Section4.3] and is natural in the sense that only the standard interpretation of efficiency is used.2.Definition2–strict/expected:This more popular(and liberal)definition requires theverifier to run in strict polynomial-time while allowing the simulator to run in expected polynomial-time.This was actually the definition proposed in the original paper on zero knowledge[29].3.Definition3–expected/expected:In this definition,both the verifier and simulator areallowed to run in expected polynomial-time.This definition is far less standard than the above two,but is nevertheless a natural one to consider.As we describe below,this definition was considered by[17],who show that(at least for one definition of expected polynomial-time)it is problematic.As we have mentioned,the standard interpretation of efficient computation is that of(strict) polynomial-time.In light of this,Definition1(strict/strict)seems to be the most natural. Despite this,expected polynomial-time was introduced in the context of zero knowledge because a number of known protocols that could be proven zero-knowledge according to the more liberal “strict/expected definition”were not known to satisfy the more severe“strict/strict defini-tion”.In particular,until very recently no constant-round zero knowledge argument(or proof)for 1In a proof system,soundness holds unconditionally and with respect to all-powerful cheating provers.In contrast, in an argument system,soundness is only guaranteed to hold with respect to polynomial-time bounded provers.We note that lower bounds for proofs do not necessarily hold for arguments,because in arguments the soundness condition is only computational.Likewise,lower bounds for arguments do not necessarily hold for proofs,because proofs are allowed to have super-polynomial honest prover strategies,whereas arguments are not.See Section2.1.N P was known to satisfy Definition1(strict/strict).2It was therefore necessary to relax the definition and allow expected polynomial-time simulation(as in Definition2).Proofs of Knowledge.An analogous situation arises in proofs of knowledge[29,33,18,6]. There,the underlying principle is that:If an efficient prover can convince the honest verifier with some probability that x∈L,then this prover can apply an efficient procedure(i.e.,extractor)to x and its privateinputs and obtain a witness for x with essentially the same probability.Again,the word“efficient”occurs twice,and again three possible definitions can be used.In par-ticular,the prover and extractor can be instantiated by strict polynomial-time machines,expected polynomial-time machines or a combination of both.The different definitions-discussion.As has been observed before(e.g.,see[17,Sec.3.2], [22,Sec.4.12.3]),the definitions that allow for expected polynomial-time computation are not fully satisfactory for several reasons:•Philosophical considerations:Equating“efficient computation”with expected polynomial-time is more controversial than equating efficient computation with(strict)probabilistic polynomial-time.For example,Levin([30],see also[20],[22,Sec.4.3.1.6])has shown that when expected polynomial-time is defined as above,the definition is too machine dependent,and is not closed under reductions.He proposed a different definition for expected polynomial-time that is closed under reductions and is less machine dependent.However,it is still unclear whether expected polynomial-time,even under Levin’s definition,should be considered as efficient computation.•Technical considerations:Expected polynomial-time is less understood than the more stan-dard strict polynomial-time.This means that rigorous proofs of security of protocols that use zero-knowledge arguments with expected polynomial-time simulators(or arguments of know-ledge with expected polynomial-time extractors)as components,are typically more complicated (see[31]for an example).Another technical problem that arises is that expected polynomial-time simulation is not closed under composition.Consider,for example,a protocol that uses zero-knowledge as a subprotocol.Furthermore,assume that the security of the larger protocol is proved in two stages.First,the zero-knowledge subprotocol is simulated for the adversary (using an expected polynomial-time simulator).This results in an expected polynomial-time adversary that runs the protocol with the zero-knowledge executions removed.Then,in the next stage,the rest of the protocol is simulated for this adversary.A problem arises because the simulation of the second stage must now be carried out for an expected polynomial-time adver-sary.However,simulation for an expected polynomial-time adversary can be highly problematic (as the protocol of[24]demonstrates,see[31,Appendix A]for details).•Practical considerations:A proof of security that uses expected polynomial-time simulation does not always achieve the“expected”level of security.For example,assume that a protocol’s security relies on a hard problem that would take100years to solve,using the best known algorithm.Then,we would like to prove that the probability that an adversary can successfully break the protocol is negligible,unless it runs for100years.However,when expected polynomial-time simulation is used,we cannot rule out an adversary who runs for1year and succeeds with probability1/100.This is a weaker level of security and may not be acceptable.See Section1.4 for a more detailed discussion of this issue.2We note that throughout this paper we always refer to protocols with negligible soundness error.The liberal“strict/expected definition”also suffers from a conceptual drawback regarding the notion of zero knowledge itself.Specifically,the idea behind the definition of zero knowledge is that anything that a verifier can learn as a result of the interaction,it can learn by just looking at its input.Therefore,it seems that the simulator should not be of a higher complexity class than the verifier.Rather,both the verifier and simulator should be restricted to the same complexity class(i.e.,either strict or expected polynomial-time).The“expected/expected definition”has the advantage of not having any discrepancy between the computational power of the verifier and simulator.However,it still suffers from the above described drawbacks with any use of expected polynomial-time.In addition,as Feige[17,Sec.3.3]pointed out,in order to prove that known protocols remain zero knowledge for expected polynomial-time verifiers,one needs to restrict the verifiers to run in expected polynomial-time not only when interacting with the honest prover but also when interacting with all other interactive machines.This restriction is somewhat controversial because any efficient adversarial strategy should be allowed.In particular,there seems to be no reason to disqualify an adversarial strategy that takes expected polynomial-time when attacking the honest prover,but runs longer otherwise(notice that the adversary is only interested in attacking the honest prover,and so its attack is efficient).In contrast,the“strict/strict definition”suffers from none of the above conceptual difficul-ties.For this reason,it is arguably a preferred definition.However,as we have mentioned,it was not known whether this definition can be satisfied by a protocol with a constant number of rounds. Thus a natural open question(posed by[17,Sec.3.4]and[22,Sec.4.12.3])was the following: Is expected polynomial-time simulation and extraction necessary in order to obtainconstant-round zero-knowledge proofs and proofs of knowledge?Afirst step in answering the above question was recently taken by Barak in[3].Specifically,[3]pre-sented a zero-knowledge argument system that is both constant-round and has a strict polynomial-time simulator.Interestingly,the protocol of[3]is not black-box zero knowledge.That is,the simulator utilizes the description of the code of the verifier.(This is in contrast to black-box zero knowledge where the simulator is only given oracle access to the verifier.)Given the existence of non-black-box zero-knowledge arguments with a constant number of rounds and strict polynomial-time simulation,it is natural to ask the following questions:1.Is it possible to obtain constant-round zero-knowledge arguments of knowledge with strictpolynomial-time extraction?2.Is the fact that the protocol of[3]is not black-box zero knowledge coincidental,or is this aninherent property of any constant-round zero-knowledge protocol with strict polynomial-time simulation?1.2Our ResultsIn this paper we resolve both the above questions.First,we show that it is possible to obtain strict polynomial-time knowledge extraction in a constant-round protocol.In fact,we show that it is possible to obtain strict polynomial-time simulation and extraction simultaneously in a zero-knowledge protocol.That is,we prove the following theorem:Theorem1Assume the existence of collision-resistant hash functions and collections of trapdoor permutations such that the domain of each permutation is the set of all strings of a certain length.3 Then,there exists a constant-round zero-knowledge argument of knowledge for N P with a strict polynomial-time knowledge extractor and a strict polynomial-time simulator.The definition of arguments of knowledge that we refer to in Theorem1differs from the standard definition of[6]in an important way.In the definition of[6],the knowledge extractor is given only black-box access to the prover.In contrast,in our definition,the knowledge extractor is given the actual description of the prover(i.e.,it has non black-box access).As we will see below,this modification is actually necessary for obtaining constant-round arguments of knowledge with strict polynomial-time extraction.In addition to the above positive result,we show that it is impossible to obtain a(non-trivial) constant-round zero-knowledge protocol that has a strict polynomial-time black-box simulator. Likewise,a strict polynomial-time extractor for a constant-round zero-knowledge argument of know-ledge cannot be black-box.That is,we prove the following two theorems:Theorem2There do not exist constant-round zero-knowledge proofs or arguments with strict polynomial-time black-box simulators for any language L∈BPP.Theorem3There do not exist constant-round zero-knowledge proofs or arguments of knowledge with strict polynomial-time black-box knowledge extractors for any language L∈BPP.We therefore conclude that the liberal definitions that allow the simulator(resp.,extractor)to run in expected polynomial-time are necessary for achieving constant-round black-box zero knowledge (resp.,arguments of knowledge).Furthermore,our use of non-black-box techniques in order to obtain Theorem1is essential.We note that Theorems2and3are tight in the sense that if any super-constant number of rounds are allowed,then zero-knowledge proofs of knowledge with strict polynomial-time black-box extraction and simulation can be obtained.This was shown by Goldreich in[22,Sec.4.7.6]. (Actually,[22]shows that a super-logarithmic number of sequential executions of the3-round zero-knowledge proof for Hamiltonicity[9]suffices.However,using the same ideas,it can be shown that by running log n parallel executions of the proof of Hamiltonicity,any super-constant number of sequential repetitions is actually enough.)Zero knowledge versusε-knowledge.Our impossibility result regarding constant-round black-box zero knowledge with strict polynomial-time simulation has an additional ramification to the question of the relation between black-boxε-knowledge[15]and black-box zero knowledge.Loosely speaking,an interactive proof is calledε-knowledge if for everyε,there exists a simulator who runs in time polynomial in the input and in1/ε,and outputs a distribution that can be distinguished from a real proof transcript with probability at mostε.Despite the fact that this definition seems to be a significant relaxation of zero knowledge,no separation betweenε-knowledge and zero know-ledge was previously known.Our lower bound indicates a separation for the black-box versions: that is,black-boxε-knowledge is strictly weaker than black-box zero-knowledge.Specifically,on the one hand,constant-round black-boxε-knowledge protocols with strict polynomial-time simulators 3By this we mean that there exists a trapdoor permutation family{f}s∈{0,1}∗such that f s:{0,1}|s|→{0,1}|s|.sIt actually suffices to assume the existence of a family of enhanced trapdoor permutations[23,Appendix C.1].Such a family can be constructed under the RSA and factoring assumptions,see[2,Section6.2]and[23,Appendix C.1].do exist.4On the other hand,as we show,analogous protocols for black-box zero-knowledge,do not exist.Witness-extended emulation.Zero-knowledge proofs of knowledge are often used as subproto-cols within larger protocols.Typically,in this context the mere existence of a knowledge extractor does not suffice for proving the security of the larger protocol.Loosely speaking,what is required is the existence of a machine that not only outputs a witness with the required probability(as is required from a knowledge extractor),but also outputs a corresponding simulated transcript of the interaction between the prover and the verifier.Furthermore,whenever the transcript of the interaction is such that the verifier accepts,then the witness that is obtained is valid.To explain this further,consider a case that the prover convinces the verifier in a real interaction with prob-ability p.Then,with probability negligibly close to p,the aforementioned machine should output an accepting transcript and a valid witness.Furthermore,with probability negligibly close to1−p, the machine should output a rejecting transcript(and we don’t care about the witness).This issue was addressed in[31],who called such a machine a“witness-extended emulator”.It was proved there that there exists such a witness extended emulator for any proof of knowledge. However,the extended emulator that is obtained runs in expected polynomial-time,even if the original knowledge extractor runs in strict polynomial-time.Unfortunately,we do not know how to prove an analogous result that,given any strict polynomial-time knowledge extractor,would provide a strict polynomial-time emulator.Instead,we directly construct a strict polynomial-time witness-extended emulator for our zero-knowledge proof of knowledge(under a slightly different definition than[31]).1.3On the Effect of Truncating Expected Polynomial-Time ExecutionsA naive approach to solving the problem of expected polynomial-time in simulation and extraction, is to simply truncate the execution of the simulator or extractor after it exceeds its expected running-time by“too much”.However,this does not necessarily work.The case of knowledge-extractors is a good example.Let usfix a proof(or argument)of knowledge for some NP-language L.Let x∈{0,1}∗,and let P∗be a polynomial-time prover that,for some ,aborts with probability 1− and convinces the honest verifier that x∈L with probability .For all previously known constant-round proofs of knowledge,the expected polynomial-time knowledge-extractor works in roughly the following way:itfirst verifies the proof from P∗,and if P∗was not convincing(which occurs in this case with probability1− )then it aborts.On the other hand,if P∗was convincing(which happens in this case with probability ),then it does expected p(n)·1work(where p(·)is somefixed polynomial),and outputs a witness for x.Clearly,the expected running time of the extractor is polynomial(in particular,it is p(n)plus the time taken to honestly verify a proof).However,if we halt this extractor before it completes1steps then,with high probability,theextractor will not output a witness.Note that1may be much larger than p(n),and therefore theextractor may far exceed its expected running-time and yet still not output anything.In contrast to the above,the knowledge extractor of the argument of knowledge presented in this paper(in Section4)runs in strict polynomial-time which is independent of the acceptance probability(i.e., ).For example,if there exists a cheating prover P∗that runs in time n2,but convinces the verifier that x∈L with probability =n−10then our extractor will always run 4Such a protocol can be constructed by taking any constant-round protocol with an expected polynomial-time simulator and truncating the simulator’s run(outputting⊥),if it runs for more than1/εtimes its expected running-time.By Markov’s inequality,the probability of this bad event happening is at mostε.in time,say,n4and output a witness with probability at least(negligibly less than)n−10.On the other hand,the extractors for previous protocols would do almost nothing with probability 1−n−10,and with probability n−10run for,say,n12steps and output a witness.1.4Trading Success Probability for Running TimeThe observation in Section1.3about how expected polynomial-time extractors typically work, raises serious security issues with respect to the application of proofs of knowledge that have such extractors.For example,suppose that we use a proof of knowledge for an identification protocol based on factoring.Suppose furthermore,that we use numbers for which the fastest known algorithms will take100years to factor.We claim that in this case,if we use a proof of knowledge with an expected polynomial-time extractor then we cannot rule out the possible existence of an adversary that will take1year of computation time and succeed in an impersonation attack with probability1/100.In order to see this,notice that the proof of security of the identification protocol works by constructing a factoring algorithm from any impersonator,using the extractor for the proof of knowledge.Thus,for typical protocols,what will actually be proven is that given an algorithm that runs for T steps and successfully impersonates with probability ,we can construct an algorithm that solves the factoring problem with probability and expected running time T.In particular,this factoring algorithm may(and actually will)work in the following way:with probability1− it will do nothing and with probability it will run in T/ steps and factor its input.Thus,the existence of an impersonator that runs for one year and succeeds with probability1/100,only implies the existence of a factoring algorithm that runs for100years.Therefore,we cannot rule out such an impersonator.We conclude that the standard proofs of knowledge potentially allow adversaries to trade their success probability for running time.In the concrete example above,the impersonator lowered its running time from100years to one year,at the expense of succeeding with probability 1/100instead of1.We stress that the fastest known algorithms for factoring do not allow such a trade-off.That is,if the parameters are chosen so that100years are required to factor,then the probability of successfully factoring after one year is extremely small,and not close to1/100.We stress that not only is it the case that the definition of expected polynomial-time extraction does not allow us to rule out such an adversary,but also such adversaries cannot be ruled out by the current proofs of security for known constant-round protocols(thus,the problem lies also with the protocols and not just with the definition).In contrast,such a trade-offis not possible if the extractor runs in strict polynomial-time.Rather,an impersonator that runs in time T and succeeds with probability yields a factoring algorithm that runs in time(polynomially related)to T and succeeds with probability .Thus,in the above concrete example,an analogous impersonator for a protocol with a strict polynomial-time extractor would yield a factoring algorithm that runs for one year and succeeds with probability1/100.However,such an algorithm is conjectured not to exist,and therefore such an impersonator also does not exist(unless the conjecture is wrong). 1.5Further Discussion of Prior WorkZero-knowledge proofs were introduced by Goldwasser,Micali and Rackoff[29],and were then shown to exist for all N P by Goldreich,Micali and Wigderson[26].Constant-round zero-knowledge arguments and proofs were constructed by Feige and Shamir[19],Brassard,Crepeau and Yung[11] and Goldreich and Kahan[24].All these constant-round protocols utilize expected polynomial-time simulators.Regarding zero-knowledge proofs of knowledge,following a discussion in[29],thefirstformal definitions were provided by Feige,Fiat and Shamir[18]and by Tompa and Woll[33].These definitions were later modified by Bellare and Goldreich[6].The issue of expected polynomial-time is treated in Feige’s thesis[17]and Goldreich’s book [22].Goldreich[22,Sec.4.7.6]also presents a construction for a proof of knowledge with strict polynomial-time extraction(and simulation)that uses any super-logarithmic number of rounds (as discussed above,a variant of this construction can be obtained that uses any super-constant number of rounds).As we have mentioned,until a short time ago,all known constant-round zero-knowledge pro-tocols had expected polynomial-time simulators.However,recently this barrier was broken by Barak[3],who provided thefirst constant-round zero-knowledge argument for N P with a strict polynomial-time simulator,assuming the existence of collision-resistant hash functions with super-polynomial hardness.Barak and Goldreich[4]later showed how to obtain the same result under the weaker assumption of the existence of standard collision-resistant hash functions(with polynomial-time hardness).The construction of[3]was also thefirst zero-knowledge argument to utilize a non-black-box simulator.In a similar fashion,the constant-round argument of knowledge pre-sented in this paper utilizes a non-black-box knowledge-extractor.We note that[5]also utilize a non-black-box knowledge extractor.However,their extractor runs in expected polynomial-time, and the non-black-box access is used there for a completely different reason(specifically,to achievea resettable zero-knowledge argument of knowledge).1.6Organization.In Section2we describe the basic notations and definitions that we use.Then,in Section3we define and construct a commit-with-extract commitment scheme,which is the main technical tool used to construct our zero-knowledge argument of knowledge.The proof of Theorem1can be found in Section4where we present the construction of a zero-knowledge argument of knowledge with strict polynomial-time extraction.Finally,in Section5we prove Theorems2and3.That is,we prove that it is impossible to construct strict polynomial-time black-box simulators and extractors for(non-trivial)constant-round protocols.2DefinitionsNotation.For a binary relation R,we denote by R(x)the set of all“witnesses”for x.That is, R(x)def={y|(x,y)∈R}.Furthermore,we denote by L R the language induced by the relation R. That is,L R def={x|R(x)=∅}.For afinite set S⊆{0,1}∗,we write x∈R S to say that x is distributed uniformly over the set S.We denote by U n the uniform distribution over the set{0,1}n.A functionµ(·)is negligible if for every positive polynomial p(·)and all sufficiently large n’s,it holds thatµ(n)<1/p(n).We letµ(·)denote an arbitrary negligible function.That is,when we say that f(n)<µ(n)for some function f(·),we mean that there exists a negligible functionµ(·)such that for every n,f(n)<µ(n).A function f(·)is noticeable if there exists a positive polynomial p(·)such that for all sufficiently large n’s,it holds that f(n)>1/p(n).We note that“noticeable”is not the complement of“negligible”.For two probability ensembles(sequences of random variables)X={X s}s∈S and Y={Y s}s∈S (where S⊆{0,1}∗is a set of strings),we say that X is computationally indistinguishable from Y, denoted X c≡Y,if for every polynomial-sized circuit family{D n}n∈N and every s∈S,it holds that|Pr[D|s|(X s)=1]−Pr[D|s|(Y s)=1]|<µ(|s|).We will sometime drop the subscripts s when they can be inferred from the context.In all our protocols,we will denote the security parameter by n.Let A be a probabilistic polynomial-time machine.We denote by A(x,y,r)the output of the machine A on input x,auxiliary-input y and random-tape r.We stress that the running-time of A is polynomial in|x|.5If M is a Turing machine,then we denote by desc n(M)the description of a circuit that computes M on inputs of size n.Note that a polynomial-time machine that receives desc n(M)for input runs in time that is polynomial in the running-time of M.Let A and B be interactive machines.We denote by view A(A(x,y,r),B(x,z,r ))the view of party A in an interactive execution with machine B,on public input x,where A has auxiliary-input y and random-tape r,and B has auxiliary input z and random-tape r .The view of party B is denoted similarly.Recall that a party’s view of an execution includes the contents of its input,auxiliary-input and random tape plus the transcript of messages that it receives during the execution.We will sometimes drop r or r from this notation,which will mean that the random tape is notfixed but rather chosen at random.For example we denote by view A(A(x,y),B(x,z))the random variableview A(A(x,y,U m),B(x,z,Um ))where m(resp.,m )is the number of random bits that A(resp.,B)uses on input of size|x|.2.1Zero KnowledgeLoosely speaking,an interactive proof system for a language L involves a prover P and a verifier V,where upon common input x,the prover P attempts to convince V that x∈L.We note that the prover is often given some private auxiliary-input that“helps”it to prove the statement in question to V.Such a proof system has the following two properties:pleteness:this states that when honest P and V interact on common input x∈L,thenV is convinced of the correctness of the statement that x∈L(except with at most negligible probability).2.Soundness:this states that when V interacts with any(cheating)prover P∗on common inputx∈L,then V will be convinced with at most negligible probability.(Thus V cannot be tricked into accepting a false statement.)There are twoflavors of soundness:unconditional(or statistical)soundness that must hold even for an all-powerful cheating prover,and computational soundness that needs only hold for(non-uniform)polynomial-time cheating provers.In proof systems[29],unconditional soundness is guaranteed;whereas in argument systems[10]only computational soundness must hold.We remark that a proof system is not necessarily an argument system,because the honest prover strategy in a proof system is not required to be polynomial-time(in contrast to arguments where the honest prover as well as the cheating provers must be non-uniform polynomial-time).Unless explicitly stated,when we mention“protocols”in discussion,we mean both proofs and arguments.Throughout this paper,we will always assume that the soundness error is at most negligible. However,we will not always require this of completeness.Specifically,our lower bounds in Section5 hold even if the completeness error is1−1/p(n)for some polynomial p(·);in this case,we will call p(n)the completeness bound.We now recall the definition of zero knowledge[29].Actually,we present(a slightly strengthened form of)the definition of auxiliary-input zero knowledge[22,Sec.4.3.3].6The main difference 5We assume that y and r are on different tapes.Therefore,even if y is very long(e.g.,|y|>poly(|x|)),it is still possible for A to read r.6We deviate from the definition of auxiliary-input zero knowledge of[22,Sec.4.3.3]by making the slightly stronger requirement that there exists a single universal simulator for all verifiers,rather than a different simulator for each。
Chapter 1-1

3
Language is ……
What is language?
4
Comments on the following ideas
1. Language is a means of communication. 2. Language has a form-meaning correspondence. 3. The function of language is to exchange information.
The subject matter of linguistics
• The subject matter of linguistics is all natural languages, living or dead. • It studies the origin, growth, organization, nature and development of languages. • It discovers the general rules and principles governing languages.
21
Phonetics (语音学)
• It is the scientific study of speech sounds, including the articulation, transmission and reception of speech sounds, the description and classification of speech sounds. • [b] 双唇爆破辅音
• Linguistics differs from traditional grammar at least in three basic ways:
二语习得引论-读书笔记-chapter-1-2
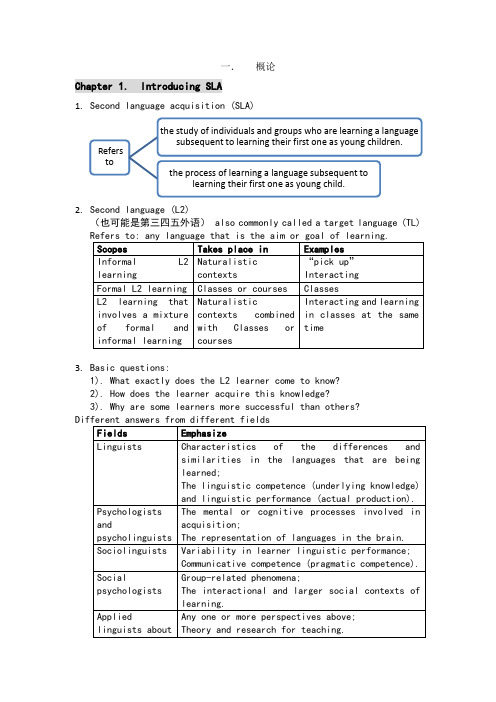
一.概论Chapter 1. Introducing SLA1.Second language acquisition (SLA)2.Second language (L2)(也可能是第三四五外语) also commonly called a target language (TL)3.Basic questions:1). What exactly does the L2 learner come to know?2). How does the learner acquire this knowledge?3). Why are some learners more successful than others?4.linguistic; psychological; social.Only one (x) Combine (√)Chapter 2. Foundations of SLAⅠ. The world of second languages1.Multi-; bi-; mono- lingualism1)Multilingualism: the ability to use 2 or more languages.(bilingualism: 2 languages; multilingualism: >2)2)Monolingualism: the ability to use only one language.3)Multilingual competence (Vivian Cook, Multicompetence)Refers to: the compound state of a mind with 2 or more grammars.4)Monolingual competence (Vivian Cook, Monocompetence)Refers to: knowledge of only one language.2.People with multicompetence (a unique combination) ≠ 2 monolingualsWorld demographic shows:3.Acquisition4.The number of L1 and L2 speakers of different languages can only beestimated.1)Linguistic information is often not officially collected.2)Answers to questions seeking linguistic information may not bereliable.3) A lack of agreement on definition of terms and on criteria foridentification.Ⅱ. The nature of language learning1.L1 acquisition1). L1 acquisition was completed before you came to school and thedevelopment normally takes place without any conscious effort.2). Complex grammatical patterns continue to develop through the1) Refers to: Humans are born with an innate capacity to learnlanguage.2) Reasons:♦Children began to learn L1 at the same age and in much the same way.♦…master the basic phonological and grammatical operations in L1 at 5/ 6.♦…can understand and create novel utterances; and are not limited to repeating what they have heard; the utterances they produce are often systematically different from those of the adults around them.♦There is a cut-off age for L1 acquisition.♦L1 acquisition is not simply a facet of general intelligence.3)The natural ability, in terms of innate capacity, is that part oflanguage structure is genetically “given” to every human child.3. The role of social experience1) A necessary condition for acquisition: appropriate socialexperience (including L1 input and interaction) is2) Intentional L1 teaching to children is not necessary and may havelittle effect.3) Sources of L1 input and interaction vary for cultural and socialfactors.4) Children get adequate L1 input and interaction→sources has littleeffect on the rate and sequence of phonological and grammatical development.The regional and social varieties (sources) of the input→pronunciationⅢ. L1 vs. L2 learningⅣ. The logical problem of language learning1.Noam Chomsky:1)innate linguistic knowledge must underlie language acquisition2)Universal Grammar2.The theory of Universal Grammar:Reasons:1)Children’s knowledge of language > what could be learned from theinput.2)Constraints and principles cannot be learned.3)Universal patterns of development cannot be explained bylanguage-specific input.Children often say things that adults do not.♦Children use language in accordance with general universal rules of language though they have not developed the cognitive ability to understand these rules. Not learned from deduction or imitation.♦Patterns of children’s language development are not directly determined by the input they receive.。
中医术语翻译

阳明病
yangbrightnessdisease
阳明经证
yangbrightnessmeridian
pattern
阳明腑证
yangbrightnessboweIpattern
阳明腑实证
YangbrightnessboweIexcess
pattern
阳明病
yangbrightnessdisease
阴虚火旺
YindeficiencywitheffuIgent
fire
五志(气)化火
fivee1ementstransforming
intofire
虚中央实
deficiencywithexcess
compIication
表虚里实
exteriordeficiencyandinteriorexcess
上虚下实
痰火扰心
phIegm-fireharassingtheheart
水气凌心
waterqiintimidatingthe
heart
风寒袭肺
wind-co1dassaiIingtheIung
风寒束肺
wind-coIdfetteringtheIung
肺热炽盛
intenseIungheat
pattern/syndrome
风寒束表
wind-co1dfetteringthe
exterior
风热犯表
wind-heatinvadingthe
exterior
暑湿袭表
summer-heatdampness
assaiIingtheexterior
卫表不固
defense-exteriorinsecurity
Part 4 social aspect
Michael Long’s Interaction Hypothesis
interaction
instruction
Learning
Input (i + 1)
Learned system
Acquisitim
output
Michael Long’s Interaction Hypothesis
Let’s recap…
• Although all theories of SLA acknowledge the need for input, they differ greatly in the importance that is attached to it. Views on input in language acquisition
The functions of motherese 1. An aid to communication 2. A language teaching aid 3. A socialization function Brown (1977): the primary motivation is “ to communicate, to understand and to be understood, to keep two minds focused on the same topic”. The effects of motherese • Little is known about the relationship between motherese and the route
科学史中“内史”与“外史”划分的消解——从科学知识社会学的立场看
Eliminate the Demarcation of Internal and External History in History of Science --From the Perspective
of SSK
作者: 刘兵[1];章梅芳[1]
作者机构: [1]清华大学人文社会科学学院,北京100084
出版物刊名: 清华大学学报:哲学社会科学版
页码: 132-138页
主题词: 科学史;科学知识社会学;内史;外史
摘要:自20世纪30年代以来,西方科学史在研究方法和解释框架上经历的一些变化和争论,大多涉及对“内史论”与“外史论”的界定、区分和评价。
就此问题,国内学者多以“内史”为重,一些关注“外史”的学者也往往坚持内外史的综合。
然而,在科学知识社会学看来,这种讨论的前提是坚持“内外史”的彼此对立存在,认为科学知识是社会建构的产物,要
求对科学知识的内容进行社会学分析。
由此科学观出发,独立于社会因素影响之外的、纯粹的
科学“内史”不复存在,“内史”与“外史”的界限相应地也被消解。
The interaction of internal and external information in a problem solving task
The Interaction of Internal and ExternalInformation in a Problem-Solving TaskJiajie ZhangDecember 1990Report 9005Department of Cognitive ScienceUniversity of California, San DiegoLa Jolla, California 92093This research was supported by a grant to Donald Norman and Edwin Hutchins from the Ames Research Center of the National Aeronautics & Space Agency, Grant NCC 2-591 in the Aviation Safety/Automation Program, technical monitor, Everett Palmer. Additional support was provided by funds from the Apple Computer Company and the Digital Equipment Corporation to the Affiliates of Cognitive Science at UCSD.This paper was developed in the environment of the Distributed Cognition Research Group led by Don Norman and Ed Hutchins. I am very grateful to Don Norman for his guidance and extensive conceptual and editorial help in every phase of this project. I thank Ed Hutchins for many inspiring comments and insights during and after these studies. Thanks are also extended to Mark St. John for many constructive criticisms on an early draft; David Kirsh, Tove Klausen, and Hank Strub for helpful discussions; and Richard Warren for his assistance in Experiments 2A and 2B. Requests for reprints should be sent to Jiajie Zhang, Department of Cognitive Science 0515; University of California, San Diego; La Jolla, California, 92093, USA. Email: jzhang@.Copyright © 1990 by Jiajie Zhang. All rights reserved.The Interaction of Internal and External Information in a Problem-Solving TaskJIAJIE ZHANG ABSTRACTIn these studies I examine the role of distributed cognition in problem solving. The major hypothesis explored is that intelligent behavior results from the interaction of internal cognition, external objects, and other people, where a distributed cognitive task can be represented as a set of modules, some internal and some external. The Tower of Hanoi problem is used as a concrete example for these studies. In Experiment 1 I ex-amine the effects of the distribution of rep-resentations among internal and external modules on problem-solving behavior. Experiments 2A and 2B focus on how the nature and number of rules affect problem-solving behavior. Experiment 3 investigates how a group’s problem-solving behavior is affected by the distribution of representations among the individuals. The results of all studies show that distributed cognitive activities are produced by the interaction among the representations in the modules involved in a given task: between internal and external representations and between internal representations. External representations are not peripheral aids. They are an indispensable part of cognition. Two of the factors determining the performance of a distributed cognitive system are the structure of the abstract task space and the distribution of representations across modules.INTRODUCTIONThe traditional approach to cognition in general and problem solving in particular focuses on an individual’s internal mental states. In the traditional view, representation and cognition are exclusively the activity of an internal mind. External objects, if they have anything to do with cognition at all, are at most peripheral aids. The cognitive properties of a group are solely determined by the structures internal to the individuals. There is no doubt that internal factors are important to cognition. They are not, however, the whole story. Much of a person’s intelligent behavior results from interactions with external objects and with other people. External and social factors also play critical roles in cognitive activities. Recently, cognitive scientists have started to address “distributed cognition,” the study of how cognitive activity is distributed across internal human minds, external cognitive artifacts, groups of people, and across space and time (Hutchins, 1990, in preparation; Hutchins & Norman, 1988; Norman, 1988, 1989, 1990). In the study of cognitive artifacts, Norman (1990) argues that artifacts not only enhance a person’s ability to perform a task, but theyalso change the nature of the task. In the study of the social organization of distributed cognition, Hutchins (1990) shows that social organizational factors often produce group properties that differ considerably from the properties of individuals.In this paper, I develop a framework, the modularity of representations, to analyze a set of distributed cognitive tasks, and to ex-plore the interactions among internal and external representations and among members of a group of people. I show that external objects are not simply peripheral aids— they provide a different form of representation. External representations are interwoven with internal representations to produce distributed cognitive activities. In addition, the share of knowledge among a set of modules is important for a system’s performance.Modularity of RepresentationsThe basic principle to be explored is that the representational system for a given task can be considered as a set, with some members internal and some external. Internal repre-sentations are in the mind, as propositions, mental images, or whatever (e.g., multipli-cation tables, arithmetic rules, logic, language, etc.). External representations are in the world, as physical symbols (e.g., written symbols, beads of an abacus, etc.) or as ex-ternal rules, constraints, or relations em-bedded in physical configurations (e.g., spa-tial relations of the items in a table, spatial configurations of the digits on a piece of pa-per, physical constraints in an abacus, etc.). The representations discussed in this paper are representations for tasks. In this sense, we can speak of not only internal represen-tations, which have their traditional meaning, but also external representations. For example, an external representation can represent the external part of the structure of a task. Generally, there are one or more internal and external representations involved in any task. Each representation is a relatively isolated functional unit in a specific medium. I call this unit, whether internal or external, a module.Figure 1 shows a representational system for a task with two internal and two external modules. Each internal module resides in a person’s mind and each external module resides in an external medium. The representations of internal and external modules involved in a given task together form a distributed representation space mapped to a single abstract task space that represents the properties of the problem. Each module sets some constraints on the abstract task space. The distributed repre-sentation space plays an important role in the studies reported here.The distributed cognition perspective demands the decomposition of the abstract task space into its internal and external components, because many cognitive tasks are distributed among internal and external modules. In the traditional studies of prob-lem solving, many abstract task spaces having internal and external components were mistakenly treated as solely internal task spaces. Generally speaking, the abstract task space of a task is not equivalent to its internal task space.The Tower of HanoiThe Tower of Hanoi problem1(Figure 2A) was chosen as a concrete example to study distributed cognitive activities in problem solving. The task of the Tower of Hanoi problem is to move all the disks from the left pole to the right pole, following two rules: Rule 1: Only one disk can be moved at a time.1 The disk sizes of the standard version of Tower of Hanoi are the reverse of those shown in Figure 2a: the largest disk is at the bottom and the smallest is at the top. The disk sizes have been reversed to make the experimental designs of all conditions consistent.Distributed Representation SpaceFIGURE 1. The distributed representation space and the abstract task space of a task with two internal and two ex-ternal modules. The abstract task space is formed by a combination of internal and external representations.Rule 2: A disk can only be moved to another pole on which it will be thelargest.The problem space for the Tower of Hanoi (Figure 2B) shows all possible states and legal moves. Each rectangle shows one of the 27 possible configurations of the three disks on the three poles. The lines between the rectangles show the transformations from one state to another when the rules are followed.The Tower of Hanoi is a well-studied problem (Hayes & Simon, 1977; Kotovsky & Fallside, 1988; Kotovsky, Hayes, & Simon, 1985; Simon & Hayes, 1976). Much of the research has focused on isomorphs of the Tower of Hanoi and their problem repre-sentations. The basic finding is that different problem representations can have dramatic impact on problem difficulty even if the formal structures are the same. External memory aid is one major factor of problem difficulty. Thus, Kotovsky et al. (1985) re-ported that the Dish-move isomorph of the Tower of Hanoi, in which all rules had to be remembered, was harder to solve than the Peg-move isomorph, in which one of the rules was embedded in physical configurations. Modifications of these two isomorphs were used in two of the three conditions in Experiment 1 of the present study (Waitress and Orange and Waitress and Donuts). Internal and External Rules. The Tower of Hanoi problem actually has three rules, not just the two stated earlier. Rule 3 is that only the largest disk on a pole can be transferred to another pole. In the representation shown in Figure 2A, Rule 3 need not be stated explicitly because the physical structure of the disks and poles coupled with Rules 1 and 2 guarantee that it will be followed. But if the(A)S1S2S3E3FIGURE 2. The Tower of Hanoi problem. (a) The task is to move all three disks from the left pole to the right pole. (b)The problem space of the Tower of Hanoi problem. Each rectangle shows one of the 27 possible configurations (states)of the three disks on the three poles. The lines between the rectangles show the transformations from one state to another when the rules are followed. S1, S2, and S3 are three starting states, and E1, E2, and E3 are three ending states. They will be used later.disks were not stacked on poles, explicit statement of Rule 3 would be necessary.In my studies I used four rules:22 The problems in Experiments 1 and3 were isomorphs of the standard Tower of Hanoi problem which only hasRule 1: Only one disk can be transferred at a time.Rule 2: A disk can only be transferred toa pole on which it will be the largest.Rule 3: Only the largest disk on a pole can be transferred to another pole.Rule 4: The smallest disk and the largest disk can not be placed on a single poleunless the medium-sized disk is alsoon that pole.Any of these four rules can be either in-ternal (memorized) or external (externalized into physical constraints).3 In the experiments that follow, I varied the numbers of external rules. In one condition, called Waitress and Oranges (Figure 5A), no rule is external. In a second condition, called Waitress and Donuts (Figure 5B), Rule 3 is external. In the Waitress and Coffee condition (Figure 5C), both Rules 2 and 3 are external. In the Waitress and Tea condition (Figure 7D), Rules 2, 3, and 4 are all external.Internal and External Problem Spaces. A problem space is composed of all possible states and all moves constrained by the rules. Figures 3A-F show the problem spaces constrained by Rules 1, 1+2, 1+3, 1+2+3, and 1+2+3+4, respectively.4 Lines with arrows are unidirectional. Lines without arrows are Rules 1, 2, and 3. Experiments 2A and 2B used all four rules.3 The rules written on the instruction sheets are not considered as external rules in the present study. These rules are internal in the sense that they are memorized by subjects before the games are played. Only those rules which are built into physical constraints and not told to the subjects are considered to be external.4 The four rules for the Tower of Hanoi are not fully orthogonal. Rules 2, 3, and 4 are orthogonal to one another, but Rules 2 and 3 are not orthogonal to Rule 1, because Rule 1 is the prerequisite of Rules 2 and 3 which are the restrictions on moving one object. When a problem solver’s task has rules which rely on other rules, its problem space can only be drawn in the context of the rules in which its rules rely.bidirectional. Note that the arrow lines in Figure 3B are in exactly opposite directions of those in Figure 3C. This implies that Rules 2 and 3 are complementary. One important point is that these five spaces can represent internal problem spaces, external problem spaces, or mixed problem spaces, depending upon how the rules constructing them are distributed across internal and external modules. A problem space constructed by external rules is an external problem space, one constructed by internal rules is an internal problem space, one constructed by a mixture of internal and external rules is a mixed problem space. Figure 3B is the internal problem space of the standard version of the Tower of Hanoi because Rules 1 and 2 are internal. If the physical constraints imposed by the disks themselves are such that only one can be moved at a time (i.e., the disks are large or heavy), then Figure 3C is its external problem space because under this cir-cumstance Rules 1 and 3 are both external. These two spaces form the distributed repre-sentation space of the Tower of Hanoi (Figure 4). The conjunction of these two spaces forms the abstract task space.Outline of the ExperimentsNormally, a cognitive task can be distributed among a set of internal and external modules. Experiment 1 examines the effects of the distribution of representations among internal and external modules on problem-solving behavior. By an analysis of the problem spaces in Figure 3 we can see that the problem space’s structure changes with the number of r u l e s.T h i s s t r u c t u r a l(a)(c) (d)FIGURE 3. Problem spaces constrained by five sets of rules. (a) Rule 1. (b) Rules 1+2. (c) Rules 1+3. (d) Rules 1+2+3. (e) Rules 1+2+3+4. They are derived from the problem space in Figure 2b. Lines with arrows are uni-directional. Lines without arrows are bi-directional. The rectangles (problem states) are not shown in this figure for the reason of clarity. (a)-(d) have the same 27 problem states as in Figure 2b. (e) only has 21 problem states, which are the outer 21 rectangles in Figure 2b.FIGURE 4. The distributed representation space and the abstract task space for the standard version of the Tower ofHanoi problem. The distributed representation space is composed of the internal and the external problem spaces,which are constrained by Rules 1+2 and Rules 1+3 (Rule 1 can be made external if the disks are big enough so that only one can be lifted at a time), respectively. The abstract task space is the conjunction of the internal and the external problem space.change might have an impact on the problem difficulty and, consequently, on problem-solving behavior. In addition, this impact, if any, might depend on the nature of the rules (internal or external). In Experiments 2A and 2B, the focus is on how the nature and number of rules affects problem solving behavior. A cognitive task can not only be distributed among internal and external modules, it can also be distributed among a set of internal modules. In Experiment 3, I investigate how a group’s problem-solving behavior is affected by the distribution of representations among the individuals.EXPERIMENT 1The standard Tower of Hanoi problem has three rules that can be distributed among internal and external modules. Different distributions may have different effects on problem-solving behavior, even if the formal structures are the same. Experiment 1investigates these effects. My hypothesis is that the more rules are distributed in external modules, the better the system’s performance.In addition, external rules might have some properties distinct from internal rules and hence change the behavior of a problem solver. There are three conditions, isomorphsWaitress and OrangesA strange, exotic restaurant requires everything to be done in a special manner. Here is an example. Three cus-tomers sitting at the counter each ordered an orange. The customer on the left ordered a large orange. The customer in the middle ordered a medium sized orange. And the customer on the right ordered a small orange. The waitress brought all three oranges in one plate and placed them all in front of the middle customer (as shown in Picture 1).Because of the exotic style of this restaurant, the waitress had to move the oranges to the proper customers follow-ing a strange ritual. No orange was allowed to touch the surface of the table . The waitress had to use only one hand to rearrange these three oranges so that each orange would be placed in the correct plate (as shown in Picture 2),following these rules:• Only one orange can be transferred at a time. (Rule 1 )• An orange can only be transferred to a plate in which it will be the largest. (Rule 2)• Only the largest orange in a plate can be transferred to another plate. (Rule 3)How would the waitress do this? That is, you solve the problem and show the movements of oranges the waitress hasto do to go from the arrangement shown in Picture 1 to the arrangement shown in Picture 2.Picture 1Picture 2(A)Picture 1Picture 1Picture 2(B) (C)FIGURE 5. (a) The complete instruction for the Waitress and Oranges (I123) condition. (b) The pictorial part of the instructions for the Waitress and Donuts (I12-E3) condition. (c) The pictorial part of the instructions for the Waitress and Coffee (I1-E23) condition.of the Tower of Hanoi, which correspond to three different distributions of the three rules between an internal and an external module. I made up three restaurant stories to explain the three conditions (see Figure 5).In the Waitress and Oranges (I123) con-dition, Rules 1, 2, and 3 were all internal (Figure 5A).In the Waitress and Donuts (I12-E3)condition, Rules 1 and 2 were internal, and Rule 3 was external. The physical constraints (coupled with Rules 1 and 2) guarantee that Rule 3 is followed. The verbal instructions for I12-E3 were the same as for I123, except that the word orange was replaced by the word donut and Rule 3 didn’t appear in the instructions. (The pictorial part of the instructions is shown in Figure 5B.)In the Waitress and Coffee (I1-E23) con-dition, Rule 1 was internal, and Rules 2 and 3were external. A smaller cup could not be placed on the top of a larger cup (Rule 2), as this would cause the coffee to spill. A cup could not be moved if there was another cup on top of it (Rule 3). The verbal part of the instructions for I1-E23 was the same as for I123, except that the word orange was re-placed by the words cup of coffee and Rules 2 and 3 didn’t appear in the instructions. (The pictorial part is shown in Figure 5C). MethodSubjects. The subjects were 18 undergraduate students enrolled in introductory psychology courses at the University of California, San Diego who volunteered for the experiment in order to earn course credit.Materials. In the I123 condition, three plastic orange balls of different sizes (small, medium, and large) and three porcelain plates were used. In the I12-E3 condition, three plastic rings of different sizes (small, medium, and large) and three plastic poles were used. In the I1-E23 condition, three plastic cups of different sizes (small, medium, and large) and three paper plates were used. All three cups were filled with coffee. The sizes of the cups were constrained such that a larger cup could be placed on the top of a smaller cup but not vice versa, in which case the coffee would spill.Design. This is a within-subject design. Each subject played all three games, one for each of the three conditions, once in a randomized order (e.g., I1-E23, I123, I12-E3). There were six possible permutations for the three games. Each permutation was assigned to a subject randomly. There were a total of eighteen subjects. Due to a limitation in the number of subjects available, the starting and ending positions were not randomized. That is, for each subject, the first, the second, and the third games always started at positions S1, S2, and S3 and ended at positions E1, E2, and E3, respectively (see Figure 2B). The starting and ending positions should not cause significient systematic deviation because the three pairs of starting and ending positions were exactly symmetric, and the order of the three games played by each subject were randomized.Procedure. Each subject was seated in front of a table and read the instructions aloud slowly. Then subjects were asked to turn the instruction sheet over and to attempt to repeat all the rules. If subjects could recite all the rules twice without error, they were instructed to start the games. Otherwise they reread the instructions and were again tested. The cycle continued until they reached the criterion. The goals were externalized by placing diagrams of the final states in front of subjects. Subjects’ hand movements and speech were monitored and recorded with a video camera. The solution time, which was from when the experimenter said “start” to when a subject finished the last move, were recorded by a timer synchronized with the video camera.ResultsThe average solution times, solution steps, and errors are shown in Table 1. The p values for the main effects and multiple comparisons are shown in Table 2. Problem difficulty measured in solution times, solution steps, and errors for the three problems was consistent. Problem difficulty was inversely proportional to the number of external rules used. The order of difficulty was, from hardest to easiest: I123 > I12-E3 ≥ I1-E23. The difference between I12-E3and I1-E23 was not statistically significant. All errors made were for internal rules; no errors made were for external rules (Table 3).TABLE 1. The Results of Experiment 1Conditions Measurements I123I12-E3I1-E23 Times (sec)131.083.053.9 Steps19.714.011.4 Errors 1.40.610.22TABLE 2. The p Values of Experiment 1Measurements Comparisons Times Steps Errors Main Effect< .05= .05< .005 I123 vs. I12-E3< .1< .1< .03 I123 vs. I1-E23< .01< .02= .001 I12-E3 vs. I1-E23> .3> .4> .2 NOTE: Fisher PLSD test was used for the multiple comparisons.TABLE 3. The Pattern of Errors in Experiment 1ConditionsRules I123I12-E3I1-E23 Rule 1104 Rule 210110 Rule 31400DiscussionTwo of the three conditions in this experi-ment, Waitress and Oranges (I123) and Waitress and Donuts (I12-E3), were modifi-cations of the Dish-move and Peg-move problems used by Kotovsky, Hayes, and Simon (1985), respectively. The results from the present study are consistent with their results: Subjects took more time to solve I123 than I12-E3. Kotovsky et al. only reported solution times in their study. The number of steps and errors in this study are all consistent with solution times. In this experiment, the more rules externalized, the easier the task. External representations are not just memory aids as claimed by Kotovsky et al. They have properties that are different from those of internal representations. The nature of external representations is discussed in the General Discussion section below, but one point worth mentioning here is that subjects made no errors for external rules. Rules, once externalized, seem to be error-proof.EXPERIMENT 2AExperiment 1 examined the effects of the distributions of representations between an internal and an external module on problem-solving behavior. Another factor affecting performance is the structure of problem space. Different number of rules gives rise to different problem space. Figure 3 shows that the problem space structure changes with the number of rules. How does the structural change of a problem change the difficulty of the problem and the behavior of a problemWaitress and OrangesA strange, exotic restaurant requires everything to be done in a special manner. Here is an example. Three cus-tomers sitting at the counter each ordered an orange. The customer on the left ordered a large orange. The customer in the middle ordered a medium sized orange. And the customer on the right ordered a small orange. The waitressbrought all three oranges in one plate and placed them all in front of the middle customer. Because of the exotic style of this restaurant, the waitress had to move the oranges to the proper customers following a strange ritual. No or-ange was allowed to touch the surface of the table. The waitress had to use only one hand to rearrange these three oranges so that each orange would be placed in the correct plate, following these rules:• Only one orange can be transferred at a time. (Rule 1)• Only the largest orange in a plate can be transferred to another plate. (Rule 3)• An orange can only be transferred to a plate in which it will be the largest. (Rule 2)• The small orange and the large orange can NOT be in a single plate the medium sized orange is also in that plate. (Rule 4)How would the waitress do this? That is, you solve the problem and show the movements of oranges the waitress has to do so that each customer will get his own orange.FIGURE 6. The instructions for Condition I1234 of Experiment 2A. The instructions for I123, I13, and I1 were exactly the same as for I1234, except that Rule 4 was absent in I123, Rules 2 and 4 absent in I13, and Rules 2, 3, and 4 absent in I1.solver? There are at least two rival factors involved. On the one hand, the fewer rules,the more paths there are from an initial state to a final state. Hence, fewer rules might make the problem easier. On the other hand,the more rules, the fewer the choices. The problem solver can simply follow where the highly constrained structure forces one to go.So, more rules might make the problem easier.My hypothesis is that the hardest problem is neither the one with the most nor the fewest rules, but one with an intermediate number of rules. Experiments 2A and 2B test this hypothesis, with Experiment 2A focusing on a change of internal rules and Experiment 2B on a change of external rules.Experiment 2A has four conditions, with four restaurant stories similar to those in Experiment 1. All rules were internal.Condition I1 has Rule 1, Condition I13 has Rules 1 and 3, Condition I123 has Rules 1, 2,and 3, and Condition I1234 has Rules 1, 2, 3,and 4. The instructions for Condition I1234are shown in Figure 6. The instructions for Conditions I123, I13, and I1 were exactly the same as for I1234, except that Rule 4 was ab-sent in I123, Rules 4 and 2 absent in I13, and Rules 4, 3, and 2 absent in I1.MethodSubjects . The subjects were 24 undergraduate students enrolled in introductory psychology courses at the University of California, San Diego, who volunteered for the experiment to earn course credit.Materials . Exactly the same materials used in the Waitress and Oranges problem in Experiment 1 were used in all four conditions of the present experiment.Design . Each subject played all four games,once each. There were 24 possible permuta-tions for the four games. The 24 subjects were assigned to these permutations randomly.Due to a limitation in the number of subjects available, the first, the second, the third, and the fourth games always started at positions S1, S2, S3, and S1 and ended at positions E1,E2, E3, and E1, respectively (see Figure 2B).This treatment should not cause significant systematic deviation because the task structures of the four problems each subject solved were different from each other, and the games were randomized.Procedure . The procedure was the same as in。
社会学理论的结构。特纳。第9章,中英对照
THE MICRO BASIS OF SOCIAL ORGANIZATION
Randall Collies has developed a conflict approachl that, at its core, is Weberian but that adds elements from Emile Durkheim's analysis of rituals, Erving Gofhnan's dramaturgy; (Chapter 24), conversation analysis within eth- nomethodology (Chapter 25), and other micro-level theoretical perspectives. Collins's argument is that macro-level phenomena are, ultimately, created and sustained by micro encounters among individuals.In essence, large and long-term social structures are built from what he terms interaction rituals that have been strung together over time in complex patterns., If true understandingof social reality is to be achieved sociological theorizing, what transpires in face-to-face interaction must be examined, even if this examination only involves sampling of interaction rituals within a macrostructure.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The Interaction of Internal and ExternalInformation in a Problem-Solving TaskJiajie ZhangDecember 1990Report 9005Department of Cognitive ScienceUniversity of California, San DiegoLa Jolla, California 92093This research was supported by a grant to Donald Norman and Edwin Hutchins from the Ames Research Center of the National Aeronautics & Space Agency, Grant NCC 2-591 in the Aviation Safety/Automation Program, technical monitor, Everett Palmer. Additional support was provided by funds from the Apple Computer Company and the Digital Equipment Corporation to the Affiliates of Cognitive Science at UCSD.This paper was developed in the environment of the Distributed Cognition Research Group led by Don Norman and Ed Hutchins. I am very grateful to Don Norman for his guidance and extensive conceptual and editorial help in every phase of this project. I thank Ed Hutchins for many inspiring comments and insights during and after these studies. Thanks are also extended to Mark St. John for many constructive criticisms on an early draft; David Kirsh, Tove Klausen, and Hank Strub for helpful discussions; and Richard Warren for his assistance in Experiments 2A and 2B. Requests for reprints should be sent to Jiajie Zhang, Department of Cognitive Science 0515; University of California, San Diego; La Jolla, California, 92093, USA. Email: jzhang@.Copyright © 1990 by Jiajie Zhang. All rights reserved.The Interaction of Internal and External Information in a Problem-Solving TaskJIAJIE ZHANG ABSTRACTIn these studies I examine the role of distributed cognition in problem solving. The major hypothesis explored is that intelligent behavior results from the interaction of internal cognition, external objects, and other people, where a distributed cognitive task can be represented as a set of modules, some internal and some external. The Tower of Hanoi problem is used as a concrete example for these studies. In Experiment 1 I ex-amine the effects of the distribution of rep-resentations among internal and external modules on problem-solving behavior. Experiments 2A and 2B focus on how the nature and number of rules affect problem-solving behavior. Experiment 3 investigates how a groupÕs problem-solving behavior is affected by the distribution of representations among the individuals. The results of all studies show that distributed cognitive activities are produced by the interaction among the representations in the modules involved in a given task: between internal and external representations and between internal representations. External representations are not peripheral aids. They are an indispensable part of cognition. Two of the factors determining the performance of a distributed cognitive system are the structure of the abstract task space and the distribution of representations across modules.INTRODUCTIONThe traditional approach to cognition in general and problem solving in particular focuses on an individualÕs internal mental states. In the traditional view, representation and cognition are exclusively the activity of an internal mind. External objects, if they have anything to do with cognition at all, are at most peripheral aids. The cognitive properties of a group are solely determined by the structures internal to the individuals. There is no doubt that internal factors are important to cognition. They are not, however, the whole story. Much of a personÕs intelligent behavior results from interactions with external objects and with other people. External and social factors also play critical roles in cognitive activities. Recently, cognitive scientists have started to address Òdistributed cognition,Ó the study of how cognitive activity is distributed across internal human minds, external cognitive artifacts, groups of people, and across space and time (Hutchins, 1990, in preparation; Hutchins & Norman, 1988; Norman, 1988, 1989, 1990). In the study of cognitive artifacts, Norman (1990) argues that artifacts not only enhance a personÕs ability to perform a task, but theyalso change the nature of the task. In the study of the social organization of distributed cognition, Hutchins (1990) shows that social organizational factors often produce group properties that differ considerably from the properties of individuals.In this paper, I develop a framework, the modularity of representations, to analyze a set of distributed cognitive tasks, and to ex-plore the interactions among internal and external representations and among members of a group of people. I show that external objects are not simply peripheral aidsÑ they provide a different form of representation. External representations are interwoven with internal representations to produce distributed cognitive activities. In addition, the share of knowledge among a set of modules is important for a systemÕs performance.Modularity of RepresentationsThe basic principle to be explored is that the representational system for a given task can be considered as a set, with some members internal and some external. Internal repre-sentations are in the mind, as propositions, mental images, or whatever (e.g., multipli-cation tables, arithmetic rules, logic, language, etc.). External representations are in the world, as physical symbols (e.g., written symbols, beads of an abacus, etc.) or as ex-ternal rules, constraints, or relations em-bedded in physical configurations (e.g., spa-tial relations of the items in a table, spatial configurations of the digits on a piece of pa-per, physical constraints in an abacus, etc.). The representations discussed in this paper are representations for tasks. In this sense, we can speak of not only internal represen-tations, which have their traditional meaning, but also external representations. For example, an external representation can represent the external part of the structure of a task. Generally, there are one or more internal and external representations involved in any task. Each representation is a relatively isolated functional unit in a specific medium. I call this unit, whether internal or external, a module.Figure 1 shows a representational system for a task with two internal and two external modules. Each internal module resides in a personÕs mind and each external module resides in an external medium. The representations of internal and external modules involved in a given task together form a distributed representation space mapped to a single abstract task space that represents the properties of the problem. Each module sets some constraints on the abstract task space. The distributed repre-sentation space plays an important role in the studies reported here.The distributed cognition perspective demands the decomposition of the abstract task space into its internal and external components, because many cognitive tasks are distributed among internal and external modules. In the traditional studies of prob-lem solving, many abstract task spaces having internal and external components were mistakenly treated as solely internal task spaces. Generally speaking, the abstract task space of a task is not equivalent to its internal task space.The Tower of HanoiThe Tower of Hanoi problem1(Figure 2A) was chosen as a concrete example to study distributed cognitive activities in problem solving. The task of the Tower of Hanoi problem is to move all the disks from the left pole to the right pole, following two rules: Rule 1: Only one disk can be moved at a time.1 The disk sizes of the standard version of Tower of Hanoi are the reverse of those shown in Figure 2a: the largest disk is at the bottom and the smallest is at the top. The disk sizes have been reversed to make the experimental designs of all conditions consistent.Distributed Representation SpaceFIGURE 1. The distributed representation space and the abstract task space of a task with two internal and two ex-ternal modules. The abstract task space is formed by a combination of internal and external representations.Rule 2: A disk can only be moved to another pole on which it will be thelargest.The problem space for the Tower of Hanoi (Figure 2B) shows all possible states and legal moves. Each rectangle shows one of the 27 possible configurations of the three disks on the three poles. The lines between the rectangles show the transformations from one state to another when the rules are followed.The Tower of Hanoi is a well-studied problem (Hayes & Simon, 1977; Kotovsky & Fallside, 1988; Kotovsky, Hayes, & Simon, 1985; Simon & Hayes, 1976). Much of the research has focused on isomorphs of the Tower of Hanoi and their problem repre-sentations. The basic finding is that different problem representations can have dramatic impact on problem difficulty even if the formal structures are the same. External memory aid is one major factor of problem difficulty. Thus, Kotovsky et al. (1985) re-ported that the Dish-move isomorph of the Tower of Hanoi, in which all rules had to be remembered, was harder to solve than the Peg-move isomorph, in which one of the rules was embedded in physical configurations. Modifications of these two isomorphs were used in two of the three conditions in Experiment 1 of the present study (Waitress and Orange and Waitress and Donuts). Internal and External Rules. The Tower of Hanoi problem actually has three rules, not just the two stated earlier. Rule 3 is that only the largest disk on a pole can be transferred to another pole. In the representation shown in Figure 2A, Rule 3 need not be stated explicitly because the physical structure of the disks and poles coupled with Rules 1 and 2 guarantee that it will be followed. But if the(A)S1S2S3E3FIGURE 2. The Tower of Hanoi problem. (a) The task is to move all three disks from the left pole to the right pole. (b)The problem space of the Tower of Hanoi problem. Each rectangle shows one of the 27 possible configurations (states)of the three disks on the three poles. The lines between the rectangles show the transformations from one state to another when the rules are followed. S1, S2, and S3 are three starting states, and E1, E2, and E3 are three ending states. They will be used later.disks were not stacked on poles, explicit statement of Rule 3 would be necessary.In my studies I used four rules:22 The problems in Experiments 1 and3 were isomorphs of the standard Tower of Hanoi problem which only hasRule 1: Only one disk can be transferred at a time.Rule 2: A disk can only be transferred toa pole on which it will be the largest.Rule 3: Only the largest disk on a pole can be transferred to another pole.Rule 4: The smallest disk and the largest disk can not be placed on a single poleunless the medium-sized disk is alsoon that pole.Any of these four rules can be either in-ternal (memorized) or external (externalized into physical constraints).3 In the experiments that follow, I varied the numbers of external rules. In one condition, called Waitress and Oranges (Figure 5A), no rule is external. In a second condition, called Waitress and Donuts (Figure 5B), Rule 3 is external. In the Waitress and Coffee condition (Figure 5C), both Rules 2 and 3 are external. In the Waitress and Tea condition (Figure 7D), Rules 2, 3, and 4 are all external.Internal and External Problem Spaces. A problem space is composed of all possible states and all moves constrained by the rules. Figures 3A-F show the problem spaces constrained by Rules 1, 1+2, 1+3, 1+2+3, and 1+2+3+4, respectively.4 Lines with arrows are unidirectional. Lines without arrows are Rules 1, 2, and 3. Experiments 2A and 2B used all four rules.3 The rules written on the instruction sheets are not considered as external rules in the present study. These rules are internal in the sense that they are memorized by subjects before the games are played. Only those rules which are built into physical constraints and not told to the subjects are considered to be external.4 The four rules for the Tower of Hanoi are not fully orthogonal. Rules 2, 3, and 4 are orthogonal to one another, but Rules 2 and 3 are not orthogonal to Rule 1, because Rule 1 is the prerequisite of Rules 2 and 3 which are the restrictions on moving one object. When a problem solverÕs task has rules which rely on other rules, its problem space can only be drawn in the context of the rules in which its rules rely.bidirectional. Note that the arrow lines in Figure 3B are in exactly opposite directions of those in Figure 3C. This implies that Rules 2 and 3 are complementary. One important point is that these five spaces can represent internal problem spaces, external problem spaces, or mixed problem spaces, depending upon how the rules constructing them are distributed across internal and external modules. A problem space constructed by external rules is an external problem space, one constructed by internal rules is an internal problem space, one constructed by a mixture of internal and external rules is a mixed problem space. Figure 3B is the internal problem space of the standard version of the Tower of Hanoi because Rules 1 and 2 are internal. If the physical constraints imposed by the disks themselves are such that only one can be moved at a time (i.e., the disks are large or heavy), then Figure 3C is its external problem space because under this cir-cumstance Rules 1 and 3 are both external. These two spaces form the distributed repre-sentation space of the Tower of Hanoi (Figure 4). The conjunction of these two spaces forms the abstract task space.Outline of the ExperimentsNormally, a cognitive task can be distributed among a set of internal and external modules. Experiment 1 examines the effects of the distribution of representations among internal and external modules on problem-solving behavior. By an analysis of the problem spaces in Figure 3 we can see that the problem spaceÕs structure changes with the number of r u l e s.T h i s s t r u c t u r a l(c)(d)(e)FIGURE 3. Problem spaces constrained by five sets of rules. (a) Rule 1. (b) Rules 1+2. (c) Rules 1+3. (d) Rules 1+2+3. (e) Rules 1+2+3+4. They are derived from the problem space in Figure 2b. Lines with arrows are uni-directional. Lines without arrows are bi-directional. The rectangles (problem states) are not shown in this figure for the reason of clarity. (a)-(d) have the same 27 problem states as in Figure 2b. (e) only has 21 problem states, which are the outer 21 rectangles in Figure 2b.FIGURE 4. The distributed representation space and the abstract task space for the standard version of the Tower ofHanoi problem. The distributed representation space is composed of the internal and the external problem spaces,which are constrained by Rules 1+2 and Rules 1+3 (Rule 1 can be made external if the disks are big enough so that only one can be lifted at a time), respectively. The abstract task space is the conjunction of the internal and the external problem space.change might have an impact on the problem difficulty and, consequently, on problem-solving behavior. In addition, this impact, if any, might depend on the nature of the rules (internal or external). In Experiments 2A and 2B, the focus is on how the nature and number of rules affects problem solving behavior. A cognitive task can not only be distributed among internal and external modules, it can also be distributed among a set of internal modules. In Experiment 3, I investigate how a groupÕs problem-solving behavior is affected by the distribution of representations among the individuals.EXPERIMENT 1The standard Tower of Hanoi problem has three rules that can be distributed among internal and external modules. Different distributions may have different effects on problem-solving behavior, even if the formal structures are the same. Experiment 1investigates these effects. My hypothesis is that the more rules are distributed in external modules, the better the systemÕs performance.In addition, external rules might have some properties distinct from internal rules and hence change the behavior of a problem solver. There are three conditions, isomorphsWaitress and OrangesA strange, exotic restaurant requires everything to be done in a special manner. Here is an example. Three cus-tomers sitting at the counter each ordered an orange. The customer on the left ordered a large orange. The custom in the middle ordered a medium sized orange. And the customer on the right ordered a small orange. The waitress brought all three oranges in one plate and placed them all in front of the middle customer (as shown in Picture 1).Because of the exotic style of this restaurant, the waitress had to move the oranges to the proper customers follow ing a strange ritual. No orange was allowed to touch the surface of the table . The waitress had to use only one hand to rearrange these three oranges so that each orange would be placed in the correct plate (as shown in Picture 2),following these rules:¥ Only one orange can be transferred at a time. (Rule 1 )¥ An orange can only be transferred to a plate in which it will be the largest. (Rule 2)¥ Only the largest orange in a plate can be transferred to another plate. (Rule 3)How would the waitress do this? That is, you solve the problem and show the movements of oranges the waitress hato do to go from the arrangement shown in Picture 1 to the arrangement shown in Picture 2.Picture 1Picture 2(A)Picture 1Picture 2Picture 1Picture 2(B) (C)FIGURE 5. (a) The complete instruction for the Waitress and Oranges (I123) condition. (b) The pictorial part of the instructions for the Waitress and Donuts (I12-E3) condition. (c) The pictorial part of the instructions for the Waitress and Coffee (I1-E23) condition.of the Tower of Hanoi, which correspond to three different distributions of the three rules between an internal and an external module. I made up three restaurant stories to explain the three conditions (see Figure 5).In the Waitress and Oranges (I123) con-dition, Rules 1, 2, and 3 were all internal (Figure 5A).In the Waitress and Donuts (I12-E3)condition, Rules 1 and 2 were internal, and Rule 3 was external. The physical constraints (coupled with Rules 1 and 2) guarantee that Rule 3 is followed. The verbal instructions for I12-E3 were the same as for I123, except that the word orange was replaced by the word donut and Rule 3 didnÕt appear in the instructions. (The pictorial part of the instructions is shown in Figure 5B.)In the Waitress and Coffee (I1-E23) con-dition, Rule 1 was internal, and Rules 2 and 3were external. A smaller cup could not be placed on the top of a larger cup (Rule 2), as this would cause the coffee to spill. A cup could not be moved if there was another cup on top of it (Rule 3). The verbal part of the instructions for I1-E23 was the same as for I123, except that the word orange was re-placed by the words cup of coffee and Rules 2 and 3 didnÕt appear in the instructions. (The pictorial part is shown in Figure 5C). MethodSubjects. The subjects were 18 undergraduate students enrolled in introductory psychology courses at the University of California, San Diego who volunteered for the experiment in order to earn course credit.Materials. In the I123 condition, three plastic orange balls of different sizes (small, medium, and large) and three porcelain plates were used. In the I12-E3 condition, three plastic rings of different sizes (small, medium, and large) and three plastic poles were used. In the I1-E23 condition, three plastic cups of different sizes (small, medium, and large) and three paper plates were used. All three cups were filled with coffee. The sizes of the cups were constrained such that a larger cup could be placed on the top of a smaller cup but not vice versa, in which case the coffee would spill.Design. This is a within-subject design. Each subject played all three games, one for each of the three conditions, once in a randomized order (e.g., I1-E23, I123, I12-E3). There were six possible permutations for the three games. Each permutation was assigned to a subject randomly. There were a total of eighteen subjects. Due to a limitation in the number of subjects available, the starting and ending positions were not randomized. That is, for each subject, the first, the second, and the third games always started at positions S1, S2, and S3 and ended at positions E1, E2, and E3, respectively (see Figure 2B). The starting and ending positions should not cause significient systematic deviation because the three pairs of starting and ending positions were exactly symmetric, and the order of the three games played by each subject were randomized.Procedure. Each subject was seated in front of a table and read the instructions aloud slowly. Then subjects were asked to turn the instruction sheet over and to attempt to repeat all the rules. If subjects could recite all the rules twice without error, they were instructed to start the games. Otherwise they reread the instructions and were again tested. The cycle continued until they reached the criterion. The goals were externalized by placing diagrams of the final states in front of subjects. SubjectsÕ hand movements and speech were monitored and recorded with a video camera. The solution time, which was from when the experimenter said ÒstartÓ to when a subject finished the last move, were recorded by a timer synchronized with the video camera.ResultsThe average solution times, solution steps, and errors are shown in Table 1. The p values for the main effects and multiple comparisons are shown in Table 2. Problem difficulty measured in solution times, solution steps, and errors for the three problems was consistent. Problem difficulty was inversely proportional to the number of external rules used. The order of difficulty was, from hardest to easiest: I123 > I12-E3 ≥ I1-E23. The difference between I12-E3and I1-E23 was not statistically significant. All errors made were for internal rules; no errors made were for external rules (Table 3).TABLE 1. The Results of Experiment 1Conditions Measurements I123I12-E3I1-E23 Times (sec)131.083.053.9 Steps19.714.011.4 Errors 1.40.610.22TABLE 2. The p Values of Experiment 1Measurements Comparisons Times Steps Errors Main Effect< .05= .05< .005 I123 vs. I12-E3< .1< .1< .03 I123 vs. I1-E23< .01< .02= .001 I12-E3 vs. I1-E23> .3> .4> .2 NOTE: Fisher PLSD test was used for the multiple comparisons.TABLE 3. The Pattern of Errors in Experiment 1ConditionsRules I123I12-E3I1-E23 Rule 1104 Rule 210110 Rule 31400DiscussionTwo of the three conditions in this experi-ment, Waitress and Oranges (I123) and Waitress and Donuts (I12-E3), were modifi-cations of the Dish-move and Peg-move problems used by Kotovsky, Hayes, and Simon (1985), respectively. The results from the present study are consistent with their results: Subjects took more time to solve I123 than I12-E3. Kotovsky et al. only reported solution times in their study. The number of steps and errors in this study are all consistent with solution times. In this experiment, the more rules externalized, the easier the task. External representations are not just memory aids as claimed by Kotovsky et al. They have properties that are different from those of internal representations. The nature of external representations is discussed in the General Discussion section below, but one point worth mentioning here is that subjects made no errors for external rules. Rules, once externalized, seem to be error-proof.EXPERIMENT 2AExperiment 1 examined the effects of the distributions of representations between an internal and an external module on problem-solving behavior. Another factor affecting performance is the structure of problem space. Different number of rules gives rise to different problem space. Figure 3 shows that the problem space structure changes with the number of rules. How does the structural change of a problem change the difficulty of the problem and the behavior of a problemWaitress and OrangesA strange, exotic restaurant requires everything to be done in a special manner. Here is an example. Three cus-tomers sitting at the counter each ordered an orange. The customer on the left ordered a large orange. The custom in the middle ordered a medium sized orange. And the customer on the right ordered a small orange. The waitress brought all three oranges in one plate and placed them all in front of the middle customer. Because of the exotic sty of this restaurant, the waitress had to move the oranges to the proper customers following a strange ritual. No or-ange was allowed to touch the surface of the table. The waitress had to use only one hand to rearrange these three oranges so that each orange would be placed in the correct plate, following these rules:¥ Only one orange can be transferred at a time. (Rule 1)¥ Only the largest orange in a plate can be transferred to another plate. (Rule 3)¥ An orange can only be transferred to a plate in which it will be the largest. (Rule 2)¥ The small orange and the large orange can NOT be in a single plate the medium sized orange is also in that plate. (Rule 4)How would the waitress do this? That is, you solve the problem and show the movements of oranges the waitress ha to do so that each customer will get his own orange.FIGURE 6. The instructions for Condition I1234 of Experiment 2A. The instructions for I123, I13, and I1 were exactly the same as for I1234, except that Rule 4 was absent in I123, Rules 2 and 4 absent in I13, and Rules 2, 3, and 4 absent in I1.solver? There are at least two rival factors involved. On the one hand, the fewer rules,the more paths there are from an initial state to a final state. Hence, fewer rules might make the problem easier. On the other hand,the more rules, the fewer the choices. The problem solver can simply follow where the highly constrained structure forces one to go.So, more rules might make the problem easier.My hypothesis is that the hardest problem is neither the one with the most nor the fewest rules, but one with an intermediate number of rules. Experiments 2A and 2B test this hypothesis, with Experiment 2A focusing on a change of internal rules and Experiment 2B on a change of external rules.Experiment 2A has four conditions, with four restaurant stories similar to those in Experiment 1. All rules were internal.Condition I1 has Rule 1, Condition I13 has Rules 1 and 3, Condition I123 has Rules 1, 2,and 3, and Condition I1234 has Rules 1, 2, 3,and 4. The instructions for Condition I1234are shown in Figure 6. The instructions for Conditions I123, I13, and I1 were exactly the same as for I1234, except that Rule 4 was ab-sent in I123, Rules 4 and 2 absent in I13, and Rules 4, 3, and 2 absent in I1.MethodSubjects . The subjects were 24 undergraduate students enrolled in introductory psychology courses at the University of California, San Diego, who volunteered for the experiment to earn course credit.Materials . Exactly the same materials used in the Waitress and Oranges problem in Experiment 1 were used in all four conditions of the present experiment.Design . Each subject played all four games,once each. There were 24 possible permuta-tions for the four games. The 24 subjects were assigned to these permutations randomly.Due to a limitation in the number of subjects available, the first, the second, the third, and the fourth games always started at positions S1, S2, S3, and S1 and ended at positions E1,E2, E3, and E1, respectively (see Figure 2B).This treatment should not cause significant systematic deviation because the task structures of the four problems each subject solved were different from each other, and the games were randomized.Procedure . The procedure was the same as in。
