高考数列公式总结

合集下载

2024高考数学数列知识点总结与题型分析

2024高考数学数列知识点总结与题型分析数列是高中数学中的重要内容，作为数学的一个分支，数列的掌握对于高考数学的考试非常关键。

在本文中，我们将对2024年高考数学数列的知识点进行总结，并分析可能出现的相关题型。

一、等差数列与等差数列的通项公式等差数列是数学中最常见的数列类型之一。

对于等差数列，首先要了解等差数列的概念：如果一个数列中任意两个相邻的项之差都相等，则称该数列为等差数列。

1.1 等差数列的通项公式等差数列的通项公式是等差数列中非常重要的一个公式，它可以用来求解等差数列中任意一项。

设等差数列的首项为$a_1$，公差为$d$，第$n$项为$a_n$，则等差数列的通项公式为：$a_n = a_1 + (n-1)d$1.2 等差数列的性质与常用公式等差数列有一些重要的性质与常用的公式，掌握这些性质与公式可以帮助我们更好地解决与等差数列相关的题目。

（1）等差数列中，任意三项可以构成一个等差数列。

（2）等差数列的前$n$项和公式为：$S_n = \frac{n}{2}(a_1 + a_n)$（3）等差数列的前$n$项和的差为：$S_n - S_m = (n-m+1)\frac{a_1 + a_{n+m}}{2}$二、等比数列与等比数列的通项公式等比数列也是数学中常见的数列类型之一。

与等差数列不同的是，等比数列中的任意两项的比值都相等。

2.1 等比数列的通项公式等比数列的通项公式可以用来求解等比数列中的任意一项。

设等比数列的首项为$a_1$，公比为$q$，第$n$项为$a_n$，则等比数列的通项公式为：$a_n = a_1 \cdot q^{(n-1)}$2.2 等比数列的性质与常用公式等比数列也有一些重要的性质与常用的公式，下面我们来了解一下：（1）等比数列中，任意三项可以构成一个等比数列。

（2）等比数列的前$n$项和公式为（$q\neq1$）：$S_n = \frac{a_1(1-q^n)}{1-q}$（3）当公比$q \neq 1$时，等比数列的前$n$项和与第$n$项的关系为：$S_n = \frac{a_nq - a_1}{q - 1}$三、数列题型分析与解题技巧在高考数学中，对于数列的考察主要包括以下几个方面：3.1 数列的递推关系与通项公式的应用常见的数列题目往往要求我们根据已知的递推关系或者通项公式来求解数列中的某一项或者求解前$n$项的和。

(完整版)高考数列公式总结

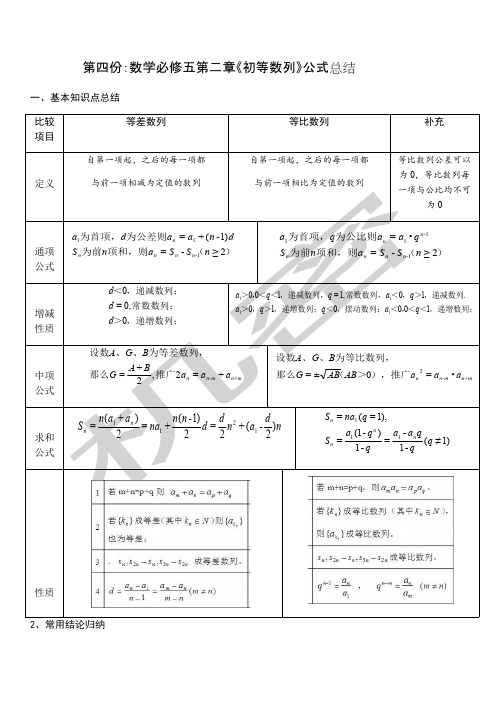
第四份：数学必修五第二章《初等数列》公式总结一、基本知识点总结aregoodfor 2、常用结论归纳ooso 1.{}{}1-21-2=nnnnnnnn TSbanbaTS项和，那么有的前、分别为等差数列、设2.常见的数列前n项和公式3.)8()6()5()4()2(=1+2•11an）（则4.构造法求数列通项公式（数量众多，此处仅为举例）(1)构造等比数列：形如的数列，可设，其中，那么qpaann+=1+)+(=+1+kapkann1-=pqk是公比为q的等比数列；举例，，则，则{}kan+1+2=1+nnaa1=,1=,2=kqp)1+(2=1+1+nnaa为公比为2的等比数列.{}1+na(2)构造等差数列：形如的数列，可以等式左右两边同时除以得，nnnpqpaa•+=1+np qpapannnn+=1-1+故，故数列是公差为q的等差数列.qpapannnn=-1-1+nnpad A l {}表示数列S n 1+2 5.累加法与累乘法举例：（1）累加法：左边加左边，右边加右边，最后把左右相同部分消除.举例：已知数列满足，求数列的通项公式。

{}n a 11211n n a a n a +=++=，{}n a （2）举例：。

等比数列数学公式高中有哪些

等比数列数学公式高中有哪些等比数列数学公式高中1、等比数列的通项公式是：An=A1__q^(n-1)2、前n项和公式是：Sn=[A1(1-q^n)]/(1-q)且任意两项am,an的关系为an=am·q^(n-m)3、从等比数列的定义、通项公式、前n项和公式可以推出：a1·an=a2·an-1=a3·an-2=…=ak·an-k+1,k∈{1,2,…,n}4、若m,n,p,q∈N__,则有：ap·aq=am·an,等比中项：aq·ap=2arar则为ap,aq等比中项.记πn=a1·a2…an,则有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1另外,一个各项均为正数的等比数列各项取同底数数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列.在这个意义下,我们说：一个正项等比数列与等差数列是“同构”的.性质：①若m、n、p、q∈N,且m+n=p+q,则am·an=ap__aq;②在等比数列中,依次每k项之和仍成等比数列.“G是a、b的等比中项”“G^2=ab(G≠0)”.在等比数列中,首项A1与公比q都不为零.数学答题技巧一、调整好状态，控制好自我。

高考数学解题技巧15篇保持清醒。

数学的考试时间在下午，建议同学们中午最好休息半个小时或一个小时，其间尽量放松自己，从心理上暗示自己：只有静心休息才能确保考试时清醒。

提前进入角色，考前做好准备。

按清单带齐一切用具，提前半小时到达考区，一方面可以消除紧张、稳定情绪、从容进场，另一方面也留有时间提前进入角色让大脑开始简单的数学活动，进入单一的数学情境。

如：1.清点一下用具是否带齐(笔、橡皮、作图工具、身份证、准考证等)。

2.把一些基本数据、常用公式、重要定理在脑子里过过电影。

3.最后看一眼难记易忘的知识点。

高考数学常用公式：数列

高考数学常用公式：数列等差数列
(1)数列的通项公式an=f(n)
(2)数列的递推公式
(3)数列的通项公式与前n项和的关系
an+1-an=d
an=a1+(n-1)d
a，A，b成等差2A=a+b
m+n=k+lam+an=ak+al
等比数列常用求和公式
an=a1qn_1
a，G，b成等比G2=ab
m+n=k+laman=akal
不等式
不等式的基本性质重要不等式
a>bb
a>b，b>ca>c
a>ba+c>b+c
a+b>ca>c-b
a>b，c>da+c>b+d
a>b，c>0ac>bc
a>b，c<0ac
a>b>0，c>d>0ac
a>b>0dn>bn(n∈Z，n>1)
a>b>0>(n∈Z，n>1)
(a-b)2≥0
a，b∈Ra2+b2≥2ab
|a|-|b|≤|a±b|≤|a|+|b|
证明不等式的基本方法
比较法
(1)要证明不等式a>b(或a
a-b>0(或a-b<0=即可
(2)若b>0，要证a>b，只需证明，
要证a
综合法综合法就是从已知或已证明过的不等式出发，根据不等式的性质推导出欲证的不等式(由因导果)的方法。

分析法分析法是从寻求结论成立的充分条件入手，逐步寻求所需条件成立的充分条件，直至所需的条件已知准确时为止，明显地表现出“持果索因”。

高职高考数列知识点归纳总结

高职高考数列知识点归纳总结一、等差数列等差数列是指一个数列中的任意两个相邻的项之差都相等的数列。

等差数列的通项公式为：an = a1 + (n-1)d，其中a1为首项，d为公差，n为项数。

1. 等差数列的概念及性质：- 定义：若数列{an}满足an+1 - an = d (常数d)，则称其为等差数列。

- 通项公式：an = a1 + (n-1)d。

- 项数公式：n = (an - a1)/d + 1。

- 末项公式：an = a1 + (n-1)d。

- 首项、公差和末项的关系：若已知首项a1、公差d和末项an，则有an = a1 + (n-1)d。

2. 常见问题及解答：- 如何判断一个数列是否为等差数列？答：判断数列中任意两个相邻的项之差是否相等，若相等，则该数列为等差数列。

- 如何确定等差数列的首项和公差？答：已知等差数列的前两项a1和a2，则公差d = a2 - a1，首项a1可通过通项公式an = a1 + (n-1)d求得。

- 如何求等差数列的项数？答：已知等差数列的首项a1、公差d和末项an，则项数n = (an -a1)/d + 1。

二、等比数列等比数列是指一个数列中的任意两个相邻的项之比都相等的数列。

等比数列的通项公式为：an = a1 * r^(n-1)，其中a1为首项，r为公比，n为项数。

1. 等比数列的概念及性质：- 定义：若数列{an}满足an+1 / an = r (常数r)，则称其为等比数列。

- 通项公式：an = a1 * r^(n-1)。

- 项数公式：n = log(r, (an / a1)) + 1。

2. 常见问题及解答：- 如何判断一个数列是否为等比数列？答：判断数列中任意两个相邻的项之比是否相等，若相等，则该数列为等比数列。

- 如何确定等比数列的首项和公比？答：已知等比数列的前两项a1和a2，则公比r = a2 / a1，首项a1可通过通项公式an = a1 * r^(n-1)求得。

高考数列基本公式是什么

高考数列基本公式是什么高考数列基本公式1、一般数列的通项an与前n项和Sn的关系：an=2、等差数列的通项公式：an=a1+(n-1)d an=ak+(n-k)d (其中a1为首项、ak为已知的第k项) 当d≠0时，an是关于n的一次式;当d=0时，an是一个常数。

3、等差数列的前n项和公式：当d≠0时，Sn是关于n的二次式且常数项为0;当d=0时(a1≠0)，Sn=na1是关于n的正比例式。

4、等比数列的通项公式： an= a1qn-1an= akqn-k(其中a1为首项、ak为已知的第k项，an≠0)5、等比数列的前n项和公式：当q=1时，Sn=n a1 (是关于n的正比例式);高考数学等差、等比数列的结论1、等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m- S3m、……仍为等差数列。

4、等比数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m- S3m、……仍为等比数列。

5、两个等差数列{an}与{bn}的和差的数列{an+bn}、{an-bn}仍为等差数列。

6、两个等比数列{an}与{bn}的积、商、倒数组成的数列7、等差数列{an}的任意等距离的项构成的数列仍为等差数列。

8、等比数列{an}的任意等距离的项构成的数列仍为等比数列。

9、三个数成等差数列的设法：a-d,a,a+d;四个数成等差的设法：a-3d,a-d,,a+d,a+3d10、三个数成等比数列的设法：a/q,a,aq;用构造数列方法求通项公式题目中若给出的是递推关系式，而用累加、累积、迭代等又不易求通项公式时，可以考虑通过变形，构造出含有 an(或Sn)的式子，使其成为等比或等差数列，从而求出an(或Sn)与n的关系，这是近一、二年来的高考热点，因此既是重点也是难点。

例：已知数列{an}中，a1=2，an+1=(--1)(an+2)，n=1,2,3,……(1)求{an}通项公式 (2)略解：由an+1=(--1)(an+2)得到an+1--= (--1)(an--)∴{an--}是首项为a1--，公比为--1的等比数列。

第四章数列(公式、定理、结论图表)--2023年高考数学必背知识手册(新教材)

第四章数列（公式、定理、结论图表）一．数列的概念：1.定义：数列是一个定义域为正整数集N*（或它的有限子集｛1,2，3，…，n｝）的特殊函数，数列的通项公式也就是相应函数的解析式。

2．数列是按一定顺序排列的一列数，记作,,,,321 n a a a a 简记{}n a .3．数列{}n a 的第n 项n a 与项数n 的关系若用一个公式)(n f a n =给出，则这个公式叫做这个数列的通项公式。

4．数列的项为当自变量由小到大依次取值时对应的一列函数值，它的图像是一群孤立的点。

5、数列的递推公式：表示任一项n a 与它的前一项1n a -（或前几项）间的关系的公式．6、求数列中最大最小项的方法：最大⎩⎨⎧≥≥-+11n n n n a a a a 最小⎩⎨⎧≤≤-+11n n n n a a a a 考虑数列的单调性二、等差数列1、定义：（1）文字表示：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，则这个数列称为等差数列，这个常数称为等差数列的公差．（2）符号表示：11(2)(1)n n n n a a d n a a d n -+-=≥-=≥或2、通项公式：若等差数列{}n a 的首项是1a ，公差是d ，则()11n a a n d =+-．通项公式的变形：①()n m a a n m d =+-；②n ma a d n m-=-．通项公式特点：1()n a d n a d =+-),为常数，（m k m kn a n +=是数列{}n a 成等差数列的充要条件。

3、等差中项若三个数a ，A ，b 组成等差数列，则A 称为a 与b 的等差中项．若2a cb +=，则称b 为a 与c 的等差中项．即a 、b 、c 成等差数列<=>2a cb +=4、等差数列{}n a 的基本性质),,,(*∈N q p n m 其中（1）q p n m a a a a q p n m +=++=+，则若。

等比数列数学高中公式有哪些

等比数列数学高中公式有哪些等比数列数学高中公式有哪些等比数列数学高中公式1、等比数列的通项公式是：An=A1__q^(n-1)2、前n项和公式是：Sn=[A1(1-q^n)]/(1-q)且任意两项am,an的关系为an=am·q^(n-m)3、从等比数列的定义、通项公式、前n项和公式可以推出：a1·an=a2·an-1=a3·an-2=。

=ak·an-k+1,k∈{1,2,。

,n}4、若m,n,p,q∈N__,则有：ap·aq=am·an,等比中项：aq·ap=2arar则为ap,aq等比中项.记πn=a1·a2。

an,则有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1另外,一个各项均为正数的等比数列各项取同底数数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列.在这个意义下,我们说：一个正项等比数列与等差数列是“同构”的.性质：①若m、n、p、q∈N,且m+n=p+q,则am·an=ap__aq;②在等比数列中,依次每k项之和仍成等比数列.“G是a、b的等比中项”“G^2=ab(G≠0)”.在等比数列中,首项A1与公比q都不为零.提高数学成绩的窍门一、课内重视听讲，课后及时复习。

新知识的接受，数学能力的培养主要在课堂上进行，所以要特点重视课内的学习效率，寻求正确的学习方法。

上课时要紧跟老师的思路，积极展开思维预测下面的步骤，比较自己的解题思路与教师所讲有哪些不同。

特别要抓住基础知识和基本技能的学习，课后要及时复习不留疑点。

首先要在做各种习题之前将老师所讲的知识点回忆一遍，正确掌握各类公式的推理过程，庆尽量回忆而不采用不清楚立即翻书之举。

认真独立完成作业，勤于思考，从某种意义上讲，应不造成不懂即问的学习作风，对于有些题目由于自己的思路不清，一时难以解出，应让自己冷静下来认真分析题目，尽量自己解决。

高中数学高考数列公式总结

第四份：数学必修五第二章《初等数列》公式总结比较项目等差数列等比数列补充定义自第一项起，之后的每一项都与前一项相减为定值的数列自第一项起，之后的每一项都与前一项相比为定值的数列等比数列公差可以为0，等比数列每一项与公比均不可为0通项公式）（项和，则为前为公差则为首项，2≥-=)1-(+=1-11n S S a n S d n a a d a n n n n n）（项和，则为前为公比则为首项，2≥-=•=1-1-11n S S a n S q a a q a n n n n n n增减性质，递增数列；＞常数数列；，递减数列；＜0,0=0d d d，递增数列；＜＜，＜，摆动数列；＜，递增数列；＞，＞，递减数列＞，＜常数数列，，递减数列，＜＜，＞100010.10,1=1001111q a q q a q a q q a中项公式mn m n n a a a BA GB G A +-+=2,2+=推广那么为等差数列，、、设数m n m n n a a a AB AB G B G A +-2•=0±=），推广＞（那么为等比数列，、、设数求和公式 nd a n d d n n na a a n S n n )2-(+2=2)1-(+=2)+(=1211)1≠(-1-=-1)-1(=),1=(=111q q qa a q q a S q na S n n n n性质1.{}{}1-21-2=n n n nnnnnT S b an b a T S 项和，那么有的前、分别为等差数列、设2.常见的数列前n 项和公式3.裂项相消法的运用公式：)tan tan -1)(-tan(=tan -tan )8(!-)!1+(=!•7......................lg -)+lg(=+lg )6()-+(1=++1)5()2+)(1+(1-)1+(121=)2+)(1+(1)4()+1-1(=)+()3.(....................).........1-1(21=•1)2(,+1-+1-=)+)(+(=1)+)(+(=1+1-1=1+1-1+1-1-1+...+41-31+31-21+21-1=)1+(1+)1-(1+...+4•31+3•21+2•11,1+1-1)1+(1,1+1-1=)1+(1=2+1+βαβαβαn n n n n k n nkn n k n k k n n n n n n n n n k n n k A k n n A a a d a a CAn B An B C k C An B An k a C An B An ka n n n n n n n n n n n n n n S n n n a n n n n n n n n 三角函数形式：）阶乘数列：（对数形式：根式数列：）（三重分式：分式数列：等差数列：继而求和）（）（的数列裂项公式：到形如受此启发：我们可以得则裂项为方法是项和的前举例：求数列4.构造法求数列通项公式（数量众多，此处仅为举例） (1)构造等比数列：形如qpa a n n +=1+的数列，可设)+(=+1+k a p k a n n ，其中1-=p qk ，那么{}k a n +是公比为q 的等比数列；举例1+2=1+n n a a ， 1=,1=,2=k q p ，则)1+(2=1+1+n n a a ，则{}1+na 为公比为2的等比数列. (2)构造等差数列：形如n n n p q pa a •+=1+的数列，可以等式左右两边同时除以n p 得q p a p a n nn n +=1-1+，故q p a p a n n n n =-1-1+，故数列nnp a 是公差为q 的等差数列.5.累加法与累乘法举例：（2）累乘法：每个是式子都写出来，全部乘起来，最后把相同的消除.举例：已知数列{}n a 满足11(2)n n a n n a +=+≥，求该数列通项公式13222122![(1)43].2n n n n n a a a n a a n n a a a a a ---=⋅⋅⋅⋅=-⋅⋅⨯=L L 每个都写出来，依次乘起来得到：（1）累加法：左边加左边，右边加右边，最后把左右相同部分消除. 举例：已知数列{}n a 满足11211n n a a n a +=++=，，求数列{}n a 的通项公式。

等差等比数列求和公式(2024高考必考)

等差等比数列求和公式（2024高考必考）等比数列求和公式通项公式 an=a1×q^(n-1)求和公式 a1(1-q^n)/(1-q)Sn=a1(1-q^n)/(1-q)(q≠1)求和公式推导(1)Sn=a1+a2+a3+...+an(公比为q)(2)qSn=a1q + a2q + a3q +...+ anq = a2+ a3+ a4+...+ an+ a(n+1)(3)Sn-qSn=(1-q)Sn=a1-a(n+1)(4)a(n+1)=a1q^n(5)Sn=a1(1-qn)/(1-q)(q≠1)等差数列求和公式Sn=n(a1+an)/2Sn=na1+n(n-1)d/2=dn^2/2+(a1-d/2)n末项=首项+(项数-1)×公差项数=(末项-首项)÷公差+1首项=末项-(项数-1)×公差和=(首项+末项)×项数÷2末项:最后一位数首项:第一位数项数:一共有几位数和:求一共数的总和高中数学学习方法明晰概念高中数学中的概念是比较严谨的，各个定义间都有很强的逻辑联系，逐个理解后就应把概念记牢，高考的选择题会涉及这方面的内容，而某些解答题也会由于概念定义所限而由繁变简，掌握好概念之后，有利于基础打牢，要做到“明晰”，关键是要多查书，勤查书，不要一知半解。

刻苦练习熟能生巧，对数学而言，也是如此。

做题能提高对题型的熟识度，对技巧的熟识度，以及计算的准确度。

而以上这些，会大大提高解题速度和准确率。

而练习，也是要掌握方法的，习题太易，会使人生厌;习题太难，会让人胆怯。

调整状态状态对于考生来讲，非常重要，考试中状态的差异，会带来成绩上巨大的波动。

一般考前一段时间，老师会发很多练习以强化训练，而实际上，状态的调整因人而异。

有的人在训练之后对题目很厌烦，即使在考场上题目会做，往往草草收笔，过程简略，以致痛失步骤分;有的人训练得不够时，找不到做题的感觉，思维僵了，愣是解不出本在自己实力范围之内的题。

高三数学知识点归纳公式大全总结

高三数学知识点归纳公式大全总结高三是学生们备战高考的决战之年，在这个阶段，数学作为一门重要的学科，占据着学生们学习的重要部分。

为了帮助同学们更好地复习数学知识，下面将对高三数学知识点进行归纳和总结，提供一些常用的公式作为参考，希望对同学们有所帮助。

一、数列和数列的通项公式数列是由若干项依照一定规律排列而成的序列，而数列的通项公式则是描述数列的每一项与项号之间的关系的公式。

常见的数列包括等差数列、等比数列和斐波那契数列。

1. 等差数列的通项公式等差数列是指数列中相邻两项之差恒定的数列。

其通项公式为：An = A1 + (n-1)d其中，An为第n项，A1为第一项，d为公差。

2. 等比数列的通项公式等比数列是指数列中相邻两项之比恒定的数列。

其通项公式为：An = A1 * q^(n-1)其中，An为第n项，A1为第一项，q为公比。

3. 斐波那契数列的通项公式斐波那契数列是一个特殊的数列，其前两项均为1，从第三项开始，每一项都等于前两项之和。

其通项公式为：Fn = Fn-1 + Fn-2其中，Fn为第n项，Fn-1为第n-1项，Fn-2为第n-2项。

二、函数与方程函数和方程是数学中的重要概念，掌握了函数和方程的性质和求解方法，就能更好地解决数学问题。

1. 一次函数的一般式及斜率公式一次函数可以用一般式表示为：y = ax + b其中，a为斜率，b为截距。

一次函数的斜率公式为：a = (y2 - y1) / (x2 - x1)其中，(x1, y1)和(x2, y2)为直线上两点的坐标。

2. 二次函数的顶点坐标及对称轴公式二次函数的标准形式为：y = ax^2 + bx + c其中，a、b、c为常数，a≠0。

二次函数的顶点坐标公式为：顶点坐标为：(h, k)其中，h = -b / (2a)，k = f(h) = ah^2 + bh + c。

二次函数的对称轴公式为：x = h其中，h为顶点的横坐标。

3. 二次方程的求根公式二次方程一般形式为：ax^2 + bx + c = 0二次方程的求根公式为：x = (-b ± √(b^2 - 4ac)) / (2a)其中，±表示两个解，即正负号分别取一次。

高考数学复习知识点：数学数列公式大全

2019高考数学复习知识点：数学数列公式大全2019高考各科复习资料2019年高三开学已经有一段时间了，高三的同学们是不是已经投入了紧张的高考一轮复习中，数学网高考频道从高三开学季开始为大家系列准备了2019年高考复习，2019年高考一轮复习，2019年高考二轮复习，2019年高考三轮复习都将持续系统的为大家推出。

一、高中数列基本公式：1、一般数列的通项an与前n项和Sn的关系：an=2、等差数列的通项公式：an=a1+(n-1)d an=ak+(n-k)d (其中a1为首项、ak为已知的第k项) 当d≠0时，an是关于n 的一次式;当d=0时，an是一个常数。

3、等差数列的前n项和公式：Sn=Sn=Sn=当d≠0时，Sn是关于n的二次式且常数项为0;当d=0时(a1≠0)，Sn=na1是关于n的正比例式。

4、等比数列的通项公式： an= a1 qn-1 an= ak qn-k (其中a1为首项、ak为已知的第k项，an≠0)5、等比数列的前n项和公式：当q=1时，Sn=n a1 (是关于n的正比例式);当q≠1时，Sn=Sn=三、高中数学中有关等差、等比数列的结论1、等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等差数列。

2、等差数列{an}中，若m+n=p+q，则3、等比数列{an}中，若m+n=p+q，则4、等比数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等比数列。

5、两个等差数列{an}与{bn}的和差的数列{an+bn}、{an-bn}仍为等差数列。

6、两个等比数列{an}与{bn}的积、商、倒数组成的数列{anbn}、仍为等比数列。

7、等差数列{an}的任意等距离的项构成的数列仍为等差数列。

8、等比数列{an}的任意等距离的项构成的数列仍为等比数列。

9、三个数成等差数列的设法：a-d,a,a+d;四个数成等差的设法：a-3d,a-d,,a+d,a+3d10、三个数成等比数列的设法：a/q,a,aq;四个数成等比的错误设法：a/q3,a/q,aq,aq3 (为什么?)11、{an}为等差数列，则(c0)是等比数列。

高考数列公式总结

）（项和，则为前为公差则为首项，2≥-=)1-(+=1-11n S S a n S d n a a d a n n n n n ）（项和，则为前为公比则为首项，2≥-=•=1-1-11n S S a n S q a a q a n n n n n n ，递增数列；＞常数数列；，递减数列；＜0,0=0d d d mn m n n a a a BA GB G A +-+=2,2+=推广那么为等差数列，、、设数mn m n n a a a AB AB G B G A +-2•=0±=），推广＞（那么为等比数列，、、设数第四份：数学必修五第二章《初等数列》公式总结一、基本知识点总结比较项目等差数列等比数列补充定义自第一项起，之后的每一项都与前一项相减为定值的数列自第一项起，之后的每一项都与前一项相比为定值的数列等比数列公差可以为0，等比数列每一项与公比均不可为0通项公式增减性质，递增数列；＜＜，＜，摆动数列；＜，递增数列；＞，＞，递减数列＞，＜常数数列，，递减数列，＜＜，＞100010.10,1=1001111q a q q a q a q q a中项公式求和公式 n da n d d n n na a a n S n n )2-(+2=2)1-(+=2)+(=1211)1≠(-1-=-1)-1(=),1=(=111q qqa a q q a S q na S n n n n 性质二、常用结论归纳1.{}{}1-21-2=nnnnnnnn TSbanbaTS项和，那么有的前、分别为等差数列、设2.常见的数列前n项和公式3.裂项相消法的运用公式：)tantan-1)(-tan(=tan-tan)8(!-)!1+(=!•7......................lg-)+lg(=+lg)6()-+(1=++1)5()2+)(1+(1-)1+(121=)2+)(1+(1)4()+1-1(=)+()3.(....................).........1-1(21=•1)2(,+1-+1-=)+)(+(=1)+)(+(=1+1-1=1+1-1+1-1-1+...+41-31+31-21+21-1=)1+(1+)1-(1+...+4•31+3•21+2•11,1+1-1)1+(1,1+1-1=)1+(1=2+1+βαβαβαnnnnnknnknnknkknnnnnnnnnknnkAknnAaadaaCAnBAnBCkCAnBAnkaCAnBAnkannnnnnnnnnnnnnSnnnannnnnnnn三角函数形式：）阶乘数列：（对数形式：根式数列：）（三重分式：分式数列：等差数列：继而求和）（）（的数列裂项公式：到形如受此启发：我们可以得则裂项为方法是项和的前举例：求数列4.构造法求数列通项公式（数量众多，此处仅为举例）(1)构造等比数列：形如qpaann+=1+的数列，可设)+(=+1+kapkann，其中1-=pqk，那么{}kan+是公比为q的等比数列；举例1+2=1+nnaa，1=,1=,2=kqp，则)1+(2=1+1+nnaa，则{}1+n a为公比为2的等比数列.{}项和的前表示数列nn S n 1+21+213222122![(1)43].2n n n n n a a a n a a n n a a a a a ---=⋅⋅⋅⋅=-⋅⋅⨯=(2)构造等差数列：形如n n n p q pa a •+=1+的数列，可以等式左右两边同时除以n p 得q p a p a n nn n +=1-1+，故qp a p a n n n n =-1-1+，故数列nnp a 是公差为q 的等差数列.5.累加法与累乘法举例：（1）累加法：左边加左边，右边加右边，最后把左右相同部分消除. 举例：已知数列{}n a 满足11211n n a a n a +=++=，，求数列{}n a 的通项公式。

高考数列知识点细目表

高考数列知识点细目表一、等差数列1. 等差数列的定义：若数列 a1, a2, a3, ... 满足 a_(n+1) - a_n = d，其中 d 为常数，则称该数列为等差数列。

2. 等差数列的通项公式：an = a1 + (n-1)d，其中 a1 为首项，d为公差。

3. 等差数列的前 n 项和公式：Sn = (n/2)(2a1 + (n-1)d)，其中 Sn 表示前 n 项和。

4. 等差数列的性质：首项与末项的和等于中间各项之和的两倍：a1 + an = a2 + a_n-1 = ... = (n/2)(a1 + an)。

二、等比数列1. 等比数列的定义：若数列 a1, a2, a3, ... 满足 a_(n+1) / a_n = q，其中 q 为常数，则称该数列为等比数列。

2. 等比数列的通项公式：an = a1 * q^(n-1)，其中 a1 为首项，q为公比。

3. 等比数列的前 n 项和公式（当q ≠ 1）：Sn = a1 * (q^n - 1) / (q - 1)，其中 Sn 表示前 n 项和。

4. 等比数列的性质：任意一项等于其前一项乘以公比：an =a_(n-1) * q。

三、公差和公比的关系1. 对于等差数列和等比数列，若形成了一个新的数列，其通常记为 b1, b2, b3, ...，则有如下关系：- 当 b_(n+1) - b_n = c1 时，c1 为公差的差数列，其首项为 d，公差为 0。

- 当 b_(n+1) / b_n = c2 时，c2 为公比的比值数列，其首项为 q，公比为 1。

四、数列问题的应用1. 等差数列的应用- 计算连续整数的和：当公差为 1 时，连续整数的和可以表示为 n(n+1)/2。

- 求解速度、加速度等变化规律：当问题中存在等差关系时，可以通过设定未知数和列方程来求解。

2. 等比数列的应用- 计算复利：当公比为 1 + r（其中 r 为利率）时，等比数列可以用于计算复利的金额。

数列高考知识点大全总结

数列高考知识点大全总结一、数列的概念1. 数列的定义数列是由一系列有限或无限个数按照一定的顺序排列组成的。

用数学语言描述就是一个由实数构成的序列。

一般用字母或符号表示，如{an}、{bn}等。

2. 数列中的相关概念（1）通项公式：数列中的第n个数的一般表达式，通常用an表示。

（2）前n项和：数列前n项的和，通常用Sn表示。

3. 数列的分类（1）等差数列：若数列中相邻两项的差恒定，称其为等差数列。

其通项公式为an=a1+(n-1)d。

（2）等比数列：若数列中相邻两项的比恒定，称其为等比数列。

其通项公式为an=a1*q^(n-1)。

（3）常数数列：数列中的每一项都相等的数列称为常数数列。

二、数列的性质1. 数列的有界性（1）有界数列：当数列中的数有上界和下界时，称其为有界数列。

（2）无界数列：当数列中的数没有上界和下界时，称其为无界数列。

2. 数列的单调性若数列中的每一项都满足an≤an+1或者an≥an+1时，称其为单调递增数列或者单调递减数列。

3. 数列的性质（1）数列的线性组合：若an和bn是两个数列，k和m是任意常数，那么k*an+m*bn 也是一个数列。

（2）数列的绝对值：若an是一个数列，那么|an|也是一个数列。

三、常见数列1. 等差数列（1）性质：等差数列的前n项和Sn=a1*n+n(n-1)d/2。

（2）求通项公式：an=a1+(n−1)d。

（3）常用公式：Sn=n/2(a1+an)。

2. 等比数列（1）性质：等比数列的前n项和Sn=a1*(q^n-1)/(q-1)，|q|>1。

（2）求通项公式：an=a1*q^(n-1)。

（3）常用公式：Sn=a1*(q^n-1)/(q-1)。

3. 斐波那契数列（1）定义：斐波那契数列是一个典型的递推数列，前两项都为1，从第三项开始，每一项都等于前两项之和。

（2）通项公式：an=f(n)=f(n-1)+f(n-2)。

（3）性质：斐波那契数列是一个无界数列。

高考数列知识点归纳总结

高考数列知识点归纳总结一、等差数列等差数列是指数列中任意两项之间的差值恒定的数列。

常用的表示方式是：a，a + d，a + 2d，a + 3d...，其中a为首项，d为公差。

1. 等差数列的通项公式为了快速计算等差数列中任意一项的数值，我们可以使用通项公式。

对于等差数列{an}，其通项公式为：an = a + (n - 1)d其中，an表示第n项的值，a为首项，d为公差。

2. 等差数列的前n项和公式等差数列的前n项和可以通过求和公式来计算，公式为：Sn = (n/2)(a + l)其中，Sn表示前n项和，n为项数，a为首项，l为末项。

3. 等差数列性质等差数列具有以下性质：- 任意三项成等差数列，当且仅当它们的差值相等。

- 等差数列中，如果知道了首项、末项和项数，就可以计算出公差。

或者前n项和。

二、等比数列等比数列是指数列中任意两项之间的比值恒定的数列。

常用的表示方式是：a，ar，ar^2，ar^3...，其中a为首项，r为公比。

1. 等比数列的通项公式为了快速计算等比数列中任意一项的数值，我们可以使用通项公式。

对于等比数列{an}，其通项公式为：an = ar^(n-1)其中，an表示第n项的值，a为首项，r为公比。

2. 等比数列的前n项和公式等比数列的前n项和可以通过求和公式来计算，公式为：Sn = a(r^n - 1) / (r - 1)其中，Sn表示前n项和，n为项数，a为首项，r为公比。

3. 等比数列性质等比数列具有以下性质：- 任意三项成等比数列，当且仅当它们的比值相等。

- 等比数列中，如果知道了首项、末项和项数，就可以计算出公比。

或者前n项和。

三、数列的求和运算在高考数学中，常常会遇到需要计算数列前n项和的情况。

数列的求和运算可以通过特定的公式或者方法来实现。

1. 等差数列的求和等差数列的前n项和可以通过求和公式来计算，公式为：Sn = (n/2)(a + l)其中，Sn表示前n项和，n为项数，a为首项，l为末项。

高中数学数列知识点归纳

高中数学数列知识点归纳摘要：一、数列的定义与性质1.等差数列的定义与性质2.等比数列的定义与性质二、数列的求和公式1.等差数列的前n 项和公式2.等比数列的前n 项和公式三、数列的应用1.高考数学中数列的知识点考察2.数列在实际问题中的应用正文：高中数学数列知识点归纳数列是高中数学中的一个重要知识点，它在历年的高考中都占有重要的地位。

本文将对数列的定义、性质、求和公式以及应用进行归纳总结。

一、数列的定义与性质1.等差数列的定义与性质等差数列是指一个数列，它的相邻两项之差是一个常数，这个常数称为公差。

等差数列的通项公式为：an = a1 + (n-1)d，其中a1 是首项，d 是公差，n 是项数。

等差数列的前n 项和公式为：sn = n/2 * (a1 + an) = n/2 * (2a1 + (n-1)d)。

2.等比数列的定义与性质等比数列是指一个数列，它的相邻两项之比是一个常数，这个常数称为公比。

等比数列的通项公式为：an = a1 * q^(n-1)，其中a1 是首项，q 是公比，n 是项数。

等比数列的前n 项和公式为：sn = a1 * (1 - q^n) / (1 - q)，当q = 1 时，等比数列变为等差数列。

二、数列的求和公式1.等差数列的前n 项和公式等差数列的前n 项和公式为：sn = n/2 * (a1 + an) = n/2 * (2a1 + (n-1)d)。

2.等比数列的前n 项和公式等比数列的前n 项和公式为：sn = a1 * (1 - q^n) / (1 - q)，当q = 1 时，等比数列变为等差数列。

三、数列的应用1.高考数学中数列的知识点考察高考数学中，数列是一个重要的考点，主要考察等差数列和等比数列的性质、通项公式、前n 项和公式，以及数列的求和、递推关系、极限等。

2.数列在实际问题中的应用数列在实际问题中有很多应用，如在金融领域，等比数列可以用来计算复利的未来值；在生物领域，等差数列可以用来描述种群数量的增长；在物理领域，等差数列可以用来描述匀速运动的速度等。

2024年高考数学数列易错知识点总结

2024年高考数学数列易错知识点总结在2024年高考中，数学数列是一个常见的考点，也是一道容易出错的题型。

为了帮助考生顺利应对数列相关的考试题目，下面总结了一些常见的易错知识点。

一、等差数列的通项公式：等差数列是指数列中任意两项之间的差相等的数列。

它的通项公式为：$a_n = a_1 + (n-1)d$。

对于等差数列来说，考生容易犯的错误有：1. 弄混公差和公比。

公差指的是等差数列中任意两项之间的差，公比指的是等比数列中任意两项之间的比值。

考生在计算等差数列的时候，应该注意区分这两个概念。

2. 弄混首项和通项。

首项指的是数列中的第一项，通项指的是数列中第n项的表达式。

在计算等差数列的时候，考生应该注意首项和通项的区别。

3. 对于计算等差数列的题目，考生有时会直接套用公式，而忽略对问题的分析和推理。

在解题过程中，不应只关注于公式的使用，还应注重思考问题的本质，并结合实际情况进行合理的推理和分析。

二、等差数列的前n项和公式：等差数列的前n项和公式为：$S_n = \\frac{n}{2}(a_1 +a_n)$。

在计算等差数列前n项和的过程中，考生容易犯的错误有：1. 弄混首项和末项。

求前n项和的公式中，首项$a_1$和末项$a_n$都是需要用到的。

考生容易弄混这两个项，在计算过程中应该注意清楚。

2. 计算公式时漏写除以2。

前n项和的公式是$\\frac{n}{2}(a_1 + a_n)$，但考生在计算的时候经常漏写除以2的操作，导致结果错误。

3. 求前n项和时，考生有时对问题的理解不准确。

在一些应用题中，需要根据题目给出的条件和要求来求解前n项和。

考生如果对问题的理解不准确，很容易在计算过程中出错。

三、等比数列的通项公式：等比数列是指数列中任意两项之间的比值相等的数列。

它的通项公式为：$a_n = a_1 \\times q^{(n-1)}$。

对于等比数列来说，考生容易犯的错误有：1. 弄混公比和公差。

2024年高考数学数列易错知识点总结

2024年高考数学数列易错知识点总结（____字）数列是高中数学中的重要内容之一，也是高考数学中的必考内容。

在2024年的高考中，关于数列的考点可能会有一些易错的地方，下面我将对2024年高考数学中数列的易错知识点进行总结。

一、概念和性质1. 数列的概念数列是指按照一定规律排列的一列数，数列中的每一个数称为数列的项。

数列可以用通项公式表示，例如等差数列的通项公式为an=a1+(n-1)d，等比数列的通项公式为an=a1*r^(n-1)，其中a1为首项，d为公差（等差数列）或公比（等比数列），n为项数。

2. 数列的递推公式数列的递推公式是指通过前一项和公式推导出后一项的公式，例如等差数列的递推公式为an=an-1+d，等比数列的递推公式为an=an-1*r。

3. 数列性质的判断判断一个数列是等差数列还是等比数列，可以通过计算相邻两项的比值（等比数列）或差值（等差数列）是否相等来进行判断。

二、常用数列类型1. 等差数列等差数列是指相邻两项之差都相等的数列。

求等差数列的通项公式可以通过计算相邻两项之差来得到，也可以通过已知首项和公差来得到。

在解题过程中，容易混淆首项和公差的顺序，需要注意。

2. 等比数列等比数列是指相邻两项之比都相等的数列。

求等比数列的通项公式可以通过计算相邻两项之比来得到，也可以通过已知首项和公比来得到。

在解题过程中，需要注意公比为零或负数时的特殊情况。

3. 斐波那契数列斐波那契数列是指从第3项开始，每一项都等于前两项之和的数列。

斐波那契数列的通项公式可以通过递推公式an=an-1+an-2得到。

4. 递推数列递推数列是指通过递推公式得到后一项的数列。

在解题过程中，容易出现递推公式写错或计算错误的情况，需要仔细注意。

三、数列的运算1. 数列的加法运算对于等差数列和等比数列，相同位置的项可以进行加法运算。

对于等差数列，可以通过逐项相加得到结果；对于等比数列，可以通过求和公式得到结果。

2. 数列的乘法运算对于等差数列和等比数列，相同位置的项可以进行乘法运算。

高考数列公式总结

2024高考数学数列知识点总结与题型分析

(完整版)高考数列公式总结

等比数列数学公式高中有哪些

高考数学常用公式：数列

高职高考数列知识点归纳总结

高考数列基本公式是什么

第四章 数列(公式、定理、结论图表)--2023年高考数学必背知识手册(新教材)

等比数列数学高中公式有哪些

高中数学高考数列公式总结

等差等比数列求和公式(2024高考必考)

高三数学知识点归纳公式大全总结

高考数学复习知识点：数学数列公式大全

高考数列公式总结

高考数列知识点细目表

数列高考知识点大全总结

高考数列知识点归纳总结

高中数学数列知识点归纳

2024年高考数学数列易错知识点总结

2024年高考数学数列易错知识点总结

第四章数列(公式、定理、结论图表)--2023年高考数学必背知识手册(新教材)