第8章圆锥曲线专练14—探索性问题2-高三数学一轮复习
2024届新高考一轮总复习人教版 第八章重难突破系列(六)圆锥曲线中的证明、探索性问题课件(31张)

令 y=-1,得点 A 的横坐标 xA=-xy11, 同理得 B 的横坐标 xB=-xy22. 设点 D(0,n),则D→A=-yx11,-1-n,D→B=-yx22,-1-n, D→A·D→B=xy11xy22+(n+1)2=-x4x121x-2 x422+(n+1)2=x116x2+(n+1)2=-4+(n+1)2. 令D→A·D→B=0,即-4+(n+1)2=0,得 n=1 或 n=-3. 综上,以 AB 为直径的圆经过 y 轴上的定点(0,1)和(0,-3).
题型一 圆锥曲线中的证明问题 数量关系的证明 [例 1] 设椭圆 C:x22+y2=1 的右焦点为 F,过 F 的直线 l 与 C 交于 A,B 两点,点 M 的坐标为(2,0). (1)当 l 与 x 轴垂直时,求直线 AM 的方程; (2)设 O 为坐标原点,证明:∠OMA=∠OMB.
[思维建模]
位置关系的证明 [例 2] (2021·新高考Ⅱ卷)已知椭圆 C 的方程为ax22+by22=1(a>b>0),右焦点为 F( 2, 0),且离心率为 36. (1)求椭圆 C 的方程; (2)设 M,N 是椭圆 C 上的两点,直线 MN 与曲线 x2+y2=b2(x>0)相切.证明:M, N,F 三点共线的充要条件是|MN|= 3.
第(1)问
求什么 想什么
求直线 AM 的方程,想到求直线 AM 的斜率或直线上的点的坐标
给什么 题目给出 M 的坐标及 l 与 x 轴垂直,可利用 l 与 x 轴垂直求出 l 的方程,进
用什么 而求出 A 点坐标,并求出直线 AM 的方程
第(2)问 求什么
证明∠OMA=∠OMB.可转化为证明直线 MA 与 MB 的斜率间的关系 想什么 给什么 题目中给出 O 点及 M 点的坐标,可求得 l 与 x 轴重合、垂直两种特殊情况下 用什么 ∠OMA=∠OMB 缺什么 缺少直线(不与 x 轴重合或垂直时),直线 l 的方程及直线 l 与椭圆交点 A,B 找什么 的坐标,可设直线 l 的方程及 A,B 两点的坐标求解
新教材适用2024版高考数学一轮总复习第8章解析几何第8讲第3课时定点定值探索性问题课件

kPA·kPB=x+y2
y 2·x-2
2=x2y-2 8=-34,
整理得 C 的方程为x82+y62=1(x≠±2 2).
(2)直线 l 的斜率存在时,可设其方程为 y=kx+m, y=kx+m,
联立x82+y62=1, 化简得 (3+4k2)x2+8kmx+4m2-24=0, 设 M(x1,y2),N(x2,y2), 则 Δ=(8km)2-4(3+4k2)(4m2-24)=48(8k2+6-m2)>0, x1+x2=-3+8km4k2,x1x2=43m+2-4k224,
显然成立, 综上,可得直线 HN 过定点(0,-2).
例3
(2023·河 南 信 阳 高 级 中 学 开 学 考 ) 已 知 椭 圆
C
:
x2 a2
+
y2 b2
=
1(a>b>0)的右焦点为 F,上顶点为 A,直线 FA 的斜率为- 33,且原点 O
到直线
FA
的距离为
3 2.
(1)求椭圆 C 的标准方程;
直线 l 交椭圆 E 于点 A,B,直线 m 交椭圆 E 于点 C,D,探究:A、B、
即:y=y90(x+3),
联立直线 AP 的方程与椭圆方程可得:
x92+y2=1
,
y=y90x+3
整理得:(y20+9)x2+6y20x+9y20-81=0, 解得:x=-3 或 x=-3y20y+20+927 将 x=-3y20y+20+927代入直线 y=y90(x+3)可得: y=y206+y09, 所以点 C 的坐标为-y320y+20+927,y206+y09.
[解析] (1)依据题意作出如下图形, 由椭圆方程 E:ax22+y2=1(a>1)可得:A(-a,0),B(a,0),G(0,1) 所以A→G=(a,1),G→B=(a,-1), 所以A→G·G→B=a2-1=8,∴a2=9, 所以椭圆 E 的方程为:x92+y2=1.
2020高三数学一轮复习(人教版理):圆锥曲线的综合问题 ——定点、定值、探索性问题

→ 则OT=
5511+6k42k2,-1+4k4k2。
因为点 T 在圆 x2+y2=1 上,
所以1511+6k42k22+-1+4k4k22=1,
化简得 176k4-24k2-5=0,
解得 k2=14(负值舍去),所以 k=±12,
经检验,此时(*)对应的判别式 Δ>0,满足题意。
又因为△MOF1 的面积为34,即12×
3×y=34,得 y=
23,所以 M
1,
23,
代入椭圆方程,得a12+43b2=-1②。 由①②解得 a2=4,b2=1。 故椭圆 C 的标准方程为x42+y2=1。 (2)假设存在过点 A(2,0)的直线 l 符合题意,则结合图形(图略)易知直线 l 的斜率必存在,于是可设直线 l 的方程为 y=k(x-2),
(2)证明:设 A(x1,y1),B(x2,y2)。 由(1)知 x1+x2=-2kk-2 4,x1x2=k12。
直线 PA 的方程为 y-2=yx11--21(x-1)。 令 x=0,得点 M 的纵坐标为 yM=-x1y-1+12+2=-xk1x-1+1 1+2。
同理得点 N 的纵坐标为 yN=-xk2x-2+1 1+2。 → →→ →
设 l:y=kx+m(m≠1)。
将 y=kx+m 代入x42+y2=1,得(4k2+1)x2+8kmx+4m2-4=0,由题设 可知 Δ=16(4k2-m2+1)>0。
设 A(x1,y1),B(x2,y2), 则 x1+x2=-4k82k+m1,x1x2=44mk22+-14。
而 k1+k2=y1x-1 1+y2x-2 1=kx1+xm1 -1+kx2+xm2 -1= 2kx1x2+mx1-x21x1+x2。 由题设知 k1+k2=-1,故(2k+1)x1x2+(m-1)(x1+x2)=0。即(2k+1)· 44mk22+-14+(m-1)·4-k28+km1=0。解得 k=-m+2 1。
2020高考新课标数学(文)一轮复习教材:专题研究圆锥曲线中的定点、定值、探索性问题

专题研究(二)圆锥曲线中的定点、定值、探索性问题专题概述:1.证明直线过定点,应根据已知条件建立直线方程中斜率k或截距b的关系式,此类问题中的定点多在坐标轴上;2•解决定值问题应以坐标运算为主,需建立相应的目标函数,然后代入相应的坐标运算,结果即可得到;3•无论定点或定值问题,都可先用特殊值法求出,然后再验证即可,这样可确定方向和目标;4•探索性问题通常采用“肯定顺推法”,将不确定性问题明朗化.其步骤为:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于待定系数的方程组,若方程组有实数解,贝加素(点、直线、曲线或参数)存在;否则,元素(点、直线、曲线或参数)不存在.[专题讲解]题型一定点问题【典例1】(2019甘肃兰州模拟)已知椭圆C:a2+ ^2= 1(a>b>0)短轴的一个端点与其两个焦点构成面积为3的直角三角形.(1)求椭圆C的方程;⑵过圆E: x2+ y2= 2上任意一点P作圆E的切线I, I与椭圆C 交于A, B 两点,以AB为直径的圆是否过定点,若过定点,求出该定点;若不过定点,请说明理由.[审题程序]第一步:待定系数法求C的方程;第二步:依据特殊情形确定定点;第三步:应用根与系数的关系,转化证明方向;第四步:计算推证.[规范解答](1)因为椭圆C短轴的一个端点和其两个焦点构成1 1 2直角三角形,所以b = c , S =㊁2c b = 2a = 3,所以 a=,6, b = , 3. x 2 y故椭圆C 的方程为§ + 3 = 1.(2)圆E 的方程为x 2 + y 2 = 2,设0为坐标原点,当直线I 的斜率不存在时,不妨设直线 AB 的方程为x = 2, 则 A(,2, 2), B(.2,—「2),所以Z AOB =扌, 所以以AB 为直径的圆过坐标原点.当直线I 的斜率存在时,设其方程为y = kx + m , A(x i , y i ), B (X 2, y 2)•因为直线与相关圆相切, 所以 d =—^=爲=飞=J 2,所以 m 2 = 2 + 2k 2.p 1 + k 2 \l 1+ ky = kx + m ,联立方程组 x 2 y得 x 2 + 2(kx + m)2= 6,即(1 + 2k 2)x 2 + 〔石 +3 = 1,4kmx + 2m 2— 6 = 0,A= 16k 2m 2— 4(1 + 2k 2)(2m 2— 6)= 8(6k 2— m 2 + 3)=8(4k 2 + 1)>0,4km 1 + 2k 2,X1^ =由根与系数的关系得2m 2 — 6所以X1X2 + y〃2 = (1 + k )X1X2 + km(X1 + X2)+ m1 + k2 2m 2- 6 4k 2m 2 2 3m 2 — 6k 2— 6= --------- : -- —+ m = -------- : - = 0. 所以OA 丄OB ,所以以AB 为直径的圆恒过坐标原点 O.[答题模板]解决这类问题的答题模板如下:[题型专练]1. (2019 广东佛山一中第二次段考)椭圆C :肇+ £ = 1(a>b>0)1的离心率为刁 其左焦点到点P(2,1)的距离为10.(1) 与椭圆C 的标准方程;(2) 若直线I : y = kx + m 与椭圆C 相交于A , B 两点(A , B 不是左 右顶点),且以AB 为直径的圆过椭圆C 的右顶点.求证:直线I 过定 点,并求出该定点的坐标.[解](1)v 左焦点(—c,0)到点P(2,1)的距离为.石, —2+c 2+ 1= 10,解得 c = 1.又 e = a = 2,解得 a = 2,「・b 2= a 2 — c 2 = 3.一x 2 y 2m 2= 1+ 2k 21 + 2k2 1 + 2k 2定目标选参数建联系v确定与参数无关的点中即为所求.•••所求椭圆C的方程为:4 + 3 = 1.⑵证明:设 A(x i , y i ), B(X 2, y 2),y = kx + m由 x 2 y 得(3+ 4『)x 2 + 8mkx + 4(m 2 — 3) = 0,4 + 3 = 1A= 64m 2k 2— 16(3 + 4k 2)(m 2— 3)>0, 化简得3+ 4k 2>m 2.2 2y 〃2 = (kx i + m)(kx 2 + m)= k X 1X 2 + mk(x i + 血)+ m =•••以AB 为直径的圆过椭圆的右顶点 D(2,0),kADkBD一2 X —2= — 1,:沁2 + X 1X 2 — 2(X 1 + X 2)+ 4= 0,3m2—4k 24 m 2—316mk •- 2+2+2+ 4= 0.3 + 4k 2 3+ 4k 2 3 + 4k 2化简整理得 7m 2 + 16mk + 4k 2= 0,解得 m 1 = — 2k , m 2 =—于, 且满足 3+ 4k 2 — m 2>0.当m = — 2k 时,I : y = k(x — 2),直线过定点(2,0)与已知矛盾; 2k ( 2) 2\当m = — y 时,I : y = k x — 7J,直线过定点J, 0J.(2综上可知,直线I 过定点,定点坐标为 J, 0 .—8km•・X l + X 2 2 3 + 4k 2x i x 2 = 4 m 2— 33+4k 23 m 2 —4k 23 + 4k 2题型二定值问题2 2【典例2] (2019北京石景山区一模)已知椭圆E:字+1(a>b>0)过点(0,1),且离心率为守3.(1)求椭圆E的方程;1⑵设直线I: y= 2X+ m与椭圆E交于A, C两点,以AC为对角线作正方形ABCD,记直线I与x轴的交点为N,问B,N两点间的距离是否为定值?如果是,求出定值;如果不是,请说明理由.[审题程序]第步:待定系数法求出椭圆方程;第二步:弦长公式求|AC|;第三步:求出中点M,利用勾股定理求出|BN|.[规范解答](1)由题意可知,椭圆的焦点在x轴上,椭圆过点(0,1),则b= 1.由椭圆的离心率e= £= ... 1 —字=~2,解得a= 2,所以椭圆E 一x22的标准方程为+ y = 1.(2)设A(X1, y) C(X2, yj,线段AC 的中点为M(x。
2023届高考数学一轮复习作业圆锥曲线中的证明探索性问题新人教B版

圆锥曲线中的证明、探索性问题1.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,左、右顶点分别是A 1,A 2,上顶点为B (0,b ),△A 1A 2B 的面积等于2.(1)求椭圆C 的方程;(2)设点Q (1,0),P (4,m ),直线PA 1,PA 2分别交椭圆C 于点M ,N ,证明:M ,Q ,N 三点共线.[解](1)由离心率为32得,c a =32①. 由△A 1A 2B 的面积为2得,ab =2 ②.a 2=b 2+c 2 ③,∴联立①②③解得,a =2,b =1, ∴椭圆C 的方程为x 24+y 2=1. (2)记点M ,N 的坐标分别为M (x 1,y 1),N (x 2,y 2).注意到A 1(-2,0),∴直线PA 1的方程为y =m 6(x +2),与椭圆x 24+y 2=1联立并整理得(m2+9)x 2+4m 2x +4m 2-36=0,由-2+x 1=-4m 2m 2+9得x 1=18-2m2m 2+9,代入直线PA 1的方程得y 1=6m m 2+9,即M ⎝ ⎛⎭⎪⎫18-2m 2m 2+9,6m m 2+9.同理可得N ⎝ ⎛⎭⎪⎫2m 2-2m 2+1,-2m m 2+1.∵Q (1,0),∴QM →=⎝ ⎛⎭⎪⎫9-3m 2m 2+9,6m m 2+9,QN →=⎝ ⎛⎭⎪⎫m 2-3m 2+1,-2m m 2+1, 由9-3m 2m 2+9·-2m m 2+1=m 2-3m 2+1·6mm 2+9知,M ,Q ,N 三点共线. 2.(2021·河南开封高三期末)已知点⎝ ⎛⎭⎪⎫-233,2,⎝ ⎛⎭⎪⎫1,-32都在椭圆C 上,点A 为椭圆C 的上顶点,点F 为椭圆C 的右焦点.(1)求椭圆C 的标准方程;(2)已知直线l 的倾斜角为30°,且与椭圆C 交于M ,N 两点,问是否存在这样的直线l 使得FA →+FM →+FN →=0?若存在,求l 的方程;若不存在,说明理由.[解](1)设椭圆C 的方程为mx 2+ny 2=1,由已知有⎩⎪⎨⎪⎧m +94n =1,43m +2n =1,解得⎩⎪⎨⎪⎧m =14,n =13,所以椭圆C 的标准方程为x 24+y 23=1.(2)由(1)知,A (0,3),F (1,0),假设存在直线l 满足题意,并设l 的方程为y =33x +t ,M (x 1,y 1),N (x 2,y 2).由⎩⎪⎨⎪⎧y =33x +tx 24+y 23=1,得13x 2+83tx +12(t 2-3)=0,由Δ=(83t )2-4×13×12(t 2-3)>0,得-393<t <393,又因为x 1+x 2=-83t 13, 由题意易知点F 为△AMN 的重心,所以x 1+x 2+x A =3x F ,即-83t13+0=3,解得t =-1338, 当t =-1338时,不满足-393<t <393,所以不存在直线l 使得FA →+FM →+FN →=0.3.设D 是圆O :x 2+y 2=16上的任意一点,m 是过点D 且与x 轴垂直的直线,E 是直线m 与x 轴的交点,点Q 在直线m 上,且满足2|EQ |=3|ED |.当点D 在圆O 上运动时,记点Q 的轨迹为曲线C .(1)求曲线C 的方程;(2)已知点P (2,3),过F (2,0)的直线l 交曲线C 于A ,B 两点,交直线x =8于点M .试判断直线PA ,PM ,PB 的斜率是否依次构成等差数列,并说明理由.[解](1)设点Q (x ,y ),D (x 0,y 0), 因为2|EQ |=3|ED |,点Q 在直线m 上, 所以x 0=x ,|y 0|=23|y |. ①因为点D 在圆O :x 2+y 2=16上运动,所以x 20+y 20=16. ②将①代入②,可得x 2+⎝ ⎛⎭⎪⎫23y 2=16.即曲线C 的方程为x 216+y 212=1.(2)直线PA ,PM ,PB 的斜率依次构成等差数列,理由如下.由题意可知直线l 的斜率存在,设直线l 的方程为y =k (x -2),令x =8,得点M 的坐标为(8,6k ).由⎩⎪⎨⎪⎧y =k x -2,x 216+y 212=1消去y ,并整理得(4k 2+3)x 2-16k 2x +16(k 2-3)=0.设A (x 1,y 1),B (x 2,y 2),则有x 1+x 2=16k 24k 2+3,x 1x 2=16k 2-34k 2+3. ③ 记直线PA ,PB ,PM 的斜率分别为k 1,k 2,k 3, 从而k 1=y 1-3x 1-2,k 2=y 2-3x 2-2,k 3=6k -38-2=k -12. 因为直线AB 的方程为y =k (x -2),所以y 1=k (x 1-2),y 2=k (x 2-2), 所以k 1+k 2=y 1-3x 1-2+y 2-3x 2-2=y 1x 1-2+y 2x 2-2-3⎝ ⎛⎭⎪⎫1x 1-2+1x 2-2=2k -3×x 1+x 2-4x 1x 2-2x 1+x 2+4. ④把③代入④,得k 1+k 2=2k -3×16k24k 2+3-416k 2-34k 2+3-32k24k 2+3+4=2k -1. 又k 3=k -12,所以k 1+k 2=2k 3,于是直线PA ,PM ,PB 的斜率依次构成等差数列.。
高三数学高考一轮复习系列教案第八章 圆锥曲线 大纲版
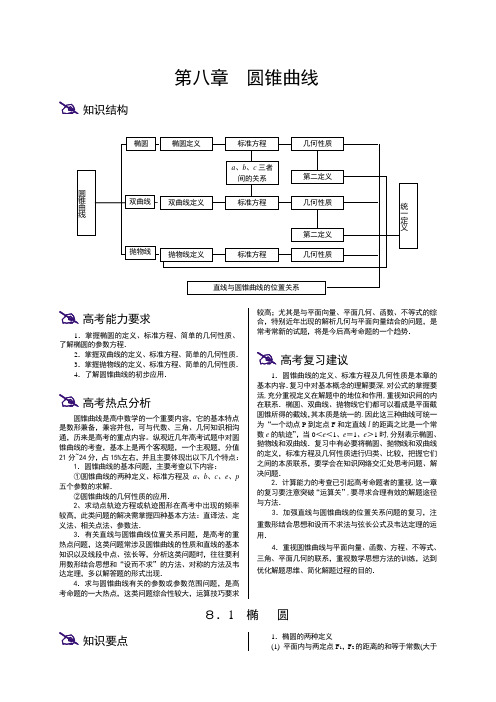
第八章圆锥曲线知识结构高考能力要求1.掌握椭圆的定义、标准方程、简单的几何性质、了解椭圆的参数方程.2.掌握双曲线的定义、标准方程、简单的几何性质.3.掌握抛物线的定义、标准方程、简单的几何性质.4.了解圆锥曲线的初步应用.高考热点分析圆锥曲线是高中数学的一个重要内容,它的基本特点是数形兼备,兼容并包,可与代数、三角、几何知识相沟通,历来是高考的重点内容。
纵观近几年高考试题中对圆锥曲线的考查,基本上是两个客观题,一个主观题,分值21分~24分,占15%左右,并且主要体现出以下几个特点:1.圆锥曲线的基本问题,主要考查以下内容:①圆锥曲线的两种定义、标准方程及a、b、c、e、p 五个参数的求解.②圆锥曲线的几何性质的应用.2、求动点轨迹方程或轨迹图形在高考中出现的频率较高,此类问题的解决需掌握四种基本方法:直译法、定义法、相关点法、参数法.3.有关直线与圆锥曲线位置关系问题,是高考的重热点问题,这类问题常涉及圆锥曲线的性质和直线的基本知识以及线段中点、弦长等,分析这类问题时,往往要利用数形结合思想和“设而不求”的方法、对称的方法及韦达定理,多以解答题的形式出现.4.求与圆锥曲线有关的参数或参数范围问题,是高考命题的一大热点,这类问题综合性较大,运算技巧要求较高;尤其是与平面向量、平面几何、函数、不等式的综合,特别近年出现的解析几何与平面向量结合的问题,是常考常新的试题,将是今后高考命题的一个趋势.高考复习建议1.圆锥曲线的定义、标准方程及几何性质是本章的基本内容.复习中对基本概念的理解要深,对公式的掌握要活,充分重视定义在解题中的地位和作用,重视知识间的内在联系.椭圆、双曲线、抛物线它们都可以看成是平面截圆锥所得的截线,其本质是统一的.因此这三种曲线可统一为“一个动点P到定点F和定直线l的距离之比是一个常数e的轨迹”,当0<e<1、e=1、e>1时,分别表示椭圆、抛物线和双曲线.复习中有必要将椭圆、抛物线和双曲线的定义,标准方程及几何性质进行归类、比较,把握它们之间的本质联系,要学会在知识网络交汇处思考问题、解决问题.2.计算能力的考查已引起高考命题者的重视,这一章的复习要注意突破“运算关”,要寻求合理有效的解题途径与方法.3.加强直线与圆锥曲线的位置关系问题的复习,注重数形结合思想和设而不求法与弦长公式及韦达定理的运用.4.重视圆锥曲线与平面向量、函数、方程、不等式、三角、平面几何的联系,重视数学思想方法的训练,达到优化解题思维、简化解题过程的目的.8.1 椭圆知识要点1.椭圆的两种定义(1) 平面内与两定点F1,F2的距离的和等于常数(大于21F F )的点的轨迹叫椭圆,这两个定点叫做椭圆的 , 之间的距离叫做焦距.注:①当2a =|F 1F 2|时,P 点的轨迹是 .②当2a <|F 1F 2|时,P 点的轨迹不存在.(2) 椭圆的第二定义:到 的距离与到 的距离之比是常数e ,且∈e 的点的轨迹叫椭圆.定点F 是椭圆的 ,定直线l 是 ,常数e 是 .2.椭圆的标准方程(1) 焦点在x 轴上,中心在原点的椭圆标准方程是:12222=+b y a x ,其中( > >0,且=2a ) (2) 焦点在y 轴上,中心在原点的椭圆标准方程是12222=+bx ay ,其中a ,b 满足: .3.椭圆的几何性质(对12222=+by a x ,a > b >0进行讨论)(1) 范围: ≤ x ≤ , ≤ y ≤ (2) 对称性:对称轴方程为 ;对称中心为 .(3) 顶点坐标: ,焦点坐标: ,长半轴长: ,短半轴长: ;准线方程: .(4) 离心率:=e ( 与 的比),∈e ,e 越接近1,椭圆越 ;e 越接近0,椭圆越接近于 .(5) 焦半径公式:设21,F F 分别为椭圆的左、右焦点,),(00y x P 是椭圆上一点,则=1PF ,122PF a PF -== .(6) 椭圆的参数方程为 . 4.焦点三角形应注意以下关系: (1) 定义:r 1+r 2=2a(2) 余弦定理:21r +22r -2r 1r 2cos θ=(2c )2(3) 面积:21F PF S ∆=21r 1r 2 sin θ=21·2c | y 0 |(其中P(00,y x )为椭圆上一点,|PF 1|=r 1,|PF 2|=r 2,∠F 1PF 2=θ)例题讲练【例1】 中心在原点,一个焦点为F 1(0,52)的椭圆被直线y =3x -2截得的弦的中点的横坐标为21,求此椭圆的方程.【例2】 已知点P(3, 4)是椭圆2222b y a x +=1 (a >b >0) 上的一点,F 1、F 2是它的两焦点,若PF 1⊥PF 2,求:(1) 椭圆的方程; (2) △PF 1F 2的面积.【例3】如图,射线OA 、OB 分别与x 轴、 y 轴所成的角均为︒30;已知线段PQ 的长度为2,并且保持线段的端点),(11y x P 在射线OA 上运动,点),(22y x Q 在射线OB 上运动(1) 试求动点),(21x x M 的轨迹C 的方程(2) 求轨迹C 上的动点N 到直线03=--y x 的距离的最大值和最小值.【例4】 (2005年全国卷I )已知椭圆的中心在原点,焦点在x 轴上,斜率为1且过椭圆右焦点F 的直线交椭圆于A 、B 两点,+与=(3, -1)共线.(1) 求椭圆的离心率;(2) 设M 是椭圆上任意一点,且=μλ+(λ、μ∈R),证明22μλ+为定值.小结归纳 1.在解题中要充分利用椭圆的两种定义,灵活处理焦半径,熟悉和掌握a 、b 、c 、e 关系及几何意义,能够减少运算量,提高解题速度,达到事半功倍之效.2.由给定条件求椭圆方程,常用待定系数法.步骤是:定型——确定曲线形状;定位——确定焦点位置;定量——由条件求a 、b 、c ,当焦点位置不明确时,方程可能有两种形式,要防止遗漏.3.解与椭圆的焦半径、焦点弦有关的问题时,一般要从椭圆的定义入手考虑;椭圆的焦半径的取值范围是],[c a c a +-.4.“设而不求”,“点差法”等方法,是简化解题过程的常用技巧,要认真领会.5.解析几何与代数向量的结合,是近年来高考的热点,在2005年的考题中足以说明了这一点,应引起重视.基础训练题 一、选择题1. 动点M 到定点)0,4(1-F 和)0,4(2F 的距离的和为8,则动点M 的轨迹为 ( ) A .椭圆 B .线段 C .无图形 D .两条射线2. (2005年全国高考试题III) 设椭圆的两个焦点分别为F 1、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 ( )A .22 B .212- C .2-2D .2-13. (2004年高考湖南卷)F 1、F 2是椭圆C :14822=+y x 的焦点,在C 上满足PF 1⊥PF 2的点P 的个数为( ) A .2个 B .4个 C .无数个 D .不确定4. 椭圆171622=+y x 的左、右焦点为F 1、F 2,一直线过F 1交椭圆于A 、B 两点,则△ABF 2的周长为 ( ) A .32 B .16 C .8 D .45. 已知点P 在椭圆(x -2)2+2y 2=1上,则xy的最小值为( )A .36-B .26-C .6-D .66-6. 我们把离心率等于黄金比215-的椭圆称为“优美椭圆”,设)0(12222>>=+b a by a x 是优美椭圆,F 、A 分别是它的左焦点和右顶点,B 是它的短轴的一个端点,则ABF ∠等于 ( ) A .︒60 B .︒75 C .︒90 D .︒120二、填空题 7. 椭圆400162522=+y x 的顶点坐标为 和 ,焦点坐标为 ,焦距为 ,长轴长为 ,短轴长为 ,离心率为 ,准线方程为 .8. 设F 是椭圆16722=+y x 的右焦点,且椭圆上至少有21个不同的点P i (i =1,2, ),使得|FP 1|、|FP 2|、|FP 3|…组成公差为d 的等差数列,则d 的取值范围是 . 9. 设1F ,2F 是椭圆14322=+y x 的两个焦点,P 是椭圆上一点,且121=-PF PF ,则得=∠21PF F . 10.若椭圆2222)1(-+m y m x =1的准线平行于x 轴则m 的取值范围是 .三、解答题11.根据下列条件求椭圆的标准方程(1) 和椭圆1202422=+y x 共准线,且离心率为21.(2) 已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为534和532,过P 作长轴的垂线恰好过椭圆的一个焦点.12.椭圆14922=+y x 的焦点为21,F F ,点P 为其上的动点,当∠21PF F 为钝角时,求点P 横坐标的取值范围.13.(2005年高考湖南卷)已知椭圆C :12222=+by a x (a >0,b >0)的左、右焦点分别是F 1、F 2,离心率为e .直线l :y =ex +a 与x 轴,y 轴分别交于点A 、B 、M 是直线l 与椭圆C 的一个公共点,P 是点F 1关于直线l 的对称点,设=λ. (Ⅰ)证明:λ=1-e 2;(Ⅱ)若λ=43,△MF 1F 2的周长为6,写出椭圆C 的方程;(Ⅲ)确定λ的值,使得△PF 1F 2是等腰三角形.提高训练题14.(2006年高考湖南卷)已知C 1:13422=+y x ,抛物线C 2:(y -m )2=2px (p >0),且C 1、C 2的公共弦AB 过椭圆C 1的右焦点.(Ⅰ)当AB ⊥x 轴时,求p 、m 的值,并判断抛物线C 2的焦点是否在直线AB 上;(Ⅱ)若p =34,且抛物线C 2的焦点在直线AB 上,求m 的值及直线AB 的方程.15.(成都市2006届毕业班摸底测试)设向量i =(1, 0),j =(0, 1),=(x +m )i +y j ,=(x -m )i +y j ,且||+||=6,0< m < 3,x >0,y ∈R . ( I )求动点P(x ,y )的轨迹方程;( II ) 已知点A(-1, 0),设直线y =31(x -2)与点P 的轨迹交于B 、C 两点,问是否存在实数m ,使得AC AB ⋅=31?若存在,求出m 的值;若不存在,请说明理由.8.2 双 曲 线知识要点 1.双曲线的两种定义(1) 平面内与两定点F 1,F 2的 常数(小于 )的点的轨迹叫做双曲线.注:①当2a =|F 1F 2|时,p 点的轨迹是 .②2a >|F 1F 2|时,p 点轨迹不存在.(2) 平面内动点P 到一个定点F 和一条定直线l (F 不在 上)的距离的比是常数e ,当∈e 时动点P 的轨迹是双曲线.设P 到1F 的对应准线的距离为d ,到2F 对应的准线的距离为2d ,则e d PF d PF ==22112.双曲线的标准方程 (1) 标准方程:12222=-b y a x ,焦点在 轴上;12222=-bx ay ,焦点在 轴上.其中:a 0,b 0,=2a .(2) 双曲线的标准方程的统一形式:)0(122<=+nm ny mx3.双曲线的几何性质(对0,0,122>>=-b a b y a x 进行讨论)(1) 范围:∈x ,∈y .(2) 对称性:对称轴方程为 ;对称中心为 .(3) 顶点坐标为 ,焦点坐标为 ,实轴长为 ,虚轴长为 ,准线方程为 ,渐近线方程为 .(4) 离心率e = ,且∈e ,e 越大,双曲线开口越 ,e 越小,双曲线开口越 ,焦准距P = .(5) 焦半径公式,设F 1,F 2分别是双曲线的左、右焦点,若),(00y x P 是双曲线右支上任意一点,=1PF ,=2PF ,若),(00y x P 是双曲线左支上任意一点,=1PF ,=2PF . (6) 具有相同渐近线x aby ±=的双曲线系方程为 (7) 的双曲线叫等轴双曲线,等轴双曲线的渐近线为 ,离心率为 .(8) 12222=-b y a x 的共轭双曲线方程为 .例题讲练【例1】 根据下列条件,写出双曲线的标准方程 (1) 中心在原点,一个顶点是(0,6),且离心率是1.5.(2) 与双曲线x 2-2y 2=2有公共渐近线,且过点M(2,-2).【例2】 (04年高考湖北卷)直线l :y =kx +1与双曲线C :2x 2-y 2=1的右支交于不同的两点A 、B .(1)求实数k 的取值范围;(2)是否存在实数k ,使得以线段AB 为直径的圆经过双曲线C 的右焦点F ?若存在,求出k 的值;若不存在,说明理由.【例3】 在双曲线1121322-=-y x 的一支上有不同的三点A(x 1,y 1),B(x 2,6),C(x 3,y 3)与焦点F(0,5)的距离成等差数列.(1)求y 1+y 3;(2)求证:线段AC 的垂直平分线经过某一定点,并求出这个定点的坐标.【例4】 (2004年高考全国卷II )设双曲线C :)0(1222>=-a y a x 与直线l :x +y =1相交于两个不同的点.(1) 求双曲线C 的离心率e 的取值范围;(2) 设直线l 与y 的交点为P ,且=125,求a的值.小结归纳1.复习双曲线要与椭圆进行类比,尤其要注意它们之间的区别,如a 、b 、c 、e 的关系.2.双曲线的渐近线的探求是一个热点.①已知双曲线方程求渐近线方程;②求已知渐近线方程的双曲线方程.3.求双曲线的方程,经常要列方程组,因此,方程思想贯穿解析几何的始终,要注意定型(确定曲线形状)、定位(曲线的位置)、定量(曲条件求参数).4.求双曲线的方程的常用方法: (1) 定义法.(2) 待定系数法.涉及到直线与圆锥曲线的交点问题,经常是“设而不求”.5.例2的第(1)问是数材P 132第13题的引申,因此高考第一轮复习要紧扣教材.6.对于直线与双曲线的位置关系,要注意“数形转化”“数形结合”,既可以转化为方程组的解的个数来确定,又可以把直线与双曲线的渐近线进行比较,从“形”的角度来判断.基础训练题 一、选择题1. A 、B 是平面内两定点,动点P 到A 、B 两点的距离的差是常数,则P 的轨迹是 ( ) A .双曲线 B .椭圆 C .双曲线的一支 D .不能确定2. (04年高考湖南卷)如果双曲线1121322=-y x 上一点p 到右焦点的距离等于13,那么点p 到右焦线的距离是 ( )A .513 B .13 C .5D .1353. 已知双曲线的渐近线方程是2xy ±=,焦点在坐标轴上且焦距是10,则此双曲线的方程为 ( )A .152022=-y x B .152022±=-y x C .120522=-y xD .120522±=-y x4. (2005年高考湖南卷)已知双曲线12222=-by a x (a >0,b >0)的右焦点为F ,右焦线与一条渐近线交于点A ,△OAF 的面积为22a ,(0为原点)则两条渐近线的夹角为( ) A .30° B .45° C .60°D .90°5. 已知双曲线14922=-y x ,则过点A(3,1)且与双曲线仅有唯一的公共点的直线有 ( ) A .1条 B .2条 C .3条 D .4条6. (2005年江苏高考最后冲刺题) 设双曲线16x 2-9y 2=144的右焦点为F 2,M 是双曲线上任意一点,点A 的坐标为(9,2),则|MA|+53|MF 2|的最小值为( )A .9B .536C .542D .554二、填空题7. 中心在原点,坐标轴为对称轴,实轴与虚轴长之差为2,离心率为45的双曲线方程为 .8. (2004年高考·吉林、四川)设中心在原点,坐标轴为对称轴的椭圆与双曲线12222=-y x 有公共焦点,且它们的离心率互为倒数,则椭圆方程为 .9. (2006年高考湖南卷)过双曲线M :1222=-b y x 的左顶点A 作斜率为1的直线l ,若l 与双曲线M 的两条渐近线分别相交于点B 、C ,且|AB|=|BC|,则双曲线M 的离心率是 .10.可以证明函数x bax y +=(b ≠0)的图象是双曲线,试问双曲线C :xx y 33+=的离心率e 等于 .三、解答题11.(1) 已知双曲线的渐近线方程为032=±yx ,且过点(2,-6),求双曲线的方程;(2) 已知双曲线的右准线为x =4,右焦点为F(10,0),离心率为e =2,求双曲线的方程. 12.ABC ∆中,固定底边BC ,让顶点A 移动,已知4=BC ,且A B C sin 21sin sin =-,求顶点A 的轨迹方程.13.双曲线12222=-by a x )0,0(>>b a 的右支上存在与右焦点和左准线等距离的点,求离心率e 的取值范围.提高训练题 14.已知动点p 与双曲线13222=-y x 的两个焦点F 1、F 2的距离之和为定值,且cos ∠F 1PF 2的最小值为-91.(1) 求动点p 的轨迹方程;(2) 若已知点D(0,3),点M 、N 在动点p 的轨迹上且λ=,求实数λ的取值范围.15.(2005年武汉市高三调考)已知等轴双曲线C :)0(222>=-a a y x 上一定点P(00,y x )及曲线C 点上两个动点A 、B ,满足0=⋅PB PA(1) M 、N 分别为PA 、PB 中点,求证:0=⋅ON OM (O 为坐标原点);(2) 求|AB|的最小值及此时A 点坐标.抛 物 线 1.抛物线定义:离 的点的轨迹叫抛物线,焦点, 叫做抛物线的准线2.抛物线的标准方程和焦点坐标及准线方程① px y 22=,焦点为 ,准线为 . ② px y 22-=,焦点为 ,准线为 . ③ py x 22=,焦点为 ,准线为 . ④ py x 22-=,焦点为 ,准线为 . 3.抛物线的几何性质:对)0(22>=p px y 进行讨论. ① 点的范围: 、 . ② 对称性:抛物线关于 轴对称. ③ 离心率=e .④ 焦半径公式:设F 是抛物线的焦点,),(o o y x P 是抛物线上一点,则=PF .⑤ 焦点弦长公式:设AB 是过抛物线焦点的一条弦(焦点弦)i) 若),(11y x A ,),(22y x B ,则AB = ,21y y .ii) 若AB 所在直线的倾斜角为θ()0≠θ则AB = .特别地,当θ2π=时,AB 为抛物线的通径,且AB = .iii) S △AOB = (表示成P 与θ的关系式).iv) ||1||1BF AF +为定值,且等于 . 例题讲练【例1】 已知抛物线顶点在原点,对称轴是x 轴,抛物线上的点),3(n A -到焦点的距离为5,求抛物线的方程和n 的值.【例2】 已知抛物线C :x y 42=的焦点为F ,过点F 的直线l 与C 相交于A 、B .(1) 若316=AB ,求直线l 的方程.(2) 求AB 的最小值.【例3】 若A(3,2),F 为抛物线x y 22=的焦点,P 为抛物线上任意一点,求PA PF +的最小值及取得最小值时的P 的坐标.【例4】 (05全国卷(Ⅲ))设A(x 1,y 1),B(x 2,y 2),两点在抛物线y =2x 2上,l 是AB 的垂直平分线.(1)当且仅当x 1+x 2取何值时,直线l 经过抛物线的焦点F ?证明你的结论?(2)当直线l 的斜率为2时,求在y 轴上的截距的取值范围.小结归纳 1.求抛物线方程要注意顶点位置和开口方向,以便准确设出方程,然后用待定系数法.2.利用好抛物线定义,进行求线段和的最小值问题的转化.3.涉及抛物线的弦的中点和弦长等问题要注意利用韦达定理,能避免求交点坐标的复杂运算.4、解决焦点弦问题时,抛物线的定义有广泛的应用,应注意焦点弦的几何性质.基础训练题 一、选择题1. 过抛物线)0(22>=P px y 的焦点作直线交抛物线于),(11y x A ,),(22y x B 两点,若P x x 321=+,则AB等于( )A .2PB .4PC .6PD .8P2. 已知动点),(y x P 满足22)2()1(5-+-y x =|1243|++y x ,则P 点的轨迹是 ( )A .两条相交直线B .抛物线C .双曲线D .椭圆3. 已知抛物线212:x y C =与抛物线2C 关于直线x y -=对称,则2C 的准线方程是( )A .81-=x B .21=xC .81=x D .21-=x4. (2005年高考上海卷)过抛物线y 2=4x 的焦点作一条直线与抛物线相交于A 、B 两点,它们的横坐标之和等于5,则这样的直线 ( ) A .有且仅有一条 B .有且仅有两条 C .有无数条 D .不存在5. (2003年新课程卷)抛物线2ax y =的准线方程是2=y ,则a 的值为 ( )A .81B .81-C .8D .8-6. (04年高考湖北卷)与直线2x -y +4=0平行的抛物线y =x 2的切线方程是 ( ) A .2x -y +3=0 B .2x -y -3=0 C .2x -y +1=0 D .2x -y -1=0二、填空题7. 点M 与点F(4,0)的距离比它到连线l :x +5=0的距了小1,则点M 的轨迹方程为 . 8. 某桥的桥洞是抛物线,桥下水面宽16米,当水面上涨2米后达警戒水位,水面宽变为12米,此时桥洞顶部距水面高度为 米(精确到0.1米). 9. 过点(3,3)的直线与抛物线y 2=3x 只有一个公共点,则这样的直线的条数为 .10.一个酒杯的轴截面是抛物线的一部分,它的方程是x 2)200(2≤≤=y y ,在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r 的取值范围是三、解答题11.求顶点在原点,对称轴是x 轴,并且顶点与焦点的距离等于6的抛物线方程.12.正方形ABCD 中,一条边AB 在直线y =x +4上,另外两顶点C 、D 在抛物线y 2=x 上,求正方形的面积.13.设A 和B 为抛物线y 2=4px (p >0)上原点以外的两个动点,已知OA ⊥OB ,OM ⊥AB ,求点M 的轨迹方程,并说明它表示什么曲线?提高训练题 14.过抛物线y 2=2px (p >0)的焦点F 作直线交抛物线于A 、B 两点,试问:以AB 为直径的圆与抛物线的准线是相交、相切还是相离?若把抛物线改为椭圆12222=+b y a x 或双曲线12222=-b y a x ,结果又如何呢?15.(2004年高考上海卷)如图,直线x y 21=与抛物线4812-=x y 交于A 、B 两点,线段AB 的垂直平分线与直线5-=y 交于Q 点. (1) 求点Q 的坐标;(2) 当P 为抛物线上位于线段AB(含点A 、B)下方的动点时,求OPQ ∆面积的最大值.8.4 直线与圆锥曲线的位置关系知识要点 1.直线与圆锥曲线的位置关系,常用研究方法是将曲线方程与直线方程联立,由所得方程组的解的个数来决定,一般地,消元后所得一元二次方程的判别式记为△,△>0时,有两个公共点,△=0时,有一个公共点,△<0时,没有公共点.但当直线方程与曲线方程联立的方程组只有一组解(即直线与曲线只有一个交点)时,直线与曲线未必相切,在判定此类情形时,应注意数形结合.(对于双曲线,重点注意与渐近线平行的直线,对于抛物线,重点注意与对称轴平行的直线)2.直线与圆锥曲线的交点间的线段叫做圆锥曲线的弦.设弦AB 端点的坐标为A(x 1,y 1),B(x 2,y 2),直线AB 的斜率为k ,则:|AB |=————————或:—————————.利用这个公式求弦长时,要注意结合韦达定理. 当弦过圆锥曲线的焦点时,可用焦半径进行运算. 3.中点弦问题:设A(x 1,y 1),B(x 2,y 2)是椭圆12222=+b y a x 上不同的两点,且x 1≠x 2,x 1+x 2≠0,M(x 0,y 0)为AB 的中点,则 ⎪⎪⎩⎪⎪⎨⎧=+=+11222222221221b y ax b y a x 两式相减可得2221212121ab x x y y x x y y -=++⋅--即 .对于双曲线、抛物线,可得类似的结论.例题讲练 【例1】 直线y =ax +1与双曲线3x 2-y 2=1相交于A 、B 两点.(1) 当a 为何值时,A 、B 两点在双曲线的同一支上?当a 为何值时,A 、B 两点分别在双曲线的两支上?(2) 当a 为何值时,以AB 为直径的圆过原点?x【例2】 已知双曲线方程2x 2-y 2=2.(1) 求以A(2,1)为中点的双曲线的弦所在直线方程; (2) 过点B(1,1)能否作直线l ,使l 与所给双曲线交于Q 1、Q 2两点,且点B 是弦Q 1Q 2的中点?这样的直线l 如果存在,求出它的方程;如果不存在,说明理由.【例3】 在抛物线y 2=4x 上恒有两点关于直线y =kx +3对称,求k 的取值范围.【例4】 (2006届苏州市高三调研测试)已知椭圆222y ax +=1(a 为常数,且a >1),向量m =(1, t ) (t >0),过点A(-a , 0)且以为方向向量的直线与椭圆交于点B ,直线BO 交椭圆于点C (O 为坐标原点).(1) 求t 表示△ABC 的面积S( t );(2) 若a =2,t ∈[21, 1],求S( t )的最大值.小结归纳1.判断直线与圆锥曲线的位置关系时,注意数形结合;用判别式的方法时,若所得方程二次项的系数有参数,则需考虑二次项系数为零的情况.2.涉及中点弦的问题有两种常用方法:一是“设而不求”的方法,利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率的关系,它能简化计算;二是利用韦达定理及中点坐标公式.对于存在性问题,还需用判别式进一步检验.3.对称问题,要注意两点:垂直和中点.基础训练题 一、选择题1. 曲线x 2+4y 2+D x +2E y +F =0与x 轴有两个交点,且这两个交点在原点的两侧的充要条件是 ( ) A .D ≠0,E =0,F >0 B .E =0,F <0 C .D 2-F >0 D .F <0 2. 若椭圆193622=+y x 的弦被点(4,2)平分,则此弦所在直线的斜率为 ( ) A .2 B .-2C .31D .-213. 经过抛物线)0(22>=p px y 的所有焦点弦中,弦长的最小值为 ( ) A .p B .2p C .4p D .不确定4. 过双曲线1222=-y x 的右焦点作直线l ,交双曲线于A 、B 两点,若∣AB ∣=4,则这样的直线l 有( ) A .1条 B .2条 C .3条 D .4条5. (华师大二附中2005年模拟试卷2) 直线l :y =kx +1(k ≠0)椭圆E :1422=+y m x ,若直线l 被椭圆E 所截弦长为d ,则下列直线中被椭圆E 截得的弦长不是d 的是 ( ) A .kx +y +1=0 B .kx -y -1=0 C .kx +y -1=0 D .kx +y =06. 椭圆mx 2+ny 2=1与直线y =1-x 交于M 、N 两点,过两点O 与线段MN 之中点的直线的斜率为22,则xnm的值是 ( )A .22B .332 C .229D .2732二、填空题7. 已知直线x -y =2与抛物线y 2-4x 交于A 、B 两点,那么线段AB 的中点坐标是 .8. 对任意实数k ,直线y =kx +b 与椭圆⎩⎨⎧==θθs i n 4c o s 2y x (0≤θ<2π)恒有公共点,则b 的取值范围是 .9. 已知抛物线y 2=4x 的一条弦AB ,A(x 1,y 1),B(x 2,y 2),AB 所在直线与y 轴交点坐标为(0,2),则2111y y += .10.若直线mx +ny -3=0与圆x 2+y 2=3没有公共点,则m 、n 的关系式为___________;以(m ,n )为点P 的坐标,过点P 的一条直线与椭圆13722=+y x 的公共点有____个.三、解答题 11.已知直线l 交椭圆162022y x +=1于M 、N 两点,B(0,4)是椭圆的一个顶点,若△BMN 的重心恰是椭圆的右焦点,求直线l 的方程.12.已知直线y =(a +1)x -1与曲线y 2=ax 恰有一个公共点,求实数a 的值.13.(05重庆)已知椭圆C 1的方程为1422=+y x ,双曲线C 2的左、右焦点分别为C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点. (1)求双曲线C 2的方程;(2)若直线l :y =kx +2与椭圆C 1及双曲线C 2恒有两个不同的交点,且l 与C 2的两个交点A 和B 的满足6<⋅(其中O 为原点),求k 的取值范围. 提高训练题14.已知椭圆的一个顶点为A(0,-1),焦点在x 轴上,若右焦点到直线022=+-y x 的距离为3. ⑴ 求椭圆的方程;⑵ 设椭圆与直线y =kx +m (k ≠0)相交于不同的两点M 、N ,当AN AM =时,求m 的取值范围.15.(04湖南)过抛物线x 2=4y 的对称轴上任一点P(0,m )(m >0),作直线与抛物线交于A 、B 两点,点Q 是点P 关于原点的对称点. (Ⅰ)设点P 分有向线段所成的比为λ,证明:)(λ-⊥;(Ⅱ)设直线AB 的方程是x -2y +12=0,过A 、B 两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.8.5 轨迹方程知识要点1.直接法求轨迹的一般步骤:建系设标,列式表标,化简作答(除杂).2.求曲线轨迹方程,常用的方法有:直接法、定义法、代入法(相关点法、转移法)、参数法、交轨法等.例题讲练【例1】一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么样的曲线.【例2】已知抛物线过点N(1,-1),且准线为l:x =-3,求抛物线顶点M的轨迹.【例3】已知直线l与椭圆12223=+byax(a>b>0)有且仅有一个交点Q,且与x轴、y轴交于R、S,求以线段SR 为对角线的矩形ORPS的顶点P的轨迹方程.【例4】已知点H(0,-3),点P在x轴上,点Q 在y轴正半轴上,点M在直线PQ上,且满足PMHP⋅=0,MQPM23-=.(1) 当点P在x轴上移动时,求动点M的轨迹曲线C 的方程;(2) 过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切线的交点B恒在一条直线上.小结归纳1.直接法求轨迹方程关键在于利用已知条件,找出动点满足的等量关系,这个等量关系有的可直接利用已知条件,有的需要转化后才能用.2.回归定义是解决圆锥曲线轨迹问题的有效途径.3.所求动点依赖于已知曲线上的动点的运动而运动,常用代入法求轨迹.4.参数法求轨迹关键在于如何选择好参数,建立起x ,y 的参数方程,以便消参,选择n 个参数,要建立n +1个方程,消参时,要注意等价性.5.求轨迹比求轨迹方程多一个步骤,求轨迹最后须说明轨迹的形状、大小、位置、方向.基础训练题 一、选择题1. 已知椭圆的焦点是F 1、F 2,P 是椭圆上的一个动点,如果延长F 1P 到Q ,使得| PQ |=| PF 2 |,那么动点Q 的轨迹是 ( ) A .圆 B .椭圆 C .双曲线的一支 D .抛物线2. 动点P 与定点)0,1(,)0,1(B A -的连结的斜率之积为1-,则P 点的轨迹方程是( ) A .x 2+y 2=1 B .x 2+y 2=1)1(±≠x C .x 2+y 2=1)0(≠x D .21x y -=3. 已知动点P(x 、y )满足1022)2()1(-+-y x =|3x +4y+2|,则动点P 的轨迹是( )A .椭圆B .双曲线C .抛物线D .无法确定4. 设P 为椭圆12222=+by a x 上一点,过右焦点F 2作∠F 1PF 2的外角平分线的垂线,垂足为Q ,则点Q 的轨迹是( ) A .直线 B .抛物线 C .圆 D .双曲线 5. 设P 为双曲线12222=-b y a x 上一点, 过右焦点F 2作∠F 1PF 2的内角平分线的垂线,垂足为Q ,则点Q 的轨迹是 ( ) A .圆 B .抛物线 C .直线 D .椭圆 6. 已知点P(x ,y )在以原点为圆心,半径为1的圆上运动,则点(x +y ,xy )的轨迹是 ( ) A .半圆 B .抛物线的一部分 C .椭圆 D .双曲线的一支二、填空题7. 长为2a 的线段AB 的两个端点分别在x 轴、y 轴上滑动,则AB 中点的轨迹方程为 .8. 经过定点M(1,2),以y 轴为准线,离心率为21的椭圆左顶点的轨迹方程 . 9. 已知抛物线)(12R m mx x y ∈-+-=,当m 变化时抛物线焦点的轨迹方程为 . 10.(04北京)在正方体ABCD —A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与到直线C 1D 1的距离相等,则动点P 的轨迹是 .三、解答题 11.以动点P 为圆心的圆与圆A :(x +5)2+y 2=49及圆B :(x -5)2+y 2=1都外切,求动点P 的轨迹.12.已知双曲线2222ny m x -=1(m >0,n >0)的顶点为A 1、A 2,与y 轴平行的直线l 交双曲线于点P 、Q. (1) 求直线A 1P 与A 2Q 交点M 的轨迹方程; (2) 当m ≠n 时,求所得圆锥曲线的焦点坐标、准线方程和离心率.13.设直线l :y =kx +1与椭圆C :ax 2+y 2=2(a >1)交于A 、B 两点,以OA 、OB 为邻边作平行四边形OAPB (O 为坐标原点).(1)若k =1,且四边形OAPB 为矩形,求a 的值; (2)若a =2,当k 变化时,(k ∈R),求点P 的轨迹方程.提高训练题14.设椭圆方程为1422=+y x ,过点M(0,1)的直线l 交椭圆于点A 、B ,O 是坐标原点,点P 满足)(21OB OA OP +=,点N 的坐标为)21,21(,当l 绕点M 旋转时,求:(1) 动点P 的轨迹方程; (2) ||NP 的最小值与最大值.A1。
2023年高考数学(理科)一轮复习课件——圆锥曲线的综合问题 第四课时 证明、探索性问题
1234
索引
又 B(0,-1),所以直线 QB 的方程为 y=-2kx-1, 代入x42+y2=1,得(16k2+1)x2+16kx=0, 所以 xQ=-161k62+k 1,yQ=163k22k+2 1-1=1166kk22- +11,即点 Q-161k62+k 1,1166kk22- +11.
索引
(2)过点 M 的直线 l 与圆 E 交于 A,B 两点,与 Γ 交于 C,D 两点,求证:|CD|> 2|AB|.
证明 由题意知,直线l的斜率存在.
设l的斜率为k,那么其方程为y=k(x+1)(k≠0). 则 E(-2,-1)到 l 的距离 d= |kk-2+11| ,
因为l与E交于A,B两点,所以d2<r2,
综合①②知∠ANM=∠BNM.
1234
索引
2.(2022·郑州调研)已知椭圆xa22+by22=1(a>b>0)的上、下顶点分别为 A,B,左、 右顶点分别为 C,D,A→C·A→D=-3,四边形 ACBD 的面积为 4.
(1)求椭圆的标准方程;
解 由题意得A(0,b),B(0,-b),C(-a,0),D(a,0), 所以A→C=(-a,-b),A→D=(a,-b), 则A→C·A→D=-a2+b2=-3.①
索引
感悟提升
此类问题一般分为探究条件、探究结论两种.若探究条件,则可先假设条件成 立,再验证结论是否成立,成立则存在,否则不存在;若探究结论,则应先求 出结论的表达式,再针对其表达式进行讨论,往往涉及对参数的讨论.
圆锥曲线—定点、定值、探究性问题
高考一轮总复习 • 数学
返回导航
名师点拨:圆锥曲线中定值问题的特点及解法 1.特点:待证几何量不受动点或动线的影响而有固定的值. 2.解法: (1)从特殊入手,求出定值,再证明这个值与变量无关; (2)引进变量法:其解题流程为
第八章 平面解析几何
高考一轮总复习 • 数学
返回导航
第八章 平面解析几何
高考一轮总复习 • 数学
返回导航
若mm2t+-24+y1=0, 将 y1=-mt±2m2-m24+t2-4 代入得 m± m2+t2-4=0,∴t=±2, ∴MN 过双曲线的顶点,与题意不符,故舍去,∴t=4, 直线 MN 过定点(4,0).
第八章 平面解析几何
高考一轮总复习 • 数学
圆锥曲线——定点、定值、探究性问题
提能训练 练案[59]
高考一轮总复习 • 数学
定点问题
返回导航
第八章 平面解析几何
高考一轮总复习 • 数学
返回导航
第八章 平面解析几何
高考一轮总复习 • 数学
返回导航
[解析]
(1)由题意baa9=2-124,5b2=1,
得ab= =21, ,
∴双曲线 C:x42-y2=1.
第八章 平面解析几何
高考一轮总复习 • 数学
返回导航
(2)设直线 MN 的方程为 y=kx+m,M(x1,y1),N(x2,y2), y=kx+m,
联立x32-y32=1, 得(1-k2)x2-2kmx-m2-3=0, 则 1-k2≠0 得 k2≠1, Δ=4k2m2+4(1-k2)(m2+3)>0,得 m2>3k2-3, x1+x2=12-kmk2,x1x2=-1m-2-k2 3,
高三数学一轮复习:1208圆锥曲线中的探索性问题
例 2 已知中心在坐标原点 O 的椭圆 C 经过点 A(2,3),且点 F(2,0)为其右焦点. (1)求椭圆 C 的方程;(椭圆 C 的方程为1x62 +1y22 =1) (2)是否存在平行于 OA 的直线 l,使得直线 l 与椭圆 C 有公共点,且直线 OA 与 l 的距离等于 4?若存在, 求出直线 l 的方程;若不存在,请说明理由.
备用:已知圆 C:(x-1)2+y2=14,一动圆与直线 x=-12相切且与圆 C 外切. (1)求动圆圆心 P 的轨迹 T 的方程;(y2=4x) (2)若经过定点 Q(6,0)的直线 l 与曲线 T 交于 A,B 两点,M 是线段 AB 的中点,过 M 作 x 轴的平行线与 曲线 T 相交于点 N,试问是否存在直线 l,使得 NA⊥NB,若存在,求出 l 的方程;若不存在,请说明理由.
圆锥曲线中的探索性问题
探索性问题通常采用“肯定顺推法”,一般步骤为: (1)假设满足条件的元素(常数、点、直线或曲线)存在,引入参变量,列出方程(组)或不等式(组); (2)解此方程(组)或不等式(组); (3)若方程(组)有实数解,则元素(常数、点、直线或曲线)存在,否则不存在.
例 1(2019·全国Ⅰ) 已知点 A,B 关于坐标原点 O 对称,AB=4,⊙M 过点 A,B 且与直线 x+2=0 相切. (1)若 A 在直线 x+y=0 上,求⊙M 的半径; (2)是否存在定点 P,使得当 A 运动时,MA-MP 为定值?并说明理由.
பைடு நூலகம்
例 3 已知焦点在 y 轴上的椭圆 E 的中心是原点 O,离心率等于 23,以椭圆 E 的长轴和短轴为对角线的四
边形的周长为 4 5.直线 l:y=kx+m 与 y 轴交于点 P,与椭圆 E 交于 A,B 两个相异点,且A→P=λP→B.
高中数学考前归纳总结圆锥曲线中的探索性问题
即
k
2
(
3
8k 2 4k
2
2)
8k2 3 4k2
2m
0,
由已知条件知 k
0且 k
R,
m
k2 3 4k 2
1
1
,0 m
3 k2 4
4
故存在满足题意的点 P 且 m的取值范围是 (0, 1 ) 。 4
2. 直 线 l 与 椭 圆 y 2 4
x2
1 交 于 A(x1, y1 ) , B( x2 , y2 ) 两 点 , 已 知 m
k( x1 x2 2) ,
若存在点 P ( m,0) ,使得以 PM,PN为邻边的平行四边形是菱形,
由于菱形对角线垂直,所以 (PM PN).MN 0
又 PM PN (x1 m, y2 ) (x1 m, y2 ) (x1 y2 2m, y1 y2 )
MN 的方向向量是 (1,k ) ,故 k( y1 y2 ) x1 x2 2m 0 , 则 k2 (x1 x2 2) x1 x2 2m 0,
例 4、已知 B、C 是曲线 C: y2 4( x 1) 上不同两点,满足 OB OC ( 0, R) ,在
x 轴上是否存在点 A( m, 0) ,使得 AB AC ,若存在,求出实数
若不存在, 说明理由。 解: 设 BC : x ky 设 B( x 1,y 1),C ( x 2,y 2)
m 的取值范围;
1 |t | 2
( x1
x2 )2
4 x1 x1
| t | 4k 2 4t 2 16 k2 4
4t 2 1
2|t |
所以 AOB 的面积为定值 .
x m , m R . 若直线 l 关于 x 轴对称的直线为 l ,问直线 l 与抛
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥曲线专练14——圆锥曲线中的探索问题2(1)求椭圆的方程;(2)若动直线l 与椭圆E 交于A ,B 两点,且恒有0OA OB =,是否存在一个以原点O 为圆心的定圆C ,使得动直线l 始终与定圆C 相切?若存在,求圆C 的方程,若不存在,请说明理由.【解答】解:(1)由题意可得c e a ==, 设12F PF θ∠=,1||PF m =,2||PF n =,由椭圆的定义可得2m n a +=,由余弦定理可得2222242cos ()2(1cos )42(1cos )c m n mn m n mn a mn θθθ=+-=+-+=-+,所以22222222()2221cos ()2a c b b b mn mn m n aθ-+===+,当且仅当m n =(即P 为椭圆的短轴端点时)取得等号,且12F PF ∠取得最大值,此时△12PF F 的面积是122c b bc =②由222a b c =+,③,联立①②③解得2a =,1b =,c =则椭圆的方程为221:4x y +=(2)当直线l 的斜率不存在时,直线l 的方程设为x n =,由0OA OB =,可得AOB ∆为等腰直角三角形,则可设(,)A n n ,所以2244n n +=,即245n =,此时原点到直线l 的距离为d =;当直线l 的斜率存在时,设直线l 的方程为y kx m =+,1(A x ,1)y ,2(B x ,2)y ,原点O 到直线l 的距离为d ,所以d =,即为222(1)m d k =+,由2244y kx m x y =+⎧⎨+=⎩可得222(14)8440k x kmx m +++-=, △222(8)4(14)(44)0km k m =-+->,即2214k m +>,122814kmx x k +=-+,21224414m x x k -=+,2222222121212122224484()()()()141414m km m k y y kx m kx m k x x km x x m k km m k k k --=++=+++=+-+=+++,2222212122224445440141414m m k m k OA OB x x y y k k k----=+=+==+++,即225440m k --=,即2225(1)440d k k +--=恒成立,即22(54)(1)0d k -+=恒成立,所以2540d -=,所以d , 所以定圆C 的方程为2245x y +=, 所以当0OA OB =时,存在定圆C 始终与直线l 相切,其方程为2245x y +=. 2.在直角坐标系xOy 中,已知抛物线2:2(0)C x py p =>的焦点为F ,若椭圆(1)求抛物线C 和椭圆M 的方程;(2)是否存在正数m ,对于经过点(0,)P m 且与抛物线C 有A ,B 两个交点的任意一条直线,都有焦点F 在以AB 为直径的圆内?若存在,求出m 的取值范围;若不存在,请说明理由.【解答】解:(1)因为抛物线2:2(0)C x py p =>经过点2(,)3E t ,且8||3EF =.所以28323p +=,解得4p =,所以抛物线2:8C x y =,焦点(0,2)F ,2163t =由题意知221641392a bb ⎧+=⎪⎨⎪=⎩解得2264a b ⎧=⎨=⎩所以椭圆22:164x y M +=; 故抛物线C 的方程为28x y =,椭圆M 的方程为22164x y +=.(2)假设存在正数m 适合题意,由题意知直线AB 的斜率一定存在,设直线AB 的方程为y kx m =+,由28x yy kx m⎧=⎨=+⎩消去y ,整理得2880x kx m --= 因为直线与抛物线有两个交点且0m >,所以△264320k m =+> 设1(A x ,1)y ,2(B x ,2)y ,则128x x k +=,128x x m =-,所以222222121212121212()2()82,8864x x x x x x x x y y k m y y m ++-+===+==因为1122(,2),(,2)FA x y FB x y =-=-,所以221212122()412416FA FB x x y y y y m m k =+-++=-+-由题意知0FA FB <恒成立, 所以2212416m m k -+<恒成立因为k R ∈,所以21240m m -+<,解得66m -<<+又因为0m >,所以66m -<<+故存在正数m 适合题意,此时m的取值范围为(6-+.A ,过原点O 的直线l 与椭圆G 交于P ,Q 两点(点Q 在第一象限),且与线段AB 交于点M . (Ⅰ)求椭圆G的标准方程;(Ⅱ)是否存在直线l ,使得BOP ∆的面积是BMQ ∆的面积的3倍?若存在,求直线l 的方程;若不存在,请说明理由.【解答】解:(Ⅰ)由题意可知:2221b ca abc =⎧⎪⎪=⎨⎪=+⎪⎩,解得21a b c ⎧=⎪=⎨⎪=⎩.∴椭圆G 的标准方程为2214x y +=.(Ⅱ)设0(Q x ,0)y ,则0(P x -,0)y -,可知002x <<,001y <<. 若使BOP ∆的面积是BMQ ∆的面积的3倍,只需使得||3||OQ MQ =, 即00222(,)333OM OQ x y ==,即0022(,)33M x y .由(2,0)A ,(0,1)B ,∴直线AB 的方程为220x y +-=.点M 在线段AB 上,∴00242033x y +-=,整理得0032x y =-,① 点Q 在椭圆G 上,∴220014x y +=,②把①式代入②式可得2081250y y -+=, 判别式小于零,该方程无解.∴不存在直线l ,使得BOP ∆的面积是BMQ ∆的面积的3倍.(1)求椭圆E 的方程;(2)若A 是椭圆E 上的一个动点,求12AF AF 的最大值和最小值;(3)过椭圆E 的右焦点且与坐标轴不垂直的直线交椭圆于P ,Q 两点,线段2OF 上是否存在点(,0)M m ,使得OP MP PQ MQ =?若存在,求出实数m 的取值范围;若不存在,请说明理由(O 为坐标原点).【解答】解:(1)以双曲线2213x y -=的右焦点为右顶点,2a ∴,椭圆2222:1(0)x y E a b a b +=>>经过点3(1,)2,∴221914a b +=,b ∴∴椭圆E 的方程为22143x y +=,(2)设(2cos )A θθ,1(1,0)F -,2(1,0)F ,∴12(12cos AF AF θ=--,)(12cos θθ-,222)4cos 13sin cos 2θθθθ=-+=+,20cos 1θ,22cos 23θ∴+,即12AF AF 的最大值为2,最小值为3, (3)存在这样的点M 符合题意.设线段PQ 的中点为N ,1(P x ,1)y ,2(Q x ,2)y ,0(N x ,0)y , 直线PQ 的斜率为(0)k k ≠,注意到2(1,0)F ,则直线PQ 的方程为(1)y k x =-,由22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩消去y 得:2222(43)84120k x k x k +-+-=, 所以2122843k x x k +=+,故2012214()243k x x x k =+=+,0023(1)43ky k x k -=-=+.又点N 在直线PQ 上,所以22443k N k +,23)43kk -+,由OP MP PQ MQ =可得()20PQ MP MQ PQ MN +==, PQ MN ∴⊥,22230143443MNk k k k km k ++∴==--+,整理得22211(0,)34344k m k k ==∈++, 所以,在线段2OF 上存在点(,0)M m 符合题意,其中1(0,)4∈.2OF FA =.(1)求椭圆C 的标准方程;(2)是否存在过点A 的直线与椭圆C 相较于P 、Q 两点,且以线段PQ 为直径的圆过坐标原点O ,若存在,求出直线PQ 的方程;不存在,说明理由. 【解答】解:(1)由题意知,b =,(,0)F c ,10(A c c-,0),则(,0)OF c=,10(2,0) FA cc=-,由2OF FA=,得204c cc=-,解得:2c=.2226a b c∴=+=,∴椭圆的方程为221 62x y+=,=;(2)(3,0)A,设直线PQ的方程为(3)y k x=-,联立22(3)162y k xx y=-⎧⎪⎨+=⎪⎩,得2222(13)182760k x k x k+-+-=,设1(P x,1)y,2(Q x,2)y,则21221813kx xk+=+,212227613kx xk-=+.∴22222121212222276543[3()9](9)131313k k ky y k x x x x kk k k-=-++=-+=+++.由已知得OP OQ⊥,得1212x x y y+=,即2222222763306131313k k kk k k--+==+++,解得:k=,符合△0>,∴直线PQ的方程为3)y x=-.6.在平面直角坐标系xOy中,过定点(0,)C p作直线与抛物线22(0)x py p=>相交于A、B 两点.(Ⅰ)若点N是点C关于坐标原点O的对称点,求ANB∆面积的最小值;(Ⅱ)是否存在垂直于y 轴的直线l ,使得l 被以AC 为直径的圆截得弦长恒为定值?若存在,求出l 的方程;若不存在,说明理由.【解答】解:法1:(Ⅰ)依题意,点N 的坐标为(0,)N p -,可设1(A x ,1)y ,2(B x ,2)y ,直线AB 的方程为y kx p =+,与22x py =联立得22x py y kx p ⎧=⎨=+⎩,消去y 得22220x pkx p --=.由韦达定理得122x x pk +=,2122x x p =-.于是1212||2ABN BCN ACN S S S p x x ∆∆∆=+=-12||p x x =-=2p =∴当0k =时,2()ABN min S ∆=.(Ⅱ)假设满足条件的直线l 存在,其方程为y a =,AC 的中点为O ',l 与AC 为直径的圆相交于点P ,Q ,PQ 的中点为H ,则O H PQ '⊥,O '点的坐标为111(,)22y p x +.1||||2O P AC '=111|||||2|22y p O H a a y p +'=-=--, 22222211111||||||()(2)()()442pPH O P O H y p a y p a y a p a ''∴=-=+---=-+-,221||(2||)4[()()]2pPQ PH a y a p a ∴==-+-.令02pa -=,得2p a =,此时||PQ p =为定值,故满足条件的直线l 存在,其方程为2p y =, 即抛物线的通径所在的直线. 解法2:(Ⅰ)前同解法1,再由弦长公式得22222222121212|||()4148212AB x x x x x x k p k p p k k -=+-=++=++,又由点到直线的距离公式得d =.从而22211||2122221ABN S d AB p k k p k ∆=⋅=++=+,∴当0k =时,2()ABN min S ∆=.(Ⅱ)假设满足条件的直线l 存在,其方程为y a =,则以AC 为直径的圆的方程为11(0)()()()0x x x y p y y --+--=,将直线方程y a =代入得211()()0x x x a p a y -+--=, 则2212111||4()()4[()()]2px x x a p a y a y a p a -=---=-+-.设直线l 与以AC 为直径的圆的交点为3(P x ,3)y ,4(Q x ,4)y ,则有34||||PQ x x =-=.令02p a -=,得2p a =,此时||PQ p =为定值,故满足条件的直线l 存在,其方程为2py =,即抛物线的通径所在的直线.。
