数模:纯净水安全监控问题
第六届苏北数学建模联赛试题B题-纯净水安全监控问题模糊模型建立
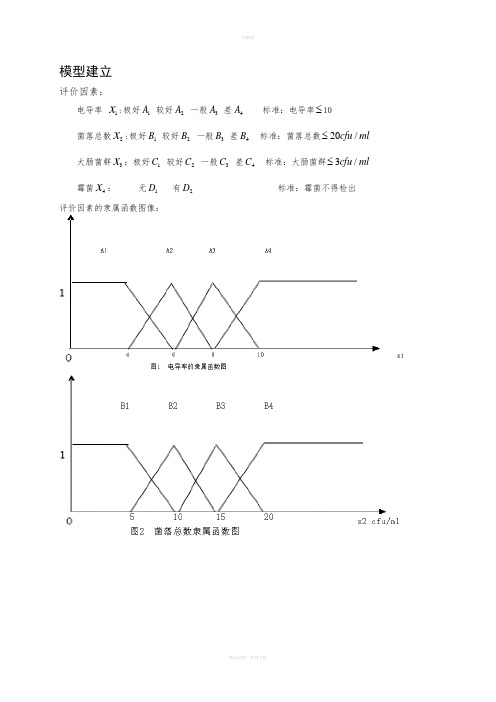
模型建立评价因素:电导率1x :极好1A 较好2A 一般3A 差4A 标准:电导率≤10菌落总数2x:极好1B 较好2B 一般3B 差4B 标准:菌落总数20/cfu ml ≤大肠菌群3x :极好1C 较好2C一般3C 差4C 标准:大肠菌群3/cfu ml ≤霉菌4x: 无1D 有2D 标准:霉菌不得检出评价因素的隶属函数图像:评价因素的隶属函数:由图1,电导率的隶属函数为:1146()4626Axxx xxμ⎧≤⎪-⎪=<≤⎨⎪>⎪⎩242820446 ()688xA xxxxxxμ--⎧≤⎪<≤⎪=⎨<≤⎪⎪<⎩3621020668()810100x A xx x x x xμ--⎧≤⎪<≤⎪=⎨<≤⎪⎪<⎩48208()810101x A x x x xμ-⎧≤⎪=<≤⎨⎪<⎩ 由图2,菌落总数的隶属函数为:110515()510100xB x x x xμ-⎧≤⎪=<≤⎨⎪<⎩ 25515505510()1015150x B xx x x x x μ--⎧≤⎪<≤⎪=⎨<≤⎪⎪<⎩31052050101015()1520200x B xx x x x xμ--⎧≤⎪<≤⎪=⎨<≤⎪⎪<⎩4155015()1520201x B x x x xμ-⎧≤⎪=<≤⎨⎪<⎩ 由图3,大肠杆菌群的隶属函数为:120.51 1.5() 1.5 2.02.00xC x x x xμ-⎧≤⎪=<≤⎨⎪<⎩ 2 1.50.52.50.50 1.51.52()2 2.52.50x C x x x x x x μ--⎧≤⎪<≤⎪=⎨<≤⎪⎪<⎩320.530.5022 2.5() 2.5330x C x x x x x xμ--⎧≤⎪<≤⎪=⎨<≤⎪⎪<⎩4 2.50.50 2.5() 2.5 3.03.01x C x x x xμ-⎧≤⎪=<≤⎨⎪<⎩ 由图4,霉菌的隶属函数为:110()00D x x x μ=⎧=⎨>⎩200()10D x x x μ=⎧=⎨>⎩纯净水质量安全评价模型建立纯净水质量安全标准111121111211112()()()P D A C B B D B C A A D A B C C =⋅⋅⋅⋅⋅⋅⋅⋅⋅()(()()())(()()())(()()())1111211121112x x x x x x x x x x D A C B B B C A A A B C C μμμμμμμμμμμ⎡⎤=∧∧∧∨∧∧∨∧∧⎢⎥⎢⎥⎣⎦对于待评定水有:评判假设:对于质量安全评估相同时,我们对于样本抽取量多的更注重其稳定性,故而排名在前,当其抽取样本数也相同时,则因环境污染而更相信从前的纯净水,从而按日期从前到后排列对于第一问:现实数据分析:质量安全评估1 1 1 1 1 1 1 1 1 1 1 0.94 0.885 0.765 0.72 0.615I0 D 0 D 0 D 0 A 0 A 0 B 0 H 0 B 0I 0 A 0 A 0 B 0 H 0 D 0 A 0 C 0 A此上为该城区所有批次的纯净水进行评判排序结果,其中1为绝对放心,0为质量最次对于第二问受检方 纯净水安全系数F 1G 1 E 1 B 0.9477 C 0.4286 A 0.35 I 0H 0 D1为绝对放心,0为质量最次,此权重值采取均值评判,纯净水安全系数i iin p P n ∑=∑,其中n 为采样品数,i p 为质量安全评判系数i n N ∑=,N 为该厂样品抽取总次数 电导率排序 受检方 纯净水安全系数 F 1 1 0 1 C 0.42861 0 1 G111E 1 1 0 1 B 0.94770.93094 0.0787 0.96406 D 0 0.4458 0.3875 0.6356A0.35 0.212250.1955I 0 0 0 0 H 0菌落总数排序受检方纯净水安全系数 F 1 1 0 1 G 1 0 0 0 E 1 1 0 1 C 0.4286 1 0 1 B 0.9477 0.6875 0 0.6875A 0.35 0.6 0 0.6 I 0 0.3333 0 0.33333 D 0 0.1667 0 0.1667H 0 0.2 00.2 大肠菌群排序受检方纯净水安全系数F 1 1 0 1G 1 1 0 1 E 1 1 0 1 B 0.9477 1 0 1 A 0.35 1 0 1 I 0 1 0 1H 0 1 0 1 D 0 1 0 1 C 0.4286 0.428570.571431霉菌和酵母排序受检方 纯净水安全系数 F 1G 1 1 E 1 1 B 0.9477 1 C 0.42861 H 0 1 I 0 1 A0.350.95D 0 0.33333观察表格可知1为绝对放心,0为质量最次,此权重值采取均值评判,纯净水安全系数i iik d d k ∑=∑,其中k 为采样品数,i d 为各指标专项质量安全评判系数i k K ∑=,K 为该采样地点样品抽取总次数1为绝对放心,0为质量最次,此权重值采取均值评判,纯净水各安全系数i iim q Q m ∑=∑,其中m 为采样品数,i q 为污染指标对应质量安全评判系数i m M ∑=,M 为该厂样品抽取总次数A 公司仓库和销售网点都管理不善B 公司仓库管理不善,但仓库更糟D 公司仓库和销售网点都管理不善,但仓库更糟,且比A 、B 公司都糟对问题四设置各公司检验批次的分布,使得抽检方案的针对性最优(即检出的风险性为最大)所以在分布在受检方 纯净水安全系数A 0.35B 0.9477 0.930940.07870.96406C 0.42861 0 1 D 0 0.44580.38750.6356E 1 1 0 1F 1 1 0 1G 1 1 0 1H 0 0 00 I 0A 0.6 0 0.6B 0.68750 0.6875C 1 0 1D 0.16670 0.1667E 1 0 1F 1 0 1G 0 0 0H 0.2 0 0.2 I0.33330.33333A101B101C0.428570.571431D101E101F101G101H101I101B1C1D0.33333E1F1G1H1I1100次抽检根据以下表格结果进行可编辑.精品文档,欢迎下载。
数学建模案例分析-- 模糊数学方法建模4控制与调节废水排放的模糊控制策略

§4 控制与调节废水排放的模糊控制策略研究一条受到污染的河流,总是先寻找其污染源在何处,然后就可采取处理措施以保护环境。
这里研究的是工业污染源(或称点源)问题,一条受到复杂的工业污染源污染的河流,如果解剖其为最基本的形态就称为污染细胞。
污染细胞不外乎如下图所示的关系造成,图中:a )系由已经汇入许多污染源的排污沟入河;b )系污染源直接入河。
在图中,无论a )或b ),总可以把它用三个断面来控制。
令排污口(或排污河)出口断面为A ;以河流接受污染物前的断面(本底断面)为B ;混合以后的干河下游断面为C 。
如果假定在中小河流中污染物一旦排入干河,则在流向下游很短的距离内即可达到断面完全混合。
因此,在制作模糊控制污染物排放策略时,不再考虑距离远近和某些污染物随时间的降解(随时间而变化的降解值,相对于模糊语言来讲,在短距离之内可以忽略),同时也不再考虑污染物的横向不均匀扩散和纵向分散以及底泥、藻类等待因素。
这样一来A 、B 、C 三者的平衡关系可表示为:A AB B A BC W L W L qQ qL Q L L +=++=(1)式中C B A L L L ,,分别表示A 、B 、C 断面监测的水质参数的浓度; Q 表示干河在汇入排污口(或排污沟)前的流量; q 表示排污口(或排污沟)的流量; A B W W ,分别表示B 、A 的权重。
一、模糊集合概念的建立如果我们把浓度为~A L 的污水在排污口(或排污沟)出口断面A 处的污水排放浓度的量级用零、小、中、大、特大等模糊语言的辞来表达,每一个辞就可以看作是基础变量为浓度值的一个模糊限制标记。
它可以由隶属函数来表征,隶属函数把基础变量的每一个值与区间[0,1]中的一个数结合起来,这个数就表示了每个值与模糊限制间的隶属度。
如果我们把某水质参数在A 断面的浓度作为语言变量在其基础变量为0,0.01,0.1,0.5……mg/L 之间的浓度值。
那么,“小”、“中”、“大”……等这些辞的语言值就可以解释是基础变量数值上的一个模糊限制的标记。
纯净水安全监控问题

2009年“百年矿大杯”第六届苏北数学建模联赛承诺书我们仔细阅读了第六届苏北数学建模联赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与本队以外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们愿意承担由此引起的一切后果。
我们的参赛报名号为:参赛组别(本科或专科):本科参赛队员(签名) :队员1:队员2:队员3:获奖证书邮寄地址:2009年“百年矿大杯”第六届苏北数学建模联赛编号专用页参赛队伍的参赛号码:(请各个参赛队提前填写好):竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):2009年“百年矿大杯”第六届苏北数学建模联赛题目纯净水安全监控问题摘要目前日趋严重的水污染对人类的生存安全构成重大威胁,因此,对饮用纯净水安全监控具有很大的必要性。
本文主要针对某城区近年的纯净水检测报告,对该城区的用水情况进行了分析和讨论。
运用层次分析法和模糊综合评价两种评价模型对已检测批次的纯净水按风险系数进行了评判排序,并用均值模型、加权均值模型和聚类分析的三种方法对各公司按风险度进行了公司的排序和分类综合评价。
用柱状图、饼图和通过MATLAB7.0和Mathematica软件模拟,得出了各危害指标的分布规律,对该城区部分公司的管理情况进行了讨论。
然后再一次运用层次分析法,另建立一个动态规划模型对总的100次检测批次进行了分配,并对该城区提出了自己的观点。
综合得到以下几点主要结论得到了各批次的纯净水的评判排序。
得到了公司的排序,并对公司进行了分类综合评价。
绘出了纯净水生产流通环节的危害指标分布规律,讨论了A、B、D公司的管理状况。
数学建模表中一条河流一年水质评价问题(一)

数学建模表中一条河流一年水质评价问题(一)数学建模表中一条河流一年水质评价问题问题背景在数学建模表中,我们需要对一条河流的水质进行评价。
该河流主要影响周围居民的饮水、农业灌溉以及生态环境等方面。
相关问题及解释1. 水质评价指标选择问题问题描述:在评价河流水质时,需要选择适当的指标来衡量水质的好坏。
解释说明:不同指标反映了水质不同的方面,例如水中溶解氧含量、水温、PH值、浊度等。
我们需要选择合适的指标来综合评价水质。
2. 数据采集问题问题描述:如何获取水质评价所需的数据?解释说明:为进行水质评价,我们需要收集一年内河流各个时刻的水质数据,包括各项指标的数值。
数据的采集方式可能包括现场监测、实验室化验等方法。
3. 数据预处理问题问题描述:在进行水质评价前,是否需要对原始数据进行预处理?解释说明:原始数据可能存在异常值、缺失值、噪声等问题。
为了保证评价结果的准确性,我们可能需要对数据进行清洗、填补缺失值、平滑等预处理操作。
4. 数据分析问题问题描述:如何利用采集到的水质数据进行评价?解释说明:通过对水质数据的分析,可以得到一些重要的统计特征,例如平均值、方差、极差等。
这些特征可以用于评价水质的稳定性、变化趋势等。
5. 水质评价模型建立问题问题描述:如何建立合适的数学模型来进行水质评价?解释说明:根据不同的水质评价目标和数据特点,我们可以选择不同的数学模型,例如线性回归模型、逻辑回归模型、支持向量机模型等。
建立合适的模型是进行准确评价的基础。
6. 模型参数估计问题问题描述:如何对水质评价模型进行参数估计?解释说明:参数估计是模型求解的关键步骤。
通过拟合已知数据,我们可以估计出模型中的参数值,以便进行后续的预测和评价。
7. 模型评价问题问题描述:如何对已建立的水质评价模型进行评价?解释说明:为了验证模型的准确性和可靠性,我们需要对模型进行评价。
常用的评价指标包括均方误差、相关系数等,通过这些指标可以衡量模型的拟合程度和预测精度。
2005全国大学生数学建模竞赛题目A

长江水质的评价和预测摘要本文用模糊数学的方法,通过计算各评价因子的隶属度和权重,得到了长江近两年多的水质情况的综合评价结论:Ⅰ类水比例为25%、Ⅱ类水比例为23%、Ⅲ类水比例为20%、Ⅳ类水比例小于1%、Ⅴ类水比例为30%、劣Ⅴ类水比例小于2%,如下面饼图,其中可饮用水比例为68%,不可饮用水比例为32%。
结果显示不可饮用水的比例很大,可以说明长江污染情况已经相当严重。
对于问题(2),我们通过建立反映长江水质的一维稳态微分方程模型,并求解得到各观测站浓度的计算公式,用Matlab编程计算,计算结果显示,高锰酸盐污染源主要在:湖北宜昌南津关和湖南岳阳城陵矶。
氨氮污染源主要在:重庆朱沱和湖南岳阳城陵矶。
对于问题(3),根据近10年的水文年数据建立灰色系统预测模型,得到了未来10年长江全流域、干流、支流河长百分比的值,据此画出相应的走势图,由此确定水质污染的发展趋势,我们的结论是:长江未来10年的污染会越来越严重。
对于问题(4),我们首先建立排污量的灰色系统预测模型,得出未来10年的排污总量,根据长江干流的Ⅳ类和Ⅴ类水的比例控制在20%以内,且没有劣Ⅴ类水的要求,建立了每年需要处理污水量的计算公式,得到了未来10年每年需要处理的污水量,见下表(单位:亿吨):年份需处理的污水量年份需处理的污水量2005 19.5390 2006 132.67772007 143.4669 2008 193.97292009 225.4419 2010 276.02932011 316.5134 2012 367.89582013 413.7736 2014 463.8682关键词:模糊数学隶属度权重微分方程灰色系统一、问题重述自2004年10月“保护长江万里行”行动发起后,考察团对沿线21个重点城市做了实地考察,认识到了母亲河长江受到了严重的污染,为此,专家提出了拯救长江的呼唤,给出了下面这些有待解决的问题。
(1)对长江近两年多的水质情况做出定量的综合评价,并分析各地区水质的污染状况。
2023华为杯数学建模b题讲解

2023华为杯数学建模b题讲解在2023华为杯数学建模竞赛中,B题是一个需要运用数学建模和优化方法的问题。
本文将对该题进行详细讲解。
题目描述:某城市的水厂需要供应4个区域的自来水。
水厂有两个供水站,每个供水站的供水量和水质不同。
假设供水站1每小时供水300立方米,水质好,水质指数为1。
供水站2每小时供水500立方米,水质较差,水质指数为0.8。
四个区域对水质的要求不同,水质指数分别为0.5、0.6、0.7和0.8。
每个区域的用水量也不同,用水量分别为200、300、400和500立方米。
为了保证供水质量,水质指数需要达到或超过该区域的水质指标。
请问,如何安排供水站的供水量,以满足四个区域的用水需求,并使得总供水量最小?解题思路:为了解决这个问题,我们需要进行数学建模和优化。
首先,我们需要定义一些变量和参数。
变量:X1:供水站1的供水量(小时为单位)X2:供水站2的供水量(小时为单位)参数:C1:供水站1的供水速率(立方米/小时)C2:供水站2的供水速率(立方米/小时)Q1:区域1的用水量(立方米)Q2:区域2的用水量(立方米)Q3:区域3的用水量(立方米)Q4:区域4的用水量(立方米)I1:供水站1的水质指数I2:供水站2的水质指数I3:区域1的水质指标I4:区域2的水质指标I5:区域3的水质指标I6:区域4的水质指标目标函数:Minimize:X1 + X2约束条件:1. 供水量必须满足各个区域的用水量:X1 + X2 >= Q1X1 + X2 >= Q2X1 + X2 >= Q3X1 + X2 >= Q42. 供水质量必须满足各个区域的水质指标:X1 * I1 + X2 * I2 >= Q1 * I3X1 * I1 + X2 * I2 >= Q2 * I4X1 * I1 + X2 * I2 >= Q3 * I5X1 * I1 + X2 * I2 >= Q4 * I63. 供水量必须大于等于0:X1 >= 0X2 >= 0通过以上的数学建模,我们可以得到一个线性规划问题。
城市纯净水供水策略数学建模
城市纯净水供水策略数学建模摘要:一、引言二、城市纯净水供水策略的现状与问题三、数学建模在城市纯净水供水策略中的应用四、具体建模方法与案例分析五、结论正文:【引言】随着城市化进程的加速,城市用水需求不断增长,保障城市居民饮用水质量已成为当前城市水资源管理的重要任务。
为了解决这一问题,本文将探讨城市纯净水供水策略数学建模的方法,以期为我国城市水资源管理提供有益参考。
【城市纯净水供水策略的现状与问题】目前,我国城市纯净水供水策略主要面临以下问题:1.水资源短缺:随着城市人口的增长,用水需求不断上升,而水资源供给却相对有限,这导致了城市水资源短缺的问题。
2.水质问题:城市水源地受到污染,使得供水水质难以达到国家相关标准,对居民生活健康造成威胁。
3.供水系统不完善:城市供水系统存在诸多问题,如水量不足、供水压力不稳定等,影响了居民用水质量。
【数学建模在城市纯净水供水策略中的应用】数学建模作为一种科学方法,可以通过建立数学模型来研究城市纯净水供水策略问题,为解决上述问题提供理论支持。
【具体建模方法与案例分析】本文以某城市为例,采用系统动力学方法建立城市纯净水供水策略的数学模型。
具体步骤如下:1.确定模型变量:根据城市水资源管理的实际情况,选取相关变量,如城市人口、用水量、水源地水质、供水设施等。
2.建立模型方程:根据水资源管理的目标,建立数学模型方程,描述各变量之间的关系。
3.模型参数估计:通过收集相关数据,对模型参数进行估计。
4.模型仿真与分析:利用计算机软件对建立的数学模型进行仿真,分析不同供水策略下的水资源管理效果。
5.模型优化与应用:根据仿真结果,对模型进行优化,为城市纯净水供水策略提供参考。
【结论】通过数学建模方法研究城市纯净水供水策略,有助于解决水资源短缺、水质问题以及供水系统不完善等问题。
水质检测的数学模型
水质指标评价问题的数学模型摘要生活用水一直是关系到民生的根本问题,是国家和政府一直在重点保护和治理的项目之一。
近年来,随着工业化、信息化步伐的加快,水质污染问题越来越突出。
本文通过对商丘某县四口水井水质标准建模分析,希望为该村,为其他有类似问题的地方,提供水质量评价标准和预防污染的借鉴方法。
针对问题一,通过主成分分析和R型聚类分析两种方法,在减少指标的同时保留尽量多的原始信息。
对主成分分析法,通过计算机模拟、软件求解,得出四口井的得分,据此得出结果;对聚类分析法,通过聚类减少指标量,然后根据密切值法得出四口井的排名。
主成分分析模型的结果南井第一,北井第二,东井第三,西井第四;R型聚类分析模型结果为东井第一,南井第二,西井第三,北井最后。
针对问题二,首先提取水质检测数据和水质分级标准表中都有的指标,然后剔除水质分级标准中各水质类型均相同的指标,确定八个指标为本问题的原始指标。
将水质分级标准表中的I类、II类、III类三类数据当作水井样本,和原来四口水井一起,组成一个样本容量为七、指标个数为八的新样本组合,利用问题一的主成分分析模型,通过软件求解,得出七个井的得分,对这七口井进行排名,然后根据排名确定水质分级。
针对问题三,结合问题一二的计算结果,从描述四口水井的概况开始,有针对性的分析污染原因,以及污染影响和对应的整治措施,为村民们提供较好的处理污染的方法,根据一些健康的饮水常识,为村民今后的饮水健康提出几点有意义的建议。
关键词:聚类分析法;主成分分析法;密切值法;水污染检测;指标;无量纲化;1问题的重述河南省商丘地区某村内有各相距500米以上的四口水井,分别位于村东、村西、村南和村北,由于农业和生活排放废物使地下浅表水遇到污染,水质监测资料如表1所示.表1:水质监测数据2009 年10月15日商丘某村井水水质监测数据报告编号:商水监/ SM089-2009 监测日期:2009.10.152009 年10月15日商丘某村井水水质监测数据/ SM089-2009 监测日期:2009.10.15报告编号:商水监(1)请用2种以上的数学方法对该村的四个井水的水质进行排序,并比较是否由于方法的不同导致存在着异,以及差异产生的原因。
水质监测的数模算法
水质评价问题分析摘要本文要求根据水质检测数据对东、西、南、北四口井进行水质评价排序并查找相应的水质污染原因,再根据题中所给附表1的水质分级标准对每口井进行水质等级的分类。
针对问题一:(1)首先运用模糊数学的思想,建立模型一:模糊排序模型,得到四口井水质的优劣排序为:南井>东井>北井>西井,其次运用层次分析法,建立模型二:综合权重模型,与模型一比较,运用M atlab软件得到排序:南井>东井>北井>西井。
然后为克服模型一、二的主观因素,建立模型三:因子分析模型,通过SP SS和M arkway软件得到四口井的排序为:南井>北井>东井>西井。
最后为了进一步检验,运用Toppsis法,建立模型四:最优综合评价模型,通过D P S演算,得出水质按由好到差排序:北井<南井<东井<西井。
(2)通过对四个模型的分析,由于各种方法所关注的环境因素不同,因此不同环境因素的评价不相同,并且有主观因素的影响,造成不同的模型得出了不同的答案。
针对问题二:首先根据模糊数学的思想,建立模型五:模糊综合评价模型,得出南井、西井的水质为第二类水,东井、北井为第三类水。
然后为了排除主观因素对结果的影响,根据灰色聚类分析法建立模型六:灰色变权聚类分析模型,对其进行再一次的等级分析,得出了相同的结果南井、西井的水质为第二类水,东井、北井为第三类水。
验证了我们结果的正确性。
针对问题三:由题目可知水质的污染主要是由于农业和生活排放的废物造成的,针对这些问题提出五点建议,同时也提出了一个生态循环模式(人畜粪便、动植物遗体→沼气→村民日常生活新能源以及农作物)来减少生活废物对水质的污染。
关键词:模糊排序模型因子分析模型综合权重灰色变权聚类分析生态循环模式一.问题重述某村内有分别位于村东、村西、村南和村北各相距500米以上的四口水井,由于农业和生活排放废物使地下浅表水遇到污染,水质监测资料如表1所示:请成以下问题:1.用2种以上的数学方法对该村的四个井水的水质进行排序,并比较方法不同所致的差异及差异产生的原因。
城市纯净水供水策略数学建模
城市纯净水供水策略数学建模摘要:一、引言1.城市供水问题的重要性2.纯净水供水策略的研究背景3.本文的研究目的和意义二、城市供水现状及挑战1.我国城市供水现状2.面临的主要挑战3.供水问题对城市发展的影响三、数学建模方法在供水策略中的应用1.数学建模方法简介2.供水策略的数学模型构建3.模型求解与分析四、城市纯净水供水策略优化建议1.水源选择与保护2.净水处理技术改进3.输配水系统优化4.用户端节水措施推广五、案例分析1.某城市供水现状简介2.应用数学模型进行供水策略优化3.优化结果与成效分析六、总结与展望1.本文研究成果总结2.研究的局限性与不足3.未来研究方向与前景正文:一、引言随着我国城市化进程的加速推进,城市供水问题日益凸显,如何保障城市居民饮用水的安全与充足,已成为当前亟待解决的问题。
本文以数学建模方法为基础,对城市纯净水供水策略进行研究,旨在为城市供水管理提供科学依据。
二、城市供水现状及挑战我国城市供水主要依赖地下水和地表水,然而随着环境污染的加剧,水质问题日益严重。
供水不足、水质不达标等问题已成为制约城市发展的瓶颈。
解决城市供水问题,对保障居民生活、促进城市可持续发展具有重要意义。
三、数学建模方法在供水策略中的应用数学建模是一种将实际问题抽象为数学问题,并加以求解的方法。
本文通过构建供水策略的数学模型,分析影响供水效果的关键因素,为供水策略优化提供理论支持。
四、城市纯净水供水策略优化建议针对供水存在的问题,本文提出从水源选择与保护、净水处理技术改进、输配水系统优化、用户端节水措施推广等方面进行策略优化,以提高供水质量和效率。
五、案例分析本文选取某城市为案例,运用数学模型对其供水策略进行优化。
结果表明,优化后的供水策略在保障供水质量和效率方面取得了显著成效。
六、总结与展望本文运用数学建模方法对城市纯净水供水策略进行了研究,并提出了优化建议。
虽然研究取得了一定的成果,但仍需进一步完善和拓展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
纯净水安全监控问题何挺 严茂花 叶宁内容摘要水是人类赖以生存的资源,日趋加剧的水污染,已对人类的生存安全构成重大威胁,成为人类健康、经济和社会可持续发展的重大障碍,对水污染的研究,在现实社会中有着重大的的意义。
本文是针对九家纯净水公司的具体检查情况建立模型对九家纯净水公司进行综合评价。
模型I:针对问题1,本文建立了综合评价模型。
首先,对题中所给的数据进行无量纲化处理, 建立纯净水风险评价指标体系,采用专家给出的各个项目(危害因素)的权值1234,,,w w w w 分别为0.17,0.25,0.28,0.30,最后给出纯净水安全风险分析的科学评价方法,即建立综合评价模型12340.170.250.280.30y x x x x =+++并对城区所有批次的纯净水进行了评价排序。
针对问题2,本文在模型I 的基础上进行求解,由九家公司每个项目(危害因素)的均值得到各公司纯净水中四个项目的得分权重,即各公司的风险度。
风险度排序评价为:D H B I A C FE G >>>>>>>>公司公司公司公司公司公司公司公司公司然后对他们分类综合评价,指出了各公司产品的主要可能的危害因素,并给出了同类公司的实际特点。
模型II :针对问题3,本文建立了熵权模型,通过熵值法求出四个危害因素在不同环节的权重,据此分析得出纯净水在生产流通环节的危害因素以及各个危害指标的分布规律,并在此基础上,讨论得出A B D 、、公司的管理状况。
模型III:针对问题4,我们在现有的历史数据下,求出各个危害因素所占的百分比,据此得到每家公司在下一年度100个批次的检验总数中的检验分配数,在此基础上,我们建立以检测出不合格品的风险度最高为目标函数的整数线性规划模型,利用LINGO 求解,可得到各公司检验批次的分布。
针对问题5,结合上述结果,本文评价了该城区的饮用水安全形势并给出了监控对策(见正文)。
关键词:综合评价 危害因素 熵权模型 熵值法 线形规划 LINGO 软件一问题重述1.1问题背景水是人类赖以生存的资源,日趋加剧的水污染,已对人类的生存安全构成重大威胁,成为人类健康、经济和社会可持续发展的重大障碍。
据世界权威机构调查,在发展中国家,各类疾病有8%是由于饮用了不卫生的水而传播的,每年因饮用不卫生水至少造成全球2000万人死亡,因此,水污染被称作"世界头号杀手"。
纯净水的安全危机的爆发,往往是日常的监控机制和管理长期存在漏洞的反映。
完整、有效的纯净水安全风险分析监测预控,为政府及有关部门实施控制措施提供决策依据和技术支持,可以有效提高纯净水安全监管效率和管理水平,及时化解可能出现的安全危机。
近年来,我国在从国家宏观层面探讨建立纯净水安全预警机制的研究方面,已取得了不少理论成果但由于我国地域辽阔,经济社会发展水平很不平衡,如何构建有效的预警机制并应用到饮用水安全监控过程还处于起步阶段。
本问题主要考虑纯净水的以下危害因素: (按照危害的严重性依次给出)“电导率”: 是纯净水的特征性指标,反映的是纯净水的纯净程度,以及生产工艺控制的好坏,“电导率”根本达不到国家卫生标准要求,与自来水无异,根本不能算做纯净水。
菌落总数: 是指纯净水检样经过处理,在一定条件下培养后所取1ml(g)检样中所含菌落的总数。
它可以作为判定纯净水被污染程度的指标之一。
大肠菌群:反映纯净水加工过程中对大便污染程度的一个指标。
数值越高证明污染越严重。
霉菌:食物霉变后产生,直接引起中毒,或产生致癌物质,毒害人体。
1.2问题的提出某城区共有九家生产并销售纯净水的公司,其中A公司和B公司规模较大,其余均为小公司。
针对该城区提供的近年的关于各公司的纯净水检测报告(见附件),请你利用数学建模的方法回答以下问题:1、结合本问题所给数据,给出纯净水安全风险分析的科学评价方法,确定评价的标准和评价的规则,对该城区所有批次的纯净水进行评判排序。
2、对该城区范围内的监控对象(各公司)按风险度进行排序评价,并对它们分类综合评价,指出各公司产品的主要可能的危害因素,并指出同类公司的实际特点。
3. 对检测出的不合格的样品成因分析:评价纯净水生产流通环节(归为仓库和销售网点两类)的危害因素以及各个危害指标的分布规律,并通过四类危害指标的分析,讨论A、B、D公司的管理状况。
4.国家相关部门每年要面对各种专项检验,对于纯净水专项检验的投入经费有限,已知该城区下一年度投在纯净水方面的检验总批次为100个批次,在现有历史数据的基础上,并考虑各公司的实际运行状况,如何设置各公司检验批次的分布,使得抽检方案的针对性最优(即检出的风险性为最大)。
5.结合你的工作,请你给该城区食品安全委员会写一篇短文,阐述你的观点,评价该城区的饮用水安全形势并给出监控对策。
二问题分析2.1问题1的分析首先,对题中所给的数据进行分析,同各个项目的标准值进行比较,得到每家公司各个批次的纯净水中不符合要求的纯净水的批次。
其次,建立纯净水风险评价指标体系,由专家打分给出的四个项目的权重。
最后,根据四个项目的权重建立综合评价模型,并利用此模型对该城区所有批次的纯净水进行评判排序。
2.2问题2的分析问题要求对城区范围内的监控公司按风险度进行排序评价,我们在找出九家公司每个指标的平均值的基础上,利用问题1中所建立的综合评价模型(模型I ),求出九家公司的纯净水中四个指标加起来的风险度,即为各公司的风险度;接着分别按四个危害因素将九家公司进行排序评价,由此评价,可以看出各公司的主要危害因素。
根据主要危害因素,我们指出了同类公司的实际特点。
2.3 问题3的分析根据题中所给数据找出的不合格的样品所对应的环节,找出四个危害因素在各个环节的权值,因为抽取的样品中,存在一定的不确定度,所以我们建立了熵权模型,利用熵值法解决这一问题,并且给出各个危害指标的分布规律。
在此基础上,我们通过分析,讨论得出A B D 、、公司的管理状况。
2.4 问题4的分析本问要求我们设置各公司检验批次的分布,使得抽样方案的针对性最优,也即根据历史数据,使得在下一年度抽样检验中各公司生产的纯净水被检验到不合格的风险度最大,由于批次的分配数目不仅仅要落实到各家公司,还要具体到各家公司的两个环节(仓库和销售网点),所以我们先根据现有的历史数据,在算出各个危害因素所占的百分比的前提下,确定分配到各家公司的检验批次,再以检测出不合格品的风险度最高为目标函数,建立线形整数规划,在LINGO 软件中求解,得到每家公司在各个环节的检验次数,也即各公司检验批次的分布。
三 模型假设1.假设项目4(霉菌和酵菌)中,标准值不得检出记为0值;2.各批次有一个危害因素不合格则视为该批次不合格;3.假设同一批次的纯净水各项检测指标都一样;4.在一年内没有被检查,则视为该批次在这一年为合格;5.所有的数据都客观准确;6.不考虑四种因素以外的因素的影响;7.在一定时期内,各公司的管理方式不变。
四 符号约定i x i i :表示第个项目(危害因素)(=1...4);, i i x x :标准化后的数据;:i i i i M x m x :表示的最大值;表示的最小值;:i w 各个项目(危害因素)的权重(i=1,2,3,4);:i w i ,第个危害因素在各个环节的权重;:=129i p i i L 第公司的不合格数(,);:;ij y i j 第个危害因素下第个时间检测样品数量:ij z i j 第个危害因素下第个时间检测的值;:Q 抽样方案风险度;ij q i j :第个公司在第个环节的风险度;:ij R i j 第个公司在第个环节抽样分配数;i N i :第个公司的抽样分配个数;j S j :第个环节抽样分配数。
五 模型的建立与求解5.1模型I 的建立与求解(针对问题1) 5.1.1 模型I 的建针对问题1,本文建立了综合评价模型。
假设A B C D E F G H I 、、、、、、、、这九个公司为评价对象,共有四个评价指标(项目)电导率、菌落总数、大肠菌群、霉菌和酵母,分别记为123x x x 、、和4x 。
首先:对四个指标进行无量纲化处理,也即标准化处理:因为这四个指标都是极小型指标,所以对数据直接进行极差变换将数据标准化,即i ii i i x m x M m -=-,,各个指标对应的数据变为如下表:表1:标准化后的数据,结合风险评价的理论及实际分析,我们建立了纯净水风险评价指标体系如图1。
从图1 中可以看出,多风险因素的递阶结构图分为二层,目标层为u ,准则层为1234,,,u u u u 。
通过建立这个评价指标体系,基本上可以反映出纯净水风险的基本情况。
图1最后:建立综合评价模型(模型I ):由四个指标的权重,可建立综合评价模型41i ii y w x ==∑5.1.2 模型I 的求解通过建立的评价指标体系(如上图1),可由专家为各个指标打分,得出各个指标的权重1234,,,w w w w 分别为0.17,0.25,0.28,0.30,所以综合评价模型为:12340.170.250.280.30y x x x x =+++利用该评价模型对城区所有批次的纯净水进行评判排序,可得下表:表2:各批次排序表排序 1 2 3 4 5 6 7受检 方 B B G C E A A 批号 20090109 20080827 20070512 20070425 20070425 20071220 20071218 得分(权重) 0.03094 0.03145 0.0545 0.0567 0.0567 0.05729 0.06749 排8 9 10 11 12 13 14受检方B B A B B B F批号20080826 20071218 20070810 20071216 20071216 20071216 20070415 得分(权重)0.07752 0.08577 0.09691 0.10651 0.116980.12087330.1598033排序15 16 17 18 19 20 21受检方B B A BC A I批号20070809 20070809 20070810 20080827 20070609 20090112 20090112 得分(权重)0.1633733330.1719633330.20724330.277540.27840670.42840.4600333排序22 23 24 25 26 27 28受检方A H D A A A D批号20090110 20071219 20080901 20070703 20080827 20080827 20090111 得分(权重)0.4726 0.4749 0.488750.65374330.70477330.74023 0.87284排序29 30 31 32 33 34 35受检方I H D H A D B批号20080902 20090112 20090111 20070704 20070704 20070704 20070704 得分(权0.92460.9992333331.4348 1.886342.090953.331903310.1467135.2 问题2的求解此问题在模型I的基础上进行求解。
