管路阻力实验报告
化工原理实验报告-流体流动阻力的测定
实验一流体流动阻力的测定一、实验目的1、掌握测定流体流经直管、管件（阀门）时阻力损失的一般实验方法。
2、测定直管摩擦系数λ与雷诺准数Re的关系，验证在一般湍流区内λ与Re的关系曲线。
3、测定流体流经管件（阀门）时的局部阻力系数ξ。
4、识辨组成管路的各种管件、阀门，并了解其作用。
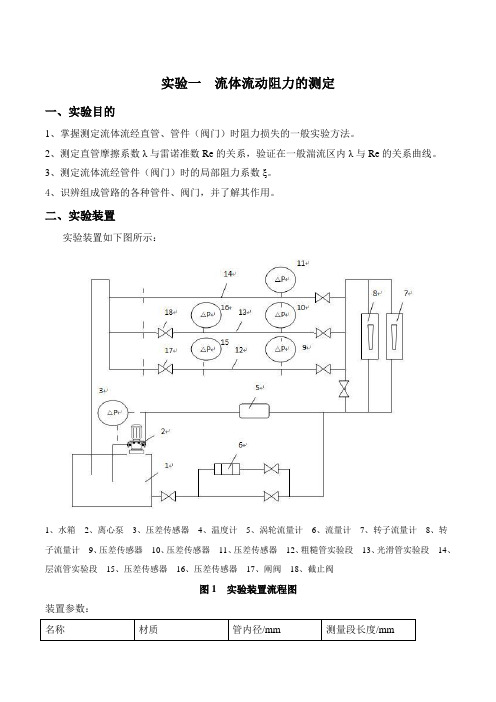
二、实验装置实验装置如下图所示：1、水箱2、离心泵3、压差传感器4、温度计5、涡轮流量计6、流量计7、转子流量计8、转子流量计9、压差传感器10、压差传感器11、压差传感器12、粗糙管实验段13、光滑管实验段14、层流管实验段15、压差传感器16、压差传感器17、阐阀18、截止阀图1 实验装置流程图装置参数：名称材质管内径/mm 测量段长度/mm三、实验原理1、直管阻力摩擦系数λ的测定流体在水平等径直管中稳定流动时，阻力损失为：2122ff p p p l u h d λρρ∆-=== ⑴即 22fd p luλρ∆=⑵Re du ρμ=⑶采用涡轮流量计测流量V2900Vu dπ=⑷ 用压差传感器测量流体流经直管的压力降f p ∆。
根据实验装置结构参数l 、d ，流体温度T （查流体物性ρ、μ），及实验时测定的流量V 、压力降ΔPf ，求取Re 和λ，再将Re 和λ标绘在双对数坐标图上。
2、局部阻力系数ζ的测定流体通过某一管件或阀门时的机械能损失表示为流体在小管径内流动时平均动能的某一倍数，这种方法称为阻力倍数法。
即：'2'2ffp u h g gζρ∆== ⑸ 故 '22fp u ζρ∆=⑹根据连接管件或阀门两端管径中小管的直径d ，流体温度T （查流体物性ρ、μ），及实验时测定的流量V 、压力降ΔPf ’，通过式⑸或⑹，求取管件（阀门）的局部阻力系数ζ。
四、实验步骤1、开启仪表柜上的总电源、仪表电源开关。
2、首先对水泵进行灌水，然后关闭出口阀，启动水泵，待电机转动平稳后，把出口阀缓缓开到最大。
3、实验从做大流量开始做起，最小流量应控制在1.5m3/h。
流体流动阻力的测定实验报告
流体流动阻力的测定实验报告一、实验目的1、掌握流体流经直管和管件时阻力损失的测定方法。
2、了解摩擦系数λ与雷诺数 Re 之间的关系。
3、学习压强差的测量方法和数据处理方法。
二、实验原理流体在管内流动时，由于黏性的存在，必然会产生阻力损失。
阻力损失包括直管阻力损失和局部阻力损失。
1、直管阻力损失根据柏努利方程，直管阻力损失可表示为：＼（h_f ＝＼frac{＼Delta p}｛ρg}＼）其中，＼（h_f\）为直管阻力损失，＼（＼Delta p\）为直管两端的压强差，＼（ρ\）为流体密度，＼（g\）为重力加速度。
摩擦系数\（λ\）与雷诺数\（Re\）及相对粗糙度\（＼frac{＼epsilon}｛d}＼）有关，其关系可通过实验测定。
当流体在光滑管内流动时，＼（Re ＜ 2000\）时，流动为层流，＼（λ ＝＼frac{64}｛Re}＼）；＼（Re ＞ 4000\）时，流动为湍流，＼（λ\）与\（Re\）和\（＼frac{＼epsilon}｛d}＼）的关系可由经验公式计算。
2、局部阻力损失局部阻力损失通常用局部阻力系数\（＼zeta\）来表示，其计算式为：＼（h_f' ＝＼frac{＼zeta u^2}｛2g}＼）其中，＼（h_f'＼）为局部阻力损失，＼（u\）为流体在管内的流速。
三、实验装置1、实验设备本实验使用的主要设备包括：离心泵、水箱、不同管径的直管、各种管件（如弯头、三通、阀门等）、压差计、流量计等。
2、实验流程水箱中的水经离心泵加压后进入实验管路，依次流经直管和各种管件，最后流回水箱。
通过压差计测量直管和管件两端的压强差，用流量计测量流体的流量。
四、实验步骤1、熟悉实验装置，了解各仪器仪表的使用方法。
2、检查实验装置的密封性，确保无泄漏。
3、打开离心泵，调节流量至一定值，稳定后记录压差计和流量计的读数。
4、逐步改变流量，重复上述步骤，测量多组数据。
5、实验结束后，关闭离心泵，整理实验仪器。
局部阻力损失实验报告
局部阻力损失实验前言：工农业生产的迅速发展, 使石油管路、给排水管路、机械液压管路等, 得到了越来越广泛的应用。
为了使管路的设计比较合理, 能满足生产实际的要求, 管路设计参数的确定显得更为重要。
管路在工作过程中存在沿程损失和局部阻力损失，合理确定阻力系数是使设计达到实际应用要求的关键。
但是由于扩张、收缩段的流动十分复杂，根据伯努利方程和动量方程推导出的理论值往往与具体的管道情况有所偏差，一般需要实验测定的局部水头损失进行修正或者得出经验公式用于工业设计。
在管路中, 经常会出现弯头, 阀门, 管道截面突然扩大, 管道截面突然缩小等流动有急剧变化的管段, 由于这些管段的存在, 会使水流的边界发生急剧变化, 水流中各点的流速, 压强都要改变, 有时会引起回流, 旋涡等, 从而造成水流机械能的损失。
例如，流体从小直径的管道流往大直径的管道, 由于流体有惯性, 它不可能按照管道的形状突然扩大, 而是离开小直径的管道后逐渐地扩大。
因此便在管壁拐角与主流束之间形成漩涡, 漩涡靠主流束带动着旋转, 主流束把能量传递给漩涡、漩涡又把得到的能量消耗在旋转中( 变成热而消散) 。
此外, 由于管道截面忽然变化所产生的流体冲击、碰撞等都会带来流体机械能的损失。
摘要：本实验利用三点法测量扩张段的局部阻力系数，用四点法量测量收缩段的局部阻力系数，然后与圆管突扩局部阻力系数的包达公式和突缩局部阻力系数的经验公式中的经验值进行对比分析，从而掌握用理论分析法和经验法建立函数式的技能。
进而加深对局部阻力损失的理解。
三、实验原理写出局部阻力前后两断面的能量方程，根据推导条件，扣除沿程水头损失可得： 1．突然扩大采用三点法计算，下式中12f h -由23f h -按流长比例换算得出。
实测 2211221212[()][()]22je f p p h Z Z h ggαυαυγγ-=++-+++理论 212(1)e AA ζ'=-2．突然缩小采用四点法计算，下式中B 点为突缩点，4f Bh -由34f h -换算得出，5fB h -由56f h -换算得出。
管道流动阻力的测定实验报告
姓名院 专业 班 年 月 日实验内容 指导教师 一、实验名称：管道流动阻力的测定二、实验目的：1. 学习U 型压差计的使用；2. 学习测量闸阀和90°弯头的局部阻力损失（h f `）的方法，计算局部阻力系数（ξ），学习直管阻力损失（h f ）的测定方法，计算出摩擦系数（λ）和雷诺准数（Re ），在双对数坐标纸上作λ-Re 关系曲线； 3. 学习流量计的标定。
三、实验原理：流体在管道中流动时，由于粘性力与涡流的存在，必然会引起能量的损失，这些损失可分为两类，即直管（沿程）阻力损失（h f ）和管件的局部阻力损失（h f `）。
1、直管阻力损失流体在圆形管流动时的阻力损失可用范宁公式计算： ]/[22kg J ud l h f ⋅=λ（1）式中： λ——摩擦系数l ——直管长[m] d ——管内径[m]u ——管内流速[m/s]，由下式计算：]/)[785.03600/(2s m d V u ⨯= （2） V ——流量[m 3/h]，由孔板流量计测定姓名院 专业 班 年月 日实验内容指导教师直管阻力损失由图2-2-1-1（a ）装置测定，原理如下： 在截面AA ’及BB ’之间列出柏努利方程： f BB BAA Ah p u gZp u gZ+++=++ρρ2222因是同内径的水平管段，故B A B A u u Z Z ==,，上式移项整理得： ]/[kg J p p h BA f ρ-=（3）在图2-2-1-1（a ）所示的U 形压差计内00`截面列能量方程： ρρρ)(R m g p gR gm p A s B ++=++(a)(b)图2-2-1-1 直管阻力测定姓名院 专业 班 年 月 日实验内容 指导教师整理上式得：]/)[(2m N gR p p S B A ρρ-=- （4） 将上式（4）代入式（3）得： ]/[)(kg J gR gR h s f =-=ρρρ（5）式中：g=9.8[N/kg]—重力加速度R ——压差读数[水]，[m]ρs=996[kg/m 3]——水的密度，由水温查表得 ρ——气体密度，本次试验记为0[kg/m 3]若用图2-2-1-1 (b)的∩压差计测压降（本实验室采用），则由式（3）得： ]/`[kg J gR p p h BBA f =-=ρ (6)或 ]`[2O mH R gp p h BA f =-=ρ (7)式中：R`——∩压差计读数[mH 2O]将式（5）或式（4）之值入（1）中，移项整理得摩擦系数计算值。
化工原理实验报告一流体阻力
实验一、管路阻力的测定一、实验目的1．学习直管阻力与局部阻力的测定方法。
2．学习计算并绘制直管摩擦系数λ与R e 的关系曲线的方法。
3．学习确定局部阻力系数ζ的方法。
二、实验原理流体在管路中的流动阻力分为直管阻力和局部阻力两种。
直管阻力也称为表皮阻力，是流体流经一定管径的直管时，由于流体内摩擦而产生的阻力， （m ） (1)gu d L g p H f 22⋅⋅=∆-=λρ局部阻力也称为形体阻力，是由于流体流经管路中的管件、阀门及管截面的突然扩大或缩小等局部地方，由于边界层分离而产生旋涡所引起的能量损失， (m)(2) gu g p H f22'⋅=∆-=ζρ管路的总能量损失等于管路中所有以上两种阻力的加和∑∑+=∑'ff f H H H 本实验所用的装置流程图如图1所示，实验装置由并联的两个支路组成，一个支路用于测定直管阻力，另一个用于测定局部阻力。
图1. 管路阻力测定实验装置流程图1-底阀2-入口真空表3-离心泵4-出口压力表5-充水阀6-差压变送器7-涡轮流量计8-差压变送器9-水箱测定直管阻力所用管子的规格：1#~2#实验装置：直管内径为27.1mm，直管管长1m。
3#~8#实验装置：直管内径为35.75mm，直管管长1m局部阻力的测定对象是两个阀门，一个闸阀，一个截止阀。
三、实验步骤1．打开充水阀向离心泵泵壳内充水。
2．关闭充水阀、出口流量调节阀，启动总电源开关，启动电机电源开关。
3．打开出口调节阀至最大，记录下管路流量最大值，即控制柜上的涡轮流量计的读数。
4．调节出口阀，流量从大到小测取8次，再由小到大测取8次，记录各次实验数据，包括涡轮流量计的读数、直管压差指示值。
5．关闭直管阻力直路的球阀，打开局部阻力的球阀，测定在三个流量下的局部压差指示值。
6．测取实验用水的温度。
7．关闭出口流量调节阀，关闭电机开关，关闭总电源开关。
注意事项：离心泵禁止在未冲满水的情况下空转。
化工原理流体流动阻力测定试验
流体流动阻力测定的实验一、实验目的及任务1 .学习直管摩擦阻力AP 八直管摩擦系数人的测定方法。
2 .掌握直管摩擦系数人与雷诺数Re 和相对粗糙度之间的关系及其变化规律。
3 .掌握局部摩擦阻力APr 局部阻力系数Z 的测定方法。
4 .学习压强差的几种测量方法和提高其测量精确度的一些技巧。
二、基本原理流体在管路中流动时，由于黏性剪应力和涡流的存在，不可避免地会引起流体压力损耗。
这种 损耗包括流体在流动时所产生的直管阻力损失和局部阻力损失。
1 .直管阻力损失流体流过直管时的摩擦系数与阻力损失之间的关系可用下式表示, l u 2h =九 x 一 x 一 f d 2式中 d 一管径，m ；1 一管长，m ； u —流速，m / s ； 九一摩擦系数。
在一定的流速下，测出阻力损失，按下式即可求出摩擦系数九7 d 2九=h x_x —f 1 u 2阻力损失h f 可通过对两截面间作机械能衡算求出(1-3)P -流体的密度，kg/m 3A f -两截面的压强差，Pa 。
由式（1-4）可知，对于水平等径直管只要测出两截面上静压强的差即可算出h f 。
两截面上静压 强的差可用压差计测出。
流速由流量计测得，在已知管径d 和平均流速u 的情况下，只需测出流体 的温度K 查出该流体的密度p 和黏度〃，则可求出雷诺数Re ，从而得出流体流过直管的摩擦系数人与雷诺数Re 的关系。
2.局部阻力损失阀门、突然扩大、突然缩小、弯头、三通等管件的局部阻力系数可用下式计算对于水平等径直管，z 1=z 2 u 1=u 2, 上式可简化为p 「P 2PA p―f P(1-4)式中p 1-p 2一两截面的压强差， Pa ；(1-1)(1-2)1 2)(1-5)三、实验装置流程和主要设备1.实验装置流程流体流动阻力实验流程如图1-1所示。
图1-1流动阻力实验流程示意图1-水箱；2-离心泵；3、4-放水阀；5、13-缓冲罐；6-局部阻力近端测压阀；7、15-局部阻力远端测压阀；8、20-粗糙管测压回水阀；9、19-光滑管测压阀；10-局部阻力管阀；11-U型管进水阀；12- 压力传感器；14-流量调节阀；15、16-水转子流量计；17-光滑管阀；18-粗糙管阀；21-倒置U型管放空阀；22-倒置U型管；23-水箱放水阀；24-放水阀;2.被测光滑直管段：管径d—0.008m；管长L—1.69m；材料一不锈钢管被测粗糙直管段：管径d—0.010m；管长L—1.69m；材料一不锈钢管被测局部阻力直管段：管径d—0.015m；管长L—1.2m；材料一不锈钢管3.压力传感器：型号:LXWY 测量范围：200 KPa4.直流数字电压表：型号：PZ139 测量范围：0〜200 KPa5.离心泵:型号：WB70/055 流量：8(m3/h) 扬程：12(m) 电机功率：550(W)6.玻璃转子流量计：型号测量范围精度LZB—40 100〜1000(L / h) 1.5LZB—10 10〜100(L/h) 2.5四、实验方法及步骤1.向储水槽内注水，直到水满为止。
管路阻力实验报告
实验三 管路阻力的测定一、实验目的1.学习管路阻力损失h f ，管子摩擦系数λ及管件、阀门的局部阻力系数ζ的测定方法，并通过实验了解它们的变化，巩固对流体阻力基本理论的认识；2.测定直管摩擦系数λ与雷诺数Re 的关系；3.测定管件、阀门的局部阻力系数。
二、基本原理流体在管路中流动时，由于粘性剪应力和涡流的存在，不可避免地会产生流体阻力损失。
流体在流动时的阻力有直管摩擦阻力（沿程阻力）和局部阻力（流体流经管体、阀门、流量计等所造成的压力损失。
1.λ－Re 关系的测定：流体流经直管时的阻力损失可用下式计算：22u d L h f⋅=λ；－直管阻力损失，式中：kg J h f / L －直管长度，m ；d －直管内径，m ； u －流体的流速，m/s ； λ－摩擦系数，无因次。
已知摩擦系数λ是雷诺数与管子的相对粗糙度（△/d ）的函数，即λ＝（Re ,△/d ）。
为了测定λ－Re 关系，可对一段已知其长度、管径及相对粗糙度的直管，在一定流速（也就是Re 一定）下测出阻力损失，然后按下式求出摩擦系数λ：为：对于水平直管，上式变：可根据伯努利方程求出阻力损失＝2)(2222121212uu p p g Z Z h h u L d h f f f-+-+-=⋅ρλρ21p p h f -=J/kg其中，21p p -为截面1与2间的压力差，Pa ；ρ流体的密度，kg/m 3。
用U 形管压差计测出两截面的压力，用温度计测水温，并查出其ρ、μ值，即可算出h f ，并进而算出λ。
由管路上的流量计可知当时的流速，从而可计算出此时的Re 数；得到一个λ－Re 对应关系，改变不同的流速，有不同的Re 及λ，可得某相对粗糙度的管子的一组λ－Re 关系。
以λ为纵坐标，Re 为横坐标，在双对数坐标纸上作出λ－Re 曲线，与教材中相应曲线对比。
2.局部阻力系数ζ的测定流体流经阀门、管件（如弯头、三通、突然扩大或缩小）时所引起的阻力损失可用下式计算：22u h f ζ= J/kg式中ζ即为局部阻力系数。
局部阻力损失实验报告
局部阻力损失实验前言：工农业生产的迅速发展, 使石油管路、给排水管路、机械液压管路等, 得到了越来越广泛的应用。
为了使管路的设计比较合理, 能满足生产实际的要求, 管路设计参数的确定显得更为重要。
管路在工作过程中存在沿程损失和局部阻力损失，合理确定阻力系数是使设计达到实际应用要求的关键。
但是由于扩张、收缩段的流动十分复杂，根据伯努利方程和动量方程推导出的理论值往往与具体的管道情况有所偏差，一般需要实验测定的局部水头损失进行修正或者得出经验公式用于工业设计。
在管路中, 经常会出现弯头, 阀门, 管道截面突然扩大, 管道截面突然缩小等流动有急剧变化的管段, 由于这些管段的存在, 会使水流的边界发生急剧变化, 水流中各点的流速, 压强都要改变, 有时会引起回流, 旋涡等, 从而造成水流机械能的损失。
例如，流体从小直径的管道流往大直径的管道, 由于流体有惯性, 它不可能按照管道的形状突然扩大, 而是离开小直径的管道后逐渐地扩大。
因此便在管壁拐角与主流束之间形成漩涡, 漩涡靠主流束带动着旋转, 主流束把能量传递给漩涡、漩涡又把得到的能量消耗在旋转中( 变成热而消散) 。
此外, 由于管道截面忽然变化所产生的流体冲击、碰撞等都会带来流体机械能的损失。
摘要：本实验利用三点法测量扩张段的局部阻力系数，用四点法量测量收缩段的局部阻力系数，然后与圆管突扩局部阻力系数的包达公式和突缩局部阻力系数的经验公式中的经验值进行对比分析，从而掌握用理论分析法和经验法建立函数式的技能。
进而加深对局部阻力损失的理解。
三、实验原理写出局部阻力前后两断面的能量方程，根据推导条件，扣除沿程水头损失可得： 1．突然扩大采用三点法计算，下式中12f h -由23f h -按流长比例换算得出。
实测 2211221212[()][()]22je f p p h Z Z h ggαυαυγγ-=++-+++理论 212(1)e AA ζ'=-2．突然缩小采用四点法计算，下式中B 点为突缩点，4f Bh -由34f h -换算得出，5fB h -由56f h -换算得出。
管路沿程阻力测定实验报告st
实验一 管路沿程阻力测定一、实验目的1、掌握流体流经管道时沿程阻力损失的测定方法。
2、测定流体流经直管时的摩擦阻力，确定摩擦系数λ与Re 的关系。
3、测定流体流经管件时的局部阻力，并求出阻力系数ξ。
4、学会压差计和流量计的使用。
二、实验原理流体在管路中流动时，引起的压强损耗包括流体流经直管的沿程阻力以及流体流动方向的改变或因管子大小、形状的改变所引起的局部阻力。
1、沿程阻力液体稳定流动时，阻力损失表现为压强（降低）损耗：12fp p h -=ρ为减少工作量，扩大实验结果的应用范围，采用因次分析法将各个变量综合成准数关系式。
影响阻力损失的因素： a 、流体的性质：密度ρ，粘度μ；b 、管路的几何尺寸：管径d,管长l,管壁粗糙度ε；c 、流动条件：u.经因次分析后，2·2==f P l u h d Δλρ 上式中：λ称为直管摩擦系数，雷诺数Re 在层流时：λ=64/ Re ; 湍流时：λ与Re和ξ/d 有关。
须由实验确定。
2、局部阻力（两种方法） ⑴当量长度法2·2e f l l u h d ⎛⎫ ⎪ ⎪ ⎪⎝⎭+=∑∑λ ⑵阻力系数法流体流经某一管件或阀门的阻力损失用流体在管路中的动能系数p h 表示：2·2p u h =ζ式中：ζ----局部阻力系数，无因次u----小截面管中的平均流速（m/s ） 2/4su V d =π（m/s ） s V ---平均流量(3m /s) p h 应用伯努利方程由液体压差计读数R 求出三、实验装置与流程1、本实验装置及设备主要参数：被测原件：镀锌水管，管长2.0m，管径（公称直径）0.021m；闸阀D=¾。
⑴测量仪表：U压差计（水银指示液）；LW-15型涡轮流量计（精度0.5级，量程0.4~4.0m3/ h，仪器编号Ⅰ的仪表常数为599.41（次/升），仪器编号为Ⅱ的仪表常数为605.30（次/升），MMD智能流量仪）。
实验一 流体力学综合实验实验报告
实验一 流体力学综合实验预习实验：一、实验目的1．熟悉流体在管路中流动阻力的测定方法及实验数据的归纳 2．测定直管摩擦系数λ和e R 关系曲线及局部阻力系数ζ 3. 了解离心泵的构造，熟悉其操作和调节方法 4. 测出单级离心泵在固定转速下的特定曲线 二、实验原理流体在管路中的流动阻力分为直管阻力和局部阻力两种。
直管阻力是流体流经一定管径的直管时，由于流体内摩擦而产生的阻力，可由下式计算：gu d l g p H f 22⋅⋅=∆-=λρ (3-1) 局部阻力主要是由于流体流经管路中的管件、阀门及管截面的突然扩大或缩小等局部地方所引起的阻力，计算公式如下：gu g p H f22''⋅=∆-=ζρ (3-2) 管路的能量损失'f f f H H H +=∑ (3-3)式中 f H ——直管阻力，m 水柱；λ——直管摩擦阻力系数；l ——管长，m ； d ——直管内径，m ；u ——管内平均流速，1s m -⋅；g ——重力加速度，9.812s m -⋅p ∆——直管阻力引起的压强降，Pa ；ρ——流体的密度，3m kg -⋅；ζ——局部阻力系数； 由式3-1可得22ludP ρλ⋅∆-=(3-4) 这样，利用实验方法测取不同流量下长度为l 直管两端的压差P ∆即可计算出λ和Re ，然后在双对数坐标纸上标绘出Re λ-的曲线图。
离心泵的性能受到泵的内部结构、叶轮形式、叶轮转速的影响。
实验将测出的H —Q 、N —Q 、η—Q 之间的关系标绘在坐标纸上成为三条曲线，即为离心泵的特性曲线，根据曲线可找出泵的最佳操作范围，作为选泵的依据。
离心泵的扬程可由进、出口间的能量衡算求得：gu u h H H H 221220-++-=入口压力表出口压力表 (3-5) 式中出口压力表H ——离心泵出口压力表读数，m 水柱；入口压力表H ——离心泵入口压力表的读数，m 水柱；0h ——离心泵进、出口管路两测压点间的垂直距离，可忽略不计；1u ——吸入管内流体的流速，1s m -⋅；2u ——压出管内流体的流速，1s m -⋅泵的有效功率，由于泵在运转过程中存在种种能量损失，使泵的实际压头和流量较理论值为低，而输入泵的功率又较理论值为高，所以泵的效率%100⨯=NN eη (3-6) 而泵的有效功率g QH N e e ρ=/（3600×1000） (3-7) 式中：e N ——泵的有效功率，K w ；N ——电机的输入功率，由功率表测出，K w ； Q ——泵的流量，-13h m ⋅；e H ——泵的扬程，m 水柱。
管路沿程阻力测定实验报告
实验一管路沿程阻力测定一实验目的1. 掌握流体流经管道时沿程阻力损失的测定方法。
2. 测定流体流过直管时的摩擦阻力，确定摩擦系数3. 测定流体流过管件时的局部阻力，并求出阻力系数4. 学会压差计和流量计的使用。
二实验原理流体在管路中流动时，由于粘性剪应力和涡流的存在，不可避免地会引起压 强损耗。
这种损耗包括流体流经直管的沿程阻力以及流体流动方向的改变或因管 子大小、形状的改变所引起的局部阻力。
1. 沿程阻力称为直管摩擦系数，滞留时，；湍流时， 与R e 的关系受管壁粗糙度的影响, 需由实验测得。
64 R e根据伯努利方程可知，流体流过的沿程阻力损失，可直接得出所测得的液柱压 差计度数R （m ）算出：p R 指-水g2）阻力系数法h pE -局部阻力系数，无因次；u-在小截面管中流体的平均流速（m/s ）三实验装置与流程1.本实验装置及设备主要参数：被测元件：镀锌水管，管长2.0m ，管径（公称直径）0.021m ；闸阀D=3/4.1）测量仪表：U 型压差计（水银指示液）；LW — 15型涡轮流量计（精度0.5级, 量程0.4~4.0m /h,仪器编号I 的仪表常数为 599.41 （次/升），仪器编号II 的仪表常数为605.30 （次/ 升）, MM 智能流量仪）。
与Re 的关系2.局部阻力 1）当量长度法h fl e d2） 循环水泵。
3） 循环水箱。
4） DZ15-40型自动开关。
X- 2X 流体流动阻力损失实验流程图1) 水箱 6 ）放空阀 11 ）取压孔 2) 控制阀 7 ）排液阀 12 ）U 形压差计 3) 放空阀8 ）数显温度表 13 ）闸阀 4) 5) U 形压差计 平衡阀 9 ）泵10）涡轮流量计14取压孔四实验操作步骤及注意事项1. 水箱充水至80%2. 仪表调整（涡轮流量计、MM 智能流量计仪按说明书调节）3. 打开压差计上平衡阀，关闭各放气阀。
4. 启动循环水泵（首先检查泵轴是否转动，开全阀 13,全关阀2,后启动）。
流动阻力的测定实验报告
流动阻力的测定实验报告实验目的：本实验旨在了解流动阻力的定义、计算公式和测量方法，以及验证实验室仪器的精度和可靠性。
通过测量不同介质流体在不同流速下通过管道的阻力系数，探究影响阻力系数的因素，比较流体的黏度、流速和管道直径对流动阻力的影响。
实验原理：流体运动是由于受到作用力而产生的运动，而阻力恰恰是一种对运动物体的反作用力。
流体在管道内流动时，由于管道表面的摩擦和阻力，会产生一定的阻碍，形成阻力系数。
阻力系数是指单位长度内管壁表面摩擦力和流体活塞面积的比值。
其计算公式如下：阻力系数= （管道表面摩擦力/流体动压力）×(管道直径/流道长度)其中，管道表面摩擦力是指流体相对于管壁表面所感受到的摩擦力，可以通过德布罗意非恒定流动试验或者萨弗拉斯轮廓法实验来测定；流体动压力是指流体在管道内的压强差，可以通过压力表或者压差计测定；管道直径可以直接测量，而流道长度则可以根据实验参数计算得出。
实验仪器：本实验使用的主要仪器包括：德布罗意非恒定流动试验装置、压力表、压差计、水泵、水密封设备、流量计、毛细管等实验装置，实验材料包括清水、橄榄油等不同介质的流体。
实验步骤：1. 选择不同的介质流体，如水、橄榄油等，准备好实验材料。
2. 在实验室设备内放入毛细管，调整毛细管底部的水平度，并通过水密封设备进行加压。
3. 打开水泵，调整水泵输出流量和流速到设定值，使液体通过管道形成稳定的非恒定流动。
4. 测量流量计的读数，记录压力表和压差计的读数，并计算出流体在管道内的平均速度。
5. 根据流速和管道直径计算出流体在管道内的雷诺数值和阻力系数。
6. 根据不同流体介质的实验参数，比较不同介质对流动阻力的影响。
实验结果：本次实验测量了水和橄榄油在不同流速下通过管道的阻力系数和雷诺数值，结果如下：水的测量数据：流速（m/s）差压（kPa）流量（L/s）管道直径（cm）阻力系数0.8 3.2 0.01 2.0 0.0191.0 5.0 0.022.0 0.0131.2 6.3 0.032.0 0.011橄榄油的测量数据：流速（m/s）差压（kPa）流量（L/s）管道直径（cm）阻力系数0.8 4.3 0.02 2.0 0.0241.0 7.2 0.032.0 0.0161.2 8.9 0.042.0 0.014通过以上数据可以发现，不同流体介质对流动阻力的影响较小，而流速和管道直径则对阻力系数有着明显的影响。
学生实验 流体流动阻力测定实验
单相流动阻力测定实验一、实验目的1. 了解流体流动阻力的测定原理及方法；2. 测定流体流过直管时的摩擦阻力,并确定摩擦系数与雷诺数的关系；3. 测定流体流过管件时的局部阻力,并求出阻力系数；4. 了解与本实验有关的各种流量测量仪表、压差测量仪表的结构特点和安装方式，掌握其测量原理、学会正确使用。
二、实验原理流体在管路中流动时，由于粘性剪应力和涡流的存在，不可避免地会引起压强损耗。
这种损耗包括流体经过直管的沿程阻力以及因流体运动方向改变或因管子大小形状改变所引起的局部阻力。
1.沿程阻力流体在水平均匀管道中稳定流动时，由截面1到截面2，阻力损失表现在压强的降低。
影响阻力损失的因素十分复杂，目前尚不能用理论方法求解，必须通过实验研究其规律。
为了减少实验工作量，扩大实验结果的应用范围，可采用因次分析法将各变量综合成准数关系式。
影响阻力损失的诸因素由：（1）流体性质：密度，粘度；（2）管路的几何尺寸：管径，管长，管壁粗糙度；（3）流动条件：流速。
2.局部阻力局部阻力通常有两种表示方法，即当量长度法和阻力系数法。
（1）当量长度法流体流过某管件或阀门时，因局部阻力造成的损失，相当于流体通过与其具有相同管径的若干米长度的直管阻力损失，这个直管长度称为当量长度。
（2）阻力系数法流体通过某一管件或阀门的阻力损失用流体在管路中的动能系数来表示。
由于管件两侧距测压孔间的直管长度很短，引起的摩擦阻力与局部阻力相比，可以忽略不计，因此动能系数之值可应用伯努利方程由压差计读数求出。
三、实验设备的功能与特点本实验装置可用于实验教学和科研。
利用该实验装置，可学习和掌握光滑直管、粗糙直管的阻力系数与雷诺准数的测量方法；也可学习局部阻力的测量方法；学习几种压差测量方法；加深对流体流动阻力概念的理解。
本实验装置的特点：⑴本实验装置数据稳定，重现性好，能给实验者明确的流体流动阻力概念。
⑵雷诺准数的数据范围宽，可作出102～104三个数量级。
流动阻力的测定实验报告
流动阻力的测定实验报告实验目的：本实验旨在通过测定不同流速下的流动阻力，探究流体在管道中流动时的阻力特性，并验证流动阻力与流速、管道直径、流体粘度等因素的关系。
实验原理：流动阻力是指流体在管道中流动时所受到的阻力，其大小与流体的粘度、流速、管道直径等因素有关。
根据流体力学原理，流动阻力可以用以下公式表示：F = kρv²L/2D其中，F为流动阻力，k为阻力系数，ρ为流体密度，v为流速，L 为管道长度，D为管道直径。
实验步骤：1. 将实验装置搭建好，调整好流量计和压力计的位置。
2. 打开水泵，调节流量计，使水流速度逐渐增加。
3. 记录不同流速下的压力差和流量。
4. 根据实验数据计算出不同流速下的流动阻力。
5. 绘制流速与流动阻力的关系曲线。
实验结果：通过实验测量，得到了不同流速下的流量和压力差数据，计算出了相应的流动阻力。
将数据绘制成图表，可以看出流速与流动阻力呈现出明显的正比关系。
同时，管道直径和流体粘度也会对流动阻力产生影响，但在本实验中未进行探究。
实验结论：本实验通过测定不同流速下的流动阻力，验证了流动阻力与流速呈正比关系的结论。
同时，实验结果也表明了流动阻力与管道直径和流体粘度等因素有关，这些因素也需要在实际应用中进行考虑。
实验中可能存在的误差：1. 流量计和压力计的精度限制。
2. 实验过程中水温的变化可能会对实验结果产生影响。
3. 实验中未考虑管道弯曲、摩擦等因素对流动阻力的影响。
4. 实验中未考虑流体的非牛顿性质对流动阻力的影响。
本实验为我们深入了解流体在管道中流动时的阻力特性提供了重要的实验数据和理论基础。
局部阻力分析实验
管道内的局部阻力实验报告一、实验目的：1.了解各种局部阻力的形成原因及影响状况。
2.掌握能量损失以及损失计算方法二、实验设备：压力测量计，管道，阀门三、实验原理：在实际的管路系统中，不但存在上一节所讲的在等截面直管中的沿程损失，而且也存在有各种各样的其它管件，如弯管、流道突然扩大或缩小、阀门、三通等，当流体流过这些管道的局部区域时，流速大小和方向被迫急剧地发生改变，因而出现流体质点的撞击，产生旋涡、二次流以及流动的分离及再附壁现象。
此时由于粘性的作用，流体质点间发生剧烈的摩擦和动量交换，从而阻碍着流体的运动。
这种在局部障碍物处产生的损失称为局部损失，其阻力称为局部阻力。
因此一般的管路系统中，既有沿程损失，又有局部损失。
四、局部损失的产生的原因及计算：一、产生局部损失的原因对于突然扩张的管道，由于流体从小管道突然进入大管道如图 4.9 （）所示，而且由于流体惯性的作用，流体质点在突然扩张处不可能马上贴附于壁面，而是在拐角的尖点处离开了壁面，出现了一系列的旋涡。
进一步随着流体流动截面面积的不断的扩张，直到 2 截面处流体充满了整个管截面。
在拐角处由于流体微团相互之间的摩擦作用，使得一部分机械能不可逆的转换成热能，在流动过程中，不断地有微团被主流带走，同时也有微团补充到拐角区，这种流体微团的不断补充和带走，必然产生撞击、摩擦和质量交换，从而消耗一部分机械能。
另一方面，进入大管流体的流速必然重新分配，增加了流体的相对运动，并导致流体的进一步的摩擦和撞击。
局部损失就发生在旋涡开始到消失的一段距离上。
图4.9（）给出了弯曲管道的流动。
由于管道弯曲，流线会发生弯曲，流体在受到向心力的作用下，管壁外侧的压力高于内侧的压力。
在管壁的外侧，压强先增加而后减小，同时内侧的压强先减小后增加，这样流体在管内形成螺旋状的交替流动。
综上所述，碰撞和旋涡是产生局部损失的主要原因。
当然在 1-2之间也存在沿程损失，一般来说，局部损失比沿程损失要大得多。
局部阻力损失实验报告解析
局部阻力损失实验前言：工农业生产的迅速发展, 使石油管路、给排水管路、机械液压管路等, 得到了越来越广泛的应用。
为了使管路的设计比较合理, 能满足生产实际的要求, 管路设计参数的确定显得更为重要。
管路在工作过程中存在沿程损失和局部阻力损失，合理确定阻力系数是使设计达到实际应用要求的关键。
但是由于扩张、收缩段的流动十分复杂，根据伯努利方程和动量方程推导出的理论值往往与具体的管道情况有所偏差，一般需要实验测定的局部水头损失进行修正或者得出经验公式用于工业设计。
在管路中, 经常会出现弯头, 阀门, 管道截面突然扩大, 管道截面突然缩小等流动有急剧变化的管段, 由于这些管段的存在, 会使水流的边界发生急剧变化, 水流中各点的流速, 压强都要改变, 有时会引起回流, 旋涡等, 从而造成水流机械能的损失。
例如，流体从小直径的管道流往大直径的管道, 由于流体有惯性, 它不可能按照管道的形状突然扩大, 而是离开小直径的管道后逐渐地扩大。
因此便在管壁拐角与主流束之间形成漩涡, 漩涡靠主流束带动着旋转, 主流束把能量传递给漩涡、漩涡又把得到的能量消耗在旋转中( 变成热而消散) 。
此外, 由于管道截面忽然变化所产生的流体冲击、碰撞等都会带来流体机械能的损失。
摘要：本实验利用三点法测量扩张段的局部阻力系数，用四点法量测量收缩段的局部阻力系数，然后与圆管突扩局部阻力系数的包达公式和突缩局部阻力系数的经验公式中的经验值进行对比分析，从而掌握用理论分析法和经验法建立函数式的技能。
进而加深对局部阻力损失的理解。
三、实验原理写出局部阻力前后两断面的能量方程，根据推导条件，扣除沿程水头损失可得：1．突然扩大采用三点法计算，下式中12f h -由23f h -按流长比例换算得出。
实测 2211221212[()][()]22je f p p h Z Z h ggαυαυγγ-=++-+++21/2e je h gαυζ=理论 212(1)e AA ζ'=-2,12je eh gαυζ'=2．突然缩小采用四点法计算，下式中B 点为突缩点，4f B h -由34f h -换算得出，5fB h -由56f h-换算得出。
阻力实验
4
实验报告格式
一、实验目的 二、实验原理 三、实验装置流程 四、实验过程及记录（实验步骤、原始数据记录表、数据计算过程<以一组数据为例>） 五、实验结果分析与总结（数据计算结果表、阻力系数与雷诺系数关系图、结果分析） 六、思考与讨论（任选讲义中 2-3 道思考题回答）
注意事项
1、因为泵是机械密封，必须在泵有水时使用，若泵内无水空转，易造成机械密封件升温
雷诺系数 Re d u
式中：d、ρ、μ— 管内径[m]、流体在测量温度下的密度和粘度 [Kg/m3]、[PaS]
2、直管摩擦阻力损失 Δpsf 及摩擦阻力系数 λ 的测定 流体在管路中流动，由于粘性剪应力的存在，不可避免的会产生机械能损耗。根据范宁
（Fanning）公式，流体在圆形直管内作定常稳定流动时的摩擦阻力损失为：
psf
l d
u2 2
[Pa]
式中： l ——沿直管两测压点间距离，m；
λ——直管摩擦系数，无因次；
由上可知，只要测得 Δpsf 即可求出直管摩擦系数 。根据柏努里方程和压差计对等径管
读数的特性可知：当两测压点处管径一样，且保证两测压点处速度分布正常时，压差计读数
Δp 即为流体流经两测压点处的直管阻力损失 Δpsf。
以上(1)和(2)式联立解得：
p
' f
2p23 p14
则局部阻力系数为：
2 (2p23 p14) u2
三、实验装置流程
实验装置示意图如下，离心泵、循环水池、管道及架子等均为不锈钢材质，工作流体 为水。其流程为：
循环水池离心泵涡轮流量计调节阀各测量管段循环水池。
φ 19×2
F1
相对细管
φ 25×2.5
局部阻力系数的实验报告
一、实验目的1. 理解局部阻力系数的概念及其在流体力学中的应用；2. 掌握局部阻力系数的测定方法；3. 通过实验，验证局部阻力系数与不同因素的关系。
二、实验原理局部阻力系数（ε）是流体在管路中通过局部收缩或扩张时，因流速变化而产生的能量损失与通过相同管径的均匀流动能量损失之比。
其计算公式为：ε = (hf_local / hf_uniform) (A_uniform / A_local)其中，hf_local为局部收缩或扩张时的能量损失，hf_uniform为均匀流动时的能量损失，A_uniform为均匀流动时的管道截面积，A_local为局部收缩或扩张时的管道截面积。
三、实验仪器与材料1. 实验台：包括直管段、局部收缩或扩张段、流量计、压力表等；2. 水源：提供实验用水；3. 计时器：用于记录实验时间；4. 计算器：用于计算实验数据；5. 实验记录表：用于记录实验数据。
四、实验步骤1. 准备实验台，连接好直管段、局部收缩或扩张段、流量计、压力表等设备；2. 打开水源，调节流量，使水在实验管路中稳定流动；3. 在直管段和局部收缩或扩张段两端安装压力表，记录压力值；4. 记录实验管路的尺寸、材料、温度等参数；5. 在流量计处测量流量，记录流量值；6. 计算直管段和局部收缩或扩张段的能量损失，即：hf_uniform = (4 f L ρ u^2) / (2 g d)hf_local = (4 f L ρ u^2) / (2 g d) (A_uniform / A_local)其中，f为摩擦系数，L为管路长度，ρ为流体密度，u为流速，g为重力加速度，d为管径；7. 计算局部阻力系数：ε = (hf_local / hf_uniform) (A_uniform / A_local)8. 改变实验管路参数（如流量、管径、材料等），重复实验步骤，记录数据；9. 分析实验数据，验证局部阻力系数与不同因素的关系。
化工原理实验报告_阻力
管路阻力的测定一、实验目的1．学习直管阻力与局部阻力的测定方法。
2．学习计算并绘制直管摩擦系数λ与R e 的关系曲线的方法。
3．学习确定局部阻力系数ζ的方法。
二、实验原理流体在管路中的流动阻力分为直管阻力和局部阻力两种。
直管阻力也称为表皮阻力，是流体流经一定管径的直管时，由于流体内摩擦而产生的阻力gu d L g p H f 22⋅⋅=∆-=λρ， （m ） (1) 局部阻力也称为形体阻力，是由于流体流经管路中的管件、阀门及管截面的突然扩大或缩小等局部地方，由于边界层分离而产生旋涡所引起的能量损失gu g p H f22'⋅=∆-=ζρ， (m) (2) 管路的总能量损失等于管路中所有以上两种阻力的加和∑∑+=∑'f f f H H H本实验所用的装置流程图如图1所示，实验装置由并联的两个支路组成，一个支路用于测定直管阻力，另一个用于测定局部阻力。
图1. 管路阻力测定实验装置流程图1-底阀 2-入口真空表 3-离心泵 4-出口压力表 5-充水阀6-差压变送器 7-涡轮流量计 8-差压变送器 9-水箱测定直管阻力所用管子的规格：1#~2#实验装置：直管内径为27.1mm ，直管管长1m 。
3#~8#实验装置：直管内径为35.75mm，直管管长1m局部阻力的测定对象是两个阀门，一个闸阀，一个截止阀。
三、实验步骤1．打开充水阀向离心泵泵壳内充水。
2．关闭充水阀、出口流量调节阀，启动总电源开关，启动电机电源开关。
3．打开出口调节阀至最大，记录下管路流量最大值，即控制柜上的涡轮流量计的读数。
4．调节出口阀，流量从大到小测取8次，再由小到大测取8次，记录各次实验数据，包括涡轮流量计的读数、直管压差指示值。
5．关闭直管阻力直路的球阀，打开局部阻力的球阀，测定在三个流量下的局部压差指示值。
6．测取实验用水的温度。
7．关闭出口流量调节阀，关闭电机开关，关闭总电源开关。
注意事项：离心泵禁止在未冲满水的情况下空转。
直管阻力测定实验报告
直管阻力测定实验报告实验目的：通过实验测定直管内径、长度和流量对其阻力的影响，了解直管阻力的原理及其计算方法。
实验仪器：直管阻力测定试验装置、水表、静压传感器、差压传感器等。
实验原理：利用直管内流经液体的阻力来测量液体的流量大小。
当液体在直管中流动时，由于摩擦和黏性等原因，液体流速会受到阻碍。
这种阻碍称为阻力。
根据伯努利原理，在等压的情况下，液体流经直管时，速度越大，静压就越小。
因此，在直管中测量液体的压差，就可以计算出液体的流速和流量大小。
根据流量和管道形状等参数，可以进一步计算出直管的阻力大小。
实验步骤：1. 将直管阻力测定试验装置连接好，开启水源，充满水道。
2. 调整管路，使水从水表中顺利地流出来，使用水表记录流量。
3. 调整实验仪器，使差压传感器和静压传感器读数稳定。
4. 分别更换不同的直管，在相同流量下，分别记录差压传感器和静压传感器的读数。
5. 记录直管的长度、内径等参数，并计算出直管的截面积和流速。
6. 根据实验数据，计算出直管的阻力，绘制出流量-阻力曲线。
实验结果：在实验中，我们根据不同的直管参数，测量出了不同的差压和静压数据。
利用这些数据，我们计算出了不同直管的截面积、流速、重力加速度、雷诺数和阻力系数等参数。
最后，我们根据实验数据绘制出了流量-阻力曲线，进一步分析了直管内径、长度和流量对其阻力的影响。
结论：通过本次实验，我们掌握了直管阻力的原理和计算方法。
实验结果表明，直管阻力与管道形状、流量大小等参数密切相关，可以通过测量差压和静压等数据来计算出。
在实际工程中，我们需要考虑直管的阻力大小，选择合适的直管参数和流量控制方法来实现高效流动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验三 管路阻力的测定
一、实验目的
1.学习管路阻力损失h f ，管子摩擦系数λ及管件、阀门的局部阻力系数ζ的测定方法，并通过实验了解它们的变化，巩固对流体阻力基本理论的认识；
2.测定直管摩擦系数λ与雷诺数Re 的关系；
3.测定管件、阀门的局部阻力系数。
二、基本原理
流体在管路中流动时，由于粘性剪应力和涡流的存在，不可避免地会产生流体阻力损失。
流体在流动时的阻力有直管摩擦阻力（沿程阻力）和局部阻力（流体流经管体、阀门、流量计等所造成的压力损失。
1.λ－Re 关系的测定：
流体流经直管时的阻力损失可用下式计算：
2
2u d L h f
⋅=
λ
；－直管阻力损失，式中：kg J h f / L －直管长度，m ；
d －直管内径，m ； u －流体的流速，m/s ； λ－摩擦系数，无因次。
已知摩擦系数λ是雷诺数与管子的相对粗糙度（△/d ）的函数，即
λ＝（Re ,△/d ）。
为了测定λ－Re 关系，可对一段已知其长度、管径及相对粗糙度的直管，在一定流速（也就是Re 一定）下测出阻力损失，然后按下式求出摩擦系数λ：
为：
对于水平直管，上式变：
可根据伯努利方程求出阻力损失＝2
)(2
22
212
1212
u
u p p g Z Z h h u L d h f f f
-+
-+
-=⋅ρ
λ
ρ
2
1p p h f -=
J/kg
其中，21p p -为截面1与2间的压力差，Pa ；ρ流体的密度，kg/m 3。
用U 形管压差计测出两截面的压力，用温度计测水温，并查出其ρ、μ值，即可算出h f ，并进而算出λ。
由管路上的流量计可知当时的流速，从而可计算出此时的Re 数；得到一个λ－Re 对应关系，改变
不同的流速，有不同的Re 及λ，可得某相对粗糙度的管子的一组λ－Re 关系。
以λ为纵坐标，Re 为横坐标，在双对数坐标纸上作出λ－Re 曲线，与教材中相应曲线对比。
2.局部阻力系数ζ的测定
流体流经阀门、管件（如弯头、三通、突然扩大或缩小）时所引起的阻力损失可用下式计算：
2
2
u h f ζ= J/kg
式中ζ即为局部阻力系数。
只要测出流体经过管件时的阻力损失h f 以及流体在相同直径的导管中的流速u ，即可算出阻力系数ζ。
三、实验装置和流程
本实验装置主要设备有水箱和离心泵，离心泵1从水槽15吸入水，经调节阀3送到管路阻力测量系统。
经直管的压口10、弯头11、涡轮测量计13后送回水槽15。
测定管子摩擦系数和阀件阻力系数时，打开离心泵进口阀2、出口阀3.直管阻力损失和弯头阻力损失用U 形压差计测定其压差，指示液为水。
管内水的流量由涡轮流量计测定。
用调节阀3可以改变流体通过管内的流速，从而计算出不同流动状态下的摩擦系数和弯头阻力系数。
1-离心泵 2-泵进口阀 3泵出口阀 4-真空表 5-压力表 6-转速表 7转速传感器 8-冷却风扇 9-加水旋塞10-测压法兰 11-弯头 12-流量显示表 13-透明涡轮流量变送器 14-计量槽 15-水槽 16-马达天平测功机 四、操作步骤
1.熟悉流程及使用的仪表；
2.实验前将水槽充满水，以后水可循环使用。
3.启动离心泵，使用离心泵时注意：
（1）离心泵在启动前要灌水排气；
（2）离心泵要在出口阀关闭的情况下启动；
（3）关闭前要先关出口阀。
4.排气：为了减少实验误差，实验前应进行排气。
（1）管路排气；（2）测压导管排气；
5.调节流量测取数据。
调节时可在流量变化的整个幅度内取8~10个读数。
每调一次流量后，应等稳定后同时读取各测定点的数据。
6.局部阻力的测定步聚与直管阻力相同，记录6~8组数据即可。
7.测定完毕，关闭出口阀，然后拉开电闸，停泵。
本实验的主要误差是压差计的读数，故每个点要多读几次数据，取其平均值。
五、实验结果以及数据处理
直管阻力数据表
图1 λ——Re 双对数图
计算范例：
涡轮流量计显示值×0.001=流量 4.19(L/s)×0.001=0.00419（m 3/s ） 流量÷面积=流速 0.00419÷3.14(0.0408/2)2=3.198473(m/s)
ρ
2
1p p h f -=
J/kg 589.9×0.001/996.7=5.78102（J/Kg ）
22
u
L d h f
⋅=λ 5.78102×0.0408×2÷1.8÷3.1984732=0.0255987 Re=du ρ/μ 0.0408m ×3.198473×996.7÷0.8737=148869.3
管件阻力数据表
图2 管件阻力图
计算范例：
涡轮流量计显示值×0.001=流量 4.19(L/s)×0.001=0.00419（m 3/s ） 流量÷面积=流速 0.00419÷3.14(0.0408/2)2=3.198473(m/s)
ρ
2
1p p h f -=
J/kg 589.9×0.001÷996.7=5.78102（J/Kg ）
Re=lu ρ/μ 1.8m ×3.198473×996.7÷0.8737=148869.3 ξ=2hf/u 2 2×5.78102÷3.1984732=0.966567
讨论与分析：
1.从图1上所绘的图线可得随着ln Re 的增大，ln λ随之减少。
对于本实验的讨论，从
22
u
L d h f
⋅=λ以及Re=lu ρ/μ来验证，得到管路中的流动情况并不是呈现为层流状态。
从实验数据Re 中可以得知，同时，图线也证实这一结论，假如流体的流动状态是层流，那么λ=64/Re 那么取对数后的就会是 ln λ=-lnRe +Ln64 在图线呈现的图线为直线，而图上的线段为高次的曲线，从而驳斥了层流的假设，一次流体的流动情况为非层流的论点得以
证实。
与此同时，从粗糙管紊流区的经验公式25.0)d 0.11(∆
=λ可以推断，本实验的流体流动
情况也不是粗糙管紊流，因为在这种情况下，雷洛数Re 与λ没有联系，图线会呈现为水平线，而从图线可知雷洛数Re 与λ存在联系，从而观点得证。
并且从无缝钢管的相对粗糙度为0.04～0.17以及Re 的数量级可以确定为非粗糙湍流区。
2.对于图2，我们可以从实验中得到的图线为一段水平线，也就是随着lnRe的变化
lnξ的变化极不明显，在考虑到有实验误差的情况下，我们可以进一步得出，管件阻力ξ与雷洛系数Re不存在必然的联系。
而在本次实验当中阻力系数的值都比较接近于1，这可能跟管件材料很有关系。
3.综上所述，直管管路的阻力与雷洛数Re，可能有关也可能无关，要对Re进行分类讨论，而本次实验得出的数据就在Re与λ存在联系的区间内。
而同时，实验可得出管件阻力ξ与雷洛数Re不存在联系，而跟它本身的材料有关系。
所以，在设计管路的时候，我们因该考虑到这几个参考数的决定因素，从而更加合理地进行设计。
思考题：
1.测压孔的大小和位置，测压导管的粗细和长短对实验无影响，为什么？
答：因为孔板式测压计的的测量原理只涉及到流量的密度、液柱差、孔板的面积，以及管道内径，与测压孔的大小和位置，测压导管的粗细和长短无关，公式Q=C0A0ρ
ρ/)
ρ
gR中可以看出与题目的量无。
2-
(
A
2.将实验曲线与教材上相应曲线比较。
分析其误差及误差产生的原因。
λ——Re双对数图
λ——Re 莫迪图
分析： 从总体趋势上讲，曲线都有下降的趋势，并且随着趋势的下降曲线渐渐趋于平缓。
成因是由于随着雷洛数的增大流动，管内的流动情况就转变为粗糙管的湍流，即雷洛数与直管阻力无关，所以两个图像在尾端都成趋于平缓的势头。
而两图在前端的趋势有所区别，莫迪图的在前端随着雷洛数的减少，越接近层流，就越接近直线而且斜率为 64/Re ，但是双对数图是因为雷
洛数越少，就越接近 hf=g
d lu 2R
e 642
方程，即 入=64/Re, 取了对数后，就越接近
水平线，所以比起莫迪图，双对数图在前端成较平缓的走势。