信号与系统实验报告
信号与系统实验报告总结
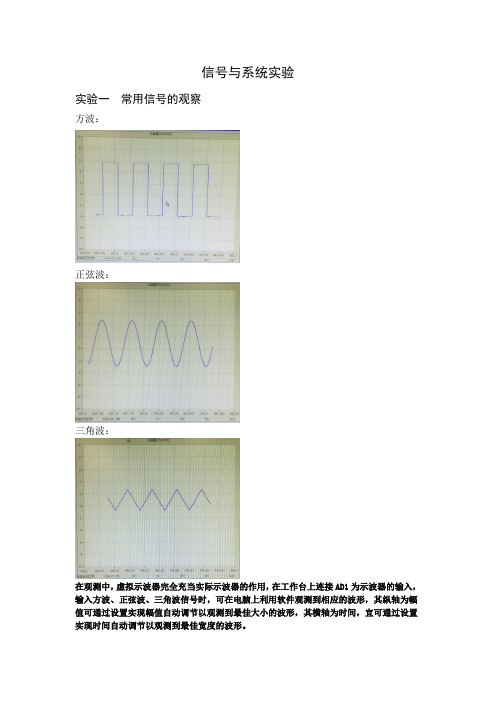
信号与系统实验实验一常用信号的观察方波:正弦波:三角波:在观测中,虚拟示波器完全充当实际示波器的作用,在工作台上连接AD1为示波器的输入,输入方波、正弦波、三角波信号时,可在电脑上利用软件观测到相应的波形,其纵轴为幅值可通过设置实现幅值自动调节以观测到最佳大小的波形,其横轴为时间,宜可通过设置实现时间自动调节以观测到最佳宽度的波形。
实验四非正弦周期信号的分解与合成方波DC信号:DC信号几乎没有,与理论相符合,原信号没有添加偏移。
方波基波信号:基波信号为与原方波50Hz信号相对应的频率为50Hz的正弦波信号,是方波分解的一次谐波信号。
方波二次谐波信号:二次谐波信号频率为100Hz为原方波信号频率的两倍,幅值较一次谐波较为减少。
方波三次谐波信号:三次谐波信号频率为150Hz为原方波信号的三倍。
幅值较一二次谐波大为减少。
方波四次谐波信号:四次谐波信号的频率为200Hz为原方波信号的四倍。
幅值较三次谐波再次减小。
方波五次谐波信号:五次谐波频率为250Hz为原方波信号的五倍。
幅值减少到0.3以内,几乎可以忽略。
综上可知:50Hz方波可以分解为DC信号、基波信号、二次、三次、四次、五次谐波信号…,无偏移时即无DC信号,DC信号幅值为0。
分解出来的基波信号即一次谐波信号频率与原方波信号频率相同,幅值接近方波信号的幅值。
二次谐波、三次谐波、四次谐波、五次谐波依次频率分别为原方波信号的二、三、四、五倍,且幅值依次衰减,直至五次谐波信号时几乎可以忽略。
可知,方波信号可分解为多个谐波。
方波基波加三次谐波信号:基波叠加上三次谐波信号时,幅值与方波信号接近,形状还有一定差异,但已基本可以看出叠加后逼近了方波信号。
方波基波加三次谐波信号加五次谐波信号:基波信号、三次谐波信号、五次谐波信号叠加以后,比基波信号、三次谐波信号叠加后的波形更加接近方波信号。
综上所述:方波分解出来的各次谐波以及DC信号,叠加起来以后会逼近方波信号,且叠加的信号越多,越是接近方波信号。
信号与系统实验实验报告

信号与系统实验实验报告一、实验目的本次信号与系统实验的主要目的是通过实际操作和观察,深入理解信号与系统的基本概念、原理和分析方法。
具体而言,包括以下几个方面:1、掌握常见信号的产生和表示方法,如正弦信号、方波信号、脉冲信号等。
2、熟悉线性时不变系统的特性,如叠加性、时不变性等,并通过实验进行验证。
3、学会使用基本的信号处理工具和仪器,如示波器、信号发生器等,进行信号的观测和分析。
4、理解卷积运算在信号处理中的作用,并通过实验计算和观察卷积结果。
二、实验设备1、信号发生器:用于产生各种类型的信号,如正弦波、方波、脉冲等。
2、示波器:用于观测输入和输出信号的波形、幅度、频率等参数。
3、计算机及相关软件:用于进行数据处理和分析。
三、实验原理1、信号的分类信号可以分为连续时间信号和离散时间信号。
连续时间信号在时间上是连续的,其数学表示通常为函数形式;离散时间信号在时间上是离散的,通常用序列来表示。
常见的信号类型包括正弦信号、方波信号、脉冲信号等。
2、线性时不变系统线性时不变系统具有叠加性和时不变性。
叠加性意味着多个输入信号的线性组合产生的输出等于各个输入单独作用产生的输出的线性组合;时不变性表示系统的特性不随时间变化,即输入信号的时移对应输出信号的相同时移。
3、卷积运算卷积是信号处理中一种重要的运算,用于描述线性时不变系统对输入信号的作用。
对于两个信号 f(t) 和 g(t),它们的卷积定义为:\(f g)(t) =\int_{\infty}^{\infty} f(\tau) g(t \tau) d\tau \在离散时间情况下,卷积运算为:\(f g)n =\sum_{m =\infty}^{\infty} fm gn m \四、实验内容及步骤实验一:常见信号的产生与观测1、连接信号发生器和示波器。
2、设置信号发生器分别产生正弦波、方波和脉冲信号,调整频率、幅度和占空比等参数。
3、在示波器上观察并记录不同信号的波形、频率和幅度。
信号与系统实验报告

信号与系统实验报告一、实验目的(1) 理解周期信号的傅里叶分解,掌握傅里叶系数的计算方法;(2)深刻理解和掌握非周期信号的傅里叶变换及其计算方法;(3) 熟悉傅里叶变换的性质,并能应用其性质实现信号的幅度调制;(4) 理解连续时间系统的频域分析原理和方法,掌握连续系统的频率响应求解方法,并画出相应的幅频、相频响应曲线。
二、实验原理、原理图及电路图(1) 周期信号的傅里叶分解设有连续时间周期信号()f t ,它的周期为T ,角频率22fT,且满足狄里赫利条件,则该周期信号可以展开成傅里叶级数,即可表示为一系列不同频率的正弦或复指数信号之和。
傅里叶级数有三角形式和指数形式两种。
1)三角形式的傅里叶级数:01212011()cos()cos(2)sin()sin(2)2cos()sin()2n n n n a f t a t a t b t b t a a n t b n t 式中系数n a ,n b 称为傅里叶系数,可由下式求得:222222()cos(),()sin()T T T T nna f t n t dtb f t n t dtTT2)指数形式的傅里叶级数:()jn tn nf t F e式中系数n F 称为傅里叶复系数,可由下式求得:221()T jn tT nF f t edtT周期信号的傅里叶分解用Matlab进行计算时,本质上是对信号进行数值积分运算。
Matlab中进行数值积分运算的函数有quad函数和int函数。
其中int函数主要用于符号运算,而quad函数(包括quad8,quadl)可以直接对信号进行积分运算。
因此利用Matlab进行周期信号的傅里叶分解可以直接对信号进行运算,也可以采用符号运算方法。
quadl函数(quad系)的调用形式为:y=quadl(‘func’,a,b)或y=quadl(@myfun,a,b)。
其中func是一个字符串,表示被积函数的.m文件名(函数名);a、b分别表示定积分的下限和上限。
信号与系统实验报告

信号与系统实验报告
实验名称:信号与系统实验
一、实验目的:
1.了解信号与系统的基本概念
2.掌握信号的时域和频域表示方法
3.熟悉常见信号的特性及其对系统的影响
二、实验内容:
1.利用函数发生器产生不同频率的正弦信号,并通过示波器观察其时域和频域表示。
2.通过软件工具绘制不同信号的时域和频域图像。
3.利用滤波器对正弦信号进行滤波操作,并通过示波器观察滤波前后信号的变化。
三、实验结果分析:
1.通过实验仪器观察正弦信号的时域表示,可以看出信号的振幅、频率和相位信息。
2.通过实验仪器观察正弦信号的频域表示,可以看出信号的频率成分和幅度。
3.利用软件工具绘制信号的时域和频域图像,可以更直观地分析信号的特性。
4.经过滤波器处理的信号,可以通过示波器观察到滤波前后的信号波形和频谱的差异。
四、实验总结:
通过本次实验,我对信号与系统的概念有了更深入的理解,掌
握了信号的时域和频域表示方法。
通过观察实验仪器和绘制图像,我能够分析信号的特性及其对系统的影响。
此外,通过滤波器的处理,我也了解了滤波对信号的影响。
通过实验,我对信号与系统的理论知识有了更加直观的了解和应用。
信号与系统实验报告

1、求门函数g4(t)的傅里叶变换,并画出其频率特性曲线。
程序如下:w=linspace(-3*pi,3*pi,512);N=length(w);F=zeros(1,N);for k=1:NF(k)=quadl('sf1',-3,3,[],[],w(k));endfigure(1);plot(w,real(F));xlabel('\omega');ylabel('F(j\omega)');figure(2);plot(w,real(F)-sinc(w/2/pi).^2);xlabel('\omega');title('计算误差');运行结果如图一、图二所示:图一g4(t)的傅里叶变换图二g4(t)傅里叶变换的计算误差2、已知频率特性函数为:H(jw)=2(jw)3+jw+4(jw)4+3(jw)3+2(jw)2+5jw+2求其幅频特性和相频特性。
程序如下:w=linspace(0,5,200);b=[2 0 1 4];a=[1 3 2 5 2];H=freqs(b,a,w);subplot(2,1,1);plot(w,abs(H));set(gca,'xtick',[0 1 2 3 4 5]);set(gca,'ytick',[0 0.4 0.707 1]);xlabel('\omega');ylabel('|H(j\omega)|');subplot(2,1,2);plot(w,angle(H));set(gca,'xtick',[0 1 2 3 4 5]);xlabel('\omega');ylabel('\phi(\omega)');运行结果如图三所示:图三幅频特性和相频特性3、设H s=s(s−p1)(s−p2)设①p1=-2,p2=-30;②p1=-2,p2=3(1)针对极点参数①②,画出系统零、极点分布图,判断该系统稳定性。
信号与系统实验报告
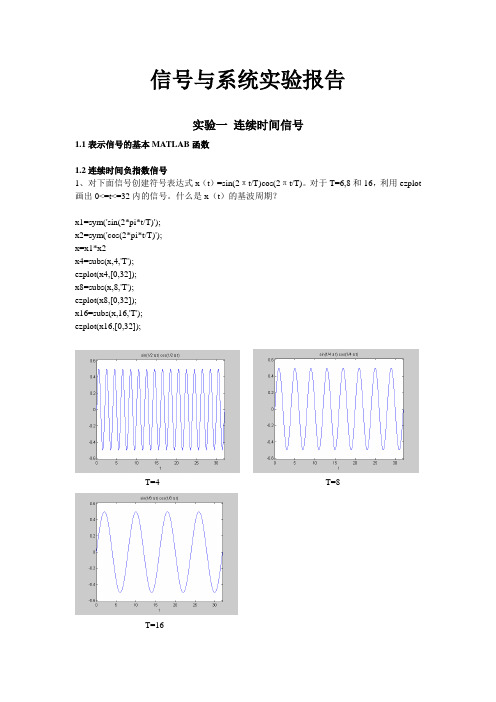
信号与系统实验报告实验一连续时间信号1.1表示信号的基本MATLAB函数1.2连续时间负指数信号1、对下面信号创建符号表达式x(t)=sin(2πt/T)cos(2πt/T)。
对于T=6,8和16,利用ezplot 画出0<=t<=32内的信号。
什么是x(t)的基波周期?x1=sym('sin(2*pi*t/T)');x2=sym('cos(2*pi*t/T)');x=x1*x2x4=subs(x,4,'T');ezplot(x4,[0,32]);x8=subs(x,8,'T');ezplot(x8,[0,32]);x16=subs(x,16,'T');ezplot(x16,[0,32]);T=4 T=8T=162、对下面信号创建一个符号表达式x(t)=exp(-at)cos(2πt)。
对于a=1/2,1/4,1/8,利用ezplot确定td,td为|x(t)|最后跨过0.1的时间,将td定义为该信号消失的时间。
利用ezplot对每一个a值确定在该信号消失之前,有多少个完整的余弦周期出现,周期数目是否正比于品质因素Q=(2π/T)/2a?x1=sym('exp(-a*t)');x2=sym('cos(2*pi*t)');x=x1*x2;xa1=subs(x,1/2,'a');ezplot(xa1);xa2=subs(x,1/4,'a');ezplot(xa2);xa3=subs(x,1/8,'a');ezplot(xa3);a=1/2 a=1/4a=1/83、将信号x(t)=exp(j2πt/16)+exp(j2πt/8)的符号表达式存入x中。
函数ezplot不能直接画出x(t),因为x*(t)是一个复数信号,实部和虚部分量必须要提取出来,然后分别画出他们。
信号与系统实验报告

信号与系统实验报告目录1. 内容概要 (2)1.1 研究背景 (3)1.2 研究目的 (4)1.3 研究意义 (4)2. 实验原理 (5)2.1 信号与系统基本概念 (7)2.2 信号的分类与表示 (8)2.3 系统的分类与表示 (9)2.4 信号与系统的运算法则 (11)3. 实验内容及步骤 (12)3.1 实验一 (13)3.1.1 实验目的 (14)3.1.2 实验仪器和设备 (15)3.1.4 实验数据记录与分析 (16)3.2 实验二 (16)3.2.1 实验目的 (17)3.2.2 实验仪器和设备 (18)3.2.3 实验步骤 (19)3.2.4 实验数据记录与分析 (19)3.3 实验三 (20)3.3.1 实验目的 (21)3.3.2 实验仪器和设备 (22)3.3.3 实验步骤 (23)3.3.4 实验数据记录与分析 (24)3.4 实验四 (26)3.4.1 实验目的 (27)3.4.2 实验仪器和设备 (27)3.4.4 实验数据记录与分析 (29)4. 结果与讨论 (29)4.1 实验结果汇总 (31)4.2 结果分析与讨论 (32)4.3 结果与理论知识的对比与验证 (33)1. 内容概要本实验报告旨在总结和回顾在信号与系统课程中所进行的实验内容,通过实践操作加深对理论知识的理解和应用能力。
实验涵盖了信号分析、信号处理方法以及系统响应等多个方面。
实验一:信号的基本特性与运算。
学生掌握了信号的表示方法,包括连续时间信号和离散时间信号,以及信号的基本运算规则,如加法、减法、乘法和除法。
实验二:信号的时间域分析。
在本实验中,学生学习了信号的波形变换、信号的卷积以及信号的频谱分析等基本概念和方法,利用MATLAB工具进行了实际的信号处理。
实验三:系统的时域分析。
学生了解了线性时不变系统的动态响应特性,包括零状态响应、阶跃响应以及脉冲响应,并学会了利用MATLAB进行系统响应的计算和分析。
信号与系统实验报告
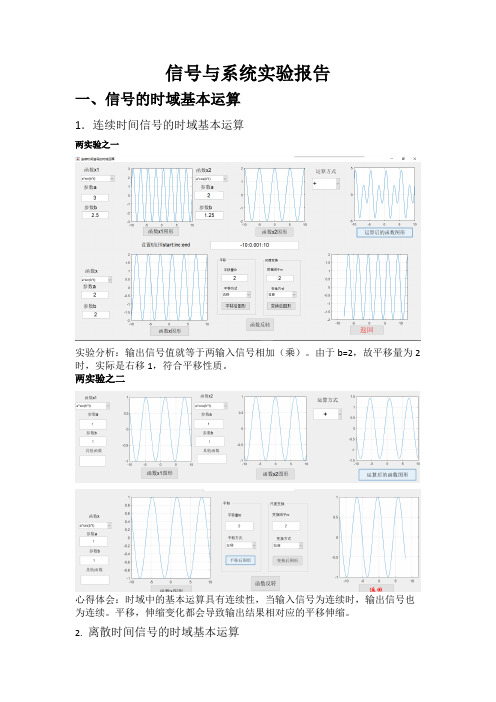
信号与系统实验报告一、信号的时域基本运算1.连续时间信号的时域基本运算两实验之一实验分析:输出信号值就等于两输入信号相加(乘)。
由于b=2,故平移量为2时,实际是右移1,符合平移性质。
两实验之二心得体会:时域中的基本运算具有连续性,当输入信号为连续时,输出信号也为连续。
平移,伸缩变化都会导致输出结果相对应的平移伸缩。
2.离散时间信号的时域基本运算两实验之一实验分析:输出信号的值是对应输入信号在每个n值所对应的运算值,当进行拉伸变化后,n值数量不会变,但范围会拉伸所输入的拉伸系数。
两实验之二心得体会:离散时间信号可以看做对连续时间信号的采样,而得到的输出信号值,也可以看成是连续信号所得之后的采样值。
二、连续信号卷积与系统的时域分析1.连续信号卷积积分两实验之一实验分析:当两相互卷积函数为冲激函数时,所卷积得到的也是一个冲激函数,且该函数的冲激t值为函数x,函数y冲激t值之和。
两实验之二心得体会:连续卷积函数每个t值所对应的卷积和可以看成其中一个在k值取得的函数与另外一个函数相乘得到的一个分量函数,并一直移动k值直至最后,最后累和出来的最终函数便是所得到的卷积函数。
3.RC电路时域积分两实验之一实验分析:全响应结果正好等于零状态响应与零输入响应之和。
两实验之二心得体会:具体学习了零状态,零输入,全响应过程的状态及变化,与之前所学的电路知识联系在一起了。
三、离散信号卷积与系统的时域分析1.离散信号卷积求和两实验之一实验分析:输出结果的n值是输入结果的k号与另一个n-k的累和两实验之二心得体会:直观地观察到卷积和的产生,可以看成连续卷积的采样形式,从这个方面去想,更能深入地理解卷积以及采样的知识。
2.离散差分方程求解两实验之一实验分析:其零状态响应序列为0 0 4 5 7.5,零输入响应序列为2 4 5 5.5 5.75,全状态响应序列为2 4 9 10.5 13.25,即全状态=零输入+零状态。
两实验之二心得体会:求差分方程时,可以根据全状态响应是由零输入输入以及零状态相加所得,分开来求,同时也加深了自己对差分方程的求解问题的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学生实验报告(理工类)课程名称:信号与系统专业班级:学生学号:学生姓名:所属院部:龙蟠学院指导教师:20 ——20 学年第学期金陵科技学院教务处制实验报告书写要求实验报告原则上要求学生手写,要求书写工整。
若因课程特点需打印的,要遵照以下字体、字号、间距等的具体要求。
纸张一律采用A4的纸张。
实验报告书写说明实验报告中一至四项内容为必填项,包括实验目的和要求;实验仪器和设备;实验内容与过程;实验结果与分析。
各院部可根据学科特点和实验具体要求增加项目。
填写注意事项(1)细致观察,及时、准确、如实记录。
(2)准确说明,层次清晰。
(3)尽量采用专用术语来说明事物。
(4)外文、符号、公式要准确,应使用统一规定的名词和符号。
(5)应独立完成实验报告的书写,严禁抄袭、复印,一经发现,以零分论处。
实验报告批改说明实验报告的批改要及时、认真、仔细,一律用红色笔批改。
实验报告的批改成绩采用百分制,具体评分标准由各院部自行制定。
实验报告装订要求实验批改完毕后,任课老师将每门课程的每个实验项目的实验报告以自然班为单位、按学号升序排列,装订成册,并附上一份该门课程的实验大纲。
实验项目名称: 常用连续信号的表示 实验学时:同组学生姓名: 实验地点: B402 实验日期: 2011年 11月10日 实验成绩: 批改教师: 杨娟 批改时间: 一、实验目的和要求熟悉MATLAB 软件;利用MATLAB 软件,绘制出常用的连续时间信号。
二、实验仪器和设备586以上计算机,装有MATLAB7.0软件三、实验过程1、打开MATLAB 界面,建立新文件。
2、根据实验要求,编写程序。
3、调试运行程序,并修改完善。
4、保存设计成果,撰写实验报告。
1. 绘制正弦信号)t Asin t (f 0ϕω+=(),其中A=1,πω2=,6/πϕ=;2. 绘制指数信号at Ae t (f =),其中A=1,0.4a -=;3. 绘制矩形脉冲信号,脉冲宽度为2;4. 绘制三角波脉冲信号,脉冲宽度为4;斜度为0.5;5. 对上题三角波脉冲信号进行尺度变换,分别得出)2t (f ,)2t 2(f -;6. 绘制抽样函数Sa (t ),t 取值在-3π到+3π之间;7. 绘制周期矩形脉冲信号,参数自定;8. 绘制周期三角脉冲信号,参数自定。
四、实验结果与分析 12345678实验项目名称:连续时间系统分析实验学时: 2同组学生姓名:实验地点: B402 实验日期: 2011年 11月17日实验成绩:批改教师:杨娟批改时间:一、实验目的和要求利用MATLAB软件对系统进行冲激响应、零状态响应、频率响应的求解并领会其物理意义;掌握周期信号的傅立叶级数系数以及功率谱的计算二、实验仪器和设备586以上计算机,装有MATLAB7.0软件三、实验过程1.一力学系统,其系统微分方程为(t)100++,求该)t(''yδ=100y(t))t('2y系统冲激响应;连续时间系统冲激响应%program8_2 Impulse response of LTI systemts=0;te=5;dt=0.01;sys=tf([10],[1 2 100]);t=ts:dt:te;y=impulse(sys,t);plot(t,y);xlabel('t(sec)');ylabel('y(t)');grid on;2.一系统微分方程为f(t)+,若t10s i n2=,求该)t(fπ)t(''y=100y(t)+)t('2y系统零状态响应;连续时间系统零状态响应%program8_1 Solution of differential equationts=0;te=5;dt=0.01;sys=tf([1],[1 2 10]);t=ts:dt:te;f=10*sin(2*pi*t);y=lsim(sys,f,t);plot(t,y);xlabel('t(sec)');ylabel('y(t)');grid on;3.一系统微分方程为3x(t)('y=+,求该系统的频率响应(绘出其幅t)3y(t)值和相位特性曲线);、%lab1.ma=[2 3];b=3;freqs(b,a);4.一系统微分方程为5x(t)(''3y+++,求该系统的频率=t)(t)4y'x'y(t))t('响应(绘出其幅值和相位特性曲线);%lab2.ma=[2 3 1]; b=[1 0 5]; freqs(b,a);5. 计算教材例3-1-2周期三角波信号的傅立叶级数系数并绘出其频谱周期三角波信号的频谱%program9_1 Frequency spectrum of periodic triangular signal N=10; n1=-N:-1;c1=-4*j*sin(n1*pi/2)/pi^2./n1.^2;%计算n=-N 到-1时的傅立叶级数系数 c0=0;%计算n=0到N 时的傅立叶级数系数 n2=1:N;c2=-4*j*sin(n2*pi/2)/pi^2./n2.^2;%计算n=1到N 时的傅立叶级数系数 cn=[c1 c0 c2]; n=-N:N;subplot(2,1,1); stem(n,abs(cn)); ylabel('cn 的幅度'); subplot(2,1,2); stem(n,angle(cn)); ylabel('cn 的相位'); xlabel('\omega/\omega_0');6. 计算信号t)f cos(2t)f 2(cos )t (x 21ππ+=的功率并绘制其功率谱,其中f 1=37Hz,f 2=219Hz 。
ts=0.001; fs=1/ts; t=[0:ts:10];x=cos(2*pi*37*t)+cos(2*pi*219*t); p=(norm(x)^2)/length(x); psd=spectrum(x,1024);pause %按任意键可看到信号的功率 ppause %按任意键可看到功率谱 specplot(psd,fs)1、打开MATLAB 界面,建立新文件。
2、根据实验要求,编写程序。
3、调试运行程序,并修改完善。
4、保存设计成果,撰写实验报告。
四、实验结果与分析123456ss实验三实验项目名称:连续时间系统的复频域分析实验学时: 2学时同组学生姓名:实验地点: B402实验日期:2011、11、24 实验成绩:批改教师:杨娟批改时间:一、实验目的和要求利用MATLAB软件掌握Laplace正变换与反变换,对F(s)进行部分分式展开,求系统函数的零极点并画出零极点分布图,并判断系统是否稳定。
二、实验仪器和设备586以上计算机,装有MATLAB7.0软件三、实验过程一、打开MATLAB 界面,建立新文件。
二、根据实验要求,编写程序。
三、调试运行程序,并修改完善。
四、保存设计成果,撰写实验报告。
1. 求函数)t ()at (sin e )t (f t ε-=的Laplace 变换;2. 求1)/(s s F(s)22+=的Laplace 反变换;3. 对3s)4s 2)/(s s (F(s)23+++=进行部分分式展开;4. 求出系统函数)22s s /()1s ()s (H 2++-=的零极点并画出零极点分布图;5. 画出系统函数)12s 2s s /(1)s (H 23+++=的零极点分布图,求出系统的单位冲激响应h(t)和幅频响应)j (H ω,并判断系统是否稳定。
四、实验结果与分析拉普拉斯正反变换%分别利用matlab 中的Laplace 和ilaplace 函数求:(1)f(t)=e-tsin(at)u(t)的Laplace 变换;(2)F(S)=S^2/(s^2+1)的Laplace 反变换%program9_12_1 Inverse Laplace transform using Laplace functionf=sym('exp(-1*t)*sin(a*t)');F=laplace(f);pauseF%program9_12_2 Inverse Laplace transform using ilaplace functionF=sym('s^2/(s^2+1)');ft=ilaplace(F);pauseft部分分式展开1%program9_7 Inverse Laplace transform by partial-fraction expansionformat rat;%将分数以近似的整数之比的形式显示,F(s)=(s+2)/(s^3+4s^2+3s) num=[1 2];%num 为分子多项式的系数向量den=[1 4 3 0];%den 为分母多项式的系数向量[r,p,k]=residue(num,den);%r 为所得部分分式展开式的系数向量,p 为极点,k 为分式的直流分量pause;r'pausep'pausek'零极点计算与分布图2%求出系统函数H(S)=(s-1)/(s^2+2s+2)的零极点,并画出零极点分布图%program9_10_1 pole-zero map of H(S) using pzmap functionb=[1 -1];a=[1 2 2];sys=tf(b,a);pzmap(sys);零极点计算与分布图%求出系统函数H(S)=(s-1)/(s^2+2s+2)的零极点,并画出零极点分布图%program9_10 pole-zero map of H(S) using plot functionb=[1 -1];a=[1 2 2];zs=roots(b);ps=roots(a);plot(real(zs),imag(zs),'o',real(ps),imag(ps),'kx','markersize',12);axis([-2 2 -2 2]);grid on;legend('零点','极点');零极点分布图与系统稳定性%画出系统函数为H(S)=1/(s^3+2s^2+2s+1)的零极点分布图;求出系统的单位冲激响应h(t)和幅频响应|H(jw)|,并判断系统是否稳定%program9_11 Impulse response,amplitude frequency response an stability analysis of LTI H(S)num=[1];den=[1 2 2 1];sys=tf(num,den);poles=roots(den);pausefigure(1);%系统函数的零极点分布图pzmap(sys);t=0:0.02:10;h=impulse(num,den,t);pausefigure(2);%系统的单位冲激响应plot(t,h);xlabel('t(s)');ylabel('h(t)');title('Impulse Respone');[H,w]=freqs(num,den);pausefigure(3);%系统的幅频响应plot(w,abs(H));xlabel('ang.freq.\omega(rad/s)');ylabel('|H(j\omega)|');title('Magnitude Respone');第一题结果F =a/((s+1)^2+a^2)第二题结果ft =dirac(t)-sin(t)第三题结果ans =-0.1667 -0.5000 0.6667ans = -3 -1 0ans = []F(s)=-0.1667/(s-3)+[ -0.5000/(s-1)]+ 0.6667/s第四题结果第五题结果实验项目名称:离散时间系统分析实验学时: 2 同组学生姓名:实验地点: B402 实验日期: 2011.12.01 实验成绩:批改教师:杨娟批改时间:一、实验目的和要求利用MATLAB软件掌握离散信号的表示,学会计算离散信号卷积,求系统的单位函数响应,求系统的零极点并画出零极点分布图,并判断系统是否稳定。
