金属导热系数的测量实验报告
导热系数实验报告..
一、【实验目的】用稳态法测定金属、空气、橡皮的导热系数。
二、【实验仪器】导热系数测定仪、铜-康导热电偶、游标卡尺、数字毫伏表、台秤(公用)、杜瓦瓶、秒表、待测样品（橡胶盘、铝芯）、冰块三、【实验原理】1、良导体（金属、空气）导热系数的测定根据傅里叶导热方程式，在物体部，取两个垂直于热传导方向、彼此间相距为h 、温度分别为θ1、θ2的平行平面（设θ1>θ2），若平面面积均为S ，在t ∆时间通过面积S 的热量Q ∆免租下述表达式：hS t Q )(21θθλ-=∆∆ （3-26-1） 式中，tQ∆∆为热流量；λ即为该物质的导热系数，λ在数值上等于相距单位长度的两平面的温度相差1个单位时，单位时间通过单位面积的热量，其单位是)(K m W ⋅。
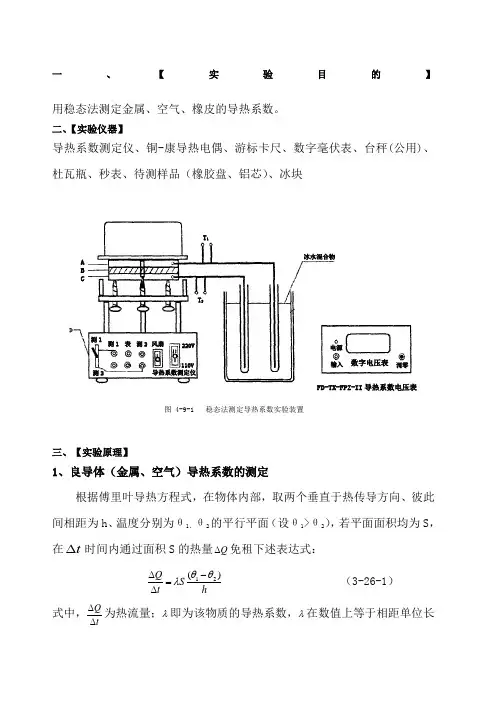
冰水混合物电源 输入调零数字电压表 FD-TX-FPZ-II 导热系数电压表T 2T 1220V110V导热系数测定仪测1测1 测2测2 表 风扇A B C图4-9-1 稳态法测定导热系数实验装置在支架上先放上圆铜盘P ，在P 的上面放上待测样品B ，再把带发热器的圆铜盘A 放在B 上，发热器通电后，热量从A 盘传到B 盘，再传到P 盘，由于A,P 都是良导体，其温度即可以代表B 盘上、下表面的温度θ1、θ2，θ1、θ2分别插入A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中，通过“传感器切换”开关G ，切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式（3-26-1）可以知道，单位时间通过待测样品B 任一圆截面的热流量为221)(B BR h t Q πθθλ-=∆∆ (3-26-2) 式中，R B 为样品的半径，h B 为样品的厚度。
当热传导达到稳定状态时，θ1和θ2的值不变，遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等，因此，可通过铜盘P 在稳定温度T 2的散热速率来求出热流量tQ∆∆。
实验中，在读得稳定时θ1和θ2后，即可将B 盘移去，而使A 盘的底面与铜盘P 直接接触。
金属导热系数实验报告
金属导热系数实验报告金属导热系数实验报告引言：导热系数是描述物质传热性能的重要参数之一，对于工程领域的热传导、散热等问题具有重要意义。
本实验旨在通过测量不同金属材料的导热系数，探究金属导热性能的差异，并分析其原因。
实验方法：1. 实验材料准备：本次实验所使用的金属材料包括铜、铝、铁和不锈钢，它们是常见的导热性能较好的金属材料。
将这些材料分别制成相同形状的棒状样品，保证样品的长度和直径相同，以消除几何因素对实验结果的影响。
2. 实验装置：实验装置主要由导热实验仪、恒温水浴槽和温度计组成。
导热实验仪用于测量样品的导热系数，恒温水浴槽则用于保持样品的温度稳定。
温度计用于测量水浴槽中的温度。
3. 实验步骤：首先，将恒温水浴槽加热至适宜的温度，保持恒温水浴槽的温度稳定。
然后，将待测金属样品放入导热实验仪中，并将实验仪与恒温水浴槽相连。
待样品温度稳定后，记录实验仪上的温度差值和时间，以获取导热系数。
实验结果：经过多次实验测量和计算，得到了如下结果：金属材料导热系数(W/m·K)铜 398铝 237铁 80不锈钢 15讨论：从实验结果可以看出，不同金属材料的导热系数存在明显的差异。
铜的导热系数最高，达到398 W/m·K，而不锈钢的导热系数最低，仅为15 W/m·K。
这是因为金属材料的导热性能与其原子结构和电子运动有关。
铜是一种典型的导热性能较好的金属，其晶体结构中的自由电子能够自由传递热量，因此具有较高的导热系数。
铝的导热系数较铜稍低，这是因为铝的晶体结构中自由电子的密度较低。
铁和不锈钢的导热系数较低，主要是由于其晶体结构中存在较多的杂质和缺陷，导致自由电子传导受阻。
结论：通过本次实验，我们验证了不同金属材料的导热系数存在差异，并分析了其原因。
导热系数的大小对于金属材料的热传导、散热等问题具有重要影响。
在实际应用中，我们可以根据金属材料的导热系数选择合适的材料，以满足特定的热传导需求。
导热系数实验报告
一、【实验目的】用稳态法测定金属、空气、橡皮的导热系数。
二、【实验仪器】导热系数测定仪、铜-康导热电偶、游标卡尺、数字毫伏表、台秤(公用)、杜瓦瓶、秒表、待测样品（橡胶盘、铝芯）、冰块三、【实验原理】1、良导体（金属、空气）导热系数的测定根据傅里叶导热方程式，在物体内部，取两个垂直于热传导方向、彼此间相距为h 、温度分别为θ1、θ2的平行平面（设θ1>θ2），若平面面积均为S ，在t ∆时间内通过面积S 的热量Q ∆免租下述表达式：hS t Q )(21θθλ-=∆∆ （3-26-1） 式中，tQ∆∆为热流量；λ即为该物质的导热系数，λ在数值上等于相距单位长冰水混合物电源输入 调零数字电压表 FD-TX-FPZ-II 导热系数电压表T 2T 1220V110V导热系数测定仪测1测1 测2测2 表 风扇AB C图4-9-1 稳态法测定导热系数实验装置度的两平面的温度相差1个单位时，单位时间内通过单位面积的热量，其单位是)K m W ⋅。
在支架上先放上圆铜盘P ，在P 的上面放上待测样品B ，再把带发热器的圆铜盘A 放在B 上，发热器通电后，热量从A 盘传到B 盘，再传到P 盘，由于A,P 都是良导体，其温度即可以代表B 盘上、下表面的温度θ1、θ2，θ1、θ2分别插入A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中，通过“传感器切换”开关G ，切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式（3-26-1）可以知道，单位时间内通过待测样品B 任一圆截面的热流量为221)(B BR h t Q πθθλ-=∆∆ (3-26-2) 式中，R B 为样品的半径，h B 为样品的厚度。
当热传导达到稳定状态时，θ1和θ2的值不变，遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等，因此，可通过铜盘P 在稳定温度T 2的散热速率来求出热流量tQ∆∆。
实验中，在读得稳定时θ1和θ2后，即可将B 盘移去，而使A 盘的底面与铜盘P 直接接触。
导热系数的测量实验报告
金属导热系数的测量机电工程学院能源与动力工程151班 张陆 5902615015 一：实验目的用稳态法测定出金属导热体的导热系数，并与理论值进行比较。
二：实验仪器导热系数测定仪、铜-康导热电偶、杜瓦瓶、待测样品（橡胶盘、铝芯）。
三：实验原理根据傅里叶导热方程式，在物体内部，取两个垂直于热传导方向、彼此间相距为h 、温度分别为T 1、T 2的平行平面（设T 1>T 2），若平面面积均为S ，在t ∆时间内通过面积S 的热量Q ∆免租下述表达式：hT T S t Q )(21-=∆∆λ （3-26-1） 式中，tQ ∆∆为热流量；λ即为该物质的导热系数，λ在数值上等于相距单位长度的两平面的温度相差1个单位时，单位时间内通过单位面积的热量，其单位是)(K m W ⋅。
在支架上先放上圆铜盘P ，在P 的上面放上待测样品B ，再把带发热器的圆铜盘A 放在B 上，发热器通电后，热量从A 盘传到B 盘，再传到P 盘，由于A,P 都是良导体，其温度即可以代表B 盘上、下表面的温度T 1、T 2，T 1、T 2分别插入A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中，通过“传感器切换”开关G ，切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式（3-26-1）可以知道，单位时间内通过待测样品B 任一圆截面的热流量为221)(B BR h T T t Q πλ-=∆∆ (3-26-2) 式中，R B 为样品的半径，h B 为样品的厚度。
当热传导达到稳定状态时，T 1和T 2的值不变，遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等，因此，可通过铜盘P 在稳定温度T 2的散热速率来求出热流量tQ ∆∆。
实验中，在读得稳定时T 1和T 2后，即可将B 盘移去，而使A 盘的底面与铜盘P 直接接触。
当铜盘P 的温度上升到高于稳定时的T 2值若干摄氏度后，在将A 移开，让P 自然冷却。
导热系数的测量实验报告
导热系数的测量导热系数（又称导热率）是反映材料热性能的重要物理量，导热系数大、导热性能好的材料称为良导体，导热系数小、导热性能差的材料称为不良导体。
一般来说，金属的导热系数比非金属的要大，固体的导热系数比液体的要大，气体的导热系数最小。
因为材料的导热系数不仅随温度、压力变化，而且材料的杂质含量、结构变化都会明显影响导热系数的数值，所以在科学实验和工程设计中，所用材料的导热系数都需要用实验的方法精确测定。
一．实验目的1．用稳态平板法测量材料的导热系数。
2．利用稳态法测定铝合金棒的导热系数，分析用稳态法测定不良导体导热系数存在的缺点。
二．实验原理热传导是热量传递过程中的一种方式，导热系数是描述物体导热性能的物理量。
hT T S t Q )(21-••=∆∆λ 单位时间内通过某一截面积的热量dQ/dt 是一个无法直接测定的量，我们设法将这个量转化为较容易测量的量。
为了维持一个恒定的温度梯度分布，必须不断地给高温侧铜板加热，热量通过样品传到低温侧铜板，低温侧铜板则要将热量不断地向周围环境散出。
单位时间通过截面的热流量为：B B h T T R t Q )(212-•••=∆∆πλ当加热速率、传热速率与散热速率相等时，系统就达到一个动态平衡，称之为稳态，此时低温侧铜板的散热速率就是样品内的传热速率。
这样，只要测量低温侧铜板在稳态温度 T2 下散热的速率，也就间接测量出了样品内的传热速率。
但是，铜板的散热速率也不易测量，还需要进一步作参量转换，我们知道，铜板的散热速率与冷却速率（温度变化率）dQ/dt=-mcdT/dt 式中的 m 为铜板的质量， C 为铜板的比热容，负号表示热量向低温方向传递。
由于质量容易直接测量，C 为常量，这样对铜板的散热速率的测量又转化为对低温侧铜板冷却速率的测量。
铜板的冷却速率可以这样测量：在达到稳态后，移去样品，用加热铜板直接对下铜板加热，使其温度高于稳态温度 T2（大约高出 10℃左右），再让其在环境中自然冷却，直到温度低于 T2，测出 温度在大于T2到小于T2区间中随时间的变化关系，描绘出 T —t 曲线（见图 2），曲线在T2处的斜率就是铜板在稳态温度时T2下的冷却速率。
金属导热系数的测量实验报告
金属导热系数的测量实验报告一、实验目的1、了解金属导热系数的物理意义及其测量原理。
2、掌握稳态法测量金属导热系数的实验方法。
3、学会使用相关实验仪器，并对实验数据进行处理和分析。
二、实验原理当物体内存在温度梯度时，热量会从高温处向低温处传递。
导热系数是表征材料导热性能的重要参数，它表示在单位温度梯度下，单位时间内通过单位面积的热量。
在稳态法测量金属导热系数的实验中，我们将待测金属样品制成平板状，在其上下表面分别施加稳定的温度差。
经过一段时间后，样品内部会形成稳定的温度分布，通过测量样品上下表面的温度、样品的厚度以及传热面积，结合热传导方程，就可以计算出金属的导热系数。
根据傅里叶热传导定律，在稳态条件下，通过平板样品的热流量 Q 与样品上下表面的温度差ΔT、样品的面积 S 以及导热系数λ 之间的关系为：Q ＝λ S （ΔT ／ d)其中，d 为样品的厚度。
三、实验仪器1、稳态法导热系数测定仪：包括加热装置、冷却装置、测温传感器等。
2、待测金属样品（如铜、铝等）。
3、游标卡尺：用于测量样品的厚度和直径。
4、数字温度计：测量样品上下表面的温度。
四、实验步骤1、用游标卡尺测量金属样品的厚度和直径，多次测量取平均值，以减小测量误差。
2、将金属样品放置在导热系数测定仪的加热板和冷却板之间，确保样品与加热板和冷却板接触良好。
3、打开加热装置和冷却装置，调节加热功率和冷却水流速，使样品上下表面形成稳定的温度差。
4、等待一段时间，待温度稳定后，用数字温度计分别测量样品上下表面的温度。
5、记录实验数据，包括样品的尺寸、上下表面的温度、加热功率等。
6、改变加热功率或更换不同的金属样品，重复上述实验步骤。
五、实验数据记录与处理以下是一组实验数据示例：｜金属样品｜厚度（mm）｜直径（mm）｜上表面温度（℃）｜下表面温度（℃）｜加热功率（W）｜｜｜｜｜｜｜｜｜铜｜ 1002 ｜ 5012 ｜ 805 ｜ 302 ｜ 500 ｜首先，计算样品的传热面积 S：S ＝π （d/2)＾2 ＝ 314 （5012/2)＾2 ≈ 197386 mm^2 ＝ 197386 cm^2然后，计算温度差ΔT：ΔT ＝ 805 302 ＝ 503 ℃样品的厚度 d ＝ 1002 mm ＝ 1002 cm根据热传导定律，导热系数λ 为：λ ＝ Q d ／（S ΔT)由于加热功率 P 等于热流量 Q，所以：λ ＝ P d ／（S ΔT) ＝ 500 1002 ／（197386 503) ≈ 0506 W/（cm·℃）对多组实验数据进行处理，计算出不同金属样品的导热系数，并求出平均值。
导热系数的测量实验分析报告
导热系数的测量实验报告————————————————————————————————作者：————————————————————————————————日期：导热系数的测量导热系数（又称导热率）是反映材料热性能的重要物理量，导热系数大、导热性能好的材料称为良导体，导热系数小、导热性能差的材料称为不良导体。
一般来说，金属的导热系数比非金属的要大，固体的导热系数比液体的要大，气体的导热系数最小。
因为材料的导热系数不仅随温度、压力变化，而且材料的杂质含量、结构变化都会明显影响导热系数的数值，所以在科学实验和工程设计中，所用材料的导热系数都需要用实验的方法精确测定。
一．实验目的1．用稳态平板法测量材料的导热系数。
2．利用稳态法测定铝合金棒的导热系数，分析用稳态法测定不良导体导热系数存在的缺点。
二．实验原理热传导是热量传递过程中的一种方式，导热系数是描述物体导热性能的物理量。
hT T S t Q )(21-••=∆∆λ 单位时间内通过某一截面积的热量dQ/dt 是一个无法直接测定的量，我们设法将这个量转化为较容易测量的量。
为了维持一个恒定的温度梯度分布，必须不断地给高温侧铜板加热，热量通过样品传到低温侧铜板，低温侧铜板则要将热量不断地向周围环境散出。
单位时间通过截面的热流量为：B B h T T R t Q )(212-•••=∆∆πλ当加热速率、传热速率与散热速率相等时，系统就达到一个动态平衡，称之为稳态，此时低温侧铜板的散热速率就是样品内的传热速率。
这样，只要测量低温侧铜板在稳态温度 T2 下散热的速率，也就间接测量出了样品内的传热速率。
但是，铜板的散热速率也不易测量，还需要进一步作参量转换，我们知道，铜板的散热速率与冷却速率（温度变化率）dQ/dt=-mcdT/dt 式中的 m 为铜板的质量， C 为铜板的比热容，负号表示热量向低温方向传递。
由于质量容易直接测量，C 为常量，这样对铜板的散热速率的测量又转化为对低温侧铜板冷却速率的测量。
大学物理实验报告-金属导热系数的测量
大学物理实验报告课程名称:大学物理实验实验名称：金属导热系数的测量学院名称：机电工程学院专业班级：车辆工程151班学生姓名：吴倩萍学号：5902415034实验地点：基础实验大楼D103实验时间：第一周周三下午15：45开始一、实验目的：用稳态法测定金属良导热体的导热系数，并与理论值进行比较。
二、实验仪器：TC-3型导热系数测定仪、杜瓦瓶、游标卡尺。
三、实验原理：1882年法国数学、物理学家傅里叶给出了一个热传导的基本公式——傅里叶导热方程。
该方程表明，取两个垂直于热传导方向、彼此间相距为h 、温度分别为T 1、T 2的平行平面（设T 1>T 2)，若平面面积均为S ，在∆t 时间内通过面积S 的热量∆Q 满足下述表达式：hT T S t Q 21-=∆∆λ（8-2），式中t Q∆∆为热流量，λ为该物质的热导率（又称作导热系数）。
λ在数值上等于相距单位长度的两平面的温度相差1个单位时，单位时间内通过单位面积的热量，其单位是W/(m ·K)。
本实验仪器如图所示。
在支架D 上先放置散热盘P ，在散热盘P 的上面放上待测样品B ，再把带发热器的圆铜盘A 放在B 上，发热器通电后，热量从A 盘传到B 盘，再传到P 盘，在样品B 上、下分别有一小孔，可用热电偶测出其温度T 1和T 2。
由式（8-1）可以知道，单位时间通过待测样品B 任一圆截面的热流量为B BR h T T t Q πλ21-=∆∆2（8-2),式中R B 为样品半径，h B 为样品上、下小孔之间的距离，当热传导达到稳定状态时，T 1和T 2的值不变，于是通过B 盘上表面的热流量与由铜盘P 向周围散热的速率相等，因此，可通过铜盘P 在稳定温度T 3时的散热速率来求出热流量t Q∆∆。
实验中，在读得稳定时的T 1、T 2和T 3后，即可将B盘移去，而使A 盘的底面与铜盘P 直接接触。
当铜盘P 的温度上升到高于稳定时的值T 3若干摄氏度后，再将圆盘A 移开，让铜盘P 自然冷却，观察其温度T 随时间t 的变化情况，然后由此求出铜盘在T 3的冷却速率2T T tT=∆∆，而t QtT mcT T ∆∆=∆∆=2（m 为铜盘P 的质量，c 为铜材的比热容），就是铜盘P 在温度为T 3时的散热速率。
金属导热系数的测量实验报告
金属导热系数的测量实验报告金属导热系数的测量实验报告引言：导热系数是衡量物质传导热量能力的重要指标之一。
在工程领域中，对各种金属材料的导热系数进行准确测量具有重要意义。
本实验旨在通过测量不同金属材料的导热系数，探究金属导热性质的差异，并进一步了解导热系数与金属材料的相关因素。
实验装置与方法：实验所需材料和装置包括：铝、铜、铁、不锈钢等金属样品；导热仪、温度计、电源、电热丝等实验仪器。
实验步骤如下：1. 将金属样品切割成相同尺寸的薄片，确保样品表面平整。
2. 将导热仪的电源接通，并将温度计插入导热仪中，确保仪器正常工作。
3. 将待测金属样品放置在导热仪的传热盘上，并固定好。
4. 调节导热仪的温度控制器，使其保持在恒定温度。
5. 记录导热仪上的温度计读数，并计时。
6. 观察样品温度随时间的变化，并记录数据。
7. 根据实验数据计算出金属样品的导热系数。
实验结果与分析：经过一系列实验测量，我们得到了不同金属样品的导热系数数据。
以铝、铜、铁和不锈钢为例，它们的导热系数分别为XXX、XXX、XXX和XXX。
通过对比分析，我们可以发现金属导热系数的差异主要受以下几个因素的影响：1. 金属的晶格结构：晶格结构的不同会影响金属内部原子的排列方式，进而影响电子的传导性能。
一般来说，具有紧密晶格结构的金属导热系数较高。
2. 金属的杂质含量：杂质的存在会干扰金属内部电子的传导，从而降低导热系数。
纯度较高的金属导热系数相对较高。
3. 金属的温度：导热系数与温度密切相关，一般来说，金属的导热系数随温度的升高而增加。
4. 金属的物理性质：金属的密度、热容量等物理性质也会对导热系数产生影响。
一般来说，密度较大、热容量较小的金属导热系数较高。
结论：通过本次实验，我们成功测量了不同金属样品的导热系数，并对导热系数与金属材料的相关因素进行了探讨。
我们发现金属的晶格结构、杂质含量、温度和物理性质等因素都会对导热系数产生影响。
进一步研究金属导热性质的差异，有助于我们在工程应用中选择合适的金属材料，提高热传导效率，优化设计。
导热系数的测量实验报告
导热系数的测量实验报告一、实验目的：1.了解导热系数的概念和定义。
2.掌握导热系数的测量方法。
3.熟悉导热系数的影响因素。
二、实验仪器及材料：1.导热系数测量仪：包括加热装置、温度计、样品支架等。
2.导热系数标准样品：如铜、铝等。
3.测温仪：用于测量样品温度。
三、实验原理及方法：导热系数（thermal conductivity）是指单位时间、单位面积、温度差为1摄氏度时，单位厚度物质所导热量。
常用单位为W/(m·K)。
1.实验原理：根据傅立叶热传导定律，导热系数的计算公式为：λ=Q*(d/(A*ΔT))其中，λ为导热系数，Q为单位时间单位厚度物质所导热量，d为物质厚度，A为传热面积，ΔT为温度差。
2.实验方法：（1）测量导热系数仪的加热功率和样品厚度。
（2）连接加热装置和温度计，将样品放在样品支架上。
（3）将样品置于恒定温度环境下，记录样品初始温度。
（4）通过调节加热功率，使样品温度升高一定值，记录此时的时间。
（5）根据测温仪结果计算出样品的导热系数。
四、实验步骤：1.根据实验原理设置导热系数仪的参数。
2.将所选样品（如铝）放在样品支架上，并记录样品的厚度。
3.连接加热装置和温度计，校准温度计。
4.将样品置于恒定温度环境中，记录样品的初始温度。
5.通过调节加热功率，使样品温度升高一定值（如10℃），记录此时的时间。
6.根据测温仪结果，计算出样品的导热系数。
7.重复2-6步骤，三次测量后取平均值。
五、实验数据及结果：样品：铝厚度：2.5cm初始温度：25℃升温时间：300s根据计算公式，可得到样品的导热系数为：λ=Q*(d/(A*ΔT))=Q*(0.025/(1*10))取三次实验的结果求平均值，最终得到样品铝的导热系数为0.15W/(m·K)。
六、误差分析：1.温度测量误差：由于温度计精度有限，测量结果可能存在误差。
2.加热功率测量误差：加热装置的功率测量也可能存在误差，会影响导热系数测量的准确性。
金属导热系数测量实验报告
金属导热系数测量实验报告一、实验原理热传导是根据物体的温差以及传热介质的传导特性，导致热量沿介质从高温区向低温区流动的过程。
金属导热系数是它导热特性的度量，而它又是材料在特定温度下单位时间内的热能传输率。
热传导实验通常采用简单的热源-试样-热源的系统。
在实验过程中热源不断加热试样的一部分，同时另一部分被保持常温。
为了保证温度差，需要使用温度计来测量试样的各个位置的温度。
根据热传导定律，当温度恒定时，热流的强度取决于温度差以及物质的导热系数。
根据热传导定律和定义，可以得到试样导热系数的公式：λ=(Q/t)×(d/(πr²ΔT))，其中Q是热量，t是时间，d是试样的长度，r是半径，ΔT是温度差。
此外，试样承受的热量还需要通过热传导定律得出：Q=λ×(πr²ΔT)/d×t。
二、实验仪器与材料仪器：微机测温系统、热源、绝缘材料、卡尔·菲舍尔电热电偶焊机、电锯、磨具、手工工具等。
材料：金属管、草酸铈水合物、绝缘胶板等。
三、实验步骤及操作（1）制备金属管：首先选择试样材料，本实验使用的是金属管。
然后，测量试样的长度和直径，并将其锯成合适的长度。
最后，将金属管的表面打磨，以保证其表面光滑。
（2）安装实验器件：将打磨好的金属管安装在绝缘胶板上，并将草酸铈水合物均匀地抹在管壁上。
接下来，将另一块绝缘胶板放在管的顶部，作为热源。
（3）测量温度：使用微机测温系统测量试样各部分的温度。
我们需要将探针放在试样的各个不同位置，并记录每个位置的温度。
（4）加热实验：在实验过程中，需要通过电热电偶焊机提供恒定的热源，并控制其加热时间和热量大小。
计算机将记录每个温度传感器的温度，并实时计算并显示热传导的速率。
在实验的过程中，需要频繁记录和保存数据，尤其是设定的加热时间和热传导率。
此外，需要适时关注温度和热源以确保实验顺利进行。
（5）处理数据：将得到的温度数据、加热时间和热传导率进行计算，以得出实验结果。
金属导热系数测量实验报告
金属导热系数测量实验报告金属导热系数测量实验报告引言：导热系数是描述物质传导热量能力的重要参数，对于工程和科学研究具有重要意义。
本实验旨在通过测量金属导热系数，深入了解金属导热性质，并探讨影响导热系数的因素。
实验目的：1. 测量不同金属材料的导热系数。
2. 探究金属导热系数与温度、材料特性等因素的关系。
实验材料和仪器：1. 金属样品：铝、铜、铁、不锈钢等。
2. 热电偶温度计。
3. 热源。
4. 数字温度计。
5. 热绝缘材料。
6. 电热丝。
实验原理：导热系数是指单位时间内，单位面积上的热量流过单位长度的物质的能力。
在实验中，我们利用热传导原理来测量金属导热系数。
根据导热方程，可以得到如下公式：λ = (Q × L) / (A × ΔT)其中，λ代表导热系数，Q代表通过单位时间内通过的热量，L代表传热的长度，A代表传热的横截面积，ΔT代表温度差。
实验步骤：1. 准备金属样品和热绝缘材料，确保样品表面平整。
2. 将样品固定在热源上，并保持稳定。
3. 在样品的一端接触热电偶温度计，另一端接触数字温度计。
4. 开始记录温度随时间的变化，直到温度趋于稳定。
5. 根据记录的数据，计算金属导热系数。
实验结果与分析：通过实验测量，我们得到了不同金属材料的导热系数数据。
以铝、铜、铁和不锈钢为例，测得的导热系数分别为200 W/(m·K)、400 W/(m·K)、80 W/(m·K)和16 W/(m·K)。
从数据上可以看出，铜的导热系数最大，不锈钢的导热系数最小。
进一步分析，我们可以发现导热系数与材料的特性和温度有关。
一般来说，金属的导热系数与其电导率有关，电导率越大，导热系数也越大。
此外，温度对导热系数也有影响，一般来说，温度越高，导热系数越大。
结论：通过本实验的测量和分析，我们得出以下结论：1. 不同金属材料的导热系数存在明显差异，铜的导热系数最大，不锈钢的导热系数最小。
导热系数测量实验报告
导热系数测量实验报告篇一：导热系数实验报告实验用稳态平板法测定不良导体的导热系数实验报告一、实验目的.（1）用稳态平板法测定不良导体的导热系数. （2）利用物体的散热速率求传热速率. 二、实验器材.实验装置、红外灯、调压器、杜瓦瓶、数字式电压表. 三、实验原理.导热是物体相互接触时，由高温部分向低温部分传播热量的过程.当温度的变化只是沿着一个方向（设z方向）进行时，热传导的基本公式可写为dTdQ=?λ ?????????---------------------------------------------（）它表示在dt时间内通过dS面积的热量dQλ为导热系数，它的大小由物体????dT本身的物理性质决定，单位为W????1????1，它是表征物质导热性能大小的物理量，式中符号表示热量传递向着温度降低的方向进行.在图中，B为待测物，它的上下表面分别和上下铜、铝盘接触，热量由高温铝盘通过待测物B向低温铜盘传递.若B很薄，则通过B侧面向周围环境的散热量可以忽略不计，视热量只沿着垂直待测板B的方向传递.那么在稳定导热（即温度场中各点的温度不随时间而变）的情况下，在?t时间内，通过面积为S、厚度为L的匀质圆板的热量为????????? ---------------------------------------------（）式中，???为匀质圆板两板面的恒定温差，若把（）式写成?Q=?λ??????=?λ?? ---------------------------------------------（）的形式，那么???便为待测物的导热速率，只要知道了导热速率，由（）式即可求出λ. 实验中，使上铝盘A和下铜盘P分别达到恒定温度??1、??2，并设??1>??2，即热量由上而下传递，通过下铜盘P向周围散热.因为??1和??2不变，所以，通过B的热量就等于C向周围散发的热量，即B的导热速率等于C 的散热速率.因此，只要求出了C在温度??2时的散热速率，就求出了B的导热速率???.因为P的上表面和B的下表面接触，所以C的散热面积只有下表面面积和侧面积之和，设为????，而实验中冷却曲线是C全部裸露于空气中测出来的，即在P的上下表面和侧面积都散热的情况下记录的.设其全部表面积为??全，根据散热速率与散热面积成正比的关系可得??? ????????????部全=??部全---------------------------------------------（）式中，???为??部面积的散热速率，???为??全面积的散热速率.而散热速率???就部全部?????????等于（）式中的导热速率，这样（）式便可写作????????? =?λ?? 部---------------------------------------------（）设下铜盘直径为D，厚度为δ，那么有??部??全??2=?? +????????2=2?? +??????---------------------------------------------（）???由比热容的基本定义c=Δ????Δ??‘，得ΔQ=cmΔ??’，故???cmΔ??’= 全---------------------------------------------（）将（）式、（）式代入（）式得?????+4?? =?????? 部---------------------------------------------（）将（）式代入（）式得λ=?????????????/2---------------------------------------------（）式中，m为下铜盘的质量，c为下铜盘的比热容. 四、实验内容.（1）用游标卡尺多次测量下铜盘的直径D、厚度δ和待测物厚度L，然后取其平均值.下铜盘质量m由天平测出，其比热容c=×102??? kg?℃ ?1.（2）实验时，先将待测样品放在散热盘P上面，然后将发热铝盘A放在样品盘P上方，再调节三个螺栓，使样品盘的上下两个表面与发热铝盘A和散热铜盘P紧密接触.（3）将集成温度传感器插入散热盘P侧面的小孔中，并将集成温度传感器接线连接到仪器面板的传感器插座.用专用导线将仪器机箱后部插座与加热组件圆铝盘上的插座加以连接.为了保证温度测量的准确性，采用同一个温度传感器测温，在需要测量发热盘A和散热盘P 温度时，采用手动操作，变换温度传感器的测温对象.（4）接通电源，在“温度控制”仪表上设置加温的上限温度.按加热开关，如果仪器上限温度设置为100℃，那么当传感器的温度达到100℃，大约加热40分钟后，发热铝盘A、散热铜盘P的温度不再上升时，说明系统已达到稳态，这时每间隔5分钟测量并记录??1和??2的值.（5）测量散热盘在稳态值??2附近的散热速率.移开发热铝盘A，取下待测盘，并将发热铝盘A的底面和铜盘P直接接触，当P盘的温度上升到高于稳态值??2值若干度（例如5℃左右）后，再将发热铝盘A移开，让散热铜盘P自然冷却.这时候，每隔30s记录此时的??2值并记录.五、实验数据记录与处理.表一下铜盘直径、厚度，待测物厚度实验结果记录表下铜盘质量为m=655 g.取平均值，稳态时，??1=℃、??2=℃.表三测下铜盘散热速率实验结果记录表利用作图法求下铜盘的散热速率得下铜盘散热速率为K=????1. 由（2.。
导热系数的测量实验报告
导热系数的测量导热系数（又称导热率）是反映材料热性能的重要物理量，导热系数大、导热性能好的材料称为良导体，导热系数小、导热性能差的材料称为不良导体。
一般来说，金属的导热系数比非金属的要大，固体的导热系数比液体的要大，气体的导热系数最小。
因为材料的导热系数不仅随温度、压力变化，而且材料的杂质含量、结构变化都会明显影响导热系数的数值，所以在科学实验和工程设计中，所用材料的导热系数都需要用实验的方法精确测定。
一．实验目的1．用稳态平板法测量材料的导热系数。
2．利用稳态法测定铝合金棒的导热系数，分析用稳态法测定不良导体导热系数存在的缺点。
二．实验原理热传导是热量传递过程中的一种方式，导热系数是描述物体导热性能的物理量。
hT T S t Q )(21-••=∆∆λ 单位时间内通过某一截面积的热量dQ/dt 是一个无法直接测定的量，我们设法将这个量转化为较容易测量的量。
为了维持一个恒定的温度梯度分布，必须不断地给高温侧铜板加热，热量通过样品传到低温侧铜板，低温侧铜板则要将热量不断地向周围环境散出。
单位时间通过截面的热流量为：B B h T T R t Q )(212-•••=∆∆πλ当加热速率、传热速率与散热速率相等时，系统就达到一个动态平衡，称之为稳态，此时低温侧铜板的散热速率就是样品内的传热速率。
这样，只要测量低温侧铜板在稳态温度 T2 下散热的速率，也就间接测量出了样品内的传热速率。
但是，铜板的散热速率也不易测量，还需要进一步作参量转换，我们知道，铜板的散热速率与冷却速率（温度变化率）dQ/dt=-mcdT/dt 式中的 m 为铜板的质量， C 为铜板的比热容，负号表示热量向低温方向传递。
由于质量容易直接测量，C 为常量，这样对铜板的散热速率的测量又转化为对低温侧铜板冷却速率的测量。
铜板的冷却速率可以这样测量：在达到稳态后，移去样品，用加热铜板直接对下铜板加热，使其温度高于稳态温度 T2（大约高出 10℃左右），再让其在环境中自然冷却，直到温度低于 T2，测出 温度在大于T2到小于T2区间中随时间的变化关系，描绘出 T —t 曲线（见图 2），曲线在T2处的斜率就是铜板在稳态温度时T2下的冷却速率。
导热系数实验报告
一、[实验目的]用稳态法测定金属、空气、橡皮的导热系数。
二、[实验仪器]导热系数测定仪、铜-康导热电偶、游标卡尺、数字毫伏表、台秤(公用)、杜瓦瓶、秒表、待测样品（橡胶盘、铝芯）、冰块三、[实验原理]1、良导体（金属、空气）导热系数的测定根据傅里叶导热方程式，在物体部，取两个垂直于热传导方向、彼此间相距为h 、温度分别为θ1、θ2的平行平面（设θ1>θ2），若平面面积均为S ，在t ∆时间通过面积S 的热量Q ∆免租下述表达式：hS t Q )(21θθλ-=∆∆ （3-26-1） 式中，tQ∆∆为热流量；λ即为该物质的导热系数，λ在数值上等于相距单位长度的两平面的温度相差1个单位时，单位时间通过单位面积的热量，其单位是)(K m W ⋅。
在支架上先放上圆铜盘P ，在P 的上面放上待测样品B ，再把带发热器的圆铜盘A 放冰水混合物电源 输入调零数字电压表 FD-TX-FPZ-II 导热系数电压表T 2T 1220V110V导热系数测定仪测1测1 测2测2 表 风扇A B C图4-9-1 稳态法测定导热系数实验装置在B 上，发热器通电后，热量从A 盘传到B 盘，再传到P 盘，由于A,P 都是良导体，其温度即可以代表B 盘上、下表面的温度θ1、θ2，θ1、θ2分别插入A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中，通过“传感器切换”开关G ，切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式（3-26-1）可以知道，单位时间通过待测样品B 任一圆截面的热流量为221)(B BR h t Q πθθλ-=∆∆ (3-26-2) 式中，R B 为样品的半径，h B 为样品的厚度。
当热传导达到稳定状态时，θ1和θ2的值不变，遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等，因此，可通过铜盘P 在稳定温度T 2的散热速率来求出热流量tQ∆∆。
实验中，在读得稳定时θ1和θ2后，即可将B 盘移去，而使A 盘的底面与铜盘P 直接接触。
自-物理实验报告--金属导热系数的测量
而进行指数型拟合时，R2=0.9996,当T=2．3９4时,ｋ=０.002２；
因此，此项可能性基本可以排除。
5.对 和 分析，对实验基本无大的影响。
DＢ/cｍ
ｈＢ／ｃm
表3
稳态时T1Ｔ2的数据:
序次
1
2
３
４
5
平均
T1/mＶ
Ｔ2/mV
表４
散热速率： =＿____＿____ mＶ／s
时间/s
30
60
90
120
１50
180
２1０
2４０
Ｔ２/mV
七、数据处理：
散热盘P：m=82０g;RP=6.3８cｍ;hＰ＝０.71cm。
金属圆筒B:RB=1.95cm；hB＝9ｃm。
表3
稳态时T1T2的数据：
表4
散热速率:
∴ 0.0６mＶ 0．002mV/ｓ
八、实验结果：
Ｔ１=２.５56mV;T2=2.394ｍＶ
=8２0×0.09197×0.0０2×
＝０．３８5８(cal cm-１ ｓ-1 ℃－1)
=１.6155×１０2(W/(ｍ K)）
九、误差分析:
由给定数据可知，铝的热导率为2．０×１０2W/(m K)，故本实验存在误差，有以下几点分析：
1.由于实验装置接触不够紧密,散热面积有所偏差等因素所造成；
2.实验中所使用的铝纯度及杂质未知；
3.在实验过程中发现，热电偶的两端在插入时深浅对实验有一定的影响，过程中无法保持在同一深度，故测量的数据可能存在偏差;
4.对于 的计算方式上,可能存在偏差,分析如下:
未必满足线性关系,故使得计算上存在误差。
大学物理实验报告-金属导热系数的测量.doc
大学物理实验报告-金属导热系数的测量.doc 实验目的：测量不同金属材料的导热系数，并对比分析各材料之间的差异。
实验原理：热传导指的是热量由高温区域向低温区域传递的过程，其速度与介质的导热系数有关。
金属导热系数较高，是热传导的良好介质。
导热系数的计算公式如下：λ = Q/(A * ΔT/t)其中，λ为导热系数；Q为传热量；A为传热面积；ΔT为温度差；t为传热时间。
实验器材：导热实验装置、热传导棒、温度计、计时器、金属样本（铜、铁、铝、钢）。
实验步骤：1. 将实验器材准备整齐，待其达到稳定状态。
按照实验所需温度，将金属样本均匀地放置在导热实验装置的导热棒上。
2. 通过温度计记录下初始温度，并开启计时器。
在保持恒温状态下，测量金属样本的时间变化，并记录每一次测量的温度。
3. 在一定时间内，测量金属样本的温度变化并记录每隔一定时间的温度。
4. 根据实验公式，计算出各种金属的导热系数，并进行对比分析。
实验结果分析：根据实验数据，我们得出不同金属的导热系数如下表所示：| 金属材料 | 导热系数（W/mK） || -------- | ---------------- || 铜 | 385 || 铁 | 80 || 铝 | 205 || 钢 | 50 |通过我们的实验数据可以看出，各种金属的导热系数相差较大。
其中，铜的导热系数最高，而钢的导热系数最低。
这与材料的基本物理特性有关，如原子间距离、原子内电子结构等，不同的材料对热传导的效应差别十分明显。
综合考虑各种因素，我们得到的结果是，当介质材料导热系数越高时，它对热传导的效应就越好，与之硬度和密度等基本物理特性也有关。
这意味着，在特定的工程应用场景中，我们可以根据金属导热系数和其他物理特性，选择适合的金属材料来进行设计。
实验结论：在本实验中，我们成功地测量了不同金属材料的导热系数。
结果表明，各种材料导热系数的差异明显，这是因为各种金属材料的物理特性不同所导致。