人教版数学七年级竞赛教程之倍数 约数附答案
倍数与约数之练习题计算倍数和约数

倍数与约数之练习题计算倍数和约数倍数与约数是初中数学中的重要概念,对于提升学生的数学运算能力和逻辑思维能力有着重要意义。
本文将以练习题的形式,帮助读者加深对倍数与约数的理解,并通过解题过程加强对相关知识点的掌握。
一、倍数的计算1. 若正整数a能被正整数b整除,我们就称a是b的倍数,记作a|b或b/a。
2. 倍数的计算可以通过以下练习题进行加强:练习题一:计算下列数的倍数1)11的倍数2)25的倍数3)98的倍数4)72的倍数解答:1)11的倍数:11、22、33、44、55、66、77、88、99、110、121……2)25的倍数:25、50、75、100、125、150、175、200、225、250、275……3)98的倍数:98、196、294、392、490、588、686、784、882、980、1078……4)72的倍数:72、144、216、288、360、432、504、576、648、720、792……二、约数的计算1. 若正整数a能被正整数b整除,我们就称b是a的约数,记作b|a 或a/b。
2. 约数的计算可以通过以下练习题进行加强:练习题二:计算下列数的约数1)12的约数2)37的约数3)60的约数4)92的约数解答:1)12的约数:1、2、3、4、6、122)37的约数:1、373)60的约数:1、2、3、4、5、6、10、12、15、20、30、604)92的约数:1、2、4、23、46、92三、倍数与约数之间的关系1. 若正整数a既是b的倍数,又是c的倍数,那么a是b与c的公倍数。
2. 若正整数a既是b的约数,又是c的约数,那么a是b与c的公约数。
3. 设a、b是两个正整数,且a≠0,b≠0,那么a与b的最小公倍数,记作[a,b],是同时是a的倍数也是b的倍数的最小正整数;a与b的最大公约数,记作(a,b),是同时是a的约数也是b的约数的最大正整数。
练习题三:计算下列数的最小公倍数与最大公约数1)4与6的最小公倍数与最大公约数2)15与20的最小公倍数与最大公约数3)24与32的最小公倍数与最大公约数4)45与60的最小公倍数与最大公约数解答:1)4与6的最小公倍数为12,最大公约数为2。
人教版数学七年级竞赛教程之倍数 约数附答案
倍数约数【知识精读】1两个整数A和B(B≠0),如果B能整除A(记作B|A),那么A叫做B的倍数,B 叫做A的约数。
例如3|15,15是3的倍数,3是15的约数。
2因为0除以非0的任何数都得0,所以0被非0整数整除。
0是任何非0整数的倍数,非0整数都是0的约数。
如0是7的倍数,7是0的约数。
3整数A(A≠0)的倍数有无数多个,并且以互为相反数成对出现,0,±A,±2A,……都是A的倍数,例如5的倍数有±5,±10,……。
4整数A(A≠0)的约数是有限个的,并且也是以互为相反数成对出现的,其中必包括±1和±A。
例如6的约数是±1,±2,±3,±6。
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,被除数=除数×商数+余数若用字母表示可记作:A=BQ+R,当A,B,Q,R都是整数且B≠0时,A-R能被B整除例如23=3×7+2则23-2能被3整除。
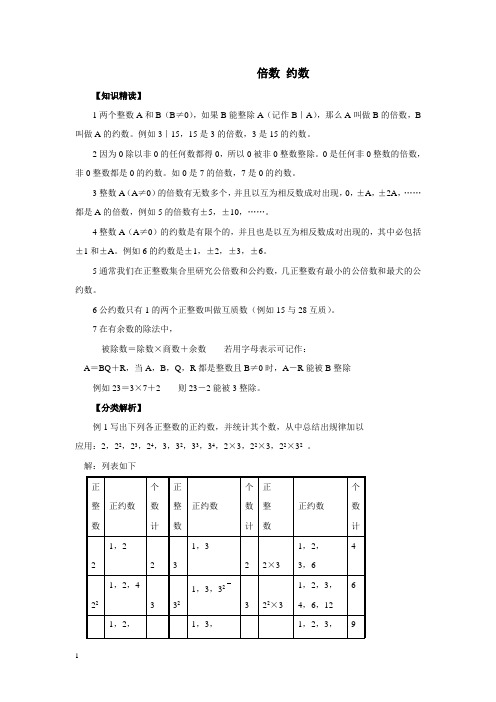
【分类解析】例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32。
解:列表如下其规律是:设A=a m b n(a,b是质数,m,n是正整数)那么合数A的正约数的个是(m+1)(n+1)例如求360的正约数的个数解:分解质因数:360=23×32×5,360的正约数的个数是(3+1)×(2+1)×(1+1)=24(个)例2用分解质因数的方法求24,90最大公约数和最小公倍数解:∵24=23×3,90=2×32×5∴最大公约数是2×3,记作(24,90)=6最小公倍数是23×32×5=360,记作[24,90]=360例3己知32,44除以正整数N有相同的余数2,求N解:∵32-2,44-2都能被N整除,∴N是30,42的公约数∵(30,42)=6,而6的正约数有1,2,3,6经检验1和2不合题意,∴N=6,3例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的最小公倍数减去1。
人教版初一下数学竞赛试题及答案

人教版初一下数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. -1C. 1D. 22. 如果a和b是两个连续的整数,且a > b,那么a-b的值是:A. 1B. 0C. -1D. 23. 一个数的平方根是它本身,这个数可以是:A. 1B. -1C. 0D. 44. 一个数的立方等于它本身,这个数有:A. 1个B. 2个C. 3个D. 4个5. 一个圆的半径是r,它的面积是:A. πr²B. 2πrC. πrD. r²6. 一个长方体的长、宽、高分别是a、b、c,它的体积是:A. abcB. 2abcC. a+b+cD. a²b²c²7. 一个等差数列的首项是a,公差是d,第n项是:A. a+(n-1)dB. a+ndC. a-dD. a-d(n-1)8. 如果一个三角形的三边长分别为a、b、c,且a² + b² = c²,那么这个三角形是:A. 直角三角形B. 等边三角形C. 等腰三角形D. 不规则三角形9. 一个分数的分子和分母同时扩大相同的倍数,其值:A. 增大B. 减小C. 不变D. 无法确定10. 一个数的绝对值是它本身,这个数:A. 必须为正数B. 必须为负数C. 可以是正数或零D. 可以是负数或零二、填空题(每题4分,共20分)11. 一个数的平方等于16,这个数是________。
12. 如果一个数的相反数是-5,那么这个数是________。
13. 一个数的绝对值等于5,这个数可以是________。
14. 一个数的立方根是2,那么这个数是________。
15. 一个数的倒数是1/4,这个数是________。
三、解答题(每题10分,共50分)16. 计算下列表达式的值:(3+5)² - 2×(4-1)。
17. 一个长方体的长是10厘米,宽是8厘米,高是6厘米,求它的表面积和体积。
初中数学竞赛-七年级 -整数问题2 - 答案

∴
,
即可.
【解答】解:385 的二位因数有 11,35,55,77, 他们不全相同,
解得,
,
故最大为 77,77,55,和为 209, 最小为 11,11,35,和为 57.
∴100x+y=352=1225, ∴x=12,y=25,
故答案为 209,57.
即:小王现在的年龄是 12 岁,
6.在 100~1999 这一千九百个自然数中,十位与个位数 字相同的共有 190 个.
结论. 【解答】解:∵2m+2006+2m =2m(22006+1) ∵22006 末位是 4, ∴22006+1 末位是 5, 而 2m 是偶数, 所以 2m+2006+2m(m 是正整数)的末位数字是 0.
则 k=0、1 或 2,(0 不合要求,舍去), 因此 A=4001 或 A=8004. 故答案为:4001 或 8004. 15.若 1+2+3+…+k 之和为一完全平方数 N2,并且 N 小 于 100,则 K 的可能值是 1,8 或 49 . 【考点】#9:完全平方数.
与最小公倍数之和等于 ab+1 .
个数仍然为完全平方数,则小王现在的年龄是 12
【考点】#6:约数与倍数. 菁优网版权所有
【分析】由于相邻的两个自然数互为质数,故他们的 最大公约数是 1,最小公倍数是 ab,从而易求答案. 【解答】解:a、b 为两个相邻的自然数,它们的最大
岁. 【考点】#9:完全平方数.
位对应着 1,2,…,19 这 19 种可能即可得出答案.
15,然后左边分解因式,右边分解因数,建立方程组
【解答】解:后两位数字相同,只有 00,11,22,33, 44,55,66,77,88,99 这 10 种可能情形, 而每一种相同的末两位数字相同的数,百位到千位对 应着 1,2,…,19 这 19 种可能,
初一数学专题复习之约数与倍数

初一数学专题复习之约数与倍数
初一数学专题复习之约数与倍数
约数和倍数:若整数a能够被b整除,a叫做b的倍数,b就叫做a的约数。
公约数:几个数公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
最大公约数的`性质:
1、几个数都除以它们的最大公约数,所得的几个商是互质数。
2、几个数的最大公约数都是这几个数的约数。
3、几个数的公约数,都是这几个数的最大公约数的约数。
4、几个数都乘以一个自然数m,所得的积的最大公约数等于这几个数的最大公约数乘以m。
例如:12的约数有1、2、3、4、6、12;
18的约数有:1、2、3、6、9、18;
那么12和18的公约数有:1、2、3、6;
那么12和18最大的公约数是:6,记作(12,18)=6;
求最大公约数基本方法:
1、分解质因数法:先分解质因数,然后把相同的因数连乘起来。
2、短除法:先找公有的约数,然后相乘。
3、辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数。
公倍数:几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
12的倍数有:12、24、36、48……;
18的倍数有:18、36、54、72……;
那么12和18的公倍数有:36、72、108……;
那么12和18最小的公倍数是36,记作[12,18]=36;
最小公倍数的性质:
1、两个数的任意公倍数都是它们最小公倍数的倍数。
2、两个数最大公约数与最小公倍数的乘积等于这两个数的乘积。
最小公倍数的求法:1、短除法;2、分解质因数。
数论--约数倍数-第4讲约数和倍数竞赛班学生

第四讲约数和倍数一、基础知识1. 1. 常用的特殊自然数的整除特征1)2系列:被2整除只需看末位能否被2整除被4整除只需看末两位能否被4整除被8整除只需看末三位能否被8整除,依次类推2)5系列:被5整除只需看末位是否为0或5被25整除只需看末两位能否被25整除,即只可能是00,25,50,75我们以被8整除看末三位为例证明以上两个系列的性质假设一个多位数末三位是abc,末三位之前的部分为x那么该数=1000x+abc,由于8|1000,所以8|1000x,因此该数能否被8整除就决定于末三位abc能否被8整除,证毕.3)3系列:被3整除只需看各位数字之和能否被3整除.被9整除只需看各位数字之和能否被9整除.我们以三位数为例来证明被9整除只需看各位数字之和这一性质假设该三位数为abc=100a+10b+c=(99a+9b)+(a+b+c)很明显第一个括号里的数是9的倍数,因此只要a+b+c,即各位数字之和能被9整除,那么这个三位数abc 就能被9整除,反之亦然。
推广到任意位数的自然数,该证明方法仍然成立,请大家自己尝试一下.4)7,11,13系列被7,11,13整除的判别方法:看多位数的末三位和前面部分之差能否被7,11,13整除[思考]:为什么要从末三位把这个数一分为二呢?仔细想一想我们会发现7x11x13=1001,正好比1000大1,由此我们可以得到如下证明和2系列的证明类似,我们仍然设一个多位数的末三位是abc,前面部分是x那么我们要证明的就是这个多位数能否被7,11,13整除决定于abc-x能否被7,11,13整除该数=1000x+abc=1001x+(abc-x)由于1001同时是7,11,13的倍数,所以这个多位数能否被7,11,13整除决定于abc-x能否被7,11,13整除,证毕.特别的,我们还有另外一种判别能否被11整除的性质,就是看奇数位数字之和与偶数为数字之和能否被11整除,若能整除则原数可被11整除,反之亦然.请大家自己想一想这个如何证明?(思考题)2.整除的性质1)已知b|c,a|c,则[a,b]|c,特别地,若(a,b)=1,则有ab|c.2)已知c|ab,(b,c)=1,则c|a.3.最大公约数和最小公倍数两个基本性质一.两个自然数分别除以它们的最大公约数,所得的商互质.即若a=a1*(a,b),b=b1*(a,b),则(a1,b1)=1二.两个数的最大公约和最小公倍的乘积等于这两个数的乘积.[a,b]*(a,b)=ab二、例题部分例1.(★★第16届希望杯第2试)我们用记号“|”表示两个正整数之间的整除关系,如3|12表示3整除12,那么满足x | (y+1)和y | (x+1)的正整数组(x,y)有__________组.例2.(★★第12届希望杯第2试) 两个正整数的和是60,它们的最小公倍数是273,则它们的乘积是__________例3.(★★★★ 1987年北京初二数学竞赛题)x,y,z均为整数,若11|(7x+2y-5z),求证:11|(3x-7y+12z)。
2023年初一数学竞赛教程含例题练习及答案⑸

初一数学竞赛讲座第5讲与年号有关的竞赛题在数学竞赛中,常可以看到某些题目中出现了当年的年号,这类题我们称之为“年号题”。
这类题趣味性强,时间性强,引起了参与竞赛的少年朋友很大的爱好。
“年号题”一般可提成两类,一类是题目的条件中出现了当年的年号,另一类是题目答案中出现了当年的年号。
下面我们分别举例说明这两类问题的解法。
一、题目条件中出现年号的问题1.题目在编制和解答中巧妙地运用了该年年号的数字特性,如年号数值的质因数分解式、是否质数、它的数的整除性等等。
例1 将19到80的两位数顺次排成数A=19202322…7980。
问:这个数A 能否被1980整除?解:由于1980=99×20,因此要考察A能否被1980整除,只需要考察A能否被99和20整除就行了。
能被20整除是显然的。
由于99除100的任何次方所得的余数都是1,所以A=19×10061+20×10060+…+79×100+80除以99的余数与B=19+20+…+79+80=99×31除以99的余数相同。
由于99|B,所以99|A。
于是A能被1980整除。
例2 用S(n)表达自然数n的各位数字之和,又n+S(n)=1999,求自然数n。
11x+2y=89。
注意到x是奇数且x,y都是一位整数,不难求得x=7,y=6,从而n=1976。
例3 在3×3的九宫格中,填上 9个不同的自然数,使得每行三数相乘,每列三数相乘所得的6个乘积都等于P 。
试拟定P 能取1996,1997, 1998,1999,2023,2023这6个数中的哪些值。
解:所填的9个数应为P 的9个不同约数,又P 不能填入九宫格内,故P 的不同约数的个数应不小于10。
1996=22×499,有6个约数; 1997和1999是质数,各有2个约数;1998=2×33×37,有16个约数; 2023=24×53,有20个约数;2023=3×23×29,有8个约数。
数的倍数与约数练习题及答案

数的倍数与约数练习题及答案一、选择题1. 下列哪个数一定是4的倍数?A. 19B. 28C. 35D. 422. 哪个数不是 7 的约数?A. 14B. 21C. 28D. 353. 若一个数同时是2和3的倍数,它最多是多少的倍数?A. 12B. 18C. 24D. 364. 一个数是5的倍数,它一定是10的倍数吗?A. 是B. 否5. 有一个数,在它的乘法表中,找到了数3,4,5,6,8,9,12,16,18,24,27分别是第几行?A. 第1 行B. 第2 行C. 第3 行D. 第4 行6. 某个数能同时被2和5整除,它能被10整除吗?A. 能B.不能7. 分解因式:36 = _____ * _____A. 3, 12B. 2, 18C. 4, 9D. 6, 68. 设 x 是3的倍数, y 是4的倍数,那么 5x + 6y 是____的倍数。
A. 3B. 4C. 5D. 69. 一个整数能同时被2和3整除,它一定是6的倍数吗?A. 是B. 否10. 分解因式:48 = _____ * _____A. 2, 24B. 3, 16C. 4, 12D. 6, 8二、填空题1. 6 的倍数的最小正整数是 ______。
2. 14 是 ______ 的倍数。
3. 有一个数,它是 3 的倍数,也是 2 的倍数,它至少是 ______ 的倍数。
4. 48 是 ______ 的约数。
5. 若一个数同时是 2 和 5 的倍数,它最小是 ______ 的倍数。
6. 20 = 4 * ______。
7. 若一个数同时是 2 和 3 的倍数,那么它一定是 ______ 的倍数。
8. 64 是 ______ 的约数。
三、解答题1. 找出 36 的所有约数。
2. 一个数被 2 除余 1,被 3 除余 2,被 5 除余 4,那么该数最小是多少?3. 分解因式:60 = ______ * ______。
4. 7 的最小倍数是多少?5. 分解因式:72 = ______ * ______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍数约数
【知识精读】
1两个整数A和B(B≠0),如果B能整除A(记作B|A),那么A叫做B的倍数,B 叫做A的约数。
例如3|15,15是3的倍数,3是15的约数。
2因为0除以非0的任何数都得0,所以0被非0整数整除。
0是任何非0整数的倍数,非0整数都是0的约数。
如0是7的倍数,7是0的约数。
3整数A(A≠0)的倍数有无数多个,并且以互为相反数成对出现,0,±A,±2A,……都是A的倍数,例如5的倍数有±5,±10,……。
4整数A(A≠0)的约数是有限个的,并且也是以互为相反数成对出现的,其中必包括±1和±A。
例如6的约数是±1,±2,±3,±6。
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,
被除数=除数×商数+余数若用字母表示可记作:
A=BQ+R,当A,B,Q,R都是整数且B≠0时,A-R能被B整除
例如23=3×7+2则23-2能被3整除。
【分类解析】
例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以
应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32。
解:列表如下
其规律是:设A=a m b n(a,b是质数,m,n是正整数)
那么合数A的正约数的个是(m+1)(n+1)
例如求360的正约数的个数
解:分解质因数:360=23×32×5,
360的正约数的个数是(3+1)×(2+1)×(1+1)=24(个)
例2用分解质因数的方法求24,90最大公约数和最小公倍数
解:∵24=23×3,90=2×32×5
∴最大公约数是2×3,记作(24,90)=6
最小公倍数是23×32×5=360,记作[24,90]=360
例3己知32,44除以正整数N有相同的余数2,求N
解:∵32-2,44-2都能被N整除,∴N是30,42的公约数
∵(30,42)=6,而6的正约数有1,2,3,6
经检验1和2不合题意,∴N=6,3
例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数
分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的最小公倍数减去1。
解:∵[10,9,8]=360,
∴所以所求的数是359
【实战模拟】
1,12的正约数有_________,16的所有约数是_________________
2,分解质因数300=_________,300的正约数的个数是_________
3,用分解质因数的方法求20和250的最大公约数与最小公倍数。
4,一个三位数能被7,9,11整除,这个三位数是_________
5,能同时被3,5,11整除的最小四位数是_______最大三位数是________
6,己知14和23各除以正整数A有相同的余数2,则A=________
7,写出能被2整除,且有约数5,又是3的倍数的所有两位数。
答____
8,一个长方形的房间长1.35丈,宽1.05丈要用同一规格的正方形瓷砖铺满,问正方形最大边长可以是几寸?若用整数寸作国边长,有哪几种规格的正方形瓷砖适合?
9,一条长阶梯,如果每步跨2阶,那么最后剩1阶,如果每步跨3阶,那么最后剩2阶,如果每步跨4阶,那么最后剩3阶,如果每步跨5阶,那么最后剩4阶,如果每步跨6阶,那么最后剩5阶,只有每步跨7阶,才能正好走完不剩一阶,这阶梯最少有几阶?
答案
1. 1,2,3,4,6,12;±1,±2,±3,±6,±9,±18
2. 22×3×52;18
3. 2×5;22×53
4. 693
5. [3,5,11]=165,1155;990
6. A=3 即求14-2与23-2的公约数
7. 30,60,90
8.(135,105)=15,正约数有1,3,5,15
9.119。
∵[2,3,4,5,6]=60,60×2-1=119。
