沪科版习题库之二次根式性质1
沪科版二次根式

1
教学目标:
1、认识二次方根,理解二次方根 的双重非负性,并会根据二次方 根的双重非负性解相关练习。
? ? 2、认识二次方根的性质1 : a 2 ? a
(a≥0)和 性质2: a 2 ? a ;并利 用它们进行计算和化简.
大家好
2
回忆
⑴什么叫做一个数的平方根?如何表示? 一般地,若一个数的平方等于a,则 这个数就叫做a的平方根.
2 3
????2
=
-6
? ?2
x xy
? 5 ? 2 ?? 5 ? 2 ?
? x3 y
=3
大家好
13
2.计算:? (? 1 )02 ? (? 3 3)2
解:? (? 10 )2 ? (? 3 3)2 ? ? 10 ? (? 3)2 ? ( 3)2
? ?10 ? 27 ? 17
大家好
14
32 ? 3
?1? x ? 3 ?
6? x
x≥3 x≤6
∴3≤x≤6
?2? 1 ? x ? x ? 1
x≥1 x≤1
∴x=1
?3? x 2 ? 2
?4? x ? 1
x为全体实数.
x为全体实数.
大家好
10
( 4 )2 ? 4
????
1 9
????2
?
1 9
( 0.01 ) 2 ? 0.01
( 0 )2 ? 0
二次根式性质1:
a(a≥ 0) 是 一 个 非 .负 数
大家好
18
结束
大家好
19
? ? 性质1 a 2 ? a (a≥0)
大家好
பைடு நூலகம்11
计算:(1)( 3)2;(2)(3 5).2 2
沪科版八年级数学下册第16章《二次根式》培优讲解与练习
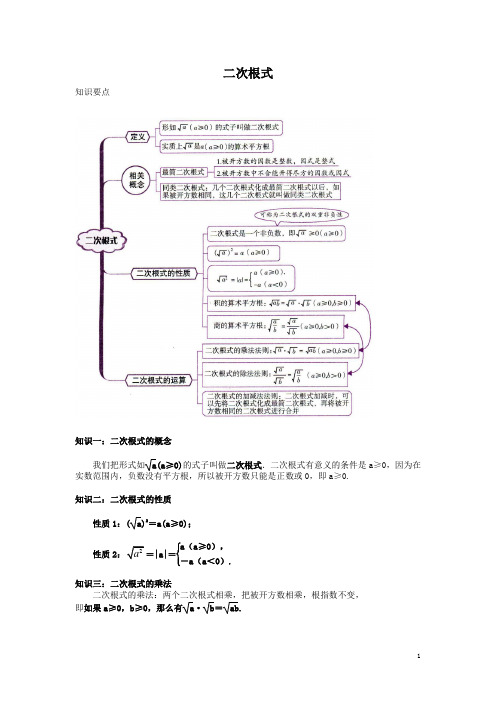
二次根式知识要点知识一:二次根式的概念我们把形式如a(a ≥0)的式子叫做二次根式.二次根式有意义的条件是a ≥0,因为在实数范围内,负数没有平方根,所以被开方数只能是正数或0,即a ≥0.知识二:二次根式的性质性质1:(a)2=a(a ≥0);性质2|a|=⎩⎪⎨⎪⎧a (a ≥0),-a (a <0).知识三:二次根式的乘法二次根式的乘法:两个二次根式相乘,把被开方数相乘,根指数不变,即如果a ≥0,b ≥0,那么有a ·b =ab.知识四:二次根式的乘法公式的逆用 二次根式乘法公式a ·b =ab(a ≥0,b ≥0),由等式对称性,也可以写成ab =a ·b(a ≥0,b ≥0).知识五:二次根式的除法两个二次根式相除,把被开方数相除作为商的被开方数,根指数不变,用字母表示为:a b =a b (a ≥0,b >0).知识六:二次根式的除法公式的逆用及分母有理化 由二次根式除法规定,a b =a b (a ≥0,b >0),反过来可得,a b =a b(a ≥0,b >0). 分母有理化:二次根式的除法运算,通常采用分子、分母同乘以一个式子化去分母中的根号的方法来进行.把分母中的根号化去,叫做分母有理化.知识七:最简二次根式满足下面两个条件的二次根式就是最简二次根式:(1)被开方数的因数是整数,因式是整式;(2)被开方数不含开得尽方的因数或因式.最简二次根式具备以下两个特点:(1)被开方数不含分母;(2)被开方数中不含开得尽方的因数或因式.在化简二次根式时要注意:(1)有时需将被开方数分解因式;(2)当一个式子的分母中含有二次根式时,一般应先分母有理化.知识八:二次根式的大小比较比较二次根式大小的常用方法有:(1)作差法:先求出a 与b 的差,再根据“当a-b<0时,a<b ;当a-b=0时,a=b ;当a-b>0时,a>b ”来比较a 与b 的大小.(2)作商法:a>0,b>0,若1a b >,则a>b ;若1a b <,则a<b ;若1a b=,则a=b. (3)倒数法:先分别求出a 与b 的倒数,再根据“当11a b <时,a>b ;当11a b =时,a=b ;当11a b >时,a<b ”来比较a 与b 的大小. (4)平方法:先将两个根式各自平方,然后比较平方后法大小,再说明原数的大小,即若a>0,b>0,且22a b >,则a>b ;若a<0,b<0,且22a b >,则a<b.(5)移动因式法:当a>0,b>0时,若要比较形如与的两数大小,可先把根号外的正因数a 与b 平方后移入根号内,再根据被开方数的大小进行比较.(6)分母有理化法:先将分式里分母中的根号化去后,再比较其结果,便可以判断原来的根式的大小.知识九:同类二次根式几个二次根式化成最简二次根式后,如果被开方数相同,像这样的二次根式称为同类二次根式.知识十:二次根式的加减二次根式相加减,先把各个二次根式化成最简二次根式,再把同类二次根式合并.二次根式的加减:①将每个二次根式化简;②找出同类二次根式;③合并同类二次根式.若有括号,一般先去括号,再合并同类二次根式.知识十一:二次根式的混合运算二次根式的混合运算顺序和实数混合运算顺序一样,先算乘方,再算乘除,最后算加减,有括号的,先算括号内的. 类型一:考查二次根式的概念(求自变量取值范围) 1、下列各式中,不是二次根式的是( ) A .45 B .3π- C .14 D .122、二次根式212--x x 有意义时,则x 的取值范围是 .3、已知: 122+--++=x x y ,则2001)(y x += .类型二:考查二次根式的性质(非负性、化简)4、实数在数轴上的位置如图所示,化简21(2)=a a -+- .5、把34-的根号外的因式移到根号内得 ;化简1x x -= .6、若代数式22(2)(4)a a -+-的值是常数2,则a 的取值范围是 .7、已知254245222+-----=x x x x y ,则22y x += . (重庆市竞赛题)8、若-3≤x ≤2时,试化简│x-2│+2(3)x ++21025x x -+.9、已知直角三角形两边x 、y 的长满足|x 2-4|+652+-y y =0,求第三边长.10、若│2016-a │,求a-20162的值.11、设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,求22223yxy x y xy x +--+的值. 12、在实数范围内分解因式: 23x -= ;4244m m -+= 429__________,2__________x x -=-+=.类型三:最简二次根式和同类二次根式13、下列各式中是最简二次根式的是( ) (A)a 18 (B)2x (C)22n m + (D)y x 23 14、如果最简二次根式83-a 与a 217-能够合并为一个二次根式,则a=__________. 类型四:二次根式计算15、计算⎪⎪⎭⎫ ⎝⎛-÷1213115 27124148÷⎪⎭⎫ ⎝⎛+28182122--⎪⎪⎭⎫ ⎝⎛+⨯2001)13(2)13(2)13(199920002001++-+-+类型五:综合提升1、若 ab ≠0,则等式ab b b a-=--351成立的条件是 .(淄博市中考题)211x -= )A .x ≥1B .x ≥-1C .-1≤x ≤1D .x ≥1或x ≤-13、如果式子2)1(2-+-x x 化简的结果为32-x ,则x 的取值范围是( )A .x ≤1B .x ≥2C .1≤x ≤2D .x >04、已知)0,0(02>>=+-y x y xy x ,则y xy x yxy x 4353-++-的值为( )A .31 B .21 C .32 D .43 5、已知233x x +=-x 3+x ,则( )(A )x ≤0 (B )x ≤-3 (C )x ≥-3 (D )-3≤x ≤06、已知21+=m ,1n =()()227143678m m a n n -+--=.则a = .7、已知139+与139-的小数部分分别是a 和b ,求ab -3a+4b+8的值.8、已知x 、y 是实数,且329922+--+-=x x x y ,求y x 65+的值.9、已知a 、b 、c 均为实数,且c c ab ab a a ===+22,1,0. 化简:。
沪教版八年级上册-二次根式的复习与练习题

二次根式知识点归纳和题型归类一、知识要点梳理知识点一、二次根式的主要性质: 1.; 2.; 3.;4. 积的算术平方根的性质:;5. 商的算术平方根的性质:.6.若,则.知识点二、二次根式的运算 1.二次根式的乘除运算(1) 运算结果应满足以下两个要求:①应为最简二次根式或有理式;②分母中不含根号. (2) 注意每一步运算的算理; (3) 乘法公式的推广:2.二次根式的加减运算 先化简,再运算,3.二次根式的混合运算 (1)明确运算的顺序,即先乘方、开方,再乘除,最后算加减,有括号先算括号里; (2)整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用. 二、分类练习与讲解: 1、 二次根式的概念我们把形如)0(≥a a 的式子叫做二次根式,如)1(1,1,32,51,32≥-+x x x 等,都是二次根式注意:① 二次根式都含有二次根号"";② 在二次根式中,被开方数a 必须满足0≥a ,当0<a 时,根式无意义; ③ 在二次根式中,a 可以是数也可以是一个代数式; ④ 二次根式)0(≥a a 是a 的算术平方根,所以0≥a 。
例1、当x 为任意实数时,下列各式有意义的是( )A .x 2-B .x21 C .32+-x D .2)1003(-x例2、当x 为何值时,下列各式有意义?⑴12+x ; ⑵xx --113 2、 二次根式的性质性质:⎩⎨⎧<-≥==)0()0(2a a a a a a 注意:性质a a =2表明:一个数的平方的算术平方根等于这个数的绝对值,需注意的是2a 不是等于a ,而是等于a ,再根据a 的正、负确定最后的结果。
例3 已知2<x ,则442+-x x 的结果是______________ 例4 已知x 满足x x x =-+-20062005,那么22005-x 的值为( )A .2004B .2005C .2006D .2007 练习:二次根式的意义及性质题组1:((0a ≥),叫做二次根式) 1.下列各式中一定是二次根式的是( )A B C D 2.下列各式中,是二次根式的有_____________________________。
2015年沪科版起点教育八年级下册数学二次根式测试题(一至四)(含答案)标准版

2015年起点教育八年级下册数学二次根式测试题(一)一、选择题1.已知233x x +=-x 3+x ,则………………………………………………( ) A .x ≤0 B .x ≤-3 C .x ≥-3 D .-3≤x ≤02.化简aa3-(a <0)A .a -B .-aC 3.当a <0,b <0时,-a +2ab -b A .2)(b a + B .-2)(b a - C .4.在根式①22b a + ②5x③xy x -2A .①② B .③④ C 5.下列二次根式中,A .23a a a 和B .232a a 和C .6.如果1122=+-+a a a ,那么a A .0=a B .1=a C .a 7.能使22-=-x x x x 成立的x A .2≠x B .0≥x C .x 8.若化简|1-x A .x 为任意实数 B .1≤x ≤4 C .x 9.已知三角形三边为a 、b 、c ,其中a 、b 么这个三角形的最大边c A .8>c B .148<<c C .610.小明的作业本上有以下四题①4416a = ③a aa a a=⋅=112; ④a a -23A .① B .② C .③ D .④二.填空题:11.021⎪⎭⎫⎝⎛-的平方根是 ,36的算术平方根是 。
12.(7-52)2008·(-7-52)2009=______________。
13.x ,y 分别为8-11的整数部分和小数部分,则2xy -y 2=____________. 14.若132-=x ,则322+-x x 的值为______。
15.已知xy <0,= 。
。
2)2-24.若x ,y 为实数,且y =x 41-+14-x +21.求x y y x ++2-xy y x +-2的值。
25.已知直角三角形的两条直角边长分别为28+=a ,28-=b ,求斜边c 及斜边上的高h 。
沪教版八年级上册-二次根式的复习与练习题(精编文档).doc

【最新整理,下载后即可编辑】二次根式知识点归纳和题型归类 一、知识要点梳理知识点一、二次根式的主要性质: 1.; 2.; 3.;4. 积的算术平方根的性质:;5. 商的算术平方根的性质:.6.若,则. 知识点二、二次根式的运算 1.二次根式的乘除运算(1) 运算结果应满足以下两个要求:①应为最简二次根式或有理式;②分母中不含根号.(2) 注意每一步运算的算理; (3) 乘法公式的推广:2.二次根式的加减运算 先化简,再运算,3.二次根式的混合运算 (1)明确运算的顺序,即先乘方、开方,再乘除,最后算加减,有括号先算括号里;(2)整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用. 二、分类练习与讲解: 1、 二次根式的概念我们把形如)0(≥a a 的式子叫做二次根式, 如)1(1,1,32,51,32≥-+x x x 等,都是二次根式注意:① 二次根式都含有二次根号"";② 在二次根式中,被开方数a 必须满足0≥a ,当0<a 时,根式无意义; ③ 在二次根式中,a 可以是数也可以是一个代数式; ④ 二次根式)0(≥a a 是a 的算术平方根,所以0≥a 。
例1、当x 为任意实数时,下列各式有意义的是( )A .x 2-B .x21 C .32+-x D .2)1003(-x例2、当x 为何值时,下列各式有意义?⑴ 12+x ; ⑵xx --1132、 二次根式的性质性质:⎩⎨⎧<-≥==)0()0(2a a a a a a 注意:性质a a =2表明:一个数的平方的算术平方根等于这个数的绝对值,需注意的是2a 不是等于a ,而是等于a ,再根据a 的正、负确定最后的结果。
例3 已知2<x ,则442+-x x 的结果是______________例4 已知x 满足x x x =-+-20062005,那么22005-x 的值为( )A .2004B .2005C .2006D .2007 3、 二次根式的乘除法法则(1)一般地,对二次根式的乘法规定 )0,0(≥≥=•b a ab b a 。
沪科版数学八下期末复习:二次根式习题课件(31张)

12.[2019·合肥瑶海区期中]阅读理解材料:把分母中的根号化去
叫做分母有理化,例如:① 2 = 5
2 5 =2 5· 5
5
5;②
21-1=
( 21-×(1)2(+12)+1)=( 22)+21-12= 2+1.根据上述材料,
回答下面问题.
(1)将下列式子分母有理化:
1 3-
; 2
解:原式=(
11.设 a,b,c 为△ABC 的三边长,化简: (a+b+c)2+ (a-b-c)2+ (b-a-c)2- (c-b-a)2.
解:根据 a,b,c 为△ABC 的三边长,得 a+b+c>0,a-b-c <0,b-a-c<0,c-b-a<0, 所以原式=|a+b+c|+|a-b-c|+|b-a-c|-|c-b-a|=a+b+ c+b+c-a+a+c-b-a-b+c=4c.
原式=3b 2b
ab=3 a
2
b.
16.[合肥庐阳区月考]计算: 8+2( 3- 2)- 2× 6. 解:原式=2 2+2 3-2 2- 2×6=2 2+2 3-2 2-2 3=0.
17.[合肥期中]你见过像 4-2 3, 48- 45,…这样的根式 吗?这一类根式叫做复合二次根式.有一些复合二次根式可 以化简,如: 4-2 3= 3-2 3+1= ( 3)2-2 3+12 = ( 3-1)2= 3-1,请用上述方法化简: 5-2 6.
21.已知 a-b= 3+ 2,b-c= 3- 2,求 2(a2+b2+c2-ab -bc-ac)的值.
解:∵a-b= 3+ 2,b-c= 3- 2, ∴(a-b)+(b-c)=( 3+ 2)+( 3- 2),即 a-c=2 3. ∴2(a2+b2+c2-ab-bc-ac)=(a2-2ab+b2)+(b2-2bc+c2)+ (a2-2ac+c2)=(a-b)2+(b-c)2+(a-c)2=( 3+ 2)2+( 3-
精选-沪教版八年级数学下册《二次根式》练习题及答案-文档资料
沪教版八年级数学下册《二次根式》练习题及答案数学是一个要求大家严谨对待的科目,有时一不小心一个小小的小数点都会影响最后的结果。
下文就为二次根式练习题及答案,希望大家认真对待。
一、填空题1. 表示二次根式的条件是_____ _.2.当x______时,有意义,当x______时,有意义.3.若无意义,则x的取值范围是______.4.直接写出下列各式的结果:(1) =_______;?(2) _______;?(3) _______;(4) _______;?(5) _______;(6)? _______.二、选择题5.下列计算正确的有(???? ).A.①、②?B .③、④?C.①、③?D.②、④6.下列各式中一定是二次根式的是 (??? ).A. ?B.? ?C. ?D.7.当x=2时,下列各式中,没有意义的是(??? ).A. ?B. ?C. ?D.8.已知那么a的取值范围是(???? ).A. ?B. ?C. ?D.三、解答题9.当x为何值时,下列式子有意义?(1) ??(2)10.计算下列各式:(1) ?(2) ? (3) ??(4)综合、运用、诊断一、填空题11. 表示二次根式的条件是______.12.使有意义的x的取值范围是____ __.13.已知,则xy的平方根为______.14.当 x=-2时, =________.二、选择题15.下列各式中,x的取值范围是x>2的是(??? ).A. ?B. ?C. ?D.16.若,则x-y的值是(??? ).A.-7?B .-5?C.3?D.7三、解答题17.计算下列各式:(1) ?(2) ?(3) ?(4)18.当a=2,b=-1,c=-1时,求代数式的值.拓广、探究、思考19.已知数a,b,c在数轴上的位置如图所示:化简:的结果是:______________________.20.已知△ABC的三边长a, b,c均为整数,且a和b满足试求△ABC的c边的长.答案与提示1.a≥-1.2.-3.3.x4.(1)7;? (2)7;? (3)7;? (4)-7;? (5)0.7;? (6)49.5.C.?6.B.?7.D.?8.D.9.(1)x≤1;(2)x=0;(3)x是任意实数;(4)x≤1且x≠-2.10.(1)18;(2)a2+1;(3)? (4)6 .11.x≤0.? 12.x≥0且?? 13.±1.? 14.0.? 15.B.? 16.D.17.(1)π-3.14;(2)-9;(3)? (4)36.? 18. 或1.19.0.? 20.提示:a=2,b=3,于是1查字典大学网为大家提供的二次根式练习题及答案,大家仔细做了吗?希望够帮助到大家。
二次根式的有关概念和性质 (知识点考点串编八年级数学下学期核心考点精讲精练(沪科版)(解析版)
专题01二次根式的概念和性质(知识点考点串编)【思维导图】◎考点1:二次根式的值例.(2022·浙江·九年级专题练习)当0x =42x + ) A .4 B .2 C 2D .0【答案】B 【解析】 【分析】把0x =42x + 【详解】解:把0x =42x +42◉知识点一:二次根式的定义知识点技巧:二次根式概念:一般地,我们把形如(a ≥0)的式子叫做二次根式,“”称为二次根号。
【注意】 1.二次根式,被开方数a 可以是一个具体的数,也可以是代数式。
2.二次根式是一个非负数。
3.二次根式与算术平方根有着内在联系,(a ≥0)就表示a 的算术平方根。
【点睛】本题考查了二次根式的定义和二次根式的性质,能灵活运用二次根式的性质进行计算是解题的关键. 练习1.(2021·全国·八年级专题练习)当a 为实数时,下列各式中是二次根式的是( )个10a +a 2a 21a -21a +()21a -A .3个 B .4个 C .5个 D .6个【答案】B 【解析】 【分析】,(0)a a >的代数进行分析得出答案. 【详解】222210,||,,1,1,(1)a a a a a a +-+-||a 2a 21a +2(1)a -4个. 故选:B . 【点睛】此题主要考查了二次根式的定义,形如,(0)a a >的代数式,正确把握定义是解题关键. 练习2.(2021·河北·222321-- ). A .321-+ B .321+- C .321++ D .321--【答案】A 【解析】 【分析】根据有理数运算和二次根式的性质计算,即可得到答案. 【详解】2223219412--=--=∵3212-+=,且选项B 、C 、D 的运算结果分别为:4、6、0 故选:A .本题考查了二次根式、有理数运算的知识;解题的关键是熟练掌握二次根式、含乘方的有理数混合运算的性质,即可得到答案.练习3.(2021·河南林州·八年级期末)已知当12a <<2(2)1a a --的值是( ) A .3- B .12a -C .32a -D .23a -【答案】C 【解析】 【分析】由题意直接根据二次根式的性质以及去绝对值的方法,进行分析运算即可. 【详解】 解:∵12a <<,2(2)1212132a a a a a a a --=---=-+-=-. 故选:C. 【点睛】本题考查二次根式和去绝对值,熟练掌握二次根式的性质以及去绝对值的方法是解题的关键.◎考点2:求二次根式中的参数例.(2021·24n n 的最小值是( ) A .2 B .4 C .6 D .8【答案】C 【解析】 【分析】24n 2426n n =6n 是完全平方数,满足条件的最小正整数n 为6. 【详解】 解:2426n n =24n∵26n 6n 是完全平方数; ∵n 的最小正整数值为6. 故选:C .本题主要考查了二次根式的定义,关键是根据乘除法则和二次根式有意义的条件,二次根式有意义的条件时被开方数是非负数进行解答练习1.(2020·甘肃·酒泉市第二中学八年级期中)若x 、y 为实数,且220x y +-=,则2019x y ⎛⎫⎪⎝⎭的值( ) A .-2 B .1 C .2 D .-1【答案】D 【解析】 【分析】根据非负数的性质可求出x 、y 的值,然后把x 、y 的值代入所求式子计算即可. 【详解】解:∵220x y +-, ∵x +2=0,y -2=0, ∵x =﹣2,y =2, ∵220190192=12x y -⎛⎫⎛⎫ ⎪⎝=- ⎪⎝⎭⎭.故选:D . 【点睛】本题主要考查了非负数的性质,明确实数绝对值和二次根式的非负性以及﹣1的奇次幂的性质是解题关键.练习2.(2020·江苏·丰县欢口镇欢口初级中学八年级阶段练习)如果22443x x y -+-,则2x y -的平方根是( ) A .-7 B .1 C .7 D .±1【答案】D 【解析】 【分析】根据二次根式的性质求出x 、y 的值,再代入求解即可.解:由题意可得:24020x x -+≠=,,解得:2x =, 故3y =,则21x y -=, 故2x y -的平方根是:±1. 故选:D . 【点睛】本题考查了关于二次根式的运算问题,掌握二次根式的性质、平方根的性质是解题的关键. 练习3.(2021·全国·20n n 的值是( ) A .0 B .1C .2D .5【答案】D 【解析】 【分析】首先化简二次根式进而得出n 的最小值. 【详解】20n =5n ∵最小正整数n 的值是5. 故选D . 【点睛】本题考查了二次根式的定义,正确化简二次根式得出是解题的关键.例.(2022·全国·九年级专题练习)在函数12y x =-中,自变量x 的取值范围是( ) A .x <2 B .x ≥2 C .x >2 D .x ≠2【答案】C 【解析】◉知识点二:二次根式有意义的条件知识点技巧:二次根式有意义的条件:由二次根式的意义可知,当a ≧0时,有意义,是二次根式,所以要使二次根式有意义,只要使被开方数大于或等于零即可。
沪科版八年级下册数学16.1二次根式同步练习含解析
Word 文档仅限参照16.1 二次根式同步练习一、选择题 ( 本大题共 8 小题 )1. 若式子 3x4 在实数范围内存心义,则 x 的取值范围是()A.. 4B.4C. 3D.3xx>xx>33442. 当 A. 为实数时,以下各式中是二次根式的有()个。
a + 10, |a| , a 2, a 2- 1, a 2+ 1, (a - 1) 2. A..3 个B.4个 C.5个 D.6个3. 已知 y = 2x5 + 5 2x + 3,则 2xy 的值为()A.. 15B. 15 C . 15D. 152 24. 若 a1,化简a 1 2 =( )2A. . a 1 B . 1 a C . a 1 D . a 15. 化简a 3)a( A.<0) 得(A.aB- aC -aDa6. k 、m 、n 为三整数,若135 k 15 , 450 15 m ,180 6 n ,则以下有对于k 、m 、 n 的大小关系,何者正确?()A. . k < m=n B . m=n < kC . m <n < kD . m <k < n7. 设实数 A. , b 在数轴上对应的地址以以下列图,化简a 2 +|A.+b| 的结果是()A..-2A.+bB.2A.+bC.-bD. b8. 若 0< x < 1,则 ( x1 )2 4 - ( x 1 ) 2 4 等于( )xx A.2B -2C - 2xD 2xxx二、填空题 ( 本大题共 6 小题)Word 文档仅限参照9. x是怎样的实数时,式子x- 3在实数范围内存心义。
10. 若 x, y 为实数,且 y= 1 4x + 4x 1 +1.求x+y的值.211.若 a+ 3+ (b - 2) 2= 0,则 A. b的值是 __________ .112.已知 x, y 为实数,且 y=2+ 8x- 1+1- 8x ,则 x∶y= __________.13.实数 A. , b 在数轴上的地址以以下列图,则(a b)2 a的化简结果为.14.若 a23a 1b22b 10,则a21|b | =_____a2三、计算题 ( 本大题共 4 小题)15.若 A.2+b- 2= 4A. - 4,求ab的值.16.已知x,y都是实数,且知足y=5- x+x- 5+ 3,求 x+y 的值.17.若|A.-b+1|与a+ 2b+ 4互为相反数,试求(A. + b) 2 017的值18.若m知足关系式3x+ 5y- 2- m+2x+ 3y- m=x- 199+ y·199- x- y,试确定 m 的值.参照答案:一、选择题 ( 本大题共 8 小题 )1.A.剖析:依照二次根式的见解解得即可。
第2课时 二次根式的性质 沪科版数学八年级下册同步练习(含答案)
16.1 第2课时 二次根式的性质知识点 1 二次根式的性质1:(√a )2=a (a ≥0)1.计算:(1)(√4)2= ;(2)(√0)2= ;(3)√1692= ;(4)(√10)2= . 2.(2021苏州)计算(√3)2的结果是( ) A .√3 B .3 C .2√3 D .9 知识点 2 二次根式的性质2:√a 2=|a|3.计算√32的值为 ( )A .3B .9C .±3D .±√34.(2021杭州)下列计算正确的是 ( )A .√22=2B .√(-2)2=-2C .√2=±2D .√(-2)2=±2 5.若x<0,则计算x+√x 2x 的结果是 ( ) A.0 B.-2 C.0或-2 D.26.(教材例3变式)化简:√(π-3)2+√(π-4)2= .7.(2020马鞍山当涂县期末)若√(a -3)2=3-a ,则a 的取值范围是 .8.计算(√2-x )2+√(x -3)2的结果是 ( )A .1B .-1C .2x-5D .5-2x9.在实数范围内分解因式:2x 2-6= .10.(教材例2变式)计算:(1)(√10)2-√(-4)2;(2)√(-34) 2×√432-√(-0.3)2.c2-4c+16.11.已知三角形的两边长分别为3和5,第三边长为c,化简:(√|2-c|)2-√1412.你见过像√4-2√3,√√48-√45,…这样的根式吗?这一类根式叫做复合二次根式,有些复合二次根式可以化简,如:√4-2√3=√3-2√3+1=√(√3)2-2√3+12=√(√3-1)2=√3-1.用上述方法化简:√6-2√5=.答案16.1 第2课时 二次根式的性质1.(1)4 (2)0 (3)169 (4)102.B (√3)2=3.3.A4.A5.A ∵x<0,∴√x 2=-x ,∴原式=x -x x =0.故选A .6.17.a ≤3 ∵√(a -3)2=3-a ,∴3-a ≥0,解得a ≤3.8.D 由题意可知2-x ≥0,∴x ≤2, ∴x-3<0,∴√(x -3)2=3-x ,∴(√2-x )2+√(x -3)2=2-x+3-x=5-2x.故选D .9.2(x+√3)(x-√3) 2x 2-6=2(x 2-3)=2[x 2-(√3)2]=2(x+√3)(x-√3).10. 根据二次根式的两个性质求解.运用√a 2=|a|计算时,注意a 的符号. 解:(1)原式=10-4=6.(2)原式=34×43-0.3=1-0.3=0.7. 11.解:由三角形三边关系可知2<c<8,∴1<12c<4,∴12c-4<0,则(√|2-c |)2-√14c 2-4c +16==4-12c =+12c=32c-6.12.√5-1 √6-2√5=√5-2√5+1=√(√5)2-2√5+12=√(√5-1)2=√5-1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1. 下列各式一定是二次根式的是()
2.
a≥2)
)A.1个B.2个C.3个D.4个
3.
2)
b≥
0)
x<
中,二次根式的个数是()
A.2个B.3个C.4个D.5个
4.
2,则a的取值范围是()
A.4
a≥B.2
a≤C.24
a
≤≤D.2
a=或4
a=
5.
()
A.1个B.2个C.3个D.4个
6. 如果2
1
21
a ab
a b
-=-
-
,则a和b的关系是()
A.a b
≤B.a b
<C.a b
≥
D.a
b
>
7. 0
=,则20062006
x y
+的值为()
A.0B.1C.1
-D.2
8. 下列式子一定是二次根式的是()
A.2
-
-x B.x C.2
2+
x D.2
2-
x
9. 若b
b-
=
-3
)
3(2,则()
A.b>3 B.b<3 C.b≥3 D.b≤3
1
2 10. 若x<0,则x x x 2
-的结果是( )
A .0
B .—2
C .0或—2
D .2
11. 已知0
a
) A. 1 B. -1 C. 1± D. 以上答案都不对
12. 把(
2x -根号外的因式移到根号内,得( )
13.
,则x 的取值范围是 ( )
A .x ≥7
B .x ≤7
C .x>7
D .x<7
14.
的值,当a=5时,得到不同的答案,如下所示,那么( ).
甲的答案是:
乙的答案是:
(A )甲的答案正确的 (B )乙的答案正确的
(C )两人都不正确 (D )以上三种说法都不对
15.
( )
A .①和③
B .②和③
C .①和④
D .③和④
16. 对于任何实数a 、b ,下列结论正确的是( )
A .a 2的算术平方根是a B
a =-
C
2= D
a =
二、填空题
17.
3x =-,则x 的取值范围为 .
3
18. 把8写成一个非负数平方的形式是________
19. 形如 的式子叫做二次根式,它的值一定是 数.
20.
0=
的值为 .
21.
m =,则代数式2
2006m -的值是 .
22.
0a =,则a 的范围是 .
23. 已知0a b <<
,化简a b -= .
24. ①=-2)3.0( ;②=-2)52( 。
25. 若m<0,则332||m m m ++= 。
26.
20x y +-=,则_________x y -=。
计算
27.
=2,且ab<0,则a-b=_______.
28.
=________. 三、计算题
29.
已知:40a -=,计算22222
a a
b a ab b a b +--的值.
四、应用题
30. 当
15x 时,化简:
一、选择题
1.C
2. C
3. C
4.C
5. C
6. B
7. A
8. C
9. D
10. D
11. B
12. D
13. B;提示:7-x≥0
14. B;
15. C
16. D
二、填空题
x
17.3
18. 2
4
19.
0)
a≥,非负
20.5
21.2007
22.0
a≤
23.b-
24.①0.3 ②2
5-
25.—m
26. 0;
27. -7;提示:a=±3,b=4,ab<0,∴a=-3,a-b=-3-4=-7
28.
=
三、计算题
29.16 81
.
四、应用题
30.26
x-;
5。
