初二下期末几何压轴题及解析
初二下期末几何压轴题及解析

初二下期末几何及解析1、以四边形ABCD 的边AB 、AD 为边分别向外侧作等边三角形ABF 和ADE ,连接EB 、FD ,交点为G .(1)当四边形ABCD 为正方形时(如图1),E B 和FD 的数量关系是_____________;(2)当四边形ABCD 为矩形时(如图2),EB 和FD 具有怎样的数量关系?请加以证明;(3)四边形ABCD 由正方形到矩形到一般平行四边形的变化过程中,∠EGD 是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD 的度数.难度一般:证全等即可(第三问,图1中就能看出是45°。
) 解 (1)EB=FD 。
(2)EB=FD 。
证:∵△AFB 为等边三角形,∴AF=AB ,∠FAB=60°∵△ADE 为等边三角形,∴AD=AE ,∠EAD=60°,∴∠FAB+∠BAD=∠EAD+∠BAD即∠FAD=∠BAE,∴△FAD ≌△BAE,∴EB=FD(3)解:∵△ADE 为等边三角形,∴∠AED=∠EDA=60° ∵△FAD ≌△BAE ,∴∠AEB=∠ADF 设∠AEB 为x °,则∠ADF 也为x °于是有∠BED 为(60-x )°,∠EDF 为(60+x )° ∴∠EGD=180°-∠BED-∠EDF =180°-(60-x )°-(60+x )°=60°2、已知:如图,在□ABCD 中,点E 是BC 的中点, 连接AE 并延长交DC 的延长线于点F ,连接BF . (1)求证:△ABE ≌△FCE ;(2)若AF =AD ,求证:四边形ABFC 是矩形.FA BC DE简单题证明:(1)如图1.在△ABE 和△FCE 中,∠1=∠2, ∠3=∠4,BE =CE , ∴△ABE ≌△FCE .(2)∵△ABE ≌△FCE ,∴AB =FC .∵AB ∥FC ,∴四边形ABFC 是平行四边形. ∵四边形ABCD 是平行四边形,∴AD =BC . ∵AF =AD ,∴AF =BC .∴四边形ABFC 是矩形.3、已知:△ABC 是一张等腰直角三角形纸板,∠B =90°,AB =BC =1. (1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC 的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.(2)按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为1S ,则1S =___________;余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3), 得到2个新的正方形,将此次所得2个正方形的面积的和.记为2S ,则2S =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形图EFA BCD 图AB C图图B图2CBA图14321EDC BAF的面积的和.记为3S;按照同样的方法继续操作下去……,第n次裁剪得到_________个新的正方形,它们的面积的和.nS=______________.(题外题:把你剪出的正方形的面积与图1中的正方形面积进行比较。
最新成都八年级下期末数学B卷几何压轴题汇编二(含答案)

最新成都八年级下期末数学B卷几何压轴题汇编二21.已知四边形ABCD为矩形,对角线AC、BD相交于点O,∠CDO=30°.点E、F为矩形边上的两个动点,且∠EOF=60°.(1)如图1,当点E、F分别位于AB、AD边上时.①求证:∠DOF=∠AOE;②若∠OEB=75°,求证:DF=AE.(2)如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试探究线段AF与线段BE的数量关系,并说明理由.22.如图1,在平面直角坐标系中,直线y=﹣x+n分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),点C为线段AB的中点.(1)求点B的坐标;(2)点P为直线AB上的一个动点,过点P作x轴的垂线,与直线OC交于点Q,设点P的横坐标为m,△OPQ的面积为S,求S与m的函数解析式;(3)当点P在直线AB上运动时,在平面直角坐标系内是否存在一点N,使得以O,B,P,N为顶点的四边形为矩形,若存在,求出N点的坐标;若不存在,请说明理由.23.如图,在菱形ABCD中,∠ABC=120°,AB=4,E为对角线AC上的动点(点E不与A,C重合),连接BE,将射线EB绕点E逆时针旋转120°后交射线AD于点F.(1)如图1,当AE=AF时,求∠AEB的度数;(2)如图2,分别过点B,F作EF,BE的平行线,且两直线相交于点G.i)试探究四边形BGFE的形状,并求出四边形BGFE的周长的最小值;ii)连接AG,设CE=x,AG=y,请直接写出y与x之间满足的关系式,不必写出求解过程.24.如图,在平面直角坐标系xOy中,直线y=﹣2x+6交x轴于点A,交y轴于点B,过点B的直线交x轴负半轴于点C,且AB=BC.(1)求点C的坐标及直线BC的函数表达式;(2)点D(a,2)在直线AB上,点E为y轴上一动点,连接DE.(ⅰ)若∠BDE=45°,求△BDE的面积;(ⅱ)在点E的运动过程中,以DE为边作正方形DEGF,当点F落在直线BC上时,求满足条件的点E 的坐标.25.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;(2)如图2,如果正方形ABCD的边长为,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG ∥BD,BG=BD.①求∠BDE的度数;②请直接写出正方形CEFG的边长的值.26.在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.(1)如图1,当菱形DEFG的一顶点F在AB边上.①若CG=OD时,求直线DG的函数表达式;②求证:△OED≌△BGF.(2)如图2,当菱形DEFG的一顶点F在AB边右侧,连接BF,设CG=a,△FBG面积为S.求S与a 的函数关系式;并判断S的值能否等于1?请说明理由;(3)如图3,连接GE,当GD平分∠CGE时,m的值为.(直接写出答案).27.等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①.(1)求证:AM=CM;(2)将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.①求证:AM=CM,AM⊥CM;②若AB=4,求△AOM的面积.28.在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.(1)求直线BC的解析式.(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.29.如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.(1)如图②,若M为AD边的中点,①△AEM的周长=cm;②求证:EP=AE+DP;(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.30.矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连接CE,若△CGE 是等腰三角形,求直线BE的解析式;(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由.31.如图为正方形ABCD中,点M、N在直线BD上,连接AM,AN并延长交BC、CD于点E、F,连接EN.(1)如图1,若M,N都在线段BD上,且AN=NE,求∠MAN;(2)如图2,当点M在线段DB延长线上时,AN=NE,(1)中∠MAN的度数不变,判断BM,DN,MN之间的数量关系并证明;(3)如图3,若点M在DB的延长线上,N在BD的延长线上,且∠MAN=135°,AB=,MB=,求DN.32.在正方形AMFN中,以AM为BC边上的高作等边三角形ABC,将AB绕点A逆时针旋转90°至点D,D点恰好落在NF上,连接BD,AC与BD交于点E,连接CD.(1)如图1,求证:△AMC≌△AND;(2)如图1,若DF=,求AE的长;(3)如图2,将△CDF绕点D顺时针旋转α(0°<α<90°),点C,F的对应点分别为C1、F1.连接AF1、BC1,点G是BC1的中点,连接AG.试探索是否为定值,若是定值,则求出该值;若不是,请说明理由.33.如图,等腰直角三角形OAB的三个定点分别为O(0,0)、A(0,3)、B(﹣3,0),过A作y轴的垂线l1.点C在x轴上以每秒的速度从原点出发向右运动,点D在l1上以每秒的速度同时从点A出发向右运动,当四边形ABCD为平行四边形时C、D同时停止运动,设运动时间为t.当C、D停止运动时,将△OAB沿y轴向右翻折得到△OAB1,AB1与CD相交于点E,P为x轴上另一动点.(1)求直线AB的解析式,并求出t的值.(2)当PE+PD取得最小值时,求PD2+PE2+2PD•PE的值.(3)设P的运动速度为1,若P从B点出发向右运动,运动时间为x,请用含x的代数式表示△P AE的面积.34.已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;①求证:点F是AD的中点;②判断BE与CF的数量关系和位置关系,并说明理由;(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.35.(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.①求证:四边形BFDE是菱形;②直接写出∠EBF的度数.(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC 上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.36.已知正方形ABCD,探究以下问题:(1)如图1,点F在BC上,作FE⊥BD于点E,取DF的中点G,连接EG、CG,将△EGC沿直线EC 翻折到△EG′C,求证:四边形EGCG′是菱形;(2)如图2,点F是BC外一点,作FE⊥BC于点E,且BE=EF,连接DF,取DF的中点G,将△EGC 沿直线EC翻折到△EG′C,作FM⊥CD于点M,请问(1)中的结论”四边形EGCG′是菱形”是否依然成立,并说明理由;(3)在(2)的条件下,若图2中AB=4,设BE长为x,四边形EGCG′的面积为S,请求出S关于x 的函数关系式,并说明理由.37.(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为;(2)【拓展研究】在(1)的条件下,如果正方形CDEF绕点C旋转,当点B,E,F三点共线时,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;(3)【问题发现】当正方形CDEF旋转到B,E,F三点共线时,求线段AF的长.38.如图1,直线y=﹣x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.(1)求OB的长;(2)如图2,F,G是直线AB上的两点,若△DFG是以FG为斜边的等腰直角三角形,求点F的坐标;(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P,Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.39.如图,矩形ABCD中,∠BAC=30°,对角线AC、BD交于点O,∠BCD的平分线CE分别交AB、BD 于点E、H,连接OE.(1)求∠BOE的度数;(2)若BC=1,求△BCH的面积;(3)求S△CHO:S△BHE.参考答案21.已知四边形ABCD为矩形,对角线AC、BD相交于点O,∠CDO=30°.点E、F为矩形边上的两个动点,且∠EOF=60°.(1)如图1,当点E、F分别位于AB、AD边上时.①求证:∠DOF=∠AOE;②若∠OEB=75°,求证:DF=AE.(2)如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试探究线段AF与线段BE的数量关系,并说明理由.【解答】证明:(1)①∵四边形ABCD是矩形,∴AC=BD,AO=CO,BO=DO,∠CDA=90°,∴AO=DO,∵∠CDO=30°,∴∠ADO=60°,∴△AOD是等边三角形,∴∠AOD=60°,∵∠EOF=60°,∴∠EOF=∠AOD,∴∠DOF=∠AOE;②在OF上截取OH=OE,连接DH,∵AO=OD,∠DOF=∠AOE,OE=OH,∴△AOE≌△DOH(SAS),∴AE=DH,∵∠OEB=75°,∴∠AEO=105°,∵∠AEO+∠EOF+∠OF A+∠DAB=360°,∴∠AFO=105°,∴∠DFH=75°,∴∠DFH=∠DHF,∴DF=DH=AE;(2)将△OAF绕点O顺时针旋转120°得到△OBN,连接NE.∴ON=OF,∠NOF=∠AOB=120°,AF=BN,∵∠AOB=120°,∠EOF=60°,∴∠BON+∠BOE=∠AOF+∠BOE=60°,∴∠EON=∠EOF,∵OF=ON,OE=OE,∴△EOF≌△EON(SAS),∴∠OEF=∠OEN,∵∠OFB=75°,∠OBF=30°,∴∠BOF=75°,∴∠BOE=75°﹣60°=15°,∴∠FEO=∠BOE+∠OBE=45°,∴∠OEF=∠OEN=45°,∴∠NEB=∠NEF=90°,∵∠OBN=∠OAF=30°,∠OBE=30°,∴∠EBN=60°,∴∠ENB=90°﹣60°=30°,∴BN=2BE,∵AF=BN,∴AF=2BE.22.如图1,在平面直角坐标系中,直线y=﹣x+n分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),点C为线段AB的中点.(1)求点B的坐标;(2)点P为直线AB上的一个动点,过点P作x轴的垂线,与直线OC交于点Q,设点P的横坐标为m,△OPQ的面积为S,求S与m的函数解析式;(3)当点P在直线AB上运动时,在平面直角坐标系内是否存在一点N,使得以O,B,P,N为顶点的四边形为矩形,若存在,求出N点的坐标;若不存在,请说明理由.【解答】解:(1)将点A的坐标代入y=﹣x+n并解得:n=3,故直线的表达式为:y=﹣x+3,令x=0,则y=3,故点B(0,3);(2)点C为线段AB的中点,则由中点公式得,点C(2,),则直线OC的表达式为:y=x,设点P(m,﹣m+3),则点Q(m,m),当点P在y轴右侧,且在点C右侧时,S=PQ•|x P|=(m+m﹣3)•m=m2﹣m;当点P在y轴右侧,且在点C左侧时,S=PQ•|x P|=(﹣m+3﹣m)•m=m﹣m2;当点P在y轴左侧时,同理可得:S=m2﹣m;故S=m2﹣m或S=m﹣m2;(3)设P(m,﹣m+3),点N(s,t),而点O、B的坐标分别为(0,0)、(0,3);①当OB是矩形的边时,则点P与点A重合,故点P(4,0),故点N(4,3);②当OB是矩形的对角线时,由中点公式得:m+s=0且﹣m+3+t=3+0①,由矩形的对角线相等得:OB=PN,即(m﹣s)2+(﹣m+3﹣t)2=32②,联立①②并解得:,故点N(﹣,);综上,点N的坐标为(4,3)或(﹣,).23.如图,在菱形ABCD中,∠ABC=120°,AB=4,E为对角线AC上的动点(点E不与A,C重合),连接BE,将射线EB绕点E逆时针旋转120°后交射线AD于点F.(1)如图1,当AE=AF时,求∠AEB的度数;(2)如图2,分别过点B,F作EF,BE的平行线,且两直线相交于点G.i)试探究四边形BGFE的形状,并求出四边形BGFE的周长的最小值;ii)连接AG,设CE=x,AG=y,请直接写出y与x之间满足的关系式,不必写出求解过程.【解答】解:(1)如图1中,∵四边形ABCD是菱形,∴BC∥AD,∠BAC=∠DAC,∴∠ABC+∠BAD=180°,∵∠ABC=120°,∴∠BAD=60°,∴∠EAF=30°,∵AE=AF,∴∠AEF=∠AFE=75°,∵∠BEF=120°,∴∠AEB=120°﹣75°=45°.(2)i)如图2中,连接DE.∵AB=AD,∠BAE=∠DAE,AE=AE,∴△BAE≌△DAE(SAS),∴BE=DE,∠ABE=∠ADE,∵∠BAF+∠BEF=60°+120°=180°,∴∠ABE+∠AFE=180°,∵∠AFE+∠EFD=180°,∴∠EFD=∠ABE,∴∠EFD=∠ADE,∴EF=ED,∴EF=BE,∵BE∥FG,BG∥EF,∴四边形BEFG是平行四边形,∵EB=EF,∴四边形BEFG是菱形,∴当BE⊥AC时,菱形BEFG的周长最小,此时BE=AB•sin30°=2,∴四边形BGFE的周长的最小值为8.ii)如图2﹣1中,连接BD,DE,过点E作EH⊥CD于H.∵AB=AD,∠BAD=60°,∴△ABD是等边三角形,∴BD=BA,∠ABD=60°,∵BG∥EF,∴∠EBG=180°﹣120°=60°,∴∠ABD=∠GBE,∴∠ABG=∠DBE,∵BG=BE,∴△ABG≌△DBE(SAS),∴AG=DE=y,在Rt△CEH中,EH=EC=x.CH=x,∴DH=|4﹣x|,在Rt△DEH中,∵DE2=EH2+DH2,∴y2=x2+(4﹣x)2,∴y2=x2﹣12x+48,∴y=(0<x<12).24.如图,在平面直角坐标系xOy中,直线y=﹣2x+6交x轴于点A,交y轴于点B,过点B的直线交x轴负半轴于点C,且AB=BC.(1)求点C的坐标及直线BC的函数表达式;(2)点D(a,2)在直线AB上,点E为y轴上一动点,连接DE.(ⅰ)若∠BDE=45°,求△BDE的面积;(ⅱ)在点E的运动过程中,以DE为边作正方形DEGF,当点F落在直线BC上时,求满足条件的点E 的坐标.【解答】解:(1)∵直线y=﹣2x+6交x轴于点A,交y轴于点B,∴A(3,0),B(0,6),∴OA=3,OB=6,∵AB=BC,OB⊥AC,∴OC=OA=3,∴C(﹣3,0),设直线BC的解析式为y=kx+b,则有,解得,∴直线BC的解析式为y=2x+6.(2)如图,取点Q(﹣1,3),连接BQ,DQ,DQ交AB于E.∵D(a,2)在直线y=﹣2x+6上,∴2=﹣2a+6,∴a=2,∴D(2,2),∵B(0,6),∴QB==,QD==,BD==2,∴BD2=QB2+QD2,QB=QD,∴∠BQD=90°,∠BDQ=45°,∵直线DQ的解析式为y=﹣x+,∴E(0,),∴OE=,BE=6﹣=,∴S△BDE=××2=.(3)如图,过点D作DM⊥OA于M,DN⊥OB于N.∵四边形DEGF是正方形,∴∠EDF=90°,ED=DF,∵∠EDF=∠MDN=90°,∴∠EDN=∠DFM,∵DE=DF,DN=DM,∴△DNE≌△DMF(SAS),∴∠DNE=∠DMF=90°,EN=FM,∴点F在x轴上,∴当点F与C重合时,FM=NE=5,此时E(0,7),同法可证,点F′在直线y=4上运动,当点F′落在BC上时,E(0,﹣1),综上所述,满足条件的点E的坐标为(0,7)或(0,﹣1).25.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;(2)如图2,如果正方形ABCD的边长为,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG ∥BD,BG=BD.①求∠BDE的度数;②请直接写出正方形CEFG的边长的值.【解答】(1)证明:∵四边形ABCD和CEFG为正方形,∴BC=DC,CG=CE,∠BCD=∠GCE=90°.∴∠BCD+∠DCG=∠GCE+∠DCG,∴∠BCG=∠DCE.在△BCG和△DCE中,,∴△BCG≌△DCE(SAS).(2)解:①连接BE.由(1)可知:BG=DE.∵CG∥BD,∴∠DCG=∠BDC=45°.∴∠BCG=∠BCD+∠GCD=90°+45°=135°.∵∠GCE=90°,∴∠BCE=360°﹣∠BCG﹣∠GCE=360°﹣135°﹣90°=135°.∴∠BCG=∠BCE.∵BC=BC,CG=CE,在△BCG和△BCE中,,∴△BCG≌△BCE(SAS).∴BG=BE.∵BG=BD=DE,∴BD=BE=DE.∴△BDE为等边三角形.∴∠BDE=60°.②延长EC交BD于点H,在△BCE和△DCE中,,∴△BCE≌△BCG(SSS),∴∠BEC=∠DEC,∴EH⊥BD,BH=.∵BC=CD=,在Rt△BCD中由勾股定理,得∴BD===2.∴CH=1.在Rt△BHE中,由勾股定理,得EH=,∴CE=﹣1.∴正方形CEFG的边长为.26.在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.(1)如图1,当菱形DEFG的一顶点F在AB边上.①若CG=OD时,求直线DG的函数表达式;②求证:△OED≌△BGF.(2)如图2,当菱形DEFG的一顶点F在AB边右侧,连接BF,设CG=a,△FBG面积为S.求S与a 的函数关系式;并判断S的值能否等于1?请说明理由;(3)如图3,连接GE,当GD平分∠CGE时,m的值为.(直接写出答案).【解答】解:(1)①∵将x=0代入y=mx+2得;y=2,∴点D的坐标为(0,2).∵CG=OD=2,∴点G的坐标为(2,6).将点G(2,6)代入y=mx+2得:2m+2=6.解得:m=2.∴直线DG的函数表达式为y=2x+2.②如图1,延长GF交y轴于点M,∵DM∥AB,∴∠GFB=∠DMG,∵四边形DEFG是菱形,∴GF∥DE,DE=GF,∴∠DMG=∠ODE,∴∠GFB=∠ODE,又∵∠B=∠DOE=90°,∴△OED≌△BGF(AAS);(2)如图2所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.∵四边形DEFG为菱形,∴GF=DE,GF∥DE.∴∠GNC=∠EDO.∴∠NGC=∠DEO.∴∠HGF=∠DEO.在Rt△GHF和Rt△EOD中,,∴Rt△GHF≌Rt△EOD(AAS).∴FH=DO=2.∴S△GBF=GB•HF=×2×(6﹣a)=6﹣a.∴S与a之间的函数关系式为:S=6﹣a.当s=1时,则6﹣a=1.解得:a=5.∴点G的坐标为(5,6).在△DCG中,由勾股定理可知;DG===.∵四边形GDEF是菱形,∴DE=DG=.在Rt△DOE中,由勾股定理可知OE===>6.∴OE>OA.∴点E不在OA上.∴S≠1.(3)如图3所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.又∵四边形DEFG为菱形,∴DM⊥GM,点M为DF的中点.∵GD平分∠CGE,DM⊥GM,GC⊥OC,∴MD=CD=4.∵由(2)可知点F的坐标为4,点D的纵坐标为2,∴点M的纵坐标为3.∴ND=1.在Rt△DNM中,MN==.∴点M的坐标为(,3).设直线DM的解析式为y=kx+2.将(,3)代入得:k+2=3.解得:k=.∴设直线MG的解析式为y=﹣x+b.将(,3)代入得:﹣15+b=3.解得:b=18.∴直线MG的解析式为y=﹣x+18.将y=6代入得:﹣x+18=6.解得:x=.∴点G的坐标为(,6).将(,6)代入y=mx+2得:m+2=6.解得:m=.故答案为:.27.等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①.(1)求证:AM=CM;(2)将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.①求证:AM=CM,AM⊥CM;②若AB=4,求△AOM的面积.【解答】解:(1)证明:∵∠OAB=90°,∴△ABD是直角三角形,∵点M是BD的中点,∴AM=BD,∵DC⊥OB,∴∠BCD=90°,∵点M是BD的中点,∴CM=BD,∴AM=CM;(2)①如图②,在图①中,∵AO=AB,∠OAB=90°,∴∠ABO=∠AOB=45°,∵DC⊥OB,∴∠OCD=90°,∴∠ODC=∠AOB,∴OC=CD,延长CM交OB于T,连接AT,由旋转知,∠COB=90°,DC∥OB,∴∠CDM=∠TBM,∵点M是BD的中点,∴DM=BM,∵∠CMD=∠TMB,∴△CDM≌△TBM(ASA),∴CM=TM,DC=BT=OC,∵∠AOC=∠BOC﹣∠AOB=45°=∠ABO,∵AO=AB,∴△OAC≌△BAT(SAS),∴AC=AT,∠OAC=∠BAT,∴∠CAT=∠OAC+∠OAT=∠BAT+∠OAT=∠OAB=90°,∴△CAT是等腰直角三角形,∵CM=TM,∴AM⊥CM,AM=CM;②如图③,在Rt△AOB中,AB=4,∴OA=4,OB=AB=4,在图①中,点D是OA的中点,∴OD=OA=2,∵△OCD是等腰直角三角形,∴DC=CO==,由①知,BT=CD,∴BT=,∴OT=OB﹣TB=3,在Rt△OTC中,CT==2,∵CM=TM=CT==AM,∵OM是Rt△COT的斜边上的中线,∴OM=CT=,∴AM=OM,过点M作MN⊥OA于N,则ON=AN=OA=2,根据勾股定理得,MN==1,∴S△AOM=OA•MN=×4×1=2.28.在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.(1)求直线BC的解析式.(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.【解答】解:(1)∵直线y=﹣x+2与x轴、y轴分别交于A、B两点,∴x=0时,y=2,y=0时,x=2,∴A(2,0),B(0,2),∴OB=AO=2,在Rt△COB中,∠BOC=90°,∠BCA=30°,∴OC=2,∴C(﹣2,0),设直线BC的解析式为y=kx+b,代入B,C两点的坐标得,,∴k=,b=2,∴直线BC的解析式为y=x+2;(2)分别过点M,N作MQ⊥x轴,NP⊥x轴,垂足分别为点Q,P.(Ⅰ)如图1,当点M在线段AB上运动时,∵CN=2t,AM=t,OB=OA=2,∠BOA=∠BOC=90°,∴∠BAO=∠ABO=45°,∵∠BCO=30°,∴NP=MQ=t,∵MQ⊥x轴,NP⊥x轴,∴∠NPQ=∠MQA=90°,NP∥MQ,∴四边形NPQM是矩形,∴NS∥x轴,∵AD⊥x轴,∴AS∥MQ∥y轴,∴四边形MQAS是矩形,∴AS=MQ=NP=t,∵NS∥x轴,AS∥MQ∥y轴,∴∠DNS=∠BCO,∠DSN=∠DAO=∠BOC=90°,∴当DS=BO=2时,△DSN≌△BOC(AAS),∵D(2,+2),∴DS=+2﹣t,∴+2﹣t=2,∴t=(秒);(Ⅱ)当点M在线段AB的延长线上运动时,如图2,同理可得,当DS=BO=2时,△DSN≌△BOC(AAS),∵DS=t﹣(+2),∴t﹣(+2)=2,∴t=+4(秒),综合以上可得,t=秒或t=+4秒时,△DSN≌△BOC.(3)存在以M、B、N、P为顶点的四边形是菱形:M(﹣2﹣2,2+4)或M(﹣2﹣4,2+6)或M(﹣2+2,2).∵M是直线AB在第二象限上的一点,点N,P分别在直线BC,直线AD上,∴设点M(a,﹣a+2),N(b,b+2),P(2,c),点B(0,2),(Ⅰ)当以BM,BP为邻边构成菱形时,如图3,∵∠CBO=60°,∠OBA=∠OAB=∠P AF=45°,∴∠DBA=∠MBN=∠PBN=75°,∴∠MBE=45°,∠PBF=30°,∴MB=ME,PF=AP,PB=2PF=AP,∵四边形BMNP是菱形,∴,解得,a=﹣2﹣2,∴M(﹣2﹣2,2+4)(此时点N与点C重合),(Ⅱ)当以BP为对角线,BM为边构成菱形时,如图4,过点B作EF∥x轴,ME⊥EF,NF⊥EF,同(Ⅰ)可知,∠MBE=45°,∠NBF=30°,由四边形BMNP是菱形和BM=BN得:,解得:a=﹣2﹣4,∴M(﹣2﹣4,2+6),(Ⅲ)当以BM为对角线,BP为边构成菱形时,如图5,作NE⊥y轴,BF⊥AD,∴∠BNE=30°,∠PBF=60°,由四边形BMNP是菱形和BN=BP得,,解得:a=﹣2+2,∴M(﹣2+2,2).综合上以得出,当以M、B、N、P为顶点的四边形是菱形时,点M的坐标为:M(﹣2﹣2,2+4)或M(﹣2﹣4,2+6)或M(﹣2+2,2).29.如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.(1)如图②,若M为AD边的中点,①△AEM的周长=6cm;②求证:EP=AE+DP;(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.【解答】解:(1)由折叠知BE=EM,∠B=∠EMP=90°.①△AEM的周长=AE+EM+AM=AE+EB+AM=AB+AM.∵AB=4,M是AD中点,∴△AEM的周长=4+2=6(cm);②现证明EP=AE+PD方法一:取EP的中点G,则在梯形AEPD中,MG为中位线,∴MG=(AE+PD),在Rt△EMP中,MG为斜边EP的中线,∴MG=EP,∴EP=AE+PD.方法二:延长EM交CD延长线于Q点.∵∠A=∠MDQ=90°,AM=DM,∠AME=∠DMQ,∴△AME≌△DMQ.∴AE=DQ,EM=MQ.又∵∠EMP=∠B=90°,∴PM垂直平分EQ,有EP=PQ.∵PQ=PD+DQ,∴EP=AE+PD.(2)△PDM的周长保持不变.设AM=x,则MD=4﹣x.由折叠性质可知,EM=4﹣AE,在Rt△AEM中,AE2+AM2=EM2,即AE2+x2=(4﹣AE)2,整理得:AE2+x2=16﹣8AE+AE2,∴AE=(16﹣x2),又∵∠EMP=90°,∴∠AME+∠DMP=90°.∵∠AME+∠AEM=90°,∴∠AEM=∠DMP.又∵∠A=∠D,∴△PDM∽△MAE.∴∴C△PDM=C△MAE•=(4+x)•=8.∴△PDM的周长保持不变.30.矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连接CE,若△CGE 是等腰三角形,求直线BE的解析式;(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由.【解答】解:(1)如图1,在矩形ABCO中,∠B=90°当点D落在边BC上时,BD2=AD2﹣AB2,∵C(0,3),A(a,0)∴AB=OC=3,AD=AO=a,∴BD=;(2)如图2,连接AC,∵a=3,∴OA=OC=3,∴矩形ABCO是正方形,∴∠BCA=45°,设∠ECG的度数为x,∴AE=AC,∴∠AEC=∠ACE=45°+x,①当CG=EG时,x=45°+x,解得x=0,不合题意,舍去;②当CE=GE时,如图2,∠ECG=∠EGC=x∵∠ECG+∠EGC+∠CEG=180°,∴x+x+(45°+x)=180°,解得x=45°,∴∠AEC=∠ACE=90°,不合题意,舍去;③当CE=CG时,∠CEG=∠CGE=45°+x,∵∠ECG+∠EGC+∠CEG=180°,∴x+(45°+x)+(45°+x)=180°,解得x=30°,∴∠AEC=∠ACE=75°,∠CAE=30°如图3,连接OB,交AC于点Q,过E作EH⊥AC于H,连接BE,∴EH=AE=AC,BQ=AC,∴EH=BQ,EH∥BQ且∠EHQ=90°∴四边形EHQB是矩形∴BE∥AC,设直线BE的解析式为y=﹣x+b,∵点B(3,3)在直线上,则b=6,∴直线BE的解析式为y=﹣x+6;(3)①∵点P为矩形ABCO的对称中心,∴P(,),∵B(a,3),∴PB的中点坐标为:(a,),∴直线PB的解析式为y PB=x,∵当P,B关于AD对称,∴AD⊥PB,∴直线AD的解析式为:y=﹣x+,∵直线AD过点(a,),∴=﹣a2+,解得:a=±3,∵a≥3,∴a=3;②存在M,N;理由:∵a=3,∴直线AD的解析式为y=﹣x+9,∴∠DAO=60°,∴∠DAB=30°,连接AE,∵AD=OA=3,DE=OC=3,∴∠EAD=30°,∴A,B,E三点共线,∴AE=2DE=6,∴E(3,6),F(,),设M(m,0),N(0,n),∵四边形EFMN是平行四边形,∴,解得:,∴M(,0),N(0,).31.如图为正方形ABCD中,点M、N在直线BD上,连接AM,AN并延长交BC、CD于点E、F,连接EN.(1)如图1,若M,N都在线段BD上,且AN=NE,求∠MAN;(2)如图2,当点M在线段DB延长线上时,AN=NE,(1)中∠MAN的度数不变,判断BM,DN,MN之间的数量关系并证明;(3)如图3,若点M在DB的延长线上,N在BD的延长线上,且∠MAN=135°,AB=,MB=,求DN.【解答】解:(1)如图1,过N作GK⊥BC,交AD于G,交BC于K,∵四边形ABCD是正方形,∴AD∥BC,∠ADB=45°,∴GK⊥AD,∴∠AGN=∠EKN=90°,∵△BNK是等腰直角三角形,∴BK=NK,∵AD=DC=GK,∴AG=BK,在Rt△AGN和Rt△NKE中,∴Rt△AGN≌Rt△NKE(HL),∴∠ANG=∠NEK,∵∠ENK+∠NEK=90°,∴∠ANG+∠ENK=90°,∴∠ANE=90°,∴△ANE是等腰直角三角形,∴∠MAN=45°;(2)MN2=DN2+BM2,理由如下:如图,将△ABM绕点A逆时针旋转90°,得到△ADH,连接NH,∴△ABM≌△ADH∴AM=AH,∠MAB=∠DAH,∠ABM=∠ADH,BM=DH∵∠ABD=∠ADB=45°∴∠ABM=∠ADH=135°∴∠NDH=90°,∵∠MAD=∠BAD+∠MAB=∠MAH+∠DAH∴∠MAH=∠BAD=90°∵∠MAN=45°,∴∠MAN=∠HAN=45°,且AM=AH,AN=AN∴△AMN≌△AHN(SAS)∴MN=NH,∵在Rt△DHN中,NH2=DN2+DH2,∴MN2=DN2+BM2,(3)如图3,过A作AK⊥AM,且AK=AM,连接MK、KB、KN,∵AB=∴BD=AB=2,∴MD=BD+BM=3∵∠KAM=∠BAD=90°,∴∠KAB=∠DAM,且AB=AD,AK=AM∴△BAK≌△DAM(SAS),∴DM=BK=3,∠ABK=∠ADM=45°,∴∠NBK=45°+45°=90°,∵∠MAN=135°,∠KAM=90°,∴∠NAK=135°=∠MAN,∵AN=AN,∴△AKN≌△AMN(SAS),∴NK=MN设DN=x,则MN=3+x,在Rt△NBK中,由勾股定理得:(2+x)2+(3)2=(3+x)2,解得:x=2∴DN=232.在正方形AMFN中,以AM为BC边上的高作等边三角形ABC,将AB绕点A逆时针旋转90°至点D,D点恰好落在NF上,连接BD,AC与BD交于点E,连接CD.(1)如图1,求证:△AMC≌△AND;(2)如图1,若DF=,求AE的长;(3)如图2,将△CDF绕点D顺时针旋转α(0°<α<90°),点C,F的对应点分别为C1、F1.连接AF1、BC1,点G是BC1的中点,连接AG.试探索是否为定值,若是定值,则求出该值;若不是,请说明理由.【解答】(1)证明:如图1中,∵四边形AMFN是正方形,∴AM=AN∠AMC=∠N=90°∴△AMC,△AND是Rt△∵△ABC是等边三角形∴AB=AC∵旋转后AB=AD∴AC=AD∴Rt△AMC≌Rt△AND(HL).(2)解:如图2中,过E作EG⊥AB于G,在BC找一点H,连接DH,使BH=HD.设AG=x,则AE=2x,GE=x.易得△GBE是等腰直角三角形∴BG=EG=x,∴AB=BC=(+1)x,易得∠DHF=30°∴HD=2DF=2,HF=3,∴BF=BH+HF=2+3,∵Rt△AMC≌Rt△AND(HL)∴易得CF=DF=∴BC=BF﹣CF=2+3﹣=3+,∴(+1)x=3+,∴x=∴AE=2x=2.(3)结论:=.理由:如图3中,延长F1G到M,延长BA交F1C1的延长线于N,使得GM=F1G,则△GMB≌△GF1C1,∴BM=F1C1=DF1,∠BMG=∠GF1N,∴BM∥F1N,∴∠MBA=∠N,∵∠NAO=∠OF1D=90°,∠AON=∠DOF1,∴∠N=∠ADF1∴∠ABM=∠ADF1,∵AB=AD,∴△ABM≌△ADF1(SAS),∴AM=AF1,∠MAB=∠DAF1,∴∠MAF1=∠BAD=90°,∴△AMF1是等腰直角三角形,∴AG⊥MF1,AG=GF1,∴AF1=AG∴=.33.如图,等腰直角三角形OAB的三个定点分别为O(0,0)、A(0,3)、B(﹣3,0),过A作y轴的垂线l1.点C在x轴上以每秒的速度从原点出发向右运动,点D在l1上以每秒的速度同时从点A出发向右运动,当四边形ABCD为平行四边形时C、D同时停止运动,设运动时间为t.当C、D停止运动时,将△OAB沿y轴向右翻折得到△OAB1,AB1与CD相交于点E,P为x轴上另一动点.(1)求直线AB的解析式,并求出t的值.(2)当PE+PD取得最小值时,求PD2+PE2+2PD•PE的值.(3)设P的运动速度为1,若P从B点出发向右运动,运动时间为x,请用含x的代数式表示△P AE的面积.【解答】解:(1)设直线AB的解析式为y=kx+b(k≠0),将A(0,3),B(﹣3,0)代入y=kx+b,得:,解得:,∴直线AB的解析式为y=x+3.设t秒后,四边形ABCD为平行四边形,依题意,得:3+t=(+)t,解得:t=2.(2)作点E关于x轴的对称点E′,连接E′D交x轴于点P,此时PE+PD取得最小值,如图1所示.由(1)可知:点C的坐标为(,0),点D的坐标为(3+,3).∵AB∥CD,∴设直线CD的解析式为y=x+c,将C(,0)代入y=x+c,得:0=+c,解得:c=﹣,∴直线CD的解析式为y=x﹣.同理,可求出直线AB′的解析式为y=﹣x+3.联立直线CD,AB′的解析式成方程组,得:,解得:,∴点E的坐标为(,),∴点E′的坐标为(,),∴PD2+PE2+2PD•PE=(PD+PE)2=E′D2=(3+﹣)2+(3﹣)2=24﹣3.(3)分两种情况考虑,如图2所示.①当0≤x≤6时,S△P AE=S△P AB′﹣S△PEB′=×3(6﹣x)﹣×(6﹣x)=(6﹣x);当x>6时,S△P AE=S△P AB′﹣S△PEB′=×3(x﹣6)﹣×(x﹣6)=(x﹣6).综上所述:△P AE的面积S△P AE=.34.已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;①求证:点F是AD的中点;②判断BE与CF的数量关系和位置关系,并说明理由;(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.【解答】(1)①证明:如图1,∵AF=CF,∴∠1=∠2,∵∠1+∠ADC=90°,∠2+∠3=90°,∴∠3=∠ADC,∴FD=FC,∴AF=FD,即点F是AD的中点;②BE=2CF,BE⊥CF.理由如下:∵△ABC和△DEC都是等腰直角三角形,∴CA=CB,CD=CE,在△ADC和△BEC中,∴△ADC≌△BEC,∴AD=BE,∠1=∠CBE,而AD=2CF,∠1=∠2,∴BE=2CF,而∠2+∠3=90°,∴∠CBE+∠3=90°,∴CF⊥BE;(2)仍然有BE=2CF,BE⊥CF.理由如下:延长CF到G使FG=CF,连接AG、DG,如图2,∵AF=DF,FG=FC,∴四边形ACDG为平行四边形,∴AG=CD,AG∥CD,∴∠GAC+∠ACD=180°,即∠GAC=180°﹣∠ACD,∴CD=CE=AG,∵△DEC绕点C顺时针旋转α角(0<α<90°),∴∠BCD=α,∴∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,∴∠GAC=∠ECB,在△AGC和△CEB中,∴△AGC≌△CEB,∴CG=BE,∠2=∠1,∴BE=2CF,而∠2+∠BCF=90°,∴∠BCF+∠1=90°,∴CF⊥BE.35.(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.①求证:四边形BFDE是菱形;②直接写出∠EBF的度数.(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC 上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.【解答】(1)①证明:如图1中,∵四边形ABCD是矩形,∴AD∥BC,OB=OD,∴∠EDO=∠FBO,在△DOE和△BOF中,,∴△DOE≌△BOF,∴EO=OF,∵OB=OD,∴四边形EBFD是平行四边形,∵EF⊥BD,∴四边形EBFD是菱形.②∵BE平分∠ABD,∴∠ABE=∠EBD,∵EB=ED,∴∠EBD=∠EDB,∴∠ABD=2∠ADB,∵∠ABD+∠ADB=90°,∴∠ADB=30°,∠ABD=60°,∴∠ABE=∠EBO=∠OBF=30°,∴∠EBF=60°.(2)结论:IH=FH,且IH⊥FH.理由:如图2中,延长BE到M,使得EM=EJ,连接MJ.∵四边形EBFD是菱形,∠B=60°,∴EB=BF=ED,DE∥BF,∴∠JDH=∠FGH,在△DHJ和△GHF中,,∴△DHJ≌△GHF,∴DJ=FG,JH=HF,∴EJ=BG=EM=BI,∴BE=IM=BF,∵∠MEJ=∠B=60°,∴△MEJ是等边三角形,∴MJ=EM=NI,∠M=∠B=60°在△BIF和△MJI中,,∴△BIF≌△MJI,∴IJ=IF,∠BFI=∠MIJ,∵HJ=HF,∴IH⊥JF,∵∠BFI+∠BIF=120°,∴∠MIJ+∠BIF=120°,∴∠JIF=60°,∴△JIF是等边三角形,在Rt△IHF中,∵∠IHF=90°,∠IFH=60°,∴∠FIH=30°,∴IH=FH,IH⊥FH.(3)结论:EG2=AG2+CE2.理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,∵∠F AD+∠DEF=90°,∴AFED四点共圆,∴∠EDF=∠DAE=45°,∠ADC=90°,∴∠ADF+∠EDC=45°,∵∠ADF=∠CDM,∴∠CDM+∠CDE=45°=∠EDG,在△DEM和△DEG中,,∴△DEG≌△DEM,∴GE=EM,∵∠DCM=∠DAG=∠ACD=45°,AG=CM,∴∠ECM=90°∴EC2+CM2=EM2,∵EG=EM,AG=CM,∴GE2=AG2+CE2.36.已知正方形ABCD,探究以下问题:(1)如图1,点F在BC上,作FE⊥BD于点E,取DF的中点G,连接EG、CG,将△EGC沿直线EC 翻折到△EG′C,求证:四边形EGCG′是菱形;(2)如图2,点F是BC外一点,作FE⊥BC于点E,且BE=EF,连接DF,取DF的中点G,将△EGC 沿直线EC翻折到△EG′C,作FM⊥CD于点M,请问(1)中的结论”四边形EGCG′是菱形”是否依然成立,并说明理由;(3)在(2)的条件下,若图2中AB=4,设BE长为x,四边形EGCG′的面积为S,请求出S关于x 的函数关系式,并说明理由.【解答】证明:(1)∵四边形ABCD为正方形,∴∠DCF=90°.∵G为线段DF的中点,∴CG=DF.∵FE⊥BD,∴∠FED=90°,∵G为线段DF的中点,∴EG=DF,∴CG=EG.∵将△EGC沿直线EC翻折到△EG′C,∴CG=CG′,EG=EG′,∴四边形EGCG′四条边相等,∴四边形EGCG′是菱形.(2)(1)中的结论”四边形EGCG′是菱形”依然成立.证明:在图2中,连接BG,GM,如图所示.∵FE⊥BC于点E,且BE=EF,∴△BEF为等腰直角三角形,∴∠EBF=45°.∵四边形ABCD为正方形,∴∠DBE=45°,∴∠DBF=∠DBE+∠EBF=90°.∵G为线段DF的中点,∴BG=DF.∵FM⊥CD于点M,∴∠DMF=90°,∵G为线段DF的中点,∴MG=DF,∴BG=MG.∵FE⊥BC,FM⊥CD,∴四边形EFMC为矩形,∴EF=CM.∴BE=EF=MC.∵BG=GD,MG=GD,∴∠DBG=∠BDG,∠GMD=∠GDM,∵∠DBC=∠CDB=45°,∴∠GBE=∠DBC﹣∠DBG=45°﹣∠BDG,∠GMC=∠GDM=∠CBD﹣∠BDG=45°﹣∠BDG,∴∠GBE=∠GMC.。
初二数学压轴几何证明题(含答案)
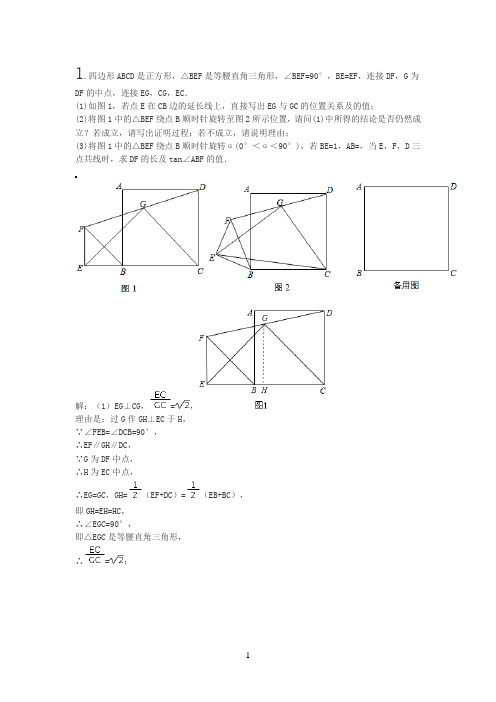
1.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及的值;(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=,当E,F,D三点共线时,求DF的长及tan∠ABF的值.解:(1)EG⊥CG,=,理由是:过G作GH⊥EC于H,∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,∵G为DF中点,∴H为EC中点,∴EG=GC,GH=(EF+DC)=(EB+BC),即GH=EH=HC,∴∠EGC=90°,即△EGC是等腰直角三角形,∴=;(2)解:结论还成立,理由是:如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,∵在△EFG和△HDG中∴△EFG≌△HDG(SAS),∴DH=EF=BE,∠FEG=∠DHG,∴EF∥DH,∴∠1=∠2=90°-∠3=∠4,∴∠EBC=180°-∠4=180°-∠1=∠HDC,在△EBC和△HDC中∴△EBC≌△HDC.∴CE=CH,∠BCE=∠DCH,∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°,∴△ECH是等腰直角三角形,∵G为EH的中点,∴EG⊥GC,=,即(1)中的结论仍然成立;(3)解:连接BD,∵AB=,正方形ABCD,∴BD=2,∴cos∠DBE==,∴∠DBE=60°,∴∠ABE=∠DBE-∠ABD=15°,∴∠ABF=45°-15°=30°,∴tan∠ABF=,∴DE=BE=,∴DF=DE-EF=-1.解析:(1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,根据梯形的中位线求出EG=GC,GH=(EF+DC)=(EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可;(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案;(3)连接BD,求出cos∠DBE==,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.2.已知正方形ABCD和等腰直角三角形BEF,BE=EF,∠BEF=90°,按图1放置,使点E在BC 上,取DF的中点G,连接EG,CG.(1)延长EG交DC于H,试说明:DH=BE.(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:EG=CG且EG⊥CG.在设法证明时他发现:若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?请写出来.(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.(1)证明:∵∠BEF=90°,∴EF∥DH,∴∠EFG=∠GDH,而∠EGF=∠DGH,GF=GD,∴△GEF≌△GHD,∴EF=DH,而BE=EF,∴DH=BE;(2)连接DB,如图,∵△BEF为等腰直角三角形,∴∠EBF=45°,而四边形ABCD为正方形,∴∠DBC=45°,∴D,E,B三点共线.而∠BEF=90°,∴△FED为直角三角形,而G为DF的中点,∴EG=GD=GC,∴∠EGC=2∠EDC=90°,∴EG=CG且EG⊥CG;(3)第2问中的结论成立.理由如下:连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,∵G为DF的中点,O为BD的中点,M为BF的中点,∴OG∥BF,GM∥OB,∴四边形OGMB为平行四边形,∴OG=BM,GM=OB,而EM=BM,OC=OB,∴EM=OG,MG=OC,∵∠DOG=∠GMF,而∠DOC=∠EMF=90°,∴∠EMG=∠GOC,∴△MEG≌△OGC,∴EG=CG,∠EGM=∠OCG,又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,∴EG=CG且EG⊥CG.解析:(1)由∠BEF=90°,得到EF∥DH,而GF=GD,易证得△GEF≌△GHD,得EF=DH,而BE=EF,即可得到结论.(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,得到D,E,B三点共线,而G为DF的中点,根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC,于是∠EGC=2∠EDC=90°,即得到结论.(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,得到OG=BM,GM=OB,而EM=BM,OC=OB,得到EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF=90°,得∠EMG=∠GOC,则△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.3.已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图①放置,使点F在BC上,取DF的中点G,连接EG、CG.(1)探索EG、CG的数量关系和位置关系并证明;(2)将图①中△BEF绕B点顺时针旋转45°,再连接DF,取DF中点G(如图②),问(1)中的结论是否仍然成立.证明你的结论;(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间),再连接DF,取DF的中点G(如图③),问(1)中的结论是否仍然成立,证明你的结论.解:(1)EG=CG且EG⊥CG.证明如下:如图①,连接BD.∵正方形ABCD和等腰Rt△BEF,∴∠EBF=∠DBC=45°.∴B、E、D三点共线.∵∠DEF=90°,G为DF的中点,∠DCB=90°,∴EG=DG=GF=CG.∴∠EGF=2∠EDG,∠CGF=2∠CDG.∴∠EGF+∠CGF=2∠EDC=90°,即∠EGC=90°,∴EG⊥CG.(2)仍然成立,证明如下:如图②,延长EG交CD于点H.∵BE⊥EF,∴EF∥CD,∴∠1=∠2.又∵∠3=∠4,FG=DG,∴△FEG≌△DHG,∴EF=DH,EG=GH.∵△BEF为等腰直角三角形,∴BE=EF,∴BE=DH.∵CD=BC,∴CE=CH.∴△ECH为等腰直角三角形.又∵EG=GH,∴EG=CG且EG⊥CG.(3)仍然成立.证明如下:如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.∵GF=GD,∠HGF=∠CGD,HG=CG,∴△HFG≌△CDG,∴HF=CD,∠GHF=∠GCD,∴HF∥CD.∵正方形ABCD,∴HF=BC,HF⊥BC.∵△BEF是等腰直角三角形,∴BE=EF,∠EBC=∠HFE,∴△BEC≌△FEH,∴HE=EC,∠BEC=∠FEH,∴∠BEF=∠HEC=90°,∴△ECH为等腰直角三角形.又∵CG=GH,∴EG=CG且EG⊥CG.解析:(1)首先证明B、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG=GF=CG,得到∠EGF=2∠EDG,∠CGF=2∠CDG,从而证得∠EGC=90°;(2)首先证明△FEG≌△DHG,然后证明△ECH为等腰直角三角形.可以证得:EG=CG且EG ⊥CG.(3)首先证明:△BEC ≌△FEH ,即可证得:△ECH 为等腰直角三角形,从而得到:EG=CG 且EG ⊥CG .已知,正方形ABCD 中,△BEF 为等腰直角三角形,且BF 为底,取DF 的中点G ,连接EG 、CG .(1)如图1,若△BEF 的底边BF 在BC 上,猜想EG 和CG 的数量关系为______;(2)如图2,若△BEF 的直角边BE 在BC 上,则(1)中的结论是否还成立?请说明理由;(3)如图3,若△BEF 的直角边BE 在∠DBC 内,则(1)中的结论是否还成立?说明理由.解:(1)GC=EG ,(1分)理由如下:∵△BEF 为等腰直角三角形, ∴∠DEF=90°,又G 为斜边DF 的中点, ∴EG=DF , ∵ABCD 为正方形, ∴∠BCD=90°,又G 为斜边DF 的中点,∴CG= DF , ∴GC=EG ;(2)成立.如图,延长EG 交CD 于M ,∵∠BEF=∠FEC=∠BCD=90°,∴EF ∥CD ,∴∠EFG=∠MDG ,又∠EGF=∠DGM ,DG=FG ,∴△GEF ≌△GMD ,∴EG=MG ,即G 为EM 的中点.∴CG 为直角△ECM 的斜边上的中线,∴CG=GE= EM ;(3)成立.取BF 的中点H ,连接EH ,GH ,取BD 的中点O ,连接OG ,OC .∵CB=CD ,∠DCB=90°,∴CO= BD1 2 1 21212.∵DG=GF,∴GH∥BD,且GH= BD,OG∥BF,且OG= BF,∴CO=GH.为等腰直角三角形.∵△BEF∴EH= BF∴EH=OG.∵四边形OBHG为平行四边形,∴∠BOG=∠BHG.∵∠BOC=∠BHE=90°.∴∠GOC=∠EHG.∴△GOC≌△EHG.∴EG=GC.此题考查了正方形的性质,以及全等三角形的判定与性质.要求学生掌握直角三角形斜边上的中线等于斜边的一半,以及三角形的中位线与第三边平行且等于第三边的一半.掌握这些性质,熟练运用全等知识是解本题的关键.解析:(1)EG=CG,理由为:根据三角形BEF为等腰直角三角形,得到∠DEF为直角,又G为DF中点,根据在直角三角形中,斜边上的中线等于斜边的一半,得到EG为DF的一半,同理在直角三角形DCF中,得到CG也等于DF的一半,利用等量代换得证;(2)成立.理由为:延长EG交CD于M,如图所示,根据“ASA”得到三角形EFG与三角形GDM 全等,由全等三角形的对应边相等得到EG与MG相等,即G为EM中点,根据直角三角形斜边上的中线等于斜边的一半得到EG与CG相等都等于斜边EM的一半,得证;(3)成立.理由为:取BF的中点H,连接EH,GH,取BD的中点O,连接OG,OC,如图所示,1212因为直角三角形DCB中,O为斜边BD的中点,根据斜边上的中线等于斜边的一半得到OC等于BD 的一半,由HG为三角形DBF的中位线,根据三角形的中位线平行于第三边且等于第三边的一半,得到GH等于BD一半,OG等于BF的一半,又根据直角三角形斜边上的中线等于斜边的一半得到EH等于BF的一半,根据等量代换得到OG与EH相等,再根据OBHG为平行四边形,根据平行四边形的性质得到对边相等,对角相等,进而得到∠GOC与∠EHG相等,利用“SAS”得到△GOC与△EHG全等,利用全等三角形的对应边相等即可得证.。
初二期末几何压轴题答案详解课件

首先分析题目给出的条件,明确所 涉及的三角形和四边形,然后根据 性质和判定定理进行推理,最后得 出结论。
角度与线段的计算题
总结词
考察角度和线段的计算
详细描述
这类题目通常涉及角度和线段的计算,需要学生掌握角度和线段的 计算公式,并能够灵活运用。
解题方法
首先根据题目给出的条件,明确所涉及的角度和线段,然后根据计 算公式进行计算,最后得出结论。
初二期末几何压轴题 答案详解课件
目录
• 几何压轴题概述 • 常见几何压轴题类型与解题方法 • 几何压轴题的解题技巧与注意事项 • 学生常见问题与解答 • 练习与巩固 • 总结与展望
01
几何压轴题概述
几何压轴题的定义与特点
定义
几何压轴题通常指在期末考试中难度较大、分值较高、考察学生综合运用几何 知识能力的题目。
解题方法
首先分析题目给出的条件,明确所涉及的折叠和旋转,然后根据性质 和判定定理进行推理,最后得出结论。
03
几何压轴题的解题技巧与 注意事项
解题技巧:如何快速找到解题突破口
仔细审题
理解题目的要求和条件,明确解题的目标。
寻找关键信息
从题目中提取关键信息,如特殊角、特殊图 形等。
利用已知条件进行推导
注重实践应用
将所学的几何知识应用到实际生活中,加深对知 识的理解,提高自己的实践能力。
3
提前预习下一学期的学习内容
提前了解下一学期的学习内容,做好预习工作, 为新的学习做好准备。
THANKS
感谢观看
答案与解析: 答案+解析 答案与解析: 答案+解析
练习题二:填空题
01
填空题一: 题 目内容
02
期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1.(三角形翻折问题)如图,在Rt ABC △中,9086ABC AB BC ∠=︒==,,,分别在AB AC ,边上取点E F ,,将AEF △沿直线EF 翻折得到A EF '△,使得点A 的对应点A '恰好落在CB 延长线上,当60EA B '∠=︒时,AE 的长为 ,当A F AC '⊥时,AF 的长为 .【答案】 32− 407【分析】由折叠的性质可得AE A E '=,先求出30A EB '∠=︒,从而可得1122A B A E AE ''==,再由勾股定理可得BE AE =,最后由AE BE AB +=,进行计算即可;令A F '交AB 于G ,连接CG ,由折叠的性质可得:A EA F '∠=∠,AFE A FE '∠=∠,AEF A EF '∠=∠,AF A F '=,由A F AC '⊥得出90A FA A FC ''∠=∠=︒,45AFE A FE '∠=∠=︒,证明()ASA A FC AFG '≌得到CF FG =,设CF FG x ==,则10AF x =−,AG ,根据1122ACG S AC FG AG BC =⋅=⋅建立方程,解方程即可得出CF 的长,即可求解.【详解】解:由折叠的性质可得:AE A E '=,90ABC ∠=︒,18090A BE ABC '∴∠=︒−∠=︒,60EA B '∠=︒,9030A EB EA B ''∴∠=︒−∠=︒,1122A B A E AE ''∴==,BE AE∴==,AE BE AB+=,8AE AE∴=,32AE∴=−如图,令A F'交AB于G,连接CG,A F AC'⊥,90A FA A FC''∴∠=∠=︒,由折叠的性质可得:A EA F'∠=∠,AFE A FE'∠=∠,AEF A EF'∠=∠,AF A F'=,90AFE A FE'∠+∠=︒,45AFE A FE'∴∠=∠=︒,设A EA Fα'∠=∠=,则45FEB AFEα∠=∠=+︒,180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠,()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−,902EA B A EBα''∴∠=︒−∠=,FA C EA B EA F Aα'''∴∠=∠−∠==∠,在A FC'和AFG中,CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩',()ASAA FC AFG'∴≌,CF FG∴=,在Rt ABC△中,9086ABC AB BC∠=︒==,,,10AC∴,设CF FG x==,则10AF x=−,AG∴==1122ACGS AC FG AG BC=⋅=⋅,106x∴⋅=,整理得:271809000x x+−=,即29014400749x⎛⎫+=⎪⎝⎭,9012077x∴+=±,解得:307x=或30x=−(不符合题意,舍去),307CF∴=,30401077AF AC CF∴=−=−=,故答案为:32−407.【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.例2.(坐标系中折叠问题)如图,在平面直角坐标系中,长方形ABCO的边OC OA、分别在x轴、y轴上,6AB=,点E在边BC上,将长方形ABCO沿AE折叠,若点B的对应点F 恰好是边OC的三等分点,则点E的坐标是.【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题,坐标与图形,由折叠的性质可得6AF AB==,BE EF=,90AFE B∠=∠=︒,再分当点F靠近点C时,24CF OF==,,当点F靠近点O 时,则42CF OF==,,两种情况利用勾股定理先求出OA的长,进而得到BC的长,设出CE 的长,进而得到EF的长,在Rt EFC△中,由勾股定理建立方程求解即可.【详解】解:在长方形ABCO 中,6CO AB ==,90BCO B AOC ∠=∠=∠=︒, 由折叠的性质可得6AF AB ==,BE EF =,90AFE B ∠=∠=︒,F 恰好是边OC 的三等分点,∴当点F 靠近点C 时,24CF OF ==,,在Rt AFO V中,OA =,∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222EF CF CE =+,∴()2222xx =+,解得x =,∴点E的坐标是⎛− ⎝⎭; 当点F 靠近点O 时,则42CF OF ==,,在Rt AFO V中,OA ==∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222CF CE =+,∴()2224x x =+,解得x =∴点E的坐标是(−;综上所述,点E的坐标是⎛− ⎝⎭或(−,故答案为:⎛− ⎝⎭或(−.例3.(四边形折叠问题)如图,已知矩形ABCD ,4AB =,5BC =,点P 是射线BC 上的动点,连接AP ,AQP △是由ABP 沿AP 翻折所得到的图形.(1)当点Q 落在边AD 上时,QC = ;(2)当直线PQ 经过点D 时,求BP 的长;(3)如图2,点M 是DC 的中点,连接MP 、MQ .①MQ 的最小值为 ;②当PMQ 是以PM 为腰的等腰三角形时,请直接写出BP 的长.【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】(1)根据折叠的性质和勾股定理进行求解即可;(2)分点P 在线段BC 上,点P 在线段BC 的延长线上,两种情况,进行讨论求解;(3)①连接AM ,勾股定理求出AM 的长,折叠求出AQ 的长,根据MQ AM AQ ≥−,求出最小值即可;②分PM MQ =和PM PQ =两种情况,再分点P 在线段BC 上,点P 在线段BC 的延长线上,进行讨论求解即可.【详解】(1)解:当点Q 落在边AD 上时,如图所示,∵矩形ABCD ,4AB =,5BC =,∴4,5CD AB AD BC ====,90BAD B BCD ADC ∠=∠=∠=∠=︒,∵翻折,∴4,90AQ AB AQP B ==∠=∠=︒,∴1DQ AD AQ =−=,在Rt CDQ △中,CQ ==(2)当直线PQ 经过点D 时,分两种情况:当点P 在线段BC 上时,如图:∵翻折,∴4AQ AB ==,90AQP B ∠=∠=︒,BP PQ =,∴90AQD ∠=︒,∴3DQ ==,设BP PQ x ==,则:5PC BC BP x =−=−,3DP DQ PQ x =+=+,在Rt PCD △中,222DP CP CD=+,即:()()222345x x +=+−,∴2x =;∴2BP =;②当P 在线段BC 的延长线上时:∵翻折,∴4,90AQ AB Q B ==∠=∠=︒,BP PQ =,∴3DQ ==,设BP PQ x ==,则:5PC BP BC x =−=−,3DP PQ DQ x =−=−,在Rt PCD △中,222DP CP CD =+,即:()()222345x x −=+−,∴8x =;∴8BP =;综上:2BP =或8BP =;(3)①连接AM ,∵M 是CD 的中点, ∴122DM CM CD ===,∴AM =∵翻折,∴4AQ AB ==,∵MQ AM AQ ≥−,∴当,,A Q M 三点共线时,MQ 的值最小,即:4MQ AM AQ =−=4;②当PM PQ =时,如图:∵翻折,∴BP PQ PM ==,设BP x =,则:,5PM x CP BC BP x ==−=−,在Rt PCM 中,222PM CM PC =+,即:()22225x x =+−,解得: 2.9x =,即: 2.9BP =;当PM QM =,点P 在线段BC 上时,如图:∵,QM PM DM CM ==,90D C ∠=∠=︒,∴()HL MDQ MCP ≌,∴CP DQ =,点Q 在AD 上,由(1)知:1DQ =,∴1CP DQ ==,∴4BP BC CP =−=;当点P 在BC 的延长线上时:如图:此时点M 在AP 上,连接BM ,∵翻折,∴BM MQ PM ==,∵MC BP ⊥,∴210BP BC ==;综上: 2.9BP =或4BP =或10BP =.质,综合性强,难度大,属于压轴题.利用数形结合和分类讨论的思想进行求解,是解题的关键.【模拟训练】1.如图,在长方形ABCD 中,点E 是AD 的中点,将ABE 沿BE 翻折得到FBE ,EF 交BC 于点H ,延长BF DC 、相交于点G ,若8DG =,10BC =,则DC = .【答案】258【分析】本题考查了全等三角形的判定与性质,折叠的性质,勾股定理,连接EG ,根据点E 是AD 的中点得DE AE EF ==,根据四边形ABCD 是长方形得90D A ∠=∠=︒,根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒,利用HL 证明Rt Rt EFG EDG △≌△,得8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG V △中,根据勾股定理得,222CG BC BG +=,进行计算即可得.【详解】解:如图所示,连接EG ,∵点E 是AD 的中点,∴DE AE EF ==,∵四边形ABCD 是长方形,∴90D A ∠=∠=︒,∵将ABE 沿BE 翻折得到FBE ,∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中,EF ED EG EG =⎧⎨=⎩,∴()Rt Rt HL EFG EDG V V ≌,∴8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG 中,根据勾股定理得,222CG BC BG +=,∴222(8)10(8)x x −+=+,解得258x =,故答案为:258.2.如图,在Rt ABC △中,90ACB ∠=︒,254AB =,154=AC ,点D 是AB 边上的一个动点,连接CD ,将BCD △沿CD 折叠,得到CDE ,当DE 与ABC 的直角边垂直时,AD 的长是 .【答案】154或54【分析】本题考查了勾股定理,平行四边形的判定和性质,折叠的性质,全等三角形的判定和性质,分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案,根据题意,正确画出图形是解题的关键.【详解】解:如图,当DE BC ⊥时,延长ED 交BC 于点F ,CE 与AB 相交于点M ,∵EF BC ⊥,∴90EFC EFB ∠=∠=︒,∴90E ECF ∠+∠=︒,由折叠得,B E ∠=∠,CE CB =,MCD FCD ∠=∠,∴90B ECF ∠+∠=︒,∴90CMB ∠=︒,即C M A B ⊥,∵90ACB ∠=︒,254AB =,154=AC ,∴5BC ==, ∵1122ABC S AC BC AB CM ==△,∴11512552424CM ⨯⨯=⨯⨯,解得3CM =,∴4BM =,∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴()AAS CFD CMD ≌,∴3CF CM ==,DF DM =,∴532BF BC CF =−=−=,设DF DM x ==,则4BD x =−,在Rt BFD 中,222DF BF BD +=,∴()22224x x +=−, 解得32x =, ∴35422BD =−=, ∴25515424AD AB BD =−=−=;当DE AB ⊥时,如图,设DE 与AC 相交于点M ,由折叠可得,BCD ECD ∠=∠,DE DB =,ED BD =,5EC BC ==,∵DE AB ⊥,90ACB ∠=︒,∴DE BC ∥,∴EDC BCD ∠=∠,∴EDC ECD ∠=∠,∴5ED EC ==,∴5BD ED ==, ∴255544AD AB BD =−=−=;综上,AD 的长是154或54, 故答案为:154或54.3.如图,等边三角形ABC 中,16AB BD AC =⊥,于点D ,点E F 、分别是BC DC 、上的动点,沿EF 所在直线折叠CEF △,使点C 落在BD 上的点C '处,当BEC '△是直角三角形时,BE 的值为 .【答案】24−或323【分析】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.由等边三角形的性质可得30DBC ∠=︒,分9090BEC BC E ''∠=︒∠=︒,两种情况讨论,由直角三角形的性质即可求解.【详解】解:ABC 是等边三角形,BD AC ⊥,30,DBC ∴∠=︒ 由折叠的性质可得:,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323.4.如图,在ABC 中,120ACB ∠=︒,8AC =,4BC =,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,使点A 落在CD 的延长线上的点A '处,两条折痕与斜边AB 分别交于点E 、F ,则线段FA '的长为 .【答案】【分析】本题考查了折叠的性质,勾股定理,直角三角形的性质,添加恰当辅助线构造直角三角形是本题的关键.过点A 作AH BC ⊥交BC 的延长线于H ,由直角三角形的性质可求142HC AC ==,AH =AB 的长,由面积法可求CE 的长,由折叠的性质可求90BEC DEC ∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,然后再求解即可.【详解】解:如图,过点A 作AH BC ⊥,交BC 的延长线于H ,120ACB ∠=︒,ACB H HAC ∠=∠+∠,30HAC ∴∠=︒,142HC AC ∴==,AH ==,448BH ∴=+=,AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯,4CE ∴=,CE ∴,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,90BEC DEC ∴∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,1602ECF ACB ∴∠=∠=︒,30CFE ∴∠=︒,EF ∴,在Rt BCE中,BE ===,AF AB EF BE ∴=−−==FA AF '∴==故答案为:5.如图,点D 是ABC 的边AB 的中点,将BCD △沿直线CD 翻折能与ECD 重合,若4AB =,2CD =,1AE =,则点C 到直线AB 的距离为 .【答案】【分析】连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质及中点性质可得AEB △为直角三角形,且G 为BE 中点,从而CG BE ⊥,由勾股定理可得BE的长,再根据2ABC BDC S S =△△,即11222AB CH CD BG ⋅=⨯⋅,从而可求得CH 的长.【详解】解:连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质可得:BD ED =,CB CE =,∴CG 为BE 的中垂线, ∴12BG BE =,∵点D 是AB 的中点,4AB =,2CD =,1AE =, ∴122BD AD AB ===,CBD CAD S S =,AD DE =,∴DBE DEB ∠=∠,DEA DAE ∠=∠,∵180EDA DEA DAE ∠+∠+∠=︒,即22180DEB DEA ∠+∠=︒,∴90DEB DEA ∠+∠=︒,即90BEA ∠=︒,∴BE∴12BG BE ==, ∵2ABC BDCS S =△△, ∴11222AB CH CD BG ⋅=⨯⋅,∴422CH =⨯,∴CH ,∴点C 到直线AB 的距离为.故答案为:.【点睛】本题考查翻折变换,线段中垂线的判定,等腰三角形的性质,点到直线的距离,直角三角形的判定,勾股定理,利用面积相等求相应线段的长,解题的关键是得出CG 为BE 的中垂线,2ABC BDC S S =△△.6.如图,在ABC 中,90,A AB AC ∠=︒==D 为AC 边上一动点,将C ∠沿过点D 的直线折叠,使点C 的对应点C '落在射线CA 上,连接BC ',当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为 .【答案】 或 【分析】由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==时,分别根据勾股定理求出AC '的长,再求出CC '的长即可 【详解】解:由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时,90,A AB AC ∠=︒==∴由勾股定理得,222BC AC AB ''−=,即222(2)AC AC ''−=,AC '∴=CC '∴CD ∴;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时,同理得AC 'CC '∴CD ∴;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==由勾股定理得,222AC BC AB ''=−,即22218AC '=−=,AC '∴=CC '∴CD ∴=,0>,CD AB ∴>,此时点D 不在边AC 上,不符合题意,舍去,综上,当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为或.故答案为:或.【点睛】本题主要考查图形的翻折变换(折叠问题),勾股定理,等腰直角三角形的性质等知识,灵活运用折叠的性质及勾股定理是解答本题的关键,同时要注意分类思想的运用.7.如图,在ABC 中,90ACB ∠=︒,3AC =,4BC =,P 为斜边AB 上的一动点(不包含A ,B 两端点),以CP 为对称轴将ACP △翻折得到A CP ',连结BA '.当A P AB '⊥时,BA '的长为 .【答案】【分析】当A P AB '⊥时,过点C 作CD AB ⊥于D ,可知125CD =,95AD =,得出PDC △为等腰直角三角形,得到PD CD =,求出PA '和BP 的长,利用勾股定理即可求出BA '的长.【详解】过点C 作CD AB ⊥于D ,在Rt ADC 中,90ACB ∠=︒,3AC =,4BC =,∴5AB = ∵1122AC BC AB CD ⨯=⨯,125CD ∴=,在Rt ADC 中,3AC =∴95AD ==,当A P AB '⊥时,如图由折叠性质可知12∠=∠,PA PA '=,又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴,又2390∠+∠=︒,345∴∠=︒,23∴∠=∠,125PD CD ∴==,又PA PD AD =+,12921555PA ∴=+=,又PA PA '=,215PA '∴=,又BP AB PA =−,214555BP ∴=−=,在Rt BPA '△中,90BPA ∠='︒,222BP PA BA ∴='+,2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭,BA '∴=,故答案为:.【点睛】本题考查了勾股定理的应用,折叠问题,熟练掌握勾股定理是解题的关键.8.如图,在ABC 中,90ACB ∠=︒,AC BC =,D 为AB 上一点,连接DC ,将BDC 沿DC 翻折,得到EDC △,连接AE ,若AE CE =,4BC =,则D 到CE 的距离是 .【答案】2【分析】本题考查等腰直角三角形中的折叠问题,涉及等边三角形判定与性质,勾股定理应用、面积法等知识.设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,根据将BDC 沿DC 翻折,得到EDC △,AC BC =,AE CE =,可得ACE △是等边三角形,即知60ACE ∠=︒,而90ACB ∠=︒,故150BCE ∠=︒,30ECF ∠=︒,可得75BCD ECD ∠=∠=︒,122EF CE ==,CF =BE =15CBE ∠=︒,可得90BGC ∠=︒,即CG BE ⊥,从而12BG BE GE ===,由勾股定理得CG ,在Rt BDG △中,DG ,即得CD DG CG =+,由面积法可得D 到CE 的距离是2. 【详解】解:设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,如图:将BDC 沿DC 翻折,得到EDC △,4BC CE ∴==,BCD ECD ∠=∠,AC BC =,AE CE =,AC BC CE AE ∴===,ACE ∴是等边三角形,60ACE ∴∠=︒,90ACB ∠=︒,150BCE ∴∠=︒,30ECF ∠=︒,75BCD ECD ∴∠=∠=︒,122EF CE ==,CF =在Rt BEF △中,BE ==BCE 中,BC CE =,150BCE ∠=︒,15CBE ∴∠=︒,18090BGC BGC BCD ∴∠=︒−∠−∠=︒,即CG BE ⊥,12BG BE GE ∴==,CG ∴===,45ABC ∠=︒,15CBE ∠=︒,30DBG ∴∠=︒,在Rt BDG△中,DG =,CD DG CG ∴=+=,设D 到CE 的距离是h ,2DCE S CE h DC GE ∆=⋅=⋅,324DC GE h CE ⋅∴===,故答案为:2.9.在生活中、折纸是一种大家喜欢的活动、在数学中,我们可以通过折纸进行探究,探寻数学奥秘.【纸片规格】三角形纸片ABC ,120ACB ∠=︒,CA CB =,点D是底边AB 上一点.【换作探究】(1)如图1,若6AC =,AD =CD ,求CD 的长度;(2)如图2,若6AC =,连接CD ,将ACD 沿CD 所在直线翻折得到ECD ,点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直,求AD 的长;(3)如图3,将ACD 沿CD 所在直线翻折得到ECD ,边CE 与边AB 交于点F ,且DE BC ∥,再将DFE △沿DF 所在直线翻折得到DFG ,点E 的对应点为点G ,DG 与CE 、BC 分别交于H ,K ,若1KH =,请直接写出AC 边的长.【答案】(1)(2)3或(3)3【分析】(1)作CE AB ⊥于E ,求得30A B ==︒∠∠,从而得出132CE AC ==,AE AC =进而得出DE AE AD =−=(2)当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,依次得出45DAE DEA ∠=∠=︒,304575CAE CAD DAE ∠=∠+∠=︒+︒=︒,75CEA CAE ∠=∠=︒,30ACE ∠=︒,15ACD DCE ∠=∠=︒,45CDG CAB DAC ∠=∠+∠=︒,从而DG CG =,进一步得出结果;当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,可推出90AVC ∠=︒,60ACE ∠=︒,从而30ACD DCE ∠=∠=︒,进一步得出结果;当DE BC ⊥时,可推出180ACB BCE ∠+∠=︒,从而90ACD DCE ∠=∠=︒,进一步得出结果;(3)可推出CKH 和CDH △及CHK 是直角三角形,且30HCK ∠=︒,30HDF ∠=︒,45DCH ∠=︒,进一步得出结果.【详解】(1)解:如图1,作CE AB ⊥于E ,90AEC ∴∠=︒,CA CB =,120ACB ∠=︒,30A B ∴∠=∠=︒,132CE AC ∴==,AE =,DE AE AD ∴=−==CD ∴=;(2)解:如图2,当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,由翻折得:AD DE =,CAD CED =∠∠,AC CE =,45DAE DEA ∠∠∴==︒,304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒,75CEA CAE ∴∠=∠=︒,30ACE ∴∠=︒,15ACD DCE ∴∠=∠=︒,45CDG CAB DAC ∴∠=∠+∠=︒,DG CG ∴=,由(1)知:3CG =,AG =3AD AG DG ∴=−=;如图3,当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,90E ACE ∴∠+∠=︒,E A ∠=∠,90A ACE ∴∠+∠=︒,90AVC ∴∠=︒,60ACE∴∠=︒,30ACD DCE∴∠=∠=︒,ACD A∴∠=∠,AD CD∴=,3CV =,CD∴=,AD CD∴==如图4,当DE BC⊥时,30E A∠=∠=︒,60BCE∴∠=︒,180ACB BCE∴∠+∠=︒,90ACD DCE∴∠=∠=︒,AD∴=,综上所述:3AD=或(3)解:如图5,∵DE BC ∥,30B C ∠=∠=︒,30BCF E ∴∠=∠=︒,30EDF B ∠=∠=︒,120ACB ∠=︒,90ACE ∴∠=︒,1452ECD ACD ACE ∴∠=∠=∠=︒,将DFE △沿DF 所在直线翻折得到DFG ,30GDF EDF ∴∠=∠=︒,60EDG ∴∠=︒,90CHK EHD ∴∠=∠=︒,DH CH ∴=1FH ∴==,1CF CH FH ∴=+,3AC ∴==.【点睛】本题考查了等腰三角形的判定和性质,直角三角形的性质等知识,解决问题的关键是正确分类,画出图形.10.如图,在ABC 中,90BAC ∠=︒,AB AC =,点D 为线段BC 延长线上一点,以AD 为腰作等腰直角DAF △,使90DAF ∠=︒,连接CF .(1)请判断CF 与BC 的位置关系,并说明理由;(2)若8BC =,4CD BC =,求线段AD 的长;(3)如图2,在(2)的条件下,将DAF △沿线段DF 翻折,使点A 与点E 重合,连接CE ,求线段CE 的长.【答案】(1)CF BC ⊥,理由见解析(2)(3)【分析】(1)证明()SAS ABD ACF △≌△,则ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,可得90FAO DCO ∠=∠=︒,进而可得CF BC ⊥;(2)如图2,过A 作AH BC ⊥于H ,则142BH CH AH BC ====,6DH =,由勾股定理得,AD =(3)由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,证明()AAS ADM DEN ≌,则46DN AM EN DM ====,,6CN =,由勾股定理得,CE =计算求解即可.【详解】(1)解:CF BC ⊥,理由如下:∵等腰直角DAF △,90DAF ∠=︒,∴AD AF =,又∵90BAC ∠=︒,∴BAC CAD DAF CAD ∠+∠=∠+∠,即BAD CAF ∠=∠,∵AB AC =,BAD CAF ∠=∠,AD AF =,∴()SAS ABD ACF △≌△,∴ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,∴90FAO DCO ∠=∠=︒,∴CF BC ⊥;(2)解:∵8BC =,4CD BC =,∴2CD =,如图2,过A 作AH BC ⊥于H ,∵ABC 是等腰直角三角形, ∴142BH CH AH BC ====,∴6DH =,由勾股定理得,AD =∴线段AD 的长为(3)解:由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,∴90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,∴90AMD DNE ∠=︒=∠,同理(2)可知,4AM =,6MD =,∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠,∴ADM DEN ∠=∠,∵90AMD DNE ∠=︒=∠,ADM DEN ∠=∠,AD DE =,∴()AAS ADM DEN ≌,∴46DN AM EN DM ====,,∴6CN =,由勾股定理得,CE =,∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质,三角形内角和定理,勾股定理,折叠的性质,等腰三角形的性质.熟练掌握全等三角形的判定与性质,折叠的性质是解题的关键.11.如图1,在Rt ABC △中,90C ∠=︒,5AC =,12BC =,点D 为BC 边上一动点,将ACD 沿直线AD 折叠,得到AFD △,请解决下列问题.(1)AB =______;当点F 恰好落在斜边AB 上时,CD =______;(2)连接CF ,当CBF V 是以CF 为底边的等腰三角形时,请在图2中画出相应的图形,并求出此时点F 到直线AC 的距离;(3)如图3,E 为边BC 上一点,且4,连接EF ,当DEF 为直角三角形时,CD = .(请写出所有满足条件的CD 长)【答案】(1)13,103(2)画图见解析,600169(3)52或或5或10【分析】(1)根据勾股定理可得AB 的长,再利用等积法求出CD 即可;(2)过点F 作FG AC ^,交CA 的延长线于G ,首先由等积法求出CH 的长,再根据勾股定理求出AH 的长,再次利用等积法可得FG 的长;(3)分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形,从而解决问题.【详解】(1)解:在Rt ABC △中,由勾股定理得,13AB ,当点F 落在AB 上时,由折叠知,CD DF =, ∴111222AC CD AB DF AC BC ⋅+⋅=⋅,51360CD CD ∴+=,103CD ∴=,故答案为:13,103;(2)过点F 作FG AC ^,交CA 的延长线于G ,BC BF =,AC AF =,AB ∴垂直平分CF , 由等积法得6013AC BC CH AB ⋅==,在Rt ACH 中,由勾股定理得,2513AH ===, 1122ACF S AC FG CF AH =⋅=⋅△,6025260013135169CF AH FG AC ⨯⨯⋅∴===;(3)当90DEF ∠=︒时,当点D 在CE 上时,作FH AC ⊥于H ,则4HF CE ==,5AF AC ==,3AH ∴=,2CH EF AC AH ∴==−=,设CD x =,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)2x x =−+, 解得52x =,52CD ∴=, 当点D 在EB 上时,同理可得538CH AC AH =+=+=,设CD DF x ==,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)8x x −+=,解得10x =,10CD ∴=,当90DFE ∠=︒时,由勾股定理得AE设CD DF x ==,则520x +=,x ∴,CD ∴=;当90FDE ∠=︒时,则45ADC ADF ∠=∠=︒,5CD AC ∴==,综上:52CD =或或5或10,故答案为:52或或5或10.【点睛】本题是三角形综合题,主要考查了翻折的性质,直角三角形的性质,勾股定理,等腰直角三角形的判定与性质等知识,利用等积法求垂线段的长是解题的关键.。
最新成都八年级下期末数学B卷几何压轴题汇编三(含答案)

最新成都八年级下期末数学B卷几何压轴题汇编三40.如图,已知平面直角坐标系中,A(1,0)、C(0,2),现将线段CA绕A点顺时针旋转90°得到点B,连接AB(1)求出直线BC的解析式;(2)若动点M从点C出发,沿线段CB以每分钟个单位的速度运动,过M作MN∥AB交y轴于N,连接AN设运动时间为t分钟,当四边形ABMN为平行四边形时,求t的值.(3)P为直线BC上一点,在坐标平面内是否存在一点Q使得以O、B、P、Q为顶点的四边形为菱形?若存在,求出此时Q的坐标;若不存在请说明理由.41.已知直线y=﹣x+6与x轴,y轴分别相交于点A,B,将∠OBA对折,使点O的对应点E落在直线AB上,折痕交x轴于点C.(1)求点C的坐标;(2)若已知第四象限内的点D(,﹣),在直线BC上是否存在点P,使得四边形OP AD为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)设经过点D(,﹣)且与x轴垂直的直线与直线BC的交点为F,Q为线段BF上一点,求|QA﹣QO|的取值范围.42.如图1,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=2AE=4.将正方形AEFG绕点A 按逆时针方向旋转α(0°≤α≤60°).(1)如图2,当α>0°时,求证:△DAG≌△BAE;(2)在旋转的过程中,设BE的延长线交直线DG于点P.①如果存在某时刻使得BF=BC,请求出此时DP的长;②若正方形AEFG绕点A按逆时针方向旋转了60°,求旋转过程中点P运动的路线长.43.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F(1)如图1,求证:DE=DF;(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E是AP的中点;(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG、BH,若BG=2,AB=6,求线段PH的长.44.如图1,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D 的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.45.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B.点C坐标是(0,1),连接AC,过点C作CE⊥AB于点E.(1)求CE的长度.(2)如图2,点D为线段EA上一动点(不与E、A重合),连接CD并延长至点F,使DC=DF,作点F关于AB的对称点G,连接DG,CG,FG,线段FG交AB于点H,AC交DG于点M.①求证:;②当∠CAB=2∠F时,求线段AD的长度.46.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG、CG.(1)如图1,若点E在CB边的延长线上时,延长线段EG,CD相交于点M,求证:GE=GM,CE=CM.(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置时,延长EG到M,使GE=GM,连接MD,MC.①求证:∠EBC=∠MDC;②判断EG与CG的关系并证明.47.如图,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG.(1)如图1,若在旋转过程中,点E落在对角线AC上,AF,EF分别交DC于点M,N.①求证:MA=MC;②求MN的长;(2)如图2,在旋转过程中,若直线AE经过线段BG的中点P,连接BE,GE,求△BEG的面积48.如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于C,且△ABC面积为10.(1)求点C的坐标及直线BC的解析式;(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作正方形FGQP,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是否存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.49.如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′.使点B的对应点B′落在AC上,B'C'交AD于点E,在B′C′上取点F,使B′F=AB.(1)求证:AE=C'E;(2)求∠BFB'的度数;(3)若AB=2,求BF的长.50.如图1.在边长为10的正方形ABCD中,点M在边AD上移动(点M不与点A,D重合),MB的垂直平分线分别交AB,CD于点E,F,将正方形ABCD沿EF所在直线折叠.则点B的对应点为点M,点C 落在点N处,MN与CD交于点P,(1)若AM=4,求BE的长;(2)随着点M在边AD上位置的变化,∠MBP的度数是否发生变化?若变化,请说明理由;若不变,请求出∠MBP的度数;(3)随着点M在边AD上位置的变化,点P在边CD上位置也发生变化,若点P恰好为CD的中点(如图2),求CF的长.51.在矩形ABCD中,AB=12,BC=25,P是线段AB上一点(点P不与A,B重合),将△PBC沿直线PC折叠,顶点B的对应点是点G,CG,PG分别交线段AD于E,O.(1)如图1,若OP=OE,求证:AE=PB;(2)如图2,连接BE交PC于点F,若BE⊥CG.①求证:四边形BFGP是菱形;②当AE=9,求的值.52.如图,已知直线y=kx+4(k≠0)经过点(﹣1,3),交x轴于点A,y轴于点B,F为线段AB的中点,动点C从原点出发,以每秒1个位长度的速度沿y轴正方向运动,连接FC,过点F作直线FC的垂线交x轴于点D,设点C的运动时间为t秒.(1)当0<t<4时,求证:FC=FD;(2)连接CD,若△FDC的面积为S,求出S与t的函数关系式;(3)在运动过程中,直线CF交x轴的负半轴于点G,+是否为定值?若是,请求出这个定值;若不是,请说明理由.53.如图,△ABC与△ADE都为等腰直角三角形,∠ABC=∠ADE=90°,连接BD,EC,且F为EC的中点.(1)如图1,若D、A、C三点在同一直线上时,请判断DF与BF的关系,并说明理由;(2)如图2,将图1中的△ADE绕点A逆时针旋转m°(0<m<90),请判断(1)中的结论是否仍然成立?并证明你的判断;(3)在(2)下,若△DEF与△BCF的面积之和于△DBF的面积,请直接写出m的值.54.已知菱形ABCD的边长为5,其顶点都在坐标轴上,且点A坐标为(0,﹣3).(1)求点B的坐标及菱形ABCD的面积;(2)点P是菱形边上一动点,沿A→B→C→D运动(到达D点时停止)①如图1,当点P关于x轴对称的点Q恰好落在直线y=x﹣3上时,求点P的坐标.②探究:如图2,当P运动到BC,CD边时,作△ABP关于直线AP的对称图形为△AB′P,是否存在这样的P点,使点B′正好在直线y=x﹣3上?若存在,求出满足条件的点P坐标;若不存在,请说明理由.55.(1)如图1,正方形ABCD中,∠PCG=45°,且PD=BG,求证:FP=FC;(2)如图2,正方形ABCD中,∠PCG=45°,延长PG交CB的延长线于点F,(1)中的结论还成立吗?请说明理由;(3)在(2)的条件下,作FE⊥PC,垂足为点E,交CG于点N,连接DN,求∠NDC的度数.56.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.(1)求直线BC和AB的解析式;(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请直接写出这两点的坐标;若不存在,请说明理由.57.在正方形ABCD中,点P是射线BC上任意一点(不与点B、C重合),连接AP,过点P作AP的垂线交正方形的外角∠DCF的平分线于点E.(1)如图1,当点P在BC边上时,判断线段AP、PE的大小关系,并说明理由;(2)如图2,当点P在BC的延长线上时,(1)中结论是否成立,若成立,请证明;若不成立,请说明理由;(3)如图3,在(2)的条件下,连接AE交CD的延长线于点G,连接GP,请写出三条线段GP、BP、GD的数量关系并证明.58.已知如图,直线y=kx+b与x轴、y轴分别交于点A、B,与直线y=3x交于点C,且|OA﹣6|+=0,将直线y=kx+b沿直线y=3x折叠,与x轴交于点D,与y轴交于点E.(1)求直线y=kx+b的解析式及点C的坐标;(2)求△BCE的面积;(3)若点P是直线y=3x上的一个动点,在平面内是否存在一点Q,使以点A、C、P、Q为顶点的四边形是矩形?若存在,请直接写出点P、点Q的坐标;若不存在,请说明理由.59.在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.(1)求直线CD和直线OD的解析式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.60.菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.(1)如图1,求∠BGD的度数;(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4,求菱形ABCD的面积.参考答案41.已知直线y=﹣x+6与x轴,y轴分别相交于点A,B,将∠OBA对折,使点O的对应点E落在直线AB上,折痕交x轴于点C.(1)求点C的坐标;(2)若已知第四象限内的点D(,﹣),在直线BC上是否存在点P,使得四边形OP AD为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)设经过点D(,﹣)且与x轴垂直的直线与直线BC的交点为F,Q为线段BF上一点,求|QA﹣QO|的取值范围.【解答】解:(1)连接CE,则CE⊥AB,y=﹣x+6与x轴,y轴分别相交于点A,B,则点A、B的坐标分别为:(8,0)、(0,6),则AB=10,设:OC=a,则CE=a,BE=OB=6,AE=10﹣6=4,CA=8﹣a,由勾股定理得:CA2=CE2+AE2,即(8﹣a)2=a2+42,解得a=3,故点C(3,0);(2)不存在,理由:将点B、C的坐标代入一次函数表达式y=kx+b并解得:直线BC的表达式为:y=﹣2x+6,设点P(m,n),当四边形OP AD为平行四边形时,OA的中点即为PD的中点,即:m+=8,n﹣=0,解得:m=,n=,当x=时,y=﹣2x+6=1,故点P不在直线BC上,即在直线BC上不存在点P,使得四边形OP AD为平行四边形;(3)当x=时,y=﹣2x+6=﹣5,故点F(,﹣5),当点Q为AO的垂直平分线与直线BC的交点时,QO=QA,则|QA﹣QO|=0,当点Q在点B处时,|QA﹣QO|有最大值,此时:点A(8,0)、点O(0,0)、点Q(0,6),则AQ=10,QO=6,|QA﹣QO|=4,故|QA﹣QO|的取值范围为:0≤|QA﹣QO|≤4.42.如图1,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=2AE=4.将正方形AEFG绕点A 按逆时针方向旋转α(0°≤α≤60°).(1)如图2,当α>0°时,求证:△DAG≌△BAE;(2)在旋转的过程中,设BE的延长线交直线DG于点P.①如果存在某时刻使得BF=BC,请求出此时DP的长;②若正方形AEFG绕点A按逆时针方向旋转了60°,求旋转过程中点P运动的路线长.【解答】(1)证明:在正方形ABCD和正方形AEFG中,AD=AB,AG=AE,∠BAD=∠EAG=90°,∵∠BAE+∠EAD=∠BAD,∠DAG+∠EAD=∠EAG,∴∠BAE=∠DAG,在△DAG和△BAE中,,∴△DAG≌△BAE(SAS);∴BE=DG;(2)解:①∵AB=2AE=4,∴AE=2,由勾股定理得,AF=AE=2,∵BF=BC=4,∴AB=BF=4,∴△ABF是等边三角形,∵AE=EF,∴直线BE是AF的垂直平分线,设BE的延长线交AF于点O,交AD于点H,如图3所示:则OE=OA===,∴OB===,∵cos∠ABO==,cos∠ABH==,∴=,∴BH=,AH===,∴DH=AD﹣AH=4﹣,∵∠DHP=∠BHA,∠BAH=∠DPH=90°,∴△BAH∽△DPH,∴=,即:=,∴DP=﹣;②∵△DAG≌△BAE,∴∠ABE=∠ADG,∵∠BPD=∠BAD=90°,∴点P的运动轨迹为以BD为直径的,BD=AB=4,∵正方形AEFG绕点A按逆时针方向旋转了60°,∴∠BAE=60°,∵AB=2AE,∴∠BEA=90°,∠ABE=30°,∴B、E、F三点共线,同理D、F、G三点共线,∴P与F重合,∴∠ABP=30°,∴所对的圆心角为60°,∴旋转过程中点P运动的路线长为:=.43.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F(1)如图1,求证:DE=DF;(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E是AP的中点;(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG、BH,若BG=2,AB=6,求线段PH的长.【解答】证明:(1)∵四边形ABCD是正方形,∴AB=AD=CD,∠A=∠ADC=90°=∠BCD,∵将直线DE绕点D逆时针旋转90°,∴∠EDF=90°,∴∠ADC=∠EDF,∴∠ADE=∠CDF,且AD=CD,∠A=∠DCF=90°,∴△ADE≌△CDF(SAS),∴DE=DF,(2)如图2,连接EH,FH,∵点D关于直线EF的对称点为H,∴EH=DE,FH=DF,且DE=DF,∴EH=DE=FH=DF,∵DE=EH,DF=HF,EF=EF,∴△DEF≌△HEF(SSS)∴∠EHF=∠EDF=90°,且PH⊥CH,∴∠PHE=∠FHC,∵∠B=∠PHC=90°,∠BGP=∠CGH,∴∠BPG=∠HCG,∴∠EPH=∠HCF,且EH=HF,∠EHP=∠CHF,∴△EHP≌△FHC(AAS)∴EP=CF,∵△ADE≌△CDF,∴AE=CF,∴AE=EP,∴点E是AP中点,(3)如图3,连接PC,EH,FH,过点E作EK∥BC,交AC于K,∵EK∥BC,∴∠AKE=∠ACB=45°=∠EAK,∠AEK=∠ABC=90°,∠EKG=∠GCF,∴AE=EK,∵AE=CF,∴EK=CF,且∠EKG=∠GCF,∠EGK=∠CGF,∴△EKG≌△FCG(AAS)∴EG=FG,∵BG=2,∴EG=FG=BG=2,∴EF=4,∵EF2=BE2+BF2,∴80=(6﹣AE)2+(6+AE)2,∴AE=2∴BP=AB﹣AE﹣EP=2∴PC===2由(2)可知△EHP≌△FHC,∴PH=CH,且PH⊥CH∴PC=PH∴PH=244.如图1,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D 的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.【解答】(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,∴∠OBC=∠ECD.∵将线段CB绕着点C顺时针旋转90°得到CD,∴BC=CD.在△BOC和△CED中,,∴△BOC≌△CED(AAS).(2)解:∵直线y=﹣x+3与x轴、y轴相交于A、B两点,∴点B的坐标为(0,3),点A的坐标为(6,0).设OC=m,∵△BOC≌△CED,∴OC=ED=m,BO=CE=3,∴点D的坐标为(m+3,m).∵点D在直线y=﹣x+3上,∴m=﹣(m+3)+3,解得:m=1,∴点D的坐标为(4,1),点C的坐标为(1,0).∵点B的坐标为(0,3),点C的坐标为(1,0),∴直线BC的解析式为y=﹣3x+3.设直线B′C′的解析式为y=﹣3x+b,将D(4,1)代入y=﹣3x+b,得:1=﹣3×4+b,解得:b=13,∴直线B′C′的解析式为y=﹣3x+13,∴点C′的坐标为(,0),∴CC′=﹣1=,∴△BCD平移的距离为.(3)解:设点P的坐标为(0,m),点Q的坐标为(n,﹣n+3).分两种情况考虑,如图3所示:①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P1的坐标为(0,);当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P2的坐标为(0,);②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P的坐标为(0,).综上所述:存在,点P的坐标为(0,)或(0,).45.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B.点C坐标是(0,1),连接AC,过点C作CE⊥AB于点E.(1)求CE的长度.(2)如图2,点D为线段EA上一动点(不与E、A重合),连接CD并延长至点F,使DC=DF,作点F关于AB的对称点G,连接DG,CG,FG,线段FG交AB于点H,AC交DG于点M.①求证:;②当∠CAB=2∠F时,求线段AD的长度.【解答】解:(1)∵直线交x轴于点A,交y轴于点B ∴A(﹣3,0),B(0,4)∴OA=3,OB=4,AB=5∵C(0,1)∴BC=3∵S△ABC==∴CE==(2)①∵F点与G点关于直线AB成轴对称∴直线AB是线段FG的垂直平分线,HF=HG∴DF=DG又∵DF=DC∴DF=DG=DC∴∠FGC=90°又∵∠HEC=∠EHG=∠HGC=90°∴四边形ECGH是矩形.∴EH=CG又∵DF=DC,HF=HG据中位线定理得DH=CG=HG=DE即DE=CG(也可以证△FDH≌△CDE得DH=DE)②∵直线AB是线段FG的垂直平分线,DF=DG∴∠FDH=∠GDH=∠EDC,且∠CDG=∠F+∠FGD=2∠F又∵∠CAB=2∠F∴∠CAB=∠CDG∴180°﹣∠ADG﹣∠CAB=180°﹣∠ADG﹣∠CDG∴∠AMD=∠BDC=∠ADG∴AD=AM∵矩形ECGH中CG∥AB易得∠CGM=∠ADM=∠AMD=∠CMG∴CM=CG设AD=AM=a,则CM=CG=﹣a∴DE=CG=∴AE=AD+DE=a+=∵Rt△AEC中,∠AEC=90°,∴AE2+CE2=AC2即()2+()2=()2解得:AD=a=.46.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG、CG.(1)如图1,若点E在CB边的延长线上时,延长线段EG,CD相交于点M,求证:GE=GM,CE=CM.(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置时,延长EG到M,使GE=GM,连接MD,MC.①求证:∠EBC=∠MDC;②判断EG与CG的关系并证明.【解答】(1)证明:如图1中,∵四边形ABCD是正方形,∴∠BCD=90°,BC=CD,∵∠CEF=90°,∴∠CEF+∠ECM=180°,∴EF∥CD,∴∠FEG=∠M,又∵G为DF中点,∴DG=FG∵∠FGE=∠DGM,∴△FGE≌△DGM(AAS),∴EG=GM,EF=DM,∵EF=BE,∴EF=DM=BE,∵CB=CD,∴BE+BC=CD+DM,∴CE=CM.(2)延长MD,BE交于点N,连接EC,①∵EG=MG,DG=FG,∠EGF=∠MGD,∴△EFG≌△MDG(SAS),∴∠EFG=∠MDG,∴EF∥DM,∴∠END=∠BEF=90°=∠BCD,∴∠CBN+∠NDC=∠CDM+∠NDC=180°,∴∠CBE=∠CDM.②结论:CG=EG,CG⊥EG.理由:∵△EFG≌△MDG,∴EF=DM=EB,又∵BC=DC,∠CBE=∠CDM,∴△CBE≌△CDM(SAS),∴EC=MC,且∠BCE=∠DCM,∴∠ECM=∠BCD=90°,∵G为EM中点,∴CG=EG,CG⊥EG.47.如图,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG.(1)如图1,若在旋转过程中,点E落在对角线AC上,AF,EF分别交DC于点M,N.①求证:MA=MC;②求MN的长;(2)如图2,在旋转过程中,若直线AE经过线段BG的中点P,连接BE,GE,求△BEG的面积【解答】(1)①证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠DCA=∠BAC,由旋转的性质得:∠F AE=∠BAC,∴∠DCA=∠F AE,∴MA=MC;②解:设MA=MC=x,则DM=8﹣x,在Rt△ADM中,62+(8﹣x)2=x2,解得:x=,在Rt△AEF中,AF===10,∴MF=AF﹣AM=,∵∠AEF=∠CEN=90°,∴∠MCA+∠CNE=∠MAC+∠AEF=90°,又∵∠MCA=∠MAC,∴∠AFE=∠CNE=∠MNF,∴MN=MF=;(2)解:分情况讨论:①如图2所示:过点B作BH⊥AE于H,则∠GAP=∠BHP=90°,在△HBP和△AGP中,,∴△HBP≌△AGP(AAS),∴AP=HP,BH=AG=6,在Rt△ABH中,AH===2,∴AP=AH=,∴PE=AE﹣AP=8﹣,∴△BEG的面积=2△GPE的面积=2××6×(8﹣)=48﹣6;②如图3所示:同①得:AH=2,AP=,∴PE=8+,∴△BEG的面积=2△GPE的面积=2××6×(8+)=48+6;综上所述,△BEG的面积为48﹣6或48+6.48.如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于C,且△ABC面积为10.(1)求点C的坐标及直线BC的解析式;(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作正方形FGQP,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是否存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.【解答】解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,∴A(﹣2,0),B(0,4),∴OA=2,OB=4,∵S△ABC=•AC•OB=10,∴AC=5,∴OC=3,∴C(3,0),设直线BC的解析式为y=kx+b,则有,∴.∴直线BC的解析式为y=﹣x+4.(2)∵F A=FB,A(﹣2,0),B(0,4),∴F(﹣1,2),设G(0,n),①当n>2时,如图2﹣1中,点Q落在BC上时,过G作直线平行于x轴,过点F,Q作该直线的垂线,垂足分别为M,N.∵四边形FGQP是正方形,易证△FMG≌△GNQ,∴MG=NQ=1,FM=GN=n﹣2,∴Q(n﹣2,n﹣1),∵点Q在直线y=﹣x+4上,∴n﹣1=﹣(n﹣2)+4,∴n=,∴G(0,).②当n<2时,如图2﹣2中,同法可得Q(2﹣n,n+1),∵点Q在直线y=﹣x+4上,∴n+1=﹣(2﹣n)+4,∴n=﹣1,∴G(0,﹣1).综上所述,满足条件的点G坐标为(0,)或(0,﹣1).(3)如图3中,设M(m,﹣m+4),∵S△AMB=S△AOB,∴S△ABC﹣S△AMC=S△AOB,∴×5×4﹣×5×(﹣m+4)=×2×4,∴m=,∴M(,),∴直线AM的解析式为y=x+,作BE∥OC交直线AM于E,此时E(,4),当CD=BE时,可得四边形BCDE,四边形BECD1是平行四边形,可得D(,0),D1(﹣,0),当点E在第三象限,根据BC=DE,可得D2(﹣,0)也符合条件,综上所述,满足条件的点D的坐标为(,0)或(﹣,0)或(﹣,0).49.如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′.使点B的对应点B′落在AC上,B'C'交AD于点E,在B′C′上取点F,使B′F=AB.(1)求证:AE=C'E;(2)求∠BFB'的度数;(3)若AB=2,求BF的长.【解答】(1)证明:∵在Rt△ABC中,AC=2AB,∴∠ACB=∠AC′B′=30°,∠BAC=60°,由旋转可得:AB′=AB,∠B′AC′=∠BAC=60°,∴∠EAC′=∠AC′B′=30°,∴AE=C′E;(2)解:由(1)得到△ABB′为等边三角形,∴∠AB′B=60°,即∠BB'F=∠AB'B+∠AB'F=150°,∵BB'=B'F,∴∠FBB′=∠B'FB=15°;(3)解:连接AF,过A作AM⊥BF,可得△AB′F是等腰直角三角形,△AB′B为等边三角形,∴∠AFB′=45°,∠BB′F=150°,∵BB′=B′F,∴∠B′FB=∠B′BF=15°,∴∠AFM=30°,∠ABF=45°,在Rt△AMF中,AM=BM=AB•cos∠ABM=2×=2,在Rt△AMF中,MF=AM=2,则BF=2+2.50.如图1.在边长为10的正方形ABCD中,点M在边AD上移动(点M不与点A,D重合),MB的垂直平分线分别交AB,CD于点E,F,将正方形ABCD沿EF所在直线折叠.则点B的对应点为点M,点C 落在点N处,MN与CD交于点P,(1)若AM=4,求BE的长;(2)随着点M在边AD上位置的变化,∠MBP的度数是否发生变化?若变化,请说明理由;若不变,请求出∠MBP的度数;(3)随着点M在边AD上位置的变化,点P在边CD上位置也发生变化,若点P恰好为CD的中点(如图2),求CF的长.【解答】解:(1)如图1中,∵四边形ABCD是正方形,∴∠A=90°,AB=AD=10,由翻折可知:EB=EM,设EB=EM=x,在Rt△AEM中,∵EM2=AM2+AE2,∴x2=42+(10﹣x)2,∴x=.∴BE=.(2)如图1﹣1中,作BH⊥MN于H.∵EB=EM,∴∠EBM=∠EMB,∵∠EMN=∠EBC=90°,∴∠NMB=∠MBC,∵AD∥BC,∴∠AMB=∠MBC,∴∠AMB=∠BMN,∵BA⊥MA,BH⊥MN,∴BA=BH,∵∠A=∠BHM=90°,BM=BM,BA=BH,∴Rt△BAM≌△BHM(HL),∴∠ABM=∠MBH,同法可证:∠CBP=∠HBP,∵∠ABC=90°,∴∠MBP=∠MBH+∠PBH=∠ABH+∠CBH=∠ABC=45°.(3)如图2中,作FG⊥AB于G.则四边形BCFG是矩形,FG=BC,CF=BG.设AM=x,∵PC=PD=5,∴PM=x+5,DM=10﹣x,在Rt△PDM中,(x+5)2=(10﹣x)2+25,∴x=,∴AM=,设EB=EM=m,在Rt△AEM中,则有m2=(10﹣m)2+()2,∴m=,∴AE=10﹣=,∵AM⊥EF,∴∠ABM+∠GEF=90°,∠GEF+∠EFG=90°,∴∠ABM=∠EFG,∵FG=BC=AB,∠A=∠FGE=90°,∴△BAM≌△FGE(AAS),∴EG=AM=,∴CF=BG=AB﹣AE﹣EG=10﹣﹣=.51.在矩形ABCD中,AB=12,BC=25,P是线段AB上一点(点P不与A,B重合),将△PBC沿直线PC折叠,顶点B的对应点是点G,CG,PG分别交线段AD于E,O.(1)如图1,若OP=OE,求证:AE=PB;(2)如图2,连接BE交PC于点F,若BE⊥CG.①求证:四边形BFGP是菱形;②当AE=9,求的值.【解答】证明:(1)∵四边形ABCD是矩形∴AB=CD,AD=BC,AD∥BC,∠A=∠B=90°∵将△PBC沿直线PC折叠,∴PB=PG,∠B=∠G=90°∵∠AOP=∠GOE,OP=OE,∠A=∠G=90°∴△AOP≌△GOE(AAS)∴AO=GO∴AO+OE=GO+OP∴AE=GP,∴AE=PB,(2)①∵△BPC沿PC折叠得到△GPC,∴∠PGC=∠PBC=90°,∠BPC=∠GPC,BP=PG,BF=FG∵BE⊥CG,∴BE∥PG,∴∠GPF=∠PFB,∴∠BPF=∠BFP,∴BP=BF∴BP=BF=PG=GF∴四边形BFGP是菱形;②∵AE=9,CD=AB=12,AD=BC=GC=25,∴DE=AD﹣AE=16,BE==15,在Rt△DEC中,EC==20∵BE∥PG∴△CEF∽△CGP∴∴==∴设EF=4x,PG=5x,∴BF=BP=GF=5x,∵BF+EF=BE=15∴9x=15∴x=∴BF=BP=5x=,在Rt△BPC中,PC==∴==52.如图,已知直线y=kx+4(k≠0)经过点(﹣1,3),交x轴于点A,y轴于点B,F为线段AB的中点,动点C从原点出发,以每秒1个位长度的速度沿y轴正方向运动,连接FC,过点F作直线FC的垂线交x轴于点D,设点C的运动时间为t秒.(1)当0<t<4时,求证:FC=FD;(2)连接CD,若△FDC的面积为S,求出S与t的函数关系式;(3)在运动过程中,直线CF交x轴的负半轴于点G,+是否为定值?若是,请求出这个定值;若不是,请说明理由.【解答】(1)证明:连接OF,如图1所示:∵直线y=kx+4(k≠0)经过点(﹣1,3),∴﹣k+4=3,解得:k=1,∴直线y=x+4,当y=0时,x=﹣4;当x=0时,y=4;∴A(﹣4,0),B(0,4),∴OA=OB=4,∵∠AOB=90°,∴△AOB是等腰直角三角形,∴∠CBF=45°,∵F为线段AB的中点,∴OF=AB=BF,OF⊥AB,∠DOF=∠AOB=45°=∠CBF,∴∠OFB=90°,∵DF⊥CF,∴∠DFC=90°,∴∠OFD=∠BFC,在△BCF和△ODF中,,∴△BCF≌△ODF(ASA),∴FC=FD;(2)解:①当0<t<4时,连接OF,如图2所示:由题意得:OC=t,BC=4﹣t,由(1)得:△BCF≌△ODF,∴BC=OD=4﹣t,∴CD2=OD2+OC2=(4﹣t)2+t2=2t2﹣8t+16,∵FC=FD,∠DFC=90°,∴△FDC是等腰直角三角形,∴FC2=CD2,∴△FDC的面积S=FC2=×CD2=(2t2﹣8t+16)=t2﹣2t+4;②当t≥4时,连接OF,如图3所示:由题意得:OC=t,BC=t﹣4,由(1)得:△BCF≌△ODF,∴BC=OD=t﹣4,∴CD2=OD2+OC2=(t﹣4)2+t2=2t2﹣8t+16,∵FC=FD,∠DFC=90°,∴△FDC是等腰直角三角形,∴FC2=CD2,∴△FDC的面积S=FC2=×CD2=(2t2﹣8t+16)=t2﹣2t+4;综上所述,S与t的函数关系式为S=t2﹣2t+4;(3)解:+为定值;理由如下:①当0<t<4时,如图4所示:当设直线CF的解析式为y=ax+t,∵A(﹣4,0),B(0,4),F为线段AB的中点,∴F(﹣2,2),把点F(﹣2,2)代入y=ax+t得:﹣2a+t=2,解得:a=(t﹣2),∴直线CF的解析式为y═(t﹣2)x+t,当y=0时,x=,∴G(,0),∴OG=,∴+=+==;②当t≥4时,如图5所示:同①得:+=+==;综上所述,+为定值.53.如图,△ABC与△ADE都为等腰直角三角形,∠ABC=∠ADE=90°,连接BD,EC,且F为EC的中点.(1)如图1,若D、A、C三点在同一直线上时,请判断DF与BF的关系,并说明理由;(2)如图2,将图1中的△ADE绕点A逆时针旋转m°(0<m<90),请判断(1)中的结论是否仍然成立?并证明你的判断;(3)在(2)下,若△DEF与△BCF的面积之和于△DBF的面积,请直接写出m的值.【解答】解:(1)如图1中,结论:DF=BF,DF⊥BF.理由:在Rt△BEC中,∵∠EBC=90°,EF=FC,∴BF=EC,在Rt△DCE中,∵∠EDC=90°,EF=FC,∴DF=EC,∴DF=BF,∵∠FCB=∠FBC,∠FED=∠FDE,∴∠BFC+∠DFE=(180°﹣2∠FCB)+(180°﹣2∠FDE)=360°﹣2(∠FCB+∠FED)=360°﹣2(45°+∠BEC+∠FCB)=360°﹣270°=90°,∴∠DFB=90°,即DF⊥BF.(2)结论成立.理由:如图2中,如图作CM∥DE交DF的延长线于M,延长DA交MC的延长线于N,DN交BC于O.∵DE∥CM,∴∠FED=∠FCM,∵∠DFE=∠MFC,EF=CF,∴△DFE≌△MFC,∴DF=FM,DE=CM=AD,∵∠EDN+∠N=180°,∠EDN=90°,∴∠N=∠ABO=90°,∵∠AOB=∠CON,∴∠DAB=∠ACM,∵BA=BC,AD=CM,∴△BAD≌△BCM,∴BD=BM,∠DBA=∠CBM,∴∠DBM=∠ABC=90°,∴△DBM是等腰直角三角形,∵DF=FM,∴BF⊥DF,BF=DF=FM.(3)如图2中,由(2)可知:△DFE≌△MFC,△BDM是等腰直角三角形,DF=FM,∴S△DEF+S△BFC=S△FCM+S△BCF=S四边形BFMC,S△BDF=S△BFM,∴当B、C、M共线时,△DEF与△BCF的面积之和于△DBF的面积,此时旋转角为45°,∴m=45°.54.已知菱形ABCD的边长为5,其顶点都在坐标轴上,且点A坐标为(0,﹣3).(1)求点B的坐标及菱形ABCD的面积;(2)点P是菱形边上一动点,沿A→B→C→D运动(到达D点时停止)①如图1,当点P关于x轴对称的点Q恰好落在直线y=x﹣3上时,求点P的坐标.②探究:如图2,当P运动到BC,CD边时,作△ABP关于直线AP的对称图形为△AB′P,是否存在这样的P点,使点B′正好在直线y=x﹣3上?若存在,求出满足条件的点P坐标;若不存在,请说明理由.【解答】解:(1)如图1中,∵四边形ABCD菱形,∴AB=BC=CD=AD=5,OA=OC,OB=OD,∵A(0,﹣3),∴OA=3,在Rt△AOD中,OD==4,∴BD=8,AC=6,∴S菱形ABCD=×BD×AC=24.(2)①如图2中,由题意B(4,0),C(0,3),∴直线BC的解析式为y=﹣x+3,由解得,∴Q(,),∴当点P坐标为(,﹣)时,点P关于x轴对称的点Q恰好落在直线y=x﹣3上,当点P′与C重合时,点P′关于x轴对称的点Q′恰好落在直线y=x﹣3上,此时P′(0,3),综上所述,满足条件的点P坐标为(,﹣)或(0,3);②如图3中,当AP平分∠BAQ时,满足条件,由题意A(0,﹣3),B(4,0),Q(,),∴AQ=,BQ=,∵=(角平分线性质定理,可以用面积法证明),∴=,∴PB=×=,∴可得P(,).当AP′⊥AP时,B″在直线AQ上,此时直线AP′的解析式为y=﹣x﹣3,直线CD的解析式为y=x+3,由,解得,∴P′(﹣,),综上所述,满足条件的点P坐标为(,)或(﹣,).55.(1)如图1,正方形ABCD中,∠PCG=45°,且PD=BG,求证:FP=FC;(2)如图2,正方形ABCD中,∠PCG=45°,延长PG交CB的延长线于点F,(1)中的结论还成立吗?请说明理由;(3)在(2)的条件下,作FE⊥PC,垂足为点E,交CG于点N,连接DN,求∠NDC的度数.【解答】解:(1)∵四边形ABCD是正方形,∴BC=CD,∠BCD=∠CBG=∠D=90°,∵BG=DP,∴△BCG≌△DCP(SAS),∴CP=CG,∠BCG=∠DCP,∵∠PCG=45°,∴∠BCG+∠DCP=45°,∴∠DCP=∠BCG=22.5°,∴∠PCF=∠PCG+∠BCG=67.5°,在△PCG中,CP=CG,∠PCG=45°,∴∠CPG=(180°﹣45°)=67.5°=∠PCF,∴PF=CF;(2)如图2,∵四边形ABCD是正方形,∴∠CBG=∠BCD=90°,过点C作CH⊥CG交AD的延长线于H,∴∠CDH=90°=∠HCG.∴∠BCG=∠DCH,∴△BCG≌△DCH(ASA),∴CG=CH,∵∠HCG=90°,∠PCG=45°,∴∠PCH=45°=∠PCG,∵CP=CP,∴△PCH≌△PCG(SAS),∴∠CPG=∠CPH,∵∠CPD+∠DCP=90°,∴∠CPF+∠DCP=90°,∵∠PCF+∠DCP=90°,∴∠CPF=∠PCF,∴PF=CF;(3)如图3,连接PN,由(2)知,PF=CF,∵EF⊥CP,∴PE=CE,∴EF是线段CP的垂直平分线,∴PN=CN,∴∠CPN=∠PCN,∵∠PCN=45°,∴∠CPN=45°,∴∠CNP=90°,∵PE=CE,∴EN=CP,在Rt△CDP中,CE=PE,∴DE=CE=CP,∴EN=DE,∴∠DNE=∠NDE,设∠DCP=α,∴∠CED=∠DCP=α,∴∠DEP=2α,∵∠PEF=90°,∴∠DEN=90°+2α,∴∠NDE=(180°﹣∠DEN)=45°﹣α,∴∠NDC=∠NDE+∠CDE=45°﹣α+α=45°.56.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.(1)求直线BC和AB的解析式;(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请直接写出这两点的坐标;若不存在,请说明理由.【解答】解:(1)在Rt△AOB中,∵OA=2,∠ABO=30°,∴OB=2,在Rt△OBC中,∵∠BCO=30°,OB=2,∴OC=6,∴B(0,2),C(﹣6,0),设直线AB的解析式为y=kx+b,则有,解得,∴直线AB的解析式为y=﹣x+2,设直线BC的解析式为y=k′x+b′则有,解得,∴直线BC的解析式为y=x+2.(2)如图1中,根据对称性可知,当点F与O重合时,∠EF′D=∠EBD=90°,此时F′(0,0),设DE交OB于K,作FH⊥DE于H.当△EFD≌△DF′E时,∠EFD=∠DF′E=90°,易证DK=EH=1,DE=AC=4,∴KH=OF=4﹣2=2,∴F(﹣2,0),综上所述,满足条件的点F坐标为(﹣2,0)或(0,0).(3)如图2中,∵B(0,2),C(﹣6,0),∴BC=4,当BC为正方形BCMN的边时,M(﹣6﹣2,6),N(﹣2,2+6)或M′(2﹣6,﹣6),N′(2,2﹣6).当BC为正方形的对角线时,M″(﹣3﹣,3+),N″(﹣3,﹣3).57.在正方形ABCD中,点P是射线BC上任意一点(不与点B、C重合),连接AP,过点P作AP的垂线交正方形的外角∠DCF的平分线于点E.(1)如图1,当点P在BC边上时,判断线段AP、PE的大小关系,并说明理由;(2)如图2,当点P在BC的延长线上时,(1)中结论是否成立,若成立,请证明;若不成立,请说明理由;(3)如图3,在(2)的条件下,连接AE交CD的延长线于点G,连接GP,请写出三条线段GP、BP、GD的数量关系并证明.【解答】解:(1)如图1,在正方形的边AB上取一点H,使BH=BP,∵四边形ABCD是正方形,∴∠ABC=∠DCF=90°,AB=CB,∴AH=PC,∠BHP=45°,∴∠AHP=135°,∵CE是∠DCF的平分线,∴∠ECF=45°,∴∠PCE=135°,∴∠AHP=∠PCE,∵AP⊥PE,∴∠APB+∠EPC=90°,∵∠APB+∠BAP=90°,∴∠BAP=∠CPE,在△AHP和△PCE中,,∴△AHP≌△PCE(ASA),∴AP=PE;(2)AP=PE,理由:如图2,∵四边形ABCD是正方形,∴∠B=∠DCF=90°,AB=AC,在BA的延长线上取一点H,使BH=BP,∴AH=CP,在△HBP中,BH=BP,∴∠BHP=45°,∵CE是∠DCF的平分线,∴∠PCE=45°,∴∠AHP=∠PCE=45°,∵AP⊥PE,∴∠EPF+∠APB=90°,。
八年级下册数学期末压轴题汇总(含解析)

(近三年)长春市八年级下数学期末压轴题(23.24题)长春市绿园区2020.7八下数学期末试题:24.(10分)如图,在矩形ABCD 中,AB=4,BC=10,E 、F 分别为BC 、AD 的中点,点P 从点A 出发,以每秒2个单位长度的速度沿AD 向终点D 速运动,作PQ ⊥BC 于Q ,当点P 不与点F 重合时,设四边形PQEF 的面积为S ,点P 的运动时间为t(秒)(1)当点P 与点D 重合时,求t 的值(2)用含t 的代数式表示线段PF (3)求S 与t 之间的函数关系式(4)当四边形PQEF 的对角线互相垂直时,直接写出的值24.(12分)如图,在平面直角坐标系中,A(-2,1),B(1,1).直线y =kx +3与y 轴相交于点C(1)在平面直角坐标系中标记出点C 的位置(2)当直线y =kx +3与直线y =2x 平行时,k 的值为;(3)当直线y =kx +3恰好经过点A 时,求直线y =kx +3的函数关系式;(4)当直线y =kx +3与线段AB 有公共点时,直接写出k 的取值范围。
B A PFDQE C01234-1-2-3-4xyAB -2-3-41234-1答案:23.(1)由题意,得2t =10(1分)t =5(2分)(2)当0≤t <25时,PF =5-2t 当25<t ≤5时,PF =2t -5(5分)(3)当0≤t <25时,S =20-8t当25<t ≤5时,S =8t -20(8分)(4)t =21或t =29(10分)评分说明:第(2)问写成PF =∣5-2t ∣或PF=∣2t -5∣扣1分第(2)间写成当0≤t ≤25一时,PF =5-2t 当25<t ≤5时,PF =2t -5不扣分第(2)、(3)问两个关系式各1分,取值范围共1分24.(1)点C 标记在(0,3)的位置(2分)(2)2(4分)(3)把(-2,1)代入y =kx +3得1=-2k +3(6分)解,得k =1(8分)∴y =x +3(10分)(4)k ≤-2或k ≥1(12分)评分说明:第(1)问只要位置标记正确即可给分长春市朝阳区2020.7数学八下期末试题23.(10分)如图在Rt ∆ABC 中∠C =90º,过点A 作线段AD 平行射线BC ,AB=10,BC=6,AD=15。
2023-2024学年八年级数学下册 专题04 勾股定理常考压轴题汇总(解析版)

专题04勾股定理常考压轴题汇总一.选择题(共23小题)1.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成一个大正方形.如图,直角三角形的直角边长为a、b,斜边长为c.若b﹣a=2,c=10,则a+b的值为()A.12B.14C.16D.18【答案】B【解答】解:由图可得,a2+b2=c2,∴且a、b均大于0,解得,∴a+b=6+8=14,故选:B.2.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是()A.B.C.D.【答案】B【解答】解:第一种情况:把我们所看到的前面和上面组成一个平面,则这个长方形的长和宽分别是6和3,则所走的最短线段是=3;第二种情况:把我们看到的左面与上面组成一个长方形,则这个长方形的长和宽分别是5和4,所以走的最短线段是=;第三种情况:把我们所看到的前面和右面组成一个长方形,则这个长方形的长和宽分别是7和2,所以走的最短线段是=;三种情况比较而言,第二种情况最短.所以它需要爬行的最短路线的长是,故选:B.3.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为()A.S1+S2+S3=S4B.S1+S2=S3+S4C.S1+S3=S2+S4D.不能确定【答案】C【解答】解:如图,设Rt△ABC的三条边AB=c,AC=b,BC=a,∵△ACG,△BCH,△ABF是等边三角形,∴S1=S△ACG﹣S5=b2﹣S5,S3=S△BCH﹣S6=a2﹣S6,∴S1+S3=(a2+b2)﹣S5﹣S6,∵S2+S4=S△ABF﹣S5﹣S6=c2﹣S5﹣S6,∵c2=a2+b2,∴S1+S3=S2+S4,故选:C.4.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI 上,若AC+BC=6,空白部分面积为10.5,则AB的长为()A.3B.C.2D.【答案】B【解答】解:∵四边形ABGF是正方形,∴∠FAB=∠AFG=∠ACB=90°,∴∠FAC+∠BAC=∠FAC+∠ABC=90°,∴∠FAC=∠ABC,在△FAM与△ABN中,,∴△FAM≌△ABN(ASA),=S△ABN,∴S△F AM=S四边形FNCM,∴S△ABC∵在△ABC中,∠ACB=90°,∴AC2+BC2=AB2,∵AC+BC=6,∴(AC+BC)2=AC2+BC2+2AC•BC=36,∴AB2+2AC•BC=36,=10.5,∵AB2﹣2S△ABC∴AB2﹣AC•BC=10.5,∴3AB2=57,解得AB=或﹣(负值舍去).故选:B.5.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.3cm2B.4cm2C.6cm2D.12cm2【答案】C【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=9cm=AE+DE=AE+BE.∴BE=9﹣AE,根据勾股定理可知AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选:C.6.如图,阴影部分表示以Rt△ABC的各边为直径向上作三个半圆所组成的两个新月形,面积分别记作S1和S2.若S1+S2=7,AC=3,则BC长是()A.3.5B.C.4D.5【答案】B【解答】解:以AC为直径的半圆的面积=×π×=π,同理:以BC为直径的半圆的面积=π,以AB为直径的半圆的面积=π,∴S1+S2=π+π+△ABC的面积﹣π,∵∠ACB=90°,∴AC2+BC2=AB2,∴S1+S2=△ABC的面积=AC•BC=7,∵AC=3,∴BC=.故选:B.7.如图,在长方体ABCD﹣EFGH盒子中,已知AB=4cm,BC=3cm,CG=5cm,长为10cm 的细直木棒IJ恰好从小孔G处插入,木棒的一端I与底面ABCD接触,当木棒的端点Ⅰ在长方形ABCD内及边界运动时,GJ长度的最小值为()A.(10﹣5)cm B.3cm C.(10﹣4)cm D.5cm【答案】A【解答】解:当GI最大时,GJ最小,当I运动到点A时,GI最大,此时GI=cm,而AC2=AB2+BC2=42+32=25,∴GI===5(cm),∴GJ长度的最小值为(10﹣5)cm.故选:A.8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,BC=10,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为()A.420B.440C.430D.410【答案】B【解答】解:如图,延长AB交KL于P,延长AC交LM于Q,由题意得,∠BAC=∠BPF=∠FBC=90°,BC=BF,∴∠ABC+∠ACB=90°=∠PBF+∠ABC,∴∠ACB=∠PBF,∴△ABC≌△PFB(AAS),同理可证△ABC≌△QCG(AAS),∴PB=AC=8,CQ=AB=6,∵图2是由图1放入长方形内得到,∴IP=8+6+8=22,DQ=6+8+6=20,∴长方形KLMJ的面积=22×20=440.故选:B.9.国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km【答案】D【解答】解:过点B作BC⊥AC,垂足为C.观察图形可知AC=9﹣7+4﹣1=5(km),BC=3+2+1=6(km),在Rt△ACB中,AB=(km).答:门口A到藏宝点B的直线距离是km,故选:D.10.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AB=9,BC=6,则BD的长为()A.3B.4C.5D.6【答案】B【解答】解:∵∠ACB=90°,AB=9,BC=6,∴,∵,∴AC•BC=AB•CD,,,∵CD⊥AB,∴∠CDB=90°,∴,故选:B.11.如图,某小区有一块长方形花圃,为了方便居民不用再走拐角,打算用瓷砖铺上一条新路,居民走新路比走拐角近()A.2m B.3m C.3.5m D.4m【答案】D【解答】解:根据勾股定理求得,AB==10(m),∴AC+BC﹣AB=6+8﹣10=4(m),故选:D.12.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是()A.148B.100C.196D.144【答案】A【解答】解:设将CA延长到点D,连接BD,根据题意,得CD=12×2=24,BC=7,∵∠BCD=90°,∴BC2+CD2=BD2,即72+242=BD2,∴BD=25,∴AD+BD=12+25=37,∴这个风车的外围周长是37×4=148.故选:A.13.如图,四边形ABCD中,AD⊥CD于点D,BC=2,AD=8,CD=6,点E是AB的中点,连接DE,则DE的最大值是()A.5B.C.6D.【答案】C【解答】解:如图,连接AC,取AC的中点为M,连接DM、EM,∵AD⊥CD,∴∠ADC=90°,∵AD=8,CD=6,∴AC=,∵M是AC的中点,∴DM=AC=5,∵M是AC的中点,E是AB的中点,∴EM是△ABC的中位线,∵BC=2,∴EM=BC=1,∵DE≤DM+EM(当且仅当点M在线段DE上时,等号成立),∴DE≤6,∴DE的最大值为6.故选:C.14.如图,长为8cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升3cm到D点,则橡皮筋被拉长了()A.2cm B.3cm C.4cm D.1cm【答案】A【解答】解:∵点C为线段AB的中点,∴AC=AB=4cm,在Rt△ACD中,CD=3cm;根据勾股定理,得:AD==5(cm);∵CD⊥AB,∴∠DCA=∠DCB=90°,在△ADC和△BDC中,,∴△ADC≌△BDC(SAS),∴AD=BD=5cm,∴AD+BD﹣AB=2AD﹣AB=10﹣8=2(cm);∴橡皮筋被拉长了2cm.故选:A.15.如图的数轴上,点A,C对应的实数分别为1,3,线段AB⊥AC于点A,且AB长为1个单位长度,若以点C为圆心,BC长为半径的弧交数轴于0和1之间的点P,则点P表示的实数为()A.B.C.D.【答案】A【解答】解:由题意可得∠BAC=90°,AB=1,AC=3﹣1=2,则CB==,那么点P表示的实数为3﹣,故选:A.16.“四千年来,数学的道理还是相通的”.运用祖冲之的出入相补原理也可证明勾股定理.若图中空白部分的面积是11,整个图形(连同空白部分)的面积是25,则大正方形的边长是()A.B.C.D.【答案】D【解答】解:如下图,设图中直角三角形的两条直角边长分别为a、b,斜边为c,∵图中空白部分的面积是11,整个图形(连同空白部分)的面积是25,∴可有,解得c2=18,解得或(不合题意,舍去),∴大正方形的边长是.故选:D.17.如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为()A.5米B.6米C.7米D.8米【答案】C【解答】解:∵△ABC是直角三角形,BC=3m,AB=5m∴AC==4(m),∴如果在楼梯上铺地毯,那么至少需要地毯为AC+BC=7米,故选:C.18.勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要细带.数学家欧几里得利用如图验证了勾股定理.以直角三角形ABC的三条边为边长向外作正方形ACKJ,正方形ABFE,正方形BCIH,连接AH.CF,具中正方形BCIH面积为1,正方形ABFE面积为5,则以CF为边长的正方形面积为()A.4B.5C.6D.10【答案】D【解答】解:过点C作CM⊥EF于点M,交AB于点N,∵正方形ABFE面积为5,正方形BCIH面积为1,∴CN⊥AB,BC=1,AB=MN=,BN=FN,∵△ABC是直角三角形,∠ACB=90°,∴AC===2,∴,即=CN,∴CN=,∴BN=FM===,∴CM=CN+MN==,∴CF=10,∴以CF为边长的正方形面积为10.故选:D.19.如图,Rt△ABC中,∠C=90°.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN.四块阴影部分的面积如图所示分别记为S、S1、S2、S3,若S=10,则S1+S2+S3等于()A.10B.15C.20D.30【答案】C【解答】解:如图,过E作BC的垂线交ED于D,连接EM.在△ACB和△BDE中,∠ACB=∠BDE=90°,∠CAB=∠EBD,AB=BD,∴△ACB≌△BND(AAS),同理,Rt△GDE≌Rt△HCB,∴GE=HB,∠EGD=∠BHC,∴FG=EH,∴DE=BC=CM,∵DE∥CM,∴四边形DCME是平行四边形,∵∠DCM=90°,∴四边形DCME是矩形,∴∠EMC=90°,∴E、M、N三点共线,∵∠P=∠EMH=90°,∠PGF=∠DGE=∠BHC=∠EHM,∴△PGF≌△MHE(AAS),∵图中S1=S Rt△EMH,S△BHC=S△EGD,∴S1+S3=S Rt△ABC.S2=S△ABC,∴S1+S2+S3=Rt△ABC的面积×2=20.故选:C.20.如图,在Rt△ABC中,∠C=90°,分别以AB、AC、BC为直径向外作半圆,它们的面积分别记作S1、S2、S3,若S1=25,S3=16,则S2为()A.9B.11C.32D.41【答案】A【解答】解:在Rt△ABC中,∠C=90°,∴AB2=AC2+BC2.∵S1=(AB)2π=AB2=25,∴AB2=25×.同理BC2=16×.∴AC2=AB2﹣BC2=25×﹣16×=9×.∴S1=(AC)2π=AC2=×9×=9.故选:A.21.如图,在Rt△ABC中,∠ACB=90°,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4.若已知S△ABC=S,则下列结论:①S4=S;②S2=S;③S1+S3=S2;④S1+S2+S3+S4=2.5S.其中正确的结论是()A.①②③B.①②④C.①③④D.②③④【答案】A【解答】解:由题意有Rt△EBD≌Rt△ABC,∴S4=S;故①正确;过F作AM的垂线交AM于N,由题意,得Rt△ANF≌Rt△ABC,Rt△NFK≌Rt△CAT,所以S2=S,故②正确;连接FP,FQ,由题意,可得△AQF≌△ACB,则F,P,Q三点共线,由Rt△NFK≌Rt△CAT可得Rt△FPT≌Rt△EMK,∴S3=S△FPT,可得Rt△AQF≌Rt△ACB,∴S1+S3=S Rt△AQF=S,故③正确;S1+S2+S3+S4=(S1+S3)+S2+S4+S Rt△ABC+S Rt△ABC=S Rt△ABC×3=S Rt△ABC=3S,故④不正确.故选:A.22.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为()尺.A.10B.12C.13D.14【答案】C【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),答:芦苇长13尺.故选:C.23.将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形ABCD和正方形EFGH.现将四个直角三角形的较长直角边分别向外延长,且A′E=ME.B′F =NF,C′G=PG,D′H=HQ,得到图2所示的“新型数学风车”的四个叶片,即△A′EF,△B′FG,△C′CH.△D′HE.若FM平分∠BFE,正方形ABCD和正方形EFGH 的边长比为1:5.若”新型数学风车”的四个叶片面积和是m,则正方形EFCH的面积是()A.B.C.3m D.【答案】B【解答】解:∵将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形ABCD和正方形EFCH.正方形ABCD和正方形EFGH的边长比为1:5.∴设正方形ABCD的边长为a,则正方形EFGH的边长为5a,设AE=BF=CG=DH=x,在△BEF中,BE2+BF2=EF2,即(x+a)2+x2=(5a)2,x2+ax﹣12a2=0,(x+4a)(x﹣3a)=0,x=﹣4a(舍去)或x=3a,∴BE=4a,BF=3a,EF=5a,∵FM平分∠BFE,∴△EMF边EF上的高为BM,+S△MBF=S△BEF,则S△BMF即,∴,∴BM=,∵A'E=ME=BE﹣BM=4a﹣a,若”新型数学风车”的四个叶片面积和是m,=S△EF A'=m,∴S△EMF∴,∴a m,∴a=∴EF=5a=,=EF=,∴S正方形EFCH故选:B.二.填空题(共14小题)24.如图①,四个全等的直角三角形与一个小正方形,恰好拼成一个大正方形,这个图形是由我国汉代数学家赵爽在为《周髀算经》作注时给出的,人们称它为“赵爽弦图”.如果图①中的直角三角形的长直角边为7cm,短直角边为3cm,连结图②中四条线段得到如图③的新图案,则图③中阴影部分的周长为32cm.【答案】32.【解答】解:由题意得:BD=7cm,AB=CD=3cm,∴BC=7﹣3=4(cm),由勾股定理得:AC==5(cm),∴阴影的周长=4(AB+AC)=4×(3+5)=32(cm).故答案为:32.25.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接PA,当△ABP为等腰三角形时,t的值为16或10或.【答案】16或10或.【解答】解:在△ABC中,∠ACB=90°,由勾股定理得:BC=cm,∵△ABP为等腰三角形,当AB=AP时,则BP=2BC=16cm,即t=16;当BA=BP=10cm时,则t=10;当PA=PB时,如图:设BP=PA=x cm,则PC=(8﹣x)cm,在Rt△ACP中,由勾股定理得:PC2+AC2=AP2,∴(8﹣x)2+62=x2,解得x=,∴t=.综上所述:t的值为16或10或.故答案为:16或10或.26.如图,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的“勾股分割点”.已知点M,N是线段AB的“勾股分割点”,若AM=4,MN=5,则斜边BN的长为.【答案】.【解答】解:当BN为最大线段时,∵点M,N是线段AB的勾股分割点,∴BN===,故答案为:.27.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形ABCD,对角线AC,BD交于点O,若AB=6,CD=10,则AD2+BC2=136.【答案】136.【解答】解:∵BD⊥AC,∴∠COB=∠AOB=∠AOD=∠COD=90°,∴BO2+CO2=CB2,OB2+OA2=AB2=36,OA2+OD2=AD2,OC2+OD2=CD2=100,∴BO2+CO2+OA2+OB2=36+100,∴AD2+CB2=BO2+CO2+OA2+OB2=136;故答案为:136.28.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(30,0)(0,12),点D是OA的中点,点P在BC上运动,当△ODP是腰长为15的等腰三角形时,点P 的坐标为(9,12)或(3,12)或(24,12).【答案】(9,12)或(6,12)或(24,12).【解答】解:由题意,当△ODP是腰长为15的等腰三角形时,有三种情况:(1)如答图①所示,PD=OD=15,点P在点D的左侧.过点P作PE⊥x轴于点E,则PE=12.在Rt△PDE中,由勾股定理得:DE===9,∴OE=OD﹣DE=15﹣9=6,∴此时点P坐标为(6,12);(2)如答图②所示,OP=OD=15.过点P作PE⊥x轴于点E,则PE=4.在Rt△POE中,由勾股定理得:OE===9,∴此时点P坐标为(9,12);(3)如答图③所示,PD=OD=5,点P在点D的右侧.过点P作PE⊥x轴于点E,则PE=4.在Rt△PDE中,由勾股定理得:DE===9,∴OE=OD+DE=15+9=24,∴此时点P坐标为(24,12).综上所述,点P的坐标为:(9,12)或(6,12)或(24,12);故答案为:(9,12)或(6,12)或(24,12).29.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门(AD和BC),门边沿D,C两点到门槛AB的距离是1尺(1尺=10寸),两扇门的间隙CD为2寸,则门槛AB长为101寸.【答案】101.【解答】解:设OA=OB=AD=BC=r寸,如图,过D作DE⊥AB于点E,则DE=10寸,OE=CD=1(寸),AE=(r﹣1)寸,在Rt△ADE中,由勾股定理得:AE2+DE2=AD2,即(r﹣1)2+102=r2,解得:r=50.5,∴2r=101,即门槛AB长为101寸,故答案为:101.30.如图,在某次军事演习中,舰艇1号在指挥中心(O处)北偏西30°的A处,舰艇2号在指挥中心南偏东60°的B处,并且OA=OB.接到行动指令后,舰艇1号向正东方向以60海里/小时的速度前进,舰艇2号沿北偏东60°的方向以m海里/小时的速度前进.1.5小时后,指挥中心观测到两舰艇分别到达点E,F处,若∠EOF=75°,EF=210海里,则m的值为80.【答案】80.【解答】解:延长AE、BF相交于点C,∵∠AOB=30°+90°+30°=150°,∠EOF=75°,∴∠EOF=∠AOB,又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(60°+60°)=180°,延长FB至D,使BD=AE,连接OD,∵∠OBD=∠OBC,∴.∠OBD=∠A,∴△OBD≌△OAE(SAS),∴OD=OE,∠BOD=∠AOE,∵∠EOF=∠AOB=∠EOD,∴.∠EOF=∠DOF,又∵OF=OF,∴△EOF≌△DOF(SAS),∴EF=AE+BF,即EF=1.5×(60+m)=210.解得m=80.故答案为:80.31.如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB=5,EF=1,则GM的长为.【解答】解:由图可知∠AED=90°,AB=5,EF=1,∵大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,故AE=BF=GC=DH,设DE=x,则在Rt△AED中,AD=AB=5,AE=1+x,根据勾股定理,得AD2=DE2+AE2,即52=x2+(1+x)2,解得:x1=3,x2=﹣4(舍去).过点M作MN⊥FB于点N,如图所示.∵四边形EFGH为正方形,EG为对角线,∴△EFG为等腰直角三角形,∴∠EGF=∠NGM=45°,故△GNM为等腰直角三角形.设GN=NM=a,则NB=GB﹣GN=3﹣a,∵MN∥AF,∴△BMN∽△BAF,∴=,将MN=a,AF=3,BN=3﹣a,BF=4代入,得=,解得a=,∴MN=GN=,在Rt△MGN中,由勾股定理,得GM===.32.如图,铁路上A、D两点相距25千米,B,C为两村庄,AB⊥AD于A,CD⊥AD于D,已知AB=15km,CD=10km,现在要在铁路AD上建一个土特产品收购站P,使得B、C 两村到P站的距离相等,则P站应建在距点A10千米.【答案】10.【解答】解:设AP=x千米,则DP=(25﹣x)千米,∵B、C两村到P站的距离相等,∴BP=PC.在Rt△APB中,由勾股定理得BP2=AB2+AP2,在Rt△DPC中,由勾股定理得PC2=CD2+PD2,∴AB2+AP2=CD2+PD2,又∵AB=15km,CD=10km,∴152+x2=102+(25﹣x)2,∴x=10.故答案为:10.33.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为20cm(杯壁厚度不计).【答案】见试题解答内容【解答】解:如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B===20(cm).故答案为20.34.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是.【答案】.【解答】解:如图,连接BP,在△ABC中,AB=AC=10,BC=12,AD=8,∴BD=DC,∴BP=PC,∴PC+PQ=BP+PQ=BQ,∴当B,P,Q共线时,PC+PQ的值最小,∴当BQ⊥AC时,BQ的值最小,令AQ'=a,则CQ'=10﹣a,∵BQ'⊥AC,∴AB2﹣AQ'2=BC2﹣CQ'2,即102﹣a2=122﹣(10﹣a)2,解得a=,∴BQ'==,∴PC+PQ的最小值为,故答案为:.35.如图,在△ABC中,∠ABC=45°,AB=,AC=6,BC>4,点E,F分别在BC,AC边上,且AF=CE,则AE+BF的最小值为2.【答案】2.【解答】解:过A点作AG∥BC,截取AG=AC,连接FG,BG,过B作BR⊥AG,交AG的反向延长线于R,则∠RBC=∠BRA=90°,∴∠GAF=∠ACE,在△AFG和△CEA中,,∴△AFG≌△CEA(SAS),∴GF=AE,∴AE+BF的最小值,即为BG的长,∵∠ABC=45°,∴∠RAB=∠EBA=45°,∵AB=4,∴BR=AR=4,∵AC=6,∴AG=AC=6,∴RG=AR+AG=4+6=10,∴BG===2,即AE+BF的最小值为2.故答案为:2.36.如图,在△ABC中,AB=9cm,AC=12cm,BC=15cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是cm.【答案】.【解答】解:∵在△ABC中,AB=9cm,AC=12cm,BC=15cm,∴BC2=AB2+AC2,∴∠A=90°,∵MD⊥AB,ME⊥AC,∴∠A=∠ADM=∠AEM=90°,∴四边形ADME是矩形,∴DE=AM,当AM⊥BC时,AM的长最短,根据三角形的面积公式得:AB•AC=BC•AM,∴9×12=15AM,AM=,即DE的最小值是cm.故答案为:.37.如图,Rt△ABC中,.点P为△ABC内一点,PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是.【答案】.【解答】解:如图所示,取AC中点O,连接PO,BO,∵PA2+PC2=AC2,∴∠APC=90°,∴,∵BP+OP≥OB,∴当B、P、O三点共线时BP+OP有最小值,即此时BP有最小值,∵∠ACB=90°,∴,∴BP=BO﹣OP=2,∴BP=PO,又∠ACB=90°,∴PC=BO=2,∴PC=PO=CO,∴△OPC是等边三角形,∴∠PCO=60°,∠PAC=30°∴AP==2,∴,故答案为:.三.解答题(共4小题)38.如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A 出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?【答案】见试题解答内容【解答】解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,∴BC=CA.设AC为x,则OC=9﹣x,由勾股定理得:OB2+OC2=BC2,又∵OA=9,OB=3,∴32+(9﹣x)2=x2,解方程得出x=5.∴机器人行走的路程BC是5cm.39.如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)求BC边的长.(2)当△ABP为等腰三角形时,求t的值.【答案】或10或16.【解答】解:在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,∴BC=,当AP=BP时,如图1,则AP=t,PC=BC﹣BP=8﹣t,在Rt△ACP中,AC2+CP2=AP2,∴62+(8﹣t)2=t2,解得t=;当AB=BP时,如图2,则BP=t=10;当AB=AP时,如图3,则BP=2BC;∴t=2×8=16,综上,t的值为或10或16.40.今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB =500km,经测量,距离台风中心260km及以内的地区会受到影响.(1)海港C受台风影响吗?为什么?(2)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?【答案】(1)海港C受台风影响,理由见解答过程;(2)台风影响该海港持续的时间为小时.【解答】解:(1)海港C受台风影响,理由:∵AC=300km,BC=400km,AB=500km,∴AC2+BC2=AB2,∴△ABC是直角三角形,∠ACB=90°;过点C作CD⊥AB于D,∵△ABC是直角三角形,∴AC×BC=CD×AB,∴300×400=500×CD,∴CD=240(km),∵以台风中心为圆心周围260km以内为受影响区域,∴海港C受台风影响;(2)当EC=260km,FC=260km时,正好影响C港口,∵ED=(km),∴EF=2ED=200km,∵台风的速度为28千米/小时,∴200÷28=(小时).答:台风影响该海港持续的时间为小时.41.请阅读下列材料:已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.【答案】见试题解答内容【解答】解:(1)DE2=BD2+EC2;(2)关系式DE2=BD2+EC2仍然成立.证明:将△ADB沿直线AD对折,得△AFD,连FE∴△AFD≌△ABD,∴AF=AB,FD=DB,∠FAD=∠BAD,∠AFD=∠ABD,又∵AB=AC,∴AF=AC,∵∠FAE=∠FAD+∠DAE=∠FAD+45°,∠EAC=∠BAC﹣∠BAE=90°﹣(∠DAE﹣∠DAB)=45°+∠DAB,∴∠FAE=∠EAC,又∵AE=AE,∴△AFE≌△ACE,∴FE=EC,∠AFE=∠ACE=45°,∠AFD=∠ABD=180°﹣∠ABC=135°∴∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,∴在Rt△DFE中,DF2+FE2=DE2,即DE2=BD2+EC2;解法二:将△EAC绕点A顺时针旋转90°得到△TAB.连接DT.∴∠ABT=∠C=45°,AT=AE,∠TAE=90°,∵∠ABC=45°,∴∠TBC=∠TBD=90°,∵∠DAE=45°,∴∠DAT=∠DAE,∵AD=AD,∴△DAT≌△DAE(SAS),∴DT=DE,∵DT2=DB2+EC2,∴DE2=BD2+EC2;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(2)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA.∴AD=DF,EF=BE.∴∠DFE=∠1+∠2=∠A+∠B=120°.若使△DFE为等腰三角形,只需DF=EF,即AD=BE,∴当AD=BE时,线段DE、AD、EB能构成一个等腰三角形,且顶角∠DFE为120°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二下期末几何及解析1、以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.(1)当四边形ABCD为正方形时(如图1),E B和FD的数量关系是_____________;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.难度一般:证全等即可(第三问,图1中就能看出是45°。
)解(1)EB=FD 。
(2)EB=FD。
证:∵△AFB为等边三角形,∴AF=AB,∠FAB=60°∵△ADE为等边三角形,∴AD=AE,∠EAD=60°,∴∠FAB+∠BAD=∠EAD+∠BAD即∠FAD=∠BAE,∴△FAD≌△BAE,∴EB=FD(3)解:∵△ADE为等边三角形,∴∠AED=∠EDA=60°∵△FAD≌△BAE,∴∠AEB=∠ADF设∠AEB为x°,则∠ADF也为x°于是有∠BED为(60-x)°,∠EDF为(60+x)°∴∠EGD=180°-∠BED-∠EDF=180°-(60-x)°-(60+x)°=60°2、已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.(1)求证:△ABE≌△FCE;(2)若AF=AD,求证:四边形ABFC是矩形.简单题证明:(1)如图1.在△ABE和△FCE中,∠1=∠2,∠3=∠4,BE=CE,∴△ABE≌△FCE.(2)∵△ABE≌△FCE,∴AB=FC.∵AB∥FC,∴四边形ABFC是平行四边形.∵四边形ABCD是平行四边形,∴AD=BC.∵AF=AD,∴AF=BC.∴四边形ABFC是矩形.FAB CDE图14321EDCBAF3、已知:△ABC 是一张等腰直角三角形纸板,∠B =90°,AB =BC =1.(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC 的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为1S ,则1S =___________;余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3), 得到2个新的正方形,将此次所得2个正方形的面积的和.记为2S ,则2S =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和.记为3S ;按照同样的方法继续操作下去……,第n 次裁剪得到_________个新的正方形,它们的面积的和.n S =______________.(题外题:把你剪出的正方形的面积与图1中的正方形面积进行比较。
) 本题相当于中考12题的简单题 解:(1)如图2;-------------1分(2)14,18,12n -,112n +. ----------6分4、已知:如图,平面直角坐标系xOy 中,正方形ABCD 的边长为4,它的顶点A 在x 轴的正半轴上运动,顶点D 在y 轴的正半轴上运动(点A ,D 都不与原点重合),顶点B ,C 都在第一象限,且对角线AC ,BD 相交于点P ,连接OP .(1)当OA =OD 时,点D 的坐标为______________, ∠POA =__________°;(2)当OA <OD 时,求证:OP 平分∠DOA ; (3)设点P 到y 轴的距离为d ,则在点A ,D 运动的 过程中,d 的取值范围是________________.(第二问:如果点P 到OP 时,求证:OP 平分∠DOA ;)图1EFA BCD 图2ABC图3图4B图2CBA解:(1)(0,,45;证明:(2)过点P 作PM ⊥x 轴于点M ,PN ⊥y 轴于点N .(如图3) ∵四边形ABCD 是正方形, ∴PD =P A ,∠DP A =90°. ∵PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,∴∠PMO =∠PNO =∠PND =90°. ∵∠NOM =90°,∴四边形NOMP 中,∠NPM =90°.∴∠DP A =∠∵∠1=∠DP A -∠NP A ,∠2=∠NPM -∠NP A ,∴∠1=∠2. 在△DPN 和△APM 中, ∠PND =∠PMA ,∠1=∠2,PD =P A , ∴△DPN ≌△APM . ∴PN =PM . ∴OP 平分∠DOA .(3)2d <≤ -5、已知:如图,平面直角坐标系xOy 中,矩形OABC 的 顶点A ,C 的坐标分别为(4,0),(0,3).将△OCA 沿直线翻折,得到△DCA ,且DA 交CB 于点E .(1)求证:EC =EA ; (2)求点E 的坐标;(3)连接DB ,请直接写出....四边形DCAB 的周长和面积.(第二问,有坐标,用代数法勾股定理可得CE=AE 的长)(第三问的证明:过D 做DM ⊥AC 于M ,过B 做BN ⊥CA 于N ,则由相似可得,DM=BN=梯形的高(能求出具体数),CM=AN (具体数)还看得DB=MN (具体数)这样即可求出周长,有可求出面积。
) 证明:(1)如图1.∵△OCA 沿直线CA 翻折得到△DCA , ∴△OCA ≌△DCA . ∴∠1=∠2. ∵四边形OABC 是矩形,∴OA ∥CB . ∴∠1=∠3.∴∠2=∠3.∴EC =EA . 解:(2)设CE = AE =x . ∵点A ,C 的坐标分别为(4,0),(0,3),∴OA =4,OC =3. ∵四边形OABC 是矩形,∴CB =OA =4,AB =OC =3,∠B =90°. 在Rt △EBA 中,222EA EB BA =+, ∴222(4)3x x =-+.解得 258x =. ∴点E 的坐标为(25,38). (3)625,19225. 6、已知:△ABC 的两条高BD ,CE 交于点F ,点M ,N 分别是AF ,BC 的中点,连接ED ,MN .(1)在图1中证明MN 垂直平分ED ; (2)若∠EBD =∠DCE =45°(如图2),判断以M ,E ,N ,D 为顶点的四边形的形状,并证明你的结论.NMABCD EF NMF EDCBA图2第一问,连接EM ,EN ,DM ,DN ,利用三角形斜边中线等于斜边一半得,ME=MD ,NE=ND ,所以点M 、N 都在线段ED 的垂直平分线上。
(有△ADF ≌△BDC ,得AF=BC ,(还得∠MDA=∠NDB ,证直角时用),进而得菱形,再证一直角得正方形,)(1)证明:连接EM ,EN ,DM ,DN .(如图2) ∵BD ,CE 是△ABC 的高, ∴BD ⊥AC ,CE ⊥AB .∴∠BDA =∠BDC =∠CEB =∠CEA =90°. ∵在Rt △AEF 中,M 是AF 的中点,∴EM =12AF . 同理,DM =12AF ,EN =12BC ,DN =12BC . ∴EM =DM , EN =DN .∴点M ,N 在ED 的垂直平分线上.∴MN 垂直平分ED . (2)判断:四边形MEND 是正方形. 证明:连接EM ,EN ,DM ,DN .(如图3) ∵∠EBD =∠DCE =45°,而∠BDA =∠CDF =90°, ∴∠BAD =∠ABD =45°,∠DFC =∠DCF =45°.∴AD =BD ,DF =DC . 在△ADF 和△BDC 中,AD =BD ,∠ADF =∠BDC ,(Rt ∠) DF =DC ,∴△ADF ≌△BDC . ∴AF =BC ,∠1=∠2. ∵由(1)知DM =12AF =AM ,DN =12BC =BN , ∴DM =DN ,∠1=∠3,∠2=∠4.∴∠3=∠4.∵由(1)知EM =DM ,EN =DN ,∴DM =DN =EM =EN . ∴四边形MEND 是菱形. ∵∠3+∠MDF =∠ADF =90°,∴∠4+∠MDF =∠NDM =90°. ∴四边形MEND 是正方形.7、(6分)如图,现有一张边长为4的正方形纸片ABCD ,点P 为AD 边上的一点(不与点A 、点D 重合),将正方形纸片折叠,使点B 落在P 处,点C 落在G 处,PG 交DC 于H ,折痕为EF ,联结BP 、BH 。
(1)求证:∠APB =∠BPH ; (2)求证:AP +HC =PH ; (3)当AP =1时,求PH 的长。
4312ABCD E F MN图3第一问,设∠EPB=∠EBP=m ,则∠BPH=90°-m ,∠PBC=90°-m ,所以∠BPH=∠PBC ,又因为∠APB=∠PBC ,所以,∠APB=∠BPH 。
第二问的题外题:将此题与北京141之东城22和平谷24 放在一起,旋转翻折共同学习;此题中用旋转把△ABP 绕点B 顺时针旋转90°不能到达目的,于是延BP 翻折,翻折后的剩余部分△BQH 与△BCH 也可全等,即可到达目的,还有意外收获:证得∠PBH=45°。
第三问,代数方法的勾股定理。
(1)证明:∵PE =BE ,∴∠EPB =∠EBP , 又∵∠EPH =∠EBC =90°,∴∠EPH -∠EPB =∠EBC -∠EBP 。
即∠BPH =∠PBC 。
又∵四边形ABCD 为正方形,∴AD ∥BC , ∴∠APB =∠PBC 。
∴∠APB =∠BPH 。
(2分) (2)证明:过B 作BQ ⊥PH ,垂足为Q , 由(1)知,∠APB =∠BPH , 又∵∠A =∠BQP =90°,BP =BP , ∴△ABP ≅△QBP ,∴AP =QP ,BA =BQ 。
又∵AB =BC ,∴BC =BQ 。
又∵∠C =∠BQH =90°,BH =BH ,∴△BCH ≅△BQH ,∴CH =QH ,∴AP +HC =PH 。
(4分)(3)由(2)知,AP =PQ =1,∴PD =3。
设QH =HC =x ,则DH =x -4。
在Rt △PDH 中,222PH DH PD =+,即()()222431x x -+=+,解得4.2=x ,∴PH =3.4(6分)8、(6分)如图,在△ABC 中,AC >AB ,D 点在AC 上,AB =CD ,E 、F 分别是BC 、AD 的中点,连结EF 并延长,与BA 的延长线交于点G ,若∠EFC =60°,联结GD ,判断△AGD 的形状并证明。
