2014年浙江普通专升本考试所有考试考纲大集锦--浙江专升本考生必备(学研教育)
2014年浙江专升本考试《英语》真题卷参考答案与解析

2014年浙江专升本考试《英语》真题卷参考答案与解析Part I Reading Comprehension (60 marks, 60 minutes)Section A (每小题2分)Format ⅠPassage One1. B【解析】主旨题。
此题解题技巧是:文章以问题开头,往往可从其后紧跟的句子中概括出主旨题的答案。
本文开头的问句有两个,涉及where与who,因此可以排除最大的干扰项C,而更有概括性的选项B为正确答案。
2. B【解析】细节题。
细节题常用的一个出题套路是正确选项不是照抄原文,而是对原文进行同义替换。
本题B选项的leftover food就同义替换了原文第二段中的scraps of food。
3. C【解析】细节题。
此题不难,定位到第三段“She replaced the soft center with spices and nut s”一句,很容易得出正确答案C4. D【解析】词汇语义题。
对词汇量较小的考生来说,代入法是针对这类题目较为实用的解题技巧。
即用四个选项逐项替代原词,看看哪个选项最符合上下文的逻辑。
定位到第三段最后一句,根据常识,用拳头击打炸面圈的中间,很可能中间会被打出一个洞来。
因此,选项D“result(后果)”一词最合题意。
5. B【解析】推断题。
倒数第二段说到,这些“Doughnut Girls(炸面圈女孩)”都在靠近士兵的危险地方工作,这里的“dangerous conditions near the soldiers(靠近士兵危险地方)”玩的是文字游戏,显然指的就是靠近前线战场的地方,因此B为正确选项。
Passage Two6.A【解析】短语语义题。
本文的前两句很容易利用对照关系确定plain是gook look的反义,即长相平凡之意。
而且本文围绕着长相与收入的关系展开,因此,可确定A为正确答案。
7. D【解析】细节题中的数学题。
首先要提醒各位考生,凡是数字题正确答案一般都要经过简单的计算,涉及原文数字的选项则多为陷阱。
2014年专升本高数真题答案解析

所以 cos 2x
n0
1n 2x2n
(2n)!
,即:
f
(x)
1 2
1 2
n0
1n 2x2n 2n!
, x(,)
13. 2
解析:
a
b
b
c
c
a
a
b
c
b
b
c
c
a
a
b
a
c
b b
b
c
c
a
a
b
a c
b
c
c
a
a
b
a c
b
c
c
a
a
b
c
a
b
a
a
c
16.
解:
lim
x 0
ln(sin2 x ex ) x ln(x2 e2x ) 2x
lim x0
ln[ex (ex sin2 ln[e2x (e2x x2
x 1)] x 1)] 2x
lim x0
ln(ex sin 2 ln(e2x x2
x 1) 1)
ex sin2 x
lim x 0
1 x 2
2 1 x 1 x
故 y 1 x0
10. ( 3 , 3) 34
解析:
求曲线的拐点,当 x
0 时,
y
2x (1 x2 )2
,
y
2(3x2 1) (1 x2 )3
,令
y 0 ,得 x 3 ,所以拐点为: ( 3 , 3)
3
34
11. 1
6
1
解析:由题意可知, S
1
(x
0
x2 )dx
浙江2014年专升本数学真题及答案

浙江2014年专升本数学真题及答案1、4.小亮用天平称得牛奶和玻璃杯的总质量为0.3546㎏,用四舍五入法将0.3546精确到0.01的近似值为()[单选题] *A.0.35(正确答案)B.0.36C.0.354D.0.3552、要使多项式不含的一次项,则与的关系是()[单选题] *A. 相等(正确答案)B. 互为相反数C. 互为倒数D. 乘积为13、16.“x2(x平方)-4x-5=0”是“x=5”的( ) [单选题] *A.充分不必要条件B.必要不充分条件(正确答案)C.充要条件D.既不充分也不必要条件4、? 是第()象限的角[单选题] *A. 一(正确答案)B. 二C. 三D. 四5、11.2020·北京,1,4分)已知集合A={-1,0,1,2},B={x|0<x<3},则A∩B=( ) [单选题] * A.{-1,0,1}B.{0,1}C.{-1,1,2}D.{1,2}(正确答案)6、14.在防治新型冠状病毒的例行体温检查中,检查人员将高出37℃的部分记作正数,将低于37℃的部分记作负数,体温正好是37℃时记作“0”。
记录一被测人员在一周内的体温测量结果分别为+1,-3,-5,+1,-6,+2,-4,那么,该被测者这一周中测量体温的平均值是(??)[单选题] *A.1℃B.31℃C.8℃(正确答案)D.69℃7、26.已知(x﹣a)(x+2)的计算结果为x2﹣3x﹣10,则a的值为()[单选题] *A.5(正确答案)B.﹣5C.1D.﹣18、48.如图,M是AG的中点,B是AG上一点.分别以AB、BG为边,作正方形ABCD和正方形BGFE,连接MD和MF.设AB=a,BG=b,且a+b=10,ab=8,则图中阴影部分的面积为()[单选题] *A.46B.59(正确答案)C.64D.819、28、若的三边之长都是整数,周长小于10,则这样的三角形共有()[单选题] *A. 6个,B. 7个,C. 8个,D. 9个(正确答案)10、已知二次函数f(x)=2x2-x+2,那么f(-2)的值为()。
浙江省普通高校“专升本”统考科目:英语考试大纲.doc
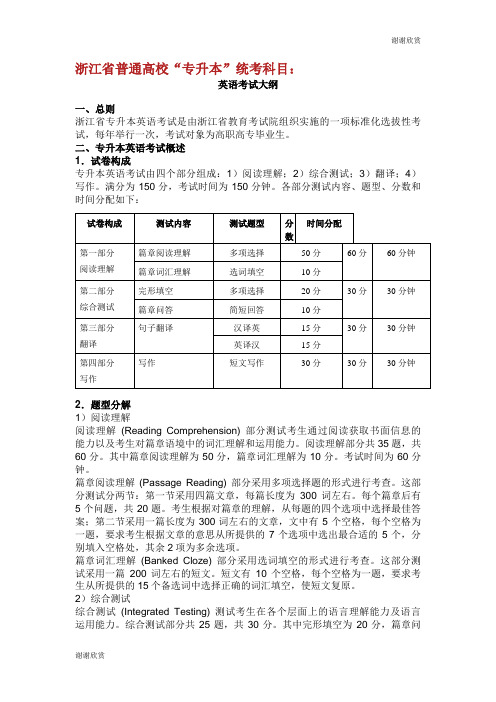
浙江省普通高校“专升本”统考科目:英语考试大纲一、总则浙江省专升本英语考试是由浙江省教育考试院组织实施的一项标准化选拔性考试,每年举行一次,考试对象为高职高专毕业生。
二、专升本英语考试概述1.试卷构成专升本英语考试由四个部分组成:1)阅读理解;2)综合测试;3)翻译;4)写作。
满分为150分,考试时间为150分钟。
各部分测试内容、题型、分数和时间分配如下:2.题型分解1)阅读理解阅读理解(Reading Comprehension) 部分测试考生通过阅读获取书面信息的能力以及考生对篇章语境中的词汇理解和运用能力。
阅读理解部分共35题,共60分。
其中篇章阅读理解为50分,篇章词汇理解为10分。
考试时间为60分钟。
篇章阅读理解(Passage Reading) 部分采用多项选择题的形式进行考查。
这部分测试分两节:第一节采用四篇文章,每篇长度为300词左右。
每个篇章后有5个问题,共20题。
考生根据对篇章的理解,从每题的四个选项中选择最佳答案;第二节采用一篇长度为300词左右的文章,文中有5个空格,每个空格为一题,要求考生根据文章的意思从所提供的7个选项中选出最合适的5个,分别填入空格处,其余2项为多余选项。
篇章词汇理解(Banked Cloze) 部分采用选词填空的形式进行考查。
这部分测试采用一篇200词左右的短文。
短文有10个空格,每个空格为一题,要求考生从所提供的15个备选词中选择正确的词汇填空,使短文复原。
2)综合测试综合测试(Integrated Testing) 测试考生在各个层面上的语言理解能力及语言运用能力。
综合测试部分共25题,共30分。
其中完形填空为20分,篇章问答为10分。
考试时间为30分钟。
完形填空(Cloze) 部分采用多项选择题的形式进行考查。
这部分测试采用一篇200词左右的短文。
短文有20个空格,空格处所删去的词既有实词也有虚词,每个空格为一题,每题有四个选择项。
要求考生选择一个最佳答案,使短文的意思和结构恢复完整。
2014年浙江普通专升本英语学习要点大集锦(学研教育,短时间提升英语的利器)

2014年浙江普通浙江普通专升本英语学习要点大集锦浙江普通专升本英语备考是个艰难的过程,考试在即?英语考试方向是什么?英语应该怎么学?词汇应该怎么记?阅读需要抓住哪些要素。
今天学研教育的资深英语老师为大家整理这篇丰富的文档,帮助大家更好地学习。
在学习浙江普通专升本英语的过程中需要大家的坚持+正确的学习方式+好的学习计划才成功地踏上本科生的诺亚方舟。
你需要做到以下几点?一、词汇应该怎么记?词汇量是确保考生顺利通过考试的基石。
背诵词汇是考生在英语学习过程中无法逃避的环节。
所以,考生要拿出毅力,勇敢闯过词汇这一关。
背单词时,考生应以词根、词缀为理解主线,通过短期内大量重复来夯实记忆效果。
从词根、词缀知识开始复习,虽然从表面上看像增加了学习内容,但实际上是“磨刀不误砍柴功”,通过此种方法能快速记住很多相关单词的意思。
同时,在背单词过程中,也要重点关注一词多义和熟词僻意的现象,并多加总结。
除此之外,重复识记单词也很重要。
只有在短期内多次接触同一个生词,而且在不同语境下看到同一个生词,对该词的印象才会深刻。
(2014年词汇手册必备手册可以向学研教育工作人员免费索取,节省大家很多准备与查找资料的时间)阅读理解阅读理解部分在浙江普通专升本英语考试中所占的分值比例很高,属于考试的重中之重。
在复习这一部分时,考生首先要走出这样一个误区:阅读练习就是逐个查生词或对照译文去理解原文,就是词典不离身,遇到生词马上查,甚至把生词整理到笔记本上。
很多考生在复习备考时都会犯这样的错误,尤其是一些养成了“踏实”的学习习惯的考生,更喜欢把这个错误的方法与“复习透彻”联系起来。
事实上,这样的方法既耗时又费力,收效也不佳。
每次考试完,考生都会抱怨平时自己做了很多练习,但考试还是不理想,上述误区就是原因之一。
考生要清楚一点:在考试现场,你不可能查单词,也不可能不计时间地去“细抠”一篇文章。
所以,考生应走出误区,找到正确而高效的复习方法。
2014专升本数学考试大纲

1、理解空间直角坐标系,理解向量的概念及其表示.
2、掌握向量的运算(线性运算、数量积、向量积),了解两个向量垂直、平行的条件.
3、理解单位向量、方向余弦、向量的坐标表达式,掌握用坐标表达式进行向量运算的方法.
4、掌握平面方程和直线方程及其求法.
5、会求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的相互关系(平行、垂直、相交等)解决有关问题.
6、掌握利用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积、平行截面面积为已知的立体体积等)及函数的平均值.
四 向量代数和空间解析几何
考试内容
向量的概念 向量的线性运算 向量的数量积和向量积 两向量垂直、平行的条件 两向量的夹角 向量的坐标表达式及其运算 单位向量 方向余弦 曲面方程和空间曲线方程的概念 平面方程 直线方程 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件 球面 柱面 旋转曲面等常用的二次曲面方程及其图形 空间曲线的参数方程和一般方程 空间曲线在坐标面上的投影曲线方程
1、理解函数的概念,掌握函数的表示法,会建立简单应用问题的函数关系.
2、了解函数的有界性、单调性、周期性和奇偶性.
3、理解复合函数及分段函数的概念,了解反函数及隐函数的概念.
4、掌握基本初等函数的性质及其图形,了解初等函数的概念.
5、理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系.
数列极限与函数极限的定义及其性质:函数的左极限与右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限 函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质
铭远教育-(历年真题)2014年浙江省专升本数学试卷及解析

25、设 lim
x 0
f x 1 ,且 f x 0 ,证明: f x x . x
26、已知
2 ln 2
dt e 1
t
x
,求 x 的值. 6
浙江省 2014 年选拔优秀高职高专毕业生进入本科学习统一 考试 《高等数学》试卷答案
一、选择题 1、D 解析:解题方法举例子。若 f x x, g x 即 f x g x 极限存在. 2、C 解析:y 3 x 2 3 , 令 y 0. 得 x 1. 当 x 1 时,y 2 ; 当 x 1 时,y 2 .
x 1
lim f x lim
x 1
x 1 是不可导点.
4、A 解析:令 t x u , 则 sin t x dt
x
0
sin udu, f x sin x sin x.
x
0
1 1 1 1 x dx x dx 5、B 解析: y e x x 2 1 e dx C x arctan x C .
所以通解为 ln xy x y C 0, C 为任意的常数
5 1 y 4e x e 2 x 2 2 15、
解析:
y C1e x C2e 2 x , r1 1, r2 2. y 3 y 2 y 1. 1 y * A.0 3 0 2 A 1, A . 2 1 C 4 5 2x 1 C C2 2 1 x 1 , C 5 y 4e e . 2 2 2 2 2 C1 2C2 1
8、曲线 y x ln e
2014年浙江专升本(高等数学)真题试卷(题后含答案及解析)

2014年浙江专升本(高等数学)真题试卷(题后含答案及解析) 题型有:1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.当x→x0时,若f(x)存在极限,g(x)不存在极限,则下列结论正确的是( )A.当x→x0时,f(x)g(x)必定存在极限B.当x→x0时,f(x)g(x)必定不存在极限C.当x→x0时,f(x)g(x)若存在极限,则此极限必为零D.当x→x0时,f(x)g(x)可能存在极限,也可能不存在极限正确答案:D解析:极限运算法则,可以举反例,若f(x)=x2,g(x)=lnx,则f(x)= x2=0,g(x)=lnx=-∞,但f(x).g(x)=x2lnx=0;若f(x)=2,g(x)=sin=2,不存在,但f(x).g(x)=不存在;可见选项D正确.2.曲线y=x3-3x上切线平行于x轴的点是( )A.(0,0)B.(1,2)C.(一1,2)D.(0,2)正确答案:C解析:由导数几何意义可知,k切=y′(x0)=3—3=0,所以切点坐标为(1,一2)或(一1,2),即选项C正确.3.函数f(x)=(x2—x一2)|x3一x|的不可导点个数是( )A.3B.2C.1D.0正确答案:B解析:导数定义,f′(0)=所以f′-(0)==2,f′+(0)==-2所以函数f(x)在x=0处不可导;同理,f′(1)=所以f′-(1)=一(x2一x—2)|x(x+1)|=4.f′+(1)=(x2一x—2)|x(x+1)|=-4,所以函数f(x)在x=1处不可导;f′(-1)==(x-2)|x3-x|=0,所以函数f(x)在x=-1处可导;综上可知,函数f(x)共有2个不可导点,选项B正确.4.若f(x=sin(t一x)dt,则f(x)= ( )A.-sinxB.-1+cosxC.sinxD.0正确答案:A解析:变限函数求导数,因为sin(t一x)dt sinudu,所以sin(t—x)dt=sinudu=0一sin(一x).(一1)=-sim,可见选项A正确.5.微分方程y′+的通解是( )A.arctanx+CB.(arctanx+C)C.arctanx+CD.+arctanx+C正确答案:B解析:一阶线性微分方程,由通解公式可得y=e-∫p(x)dx[∫Q(x).e∫p(x)dxdx+C]=.elnxdx+C]=(arctanx+C),可见选项B正确.填空题6.设f(x)在(-∞,+∞)上连续,且f(2)=3,则=___________.正确答案:9解析:利用连续性求极限,=3f(2)=9 7.设f(x)=,则f[f(x)]=___________.正确答案:解析:求复合函数的表达式,f[f(x)]=f[f(x)]=8.曲线y=xln(e+)(x>0)的渐近线方程是___________.正确答案:y=x+解析:计算斜渐近线,设直线y=ax+b为所求曲线的渐近线,则a==lne=1,b=所以,斜渐近线为y=x+.9.设y=ln,则y′|x=0=___________.正确答案:-1解析:求导函数,因为y=ln[ln(1一x)一ln(1+x)]所以y′=,故y′(0)=-1.10.曲线y=(x>0)的拐点是___________.正确答案:()解析:求曲线的拐点,当x>0时,y′=令y″=0,得x=,所以拐点为().11.由曲线y=x和y=x2所围成的平面图形的面积是___________.正确答案:解析:据题意画图,求所围平面图形的面积S=(x—x2)dx=(x2一12.将函数f(x)=sin2x展开成x的幂级数为___________.正确答案:,x∈(一∞,+∞)解析:麦克劳林展式,f(x)=sin2x=cos2x,又因cosx=x2n,x∈(一∞,+∞),所以cos2x=(2x)2n即f(x)=,x∈(一∞,+∞).13.设(a×b).c=1,则[(a+b)×(b+c)].(c+a)=___________.正确答案:2解析:混合积,向量积运算法则,在混合积计算中,如有两向量相同,则混合积为0.因此,[(a+b)×(b+c)].(c+a)=[a×(b+c)+b×(b+c)]=[a×b+a×c+b×b+b ×c].(c+a)=[a×b+a×c+b×c].(c+a)=(a×b).c+(a×b).a+(a×c).c+(a×c).a+(b×c).c+(b×c).a=(a×b).c-(b×c).a=2(a×b).c=214.微分方程(1+x)ydx+(1一y)xdy=0的通解为___________.正确答案:ln|xy|+x-y+C=0,C为任意常数解析:可分离变量的微分方程,(1+x)ydx+(1一y)xdx=0x+ln|x+C=y—ln|y|,即通解为y=x+ln|xy|+C,C为任意常数.15.设二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=C1ex+C1e2x,那么非齐次y″+ay′+by=1满足的条件y(0)=2,y′(0)=-1的解为___________.正确答案:y=4ex-解析:求二阶线性常系数非齐次方程的通解,特征方程为r2+ar+b=0,r1=1,r2=2即(r-1)(r-2)=0,r2-3r+2=0,故a=-3,b=2.所以原微分方程为y″一3y′+2y=1,由于λ=0不是特征方程的根,取k=0,因此,设特解y*=A,则(y*)′=0,(y*)″=0,代入可得A=,所以y*=,所以y″一3y′+2y=1的通解为y=C1ex+C2e2x+,再由y(0)=2,y′(0)=-1,可得C1=4,C2=,故满足初始条件的特解为y=4ex-解答题解答时应写出推理、演算步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年浙江普通专升本考试所有考试考纲大集锦--浙江专升本考生迎考必备2013年浙江普通专升本考试《大学语文》考试大纲一、考核总目标普通高校“专升本”统考科目《大学语文》主要考查考生识记、理解、分析综合、鉴赏评价、表达应用和探究六种能力,具体分为基础知识(语言知识、文学及实用文知识)和基本能力(阅读能力、写作能力)两大方面。
二、考核内容(一)基础知识1.语言知识(1)能够识记、理解常用的文言词语,掌握文言文作品中词类活用、一词多义、通假字、古今字等语言现象及常见的特殊句式,能够进行简单的文言今译。
(2)能够准确地使用汉字,识记和解释现代作品中的疑难词语(不含科技术语),了解汉语语法规范,掌握准确、简明、连贯、得体、鲜明、生动的语言表达方法。
(3)掌握文言文、现代文中常见的修辞手法。
2.文学知识(1)掌握古今中外重要作家、代表作品的基本情况。
如作家的时代、国别、字号、代表作、诗文集名称、文学主张、艺术成就等;代表作品的出处、编著年代、基本内容、主要特色和在文学史上的地位等。
(2)了解文学史中出现的重要文学流派和文学现象。
(3)默写常见的名句名篇。
(详见背诵篇目)3. 实用文知识掌握基本的实用文体的语言要求及规范的写作格式、写作要求,包括《国家行政机关公文处理办法》规定的十三种公务文书及声明、启事、证明、介绍信、求职信、演讲稿(含欢迎词、欢送词、答谢词等)、商函、计划(策划书)、总结、调查报告等事务文书。
(二)基础能力1.阅读能力(1)了解作品的题材,正确划分作品的段落层次,理解并概括段落大意及作品的主旨。
(2)能准确地分析一篇作品(文学及实用文)的材料、表现手法和表达技巧,能联系作品说明常见辞格的修辞作用。
(3)能结合不同文体的特点,分析作品语言的特色,体味富有表现力的语言的含义和表情达意的作用。
2.写作能力(1)文学写作基本要求:思想内容正确、中心明确,条理清楚、结构完整,文字通顺、标点正确、书写工整、字体行款合乎规范。
除诗歌外文体不限,字数不少于600字。
(2)实用文写作基本要求:能根据提供的材料或情境选择恰当的文种写作,主题鲜明集中、材料准确翔实、结构完整恰当、表达通顺合理。
主要文种包括公务文书中的通知、通报、报告、请示、函和事务文书中的声明、启事、证明、介绍信、求职信、演讲稿(含欢迎词、欢送词、答谢词等)、商函、计划(策划书)、总结、调查报告等。
三、考试方式与试卷结构1.考试方式:闭卷、笔试。
2.试卷分数:满分150分。
3.考试时间:150分钟。
4.试卷内容比例:语言知识约20分,文学知识约10分,实用文知识约10分,阅读约40分,写作约70分(其中实用文写作约20分,文学写作约50分)。
5.题型比例:选择题20分,填空题20分,阅读分析题40分,写作题70分。
四、背诵篇目1.《季氏将伐颛臾》《论语》2.《秋水》(节选)《庄子》3.《谏逐客书》李斯4.《郑伯克段于鄢》《左传》5.《李将军列传》(节选)《史记》6.《种树郭橐驼传》柳宗元7.《氓》《诗经》8.《陌上桑》汉乐府9.《短歌行》(对酒当歌)曹操10.《饮酒》(结庐在人境)陶渊明11.《山居秋暝》王维12.《行路难》(金樽清酒斗十千)李白13.《蜀相》杜甫14.《关山月》(和戎诏下十五年)陆游15.《炉中煤》郭沫若16.《我爱这土地》艾青17.《虞美人》(春花秋月何时了)李煜18.《水调歌头》(明月几时有)苏轼19.《水龙吟》(登建康赏心亭)辛弃疾20.《天净沙·秋思》马致远21.《前赤壁赋》苏轼2013年浙江普通专升本考试《高等数学》考试大纲考试要求考生应按本大纲的要求,掌握“高等数学”中函数、极限和连续、一元函数微分学、一元函数积分学、无穷级数、常微分方程、向量代数与空间解析几何的基本概念、基本理论和基本方法。
考生应注意各部分知识的结构及知识的联系;具有一定的抽象思维能力、逻辑推理能力、运算能力和空间想象能力;能运用基本概念、基本理论和基本方法进行推理、证明和计算;能运用所学知识分析并解决一些简单的实际问题。
更多浙江专升本考试资料可访问:( )考试内容一、函数、极限和连续 (一)函数1.理解函数的概念,会求函数的定义域、表达式及函数值,会作出一些简单的分段函数图像。
2.掌握函数的单调性、奇偶性、有界性和周期性。
3.理解函数y =ƒ(x )与其反函数y =ƒ-1(x )之间的关系(定义域、值域、图像),会求单调函数的反函数。
4.掌握函数的四则运算与复合运算; 掌握复合函数的复合过程。
5.掌握基本初等函数的性质及其图像。
6.理解初等函数的概念。
7.会建立一些简单实际问题的函数关系式。
(二)极限1.理解极限的概念(只要求极限的描述性定义),能根据极限概念描述函数的变化趋势。
理解函数在一点处极限存在的充分必要条件,会求函数在一点处的左极限与右极限。
2.理解极限的唯一性、有界性和保号性,掌握极限的四则运算法则。
3.理解无穷小量、无穷大量的概念,掌握无穷小量的性质,无穷小量与无穷大量的关系。
会比较无穷小量的阶(高阶、低阶、同阶和等价)。
会运用等价无穷小量替换求极限。
4.理解极限存在的两个收敛准则(夹逼准则与单调有界准则),掌握两个重要极限:1sin lim0=→x x x ,e )11(lim =+∞→x x x,并能用这两个重要极限求函数的极限。
(三)连续1.理解函数在一点处连续的概念,函数在一点处连续与函数在该点处极限存在的关系。
会判断分段函数在分段点的连续性。
2.理解函数在一点处间断的概念,会求函数的间断点,并会判断间断点的类型。
3.理解“一切初等函数在其定义区间上都是连续的”,并会利用初等函数的连续性求函数的极限。
4.掌握闭区间上连续函数的性质:最值定理(有界性定理),介值定理(零点存在定理)。
会运用介值定理推证一些简单命题。
二、一元函数微分学 (一)导数与微分1.理解导数的概念及其几何意义,了解左导数与右导数的定义,理解函数的可导性与连续性的关系,会用定义求函数在一点处的导数。
2.会求曲线上一点处的切线方程与法线方程。
3.熟记导数的基本公式,会运用函数的四则运算求导法则,复合函数求导法则和反函数求导法则求导数。
会求分段函数的导数。
4.会求隐函数的导数。
掌握对数求导法与参数方程求导法。
5.理解高阶导数的概念,会求一些简单的函数的n 阶导数。
6.理解函数微分的概念,掌握微分运算法则与一阶微分形式不变性,理解可微与可导的关系,会求函数的一阶微分。
(二)中值定理及导数的应用1.理解罗尔(Rolle)中值定理、拉格朗日(Lagrange)中值定理及它们的几何意义,理解柯西(Cauchy)中值定理、泰勒(Taylor)中值定理。
会用罗尔中值定理证明方程根的存在性。
会用拉格朗日中值定理证明一些简单的不等式。
2.掌握洛必达(L’Hospital)法则,会用洛必达法则求“00”,“∞∞”,“∞⋅0”,“∞-∞”,“∞1”,“00”和“0∞”型未定式的极限。
3.会利用导数判定函数的单调性,会求函数的单调区间,会利用函数的单调性证明一些简单的不等式。
4.理解函数极值的概念,会求函数的极值和最值,会解决一些简单的应用问题。
5.会判定曲线的凹凸性,会求曲线的拐点。
6.会求曲线的渐近线(水平渐近线、垂直渐近线和斜渐近线)。
7.会描绘一些简单的函数的图形。
三、一元函数积分学 (一)不定积分1.理解原函数与不定积分的概念及其关系,理解原函数存在定理,掌握不定2.熟记基本不定积分公式。
3.掌握不定积分的第一类换元法(“凑”微分法),第二类换元法(限于三角换元与一些简单的根式换元)。
4.掌握不定积分的分部积分法。
5.会求一些简单的有理函数的不定积分。
(二)定积分1.理解定积分的概念与几何意义, 掌握定积分的基本性质。
2.理解变限积分函数的概念,掌握变限积分函数求导的方法。
3.掌握牛顿—莱布尼茨(Newton —Leibniz)公式。
4.掌握定积分的换元积分法与分部积分法。
5.理解无穷区间上有界函数的广义积分与有限区间上无界函数的瑕积分的概念,掌握其计算方法。
6.会用定积分计算平面图形的面积以及平面图形绕坐标轴旋转一周所得的旋转体的体积。
四、无穷级数 (一)数项级数1.理解级数收敛、级数发散的概念和级数的基本性质,掌握级数收敛的必要条件。
2.熟记几何级数∑∞=-11n n aq,调和级数∑∞=11n n 和p —级数∑∞=11n p n的敛散性。
会用正项级数的比较审敛法与比值审敛法判别正项级数的敛散性。
3.理解任意项级数绝对收敛与条件收敛的概念。
会用莱布尼茨(Leibnitz) 判别法判别交错级数的敛散性。
(二)幂级数1.理解幂级数、幂级数收敛及和函数的概念。
会求幂级数的收敛半径与收敛区间。
2.掌握幂级数和、差、积的运算。
3.掌握幂级数在其收敛区间内的基本性质:和函数是连续的、和函数可逐项求导及和函数可逐项积分。
4.熟记e x ,sin x ,cos x ,ln(1+x ),x-11的麦克劳林(Maclaurin)级数,会将一些简单的初等函数展开为x -x 0的幂级数。
五、常微分方程 (一)一阶常微分方程1.理解常微分方程的概念,理解常微分方程的阶、解、通解、初始条件和特2.掌握可分离变量微分方程与齐次方程的解法。
3.会求解一阶线性微分方程。
(二)二阶常系数线性微分方程1.理解二阶常系数线性微分方程解的结构。
2.会求解二阶常系数齐次线性微分方程。
3.会求解二阶常系数非齐次线性微分方程(非齐次项限定为(Ⅰ) f (x )x n x P λe )(=,其中)(x P n 为x 的n 次多项式,λ为实常数;(Ⅱ))sin )(cos )(()(x x Q x x P e x f m n x ωωλ+=,其中λ,ω为实常数,)(x P n ,)(x Q m 分别为x 的n 次,m 次多项式)。
六、向量代数与空间解析几何 (一)向量代数1.理解向量的概念,掌握向量的表示法,会求向量的模、非零向量的方向余弦和非零向量在轴上的投影。
2.掌握向量的线性运算(加法运算与数量乘法运算),会求向量的数量积与向量积。
3.会求两个非零向量的夹角,掌握两个非零向量平行、垂直的充分必要条件。
(二)平面与直线1.会求平面的点法式方程与一般式方程。
会判定两个平面的位置关系。
2.会求点到平面的距离。
3.会求直线的点向式方程、一般式方程和参数式方程。
会判定两条直线的位置关系。
4.会求点到直线的距离,两条异面直线之间的距离。
5.会判定直线与平面的位置关系。
试卷结构试卷总分:150分 考试时间:150分钟 试卷内容比例:函数、极限和连续 约20% 一元函数微分学 约30% 一元函数积分学 约30% 无穷级数、常微分方程 约15% 向量代数与空间解析几何 约5% 试卷题型分值分布:选择题共 5题,每小题 4 分,总分20分;填空题共10题,每小题 4 分,总分40分; 计算题共 8题, 总分60分;综合题共 3题,每小题10分,总分30分。
