肋片散热分析—计算传热学课程设计
高等传热学肋片分析
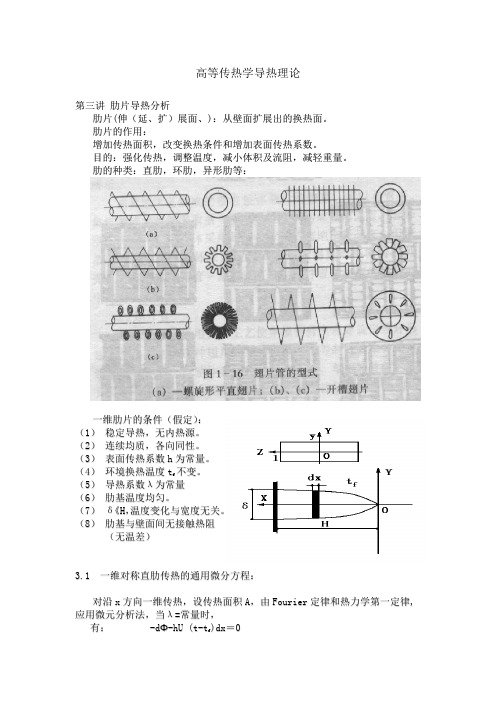
高等传热学导热理论第三讲肋片导热分析肋片(伸(延、扩)展面、):从壁面扩展出的换热面。
肋片的作用:增加传热面积,改变换热条件和增加表面传热系数。
目的:强化传热,调整温度,减小体积及流阻,减轻重量。
肋的种类:直肋,环肋,异形肋等:一维肋片的条件(假定):(1)稳定导热,无内热源。
(2)连续均质,各向同性。
(3)表面传热系数h为常量。
不变。
(4)环境换热温度tf(5)导热系数λ为常量(6)肋基温度均匀。
(7)δ《H,温度变化与宽度无关。
(8)肋基与壁面间无接触热阻(无温差)3.1一维对称直肋传热的通用微分方程:对沿x方向一维传热,设传热面积A,由F o u r i e r定律和热力学第一定律,应用微元分析法,当λ=常量时,)d x=0有:-dΦ-h U(t-tfd(λA d t/d x)-h U(t-t f)d x=(λA d2t/d x)+λ(d A/d x)d t-h U(t-tf)d x=0λA d2t/d x2+λ(d A/d x)d t/d x-h U(t-tf)=0导热面A矩形时A=2l y,U=2(l+2y),取l=1,2y<<l;A=2y,U=2,得:y d2t/d x2+(d y/d x)d t/d x-h/λ(t-tf)=0令:y=δ/2(x/H)(1-2n)/(1-n)n=1/2,y=δ/2=c o n s t,等截面肋。
n=0y=δ/2(x/H),三角形肋。
n=1/3y=δ/2(x/H)1/2,凸抛物线n=∞,y=δ/2(x/H)2,凹抛物线边界条件:x=0,肋端:(1)1stB.C:t=tf。
(2) 2ndB.C中绝热边界条件:d t/d x=0。
(3) 3rdB.C:-λd t/d x=h(t-tf)x=H,肋基:t=t。
3.2等截面直肋的导热分析上式中:n=1/2,y=δ/2=c o n s t,等截面肋。
换一下坐标得:d2t/d x2–h U/(λA)(t-tf)=0令:θ=t-tf过余温度。
利用传热学在肋片散热的改良

利用传热学在肋片散热的改良摘要:本文首先从传热学的基本概念出发,传热学的普适性不仅表现为在能源动力、石油、冶金、化工、交通、建筑建材、机械、食品、轻工、纺织、医药等传统工业部门中,而且传热学的理论和技术在生产、科学研究等领域也得到了广泛的应用。
传热学理论的应用解决了决定这些部门生产过程的热工艺技术,对一些关键技术的解决起了重要的甚至是决定性的作用。
暖气片专用管行业发展很快,但是市场存在的一些问题不容忽视,如市场无序竞争、产品质量下降、创新乏力等。
于是如何选择暖气片的肋片,成为了暖气片专用管行业的核心问题。
在这里,我们具体研究材料的选择对于肋片散热优化设计的影响。
通过对金属与非金属材料的肋片的研究,对材料导热率及材料价钱等方面的综合考虑,我们认为,现用的铝合金型散热器相对来说是比较好的一种散热器,使用范围也很广泛。
在全球经济不景气、国际市场持续低迷的情况下,我国暖气片专用管行业仍然呈现出了企稳回升、发展逐渐向好的良好局面。
虽然暖气片专用管行业发展很快,但是市场存在的一些问题不容忽视,如市场无序竞争、产品质量下降、创新乏力等。
于是如何选择暖气片的肋片,成为了暖气片专用管行业的核心问题。
根据傅里叶定律Φ=-λA(dt/dx)可知,在温差一定的条件下,增大传热量Φ就是增大导热系数λ,而在影响导热系数λ的主要因素中,肋片的材料,密度及形状起着很大的作用。
优化肋片散热主要是从这三方面着手,寻求增大肋片散热量的最佳途径。
在这里,我们具体研究材料的选择对于肋片散热优化设计的影响。
一、金属材料常用散热器材料中铜、铝、铝合金、镁、钢等,其导热性能依次递减。
但是到目前为止.最常用的散热器材料是铝。
与其他一些高热导率的材料相比,铝比较便宜,而且比较容易加工。
以LS- 6- 4 型为例, 已知室温为18℃, 散热器平均壁温80℃, 供水温度95℃, 回水温度70℃,管内水流速0.2 m/s,管内径16 mm,管外径19.2 mm,中心距600 mm, 铝合金的导热系数为λ= 170 W/(m •k).管内水以对流换热方式将热量传给管内壁,内壁以导热方式传给外壁. 外壁一方面以导热传给主肋片及支肋片表面; 另一方面以对流换热方式传给肋片间对流通道中的空气, 空气与散热器表面发生对流换热, 同时和空隙上方的环境空气直接自然对流换热.根据理论上的分析计算,可得K= 8.54 ( W/㎡•K)。
肋片散热分析—计算传热学课程设计

中国石油大学(华东)储建学院热能与动力工程系《计算传热学程^设计》设计报告学生姓名:龚波学号:08123217 专业班级:热能与动力工程08 —2班指导教师:黄善波2011年7月5日1设计题目在工程实际中,往往需要增加(对流)传热量,应用比较广泛的较为有效的一种方法就是增加换热面积,即采用肋片一在材料消耗量增加较少的条件下能较多地增大换热面积。
在一些换热设备中,肋片得到了广泛地应用,如制冷装置的冷凝器、散热器、空气加热器等等。
设计题目某等截面圆柱形直肋,设肋端是绝热的。
试分析在一定的金属消耗量下,为使肋片的散热量达到最大时所需要的肋片尺寸,并分析肋片的材料、表面传热系数对该尺寸的影响。
已知参数为了求得数值结果和利用结果进行分析,现给定题目相关已知量,包括肋片材料导热系数4二4"。
二100(1+,肋基温度7;内5 肋表度黑度£=,周围空气温度7尸20口环境辐射温度7>15r;肋表面空气的表面换热系数力广8"/位'・℃).2物理与数学模型物理模型发生在肋片的导热过程严格地说是多维的。
如图1所示,暴露于恒温流体的圆柱肋片(肋高为,直径为〃)。
由于圆柱直肋各处受热均匀,再加上肋片通常是由金属材料制成的,导热系数比较大,可以想象肋片内温度将仅沿肋高方向发生明显变化,再直径方向上变化相比很小。
因此,假设该圆柱直肋在同一截面上温度相同,则该问题可转化为等截面直肋一维稳态导热问题。
数学模型以肋基为坐标原点,圆柱肋片厚度方向为坐标正方向,建立坐标系如图2所示。
基于上述物理模型,则该问题的数学模型可描述如下:(Ha)左右两侧相应的边界条件分别是第一类边界条件和第二类边界条件,分别描述如下: 左边界(1-b)右边界(1-c)dt/dx=Odx\D图1圆柱肋片物理模型图3数值处理与程序设计数学模型无量纲化为了使数值计算结果具有更普遍的意义,—x八Tx=一,0=—— L K控制方程无量纲化后,方程整理为d20 1 dk(dO^ UZ? /7 <r\dC昔以一『如R"-,)定义1 欣_ULKj 9 Sl x9 blk dO A(N产—"一R 人一1将上述定义带入式(3)中,整理得:左边界4=0=1右边界丝=0 dx j试射法的形式令将上述数学模型无量纲化。
《传热学》课教案

《传热学》课教案本课程共27学时,讲课23学时,实验4学时。
属院级必修课。
每一节课都应做到承前启后。
(第一次课)一、主要内容第1章绪论1、引言2、热量传递的三种基本形式3、传热过程第2章导热理论和一维稳态导热1、立叶定律及导热系数二、讲课重点1、傅立叶定律2、导热系数三、讲课难点1、引言中的热量传递三种基本形式及传热量计算2、导热系数四、举例1、传热的增强和削弱技术举例为暖气供热,说明哪部分是需要增强的传热,哪部分是需要削弱传热,说明其增强和削弱传热的技术措施。
2、确定温度场和控制所需的温度举例为:研究热应力时需先确定温度场,以连铸机拉矫辊温度场的确定为例加以说明。
(第二次课)一、主要内容第2章导热理论和一维稳态导热1、导热方程及单值性条件2、单层平壁的稳态导热3、多层平壁的稳态导热二、讲课重点1、导热微分方程2、单值性条件:包括第三类边界条件(对流边界条件)、第一类边界条件(温度边界条件)和初始条件。
3、平壁导热的热阻表达式三、讲课难点1、导热微分方程的推导2、第三类边界条件中等式两端正负号一致问题四、举例1、书中例2-12、导热系数随温度变化时平壁内的温度分布3、解释温度曲线凸向的原因(第三次课)一、主要内容第2章导热理论和一维稳态导热1、无限长圆筒壁的稳态导热2、球壁的稳态导热3、通过等截面棒的稳态的导热4、各种肋片散热量的计算二、讲课重点1、无限长圆筒壁热阻的表达式2、球壁热阻的表达式3、等截面棒模型温度分布的分析及应用的场合三、讲课难点1、等截面棒温度场的推导及换热量的计算四、举例结合例题,讲述圆球法测定粒状材料的导热系数的实验,说明实验原理、方法、步骤及实验数据的处理方法。
(第四次课)一、主要内容第3章非稳态导热1、非稳态导热过程的特点2、无限大平板的加热和冷却二、讲课重点1、非稳态导热过程的特点2、无限大平板的加热或冷却问题数学模型的建立三、讲课难点1、无限大平板非稳态导热问题数学模型的求解,即分离变量法2、详细推导此数学模型的求解过程四、举例1、介绍本书中应用图表法求解无限大平板的加热或冷却问题,介绍图表法的求解思路,即:第1步:查取中心面或中心线的温度(分别对于板、圆柱体、球体来说明)第2步:查取任意点的温度第3步:查取热流量值第4步:计算Q 0第5步:计算Q 值(第五次课)一、主要内容第3章 非稳态导热1、半无限大物体非稳态导热的数学模型建立2、有限大物体温度场的求解思路(不讲具体计算方法)3、集总参数法二、讲课重点1、集总参数法的温度场及热流量计算2、集总参数法的解题思想3、集总参数法的应用条件及所适用的问题三、讲课难点1、集总参数法数学模型的求解2、详细推导此数学模型的求解过程四、举例1、结合书中的例题说明集总参数法在实际问题中的应用,首先说明热电偶的用途及特点,简单介绍热电偶的工作原理,结合其工作原理说明本例题所提到问题的实际存在性,然后说明本题的求解方法。
传热学— 肋片传热

结果分析:
于是可采用以下方法: 1.选用导热系数更小的材料作套管; 2.尽量增加套管的高度,并减小壁厚; 3.强化套管与流体的换热; 4.在储气筒或套管外包以保温材料。
圆筒壁一维导热:
假设:1)半径r<<长度l,将其看成一维问题 2)温度不随时间变化,稳态导热
Φ
tw 1 t w(n 1)
n
1 ln ri 1
i 1 2il
ri
W
研究意义
回顾上节课,我们研究了平壁一维导热和圆筒壁一维导热。它们 有个共同的特点,即在热量传递方向热流量 Φ 保持不变。
然而,在工程技术中还经常遇到另一类的一维导热问题—热量在
等截面直肋的 1.问题重导述 热
已知: (1) 矩形直肋 (2) 肋跟温度为t0,且t0 > t (3) 肋片与环境的表面传热系数为 h. (4) ,h和Ac均保持不变 求:
温度场 t 和热流量
Z
等截面直肋的
Y
2.物理模导型 热
X
分析:严格地说,肋片中的温度场是三维、稳态、无内热源、常物性、第三类边
ex ; 2
th(
x)
e e
x x
ex ex
双曲正弦函数
双曲余弦函数
双曲正切函数
稳态条件下肋片表面的散热量 = 通过肋基导入肋片的热量Leabharlann ΦAddx
x0
Ac0m th(mH )
hP m
0
th(mH )
肋端过余温度: 即 x = H
0
ch[m(H x)] ch(mH )
0
1 ch(mH )
第二章 稳态热传导
—2.4 肋片导热
主讲人:王琴 指导老师:胡烨 班级:11级交通试验班
计算传热学课程设计

计算传热学课程设计一、课程目标知识目标:1. 让学生掌握计算传热学的基本概念,理解热传导、对流和辐射的基本原理;2. 培养学生运用数学和物理知识解决传热问题的能力,掌握传热方程式的建立和求解方法;3. 引导学生了解计算传热学在实际工程中的应用,如建筑、能源、航空航天等领域。
技能目标:1. 培养学生运用计算传热软件进行传热问题模拟和分析的能力;2. 提高学生解决实际工程传热问题的能力,包括问题建模、计算和结果分析;3. 培养学生团队协作和沟通能力,能在小组讨论中发表自己的观点和倾听他人意见。
情感态度价值观目标:1. 培养学生对计算传热学领域的兴趣,激发学生探索科学问题的热情;2. 增强学生的环保意识,让学生了解传热学在节能减排中的重要作用;3. 引导学生树立正确的价值观,认识到科学技术对社会发展的推动作用。
课程性质分析:本课程属于应用物理学科,旨在培养学生运用数学、物理知识解决实际传热问题的能力。
课程内容具有较强的理论性和实践性,需要结合实际工程案例进行教学。
学生特点分析:学生为高中年级,已具备一定的数学和物理基础,但传热学相关概念和技能还需进一步培养。
学生对新鲜事物充满好奇,喜欢探索和实践。
教学要求:1. 注重理论联系实际,通过案例分析、实验演示等方式,提高学生的实践能力;2. 采用启发式教学,引导学生主动思考、提问和解决问题;3. 鼓励学生参与课堂讨论,培养团队协作和沟通能力。
二、教学内容1. 热传导理论:包括热传导基本方程、边界条件和初始条件的设定,以及稳态和非稳态热传导问题的求解方法。
教材章节:第二章 热传导理论内容列举:热传导方程、傅里叶定律、热扩散方程、边界条件、稳态解、非稳态解。
2. 对流传热原理:介绍对流传热的基本概念、流动与换热的关联,以及准则关联式的应用。
教材章节:第三章 对流传热内容列举:对流传热机理、流体力学基本方程、雷诺数、努塞尔特数、准则关联式。
3. 辐射传热基础:涵盖热辐射的基本原理、黑体辐射定律、实际表面的辐射特性以及辐射换热的计算方法。
传热学---通过肋片的导热

A
λA
+
rc
+
δB ) λ AB
(1)当热流量不变时,接触热阻 rc 较大时,必然 在界面上产生较大温差。
(2)当温差不变时,热流量必然随着接触热阻 rc 的增大而下降。
(3)即使接触热阻 rc 不是很大,若热流量很大, 界面上的温差是不容忽视的
22:58
第四节 通过肋片的导热
接触热阻的影响因素: (1)固体表面的粗糙度 (2)接触表面的硬度匹配 (3)接触面上的挤压压力 (4)空隙中的介质的性质
1 ch (mH
)
22:58
2
第四节 通过肋片的导热
几点说明: (1) 上述推导中忽略了肋端的散热(认为肋端绝热)。
对于一般工程计算,尤其高而薄的肋片,足够精确。 若必须考虑肋端散热,取:Hc=H + δ /2
(2)上述分析近似认为肋片温度场为一维。 当Bi=hδ/λ ≤ 0.05 时,误差小于1%。 对于短而厚的肋片,二维温度场,上述算式不适用; 实际上,肋片表面上表面传热系数h不是均匀一 致的—--数值计算
和其它变截面物体的导热 ¾第四节 通过肋片的导热
22:58
第四节 通过肋片的导热
第三类边界条件下通过平壁的一维稳态导热:
Φ=
1
tf1 −tf2 +δ +
1
[W ]
h1A λA h2 A
为了增加传热量,可以采取哪些措施?
(1)增加温差(tf1-tf2),但受工艺条 件限制 (2)减小热阻:
a) 金属壁一般很薄(δ 很小)、热导率很大,故导热热 阻一般可忽略。
22:58
第四节 通过肋片的导热
1 通过等截面直肋的导热 已知: (1)矩形直肋 (2)肋跟温度为t0,且t0>t∞ (3)肋片与环境的表面传热系数为h。 (4)λ,h和Ac均保持不变 求:温度场t和热流量Φ
基于MATLAB的肋片传热特性分析与优化设计

根据以上分析 , 设计肋片的高度为 0101m , 肋厚为 01001m ; 则肋片的温度分布如图 4 所示 。
14 CHEMICAL ENGINEERING DESIGN 化工设计 2005 , 15( 6)
基于 MA TL AB 的肋片传热特性分析与优化设计
叶长 Ξ 福州大学化学化工学院 福州 350002 摘要 利用 MA TLAB 对肋片传热过程进行数值模拟 , 并对肋片的传热特性进行了分析研究 。在此基
5t Φx = - λ AC 5x
而输出微元体的导热量为 :
Φx + dx = Φx + 5 5x
-λ AC
5t dx 5x
1 数学模型与数值模拟
在肋片传热中 , 常用的肋片结构主要有等横 截面直肋如矩形直肋 、圆形针肋及非等横截面肋 片如环肋 、三角形肋片等 [ 1 ] , 其中矩形 、梯形 、 三角形的环肋 t2 t′ 2 = t1
位置 x 的温度梯度 ; 利用 plot ( sol1 x - x1 , sol1 y (1 , : ) ) 和 plot ( sol1 x - x1 , sol1 y ( 2 , : ) ) 命令 即可绘制出肋片上的温度分布和温度梯度关系 图 。肋片的散热量都必须要通过肋根向外传递 , 肋片的散热量等于肋根处的传热量 , 即根据傅立 叶定律计算 :
2 h ( t 1 - t ∞) t2 1 5δ λ δ δ5 x x = t0 , t2
( x2)
( 3)
1 d
r dr
r
dt dr
=
2 h ( t - t ∞) λ δ
( 6)
( x1)
= 0 , x 1 ≤x ≤x 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国石油大学(华东)储建学院热能与动力工程系《计算传热学程序设计》设计报告学生姓名:龚波学号:08123217专业班级:热能与动力工程08-2班指导教师:黄善波2011年7 月5 日1 设计题目在工程实际中,往往需要增加(对流)传热量,应用比较广泛的较为有效的一种方法就是增加换热面积,即采用肋片—在材料消耗量增加较少的条件下能较多地增大换热面积。
在一些换热设备中,肋片得到了广泛地应用,如制冷装置的冷凝器、散热器、空气加热器等等。
1.1 设计题目某等截面圆柱形直肋,设肋端是绝热的。
试分析在一定的金属消耗量下,为使肋片的散热量达到最大时所需要的肋片尺寸,并分析肋片的材料、表面传热系数对该尺寸的影响。
1.2 已知参数为了求得数值结果和利用结果进行分析,现给定题目相关已知量,包括肋片材料导热系数λ=λοk(T)=400(1+0.0035T),肋基温度T w=95℃,肋表度黑度ε=0.80,周围空气温度T f=20℃,环境辐射温度T s=15℃,肋表面空气的表面换热系数h c=8W/(m2•℃)。
2 物理与数学模型2.1 物理模型发生在肋片的导热过程严格地说是多维的。
如图1所示,暴露于恒温流体的圆柱肋片(肋高为L,直径为D)。
由于圆柱直肋各处受热均匀,再加上肋片通常是由金属材料制成的,导热系数比较大,可以想象肋片内温度将仅沿肋高方向发生明显变化,再直径方向上变化相比很小。
因此,假设该圆柱直肋在同一截面上温度相同,则该问题可转化为等截面直肋一维稳态导热问题。
图1 圆柱肋片物理模型图2.2 数学模型以肋基为坐标原点,圆柱肋片厚度方向为坐标正方向,建立坐标系如图2所示。
基于上述物理模型,则该问题的数学模型可描述如下:()()440c f b sd dTA U h T T T Tdx dxλεσ⎛⎫⎡⎤--+-=⎪⎣⎦⎝⎭(1-a)左右两侧相应的边界条件分别是第一类边界条件和第二类边界条件,分别描述如下:左边界0wxT T==(1-b)右边界x LdTdx==(1-c)图2 圆柱肋片数学模型图3 数值处理与程序设计3.1数学模型无量纲化为了使数值计算结果具有更普遍的意义,将上述数学模型无量纲化。
为此定义xxL=,fw fT TT Tθ-=-(2)控制方程无量纲化后,方程整理为()44222321f sc b w fw f w fT Td dk d ULh T Tk d A T T T Td xd xθθθεσθθλ⎧⎫⎡⎤⎛⎫⎛⎫⎪⎪⎛⎫⎢⎥+-⨯+-+-=⎪ ⎪⎨⎬⎪ ⎪ ⎪--⎢⎥⎝⎭⎪⎪⎝⎭⎝⎭⎣⎦⎩⎭(3)定义1d dk k k d θ=,Lx UL S A =,c c h LBi ολ= , ()3b w f R T T LN οεσλ-=,f f w fT T T θ=-,ss w fT T T θ=- (4)将上述定义带入式(3)中,整理得:(){}224420Lx d c R f s S d d k Bi N k d x d xθθθθθθ⎛⎫⎡⎤+-++-= ⎪⎢⎥⎣⎦⎝⎭ (5-a ) 左边界01x θ== (5-b)右边界10x d d xθ== (5-c ) 3.2 试射法的形式令1y θ=,12dy d y d x d xθ== (6) 则有试射法形式模型12dy y d x= (7-a ) (){}4242211Lx d c R f s S dy k y Bi y N y k d xθθ⎡⎤=-+++-⎢⎥⎣⎦(7-b)左边界11121P y Q y W +=(7-c )其中,P 1=1,Q 1=0,W 1=1右边界21222P y Q y W +=(7-d )其中,P 2=0,Q 2=1,W 2=03.3 程序编写圆柱直肋一维稳态导热数学模型是二阶常微分两点边值问题,可以采用试射法求解。
其基本思想是将边值问题转换为初值问题求解。
3.3.1 设计特点在主程序外设置全局变量,为使在调用各子程序时,不会因实参与形参的作用范围而无法编译、运行程序。
在主程序头部,对参数赋值,对体积和肋高赋值应注意范围和两者的关联性。
此处赋值V=0.00002m3,L=0.5m,保证程序结果为最大传热量,而且保证了足够的计算空间又不至于过分浪费系统资源。
利用循环实现计算最大传热量的过程,首先调用肋高函数得到按线性规律递减的肋高,再调用shoot函数计算相应肋高时的肋基温度梯度,调用热量函数求解热量Q[g],输出各个肋高下的肋基温度梯度和热量,为了便于了解热量随肋高的变化关系。
比较各肋高下的热量值,将最大热量值对应下标保留。
然后,输出最大热量Q[max]和相应的肋高LG[max],再根据几何关系求解圆柱肋片的面积A,半径r和此时的最佳长径比CJB(肋高与半径的比值)。
再次调用shoot函数,求解最大传热量时圆柱肋片的温度分布和温度梯度。
求出最大传热量使用后,对程序进行验证,用户只需根据实际情况对热量函数RL,用户子程序的相关参数进行设置,不需要对验证程序进行操作,即可对程序结果进行验证。
本程序在无辐射和导热率为定值时,即λ=C(常数),N R=0时,验证程序自动执行。
本程序采用的试射法考虑了物性的变化,辐射的影响,且对模型进行了无量纲化,因此具有普遍的适用性。
3.3.2 程序流程先给程序中相关参数赋值,给定材料体积,利用试射法计算各个肋高是的肋基温度和温度梯度,根据温度梯度求肋片相应肋高的传热量,比较各个传热量值确定最大传热量,最后输出最大传热量对应结果,如果初参数满足验证程序的条件,执行验证程序并输出验证程序的结果,程序结束。
程序流程图如下。
图3 程序流程图4 模型与程序的验证4.1 模型验证为了方便利用解析解验证程序,将本题简化为常物性、无辐射等截面直肋一维稳态导热模型。
已知肋片材料导热系数λ=100 W/(m •℃),肋基温度T w =95℃,周围空气温度T f =20℃,肋表面空气的表面换热系数h c =8W/(m 2•℃)。
建立坐标系,列出其控制方程式及定解条件:222d m dxθθ= (8-a)00,;θθ===-w f x t t ,0θ==d x H dx(8-b)其中过余温度f t t θ=-,m =式(8-a )是一个二阶线性微分方程,由两边界条件可求出精确解为()()ch m x h ch mh θθ-⎡⎤⎣⎦=(9)4.2 程序验证将式(9)中参数换算成无量纲形式,然后编程,计算出每个节点温度的解析解(验证程序见附录)和数值解(验证源程序见附录),进行比较,如表格1。
表1 λ=100、无辐射圆柱直肋无量纲温度值数值解和分析解x 数值解 理论解 百分误差/% 01 1 0 0.05 0.966899 0.966899 00.1 0.935906 0.935905 0.000106850.15 0.906951 0.906951 0 0.2 0.879973 0.879973 00.25 0.854913 0.854912 0.000116970.3 0.831715 0.831715 00.35 0.81033 0.810329 0.000123410.4 0.79071 0.79071 0 0.45 0.772814 0.772813 0.0001294 0.5 0.756602 0.756601 0.00013217 0.55 0.742038 0.742037 0.00013476 0.6 0.729091 0.72909 0.00013716 0.65 0.717733 0.717732 0.00013933 0.7 0.707939 0.707938 0.00014126 0.75 0.699687 0.699686 0.00014292 0.8 0.69296 0.692959 0.00014431 0.85 0.687744 0.687742 0.00029081 0.9 0.684026 0.684024 0.00029239 0.95 0.681798 0.681797 0.00014667 10.6810560.6810550.0001468300.20.40.60.811.200.30.60.91.2无量纲位置无量纲温度图4 圆柱直肋无量纲温度分布曲线由上述图表可知圆柱肋片分析解和数值解相差不大,二者吻合较好,可以说明所编制的数值解法的程序是正确的。
5 计算结果与分析5.1 肋高与热量的关系材料的导热率λ=400(1+0.0035T),肋基温度T w=95℃,肋表度黑度ε=0.80,周围空气温度T f=20℃,环境辐射温度T s=15℃,肋表面空气的表面换热系数h c=8W/(m2•℃)时,圆柱肋片肋基无量纲温度梯度和传热量见表2。
表2 不同长度下肋片的传热量任意长度L/m 肋基温度梯度热量Φ/W0.5 10 -54.92460.49 10 -57.18930.48 -1.98619 11.83710.47 -1.92857 11.9880.46 -1.87095 12.1410.45 -1.81331 12.29570.4 -1.52509 13.08830.39 -1.46747 13.24790.36 -1.29491 13.71960.35 -1.23757 13.87210.34 -1.18038 14.02080.33 -1.12339 14.16470.32 -1.06663 14.30280.27 -0.78888 14.8590.26 -0.73514 14.93240.25 -0.68225 14.98890.24 -0.63034 15.02660.23 -0.57955 15.04320.22 -0.53001 15.03660.21 -0.48189 15.00440.2 -0.43533 14.94410.19 -0.39049 14.85290.18 -0.34756 14.72950.17 -0.30666 14.57040.1 -0.08934 12.26740.07 -0.03744 10.49210.06 -0.0256 9.76310.05 -0.01629 8.94650.04 -0.00935 8.02070.03 -0.00456 6.95490.02 -0.00166 5.69630.01 -0.00029 3.9285从表中结果易看出在肋高为0.50m和0.49m的时候,肋基温度梯度为正值,传热量为负值,与实际情况不符。
这是因为肋高增加,一定的耗材下,肋片直径变小,对流换热量处理成广义热源已不合适,即不能作为一维稳态导热模型看待。
此时,增大肋片体积、增加导热率或减小对流换热系数,又能满足模型使用调节。
