中等职业学校高一下数学试题卷
职业高中高一下学期期末数学试题卷5(含答案)

职业高中下学期期末考试 高一《 数学_》试题5一. 选择题:(每小题3分,共30分)1.函数()x a y 1-=在R 上是增函数,则a 的取值范围是( )A.a >1B.1<a <2C.a >2D.2<a <3 2.若n m ==5ln ,2ln ,则n m e +2的值为 ( )A .2B .5C .20D .103.函数2()log (1)f x x π=+的定义域是( ) A .(1,1)-B .(0,)+∞C .(1,)+∞D .R4.下列说法中,正确的是( )A. 第一象限角一定是锐角B.锐角一定是第一象限角 B. 小于90度的角一定是锐角 D.第一象限角一定是正角5.已知α为第二象限角,则=-•αα2cos 1sin 1. A. 1 B.-1 C.1或-1 D.以上都不是6.下列函数中,在区间⎪⎭⎫⎝⎛2,0π上是减函数的是( )A .x y sin =B .x y cos =C .x y tan =D .2x y =7.等差数列{n a }的通项公式是n a = -3n + 2 ,则公差d = ( )A. -4B. -3C. 3D. 48.在等差数列{n a }中,若=+173a a 10 ,则19S = ( )A. 65B. 75C. 85D. 959.已知等比数列{}n a 中,,32,832==a a 则=1a ( )A. 2B. 4C. 6D. 810.三个正数c b a ,,成等比数列, 是c b a lg ,lg ,lg 成等差数列的 A .充要条件 B .必要条件 C .充分条件 D .无法确定 二.填空题(每小题3分,共24分) 11.已知()[]0lg log log 37=x ;则=x .12.函数()lg(lg 2)f x x =-的定义域是 .13. =+2log 15514.与52π-终边相同的角中最小正角是 15.在三角形ABC 中,如果B A cos sin ⋅<0,则△ABC 是 三角形 16.已知2cos sin =+αα,则=⋅ααcos sin . 17.等比数列{}n a 中,若,2563=a a 则=72a a _______ 18.等比数列{}n a 中,若12632==a a ,,则S 6 =_______ 三.计算题:(每小题8分,共24分)19.已知:()()521322231,31-++-⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛=x x x x x g x f ,()x f >()x g ,求x 的取值范围.专业 班级 姓名 学籍号 考场 座号20.求值sin()tan()cos()cos(2)tan()sin()πααπαπαπαπα+-+++-.21.在等比数列{}n a 中,若,2,12413=-=-a a a a 求首项1a 和公比q .四.证明题:(每小题6分,共12分)22.已知(1,10)x ∈, 22lg ,lg ,lg(lg ),A x B x C x === 证明:C A B <<.23.1=-.五:综合题:(10分) 24.等比数列}{n a 中,公比q=2,25log log log 1022212=+•••++a a a ,求n a a a +•••++21.高一 《 数学__》试题5参考答案一.选择题:1---5 CCDBA 6----10 BBDAA 二.填空题11. 1000 12.[100,+∞ ) 13. 10 14.58π 15.钝角 16.2117.25 18.189 三.计算题:(每小题8分,共24分) 19.已知:()()521322231,31-++-⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛=x x x x x g x f ,()x f >()x g ,求x 的取值范围.20.求值sin()tan()cos()cos(2)tan()sin()πααπαπαπαπα+-+++-.解 原式=()()1sin tan cos cos tan sin -=---αααααα.21.在等比数列{}n a 中,若,2,12413=-=-a a a a 求首项1a 和公比q . 解 由等比数列的通项公式得()()⎩⎨⎧=-=-=-=-21112113121121q q a q a q a q a a q a 解得 ⎪⎩⎪⎨⎧==2311q a 所以2,311==q a 四.证明题:(每小题6分,共12分)22.已知(1,10)x ∈, 22lg ,lg ,lg(lg ),A x B x C x === 证明:C A B <<.(答案略)23.1=-.证明 左边=()()120cos 20sin 20cos 20sin 20cos 20sin 20cos 20sin 20cos 20sin 20cos 20sin 2-=---=--=--οοοοοοοοοοοο=右边所以1︒=-五:综合题:(10分) 24.等比数列}{n a 中,公比q=2,25log log log 1022212=+•••++a a a ,求na a a +•••++21.(答案略)。
中职数学 2018-2019学年新疆喀什地区喀什十五中职业学校高中班高一(下)期末数学试卷

2018-2019学年新疆喀什地区喀什十五中职业学校高中班高一(下)期末数学试卷一、单选题(本题共16小题,每小题2分,共32分)A .38B .39C .41D .421.(2分)在等差数列{a n }中,已知a 1=2,a 2+a 3+a 4=24,则a 4+a 5+a 6=( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.(2分)已知直线l 1:ax +y -1=0,l 2:(a -1)x -2y +1=0,则“a =2”是“l 1⊥l 2”的( )A .[-18,6]B .[-2,6]C .[-2,18]D .[4,18]3.(2分)若圆C :x 2+y 2-6x -6y -m =0上有到(-1,0)的距离为1的点,则实数m 的取值范围为( )A .652B .65C .130D .1504.(2分)已知等差数列{a n }的公差d ≠0,且a 24+a 26+40d =a 28+a210,则该数列{a n }的前13项的和为( )A .π6B .π3C .2π3D .5π65.(2分)直线y =33x +1的倾斜角为( )√A .直线l 的倾斜角为π6B .直线l 的法向量为(3,1)C .直线l 的方向向量为(1,3)D .直线l 的斜率为−36.(2分)已知直线l :3x −y +3=0,下列结论正确的是( )√√√√7.(2分)已知正n 边形的边长为a ,内切圆的半径为r ,外接圆的半径为R ,则R +r =a2tanβ,其中β=( )A .πnB .π2nC .π3nD .π4nA .24bB .22bC .4+24bD .4+22b8.(2分)已知向量a ,b 满足|a |=1,|b |=2,a 与b 的夹角为π4,则a +b 在b 上的投影向量为( )→→→→→→→→→√→√→√→√→A .30°B .60°C .120°D .150°9.(2分)直线3x +3y +1=0的倾斜角α=( )√A .−2425B .725C .2425D .-72510.(2分)若角α的终边过点P (-3,4),则cos 2α=( )A .2B .2或18C .18D .1611.(2分)设P 是双曲线x2a2-y 29=1左支上一点,该双曲线的一条渐近线方程是3x +4y =0,F 1,F 2分别是双曲线的左、右焦点,若|PF 1|=10,则|PF 2|等于( )A .-3B .-32C .3D .3212.(2分)已知向量a =(3,0),b =(x ,-2),且a ⊥(a -2b ),则x =( )→√→→→→√√√√A .110B .78C .55D .4513.(2分)若等差数列{a n }满足2a 8-a 9=6,则它的前13项和为( )A .99B .66C .297D .14414.(2分)等差数列{a n }中,a 1+a 4+a 7=39,a 3+a 5+a 9=27,则前9项的和S 9=( )15.(2分)已知等差数列前n 项和为S n .且S 13<0,S 12>0,则此数列中绝对值最小的项为( )二、填空题(本题共8小题,每小题4分,共32分)三、解答题(本题共4小题,每小题9分,共36分)A .第5项B .第6项C .第7项D .第8项A .多821斤B .少821斤C .多13斤D .少13斤16.(2分)我国南北朝时的数学著作《张邱建算经》有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下三人后入得金三斤,持出,中间四人未到者,亦依次更给,问各得金几何?“则在该问题中,等级较高的一等人所得黄金比等级较低的九等人所得黄金( )17.(4分)已知向量a =(1,m ),b =(2,-2),且 a ⊥b ,则m =.→→→→18.(4分)等比数列{a n }中,a 4,a 8是关于x 的方程x 2-10x +4=0两个实根,则a 2a 6a 10=。
中职高一(下)数学期末试卷A3

→ → 24. △ABC 中,D 是 BC 边上的中点,若 AB=→ a , AC= → b, → 则 AD=___________________. (用→ a ,→ b 表示)
31.(8 分)等比数列{an}中,a3+a6=36,
1 a4+a7=18, an=2, 求 n.
25. 已知△ABC 中,sinA=
2
衢 江 区 职 业 中 专 期末 试 卷
2012—2013 学年第 二 学期
职高数学
3 4 5 6 7
课程
1 2
专业
8 9
高职预科
10 11 12 13
年级
14 15
2012 高职
16 17 18
10.下列命题中,正确的是 A.终边相同的角都相等 C.第一象限的角都是锐角
(
) B.第一象限的角都比第二象限的角小 D.锐角都是第一象限的角 ( → C. SP ) → D. SQ
三、解答题(本题共 8 小题,共 60 分) 27.(6 分)已知角 的终边过点 P(-1,2),求角 的三角函数值。
28.(6 分) 等差数列{an}中,a1=10,a7=-38,求 d 和 S7. 33. (9 分) 已知平行四边形 ABCD, 点 A(-1,2), B(3,4), D(2,6),求 C 点坐标 (ABCD 为顺次连接)
4. 数列 4,9,16,x,36…则 x= ( ) A.25 B.20 C.18 D.30 5. 已知 sinA tanA<0,则 A 所在的象限是 ( ) A.第二或第四象限 B.第一或第三象限 C.第二或第三象限 D.第一或第四象限 6. 若 tan=﹣2,则 tan(3π -)的值为 ( ) A.3 B.﹣3 C.2 D.﹣2 7. 下列命题中的假命题是 ( ) → → A.向量 AB 与 BA 的长度相等,方向相反 B.两个相等向量若起点相同,则终点必相同 C.零向量的方向不确定 D.共线的单位向量都相等 8.等差数列{an}中,a1=-2, S11=143,则 a11= A.24 B.26 C.28 3a1+a2 9. 已知数列{an}是等比数列,q=2.则3a +a = 3 4 1 1 1 A. 3 B. 6 C. 4
中职高一下期中数学试卷

《中职高一数学期中考试》试题★注意事项:1.本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分150分,考试时间90分钟;2.请将第Ⅰ卷(选择题)的答案填写到第3页答题卡上。
第Ⅰ卷(选择题,共60分)一、选择题(本大题共15题,每题4分,共60分)1.60-︒角的终边在 ().A 、第一象限B 、第二象限C 、第三象限D 、第四象限 2.与角30︒终边相同的角是 ( ).A 、60-︒B 、390︒C 、-300︒D 、390-︒ 3.已知A (-1,3),AB (6,-2),则点B 的坐标为( )A 、(5,1)B 、(-5,-1)C 、(-7,5)D 、(7,-5) 4.角α的终边经过点P (4,-3),则tan α的值为( )A 43-B 34-C 34D 43 5.cos(﹣60°)=( )A B ﹣ C D ﹣6.如果α是锐角,那么2α是( )。
A 、第一象限角 B 、第二象限角 C 、小于180°的正角 D 、不大于直角的正角7.已知函数y= -5+4cosX ,则函数的最大值是( )。
A 、 1 B 、 -1 C 、-5 D 、-98.下列说法正确的有( )个。
①零向量长度为0,方向不确定;②单位向量是长度为1的向量;③相等向量是长度相等的向量;④平行向量是共线向量,方向相同或相反; ○5相反向量的模相等。
A 、 1 B 、2 C 、3 D 、49.已知向量)3,2(-与)1,1(-,则-2的坐标为( )得分 阅卷A 、)5,3(-B 、)7,5(-C 、)7,3(-D 、)5,5(- 10.已知点A (-1,8),B (2,4),则AB= ( )。
A 、 5 B 、 25 C 、 13 D 、11.下列说法错误的是( )A 、零向量与任一向量平行B 、零向量的方向是任意的C 、单位向量的方向与坐标轴方向相同D 、单位向量具有无数个 12. 求值5cos1803sin902tan06sin 270︒-︒+︒-︒=( ) A -2 B 2 C 3 D -313.如图,设===AB b OB a OA 则,, ( )A .b a +B .b a -C .b a +-D .b a --14.设O 为正三角形ABC 的中心,则、、是( )。
职业中等专业学校(高一数学)期末考试试题库

职业中等专业学校(高一数学)期末考试试题库1.集合{x|-1<x≤5}用区间表示为() [单选题] *A. (-1,5)B. (-1,5](正确答案)C. (-1,4)D. [-1,5]2.若函数f(X)=x²-6x+5.则f(x)的最小值为() [单选题] *A.4B.-4(正确答案)C. 5D.-53.要使有意义,则x的取值范围() [单选题] *A .空集B .R(正确答案)C.{0}D .14.若|x|>3,则x的取值范围是() [单选题] *A . {x|-3<x<3}B. {x|x<-3或x>3}(正确答案)C .{x|x>3}D. {x|x<-3}5.要使有意义,则x的取值范围() [单选题] *A. 空集B. R(正确答案)C.{0}D .16.若|x|<2,则x的取值范围是() [单选题] *A.{x|-2<x<2}B.{x|x<-2或x>2}(正确答案)C.{x|x>2}D.{x|x<-2}7.已知函数则f(2)=() [单选题] *A.11/5B .12/5C.13/5D.14/5(正确答案)8.函数y=x² +4的奇偶性是() [单选题] *A .偶函数(正确答案)B.非奇非偶函数C.既是奇函数又是偶函数D.奇函数9.函数f(x)=x+1,则此函数() [单选题] *A. 单调减区间是(0,+∞)B. 单调减区间是(-∞,0)C. 既有单调增区间又有单调减区间D. 单调增区是(-∞,+∞)(正确答案)10.已知函数f(x)=x²-7x,则f(-1)=() [单选题] *A .6B. 8(正确答案)C. 9D.-611.下列所给的不等式为一元二次不等式的是() [单选题] *A. 3x+4<0B.1/x+1>0C. x+1<0D.x²-x+10<0(正确答案)12.下列命题正确的是() [单选题] *A. 若a<b,则ac<bcB. 若a<b,则a-1>b-1C. 若a>b,则ac²<bc²D. 若a<b,则-2a>-2b(正确答案)13.算式() [单选题] *A.42B.45(正确答案)C.54D.3014.设集合A=(-∞,-1),全集为R,则集合A的补集() [单选题] *A.(-∞-1]B.[-1,+∞)(正确答案)C.(-1,+∞)D.(-∞,-1)15.若a<0,则下列不等式不正确的是() [单选题] *A.4-a>3-aB.4+a>3+aC.4a>3a(正确答案)D.3a>4a16.集合R用区间表示为() [单选题] *A.(-∞,0)B. RC. (0,+∞)D.(-∞,+∞)(正确答案)17.下列函数在区间(-∞,0)内为减函数的是() [单选题] *A.f(x)=-5x(正确答案)B.f(x)=xC.f(x)=x+5D.f(x)=-x²18.元素3属于以下哪个区间() [单选题] *A. (1,2)B. (0,2)。
山东省德州市职业中等专业学校高一数学理下学期期末试题含解析
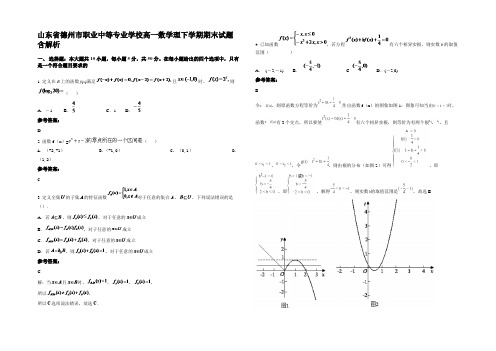
山东省德州市职业中等专业学校高一数学理下学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 定义在R上的函数f(x)满足且时,则()A.-1 B.C.1 D.参考答案:D2. 函数f(x)=()A.(-2,-1) B.(-1,0) C. (0,1) D. (1,2)参考答案:C3. 定义全集的子集的特征函数对于任意的集合、,下列说法错误的是().A.若,则,对于任意的成立B.,对于任意的成立C.,对于任意的成立D.若,则,对于任意的成立参考答案:C解:当且时,,,,所以,所以选项说法错误,故选.4. 已知函数,若方程有六个相异实根,则实数b的取值范围()A.(-2,-1) B. C. D.(-2,0)参考答案:B令,则原函数方程等价为,作出函数f(x)的图象如图1:图象可知当由时,函数有3个交点,所以要使有六个相异实根,则等价为有两个根,,且,,令,则由根的分布(如图2)可得,即,即,解得,则实数的取值范围是,故选B.5. (5分)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是()A.B.C.D.参考答案:A考点:棱柱、棱锥、棱台的侧面积和表面积;旋转体(圆柱、圆锥、圆台).专题:计算题.分析:设圆柱底面积半径为r,求出圆柱的高,然后求圆柱的全面积与侧面积的比.解答:设圆柱底面积半径为r,则高为2πr,全面积:侧面积=[(2πr)2+2πr2]:(2πr)2=.故选A.点评:本题考查圆柱的侧面积、表面积,考查计算能力,是基础题.6. 下列各组函数中,表示同一个函数的是()A.y=1,y=B.y=?,y=C.y=x与y=log a a x(a>0且a≠1)D.y=|x|,参考答案:C【考点】判断两个函数是否为同一函数.【分析】利用函数的定义域相同,解析式相同,表示同一个函数,即可判断.【解答】解:对于A,B,D,函数的定义域不同;对于C,函数的定义域相同,解析式相同,表示同一个函数,故选C.7. 已知数列{a n}为等比数列,,,则的值为()A. 7B. -5C. 5D. -7 参考答案:D【分析】利用等比数列的性质及通项公式,列方程组求解a1,q的值,再求解a1+a10的值【详解】a4+a7=2,a5?a6=﹣8,由等比数列的性质可知a5?a6=a4?a7a4?a7=﹣8,a4+a7=2,∴a4=﹣2,a7=4或a4=4,a7=﹣2,a1=1,q3=﹣2或a1=﹣8,q3a1+a10=﹣7故选:D.【点睛】本题考查了数列的基本应用,考查等比数列的性质,熟记性质准确计算是关键,是基础题8. 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A. B. C. D.参考答案:B9. 下列函数f(x)与g(x)表示同一函数的是( )A.f(x)=x0与g(x)=1 B.f(x)=2 lgx与g(x)= lgx2C.f(x)= |x| 与g(x)= D.f(x)=x与g(x)=参考答案:D略10. 2sin75°cos75°的值为A.B.C.D.参考答案:C2sin75°?cos75°=sin150°=,故选;C.二、填空题:本大题共7小题,每小题4分,共28分11. 数列{a n}的通项公式,其前n项和为S n,则等于_____.参考答案:﹣1010【分析】利用通项公式,然后分别求出,,,,得到,,…,明显,每4项相加等于2,进而利用进行求解即可【详解】解:数列的通项公式,则:当时,,当时,,当时,,当时,,…,,…,,故答案为:﹣1010.【点睛】本题考查数列递推式的运用,注意找到规律,属于基础题12. 若等比数列的前项和为,且,则=.参考答案:13. 我舰在敌岛A处南偏西50°的B处,且A,B距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行.若我舰要用2小时追上敌舰,则其速度大小为海里/小时.参考答案:14【考点】解三角形的实际应用.【分析】由题意推出∠BAC=120°,利用余弦定理求出BC=28,然后推出我舰的速度.【解答】解:依题意,∠BAC=120°,AB=12,AC=10×2=20,在△ABC中,由余弦定理,得BC2=AB2+AC2﹣2AB×AC×cos∠BAC=122+202﹣2×12×20×cos120°=784.解得BC=28.所以渔船甲的速度为=14海里/小时.故我舰要用2小时追上敌舰速度大小为:14海里/小时.故答案为:14.14. 函数的定义域集合为。
中职数学 2023-2024学年河南省中等职业学校高一(下)期末数学试卷

2023-2024学年河南省中等职业学校高一(下)期末数学试卷一、选择题(每小题3分,共30分。
每小题只有一个选项是正确的,请将正确选项涂在答题卡上)A .(-33)2=36B .(-33)2=-36C .3-3×33=0D .32×33=361.(3分)下列式子计算正确的是( )A .y =2xB .y =x 2C .y =log 2xD .y =lo x2.(3分)下列函数在区间(0,+∞)上单调递减的是( )g12A .y =30×0.2x (x ∈N *)B .y =30×(1-0.2)x (x ∈N *)C .y =30×(1+0.2)x (x ∈N *)D .y =20×0.3x (x ∈N *)3.(3分)一辆30万元的轿车,每年按照20%的折旧率折旧,设x 年后该汽车的价值为y 万元,则y 与x 之间的关系式可以表示为( )A .-1B .5C .-1或5D .1或-54.(3分)已知点A (-3,2),B (1,a ),且|AB |=5,则a =( )A .4B .-4C .D .-5.(3分)已知直线y =4x +3与直线ax -y +1=0垂直,则a =( )1414A .1B .C .2D .6.(3分)点P (1,2)到直线4x -3y -8=0的距离为( )9525A .45B .45+C .D .7.(3分)一个正三棱柱的底面边长为3,高等于5,则其表面积等于( )9M 3245M 329M 34二、填空题(每小题3分,共24分)A .正四面体B .长方体C .球D .正三棱锥8.(3分)下列各项中,三视图都相同的几何体是( )A .“买一张体育彩票中奖”是不可能事件B .“常温常压下,水加热到90℃会沸腾”是必然事件C .天气预报说明天上午10点钟下雨的概率是70%,则明天上午10点钟必定下雨D .随机事件A 发生的概率为P (A ),则0≤P (A )≤19.(3分)下列说法正确的是( )A .60人,90人,30人B .60人,60人,60人C .40人,60人,20人D .60人,100人,20人10.(3分)某地三所职业学校对2023级学生进行联合质量检测,甲校有1200名学生,乙校有1800名学生,丙校有600名学生,计划采用分层抽样法,抽取一个样本容量为180的样木,则应在这三校分别抽取学生( )11.(3分)计算:×2××= .9-2712M 811M 35612.(3分)指数函数y =a x (a >0且a ≠1)的图像过点(3,8),则当函数的自变量为时,对应的函数值是.1213.(3分)过点(,-3)且倾斜角为的直线方程为 .M 3π614.(3分)与x 2+y 2-8x -12y =0是同心圆,且半径为2的圆的标准方程为.M 315.(3分)已知圆锥的母线长为5,高为4,过圆锥的两条母线作一个截面,则截面的面积的最大值为 .16.(3分)若一个球体的表面积为36πcm 2,则其体积为.3三、解答题(每题8分,共24分)四、证明题(每题6分,共12分)五、综合题(本题10分)17.(3分)从0,1,2,3,4,5这6个数字中随机抽取2个不同的数字,则这两个数字都是奇数的概率 .18.(3分)样本数据74,81,68,69,73的样本均值为 .19.(8分)若lo (2x -1)>lo (x +3),求x 的取值范围.g12g1220.(8分)如图所示,正四棱锥P -ABCD 的底面边长是6,斜高PE =5,求该正四棱锥的侧面积和体积.21.(8分)一个罐子里有20个玻璃球,其中红色球有6个,黑色球有4个,白色球有10个,如果从罐子里随机抽取一个球,求:(1)取到红色玻璃球的概率;(2)取不到红色玻璃球的概率.22.(6分)求证:lo 3<log 32<log 23.g1223.(6分)求证:无论m 取何值,直线l :mx -y +1=0与圆C :x 2+y 2=4一定有两个交点.24.(10分)已知直线l 1过点P (1,3),直线l 2:x -y =0,l 1⊥l 2.(1)求直线l 1的方程;(2)已知圆C 的圆心在x 轴上,且圆C 与直线l 1,l 2均相切,求圆C 的标准方程.。
黑龙江省水利学校(职普融通部)2023-2024学年高一下学期期末考试数学试题

黑龙江省水利学校(职普融通部)2023-2024学年高一下学期期末考试数学试题一、单选题1.已知复数z 满足()i i 43i z -=-,则z =( )A .B .3C .D .2.已知向量(,),(1,2),(1,1)a x y b c ===-r r r ,若满足//,()a b b a c ⊥-r r r r r ,则向量a r的坐标为( ) A .11(,)24B .63(,)55-C .21(,)55D .12(,)553.甲袋中有3个红球,3个白球和2个黑球;乙袋中有2个红球,2个白球和4个黑球.先从甲袋中随机取出一球放入乙袋,分别以A ,B ,C 表示事件“取出的是红球”、“取出的是白球”、“取出的是黑球”;再从乙袋中随机取出一球,以D 表示事件“取出的是白球”,则下列结论中不正确的是( )A .事件A ,B ,C 是两两互斥的事件 B .事件A 与事件D 为相互独立事件 C .()2|9P D A =D .19()72P D =4.2021年2月20日,在党史学习教育动员大会上,习近平总书记强调这次学习教育“总的来说就是要做到学史明理、学史增信、学史崇德、学史力行,教育引导全党同志学党史、悟思想、办实事、开新局”.某单位为了解该单位党员开展学习党史知识活动情况,随机抽取了部分党员,对他们一周的党史学习时间进行了统计,统计数据如下表所示:则该单位党员一周学习党史时间的众数及第40百分位数分别是( ) A .8,8.5B .8,8C .9,8D .8,95.如图,实心正方体1111ABCD A B C D -的棱长为2,其中上、下底面的中心分别为,Q R .若从该正方体中挖去两个圆锥,且其中一个圆锥以R 为顶点,以正方形1111D C B A 的内切圆为底面,另一个圆锥以Q 为顶点,以正方形ABCD 的内切圆为底面,则该正方体剩余部分的体积为( )A .5π848-B .7π848-C .25π824-D .7π86-6.如图,在平行四边形ABCD 中,AB =1,AD =2,π3BAD ∠=,E 为BC 的中点,若AF AB λ=u u u r u u u r ,且AE ⊥DF ,则λ=( )A .45B .35C .2D .37.正四棱锥S ABCD -,O 为顶点在底面上的射影,P 为侧棱SD 的中点,且||2||SO OD =,则直线BC 与平面PAC 所成角的正弦值为( )A B C D 8.空中有一气球,在它的正西方A 点测得它的仰角为45°,同时在它南偏东60°的B 点,测得它的仰角为30°,若A 、B 两点间的距离为266米,这两个观测点均离地1米,那么测量时气球到地面的距离CD 是( )A B .1)+米 C .266米 D .米二、多选题9.已知两条直线m ,n ,两个平面α,β.下列说法正确的是( ) A .若////m n m α,,则//n α B .若//m n βαβα⊂⊂,,,则//m n C .若//m n m α⊥,,则n α⊥ D .若////m n m αβα⊥,,,则n β⊥10.已知样本1p :12,,,n ax ax ax ⋅⋅⋅的均值为4,标准差为2,样本2p :1221,21,,21n x x x --⋅⋅⋅-的方差为4,则样本1p 和样本2p 的( )A .平均数相等B .方差相等C .极差相等D .中位数相等11.先后两次掷一枚质地均匀的骰子,A 表示事件“两次掷出的点数之和是4”,B 表示事件“第二次掷出的点数是偶数”,C 表示事件“两次掷出的点数相同”,D 表示事件“至少出现一个奇数点”,则( )A .A 与C 互斥B .()34P D =C .B 与D 对立D .B 与C 相互独立三、填空题 12.已知ii 1ia b =++,a ,b ∈R ,i 是虚数单位,则||a bi -=. 13.在ABC V 中,若()7cos 9cos A B C -=,则tan C 的最小值为.14.已知ABC V 内角A 、B 、C 所对的边分别为a 、b 、c ,面积为S ,满足cos cos 1a B b A +=,且221a b +=+,则ABC V 的外接圆半径为.四、解答题15.已知ππ1sin sin 333αα⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭(1)求3πcos 2α⎛⎫- ⎪⎝⎭的值;(2)求πsin 41cos 2sin 2ααα⎛⎫+ ⎪⎝⎭-+的值. 16.矩形ATCD 中,8AD =,3DC =,B 为TC 的中点,TAB △沿AB 翻折,使得点T 到达点P 的位置.连结PD ,得到如图所示的四棱锥P ABCD -,M 为PD 的中点.(1)求线段CM 的长度;(2)若平面PAD ⊥平面ABCD ,求三棱锥P ABD -的体积.17.我校举行“两城同创”的知识竞赛答题,高二年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为[50,60),[60,70),[70,80),[80,90),[]90,100,其频率分布直方图如图所示,请你解答下列问题:(1)求m 的值;(2)若成绩不低于88分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人; (3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).18.古希腊的数学家海伦在其著作《测地术》中给出了由三角形的三边长a ,b ,c 计算三角形面积的公式:S 这个公式常称为海伦公式.其中,()12p a b c =++.我国南宋著名数学家秦九韶在《数书九章》中给出了由三角形的三边长a ,b ,c 计算三角形面积的公式:S =“三斜求积”公式. (1)利用以上信息,证明三角形的面积公式1sin 2S ac B =;(2)在ABC V 中,8a c +=,sin tan22cos B A A=-,求ABC V 面积的最大值. 19.如图,四棱锥P ABCD -的底面ABCD 为菱形,60ABC ∠=︒,PA ⊥底面ABCD ,2PA AB ==,E 为PA 的中点.(1)求证://PC 平面EBD ; (2)求三棱锥C PAD -的体积C PAD V -;(3)在侧棱PC 上是否存在一点M ,满足PC ⊥平面MBD ,若存在,求PM 的长;若不存在,说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中等职业学校高一下数学试题卷
一、单项选择题
1.下列表示 的是()
A.{x|x2<0}
B.{x|x2>0}
C.{x|x=2}
D.{x|2<x<5,x∈Z}
2.点P(-1,1)关于原点的对称点的坐标为()
A.(-1,-1)
B.(1,-1)
C.(-1,1)
D.(1,1)
3.将lga=b(a>0)化成指数式为()
A.10b=a
B.eb=a
C.ab=e
D.ea=b
4.在等比数列{an}中,若a3a5=5,则a1a7的值为()
A.5
B.10
C.15
D.25
5.已知M={y|y≥1},N={y|y≥0},则M∪N等于()
A.[0,+∞)
B.[1,+∞)
C.[2,+∞)
D.R
6.有下列事件:①若a,b∈R,则a+b=b+a;②明天是晴天;③下午刮6级阵风;④地球不停地转动.其中属于必然事件的有()
A.①②
B.②③
C.③④
D.①④
7.从3名男生和2名女生中选出3人参加座谈会,如果这3人中既有男生又有女生,那么不同的选法有()
A.5种
B.9种
C.15种
D.20种
8.下列函数在定义域上为单调递减的函数是()
A.f(x)=3
2x
⎛⎫
⎪
⎝⎭
B.f(x)=lnx
C.f(x)=2-x
D.f(x)=sinx
9.函数y=6x-x2的定义域是()
A.(-∞,6]
B.[-6,6]
C.x≤±6
D.R
10.有如下四个命题,则正确命题的个数是()
①集合N中最小的数是1②-a不属于N,则a∈N
③a∈N,b∈N,则a+b的最小值是2④x2+1=2x的解集可表示为{1,1}
A.0个
B.1个
C.2个
D.3个
11.下列表示正确的是()
A.0∈N
B.-2
3∉Q
C.π∉R
D.Z∈Q
12.等比数列{bn}中,b2b4=4,则b1b3b5=()
A.8
B.-8
C.±8
D.±16
13.集合{x∈N*|x-3<2}用列举法表示为()
A.{0,1,2,3,4}
B.{1,2,3,4}
C.{0,1,2,3,4,5}
D.{1,2,3,4,5}
14.不等式2|x|-1>3的解集是()
A.(-2,2)
B.(-1,1)
C.(-∞,-1)∪(1,+∞)
D.(-∞,-2)∪(2,+∞)
15.下列不可能为函数图象的是( )
16.方程(2x -1)2=16的根是( )
A.52
B.-32
C.-32 或52
D.-52
17.下列关系成立的是( )
A.a +5>0⇔a>5
B.a +5<0⇔a<5
C.a -5>0⇔a>-5
D.a -5<0⇔a<5
18.下列命题正确的是( )
A.若a ,b 都是单位向量,则a =
b
B.若AB
→ =DC → ,则A ,B ,C ,D 四点构成平行四边形 C.若两向量a ,b 相等,则它们是始点、终点都相同的向量
D.AB
→ 与BA → 是两平行向量 19.若数列1(1)3n n n a -=-⋅,则a4( )
A.-27
B.27
C.-81
D.81
20.区间[一3,0)∪(1,+∞)在数轴上表示正确的是( )
二、填空题
21.
+1的等比中项是 .
22.已知全集U =R ,A ={x|2<x≤3},则UA = .
23.若函数f (x )=x +1x -1
,则f (1x )= . 24.求值:(3-π)2= ,3(-9)3= , 5log = ,lg1000= ,lne2= .
25.集合中元素的三个特性是 、 、 .
26.“ab =0”是“a2+b2=0”的 条件.
27.某建筑工人在建筑工地搬砖,第1小时因为体力好共搬1000块砖,第2小时因体力消耗共搬800块砖,第3小时共搬600块砖……以此类推,设此人一共搬了5h,则总共搬了 块砖.
三、解答题
28.求等比数列1,12,14,18,…的前10项和.
29.解下列不等式:
(1)x -13+2<x -3<2x +32;
(2)3x +4-x2<0.
30.
将二项式5
2x ⎫
⎪⎭展开并化简(最后结果用指数式表示).
31.已知集合A ={1,0,x},且x2∈A ,求x 的值.
32.现有数学、语文、英语、电子、电工各一本,从中任取一本,“取出的是专业书”为事件A ,求P (A );
33.若从1,2,3中任取两个数,则这两个数都是奇数的概率为 .
34.解不等式组⎩⎪⎨⎪⎧4x +1>7(x -2),
2-2x 3≤2.
35.比较x (x-4)与(x-2)2的大小.
答案
一、单项选择题
1.A
2.B
3.A
4.A
5.A
6.D
7.B【提示】选法可分为两类:第一类为1名男生,2名女生,其选法为C13C22=3(种);第二类为2名男生,1名女生,其选法为C23C12=6(种).依据分类计数原理可得C13C22+C23C12=3+6=9(种).
8.C【提示】A,B为单调递增函数,D项中sinx为周期函数.所以答案
选C.
9.D
10.A【提示】①N中最小的数是0;②如-0.1∉N,但0.1∉N;③当a=b=0时,a+b=0<2;④与集合互异性矛盾.故正确个数为0,
选A.
11.A【提示】正确理解元素与集合、集合与集合之间的关系以及符号
的正确使用.
12.C
13.B【提示】{x∈N*|x-3<2}={x∈N*|x<5}={1,2,3,4}.
14.D【提示】2|x|-1>32|x|>4|x|>2x<-2或x>2.故选D
15.D【提示】根据函数的概念,x与y可以是一对一,也可以是多对一,但不能是一对多.
16.C【提示】∵2x-1=±4,∴x=-3
2或
5
2.
17.D【提示】根据不等式的性质进行判断.
18.D
19.B
20.C
二、填空题
21. ±1
22.{x|x≤2或x>3}
23.1+x 1-x 【提示】f (1x )=1x +11x -1
=1+x 1-x
. 24.π-3 -9 3 3 2
25.确定性、无序性、互异性 【提示】集合元素的基本特性.
26.必要不充分【提示】ab =0/⇒a2+b2=0,但a2+b2=0⇒ab =0. 27.3000【解析】1000+800+600+400+200=3000(块).
三、解答题
28.解:∵a1=1,q =12,
∴S10=101112112
⎡⎤⎛⎫⨯-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-=1023512. 29.解:(1)原不等式等价于⎩⎪⎨⎪⎧x -13+2<x -3,x -3<2x +32,
解得⎩⎪⎨⎪⎧x>7,x>-92,
∴x >7, ∴原不等式的解集为{x |x >7}.
(2)原不等式可化为x2-3x -4>0, 即(x +1)(x -4)>0,解得x <-1或x >4,
∴原不等式的解集为{x |x <-1或x >4}. 30.52x -10x +4012x --80x -2+8072
x --32x -5
31.解:若x2=0,则x =0,不符合; 若x2=x ,则x =0或1,不符合; 若x2=1,则x =±1,x =1不符合; ∴x =-1.
32.解:P (A )=25.
33.13 【提示】P =1C 23
=13 34.解:由⎩⎪⎨⎪⎧4x +1>7(x -2),2-2x 3≤2
得⎩⎪⎨⎪⎧x<5,x≥-2, ∴-2≤x<5,
∴原不等式组的解集为[-2,5).
35.解∶2(4)(2)x x x ---
()22444x x x x =---+ =4
因为4>0,
所以2(4)(2).x x x ->-。
