立体几何中的体积问题(精编版)
立体几何中的体积问题 精编版PPT文档共17页

43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
立体几何中的体积问题 精编版
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
高中数学立体几何体积计算应用例题

高中数学立体几何体积计算应用例题在高中数学中,立体几何是一个重要的章节,其中涉及到的体积计算是一个常见的考点。
本文将通过具体的例题,来说明一些常见的体积计算方法和技巧,帮助高中学生更好地理解和应用。
例题一:一个正方体的边长为3cm,求其体积。
解析:正方体的体积计算公式为 V = a^3,其中 a 表示正方体的边长。
根据题意,可以得到 a = 3cm,代入公式计算得 V = 3^3 = 27cm^3。
因此,该正方体的体积为27立方厘米。
例题二:一个圆柱体的底面半径为4cm,高度为6cm,求其体积。
解析:圆柱体的体积计算公式为V = πr^2h,其中 r 表示底面半径,h 表示高度。
根据题意,可以得到 r = 4cm,h = 6cm,代入公式计算得V = π * 4^2 * 6 = 96πcm^3。
因此,该圆柱体的体积为96π立方厘米。
例题三:一个球的半径为5cm,求其体积。
解析:球体的体积计算公式为V = (4/3)πr^3,其中r 表示球的半径。
根据题意,可以得到 r = 5cm,代入公式计算得V = (4/3)π * 5^3 = 500π/3 cm^3。
因此,该球的体积为500π/3立方厘米。
通过以上例题,我们可以看到,不同几何体的体积计算方法是不同的。
在解题过程中,我们需要根据题目给出的信息,选择合适的公式进行计算。
同时,需要注意单位的统一,确保最终的结果与题目要求的单位一致。
除了基本的体积计算,有时候我们还需要应用到一些几何体的组合和切割问题。
下面,我们通过一个例题来说明这个问题。
例题四:一个长方体的长、宽、高分别为6cm、4cm、3cm,如果将其沿着长方向切割成两个相等的部分,求切割面的面积。
解析:首先,我们需要确定切割面的形状。
根据题意,切割面是一个长方形,其中长为6cm,宽为4cm。
因此,切割面的面积为 6 * 4 = 24cm^2。
通过以上例题,我们可以看到,在解决几何体的体积计算问题时,需要根据题目的要求选择合适的计算公式,并注意单位的统一。
立体几何中的体积问题

立体几何中的体积问题立体几何中求解体积问题的技巧求解体积是立体几何的重要教学内容,也是数学竞赛的常见考查内容之一。
在解决这类问题时,除了要记住公式,还需要巧妙思考,根据具体条件灵活选择计算体积的方法。
一、公式法举例来说,对于一个四面体ABCD,已知AB=AC=AD=DB=5,BC=3,CD=4,求该四面体的体积。
根据题意,可知BC=3,CD=4,DB=5,因此∠BCD=90°。
我们可以取BD的中点E,连结AE、CE,由直角三角形的性质可知BE=CE=DE,而AB=AC=AD=5,因此△ABE≌△ACE≌△ADE。
由此可得AE⊥BD,AE⊥EC,因此AE⊥平面BCD,即AE为平面BCD上的高。
计算可知V(ABCD)=1/3×S(BCD)×AE=1/3×6×4=8/3.变式1:对于一个三棱锥P-ABC,已知PA=1,AB=AC=2,∠PAB=∠PAC=∠BAC=60°,求三棱锥A-PBC的体积。
在△PAB中,有PB²=PA²+AB²-2PA×AB×cos∠PAB=1²+2²-2×1×2×cos60°=3.同理可得PA⊥PB,PA⊥PC,因此PA⊥平面PBC。
又因为AB=AC=2,∠BAC=60°,所以△ABC为正三角形,BC=2.取BC的中点D,连结PD,则PD²=PB²-BD²=3-1=2.因此S(△PBC)=1/2×BC×PD=2.故V(A-PBC)=1/3×S(△PBC)×PA=2/3.二、分割法对于一个正四棱锥P-ABCD的体积为1,已知E、F、G、H分别是线段AB、CD、PB、PC的中点,求多面体BEG-CFH的体积。
为了求解该问题,需要将多面体BEG-CFH切割成常见的几何体。
立体几何求体积方法总结及习题演练(精)
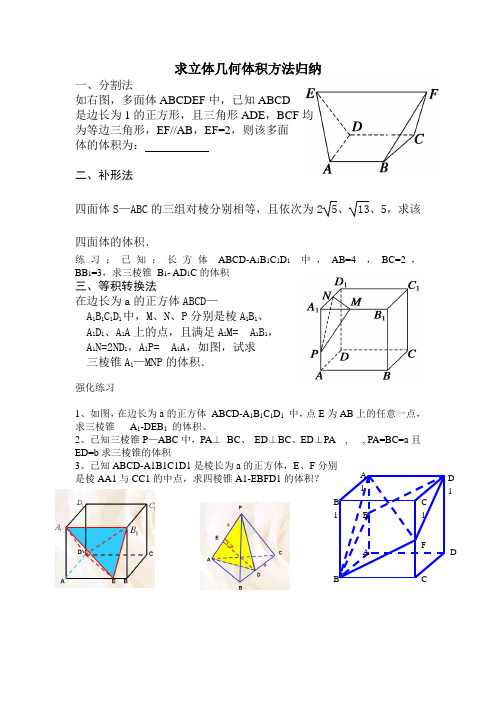
求立体几何体积方法归纳
一、分割法
如右图,多面体ABCDEF 中,已知ABCD
是边长为1的正方形,且三角形ADE ,BCF 均
为等边三角形,EF//AB ,EF=2,则该多面
体的体积为:
二、补形法
四面体S —ABC 的三组对棱分别相等,且依次为25、13、5,求该四面体的体积.
练习:已知:长方体ABCD-A 1B 1C 1D 1 中,AB=4 ,BC=2, BB 1=3,求三棱锥 B 1- AD 1C 的体积
三、等积转换法
在边长为a 的正方体ABCD —
A 1
B 1
C 1
D 1中,M 、N 、P 分别是棱A 1B 1、
A 1D 1、A 1A 上的点,且满足A 1M= A 1
B 1,
A 1N=2ND 1,A 1P= A 1A ,如图,试求
三棱锥A 1—MNP 的体积.
强化练习
1、如图,在边长为a 的正方体 ABCD-A 1B 1C 1D 1 中,点E 为AB 上的任意一点,求三棱锥 A 1-DEB 1 的体积。
2、已知三棱锥P —ABC 中,PA ⊥ BC 、 ED ⊥BC 、ED ⊥PA , , PA=BC=a 且ED=b 求三棱锥的体积
3、已知ABCD-A1B1C1D1是棱长为a 的正方体,E 、F 分别 是棱AA1与CC1的中点,求四棱锥A1-EBFD1的体积?
B B 1
C
D A C 1 D 1 A 1
E F。
(完整版)立体几何体积问题-

立体几何体积问题未命名一、解答题1.如图,在三棱锥中,,,为的中点.(1)证明:平面;(2)若点在棱上,且,求点到平面的距离.2.如图,多面体中,为正方形,,,且.(1)证明:平面平面;(2)求三棱锥的体积.3.在如图所示的几何体中,平面,四边形为等腰梯形,,,,,,.(1)证明:;(2)若多面体的体积为,求线段的长.4.如图,在四棱锥中,,,,点在线段上,且,,平面.(1)证明:平面平面;(2)当时,求四棱锥的表面积.5.如图,在四棱锥中,是等边三角形,,,.(Ⅰ)求证:(Ⅱ)若平面平面,,求三棱锥的体积6.如图,三棱柱中,平面平面,平面平面,,点、分别为棱、的中点,过点、的平面交棱于点,使得∥平面.(1)求证:平面;(2)若四棱锥的体积为,求的正弦值.7.如图,在几何体中,平面底面,四边形是正方形,,是的中点,且,.(1)证明:;(2)若,求几何体的体积.8.在多面体中,底面是梯形,四边形是正方形,,,面面,..(1)求证:平面平面;(2)设为线段上一点,,试问在线段上是否存在一点,使得平面,若存在,试指出点的位置;若不存在,说明理由?(3)在(2)的条件下,求点到平面的距离.9.已知直三棱柱,底面是边长为2的等边三角形,,为棱的中点,在棱上,且.(1)证明:平面;(2)求三棱锥的体积.10.如图,在三棱锥中,,,,,为线段的中点,将折叠至,使得且交平面于F.(1)求证:平面⊥平面PAC.(2)求三棱锥的体积.11.在矩形所在平面的同一侧取两点、,使且,若,,.(1)求证:(2)取的中点,求证(3)求多面体的体积.12.如图,在菱形中,,平面,,是线段的中点,.(1)证明:平面;(2)求多面体的表面积.13.如图,在三棱柱中,,,为的中点,.(1)求证:平面平面;(2)求到平面的距离.14.如图,四棱锥中,底面是直角梯形,,,,侧面是等腰直角三角形,,平面平面,点分别是棱上的点,平面平面(Ⅰ)确定点的位置,并说明理由;(Ⅱ)求三棱锥的体积.15.如图,三棱柱中,侧面侧面,,,,为棱的中点,为的中点.(1) 求证:平面;(2) 若,求三棱柱的体积.参考答案1.解:(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=.连结OB.因为AB=BC=,所以△ABC为等腰直角三角形,且OB⊥AC,OB==2.由知,OP⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.故CH的长为点C到平面POM的距离.由题设可知OC==2,CM==,∠ACB=45°.所以OM=,CH==.所以点C到平面POM的距离为.【解析】分析:(1)连接,欲证平面,只需证明即可;(2)过点作,垂足为,只需论证的长即为所求,再利用平面几何知识求解即可.详解:(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=.连结OB.因为AB=BC=,所以△ABC为等腰直角三角形,且OB⊥AC,OB==2.由知,OP⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.故CH的长为点C到平面POM的距离.由题设可知OC==2,CM==,∠ACB=45°.所以OM=,CH==.所以点C到平面POM的距离为.点睛:立体几何解答题在高考中难度低于解析几何,属于易得分题,第一问多以线面的证明为主,解题的核心是能将问题转化为线线关系的证明;本题第二问可以通过作出点到平面的距离线段求解,也可利用等体积法解决.2.(1)见解析;(2)【解析】分析:(1)证明面面垂直可通过证明线面垂直得到,证A平面即可,(2)由已知,连接交于,作于,由等体积法:,进而可得出结论.(1)证明:∵,由勾股定理得:又正方形中,且∴平面,又∵面,∴平面平面(2)由已知,连接交于作于,则又由(1)知平面平面,平面平面,面,得面由,知四边形为平行四边形,即,而,进而又由,所以,三棱锥的体积.点睛:考查面面垂直、几何体体积,能正确分析线条关系,利用等体积法转化求体积是解题关键.3.(1)证明见解析;(2).【解析】分析:(1)通过证明AB平面ACFE得到;(2)作于点G,设,分别计算出四棱锥的体积,再根据已知条件,求出的值,在直角三角形CFG 中求出CF的值。
高中数学立体几何——常用求体积的三种解题方法(2021年整理)

高中数学立体几何——常用求体积的三种解题方法(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学立体几何——常用求体积的三种解题方法(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学立体几何——常用求体积的三种解题方法(word版可编辑修改)的全部内容。
高中数学立体几何——常用求体积的三种解题方法1. 1(1)分割法一般的考试题目不会给你一个简单的长方体,正方体,圆等等一些能套公式就能求出体积,而是弄一些多面体,让你求它的体积。
分割法,就是把多面体分割成几个我们常见的立体,然后求各个分割体的体积,最后相加就能得出所要求的体积了。
2. 2(2)补形法多面体加以拼补,把它拼成我们常见的立体,求出该立体的体积后,把补上去的各个立体的体积算出来,相减就能得出所要求的体积了。
3。
3(3)等体积法这个方法举例比较好说明,比如,求四面体P-ABC的体积,但是顶点P到面ABC的距离不好求(即高h),然而我们把顶点和底面换一下,换成四面体A-PBC,此时,顶点A到面PBC的距离可以很容易就得到(AP⊥面PBC,即AP就是高),这样四面体A—PBC的体积就很容易就求出来了。
显然,四面体P-ABC和四面体A-PBC是同一个立体,因此,求出四面体A—PBC的体积也就是求出四面体P—ABC的体积.。
立体几何形的体积计算知识点总结

立体几何形的体积计算知识点总结体积是立体几何形的一个重要属性,它用来描述一个物体所占的空间大小。
在几何学中,我们经常需要计算不同形状的物体的体积。
为了更好地理解和掌握立体几何形的体积计算,我们需要掌握一些基本的知识点。
本文将根据不同的几何形状,总结一些常用的体积计算公式和方法。
一、正方体的体积计算正方体是最简单的立体几何形之一,它的六个面都是正方形。
计算正方体的体积非常简单,只需要将正方体的边长乘以自身再乘以自身即可。
即体积=边长×边长×边长。
例如,一个边长为5厘米的正方体的体积为5×5×5=125立方厘米。
二、长方体的体积计算长方体是更常见的一种立体几何形,它的六个面中,相对的两个面是相等的长方形。
计算长方体的体积也非常简单,只需要将长方体的长、宽和高相乘即可。
即体积=长×宽×高。
例如,一个长10厘米,宽6厘米,高8厘米的长方体的体积为10×6×8=480立方厘米。
三、圆柱体的体积计算圆柱体是一个底面为圆形的立体几何形。
要计算圆柱体的体积,需要知道底面的半径和高。
计算公式为体积=底面积×高=π×半径的平方×高。
例如,一个底面半径为3厘米,高为6厘米的圆柱体的体积为3.14×3×3×6=169.56立方厘米。
四、球体的体积计算球体是一个所有点到球心的距离都相等的立体几何形。
计算球体的体积需要知道球的半径。
计算公式为体积=4/3×π×半径的立方。
例如,一个半径为4厘米的球体的体积为4/3×3.14×4×4×4=268.08立方厘米。
五、锥体的体积计算锥体是一个底面为圆形,顶点与底面圆心相连的立体几何形。
计算锥体的体积需要知道底面的半径和高。
计算公式为体积=1/3×底面积×高=1/3×π×半径的平方×高。
立体几何中的体积计算

立体几何中的体积计算立体几何是研究空间中的图形和其属性的一门学科。
而在立体几何中,计算图形的体积是一个重要的问题。
体积是指立体图形所占据的三维空间的量度,计算体积可以帮助我们更好地理解和应用于实际问题中。
本文将介绍几种常见的立体几何形体的体积计算公式,并附上相关例子。
1. 立方体的体积计算立方体是一种边长相等的六个面都是正方形的立体图形。
它的体积计算非常简单,只需将边长的立方即可得到体积。
其计算公式为:V = a^3,其中V表示体积,a表示边长。
例如,一个边长为5厘米的立方体的体积计算如下:V = 5^3 = 125立方厘米2. 正方体的体积计算正方体是一种所有面都是正方形且边长相等的立体图形。
与立方体类似,正方体的体积计算也是将边长的立方作为计算公式。
其计算公式为:V = a^3,其中V表示体积,a表示边长。
例如,一个边长为4米的正方体的体积计算如下:V = 4^3 = 64立方米3. 长方体的体积计算长方体是一种具有长宽高三个不同边长的立体图形。
它的体积计算公式为:V = lwh,其中V表示体积,l表示长,w表示宽,h表示高。
例如,一个长为6厘米、宽为3厘米、高为2厘米的长方体的体积计算如下:V = 6 * 3 * 2 = 36立方厘米4. 圆柱体的体积计算圆柱体是由一个圆形底面和与该底面平行且高度相等的侧面组成的立体图形。
它的体积计算公式为:V = πr^2h,其中V表示体积,π表示圆周率,r表示底面半径,h表示高度。
例如,一个底面半径为2米,高度为8米的圆柱体的体积计算如下:V = 3.14 * 2^2 * 8 = 100.48立方米5. 圆锥体的体积计算圆锥体是由一个圆形底面和以该底面圆心为顶点的曲面相交而成的立体图形。
它的体积计算公式为:V = (1/3)πr^2h,其中V表示体积,π表示圆周率,r表示底面半径,h表示高度。
例如,一个底面半径为3厘米,高度为6厘米的圆锥体的体积计算如下:V = (1/3) * 3.14 * 3^2 * 6 = 56.52立方厘米总结:立体几何中的体积计算是研究图形三维空间量度的重要问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BAC 90 ,且 AB AA1 , D, E, F 分别是 B1 A, CC1 , BC 的中点。
(1)求证: DE / / 平面 ABC ; (2)求证: B1 F 平面 AEF ;
C1
B1
(3)设 AB a ,求三棱锥 D AEF 的体积。
A1
E D
F B
C A
总结
• 公式法 • 等体积法 • 割补法 • 转移法(平行、中点)(距离类)
M , N 分别是棱 CC1 , AB 中点. (Ⅰ)求证: CN 平面 ABB1A1 ; (Ⅱ)求证: CN // 平面 AMB1 ;
(Ⅲ)求三棱锥 B1 AMN 的体积.
C1
A1 M
B1
CLeabharlann ANB例4(2)
35. 如图,三棱柱 ABC A1 B1C1 中,侧棱 AA1 平面 ABC , ABC 为等腰直角三角形,
立体几何
题型一:求体积/距离类
• 熟练掌握公式(柱体、锥体、台体、球……) • 掌握一些方法与技巧:等体积法(换顶点)、
割补法、转移法(转移高)
• 直接法(公式法):几何体形状整齐,有 较明显的垂直关系且长度已知
例2.在棱长为a的正方体ABCD-A1B1C1D1中, 求点C到截面C1BD的距离.
谢谢观赏!
D1
C1
A1 F
B1
D A
E C
B
变式1.正方体ABCD-A1B1C1D1的棱长为 a,E、F分别是BB1,DD1的中点,求四 棱锥D1-AEC1F的体积?
D1
C1
A1 F
B1
D A
E C
B
例4(1)
34. 如图,已知三棱柱 ABC A1B1C1 中,AA1 底面 ABC ,AC BC 2,AA1 4 ,AB 2 2
D1
A1
B1
C1
D A
C B
• 等体积法(换顶点):大多用于与棱锥体 积有关的问题中
例3
• 割补法:通过分割或者补全几何体,可将 所求几何体体积表示成若干几何体体积的
和或差(有时无法用等体积法做时,可考 虑割补法)
变式1.正方体ABCD-A1B1C1D1的棱长为 a,E、F分别是BB1,DD1的中点,求四 棱锥D1-AEC1F的体积?
