尼科尔森《微观经济理论-基本原理与扩展》(第9版)笔记(第3章--偏好与效用)
尼科尔森《微观经济理论——基本原理与扩展》章节题库(偏好与效用)【圣才出品】

第3章偏好与效用1.A(15,15),B(14,20),C(13,23),D(14,14)四个市场篮子,每个篮子的第一个坐标值表示食品的数量,第二个坐标值表示衣服的数量。
消费者对A、B、C三个篮子同样喜欢,当A、D两个篮子可供选择时,消费者更加喜欢D;当C、D进行选择时,消费者更加喜欢C;B、D进行选择时,消费者无从选择。
请分析该消费者的偏好违反了偏好的哪些基本假定?说明你的依据。
答:(1)偏好的基本假设①完备性:即消费者可以对所有可能的篮子进行比较和排序。
对于任何两个市场篮子A 和B,消费者要么偏好其中的A,要么偏好其中的B,要么觉得两者无差异。
其中,无差异是指消费者从两个篮子中获得相同的满足程度。
②可传递性:偏好是可以传递的。
这意味着,如果消费者在市场篮子A和B中更偏好A,在B和C中更偏好B,那么消费者在A和C中更偏好A。
这一假定保证了消费者的种种偏好是一致的,因而也是理性的。
③反身性:任何一个消费束至少和它本身一样好。
这可以理解为对正常品而言,消费者总是偏好更多的商品。
(2)该消费者的偏好违背了以下基本假定:①违背了完备性假定。
因为消费者在B和D之间无法进行选择。
②违背了可传递性假定。
消费者对于A、C两个篮子同样喜欢,则有A=C;在A、D 两个篮子中,消费者更偏好D,即D>A,根据偏好的可传递性有:D>C。
但在C、D两个篮子中,消费者更偏好于C,即C>D,二者矛盾,故违背了可传递性原则。
③违背了反身性假定。
对于消费者而言,应当有A(15,15)>D(14,14),但消费者在A和D之间选择了D,故违背了反身性假定。
2.画出下述两种商品个人偏好的无差异曲线:汉堡包和软饮料。
指出个人满足(或效用)增加的方向:(1)乔的无差异曲线为凸的,汉堡包和软饮料都不喜欢。
(2)简喜欢汉堡包,但不喜欢软饮料。
如果服务员给她一杯软饮料,她会不喝倒掉。
(3)鲍勃喜欢汉堡包,但不喜欢软饮料。
但是如果服务员给他一杯软饮料,为了礼貌起见他会喝掉。
尼科尔森微观经济理论_基本原理与扩展(第9版)课后习题详解(第3章 偏好与效用)
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第2篇 选择与需求 第3章 偏好与效用课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.画出下列效用函数的无差异曲线,并判断它们是否是凸状的(即边际替代率MRS 是否随着x 的增加而递减)。
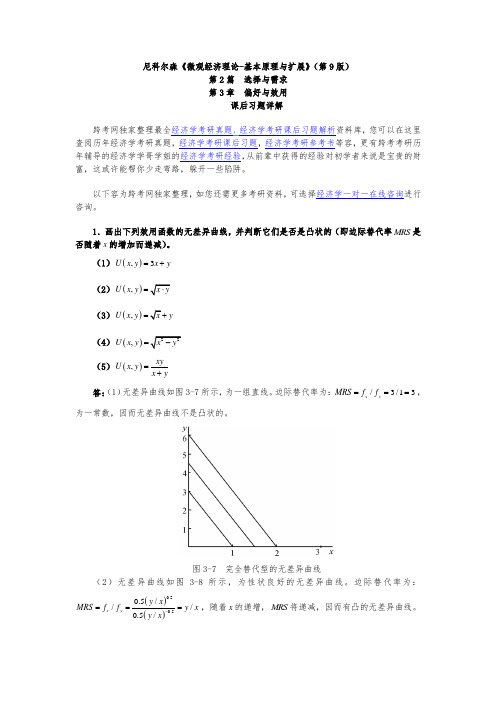
(1)(),3U x y x y =+ (2)(),U x y x y =⋅ (3)(),U x y x y =+ (4)()22,U x y x y =- (5)(),xyU x y x y=+ 答:(1)无差异曲线如图3-7所示,为一组直线。
边际替代率为:/3/13x y MRS f f ===,为一常数,因而无差异曲线不是凸状的。
图3-7 完全替代型的无差异曲线(2)无差异曲线如图3-8所示,为性状良好的无差异曲线。
边际替代率为:()()0.50.50.5///0.5/x y y x MRS f f y x y x -===,随着x 的递增,MRS 将递减,因而有凸的无差异曲线。
图3-8 凸状的无差异曲线(3)无差异曲线如图3-9所示。
边际替代率为:0.5/0.5x y MRS f f x -==,因而边际替代率递减,无差异曲线是凸状的,此为拟线性偏好的效用函数。
图3-9 拟线性型的无差异曲线(4)无差异曲线如图3-10所示。
边际替代率为:()0.522220.5/0.52/0.5()2/x y MRS f f x y x x y y x y --==-⋅-⋅=,因而边际替代率递增,无差异曲线不是凸状的。
图3-10 凹状的无差异曲线(5)无差异曲线如图3-11所示。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)课后习题详解(第4章 效用最大化与选择)

尼科尔森《微观经济理论-基本原理与扩展》(第9版)第4章 效用最大化与选择课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.三年级学生保罗每天在校用餐,它只喜欢Twinkie (t )和苏打水(s ),他从中得到的效用为:(),U t s ts =。
(1)如果每份Twinkie 为0.1美元,苏打水每瓶为0.25美元,为了使效用最大化,保罗应该如何将妈妈给他的1美元伙食费分配在这两种食物上?(2)学校为了减少Twinkie 的消费,将其价格提高到每份0.4美元,那么为了让保罗得到与(1)中相同的效用,妈妈现在要给他多少伙食费?解:(1)对效用函数(),U t s ts =进行单调变换,令()()2,,V t s U t s ts ==⎡⎤⎣⎦,这并不改变偏好次序。
保罗效用最大化问题为:max .. 0.10.251tss t t s +=设拉格朗日函数为:()(),,10.10.25L s t ts t s λλ=+--一阶条件为:0.100.25010.10.250Ls t Lt s Lt s λλλ∂=-=∂∂=-=∂∂=--=∂ 解得:2s =,5t =。
因此,他所获得的效用:10U =(2)消费品Twinkie 价格提高了,但效用水平却保持不变,则保罗面临如下的支出最小化问题:min 0.40.25..10t s s tts +=设拉格朗日函数为:()(),,0.40.2510L s t t s ts λλ=++-一阶条件为:0.40Ls tλ∂=-=∂ (1) 0.25Lt sλ∂=-=0∂ (2) 100Lts λ∂=-=∂ (3) 由上述三式解得 2.5t =,4s =,则最小支出为:10.4 2.50.2542m =⨯+⨯=,所以妈妈现在要给他2美元伙食费使他的效用水平保持不变。
尼科尔森《微观经济理论—基本原理与扩展》(第9版)课后习题详解

尼科尔森《微观经济理论—基本原理与扩展》(第9版)课后习题详解第1篇引言第1章经济模型本章没有课后习题。
本章是全书的一个导言,主要要求读者对微观经济模型有一个整体了解,然后在以后各章的学习中逐渐深化认识。
第2章最优化的数学表达1.假设。
(1)计算偏导数,。
(2)求出上述偏导数在,处的值。
(3)写出的全微分。
(4)计算时的值——这意味着当保持不变时,与的替代关系是什么?(5)验证:当,时,。
(6)当保持时,且偏离,时,和的变化率是多少?(7)更一般的,当时,该函数的等高线是什么形状的?该等高线的斜率是多少?解:(1)对于函数,其关于和的偏导数分别为:,(2)当,时,(1)中的偏微分值分别为:,(3)的全微分为:(4)当时,由(3)可知:,从而可以解得:。
(5)将,代入的表达式,可得:。
(6)由(4)可得,在,处,当保持不变,即时,有:(7)当时,该函数变为:,因而该等高线是一个中心在原点的椭圆。
由(4)可知,该等高线在(,)处的斜率为:。
2.假定公司的总收益取决于产量(),即总收益函数为:;总成本也取决于产量():。
(1)为了使利润()最大化,公司的产量水平应该是多少?利润是多少?(2)验证:在(1)中的产量水平下,利润最大化的二阶条件是满足的。
(3)此处求得的解满足“边际收益等于边际成本”的准则吗?请加以解释。
解:(1)由已知可得该公司的利润函数为:利润最大化的一阶条件为:从而可以解得利润最大化的产量为:;相应的最大化的利润为:。
(2)在处,利润最大化的二阶条件为:,因而满足利润最大化的二阶条件。
(3)在处,边际收益为:;边际成本为:;因而有,即“边际收益等于边际成本”准则满足。
3.假设。
如果与的和是1,求此约束下的最大值。
利用代入消元法和拉格朗日乘数法两种方法来求解此问题。
解:(1)代入消元法由可得:,将其代入可得:。
从而有:,可以解得:。
从而,。
(2)拉格朗日乘数法的最大值问题为:构造拉格朗日函数为:一阶条件为:从而可以解得:,因而有:。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)笔记(第3章--偏好与效用)

尼科尔森《微观经济理论-基本原理与扩展》(第9版)第2篇 选择与需求第3章 偏好与效用复习笔记跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.理性选择定理偏好是指消费者按照自己的意愿对可供选择的商品组合进行的排列。
偏好是微观经济学价值理论中的一个基础概念。
偏好是主观的,也是相对的概念。
为了便于经济分析,经济学家通常假定人们的偏好关系满足以下三个基本假设:(1)完全性(completeness ):偏好是完备的,也就是说,消费者可以在所有可能的消费组合中进行比较和排序。
例如,对于任何两个消费组合A 和B ,消费者要么偏好其中的A ,要么偏好其中的B ,要么觉得两者无差异。
其中,无差异是指消费者从两个消费选择中获得相同的满足程度。
(2)传递性(transitivity ):偏好是可以传递的,这意味着,如果消费者在消费组合A 和B 中更偏好A ,在B 和C 中更偏好B ,那么消费者在A 和C 中更偏好A 。
这一假定保证了消费者的种种偏好是一致的,因而也是理性的。
(3)连续性(continuity ):如果消费者认为消费组合A 优于B ,那么接近 A 的消费组合也一定优于接近B 的消费组合。
2.效用及其表示方法(1)效用的含义效用是指消费者消费或拥有一定数量的某种商品时所获得的满足程度。
一种商品给消费者所带来的效用不同于该商品的使用价值,它是消费者对所消费商品给予的主观评价,不同的消费者在相同的时间、地点消费相同数量的商品组合可以分别获得不同的效用,即使同一消费者在不同的时期、不同的地点消费同样数量的商品组合也可获得不同的满足程度。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)课后习题详解(第4章 效用最大化与选择)

尼科尔森《微观经济理论-基本原理与扩展》(第9版)第4章 效用最大化与选择课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.三年级学生保罗每天在校用餐,它只喜欢Twinkie (t )和苏打水(s ),他从中得到的效用为:(),U t s ts =。
(1)如果每份Twinkie 为0.1美元,苏打水每瓶为0.25美元,为了使效用最大化,保罗应该如何将妈妈给他的1美元伙食费分配在这两种食物上?(2)学校为了减少Twinkie 的消费,将其价格提高到每份0.4美元,那么为了让保罗得到与(1)中相同的效用,妈妈现在要给他多少伙食费?解:(1)对效用函数(),U t s ts =进行单调变换,令()()2,,V t s U t s ts ==⎡⎤⎣⎦,这并不改变偏好次序。
保罗效用最大化问题为:max .. 0.10.251tss t t s +=设拉格朗日函数为:()(),,10.10.25L s t ts t s λλ=+--一阶条件为:0.100.25010.10.250Ls t Lt s Lt s λλλ∂=-=∂∂=-=∂∂=--=∂ 解得:2s =,5t =。
因此,他所获得的效用:10U =(2)消费品Twinkie 价格提高了,但效用水平却保持不变,则保罗面临如下的支出最小化问题:min 0.40.25..10t s s tts +=设拉格朗日函数为:()(),,0.40.2510L s t t s ts λλ=++-一阶条件为:0.40Ls tλ∂=-=∂ (1) 0.25Lt sλ∂=-=0∂ (2) 100Lts λ∂=-=∂ (3) 由上述三式解得 2.5t =,4s =,则最小支出为:10.4 2.50.2542m =⨯+⨯=,所以妈妈现在要给他2美元伙食费使他的效用水平保持不变。
尼科尔森《微观经济理论——基本原理与扩展》第11版课后习题详解(偏好与效用)【圣才出品】

尼科尔森《微观经济理论——基本原理与扩展》第11版课后习题详解第3章偏好与效用1.画出下列函数的无差异曲线,并判断它们是否是凸的(即它们的边际替代率是否随着x 递增而递减)。
(1)U(x,y)=3x+y (2)(,)U x y x y =×(3)(,)U x y x y=+(4)22(,)y U x x y =-(5)U(x,y)=xy/(x+y)解:(1)无差异曲线如图3-7所示,为一组直线。
边际替代率为:MRS=MU x /MU y =3/1=3,为一常数,因而无差异曲线不是凸状的。
图3-7完全替代型的无差异曲线(2)无差异曲线如图3-8所示,为性状良好的无差异曲线。
其边际替代率为:()()0.50.50.50.5x y y x MU y MRS MU xy x -===即随着x的递增,MRS xy 将递减,因而是凸状的无差异曲线。
图3-8凸状的无差异曲线(3)无差异曲线如图3-9所示。
边际替代率为:MRS=MU x /MU y =0.5x -0.5即随着x 的递增,边际替代率递减,无差异曲线是凸状的,此为拟线性偏好的效用函数。
图3-9拟线性型的无差异曲线(4)无差异曲线如图3-10所示。
边际替代率为:()()0.5220.5220.520.52x y x y x MU x MRS MU y x y y ---⋅===---⋅22230dy y x dMRS x y dx dx y y--=-=>即随着x 的递增,边际替代率递增,无差异曲线不是凸状的。
图3-10凹状的无差异曲线(5)无差异曲线如图3-11所示。
边际替代率为:()()()()2222x y x y y xy x y x xy y MRS MU MU x x y x y +-+-===++即随着x 的递增,边际替代率递减,无差异曲线是凸状的。
图3-11凸状的无差异曲线2.在本章脚注7里我们曾说明,为了使两种商品的效用函数具有严格递减的边际替代率(即曲线呈严格拟凹),必须满足下列条件:2220xx y xy x y yy xU U U U U U U -+<利用这一条件检验第1题中的各效用函数无差异曲线的凸性。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)课后习题详解(第3章--偏好与效用)
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第2篇选择与需求 第3章偏好与效用课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.画出下列效用函数的无差异曲线,并判断它们是否是凸状的(即边际替代率MRS 是否随着x 的增加而递减)。
(1)(),3U x y x y =+ (2)(),U x y x y =⋅ (3)(),U x y x y =+ (4)()22,U x y x y =- (5)(),xyU x y x y=+ 答:(1)无差异曲线如图3-7所示,为一组直线。
边际替代率为:/3/13x y MRS f f ===,为一常数,因而无差异曲线不是凸状的。
图3-7 完全替代型的无差异曲线(2)无差异曲线如图3-8所示,为性状良好的无差异曲线。
边际替代率为:()()0.50.50.5///0.5/x y y x MRS f f y x y x -===,随着x 的递增,MRS 将递减,因而有凸的无差异曲线。
图3-8 凸状的无差异曲线(3)无差异曲线如图3-9所示。
边际替代率为:0.5/0.5x y MRS f f x -==,因而边际替代率递减,无差异曲线是凸状的,此为拟线性偏好的效用函数。
图3-9 拟线性型的无差异曲线(4)无差异曲线如图3-10所示。
边际替代率为:()0.522220.5/0.52/0.5()2/x y MRS f f x y x x y y x y --==-⋅-⋅=,因而边际替代率递增,无差异曲线不是凸状的。
图3-10 凹状的无差异曲线(5)无差异曲线如图3-11所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)
第2篇 选择与需求
第3章 偏好与效用
复习笔记跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.理性选择定理
偏好是指消费者按照自己的意愿对可供选择的商品组合进行的排列。
偏好是微观经济学价值理论中的一个基础概念。
偏好是主观的,也是相对的概念。
为了便于经济分析,经济学家通常假定人们的偏好关系满足以下三个基本假设:
(1)完全性(completeness ):偏好是完备的,也就是说,消费者可以在所有可能的消费组合中进行比较和排序。
例如,对于任何两个消费组合A 和B ,消费者要么偏好其中的A ,要么偏好其中的B ,要么觉得两者无差异。
其中,无差异是指消费者从两个消费选择中获得相同的满足程度。
(2)传递性(transitivity ):偏好是可以传递的,这意味着,如果消费者在消费组合A 和B 中更偏好A ,在B 和C 中更偏好B ,那么消费者在A 和C 中更偏好A 。
这一假定保证了消费者的种种偏好是一致的,因而也是理性的。
(3)连续性(continuity ):如果消费者认为消费组合A 优于B ,那么接近 A 的消费组合也一定优于接近B 的消费组合。
2.效用及其表示方法
(1)效用的含义
效用是指消费者消费或拥有一定数量的某种商品时所获得的满足程度。
一种商品给消费者所带来的效用不同于该商品的使用价值,它是消费者对所消费商品给予的主观评价,不同的消费者在相同的时间、地点消费相同数量的商品组合可以分别获得不同的效用,即使同一消费者在不同的时期、不同的地点消费同样数量的商品组合也可获得不同的满足程度。
效用有总效用和边际效用之分。
边际效用量的大小在消费者的消费决策中具有重要作用。
(2)效用的函数表示——效用函数
①效用函数的含义
经济学家常用效用函数来说明个人偏好的次序,来表示消费者的效用。
效用函数的一般形式为:
()12,,,n U X X X L ;其他事物
其中,1X 、2X 、…、n X 分别代表了某一个时期消费的每一种商品的数量。
其他事物
表示消费者的福利还来自其他许多方面,假定不变。
②效用函数的单调变换与效用测度的不唯一性
效用是用来表示个人的偏好,但个人偏好是心理的活动,因此效用的量在理论上、概念
上和实际上是不可计量的,只能根据消费者的偏好程度将它们排列为第一、第二、第三等顺序,而不能用基数1、2、3…来表示它们量的大小。
因而用于测度消费者偏好关系的效用函数也不是唯一的,效用函数的绝对值是没有意义的,效用函数值的相对大小决定了消费者的排序关系。
在用效用函数表示消费者的偏好时,效用函数的单调变化与原效用函数所代表偏好关系是相同的。
所谓单调变换是指:当12U U >时,有()()12f U f U >,则称()f U 为原效用函数()U x 的单调变换。
单调变换体现了效用测度的不唯一性,效用函数只是一种排序的工具,能够准确排序即可,其取值的绝对大小没有价值。
(3)效用的图形表示——无差异曲线
①无差异曲线的含义
无差异曲线是用来表示消费者偏好相同的两种商品的不同数量的各种组合的一簇曲线。
或者说,它是表示能给消费者带来同等效用水平或满足程度的两种商品的不同数量的各种组合。
与无差异曲线相对应的效用函数为()12,U f X X =。
其中,1X 、2X 分别为商品1和商品
2的消费数量;U 是常数,表示某个效用水平。
由于无差异曲线表示的是序数效用,所以,这里的U 只须表示某一个效用水平,而不在乎其具体数值的大小,有的经济学者称这种效用水平为效用指数。
无差异曲线可以表示为图3-1。
图3-1 无差异曲线
②无差异曲线的一般特点
第一,由于通常假定效用函数的连续性,于是,在同一坐标平面上的任何两条无差异曲线之间,存在着无数条无差异曲线。
或者说,可以有无数条无差异曲线覆盖整个坐标平面图。
离原点越近的无差异曲线所代表的效用水平越低,离原点越远的无差异曲线所代表的效用水平越高。
第二,在同一坐标平面上的任意两条无差异曲线不会相交。
此结论证明如下:
如图3-2所示,点A 和点B 在同一条无差异曲线1U 上,说明()()U A U B =,又点B 和
点C 又在同一无差异曲线2U 上,说明()()U B U C =,根据偏好的传递性,应有()()U C U A =。
然而,由于C 点代表的两种物品消费量都大于A 点代表的两种物品消费量,根据偏好的非饱和性,有()()U C U A >,这与()()U C U A >相矛盾,从而说明在同一坐标平面上的任意两条无差异曲线不会相交。
图3-2 相交的无差异曲线意味着偏好不一致
第三,在正常情况下,无差异曲线总是凸向原点的。
这一特点是由商品的边际替代率递减规律所决定的。
③无差异曲线的斜率与边际替代率
边际替代率(MRS )指在维持效用水平不变的前提下,消费者增加一单位某种商品的消费数量时所需放弃的另一种商品的消费数量。
以MRS 代表商品的边际替代率,1X ∆和2X ∆分别是商品1和商品2的消费变化量,则商品1对商品2的边际替代率的公式为:
当商品数量的变化趋于无穷小时,则商品的边际替代率公式为:
显然,无差异曲线上某一点的边际替代率就是无差异曲线在该点的斜率的绝对值。
在保持效用水平不变的前提下,消费者增加一种商品的数量所带来的效用增加量和相应减少的另一种商品数量所带来的效用减少量必定是相等的,即有:
1122
MU X MU X ⋅∆=⋅∆
上式可以写为:
这表明两种商品的边际替代率等于两种商品的边际效用之比。
这一结论也可用如下方法证明:
令效用函数为(),U U x y =,两边全微分,得:
由于U 是一个常数,所以d 0U =,代入上式,有d d 0U U x y x y
∂∂+=∂∂,所以: 1122
d d U
MU y x MRS U x MU y
∂∂=-==∂∂
④无差异曲线的凸性
无差异曲线的凸性有很强的经济和几何含义。
严格凸向原点的无差异曲线意味着边际替代率递减,也意味着人们需要消费的多元化,在大多数情况下,人们的消费行为都满足这一假设。
它同时意味着无差异曲线的斜率的绝对值递减。
(4)特定偏好的效用函数
①柯布-道格拉斯效用函数
柯布-道格拉斯效用函数为(),U X Y X Y αβ=,具有良好的性状,是经济分析中常用的一种效用函数,参数α、β反映了商品X 和Y 对于个体的相对重要性。
其边际替代率为:()/MRS Y X αβ
=。
特别地,当1αβ+=时,参数α,β分别反映了用于商品X 和Y 的支出份额,即
X P X I α=,Y P Y I β=。
柯布-道格拉斯效用函数的无差异曲线如图3-3所示。
图3-3 柯布-道格拉斯效用函数
②完全替代
线性效用函数公式为(),U X Y X Y αβ=+,表示完全替代型偏好关系,即表示消费者愿意用α单位的Y 替代β单位的X 。
如果两种商品X 和Y 之间可以按照固定的比例替代,就说商品X 是Y 的完全替代品,如图3-4所示。
特别地,当这个固定的替代比例是1∶1时,消费者只关心消费的总数。
图3-4 线性效用函数
③完全互补
里昂惕夫效用函数公式为()(),min ,U X Y X Y αβ=,表示完全互补型偏好关系。
如果消费者始终以固定的比例一起消费两种商品,就说这两种商品是完全互补品,如图3-5所示。
此时消费者关于这两种商品的无差异曲线呈L 形,所有无差异曲线的拐点的连线是一条直线,而直线的斜率就表示两种商品的搭配比率,比如鞋和袜子这两种商品。
对于里昂惕夫效用函数而言,有:X Y αβ=,即://Y X αβ=。
图3-5 里昂惕夫效用函数
④CES 效用函数
CES 效用函数:()1,X Y U X Y δδδδδ⎛⎫=+ ⎪⎝⎭,又称不变替代弹性效用函数。
当1δ=时,它是表示完全替代的线性效用函数;当0δ=时,它是柯布-道格拉斯效用函数;当δ→∞时,它是表示完全互补的里昂惕夫效用函数。
CES 效用函数的无差异曲线如图3-6所示。
图3-6 CES 效用函数
以上内容为跨考网整理的经济学考研课后习题答案解析的一部分,限于篇幅原因,如果同学还想获得更多经济学课后习题资料,可以关注微信公众平台索要经济学考研资料,你想要的资料都在这儿→jjxkyzs 。
想了解经济学考研高分的秘密吗?请点击>>>:经济学考研解题技巧
跨考经济学考研辅导提醒您: 成功的原因千千万,失败的原因就那么几个,加入我们的经济学考研交流群,考研经验交流,规避风险,锁定名校一次进!。
