最新人教版六年级数学几何典型题解:阴影部分的面积
人教版小学六年级求阴影部分面积试题和答案
解:三角形DCE的面积为: ×4×10=20平方厘米
梯形ABCD的面积为: (4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,阴影部分可补成 圆ABE的面积,其面积为:
π ÷4=9π=28.26平方厘米
(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)
例8.求阴影部分的面积。(单位:厘米)
解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为 圆,
所以阴影部分面积为: π( )=3.14平方厘米
例9.求阴影部分的面积。(单位:厘米)
解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,
例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
解:连PD、PC转换为两个三角形和两个弓形,
两三角形面积为:△APD面积+△QPC面积= (5×10+5×5)=37.5
两弓形PC、PD面积为: π -5×5
所以阴影部分的面积为:37.5+ π-25=51.75平方厘米
解:面积为4个圆减去8个叶形,叶形面积为: π -1×1= π-1
所以阴影部分的面积为:4π -8( π-1)=8平方厘米
例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?
分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去 个圆,
=3.44平方厘米
例5.求阴影部分的面积。(单位:厘米)
(完整版)小学六年级求阴影部分面积试题和答案
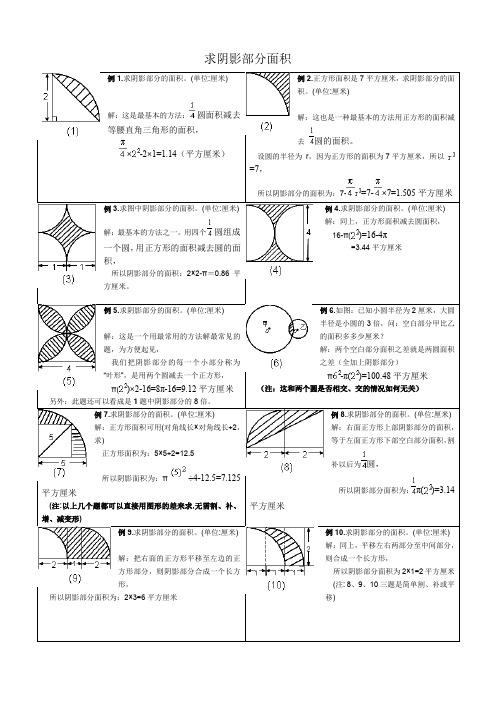
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以×7=1. 505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
小学六年级-阴影部分面积-专题复习-典型例题(含答案)

阴影部分面积专题例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小学六年级数学 阴影部分面积的计算 例题+针对性练习(带答案)

阴影部分面积的计算【例题1】求图中阴影部分的面积(单位:厘米)。
【解析】如图所示的特点,阴影部分的面积可以拼成1/4圆的面积。
62×3.14×1/4=28.26(平方厘米)答:阴影部分的面积是28.26平方厘米。
练习1:1.求下面各个图形中阴影部分的面积(单位:厘米)。
答案:18平方厘米2.求下面各个图形中阴影部分的面积(单位:厘米)。
答案:36平方厘米3.求下面各个图形中阴影部分的面积(单位:厘米)。
答案:50平方厘米【例题2】求图中阴影部分的面积(单位:厘米)。
【解析】阴影部分通过翻折移动位置后,构成了一个新的图形(如图所示)。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×4×4×1/4-4×4÷2÷2=8.56(平方厘米)答:阴影部分的面积是8.56平方厘米。
练习2:1.计算下面图形中阴影部分的面积(单位:厘米)。
答案:8平方厘米2.计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答案:8平方厘米3.计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答案:4.56平方厘米【例题3】如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO1O的面积。
【解析】因为两圆的半径相等,所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图19-10右图所示)。
所以3.14×12×1/4×2=1.57(平方厘米)答:长方形长方形ABO1O的面积是1.57平方厘米。
练习3:1.如图所示,圆的周长为12.56厘米,AC两点把圆分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD的面积。
答案:12.56平方厘米2.如图所示,直径BC=8厘米,AB=AC,D为AC的中点,求阴影部分的面积。
(完整版)小学六年级求阴影部分面积试题和答案
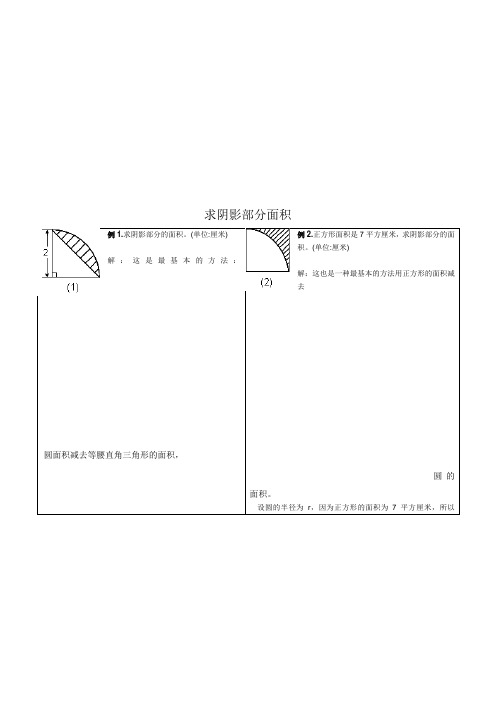
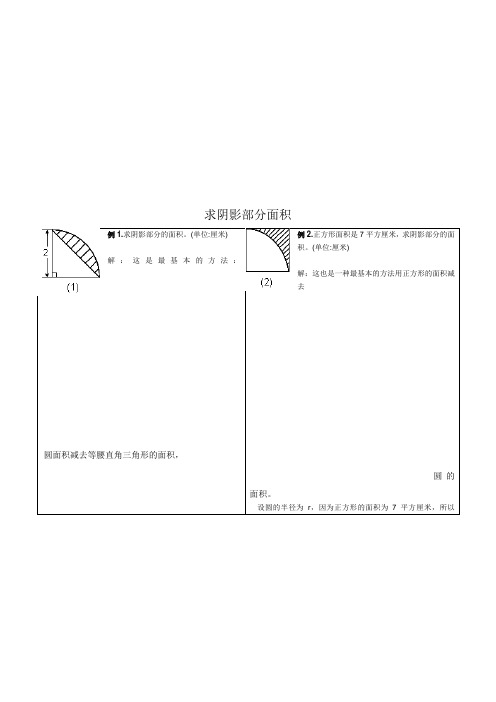
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以×7=1. 505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
(完整版)小学六年级求阴影部分面积试题和答案

例2.正方形面积是7平方厘米,求阴影部分的面 积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减 去圆面积减去等腰直角三角形的面积,面积。
设圆的半径为r ,因为正方形的面积为7平方厘米,所以求阴影部分面积例1.求阴影部分的面积。
(单位:厘米) 解:这是最基本的方法例6.如图:已知小圆半径为 2厘米,大圆 半径是小圆的3倍,问:空白部分甲比乙 的面积多多少厘米?解:两个空白部分面积之差就是两圆面积 之差(全加上阴影部分)圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部分的面积:2X 2-n= 0.86平方厘米。
)=16-4 n=3.44平方厘米505平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个X7=1.例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16- n (例6.如图:已知小圆半径为 2厘米,大圆 半径是小圆的3倍,问:空白部分甲比乙 的面积多多少厘米?解:两个空白部分面积之差就是两圆面积 之差(全加上阴影部分)例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的 题,为方便起见,我们把阴影部分的每一个小部分称为 叶形”是用两个圆减去一个正方形,◎n()X n2-16=8 n16=9.12 平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
)=100. 48平方厘米Z冗冗(注:这和两个圆是否相交、交的情况如何无关)例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积, 等于左面正方形下部空白部分面积, 割 补 以 后 为例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长X 对角线长煜, 求) 正方形面积为:5X5^2=12.5 所 以 阴 影 面 积 为:-n)—2所以阴影部分面积为: 例11.求阴影部分的面积。
(单位:厘米) 解:这种图形称为环形,可以用两个同心圆 的面积差或差的一部分来求。
最新人教版六年级数学求阴影部分面积专项训练(附答案)

最新人教版六年级数学求阴影部分面积专项训练(附答案)班级: 姓名:1、求右图中阴影图形的面积。
解:6×6÷2÷2=9(平方厘米)2、求阴影部分的面积(单位:厘米)。
解:20÷2=10 cm3.14×10×10÷2+20×10-3.14×10×10÷2=20×10=200(平方厘米)3、求阴影部分的面积(单位:厘米)解:(6+10)×6÷2=48(平方厘米)4、求阴影部分的面积(单位:厘米)解:6÷=3cm 3×3×3.14-6×6÷2=10.26(平方厘米)5、求阴影部分的面积(单位:厘米)解:20÷2=10cm 3.14×10×10 - 20×20÷2=214(平方厘米)6、求阴影部分的面积(单位:厘米)解:10×10+(10+6)×6÷2-(10+6)×6÷2 =148-48=100(平方厘米)AB CD10cm EFG66A B7、求阴影部分的面积(单位:厘米)解:10×10×3.14×1/8=39.25(平方厘米 )(10÷2)×(10÷2)×3.14-39.25=39.25(平方厘米 )8、半圆的面积是12.56平方厘米,求阴影部分的面积。
解:r=12.56×2÷3.14÷2=4cm12.56-4×4÷2 = 4.56 (平方厘米 )9.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米) 解: 设圆的半径为 r ,用正方形的面积减去 圆的面积。
因为正方形的面积为7平方厘米,所以 =7, 所以阴影部分的面积为:7-=7-×7=1.505平方厘米10、求阴影部分的面积。
(完整版)小学六年级求阴影部分面积试题和答案

求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以×7=1. 505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新人教版六年级数学几何典型题解:阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米,1S =S =DE AB)AD 2⨯+⨯阴梯形(=137)42⨯+⨯(=20(平方厘米)2、求阴影部分的面积。
解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是圆的半径,S =S 阴梯形=124)22⨯+⨯(=6(2cm )3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
解:S =AD AO ⨯ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。
由图形可知AED ∆是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。
解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
解:S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm , 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。
7、如图,正方形的面积 是10平方厘米,求圆的面积。
解:正方形的边长=圆的半径,设为r ,2r =10,2S =r π圆=3.14×10=31.42cm 。
8、如图,已知梯形的两个底分别为4厘米和7厘米,梯形的面积是多少平方厘米?解:由图,易知ABE ∆、DCE ∆是等腰直角三角形,所以AB=BE=4cm ,DC=CE=7cm ,BC=BE+CE=4+7=11cm ,1S =AB CD)BC 2⨯+⨯梯形(=147)112⨯+⨯(=60.52cm 。
9、如图,ABCD 是一个长方形,AB=10厘米,AD=4厘米,E 、F 分别是BC 、AD 的中点,G 是线段CD 上任意一点,求阴影部分的面积。
解:过G 点作GH AB ⊥,可知DAHG 、GHBC 都是长方形,根据狗牙模型,易知DAHG 1S =S 4∆GFA ,GHBC 1S =S 4∆GEC ,所以S =S +S ∆∆GFA GEC 阴=GHBC DAHG 11S +S 44=()GHBC DAHG 1S +S 4⨯=ABCD 1S 4⨯=11044⨯⨯=102cm 。
10、如图,阴影部分的面积是空白部分的2倍,求阴影部分三角形的底。
(单位:厘米)解:阴影部分的面积是空白部分的2倍,这2个三角形是等高三角形,阴影三角形的底是空白三角形的2倍,即2×4=8cm 。
11、如图,梯形的面积是60平方厘米,求阴影部分的面积。
解:S 梯形=60平方厘米,所以梯形的高=2×S 梯形÷上下底之和=2×60÷(9+11)=6cm。
11S =S -S 42⨯阴大圆小圆=()2211AB AB -422ππ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=221163.146- 3.14422⎛⎫⨯⨯⨯⨯ ⎪⎝⎭ =14.132cm 。
12、求阴影部分的面积。
解:由图可知,ABCD EFGC BFG 1S =S S S 2∆+-阴=221185(85)522⨯+-⨯+⨯ =24.52cm 。
13、已知平行四边形的面积是20平方厘米,E 是底边上的中点,求阴影部分的面积。
解:连接AC ,可知ABCD 1S =S 2∆ABC ,ABC ∆与 ABE ∆等高,BE=12BC ,所以ABC 1S =S 2∆∆ABE =ABCD 1S 4=1204⨯=52cm 。
14、如图,已知半圆的面积是31.4平方厘米,求长方形的面积。
解:S 半圆=31.4,圆的半径2r =2S π÷半圆=2×31.4÷3.14=20,。
长方形的宽为r ,长为2r ,所以长方形的面积=r ×2r=22r =2×20=402cm 。
15、求下图中阴影部分的面积和周长。
(单位:厘米) 解:S =S -S 阴正方形半圆=22122-22π⎛⎫⨯⨯ ⎪⎝⎭=2.43(2dm )3C =C +C 4阴正方形半圆=132+22π⨯⨯⨯=9.14(dm)16、如图,求阴影部分①比阴影部分②的面积少多少?(单位:厘米)解:如图,设空白部分三角形的面积为③,②①②③③①S S S S ++-=-=S S ∆-扇形=o2o13046- 3.1462360⨯⨯⨯⨯=12-9.42=2.582cm 。
17、求阴影部分的面积。
解:空白三角形是一个等腰直角三角形,且腰等于圆的半径,为3cm 。
S =S -S ∆阴半圆=9.632cm 。
18、如图所示,正方形ABCD 的边AB=4厘米,EC=10厘米,求阴影部分的面积。
解:根据沙漏模型,可知AF:FD =AB:DE=4:(10-4)=2:3,AF+FD=4,所以AF=4×223+=1.6cm ,ABF S ∆=1AF AB 2⨯⨯=11.642⨯⨯=3.22cm19、如图,在边长为6cm 的正方形内有一个三角形BEF ,线段AE=3cm ,DF=2cm ,求三角形BEF 的面积。
解:DE=AD-AE=6-3=3厘米,FC=CD-DF=6-2=4cm ,BEF ABCD ABE DEF BCF S S S S S ∆∆∆∆=---=1AB AD (AB AE BC FC DE DF)2⋅-⋅+⋅+⋅=216(636432)2-⨯⨯+⨯+⨯=122cm 。
20、已知梯形ABCD 的面积是27.5平方厘米,求三角形ACD 的面积。
解:AB=2S 梯形÷(AD+BC)=2×27.5÷(7+4)=5cm ,ACD S ∆=1AD AB 2⋅=1752⨯⨯=17.52cm 。
21、如图,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少?(单位:厘米)解:延长BC 、AD 交于点E ,可知∆ABE 、∆DEC 都是等腰直角三角形,ABCD ABE DEC S S S ∆∆=-=11AB BE DE DC 22⋅-⋅ =22119322⨯-⨯=362cm 。
22、求下图阴影部分的面积。
解:如图,阴影的上半部分是一个半圆,下半部分是长方形与2个四分之一圆的差,这3个圆的半径都相等=8÷2=4厘米。
1S S +S -2S 4⎛⎫=⨯ ⎪⎝⎭阴圆半圆长方形=S 长方形=4×8=322cm 。
此题也可以把上面的半圆切成2个四分之一圆,补到下面的四分之一圆的空白处,可直接求出面积。
23、求图中阴影部分的面积。
(单位:厘米)解:阴影部分是一个圆环。
S S =S -S =阴圆环大圆小圆 =22R r ππ-=()22R r π-=()223.1454⨯-=28.262cm 。
24、求下图中阴影部分的面积。
(单位:厘米) 解:S S -S ∆=ABCD ABE 阴=S -S ∆ABFG ABE =EFGA S 梯形 =(EF+GA)×GF ÷2=(9+20)×10÷2=1452cm 。
25、求阴影部分的面积。
(单位:厘米)解:把左上方的弓形阴影部分割补到右下方,实际上阴影部分就是一个梯形。
梯形的上底和高都是4厘米。
S S =阴梯形=(4+7)×4÷2=222cm 。
26、求下图阴影部分的面积。
(单位:厘米)解:ECG ABG S S S S ∆∆=+-阴梯形ABCE=(CE+AB)·BC ÷2+CE ·CG ÷2-AB ·(BC+CG)÷2=(2+4)×4÷2+2×2÷2-4×(4+2)÷2 =12+2-12=22cm 。
27、求下图阴影部分的面积。
(单位:厘米) 解:半圆的半径=梯形的高=4÷2=2厘米,S S -S =阴半圆梯形=(4+6)×2÷2-3.14×22÷2=10-6.28=3.722cm 。
28、四边形BCED 是一个梯形,三角形ABC 是一个直角三角形,AB=AD ,AC=AE ,求阴影部分的面积。
(单位:厘米)解:ABC S ∆=AB ·AC ÷2=BC ×高÷2,所以,高=3×4÷5=2.4厘米。
ADB AEC S S ∆∆+=(AD AE)2+⨯÷高=(3+4)×2.4÷2=8.42cm 。
29、求阴影部分的面积。
(单位:分米)解:把上面半圆的2个弓形割补到下半圆,可知阴影部分的面积=梯形的面积-三角形的面积,梯形的高=圆的半径=4dm ,梯形的上底=圆的直径=4×2=8dm ,梯形的下底=3个圆的半径=3×4=12dm ,S S -S ∆=阴梯形=(8+12)×4÷2-8×4÷2=242dm30.如图,已知AB=8厘米,AD=12厘米,三角形ABE 和三角形ADF 的面积各占长方形ABCD 的三分之一。
求三角形AEF 的面积。
解:ABCD2S =S 3梯形ABCF =28123⨯⨯=64平方厘米。
CF 2S BC-AB =÷梯形ABCF =2×64÷12-8=83厘米,同理可求出EC=4厘米,所以S ∆AEF =ABCD 1S S 3∆-ECF =8×12×13-83×4÷2=8032cm 。
