15-1 压杆稳定(10年)解析
材料力学:Ch15压杆稳定

4
1041.8kN
n PcrAC 1041 .8 5
P≤240.6kN PAC 0.866 P
例题7:已知压杆为如球果铰两,根由槽两钢根只等在边两角端钢连铆接成λ1=100,λ2=62, ,nslt==12..44cr8m,3,0[上4σ-A]述==11.2稳16×20定M28计P.9a算c,m和试2,强校铆度核钉计压孔算杆直会。不径会为发23生m变m,化P? =800kN
解:
FA
F
B
t Et cr
l 0.5 600 141.5
i 2.12
细长杆
Et π 2E 2
t
π 2E
E 2
π2
2
π2 12.5106 141.52
39.43
C
临界压力小结:
每一个压杆均有与之相应的临界应力 临界应力取决于压杆的材料、柔度
= l i
1
1
2E p
判别弹性平衡稳定性的静力学准则 (statical criterion for elastic stability)
FFPP FP
FP<FPcr :在扰动作用下,
直线平衡构形转变为弯曲 平衡构形,扰动除去后, 能够恢复到直线平衡构形, 则称原来的直线平衡构形 是稳定的。
FP FP
FP>FPcr :在扰动作用下,
55.1(< s)短粗杆
A 235106 2.3103
b a d d 752KN
i1 11.55mm
Pcr11
129.9
375KN
i2 2
16.3mm 92
Pcr 2 644KN
P i3 15.95mm 3 94
Pcr3 635KN
压杆稳定(10年)解析PPT课件

(3)当增大P至某一值 Pcr 时: 小的横向干扰 就会使杆失稳;
Pcr: 临界载荷(critical load)
扰动的种类:小的横向力;杆件表面凹坑; 杆件初始曲率等。
扰动是失稳的外因,杆件在外载作用下处于临界状态是内因。
2020年9月28日
14
P
P
压杆的实验观察
横向扰动
横向扰动
测试二
(1)将杆加粗或变短, 杆不容易失稳。
P Pcr 理想压杆曲线 B
实际压杆实验曲线
O
2020年9月28日
ymax
24
讨论
4. 精确微分方程
y
M
(1
y2
3
)2
EI
P
P Pcr
P Pcr
精确微分方程
P1.01P5cr
B
近似微分方程
实际压杆实验曲线
③稳定性 外力—?—稳定性条件
失去稳定性 后果更严重!
2020年9月28日
12
稳定性: 指平衡状态的稳定性 1.稳定平衡与不稳定平衡
不稳定平衡
2020年9月28日
稳定平衡
13
压杆的实验观察
测试一
P
(1) P=0或为拉时: 小的横向干扰不会使杆
离开起初始平衡位置(或失稳);
横向扰动 (2)增大P: 小的横向干扰仍不会使杆失稳;
2020年9月28日
1
第15章 压杆稳定
15.1 压杆稳定的概念 15.2 两端铰支细长压杆的临界力 15.3 两端约束不同时的临界力 15.4 临界力、经验公式、临界力总图 15.5 压杆的稳定校核 15.6 压杆稳定计算的折减系数法 15.7 提高压杆稳定性的措施
10压杆稳定解析

第十章压杆稳定30mm1m两根相同材料(松木)制成的杆,σb =20MPa ;A =10mm ×30mm短杆长:l =30mm ; FFFF长杆长:l =1000mm第一节 压杆稳定的概念一、稳定问题的提出若按强度条件计算,两根杆压缩时的极限承载能力均应为:F = σb A =6kN(1)短杆在压力增加到约为6kN时,因木纹出现裂纹而破坏。
(2)长杆在压力增加到约4kN时突然弯向一侧,继续增大压力,弯曲迅速增大,杆随即折断。
30mm1m FFFF压杆的破坏实验结果:• 短压杆的破坏属于强度问题;30mm1mFFFF• 长压杆的破坏则属于能否保持其原来的直线平衡状态的问题结论:短压杆与长压杆在压缩时的破坏性质完全不同压杆稳定性:压杆保持其原来直线平衡状态的能力。
压杆不能保持其原来直线平衡状态而突然变弯的现象,称为压杆的直线平衡状态丧失了稳定,简称为压杆失稳。
压杆失稳的严重后果:19世纪,瑞士的孟汗太因桥突然倒塌,造成200人遇难。
1907年加拿大的魁北克桥在建造时突然倒塌,其原因都是因为桥梁桁架中的受压杆失稳引起的。
1909年12月汉堡一个60万m3的大型贮气罐因一个受压构件失稳而突然倒塌。
研究压杆稳定性的意义:压杆因强度或刚度不足而造成破坏之前一般都有先兆;压杆由于失稳而造成破坏之前没有任何先兆,当压力达到某个临界数值时就会突然破坏,因此这种破坏形式在工程上具有很大的破坏性。
在建筑工程中的受压上弦杆、厂房的柱子等设计中都必须考虑其稳定性要求。
二、平衡状态的类型稳定平衡:干扰平衡的外力消失后,物体能自动恢复到原来的平衡位置的平衡不稳定平衡:即使干扰平衡的外力消失后,物体仍继续向远离原来平衡位置的方向继续运动的平衡。
随遇平衡:干扰平衡的外力消失后,物体可在任意位置继续保持平衡。
显然,随遇平衡是界于稳定平衡与不稳定平衡之间的状态,称为临界平衡状态。
F PF P 三、压杆临界力F crlF PF PF FF P F P F < F PcrF P F PF= F PcrF P F PF> F Pcr稳定直线平衡状态 不稳定平衡状态临界状态 压杆处于临界状态时的轴向压力称为压杆的临界力F cr 。
材料力学答案- 压杆稳定
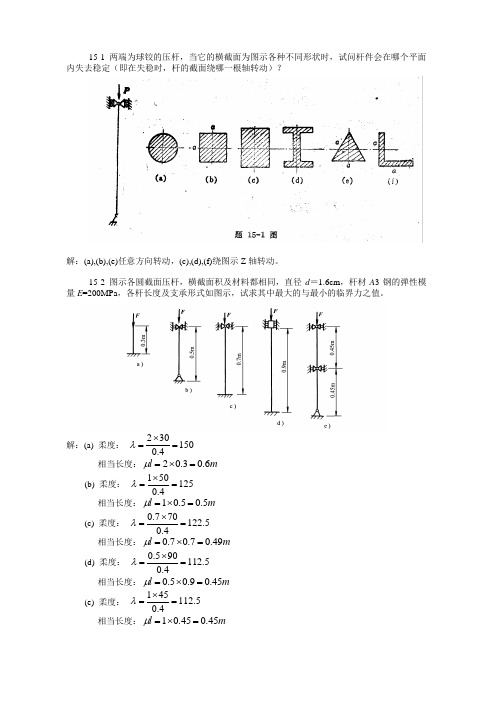
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
第15章压杆稳定

目录
§15.1 压杆稳定的概念(The basic concepts of
columns)
危害:
临界应力往往低于材料的屈服极限甚至比例极 限,破坏具有突然性
特点:
压杆临界力与压杆的材料性质、长度、截面尺 寸和形状、受到的约束情况有关
防止压杆失稳的关键所在:
压杆工作时所受到的压力(工作压力)必须小 于其临界力
3、在 Fcr作用下,
x
k ,wAsin 挠曲线为一条半波正弦曲线
l x
l
,w A
l
即 A 为跨度中点的挠度
2
目录
§15.2 临界荷载的欧拉公式
例题
解: 截面惯性矩
临界压力
269103N269kN
目录
§15.2 临界荷载的欧拉公式
两端非铰支细长压杆的临界压力
对于其他支座条件下细长压杆,求临界压力有两种方法:
3、熟知压杆临界应力总图,能根据压杆的 类别选用合适的公式计算临界应力
4、掌握简单压杆的稳定计算方法 5、了解提高压杆稳定性的主要措施
目录
作业 15-7; 15-9
34 目录
45钢。最大起重量F=80kN,规定
的稳定安全系数nst=4。试校核丝 杠的稳定性。
(1)计算柔度
dl
i
I A
d44 64 d2
d41cm 44
l 237.575
i1
查得45钢的2=60,1=100,2<<1,属于中柔度杆。
目录
§15.4 压杆稳定条件与合理设计
第十五章 压杆稳定问题
Chapter 15 Buckling of Columns
第十五章 压杆稳定问题
第十五章压杆稳定问题

5.压杆稳定条件与合理设计
因此,压杆将在正 视图平面内屈曲。
z=z l / iz ,
z > p应用欧拉公式
FPcr
(
z)
cr
A
π
2E
2
π
d2 4
276.2kN
工作安全因数 :
nw
cr wr
FPcr FP
276.2 150
1.834
5.压杆稳定条件与合理设计
1. 压杆稳定性的概念
压杆稳定性实验
1. 压杆稳定性的概念
稳定平衡与不稳定平衡 :
1. 不稳定平衡
1. 压杆稳定性的概念
2. 稳定平衡
1. 压杆稳定性的概念
3. 稳定平衡和不稳定平衡
1. 压杆稳定性的概念
压杆失稳与临界压力 :
1 压杆的稳定平衡与不稳定平衡:
稳 定 平 衡
不 稳 定 平 衡
1. 压杆稳定性的概念 F
k l
F δ kδ
F δ<k δl F δ>k δl F δ= k δl
F <k l 稳定平衡 F >k l 不稳定平衡
F = k l 临界状态
1. 压杆稳定性的概念
2 压杆失稳:
3 压杆的临界压力
临界状态
稳
对应的
定过
渡
平
衡
压力
不 稳 定 平 衡
临界压力: F=Fcr
F<Fcr稳定平衡
L EI
2.两端铰支细长压杆的临界载荷
临界力 Fcr 是微弯下的最小压力,故, 只能取n=1 ;且杆将绕惯性矩最小的轴弯曲。
Fcr
15压杆稳定

Fcr 269kN
图示结构ABC为矩形截面杆,b=60mm,h=100mm,l=4m, BD为圆截面杆,d=60mm,两杆材料均为A3钢,E=200GPa, σp =200MPa,均布载荷 q=1kN/m,稳定安全系nst=3。校核BD杆 的稳定性。 解:通过外力分析可知BD杆件为受 压杆件,根据静力学计算FBD:
M
A
0
FBD l si n45o 2ql 2 0 FBD 11.3kN
计算最大柔度
BD
l
i
2 4
d 4 6 4 d 2 4
3 7 7.1
p
2E 101 p
l
A3钢:a=304MPa,b=1.12MPa;E=206GPa, p=200MPa, s =235MPa
p
2E p
2 206 109
200 10
6
100
a s 304 235 0 61.6 b 1.12 0 max p 所以,应由经验公式求临界应力。
i
L2
(1)
(2)
(3)
3
L3
i
1 125 p
2 E d 2 ( Fcr )1 cr A 2 2540KN 1 4
L2 L3
0 2 62.5 p
( Fcr )2 cr A (a b2 ) 4705KN
2E 即: cr 2
l
i
I min i A
惯性半径。
3.柔度:
— —杆的柔度(或长细比 )
4.大柔度杆的分界:
cr
2E 2 P
2E P P
工程力学15-压杆稳定详解

§15-3 临界载荷的欧拉公式
一、两端铰支细长压杆的临界载荷
1、挠曲线近似微分方程: EIy" M(x) Fy
引用记号:k 2 F y" k 2 y 0 EI
2、该微分方程的通解为
y Asin kx Bcoskx
压 杆
式中A、B为积分常数
在
微
3、杆的边界条件
FN
5 2
F
150kN
2.CD杆的临界压力:
xA A
C
F
B
yA 2m
3m FN
I (D4 d 4 ) (1004 804 ) 1012 2.9 106 m4
64
64
2.9106 mm4
16
Fcr
2
l
EI
2
2
200103 2.9 3.52 106
106
467103 N 467kN
态
FFF===cccr
rr
b) 微
弯 F1
平 衡
F>FF>cFr cr
c)
失 稳
F1
干扰力去除后恢 复直线状态
干扰力去除后 保持微弯
干扰力去除后继续 变形,直至倒塌
1.临界状态: 由稳定平衡向微弯平衡过度的状态。
2.临界载荷Fcr: 保 持 压 杆 稳 定 的 最 大 轴 向 压 力 , 使 压 杆 失
公式。
解:变形如图,其挠曲线近似微分方程为:
L
P
P
EIyM (x)PyM
M0
令:k 2 P
EI
x
Px
y k 2 y k 2 M
M0
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定义
稳定平衡:去掉干扰后,能恢复到原直线形式的平 衡位置。 不稳定平衡:去掉干扰后,不能恢复到原直线形式平 衡位置。 临界力:压杆从稳定平衡过渡到不稳定平衡轴线压力 的临界值。 Pcr: 临界载荷(critical load)——压杆破坏载荷
17
理想压杆:
1)杆件轴线是理想直线;
2)无初弯曲; 3)载荷沿轴线方向作用,无偏心; 4)材料均匀。
2 EI
(2l )
2
Pcr
2 EI
l2
32
长度系数μ
=1
0.7
=0.5
=2
=1
0.5l
支承对压杆临界载荷的影响
各种支承压杆临界载荷的通用公式
P cr =
( l)2
2EI
一端自由,一端固定 =2.0
一端铰支,一端固定 =0.7 两端固定 两端铰支
=0.5 =1.0
P Pcr
实际压杆实验曲线
O
ymax
24
讨论
4. 精确微分方程 P
P Pcr
P Pcr
精确微分方程
P 1.015 Pcr
M 3 2 2 EI (1 y )
y
B
近似微分方程
实际压杆实验曲线
5. 欧拉公式的应用条件:
o
1.理想压杆;
2.线弹性、比例极限以内; 3. 平面弯曲。
边界条件为: x 0, y y 0; x l , y y 0
34
P
M0
P
M0
M0 c , P
d 0,
kl 2n 并 kl n
kl 2n
为求最小临界力,“k”应取除零以外的最小值,即取:
n 1, kl 2
4 2 EI 2 EI 所以,临界力为: Pcr 2 l ( l / 2) 2
二.两端铰支细长压杆的临界力、欧拉公式
临界力概念:干扰力去除后,杆保持微弯状态。 从挠曲线入手,求临界力。 y
P cr
① 弯矩: M ( x , y ) Py
P cr ② 挠曲线近似微分方程:
x
P cr
x
x y M
P cr
M P y y EI EI P y k 2 y 0 y y0 EI
9
工程事故2
2004.5.23清晨7点左右, 法国戴高乐机场的候机楼发 生屋顶坍塌事故,造成至少6 人死亡,3人受伤。 该候机楼2003年的6月17日 举办了落成典礼,但直到11 月份才正式投入使用。
法国巴黎郊外戴高乐机场的候机厅
戴高乐机场坍塌事故现场
就地展开医疗救助
10
工程背景
1983年10月4日, 高54.2m、长 17.25m、总重 565.4kN大型脚手
P
P
100
40
2)中小柔度杆的临界应力计算
P —中小柔度杆 中柔度杆: o P
① P<<S
p, 欧拉公式不适用。
强度、稳定兼而有之
— 经验公式
a. 直线型经验公式
cr a b
cr a1 b2
a s ( b ) o b
四.压杆的临界应力
1.临界应力概念 压杆处于临界状态时横截面上的平均应力。
Pcr A
Pcr 2E 2 EI 2 E cr 2 2 A ( l ) A ( l / i ) 2
i I — —惯性半径。 A
cr
临界应力的欧拉公式
2E 即: cr 2
B0 A 0 A sin kl 0 sin kl 0
P 由于 : k EI
2
2 2 n 2 Pcr EIk EI 2 l
kl n
n k l ( n 1,2,3...)
22
讨论
1. 临界力 Pcr 是微弯下的最小载荷,故:取
n=1 ,I=Imin。
P 其 中: k EI
2
21
考虑x段平衡:
③微分方程的解: ④确定积分常数:
y A sin kx B cos kx y ( 0) y ( l源自) 0y k 2 y 0
0 1 A A 0 B 0 0 即: sin kl cos kl B A sin kl B cos kl 0
凝土空 心板现场浇筑施工时, 发生模板支撑体系坍塌 事故,造成 8 人死亡、 21 人受伤的重大伤亡事故。
事故现场120救护车在出口等候救援 民工们守候在事故现场外等候消息 7
工程事故1 一个班组的人掉了下来, 在6层打灰的四十多人全都不见了。 由于工作业面距地面20多米,发生坍塌 后,工人被砸、埋其中。
材料性质 元件性质
39
2.临界应力曲线
1)欧拉公式适用范围(大柔度杆的分界) 欧拉公式应用条件:比例极限以内;平面弯曲。
E cr 2 P
2
P 当: P — —大柔度杆(或细长杆 ), 求临界力— —欧拉公式。
E
E
P
A3钢,E=200GPa , 比例极限p=200MPa,
不稳定平衡
稳定平衡
13
压杆的实验观察
P 测试一 (1) P=0或为拉时: 小的横向干扰不会使杆 离开起初始平衡位置(或失稳); (2)增大P: 小的横向干扰仍不会使杆失稳;
横向扰动
(3)当增大P至某一值 Pcr 时: 小的横向干扰 就会使杆失稳; Pcr: 临界载荷(critical load)
扰动的种类:小的横向力;杆件表面凹坑; 杆件初始曲率等。 扰动是失稳的外因,杆件在外载作用下处于临界状态是内因。
Pcr
2 EI min
l2
y z x
两端铰支压杆临界力的欧拉公式
在x-y面内失稳!
Imin=Iz
23
讨论
2. n=2、3、4 n=2
n y A sin kx A sin x l
n=3
3. y A sin kx曲线
P A
P Pcr
理想压杆曲线 B
P Pcr : OA线 P Pcr : AB线
——长度系数(或约束系数)
L——相当长度。
2 EI min 比较: P cr l2
两端铰支压杆的约束系数
=1
27
1. 一端固定一端自由
相当于长度 为 2l 两端 铰支压杆的临界力
Pcr
EI
2
2l
2
2. 一端固定一端铰支
相当于长度为0.7l 两端铰支压杆的临界力。
Pcr
架屈曲坍塌,5人
死亡、7人受伤 。
11
材料力学基本任务 构件的承载能力
问题 ①强度 ②刚度 ③稳定性
分析设计过程
外力—内力—应力—强度条件 外力—变形—刚度条件 外力—?—稳定性条件
失效方式
塑性屈服或脆断
变形过大失去工作能力 失去稳定性 后果更严重!
12
稳定性: 指平衡状态的稳定性 1.稳定平衡与不稳定平衡
P 图(b)
L
I min I y 3.89 108 m4
图 (a) : 一端固支, 一端铰支 (4545 6) 等边角钢
L
y
z
2 I min E Pcr ( 2l ) 2
2 0.389 200
(2 0.5)
2
76.8kN
37
图 (b): 一端固支,一端自由
33
例1
试由挠曲线近似微分方程,导出下述两种细长压杆的临 界力公式。
解:变形如图,其挠曲线近似微分方程为:
P P M0
x L
P
x
M0
EIy M ( x ) Py M 0 P 2 令:k EI 2 2 M0 EIy k y k P M0 y c cos kx d sin kx P
0.7l
EI
2 2
3. 两端固定
相当于长度为0.5l 两端铰支压杆的临界力。
Pcr
0.5l
EI
2 2
支承对压杆临界载荷的影响
31
表15–1 各种支承约束条件下等截面细长压杆临界力的欧拉公式 支承情况 两端铰支 一端固定 两端固定 另端铰支
一端固定 另端自由
Pcr
两端固定但可沿 横向相对移动 Pcr
14
P
P
压杆的实验观察
测试二
横向扰动
横向扰动
(1)将杆加粗或变短, 杆不容易失稳。 (2)增加杆的约束,
杆也不容易失稳。
压杆的实验观察结论
(1)压杆稳定与外载的大小、方式和杆端约束有关;
(2)压杆稳定与杆件几何尺寸有关;
15
(2)压杆的平衡状态
P< PP < crPcr P≥Pcr
稳定的
不稳定的
l
i
— 杆的柔度(或长细比)
柔度综合反映了:杆端约束、截面几何性质、
杆长对压杆稳定的影响
38
cr 与 s的比较
保证强度— — S 1)与 s 相同处: 保证稳定— — cr
S:只同材料有关 2)与 s不同处: cr:同支撑、杆长有关
= 0.5
35
x L z
例2
y
求下列细长压杆的临界力。
y z
h
b
EI y b3h 解:①绕 y 轴,两端铰支: =1.0, I y 12 , Pcry (1 L) 2
2
②绕 z 轴,
2 EI z bh3 , Pcrz 下端固定,上端铰支: =0.7 , I z (0.7 L )2 12
