五年级数学 平面几何图形的面积训练题 带详细答案
(完整版)五年级奥数平面图形面积计算

1 / 4五年级奥数第六讲———平面图形面积的计算一、知识重点1. 基本平面图形特点及面积公式特点面积公式① 四条边都相等。
正方形② 四个角都是直角。
S=aa③ 有四条对称轴。
①对边相等。
长方形②四个角都是直角。
S=ab③有二条对称轴。
平行四边形三角形梯形① 两组对边平行且相等。
② 对角相等,相邻的两个角之和为180°③ 平行四边形简单变形。
①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是④有三条边和三个角,拥有稳固性。
① 只有一组对边平行。
② 中位线等于上下底和的一半。
S=ahS=ah ÷ 2S=(a+b)h ÷22. 基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先依据图形的基本关系,再运用分解、组合、平移、割补、添协助线等几种方法将图形变为基本图形分别计算。
【典型例题】【例 1】 已知平行四边表的面积是28 平方厘米,【练一练】假如用铁丝围成以下列图同样的求暗影部分的面积。
平行四边形,需要用多少厘米铁丝?(单位:厘米)1 / 4180°。
【例 2】求图中暗影部分的面积。
【练一练】下列图中甲和乙都是正方形,求暗影部分(单位:厘米)的面积。
(单位:厘米)【例 3】以下图,甲三角形的面积比【练一练】平行四边形ABCD 的边长乙三角形的面积大 6 平方厘米,求CE 的长度。
BC=10 厘米,直角三角形 BCE 的直角边 EC 长 8 厘米,已知暗影部分的面积比三角形 EFG 的面积大10 平方厘米。
求 CF 的长。
【例 4】两条对角线把梯形 ABCD 切割成四个三角形。
【练一练】下边的梯形 ABCD 中,下底是已知两个三角形的面积(以下图),求另两个三角形上底的 2 倍, E 是 AB 的中点,求梯形 ABCD 的面积各是多少?(单位:厘米)的面积是三角形EDB 面积的多少倍?B【练一练】【练一练】计算下边图形的面积。
小学数学竞赛《几何图形》专题训练30道题含答案

小学数学竞赛《几何图形》专题训练30题含答一、单选题1.如图,一串黑白相间的珠子,被盒子遮住了一部分.如果这串珠子中白珠子有20个,那么黑珠子共有()A.19B.20C.212.一个三角形三个内角度数的比是2:1:1,这个三角形是()A.钝角三角形B.锐角三角形C.等腰三角形D.等边三角形3.下图中的∠1和∠2相比,()。
A.∠1大B.一样大C.∠2大D.无法确定4.一条直线和它上面的两点组成的图形中含有()条射线。
A.2B.3C.45.用()这几根小棒可以围成一个长方形。
A.6cm、2cm、6cm、2cm B.5cm、3cm、5cm、2cm C.5cm、2cm、6cm、6cm二、填空题6.看一看,写一写,填一填。
(1)(2)个十个一7.(如图)把底面半径3厘米、高10厘米的圆柱切成若干等份,拼成一个近似的长方体。
这个长方体的表面积是平方厘米,体积是立方厘米。
8.一些相同的小方块放在桌面上,小明从正面、上面、左面三个方向观察,图形都是一样的(如图)。
这些小方块最多有个,最少有个。
9.求角的度数.∠2=°10.观察下列各数组成的三角形,根据各数阵的排列规律,写出第五行的数(从左到右填写)11.求下面花园的面积与周长.周长m面积m212.数一数,填一填。
个,个,个,个。
13.把一个棱长为4dm的正方体木块外面涂上红色,然后切割成棱长是1dm的小正方体,一面涂红色的小正方体有块,两面涂红色的小正方体有块。
14.在下图中,一共有个小正方体,从面看到的形状是。
三、作图题15.下面是一个正方形,共16个方格。
其中有4个方格中分别画了一只小兔,请你把这个正方形分成大小、形状完全相同的4块,使每一块中都有1只小兔应怎样分割?(画粗线)16.根据要求在下列图形中分别画一条线段.(1)将图1分成两个钝角三角形.(2)将图2分成一个平行四边形和一个三角形.四、解答题17.填一填,想一想18.找规律填数.19.观察下面数的排列规律。
沪教版五年级上册《第5章_几何小实践》小学数学-有答案-单元检测训练卷A(一)

沪教版五年级上册《第5章几何小实践》单元检测训练卷A(一)一.判断.1. 三角形的面积等于与它等底等高的平行四边形面积的一半,所以任何三角形的面积都比平行四边形的面积小。
________.(判断对错)2. 有两个梯形,它们的上底、下底和高都不相等,它们的面积不可能相等。
________(判断对错)3. 两条平行线之间可以画无数条垂线段。
________.2011−2012学年湖北省咸宁市咸安区三年级(上)数学调研试卷二(第3−4单元)4. 平行四边形的对边平行且相等。
________.(判断对错)5. 梯形有一条对称轴。
________(判断对错).6. 两个面积相等的平行四边形一定等底等高。
________.(判断对错)7. 在一个三角形中,一条高只有一条对应的底边。
________.(判断对错)8. 直角三角形的两条直角边就是它的两条高。
________.(判断对错)9. 平行四边形变形后,与原来比较,周长相等,面积变小。
________.(判断对错)10. 两个面积相等的梯形一定可以拼成一个平行四边形。
________.(判断对错)二.选择.下列图形中,不是轴对称图形的是()A.圆B.正方形C.平行四边形D.等腰梯形如图,平行四边形的面积是3.6平方厘米,阴影部分的面积是()A.1.2平方厘米B.3.6平方厘米C.1.8平方厘米D.7.2平方厘米一个平行四边形的面积是80平方厘米,高是5厘米,与这条高对应的底边长是()A.8厘米 B.16厘米 C.10厘米 D.32厘米A.2.5平方厘米B.7.2平方厘米C.7.5平方厘米D.22.5平方厘米三.画出下列各图形底边上的高.画出图形底边上的高画出图形底边上的高画出图形底边上的高画出图形底边上的高画出图形底边上的高画出图形底边上的高四.画出下列梯形的高.画出下列梯形的高五.求下列图形的面积.求图形的面积求图形的面积求图形的面积求图形的面积六.求下列各图形中的未知量.求图形中的未知量求图形中的未知量求图形中的未知量七、解答题(共2小题,满分0分)有一块平行四边形的萝卜地,底长为30米,高为18米。
小学五年级平面几何必会的思想方法(典藏版)

平面几何必会的思想方法(典藏版)1.转化思想:【要点】求一些不规则图形的面积,重点在于把不规则图形转化为规则图形。
【例题】如图所示,两个相同的直角梯形重叠在一起,求阴影部分的面积。
(单位:厘米)【答案】140平方厘米【解析】可以将不规则图形面积转化成规则图形的面积来求。
题目中阴影部分的面积与下图中阴影部分的面积都等于大梯形面积减去中间重叠的小梯形面积,所以下图中阴影部分的面积等于题目中阴影部分面积,那么阴影部分面积为(20-5+20)×8÷2=140(平方厘米)。
2.分割法:【要点】把组合图形分割为常见的几何图形,以便利用面积公式计算。
【例题1】将两个相等的长方形重合在一起,求组合图形的面积.(单位:厘米)【解析】将图形分割成两个全等的梯形.(7-2+7)×2÷2×2=24(平方厘米)【例题2】如图所示,两个正方形并排放置,求阴影部分的面积是多少?【解析】将阴影部分分割成两个三角形.5×(5-3)÷2+3×3÷2=9.5【例题3】左图中两个正方形的边长分别为8厘米和6厘米.求阴影部分面积.解:将阴影部分分割成两个三角形.8×(8+6)÷2+8×6÷2=80(平方厘米)3.添补法:【要点】通过添补的方法,把不规则图形转化为能直接计算的图形【例题】AD垂直于DC,AB垂直于BC, 其余条件如图所示,求四边形ABCD的面积.(单位:厘米)【答案】32平方厘米【解析】尝试进行分割会发现,分割后仍然无法计算四边形的面积,所以考虑进行添补,如图所示.补上三角形ADE后,整个图形变成了等腰直角三角形,而且三角形ADE也是等腰直角三角形,四边形ABCD的面积:10×10÷2-6×6÷2=32(平方厘米)。
4.割补法:【要点】割下图形的一部分,通过旋转、平移等方法补成常见的几何图形。
多边形面积练习题及答案

多边形面积练习题及答案多边形面积练习题及答案多边形是几何学中常见的图形,它由多条线段组成,每条线段称为边。
多边形的面积是一个重要的几何概念,它可以通过不同的方法计算。
本文将介绍一些多边形面积的练习题及其解答。
一、三角形的面积计算三角形是最简单的多边形,其面积计算公式为:面积 = 底边长度× 高÷ 2。
假设有一个底边长度为6cm,高为4cm的三角形,其面积可以计算为:6 × 4 ÷ 2 = 12 cm²。
二、矩形的面积计算矩形是一种特殊的四边形,其相邻两边相等且相互垂直。
矩形的面积计算公式为:面积 = 长× 宽。
例如,一个长为5cm,宽为3cm的矩形,其面积为:5 ×3 = 15 cm²。
三、正方形的面积计算正方形是一种特殊的矩形,其四条边相等且相互垂直。
正方形的面积计算公式同样为:面积 = 边长× 边长。
举例来说,一个边长为4cm的正方形,其面积为:4 × 4 = 16 cm²。
四、梯形的面积计算梯形是一种具有两条平行边的四边形,其面积计算公式为:面积 = (上底 + 下底)× 高÷ 2。
假设一个梯形的上底长为5cm,下底长为8cm,高为3cm,其面积可以计算为:(5 + 8)× 3 ÷ 2 = 19.5 cm²。
五、菱形的面积计算菱形是一种具有四条边相等的四边形,其面积计算公式为:面积 = 对角线1 × 对角线2 ÷ 2。
例如,一个菱形的对角线1长为6cm,对角线2长为8cm,其面积为:6 × 8 ÷ 2 = 24 cm²。
六、多边形的面积计算对于不规则的多边形,我们可以将其分割成多个三角形或梯形,然后分别计算每个部分的面积,最后将它们相加。
假设一个不规则多边形可以分割成两个三角形,其面积分别为10 cm²和15 cm²,那么整个多边形的面积为:10 + 15 =25 cm²。
五年级下册数学试题-几何图形面积计算练习一(无答案)人教版
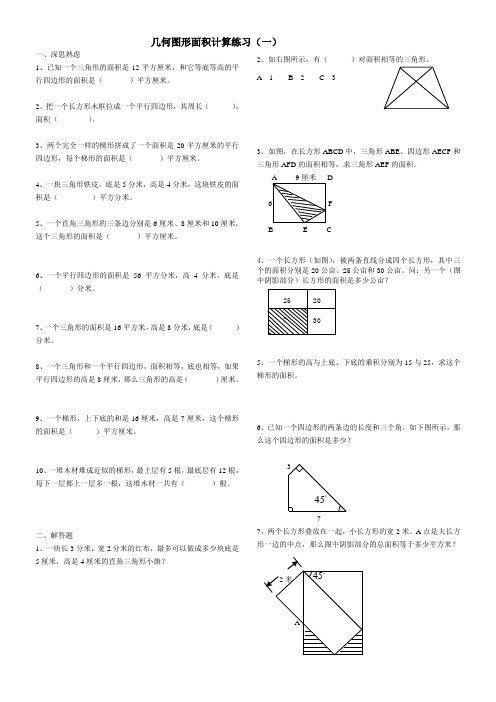
几何图形面积计算练习(一)一、深思熟虑1、已知一个三角形的面积是12平方厘米,和它等底等高的平行四边形的面积是()平方厘米。
2、把一个长方形木框拉成一个平行四边形,其周长(),面积()。
3、两个完全一样的梯形拼成了一个面积是20平方厘米的平行四边形,每个梯形的面积是()平方厘米。
4、一块三角形铁皮,底是5分米,高是4分米,这块铁皮的面积是()平方分米。
5、一个直角三角形的三条边分别是6厘米、8厘米和10厘米,这个三角形的面积是()平方厘米。
6、一个平行四边形的面积是56平方分米,高4分米,底是()分米。
7、一个三角形的面积是16平方米,高是8分米,底是()分米。
8、一个三角形和一个平行四边形,面积相等,底也相等,如果平行四边形的高是8厘米,那么三角形的高是()厘米。
9、一个梯形,上下底的和是16厘米,高是7厘米,这个梯形的面积是()平方厘米。
10、一堆木材堆成近似的梯形,最上层有5根,最底层有12根,每下一层都上一层多一根,这堆木材一共有()根。
二、解答题1、一块长3分米,宽2分米的红布,最多可以做成多少块底是5厘米,高是4厘米的直角三角形小旗?2、如右图所示,有()对面积相等的三角形。
A 1B 2C 33、如图,在长方形ABCD中,三角形ABE、四边形AECF和三角形AFD的面积相等,求三角形AEF的面积。
A 9厘米 D6 FB E C4、一个长方形(如图),被两条直线分成四个长方形,其中三个的面积分别是20公亩、25公亩和30公亩。
问:另一个(图中阴影部分)长方形的面积是多少公亩?25 20? 305、一个梯形的高与上底、下底的乘积分别为15与25,求这个梯形的面积。
6、已知一个四边形的两条边的长度和三个角,如下图所示,那么这个四边形的面积是多少?34577、两个长方形叠放在一起,小长方形的宽2米。
A点是大长方形一边的中点,那么图中阴影部分的总面积等于多少平方米?。
【平面图形的面积问题】2023年小升初数学无忧衔接 (通用版)(解析版)

平面图形的面积问题在初中几何中,随着变量和演绎推理证明等知识的进入,初中学生学习几何就需要提高相应的思维能力,比如抽象思维,推理等等。
难度自不必说,思维的层次也大为不同。
甚至一些证明,必须用演绎推理来完成,比如“两直线垂直于同一条直线,那么这两条直线平行”,这个命题就需要演绎推理思维,学生必须要在自己的心中构建直观图形,难度加大了。
如“三角形的内角和等于180°”这个定理,在小学教材中是由实验得出的,学生较熟悉。
因此,在教学中既让学生通过实验得出结论,又要强调说明不能满足于实验,而必须从理论上给予严格论证。
求几何图形面积常见方法及运用:【解题技巧】常见模型例1.(2022春·六年级统考期末)下图中阴影部分的面积是( )平方厘米。
【答案】8平方厘米【分析】观察图形可知,小正方形部分阴影面积等于长方形空白处面积,如下图:阴影部分面积等于长是(2+2)厘米,宽是2厘米长方形面积;根据长方形面积公式:面积=长×宽,代入数据,即可解答。
【详解】(2+2)×2=4×2=8(平方厘米)【答案】4平方厘米【分析】通过观察图形可知,把阴影部分通过“旋转”或“割补”法,把阴影部分拼成三角形的面积,根据三角形的面积公式:S=ah÷2,求出大三角形的面积,再除以2,即可求出阴影部分的面积。
【详解】如图:4×4÷2÷2=16÷2÷2=8÷2=4(平方厘米)变式1.(2023秋·北京西城·五年级统考期末)将等腰三角形ABC沿虚线对折,折下来的部分恰好拼成了一个长方形(如图)。
已知三角形ABC的底是6cm,高是4cm,图中涂色部分的面积是()cm2。
A.24 B.12 C.6 D.3【答案】D【分析】如图:观察图形可知,三角形ABC左右两边的涂色小三角形完全一样,把左边的涂色小三角形平移至右边,与右边涂色小三角形组合成一个与①一样大的三角形;这样三角形ABC平均分成4份,涂色部分占其中的一份;根据三角形的面积=底×高÷2,求出三角形ABC的面积,再除以4即是涂色部分的面积。
北师大版小学数学五年级下册《图形与几何》教材同步练习带答案

《图形与几何》同步习题1.下面的立体图形都是由棱长为1 cm的小正方体搭成的,它们的体积分别是多少?填一填。
2.下面是某种饮料的三种不同包装,买哪种比较便宜?请写出你的思考过程。
3.淘气爸爸制作了一个长方体鱼缸,下面的两块玻璃正好是这个鱼缸的两个面,你能计算出这个鱼缸的容积是多少立方分米吗?(玻璃厚度忽略不计)4.制作这样一个纸袋(如下图),大约需要多少包装纸?(接口处忽略不计)5.要在一个长2 m、宽1.5 m的长方形沙坑里铺上15 cm厚的沙子,需要多少立方米的沙子?6.制作一个如右图的储物柜。
(1)需要多少平方米的木板?(2)这个储物柜的占地面积是多少?7.量一量,填一填。
(1)邮局在君君家的()方向上,距离君君家约()m;学校在君君家的()偏()()°方向上,距离君君家约()m。
(2)学校在邮局的()方向上,距离邮局()m;君君家在邮局的()方向上,距离邮局()m。
8.公园内5个景点的路线图如下。
小明从A景点出发到D景点,可以怎样走?请你描述出他的行走路线。
参考答案1.8 cm 3 13 cm 3 11 cm 32.150 mL =0.15L4÷0.15≈26.7(元/L )15÷1=15(元/L )20÷1.5≈13.3(元/L )因为26.7>15>13.3 ,所以第三种最便宜。
3. ()3684192dm ××=答:这个鱼缸的容积是192 dm 3。
4. ()()305301515521200cm ×+×+××=2 答:大约需要1200 cm 2。
5.15 cm =0.15 m ()32 1.50.150.45m ××=答:需要0.45 m 3的沙子。
6.(1)(0.6×0.8+0.6×1.5+0.8×1.5)×2=()25.16m ()20.60.82 5.16 6.12m ××+=答:需要6.12 m 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面几何图形的面积
板块一:基础巩固
1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是()平方分米,三角形的面积是()平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?
3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?
3
2
4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
板块二:拓展提高
【例题1】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积
.
【例题2】右图中甲的面积比乙的面积大__________平方厘米.
6厘米
8厘米4厘米
【例3】右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.
A B
C D
E
F
【巩固】如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?
A B
E
C
D
【例4】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?
12
152
2
2
【巩固】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?
5×22
5
【例5】下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。
【例6】四边形ABCD是直角梯形,AD=12厘米,AB=8厘米,BC=15厘米,且三角形ADE,四边形DEBF,三角形CDF的面积相等,求阴影三角形的面积是多少平方厘米?
【例7】一块长方形,用垂直于长和宽的两条线分成四块,其中三块面积分别为15、18、30平方米。
第四块面积是多少平方米?
【巩固】如图有9个小长方形,其中的5个小长方形的面积分别为4、8、12、16、20平方米,其余4个长方形的面积分别是多少平方米?
【例8】如下图,在一个之间三角形铁皮上剪下一个正方形,并且使正方形的面积尽可能的大,正方形的面积最大是多少?
【巩固】如图,直角三角形ABC套住了一个正方形CDEF,E恰好在AB边上,直角边AC长40厘米,BC长12厘米,求正方形的边长是多少?
【例9】如图,长方形ABCD 长是8厘米,宽是7厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.
E
【巩固】如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.
F
E D
C B
A
【例10】如图,三角形ABC 中,DC=2BD ,CE=3AE ,三角形ADE 的面积是20平方厘米,三角形ABC 的面积是多少?
E
D C
B A
【巩固】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?
C B
【答案】
板块一:
1、24 12
2、上底+下底=20.5-8.5=12(米)
梯形面积=12×8.5÷2=51(平方米)
3、原长方形的长:24÷2=12(米)
原长方形的宽:24÷3=8(米)
原来长方形的面积:12×8=96(平方米)
4、方法一:可以分割成两个钝角三角形
第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)
方法二:两个正方形的面积-2处空白的面积
=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)
方法一:可以分割成三个钝角三角形
第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)
第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)
一共的面积:8+16+24=48(平方厘米)
方法二:把右上角补起来
阴影面积=三个正方形的面积+小长方形面积-两处空白的面积
=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)
板块二:拓展提高
【例题1】、阴影部分+中间空白=中间空白+下面空白
所以阴影部分=下面空白
20-5=15(厘米)
(15+20)×8÷2=140(平方厘米)
【例题2】、利用同增同减差不变
甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积
=6×8÷2-4×8÷2
=24-16
=8(平方厘米)
【例题3】、利用同增同减差不变
三角形ABF-三角形EDF的面积=9平方厘米
同时增加梯形BCDF的面积,则:
长方形ABCD-三角形BCE=9
长方形ABCD的面积=4×6=24(平方厘米)
则三角形BCE的面积=24-9=15(平方厘米)
EC=15×2÷6=5(厘米)
ED=5-4=1(厘米)
【巩固】、利用同增同减差不变
三角形CDE-三角形ABE的面积=2平方厘米
同时增加三角形BCE的面积,则:
三角形BCD-三角形ABC=2
三角形ABC的面积=4×4÷2=8(平方厘米)
则三角形BCD的面积=8+2=10(平方厘米)
CD=10×2÷4=5(厘米)
【例题4】原来的面积=15×12=180(平方分米)
现在的的面积=(15-2)×(12-2)=130(平方厘米)
减少的面积:180-130=50(平方厘米)
【巩固】66-2×5=56(平方厘米)
设剩下的部分正方形的边长为x厘米
5x+2x=56
X=8
原来长方形的长:8+5=13(厘米)
原来长方形的宽:8+2=10(厘米)
原来长方形的面积:13×10=130(平方厘米)
【例题5】三角形ADF的面积:32÷2÷2=8(平方厘米)三角形ABE的面积:32÷2÷2=8(平方厘米)
三角形CEF的面积:32÷2÷2÷2=4(平方厘米)
三角形AEF的面积:32-8-8-4=12(平方厘米)
【例题6】梯形的面积:(12+15)×8÷2=108(平方厘米)三角形ADE的面积:108÷3=36(平方厘米)
AE 的长:36×2÷12=6(厘米)
三角形ACF 的面积:108÷3=36(平方厘米)
CF 的长:36×2÷8=9(厘米)
BE 的长:8-6=2(厘米)
BF 的长:15-9=6(厘米)
阴影部分面积=2×6÷2=6(平方厘米)
【例题7】15×30÷18=25(平方米)
【巩固】A 面积:4×16÷8=8(平方米)
B 面积:16×12÷8=24(平方米)
D 面积:20×24÷16=30(平方米)
C 面积:8×20÷16=10(平方米)
【例题8】连接DB ,把大三角形分成两个小三角形,正方形的边长就是这两个三角形的高
大三角形ABC 的面积是:40×10÷2=200(平方厘米)
设正方形的边长为x 厘米
40x÷2+10x÷2=200
25x=200 X=8
正方形面积=8×8=64(平方厘米)
【巩固】连接CE ,把大三角形分成两个小三角形,正方形的边长就是这两个三角形的高
大三角形ABC 的面积是:40×12÷2=240(平方厘米)
设正方形的边长为x 厘米
40x÷2+12x÷2=240
26x=240
X=120/13
【例题9】长方形的面积:8×7=56(平方厘米) A B C D
阴影部分面积:56÷2=28(平方厘米)
【巩固】24÷2÷2÷2=3
【例题10】三角形CDE的面积:20×3=60(平方厘米)三角形ADC的面积:20+60=80(平方厘米)
三角形ABD的面积:80÷2=40(平方厘米)
三角形ABC的面积:40+80=120(平方厘米)
【巩固】三角形ABD的面积:180÷2=90(平方厘米)三角形ABE的面积:90÷3=30(平方厘米)
三角形AEF的面积:30÷4×3=22.5(平方厘米)。
