压杆稳定实验
压杆稳定试验

压杆稳定试验一、目的:(1)观察和了解两端铰支细长中心受压杆件将要丧失稳定时的现象。
(2)用电测法测定两端铰支压杆的临界载荷cr F ,并与理论计算结果进行比较。
二、原理:矩形界面压杆试件及夹具如图14-1(a )所示。
试件由弹簧刚制成,两端是带圆角的刀刃。
夹具开有V 形槽,V 形槽两侧装有可伸缩的螺钉,用以改变压杆的约束状态。
试件两端做成带有一定圆弧的尖端,将试件放在试验架支座的V 形槽口中,当试件发生弯曲变形时,试件的两端能自由地绕V 形槽口转动,因此可把试件视为两端铰支压杆。
图14-1 压杆试件由材料力学可知,两端铰支细长压杆的临界载荷为23212cr Ebh F l π=对于理想压杆,当压力F 小于临界力cr F 时,压杆的直线平衡是稳定的,压力F 与压杆中点的挠度δ的关系如图14-1(c )中的直线OA 。
当压力达到临界压力cr F 时,按照小挠度理论,F 与δ的关系时图中的水平线AB 。
实际的压杆难免有初曲率,在压力偏心及材料不均匀等因素的影响下,使得F 远小于cr F 时,压杆便出现弯曲。
但这阶段的挠度δ不很明显,且随F 的增加而缓慢增长,如图中的OC 所示。
当F 接近cr F 时,δ急剧增大,如图中CD所示,它以直线AB 为渐近线。
因此,根据实际测出的F -δ曲线图,由CD 的渐近线即可确定压杆的临界载荷cr F 。
实验时,将矩形截面试件的两端,放在“V ”形支座中,则试件两端所受的约束可视为铰支。
为测定cr F ,压杆中点的变形可采用不同的测量方法。
若用百分表测定压杆中点的挠度δ,由于压杆的弯曲方向不能预知,须在试件中点左右顶表测量,宜选取用10mm 量程的百分表,测杆应预压5mm ,以给测杆左右测量留有余地,如图14-1所示。
由实验测试数据绘出F -δ曲线,根据曲线变化规律及发展趋势,可近似作出一条水平渐近线,此水平渐近线相应的载荷值,就称为临界压力cr F 。
另一种方法是在压杆中点两侧贴应变片,如图14-2(a )所示。
压杆稳定性实验(含纸桥案例分析)

压杆稳定性实验潘哲鑫2012011680 祝世杰2012010407一.实验分析对于立柱材料而言,损坏往往不是来源于直接受压的损坏,而大都来自于杆件失稳导致的折断或者倾倒。
因此研究杆件在受压情况下的失稳特性就非常有意义。
在本实验中,我们使用的是环氧树脂杆,弹性模量59.2E GPa =,500MPa σ=⎢⎥⎣⎦ 通过测量可知,杆的有效长度为,8412mm L cmd ==直径 实验一:双端铰支的情况下临界载荷22(KL)K EIP π=其中K=1,故可算得,临界842.9K P N =考虑杆件达到其许应力的最大值, K K P P A Wδσ+=⎢⎥⎣⎦ 则 3d ())42K k P W W A P πδσ=-=⎢⎥⎣⎦其中( 则算得,9.86cm δ=因此我们根据上述计算结果,进行了实验,为了防止实验材料被破坏,我们仅仅加载到最大横向位移的0.8倍。
可以观察到,当加载的力值迅速升高至临界载荷后,再继续向下加载,杆件上的力并不会变大,取而代之的是杆件向铰支允许的方向的的弯曲。
实验二:一端铰支,一段固支的情况下 临界载荷22(KL)K EIP π=其中K=0.7,故可算得,临界1720.1K P N =同理可计算得,达到杆件的最大拉伸应力时, 4.78cm δ=,于是在实验中,我们加载到约3cm 处停止。
在第二次实验中,我们遇到一个问题,即当杆件开始弯曲时,由于可能杆件安装时的偏心误差,它弯曲的方向并不是我们希望测量的方向,因此,在弯曲过程中,为了能使其向我们偏好的方向弯曲,我主动给它提供了一个水平方向的扰动的力,从而使得其改变弯曲的方向。
但这也导致了在我们实验的曲线上加载阶段,并不是完全和理论相符,而一定程度上小于本应该出现的值。
而某种程度上,呈现出线性的关系。
不过可以解释为,由于我的外加力的作用,阻碍了杆件通过弯曲来抵抗载荷,因此,杆件此时纵向的形变完全来自于由于轴向应力产生的应变,满足胡克定律,故一定程度上呈现出线性的状态。
压杆稳定 实验报告

压杆稳定实验报告压杆稳定实验报告一、引言在物理学中,稳定性是一个重要的概念。
对于一个物体或系统来说,稳定性意味着它能够保持在一个平衡状态,不会因外界干扰而倾倒或崩溃。
压杆稳定是一个经典的物理实验,通过改变杆的长度和重心位置,我们可以探索压杆在不同条件下的稳定性。
二、实验目的本实验的目的是通过改变压杆的长度和重心位置,观察和分析压杆在不同条件下的稳定性。
通过实验,我们可以进一步了解压杆稳定的物理原理,并探讨压杆稳定性与杆长、重心位置之间的关系。
三、实验装置和方法1. 实验装置:压杆、支架、重物、测量工具(如尺子和天平)等。
2. 实验方法:a. 将支架放置在水平的桌面上,并固定好。
b. 将压杆放在支架上,调整杆的位置和角度,使其保持平衡。
c. 在压杆的一端悬挂一个重物,称为A端。
d. 在压杆的另一端悬挂一个重物,称为B端。
e. 记录下A端和B端的质量,以及压杆的长度和角度。
f. 通过改变A端和B端的质量、压杆的长度和角度等条件,重复实验,记录数据。
四、实验结果与分析在实验中,我们通过改变A端和B端的质量、压杆的长度和角度等条件,观察压杆在不同条件下的稳定性。
下面是我们的实验结果和分析:1. 改变质量:我们分别改变A端和B端的质量,观察压杆的稳定性。
实验结果表明,当A端和B端的质量相等时,压杆更容易保持平衡。
这是因为在这种情况下,压杆的重心位置更接近中间,稳定性更高。
当A端或B端的质量增加时,压杆的稳定性减弱,容易发生倾倒。
2. 改变长度:我们改变压杆的长度,观察压杆的稳定性。
实验结果显示,当压杆的长度较短时,压杆更容易保持平衡。
这是因为较短的压杆有更小的杆长,重心位置更接近中间,稳定性更高。
当压杆的长度增加时,压杆的稳定性减弱,容易发生倾倒。
3. 改变角度:我们改变压杆的角度,观察压杆的稳定性。
实验结果表明,当压杆的角度接近水平时,压杆更容易保持平衡。
这是因为在这种情况下,压杆的重心位置更接近支点,稳定性更高。
压杆稳定实验
压杆稳定实验1实验目的(1).观察细长中心受压杆丧失稳定的现象。
⑵.用电测实验方法测定各种支承条件下压杆的的临界压力Pcr实,增强对压杆承载及失稳的感性认识。
⑶.实测临界压力P cr实与理论计算临界压力P cr理进行比较,并计算其误差值。
2设备和仪器⑴.50KN微机控制电子万能试验机。
⑵).计算机。
⑶.游标卡尺。
3实验原理及试件当细长杆受轴向压力转小时,杆的轴向变形较小,它与载荷是线弹性关系。
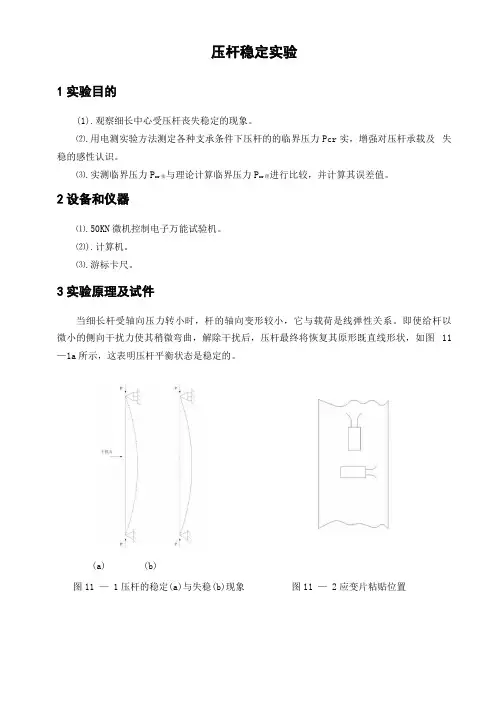
即使给杆以微小的侧向干扰力使其稍微弯曲,解除干扰后,压杆最终将恢复其原形既直线形状,如图11 —1a所示,这表明压杆平衡状态是稳定的。
(b)(a)图11 — 1压杆的稳定(a)与失稳(b)现象图11 — 2应变片粘贴位置图11-3应变片组成的全桥当轴向压力逐渐增大,超过某一值时,压杆受到微小的干扰力后弯曲,解除干扰后,压杆不能恢复直线形状,将继续弯曲,产生显著的弯曲变形,既丧失了原有的平衡状态,这表明压杆的平衡状态是不稳定的。
使压杆直线形态的平衡状态开始由稳定转变为不稳定的轴向压力值,称为压杆的临界载荷,用P cy实表示,如图11-1 b所示。
压杆丧失其直线形状的平衡而过度为曲线平衡,称为丧失稳定或简称失稳,由失稳造成的失效,失效并非强度不足,而是稳定性不够。
在压杆中部两面纵横粘贴四枚应变片组成全桥,如图11-2、图11-3所示,应变片的阻值是350Q电桥的AC和BD端的输出信号输入计算机进行数据处理并放大3 . 76x 103倍,经窗口显示压杆的变形量,将变形量除以放大倍数3.76x 103可计算出压杆的应变£。
再由应变算出压杆在临界力作用下的应力。
二E£。
从压杆的临界应力可见,细长杆弹簧钢的临界应力比比例极限应力小得多。
所以细长压杆丧失承载能力并不是材料强度不够,而是由于稳定性不够。
试件:材料为弹簧钢,E=210GP,长度L=300mm,宽度b=20mm,厚度h=2.96mm。
在试件的中部粘贴四枚应变片组成全桥,用来测量压杆的变形。
压杆稳定实验

压杆稳定实验一、实验目的1.观察压杆失稳现象,理解压杆“失稳”的实质。
2.测定四种刚性支承条件下压杆失稳的临界载荷F jx,分析支承条件对压杆失稳临界载荷的影响,并与相应的欧拉载荷F cr进行比较。
3.绘制出四种刚性支承条件下压杆失稳的屈曲模态。
二、预习思考要点1.欧拉的理想压杆模型有何特征?实验中的压杆与理想压杆有何区别?2.为什么说欧拉压杆承载力公式是在小变形条件下导出的?3.不同的支承方式对压杆的临界载荷有何影响?材料力学中是以什么参量来表示这种影响的?三、实验仪器和装置1.微型计算机2.压杆稳定试验台试验台的结构简图如图(1-35)所示,它由底板、顶板和四根立柱构成加力架。
在顶板上安装了加力和测力系统。
采用螺旋加力方式,拧进顶部的旋钮使丝杠顶推压头向下运动,即可对压杆加载。
测力传感器中的弹性敏感元件置于丝杠和压头的芯轴之间。
位移传感器为机电百分表,也装于顶板,通过承托卡感应压头的位移。
这两种传感器的弹性元件上的电阻应变计均联接成全桥电路,输出的应变信号通过电缆接入仪器的相应插座,经放大和模数(A/D)转换,在计算机上直接显示为力值和位移值。
图1-35 压杆稳定试验台 图1-36 压杆稳定试样试验台配备的支承有:下铰支承2副,中间支承卡1副;上铰支承(滚珠帽)1副。
3.压杆试件压杆试件如图1-36所示,其压杆和托梁均由弹簧钢制成,其弹性模量E=210GPa ,试件截面尺寸:20×2mm 2,各种支承条件下压杆的计算长度参考图中的有关尺寸(L i )。
4.游标卡尺、钢直尺四、实验原理对于轴向受压的理想细长直杆(即柔度λ≥λP ),按小变形理论,其临界载荷可由欧拉公式求得:2min 2)(l EI F cr μπ= (1-67)式中:E 为材料的弹性模量;I min 为压杆截面的最小轴惯性矩;l 为压杆长度;μ为长度系数。
本实验所采用的压杆稳定试验台为了简化测量装置,以压杆受压时产生的轴向位移Δ替代压杆中点的侧向位移(挠度)f,因为二者在数学上是相关的,当然不同支承条件2。
压杆稳定性实验

实验五压杆稳定性实验一、试验目的1.测定两端铰支压杆的临界载荷Fcr,验证欧拉公式。
2.观察两端铰支压杆的失稳现象。
二、设备和仪器1.多功能力学实验台2.游标卡尺、钢板尺。
三、试样试样是用弹簧钢60Si2Mn 制成的矩形截面细长杆,名义尺寸为3mm×20mm×300mm,两端制成刀口,以便安装在试验台的V 形支座内。
试样经过热处理:870℃淬油,480℃回火。
四、实验原理两端铰支的细长压杆,临界载荷Fcr 用欧拉公式计算:式中E 是材料弹性模量,I 为压杆横截面的最小惯性矩,L 为杆长。
这公式是在小变形和理想直杆的条件下推导出来的。
当载荷小于Fcr 时,压杆保持直线形状的平衡,即使有横向干扰力使压杆微小弯曲,在撤除干扰力以后仍能回复直线形状,是稳定平衡。
当载荷等于Fcr 时,压杆处于临界状态,可在微弯情况下保持平衡。
把载荷F 为纵坐标,把压杆中点挠度δ为横坐标,按小变形理论绘制的F- δ曲线为图14-1 中的OAB 折线。
但实际的杆总不可能理想地直,载荷作用线也不可能理想地与杆轴重合,材料也不可能理想地均匀。
因此,在载荷远小于Fcr 时就有微小挠度,随着载荷的增大,挠度缓慢地增加,当载荷接近Fcr 时,挠度急速增加。
其F- δ曲线如图中OCD 所示。
工程上的压杆都在小挠度下工作,过大的挠度会产生塑性变形或断裂。
只有比例极限很高的材料制成的细长杆才能承受很大的挠度使载荷稍高于Fcr(如图中虚线DE 所示)。
实验测定Fcr,在杆中点处两侧各粘贴一枚应变片,将它们组成半桥,记录应变仪读数εdu,绘制F-εdu曲线。
作F- εdu曲线的水平渐近线,就得到临界载荷Fcr。
五、试验步骤1.测量试样尺寸用钢板尺测量试样长度L,用游标卡尺测量试样上、中、下三处的宽度b 和厚度t,取其平均值。
用来计算横截面的最小惯性矩I。
2.拟定加载方案,并估算最大容许变形按欧拉公式计算Fcr,在初载荷(200N)到0.8Fcr 间分4—5 级加载,以后应变仪读数εdu每增加20 με读一次载荷值(应变仪测变形时)。
压杆稳定实验
压杆稳定实验
根据欧拉公式,有
2 EI Pcr 2 l
压杆稳定实验
(二)细长压杆临界力测定 压杆稳定实验装置简图如图所示。
压杆稳定实验
1、实验值确定: 实验采用矩形截面薄钢杆6作为压杆试样,两端放 在V形槽内,相当于两端铰支。压力P通过加载杠杆4 、固定砝码2和移动砝码3加在压杆的A端,通过调节两 个砝码的重力和位置可以改变压力P。用两个涡流传感 器5和7对称的装在试样6中点E的两边,当试样6在轴向 力P作用下变弯时,用涡流传感器和计算机测出中点E 两边的位移。实验过程中一边加力一边注意监测变形 ,如果变形显著增加时,意味着试样有较大弯曲,这 时所对应的轴向力P即为临界力Pcr。 根据平衡条件,压力P与作用在B,C点砝码重力QB , QC及作用位置的关系为:
压杆稳定实验
QB BD QC CD P AD
根据实验记录的砝码重量和变形值按一定比例 绘制P- δ曲线图,从稳定图中确定临界力Pcr 。 2、理论计算: 图示约束和截面情况下,压杆的临界压力的理论值 为:
EI Eba Pcr 2 12l 2 l
2 2
3
压杆稳定实验
3、误差计算:
对杆件6的临界力Pcr计算相对误差:
Pcr Pcr e % Pcr
四、试验步骤 1、测量原始尺寸
将试样和传感器安装在相应的卡具中,测量并 记录有关数据。包括断面尺寸、位置尺寸。
压杆稳定实验
预习要求:1.复习压杆失稳的概念和计算临界应力欧拉公式;2.复习大挠度稳定性概念。
一.实验目的1.观察压杆失稳现象;2.通过实验确定临界载荷F cr,并与理论结果比较;3.自主设计实验步骤,进行实验结果处理和撰写实验报告。
二.实验设备和仪器1.压杆失稳试验装置;2.电阻应变仪;三.实验试件1.单压杆(如图1所示)压杆材料为65Mn弹簧钢,σS=780MPa,σP=980Mpa弹性模量E=200GPa。
四.实验方法FF 压杆实验装置图为了保证试件失稳后不发生屈服,实验前后应估算试件最大许可载荷F max ,并估算最大失稳许可挠度δmax ,计算δmax 的方程为:m ax[]F F A wδσ⋅+≤实验时画出载荷—位移曲线,根据载荷—曲线的变化趋势来判断压杆的临界载荷。
注意事项:(1)为保证试件失稳后不发生屈服,估算最大许用载荷。
(2)分析压杆失稳时最大挠度发生的位置。
五.实验步骤(1)测量板条长L ,宽B ,厚H 。
(2) 选定实验组合方式,根据需要任选1—2种组合方式进行实验,在实验台上装夹好试件及配件。
压杆稳定有四种情况:(1)两端铰支。
(2)一端固定另一端铰支。
(3)两端固定。
它们的临界载荷的一般表达方式为F C r =π2EI (μL )式中μ为长度因素,支承不同μ值不同(μ=1、21、0.7)。
(3) 对于3个安装状态,各实验2遍,用百分表测压头的位移,用应变仪测压力P =ϵP EBH 和纯弯应变ϵM ,画出曲线,确定失稳压力,算出相对理论值的误差。
六.数据处理 1. 原始数据表1 基本长度注:表格里的P的公式:P=ϵEBH−33P表2两端铰支第一次:第二次:表3 一端固定另一端铰支第一次:第二次表4两端固定第一次:第二次:画出相应的P−εM曲线(绘图时横坐标表示2ε的大小,纵坐标表示压力PM的大小)图1 两端铰支图2一端固定另一端铰支图3两端固定结果表示为:。
压杆稳定
5.11 压杆稳定当作用在细长杆上的轴向压力达到或超过一定限度时,杆件可能突然变弯,即产生失稳现象。
杆件的失稳往往产生很大的变形甚至导致系统的破坏。
因此对轴向受压的杆件,除了考虑其强度与刚度外,还应考虑其稳定性问题。
一.实验目的1.观察和了解细长杆轴向受压时丧失稳定的现象;2.用电测法确定两端铰支压杆的临界载荷F cr ,并与理论计算的结果进行比较。
二.实验原理根据欧拉小挠度理论,对于两端铰支的大柔度杆(低碳钢λ≥λp=100),压杆保持直线平衡最大的载荷,保持曲线平衡最小载荷即为临界载荷F cr ,按照欧拉公式可得:22)(l EIF cr μπ(5.11-1)式中E ―材料的弹性模量,I ―试件截面的最小轴惯性矩,l ―压杆长度,μ―和压杆端点支座情况有关的系数,两端铰支杆 μ=1。
当压杆所受的荷载F 小于试件的临界力F cr ,压杆在理论上应保持直线形状,压杆处于稳定平衡状态;当F =F cr 时,压杆处于稳定与不稳定平衡之间的临界状态,稍有干扰,压杆即失稳而弯曲,其挠度迅速增加。
若以载荷F 为纵坐标,压杆中点挠度δ为横坐标,按欧拉小挠度理论绘出的F-δ图形即为折线OAB ,如图5.11-1 (b)所示.由于试件可能有初曲率,荷载可能有微小的偏心,以及材料的不均匀等因素,压杆在受力后就会发生弯曲,其中点挠度δ随荷载的增加而逐渐增大.当F<<F cr 时, δ增加缓慢。
当F 接近F cr 时,虽然载荷增加很慢,而δ却迅速增大,如OA´B´或OA´´B´´所示。
曲线OA´B´或OA´´B´´与折线OAB 的偏离,就是由于初曲率载荷偏心等影响造成,此影响越大,则偏离也越大。
若令杆件轴线为x 坐标轴,杆件下端为坐标轴原点,则在x=l/2处横截面上的内力如图5.11-1(a)(a)(b)图5.11-1所示,弯矩22/l l F M δ= ,内力F N -=,横截面上的应力:IM A F y±-=σ(5.11-2)当用半桥温度自补偿的方法将电阻应变片接到静态电阻应变仪后,可消除由轴向压力产生的应变读数,在应变仪上读数就是测点处由弯矩M 产生的真实应变的两倍。
压杆稳定性实验(含纸桥案例分析)
压杆稳定性实验潘哲鑫2012011680 祝世杰2012010407一.实验分析对于立柱材料而言,损坏往往不是来源于直接受压的损坏,而大都来自于杆件失稳导致的折断或者倾倒。
因此研究杆件在受压情况下的失稳特性就非常有意义。
在本实验中,我们使用的是环氧树脂杆,弹性模量59.2E GPa =,500MPa σ=⎢⎥⎣⎦ 通过测量可知,杆的有效长度为,8412mm L cmd ==直径 实验一:双端铰支的情况下临界载荷22(KL)K EIP π=其中K=1,故可算得,临界842.9K P N =考虑杆件达到其许应力的最大值, K K P P A Wδσ+=⎢⎥⎣⎦ 则 3d ())42K k P W W A P πδσ=-=⎢⎥⎣⎦其中( 则算得,9.86cm δ=因此我们根据上述计算结果,进行了实验,为了防止实验材料被破坏,我们仅仅加载到最大横向位移的0.8倍。
可以观察到,当加载的力值迅速升高至临界载荷后,再继续向下加载,杆件上的力并不会变大,取而代之的是杆件向铰支允许的方向的的弯曲。
实验二:一端铰支,一段固支的情况下 临界载荷22(KL)K EIP π=其中K=0.7,故可算得,临界1720.1K P N =同理可计算得,达到杆件的最大拉伸应力时, 4.78cm δ=,于是在实验中,我们加载到约3cm 处停止。
在第二次实验中,我们遇到一个问题,即当杆件开始弯曲时,由于可能杆件安装时的偏心误差,它弯曲的方向并不是我们希望测量的方向,因此,在弯曲过程中,为了能使其向我们偏好的方向弯曲,我主动给它提供了一个水平方向的扰动的力,从而使得其改变弯曲的方向。
但这也导致了在我们实验的曲线上加载阶段,并不是完全和理论相符,而一定程度上小于本应该出现的值。
而某种程度上,呈现出线性的关系。
不过可以解释为,由于我的外加力的作用,阻碍了杆件通过弯曲来抵抗载荷,因此,杆件此时纵向的形变完全来自于由于轴向应力产生的应变,满足胡克定律,故一定程度上呈现出线性的状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-9 压杆稳定性实验
工程实际中,失稳破坏往往是突然发生的,危害性很大,因此充分认识压杆的失稳现象,测定压杆的临界载荷,具有十分重要的工程意义。
一、试验目的
1.测定两端铰支细长压杆的临界载荷F cr ,并与理论值进行比较,验证欧拉公式。
2.观察两端铰支细长压杆的失稳现象。
二、设备和仪器
1.力学实验台;
2.百分表(或电阻应变仪); 3.游标卡尺、钢板尺。
三、试样
弹簧钢(60Si 2Mn )制成的矩形截面细长杆,经过热处理。
两端制成刀刃,以便安装在试验台的V 形支座内。
四、实验原理
对于轴向受压的理想细长直杆,按小变形理论其临界载荷可由欧拉公式求得: 2
cr 2()
EI
F L πμ=
(3-32)
式中:E 为材料的弹性模量,I 为压杆横截面的最小惯性矩,l 为压杆的长度;μ为长度系数,对于二端铰支情况,μ=1。
当载荷小于F cr 时,压杆保持直线形状的平衡,即使有横向干扰力使压杆微小弯曲,在撤除干扰力以后压杆仍能回复直线形状,是稳定平衡。
当载荷等于F cr 时,压杆处于临界状态,可在微弯情况下
保持平衡。
如以压力F 为纵坐标,压杆中点挠度w 为横坐标。
按小变形理论绘出的F -w 图形可由二段折线OA 和AB 来描述,如图3-32所示。
而实际压杆由于不可避免地存在初始曲率,或载荷可能有微小偏心以及材料不均匀等原因,在加载初始就出现微小挠度,开始时其挠度w 增加较慢,但随着载荷增加,挠度也
不断增加,当载荷接近临界载荷时,挠度急速增加,其F -w
曲线如图3-32中OCD 所示。
实际曲线OCD 与理论曲线之间
的偏离,表征初始曲率、偏心以及材料不均匀等因素的影响,
这种影响愈大,偏离也愈大。
显然,实际曲线的水平渐进线即代表压杆的临界载荷F cr 。
工程上的压杆都在小挠度下工作,过大的挠度会产生塑性变形或断裂。
仅有部分材料制成的细长杆能承受较大的挠度使载荷稍高于cr F (图3-32中虚线DE 所示)。
实验测定临界载荷,可用百分表测杆中点处挠度w ,如图3-33a 所示。
绘制F -w 曲线,作F -w 曲线的水平渐近线就得到临界载荷F cr 。
当采用百分表测量杆中点挠度时,由于压杆的弯曲方向不能预知,应预压一定量程,以给杆向左、右弯曲留有测量余地。
由于弯曲变形的大小也反映在试件中点的应变上,所以,也可在杆中点处两侧各粘贴一枚应变片,见图3-33b ,将它们接成半桥,记录应变仪读数du ε,绘制F -du ε曲线,作F -du ε曲线的水平渐近线,就得到临界载荷F cr 。
若用电测法测量杆中点应变时,被测量应变ε应包含二个部分,即轴力引起的应变和附加弯矩引起的应变:
F M εεε=+ 若将二个应变片作为工作片组成半桥,注意到二侧弯曲应变符号相异,则有:
du M 2εε=
可见此时已消除了由轴向压力产生的应变,其读数就是测点处由弯矩M 产生的真实应变的两倍。
因此由弯矩产生的测点处的正应力为
du 222
t t M Fw E E I I εσε==== (3-33) 即
du E I w F t
ε=
(3-34)
由上式可见,在一定的荷载F 作用下,应变仪读数du ε的大小反映了压杆挠度w 的大小,因此可用电测法来确定临界载荷F cr 。
五、实验步骤
1.测量试样尺寸
用钢板尺测量试样长度L ,用游标卡尺测量试样上、中、下三处的宽度b 和厚度t ,取其平均值。
用来计算横截面的最小惯性矩m in I 。
2.拟定加载方案,并估算最大容许变形
如采用百分表或电阻应变仪测量杆件中点变形,在初载荷F 0到0.8F cr 间的范围内,曲线比较陡直,宜采用分级加载(4~5级),进行载荷控制;载荷每增加一级F ∆,即测定一个相应的变形量(挠度w 或应变仪读数du ε)。
当接近失稳时,变形量快速增加,此时应改为位移控制;挠度w 每增加一定数值(如0.10mm ),或应变仪读数du ε每增加一定读数(如
20με)时,即读取一个相应的载荷数i F 。
取许用应力[]200M Pa σ=,计算临界载荷理论值:
()
2
cr 2
EI
F L πμ=
按下列公式估算容许最大挠度max w 或容许最大应变仪读数:
[]c r
c r
m a x
F
F
w
b t
W
σ+
≤ (3-35) (百分表测变形时)
图3-33压杆稳定实验装置简图
cr du m ax
[]2
F E bt
εσ+
≤ (3-36) (应变仪测变形时)
3.安装试样,准备测变形仪器,加初载荷,记录初读数。
试样两端应尽量放置在上、下V 形座正中央。
根据实验室设备条件确定实验方案。
若用百分表测挠度:加初载荷(如200N ),安装百分表,使表测杆在试样正中位置,预压约5mm ,调整表盘,使小指针指整数时,大指针在“0”附近,记录百分表读数。
若用应变仪测变形:将试样两侧的应变片组成半桥,设置应变仪测应变通道参数(桥路、灵敏系数、应变片电阻值),加载前调试所选应变通道电桥。
加初载荷(如200N )后,记录应变仪读数。
4. 力传感器接线、设置参数。
力传感器接线,设置参数(校正系数、载荷限值)。
5.按实验方案加载,记录数据。
按实验方案每级加载后,读取载荷值和百分表读数A i (或应变仪读数du i
ε
)。
当载荷增
量很小(但变形不超过max w 或du max ε)时,即可停止试验。
实验数据以表格形式记录。
6.卸去载荷,实验台回复原状。
六、实验结果处理
1.据测量数据计算试件宽度和厚度平均值,从而计算最小惯性矩I min 。
原始数据以表格形式示出,可参考表3-11。
表3-11 测定压杆临界载荷数据列表
2.据实验数据在方格纸上画出F -w (或F -du ε)曲线,作它的水平渐近线,确定临界载荷F cr 实验值。
3. 用欧拉公式计算临界载荷th
cr F 理论值,计算临界载荷实验值的相对误差。
th
R
cr cr
th cr
100%%
F F F -⨯= (3-37)
七、实验报告要求
实验报告应包括实验目的,原理,加载方案,实验数据记录和处理,以及误差分析等。
八、思考题
1. 如以1ε和2ε分别表示左右二侧的应变,显然随着F 的增加,二者差异也愈大。
如以压力F 为纵坐标,压应变ε为横坐标,可绘出1ε-F 和2ε-F 两种曲线。
两种ε-F 曲线的水平渐近线是否一致?
2. 本试验装置与理想情况有什么不同?对实验结果会产生哪些影响?
3. 对同一压杆,如支承条件不同,对其临界力的影响大吗?为什么?
九、预习要求
1. 预习压杆稳定相关内容,了解压杆临界载荷测量的原理和方法。
2. 对于给定压杆试件。
若已知材质和相应弹性模量以及压杆的名义尺寸l t b ⨯⨯(如4mm ×20mm ×300mm )。
估算临界载荷,拟定加载方案。
3. 参考数据处理列表,按实验要求,绘制好本实验记录表。
(宽度B=10cm 厚度d=4mm 长度l=300mm 弹性模量E=200GPa)。
