大偏心受压柱汇总
大偏心受压柱对称与非对称配筋的钢筋用量对比

1 大 偏 心 受压 柱 非 对 称 配 筋 的 计 算
水工 钢筋 混凝 土结构 大偏 心受 压柱 非对 称配 筋 的计算 公式 为
P ≤ ( x+ b 一 , / d fa ) () 1
P e≤ [ x h b ( 。一0 5 )+ A h , x ( 。一a ) ,/ 式中
摘 要 : 压 构 件 有 非 对 称 配 筋 和 对 称 配 筋 两种 情 况 。实 际 工 程 中 多 采 用施 工 方 便 的 对 称 配 筋 , 大 偏 心 受 压 受 而
柱 对 称 配筋 的钢 筋 总 用 量 多 于 非 对 称 配 筋 , 增 加 数 量 不 太 清 楚 。本 文 通 过 实 例 计 算 和理 论 分 析 , 出 对 称 但 得 配筋 钢 筋 总 面积 较非 对 称 配 筋 钢 筋 总 面 积 增 加 的 钢 筋 数 量 的 计算 公 式 , 及 钢 筋 增 加 数 量 与 压 力 P 和 偏 心 以 距e 。的关 系 。 关 键 词 : 偏 心 受 压 柱 ; 称 配 筋 ; 对 称 配 筋 ; 筋 总 用 量 大 对 非 钢
凝土 ( . :1 . / m ) Ⅱ级 钢 筋 ( = =3 0 / , 7 = 0 m, 顶 承 受 的轴 向压 力设 计 值 2 5N m , 1 N mm ) 口 =1 4 r 柱 , a P= 0 k e 从 0 4 。 渐增 大 , 别 按非 对称 配筋 和对 称配筋 计算 A 、 及 总 面积 , 5 0 N,。 .^ 逐 分 ,A 然后 , 他条件 不 其 变 , 5 0 6 0 6 0 7 0 N时 , 上 述方 法 分别 进 行计 算 。计 算 结果 见 表 1 P= 5 、0 、5 、0 k 按 。表 中 F为 对称 配 筋 钢 筋 总面 积 A 比非 对称配 筋钢 筋总 面积 A 增加 的钢 筋用 量 ( △A=A 一 占非 对 称 配 筋钢 筋 总用 量 A 。 A)
HRBF500钢筋混凝土大偏心受压柱承载力的试验研究

Ex e i e t lRe e r h o a i pa iy o p r m n a s a c n Be r ng Ca c t f HRBF5 0 0 S e lBa Re nf r e r e Ec e r c lCo p e so l m n t e r i o c d La g c nt i a m r s i n Co u
p r o ma c fc n r t o u e f r n e o o c e e c l mn e n o c d b RBF 0 t e a s i v s i a e . h o d sr i fr e y H 5 O s e lb r i n e tg t d t e l a - s r i u v s o t e a , t an c r e f c n r t , n h h r c e i t s o a l r d s t a n c r e f s e 1b r s r i u v s o o c e e a d t e c a a t rs i ff i e mo e c u a e a a y e . Th x e i e t l e e r h i d c t s t a o h 5 0 Pa f eg a n h tr l d b r r n lzd e e p rm n a s a c ia e h tb t 0 M r n i r i o o l a n e a d H RB4 0 s e lb r r a e s l n iu i a i a n t e c mp e s d m e b r n 0 t e a s a e t k n a o g t d n lma n b r i h o r s e m e ,Th e
2 C n r l e e rh I s tt f ulig a d C n t ci f . e t s ac n t u e i n n o s u t n o C G o p e ig 1 0 8 , hn ) aR i o B d r o MC r u ,B in 0 0 8 C ia j
钢筋混凝土受压构件和受拉构件—偏心受压柱计算
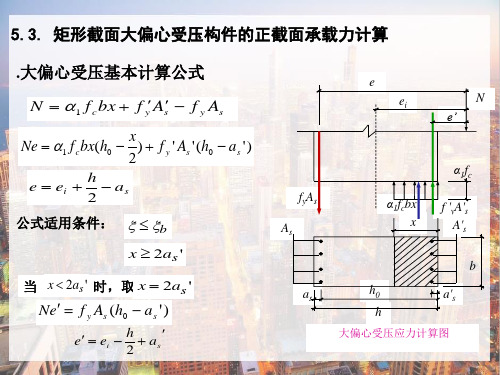
① 当同一主轴方向的杆端弯矩比: M1 0.9
M2
② 轴压比:
N 0.9
fc A
③ 构件的长细比满足要求: l0 34 12( M1 )
i
M2
M1、M2:分别为已考虑侧移影响的偏心受压构件两端截面按结构弹性
分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为M2,绝对值较小 端为 M1;当构件按单曲率弯曲时, M1/M2取正值,否则取负值。
α1fc
α1fcbx x=ξh0
f 'yA's A's
b
h0用平面的受压承载力计算
可能垂直弯矩作用平面先破坏,按非偏心方向的轴心受 压承载力计算
N Nu 0.9 ( fc A f yAs )
2.对称配筋矩形截面小偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
Ne f y As (h0 as ')
e
ei
h 2
as
e ei
N e’
fyAs As
α1fcbx x
α1fc
f 'yA's A's
b
as
h0
a's
h
大偏心受压应力计算图
2.对称配筋矩形截面大偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
5.3. 矩形截面大偏心受压构件的正截面承载力计算
.大偏心受压基本计算公式
N 1 f cbx f y As f y As
混凝土结构:2-2_偏心受压柱设计讲解
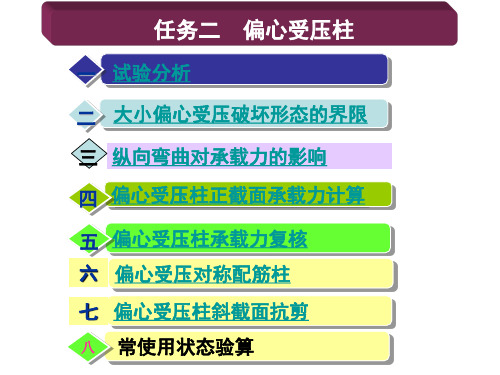
距轴向压力较近的一侧钢筋为As′, 距轴向压力较远的一侧钢筋为As。
载小 力偏 计心 算受 简压 图柱
承
图 3-15
根据承载力计算简图和内力平衡条件,并满足承载能力
极限状态设计表达式的要求,可建立基本公式如下:
若ξ≥1.6–ξb,取σs= – fy´及ξ=1.6-ξb(当ξ>h/h0时,取 ξ=h/h0),代入式(3-10)和式(3-11)求得As和As´,计算完 毕。
求出的As和As´必须满足最小配筋率要求。 小偏心受压柱正截面设计步骤见图3-17。
已知:M、N、b、h、fc、fy、f y'、l0、 as、as'
当x<2a′时,受压钢筋的应力达不到fy′,截面承载力可按 下式计算:
KNe f y As (h0 a )
式中e′——轴向压力作用点至受压钢筋As′合力点的距离。
小偏心受压柱
小偏心受压破坏时,受压区混凝土被压碎,近侧钢筋As´ 的应力达到fy´,而远侧钢筋As可能受拉,也可能受压,一般不 会达到屈服强度。
则按As=ρminbh0配筋。
(2)已知As´,求As 这种情况下,基本公式中有两个未知数ξ和As,直接利用 基本公式求出两个未知数ξ和As,步骤如下:
s
KNe
f
' y
As'
(h0
f cbh02
a' )
1 1 2s
x = ξ h0 若2a′≤x≤ξbh0时,由实用公式计算As。
h0——截面有效高度; A——构件截面面积;
ξ1 ——考虑截面应变对截面曲率的影响系数,当>1时,取 =1;对于大偏心受压柱,直接取=1;
预应力CFRP布加固混凝土大偏心受压柱试验研究

2 0 1 3年 2月
水 利与建 筑 工程学 报
J o u r n a l o f Wa t e r R e s o u r c e s a n d A r c h i t e e t u r a l E n g i n e e r i n g
Z H A I A i - l i a n g ,S U N Mi n g — j i e ,J I C h a n g - l i a n g ,C H E N S h u — j i n, a WA N G C h u n - h e
( C o l l e g e o fW a t e r C o n s e r v a n c y a n d C i v i l E n g i n e e r i n g,S h a n d o g n A g r i c u l t u r a l U n i v e r s i t y ,T a i a n ,S h a n d o g n 2 7 1 0 1 8 ,C h i n a )
V0 1 . 1 1 No . 1 F e b .. 20 1 3
预应 力 C F R P布 加 固混凝 土大 偏 心 受 压 柱 试 验 研 究
翟爱 良, 孙 明杰 , 季 昌良, 陈树建 , 王纯合
( 山东农业 大学 水利土木工程学 院,山东 泰安 2 7 1 0 1 8 )
Ex pe r i me n t a l St u d y o n Re i n f o r c e me n t f o r La r g e - e c c e nt r i c a l l y Co mp r e s s e d RC Co l u mn wi t h Pr e s t r e s s e d CFRP
混凝土偏心受压构件相关知识点总结

偏心受压构件一、偏心受压构件包括大偏心受压和小偏心受压两种情况,无论是大偏心受压还是小偏心受压均要考虑偏心距增大系数η。
2012.11400i l e h h ξξη⎛⎫=+ ⎪⎝⎭10.5.c f A Nξ=02 1.150.01l hξ=-此公式中要注意如下几点:①h ——截面高度。
环形截面取外直径;圆形截面取直径。
②0h ——截面有效高度。
对环形截面取02s h r r =+;对圆形截面取0s h r r =+。
r 、2r 、s r 按《混凝土结构设计规范》第7.3.7条和7.3.8条取用。
③A ——构件的截面面积。
对T 形截面和工形截面,均取()''.2.f fA b h b b h =+-④1ξ——偏心受压构件的截面曲率修正系数,当1 1.0ξ>取1 1.0ξ=; 2ξ——构件长细比对截面曲率的影响系数,当015l h<时,取2 1.0ξ=;⑤当偏心受压构件的长细比017.5l i ≤(或05l h≤)时,可直接取 1.0η=。
注意:017.5l i≤与05l h≤基本上是等价的。
准确地说是0 5.05l h≤二、两种破坏形态的含义截面进入破坏阶段时,离轴向力较远一侧的纵向钢筋受拉屈服,截面产生较大的转动,当截面受压区边缘的混凝土压应变达到其极值后,混凝土被压碎,截面破坏。
截面进入破坏阶段后,离轴向力较远一侧的纵向钢筋或者受拉或者受压但始终不屈服,截面转动较小,当截面受压区边缘的混凝土压应变达到其极限值后,混凝土被压碎,截面破坏 。
两种破坏形态的相同点:截面最终破坏都是由于受压区边缘混凝土被压碎而产生的,并且离轴向力较近一侧的钢筋(或曰受压钢筋's A )都受压屈服。
两种破坏形态的不同点:起因不同。
大偏心受压破坏的起因是离轴向力较远一侧的钢筋(或曰受拉钢筋s A )受拉屈服;而小偏心受压破坏则是由于截面受压区边缘混凝土压应变接近其极值。
所以大偏心受压破坏也被称为“受拉破坏”——延性破坏;小偏心受压破坏也被称为“受压破坏”——脆性破坏。
纤维布加固钢砼大偏心受压柱的强度和变形特性分析

tn e h da d f e y e .Th r u db e t i n h rg d h,a c o a es a ig,a dn mb ro ig m t o n i rt p s b e ewo l eac ran a c o a ewit n h rg p cn n u e f a c o a er i fr e e tly r o m a et eb a ig c p ct f h o u n a i u n h r g en o c m n a e st k h e rn a a iyo ec lm sm xm m.Th ih rt ef t ehg e h i —
p ro m a c n cin m e h ns o h te g h n d c lm n r n l zd e f r n ea d a to c a im ft e sr n t e e o u swe ea ay e .Th e u t n iae h t er s lsidc t d t a t e fi r f h ou h al eo ec l mn e an dt ep a tcd sr c in u t srm ie o b lsi e tu t .Th i h n ei te g h a dd fr t nd — o erc a g nsr n t n eo ma i e o p n e i l n s c a tr st en m b ro ie lt a e s e d d man yo u h fco sa h u e ffb rco h ly r ,wit fa c o ,a c o p cn d h o n h r n h rs a ig,p s a—
第3 7卷 第 3 期
21 年 6 01 月
钢筋混凝土受压柱大小偏心判断方法的讨论

钢筋混凝土受压柱大小偏心判断方法的讨论王中发【摘要】本文就钢筋混凝土受压柱的受力特点进行探讨,以探寻更有效的大小偏心判断方法。
%This paper discusses the mechanical characteristics of reinforced concrete compression column to explore more effective method to determine the size of the eccentric.【期刊名称】《价值工程》【年(卷),期】2015(000)003【总页数】2页(P128-129)【关键词】钢筋混凝土;偏心受压柱;承载力计算;判断【作者】王中发【作者单位】湖北水利水电职业技术学院水利建筑工程系,武汉430070【正文语种】中文【中图分类】U441钢筋混凝土偏心受压柱根据破坏时的特征分为大偏心受压和小偏心受压,其区别在于远离偏心压力一侧的纵向受力钢筋在柱发生破坏时是否达到屈服强度(即该侧纵筋的应力σx=fy)。
《混凝土结构设计规范》(GB50010-2011)给出的判断条件为:当满足x≤h0ξb或ξ≤ξb的条件时,受压柱为大偏心受压,反之为小偏心受压。
但在进行柱的设计时,通常柱两侧的纵向受力钢筋是未知的,也就无法直接计算x或ξ,也就无法直接判断要设计的柱是大偏心还是小偏心,因大小偏心的承载力计算公式不同,导致设计计算无法进行。
钢筋混凝土受压柱大小偏心判断方法如下:《混凝土结构设计规范》给出的偏心受压柱正截面承载力计算公式如下:①对于对称配筋,比较好判断。
先假定为大偏心受压(σx=fy),根据公式(1)取极限状态,公式按等号计算,计算出,然后根据x和ξbh0的大小关系判断。
若x≤h0ξb则表明假设正确,确为大偏心受压,反之为小偏心受压。
②对于非对称配筋,由于无法直接计算出受压区计算高度x,上述方法就不再适用了,需要另外的方法,本文重点讨论这个问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同济大学混凝土结构基本原理实验报告(共页)9姓名梁炜炼号学1350240专业建筑工程学院土木工程学院指导老师鲁亮同济大学结构工程与防灾研究所年月日20151228页9共混凝土结构基本原理实验报告第1页实验目的和内容.1、试验目的1.1通过试验研究认识混凝土结构构件的破坏全过程,掌握测试混凝土大偏心受压构件基本性能的试验方法。
、试验内容1.2对大偏心短柱施加轴向荷载直至破坏。
观察加载过程中裂缝的开展情况,将得到的极限荷载与计算值相比较。
试件介绍2.)试件设计的依据1(l0/h≤5。
通过为减少“二阶效应”的影响,将试件设计为短柱,即控制使试件的破坏状态为大偏心受压e0=200mm,调整轴向力的作用位置,即偏心距破坏。
)试件的主要参数2(①试件尺寸22);中部(两端);200×200mm(截面尺寸:200×400mm;试件长度:1300mmC25②混凝土强度等级:页共混凝土结构基本原理实验报告9第2页。
));4B18(中部③纵向钢筋:8B18(两端;(中部);4Φ8@100④箍筋:8Φ8@50(两端)25mm⑤纵向钢筋混凝土保护层厚度:;⑥试件的配筋情况(如上图所示)e0=200mm⑦取偏心距试件材料力学性能试验结果3.钢筋力学性能试验结果)/kN)平均值(MPa%)/mm延伸率(面积极限强度屈服强度/kN屈服强度(MPa)平均值(MPa)极限抗拉强度(钢筋类型MPa钢筋直481.46.055.48436.117477.9光圆钢12.574430.1474.35.96424.120 5.33637.31118.02554.615.68640.3628.27螺纹钢573.0643.31118.1916.72591.3545.715.43400.411.3222光圆钢628.27547.3392.2548.920384.110.8615.52691.132.911734.74654.7691.3螺纹钢850.27646.7691.5638.632.11634.76570.220.63410.428.662150.278光圆钢570.9413.3571.6416.228.732420.92618.82395.2582.09533.3618.4153.94螺纹钢14533.6618.11882.18533.995.15625.822118.17464.4159.24254.47螺纹钢18624.8467.2623.824119.59470.0158.74595.0186.94410.8129.0725596.4314.16螺纹钢20414.9597.8187.81419.026131.62混凝土试块强度试验结果序号试块尺寸荷载(kN)强度(MPa)33.2746.91150*150*15033.32749.132.83737.6)MPa平均值(33.14.试件验算柱极限承载力2bhf????,,,01c)A(h?af?)?(f?BbhehC?不妨令:A??ss0yc1002?从而有:?A2.2?4ACB?B?页93页共混凝土结构基本原理实验报告第??fbhN?occu1')(10.52Afbh??eN?f???Sycuco1'')(?h?mmee???s0?0.238??s0,2660.5h-a261.5KNN?cu试验方法.5加载装置5.1柱偏心受压试验的加载装置如图所示。
采用千斤顶加载,支座一端为固定铰支座,另一端为滚动铰支座。
铰支座垫板应有足够的刚度,避免垫板处混凝土局压破坏。
Pe0e0P图5.1柱偏心受压试验加载装置5.2加载方式(1)单调分级加载机制实际的加载等级为0-20kN-40kN-60kN-80kN-100kN-120kN-破坏5.3量测内容(1)纵筋应变由布置在柱内部纵筋表面的应变计量测,钢筋应变测点布置如下图。
页9共混凝土结构基本原理实验报告第4页)、4纵筋C)纵筋A(应变1、3(应变2)、B纵筋(应变57、D纵筋)(应变66页共5页9混凝土结构基本原理实验报告第大偏心受压柱试验纵向钢筋应变测点布置 5.3.1图)侧向挠度2(个位移计以测量柱侧向挠度,侧向挠度测点布置如下图。
5柱长度范围内布置大偏心受压柱试验侧向挠度测点布置5.3.2图)裂缝3(的网格。
试验时借助放大镜50mm×50mm试验前将柱四面用石灰浆刷白,并绘制查找裂缝。
页6页9混凝土结构基本原理实验报告共第试验过程.6破坏时加载过程中背部首先出现裂缝,并随着荷载的不断增大,不断扩大,随后与两侧裂缝相连接。
破坏后构件破坏主裂缝在上端且裂缝与偏心方向平行,说明构件本身存在问题;破坏时,构件受压处没有明显压碎痕迹;但背部裂缝呈平行均匀分布,间距基,与理论分析结果较为符合。
10cm本在试验结果分析.7实际试验数据共9页混凝土结构基本原理实验报告页第7k荷载纵筋应变位移测量m上支侧向上下支侧向中侧向下115-1310-0.21.0-1.-2.0-0.3-11-81313-1339.233-17-29-28-22-0.138391.829-0.5-2.0-0.559.-440.02.40.062536250-26-30-42-1.9-0.681.2-600.-41-583. 1870.772-1.8-0.68775-36101.2113-7799-46960.4-74-523.81.5-1.6-0.6113121.24.60.6138-94120-1.5139-0.7123-592.-91-66122.-954.8-69-620.7-99-1.4 -0.72.6143125144128121431441254.81280.7-63-96-99-70-1.4-0.72.6125.24.90.7-71-100146-1.4144126130-0.7-64-972.612-984.90.7-72-65128-102-1.4-0.71482.7132147130.71355.00.7149131-66-1.4151-0.7-1002.8-73-103133.5.00.-1.4154-75-0.71372.8152134-67-105-102135.7-1035.10.8-69-76-1.41551 36-0.71562.9140-107137.71425.20.8-70157159139-1.4-105-0.73.0-77-108139.-78-1.1610.81445.33.1-71-0.7-110160141-10614162143-108-1.30.8-72-79 1635.33.2147-111-0.714-1.3-730.5.43.2164145149-109-113-0.7-81165144.7168-1.30.95.5151-82-753.3-115-111-0.7166148146.2-113168150-1.30.9-831 705.3.4154-116-76-0.7148.2-1.30.9-1143.5-77171152-118-85172-0.75.6156150.7158-1.30.9-791753.6-86-120-116-0.71731555.7155.2178160-1.2180-89 1.03.8164-123-82-0.75.9-12015-1.2-1231.04.0183165-127185-92-0.71696.0-85162.24.-87-1.2-0.7174-131-1271.01881701906.2-95165.7-991794.3-1.1-90193175195-135-0.76.4-1301.1169.24.5-1.1197180200-102-138-134184-0.76.5-931.172.4.7-1.-138-96-142205-0.72021856.7188-1051.2176.24.9-99-1. 0-146193-108-142-0.72106.82071901.2179.5.1198-111-150214-102212194-0.77.01.2-146-1.0182.75.2219216199-154-0.-114203-1497.2-1051.3-185.4-15 8-153-0.72247.31.221204207-118-0.9-10918-1125.6-162-121-0.7-1577.52281.4-0.922520821219216-1241.4-166-1155.82292137.-0.-160-0.9233194.7237 -1702342171.4-127221-1647.8-1186.0-0.8-0.197.7-174-1681.52418.06.2238221-130225-0.8-0.-121200.7-1771.58.1-171-1242466.-0.-0.7242225229-133 203.2-181-1271.68.3233-136-1756.5250-0.7-0.246229202378.5-1391.6-129-185250233-0.7-0.-1786.7254208.2588.62532371.6-142241-181-188-132-0.-0 .6.9218.8-1852571.6257241-192-0.6245-145-0.-1357.219.01.7-188-0.6-137259-0.2602457.2249-148-196219.1-1401.7-150-0.-192-0.2607.4262249-1992 5321-152-0.51.8-1429.32542597.6-203-196259-0.263218.2-0.5-1542671.89.5253262262-1447.-209-0.8-201219.7-0.42492622701.9-155-2072768.1-214-1 46-0.89.622-212-0.41.92632762488.3-157-219282-0.8-1489.8220.78.5-0.4-217-151250264274-0.8-224-16026510.01.9220.8.8-0.3-222-230-155-0.26427 210.1251-1642.0257220.79.1-160-0.3-235-0.8260-22810.32632712.0253-168221.9.4264-241-165253-0.8-17310.5-2342622702.1-0.3222.7-1789.7266-247 -0.8254-17010.72.1-0.2-240263270222.7-252-1852542.210.927026510.1-176-0.2-0.8-242264222.2-243-2542.3254-19211.226126926010.5-0.1-183-0.822 2.2-24511.52.4-256-200255257268-0.1256-0.8-18911.0221.25726611.7-2462.-258-195-208253-0.0250-0.811.4220.26425512.0-246-0.02.5-20011.9-215-0.8253-260248220.0256263-2052.612.3256-24712.3-221-263252-0.219.2772662630.0-210-0.812.7251-247-2652.7-22912.62125213.22912623220.1-268-21 5-0.-24712.9-2382.82113.6260337251-270424-0.-21913.1-2472.90.1-247216.7-2723.0376********.453414.-2240.-246-0.-258215.213.72504493.-275265 0.2443-229-0.-24614.5-269213.20.25052473.214.014.9297-0.401-235-278-246-289211.224653215.40.3-0.-2733.3387405-23714.-245-300209.2495193.4-26915.814.-0.0.3553401-238-245-3002048614.83.5-2670.4-0.16.2259-239727403-244-3012016.0.4-0.7-25815.13.6486289-306-239853402-2440200.7515.20.46-2529-0.7916.75306648073.76-3030-236339378543-2407198.75-0.783.7316.750.4615.2-2499-3023-2395-23503877839030954762.共9混凝土结构基本原理实验报告第8页页页9共混凝土结构基本原理实验报告第9页实验体会与建议8.小,可能原因如下:261.5kN实测值为222.25kN,比预估值1.①混凝土构件浇筑过程中存在缺陷;②构件加载过程中偏心距大于设计值;③混凝土计算公式本身的不确定性以及材料性质的不确定性导致;4○构件实际尺寸比设计值偏小一些。
