2023年河北省中考数学试卷真题(含答案)原版高清
2023年河北省石家庄市十八县部分重点中学中考数学大联考试卷及答案解析

2023年河北石家庄市十八县部分重点中学中考数学大联考试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)﹣2的绝对值是()A.B.﹣C.2D.﹣22.(3分)下列立体图形中,主视图是圆的是()A.B.C.D.3.(3分)下列计算正确的是()A.=2B.=﹣3C.2+3=5D.(+1)2=3 4.(3分)若﹣1这个数介于整数n和n+1之间,则n+1的值是()A.0B.1C.2D.35.(3分)一家鞋店在一段时间内销售了某种女鞋20双,各种尺码鞋的销售量如表所示.则所销售的女鞋尺码的众数是()尺码/cm22.52323.52424.5销售量/双14681 A.23.5B.23.6C.24D.24.56.(3分)下列说法正确的是()A.了解一批灯泡的使用寿命,应采用抽样调查的方式B.如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖C.若甲、乙两组数据的平均数相同,S甲2=2.5,S乙2=8.7,则乙组数据较稳定D.“任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件7.(3分)将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为()A.45°B.65°C.75°D.85°8.(3分)如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于M,N两点,作直线MN.直线MN与AB相交于点D,连接CD,若AB=3,则CD的长是()A.1B.1.5C.3D.69.(3分)如图,在矩形ABCD中,AB=2,BC=,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为()A.B.C.D.10.(3分)如图,AB,BC为⊙O的两条弦,连接OA,OC,点D为AB的延长线上一点,若∠CBD=62°,则∠AOC的度数为()A.100°B.118°C.124°D.130°11.(2分)2021年3月考古人员在山西阳泉发现目前中国规模最大、保存最完好的战国水井,井壁由等长的柏木按原始榫卯结构相互搭接呈闭合的正九边形逐层垒砌,关于正九边形下列说法错误的是()A.它是轴对称图形B.它是中心对称图形C.它的外角和是360°D.它的每个内角都是140°12.(2分)如图,在矩形ABCD中,点M在AB边上,把△BCM沿直线CM折叠,使点B 落在AD边上的点E处,连接EC,过点B作BF⊥EC,垂足为F,若CD=1,CF=2,则线段AE的长为()A.﹣2B.﹣1C.D.13.(2分)如图,平行四边形OABC的周长为7,∠AOC=60°,以O为原点,OC所在直线为x轴建立直角坐标系,函数y=(x>0)的图象经过▱OABC顶点A和BC的中点M,则k的值为()A.4B.12C.D.614.(2分)如图,一只正方体箱子沿着斜面CG向上运动,∠C=α,箱高AB=1米,当BC =2米时,点A离地面CE的距离是()米.A.B.C.cosα+2sinαD.2cosα+sinα15.(2分)用正方形纸片剪出一副七巧板,并将其拼成如图的“小天鹅”,设小天鹅的水平宽度为l(左右最大距离),铅垂高度为h(上下最大距离),则的值为()A.B.C.D.16.(2分)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a=.其中正确的有()A.1个B.2个C.3个D.4个二、填空题(本大题有3个小题,共12分.第17、18小题,每小题3分;第19小题有两个空,每空3分.把答案写在题中横线上)17.(3分)如图,用大小相同的小正方形拼图形,第1个图形是一个小正方形;第2个图形由9个小正方形拼成;第3个图形由25个小正方形拼成,依此规律,若第n个图形比第(n﹣1)个图形多用了72个小正方形,则n的值是.18.(3分)育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了h第一次返回到自己班级,则七(2)班需要h才能追上七(1)班.19.(6分)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD 与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.三、解答题(本大题有7个小题,共66分。
2023年河北数学中考卷

2023年河北数学中考卷一、选择题(每题1分,共5分)1. 下列函数中,不是增函数的是()A. y=2x+1B. y=x^2C. y=3^xD. y=ln(x)2. 在三角形ABC中,若∠A=60°,AB=AC,则三角形ABC是()A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形3. 下列各数中,是无理数的是()A. √9B. √16C. √3D. √14. 已知一组数据2,3,5,7,x,方差是4,则x的值为()A. 2B. 3C. 4D. 55. 下列命题中,真命题的是()A. 对顶角相等B. 相等的角是对顶角C. 同位角相等D. 内错角相等二、判断题(每题1分,共5分)1. 任何两个无理数之和一定是无理数。
()2. 两个平行线的斜率相等。
()3. 一元二次方程的解一定是实数。
()4. 函数y=f(x)与y=f(x)关于y轴对称。
()5. 互为相反数的两个数的和为0。
()三、填空题(每题1分,共5分)1. 若a+b=6,ab=2,则a=____,b=____。
2. 已知一组数据3,5,7,x,y,平均数为6,则x+y=____。
3. 二次函数y=ax^2+bx+c的图像开口向上,则a____0。
4. 平行线l1:2x+3y+1=0,l2:2x+3y+c=0,则c____1。
5. 在直角坐标系中,点A(2,3)关于原点对称的点是____。
四、简答题(每题2分,共10分)1. 简述概率的基本性质。
2. 解释什么是函数的单调性。
3. 简述平行线的性质。
4. 请写出勾股定理的内容。
5. 简述一元二次方程的求解步骤。
五、应用题(每题2分,共10分)1. 某商店将一件商品提价20%后,售价为120元,求原价。
2. 在直角三角形ABC中,∠C=90°,AC=3,BC=4,求AB的长度。
3. 已知函数f(x)=2x^24x+1,求f(3)的值。
4. 解方程:2x5=3x+1。
2023年河北省中考数学真题(原卷与解析)
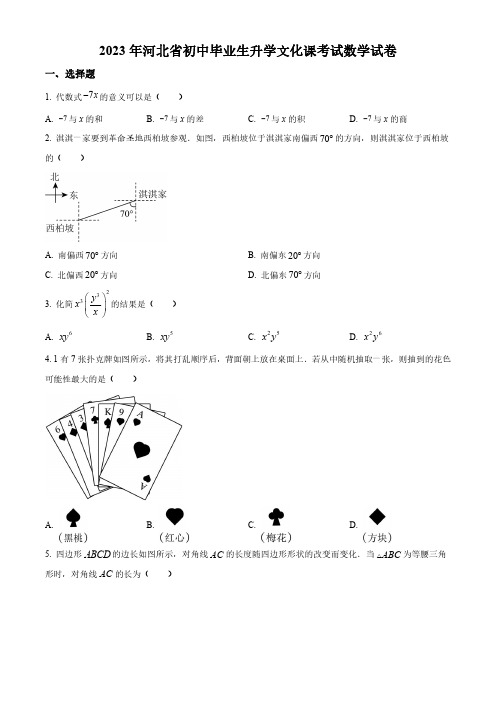
2023年河北省初中毕业生升学文化课考试数学试卷一、选择题1.代数式7x -的意义可以是()A.7-与x 的和 B.7-与x 的差C.7-与x 的积D.7-与x 的商2.淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西70︒的方向,则淇淇家位于西柏坡的()A.南偏西70︒方向B.南偏东20︒方向C.北偏西20︒方向D.北偏东70︒方向3.化简233y x x ⎛⎫ ⎪⎝⎭的结果是()A.6xyB.5xyC.25x yD.26x y 4.1有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上.若从中随机抽取一张,则抽到的花色可能性最大的是()A. B. C. D.5.四边形ABCD 的边长如图所示,对角线AC 的长度随四边形形状的改变而变化.当ABC 为等腰三角形时,对角线AC 的长为()A.2B.3C.4D.56.若k 为任意整数,则22(23)4k k +-的值总能()A .被2整除 B.被3整除 C.被5整除 D.被7整除7.若27a b ==,2214a b=()A.2 B.4 C.7 D.28.综合实践课上,嘉嘉画出ABD △,利用尺规作图找一点C ,使得四边形ABCD 为平行四边形.图1~图3是其作图过程.(1)作BD 的垂直平分线交BD 于点O ;(2)连接AO ,在AO 的延长线上截取OC AO =;(3)连接DC ,BC ,则四边形ABCD 即为所求.在嘉嘉的作法中,可直接判定四边形ABCD 为平行四边形的条件是()A.两组对边分别平行B.两组对边分别相等C.对角线互相平分D.一组对边平行且相等9.如图,点18~P P 是O 的八等分点.若137PP P ,四边形3467P P P P 的周长分别为a ,b ,则下列正确的是()A.a b <B.a b =C.a b >D.a ,b 大小无法比较10.光年是天文学上的一种距离单位,一光年是指光在一年内走过的路程,约等于129.4610km ⨯.下列正确的是()A.12119.4610109.4610⨯-=⨯B.12129.46100.46910⨯-=⨯C.129.4610⨯是一个12位数D.129.4610⨯是一个13位数11.如图,在Rt ABC △中,4AB =,点M 是斜边BC 的中点,以AM 为边作正方形AMEF ,若16AMEF S =正方形,则ABC S = ()A.3B.3C.12D.1612.如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至还需再放这样的正方体()A .1个 B.2个 C.3个 D.4个13.在ABC 和A B C ''' 中,3064B B AB A B AC A C '''''∠=∠=︒====,,.已知C n ∠=︒,则C '∠=()A.30︒B.n ︒C.n ︒或180n ︒-︒D.30︒或150︒14.如图是一种轨道示意图,其中ADC 和ABC 均为半圆,点M ,A ,C ,N 依次在同一直线上,且AM CN =.现有两个机器人(看成点)分别从M ,N 两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M A D C N →→→→和N C B A M →→→→.若移动时间为x ,两个机器人之间距离为y ,则y 与x 关系的图象大致是()A. B.C. D.15.如图,直线12l l ∥,菱形ABCD 和等边EFG 在1l ,2l 之间,点A ,F 分别在1l ,2l 上,点B ,D ,E ,G 在同一直线上:若50α∠=︒,146ADE ∠=︒,则β∠=()A.42︒B.43︒C.44︒D.45︒16.已知二次函数22y x m x =-+和22y x m =-(m 是常数)的图象与x 轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为()A.2B.2mC.4D.22m 二、填空题17.如图,已知点(3,3),(3,1)A B ,反比例函数(0)k y k x=≠图像的一支与线段AB 有交点,写出一个符合条件的k 的数值:_________.18.根据下表中的数据,写出a 的值为_______.b 的值为_______.x结果代数式2n31x +7b 21x x +a 119.将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l 上,两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l 平行,有两边分别经过两侧正六边形的一个顶点.则图2中(1)α∠=______度.(2)中间正六边形的中心到直线l 的距离为______(结果保留根号).三、解答题20.某磁性飞镖游戏的靶盘如图.珍珍玩了两局,每局投10次飞镖,若投到边界则不计入次数,需重新投,计分规则如下:投中位置A 区B 区脱靶一次计分(分)312-在第一局中,珍珍投中A 区4次,B 区2次,脱靶4次.(1)求珍珍第一局的得分;(2)第二局,珍珍投中A 区k 次,B 区3次,其余全部脱靶.若本局得分比第一局提高了13分,求k 的值.21.现有甲、乙、丙三种矩形卡片各若干张,卡片的边长如图1所示(1)a >.某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图2和图3,其面积分别为12,S S .(1)请用含a 的式子分别表示12,S S ;当2a =时,求12S S +的值;(2)比较1S 与2S 的大小,并说明理由.22.某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,调意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,下图是根据这20份问卷中的客户所评分数绘制的统计图.(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改;(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评分数为几分?与(1)相比,中位数是否发生变化?23.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.如图,在平面直角坐标系中,一个单位长度代表1m 长.嘉嘉在点(6,1)A 处将沙包(看成点)抛出,并运动路线为抛物线21:(3)2C y a x =-+的一部分,淇淇恰在点(0)B c ,处接住,然后跳起将沙包回传,其运动路线为抛物线221:188n C y x x c =-+++的一部分.(1)写出1C 的最高点坐标,并求a ,c 的值;(2)若嘉嘉在x 轴上方1m 的高度上,且到点A 水平距离不超过1m 的范围内可以接到沙包,求符合条件的n 的整数值.24.装有水的水槽放置在水平台面上,其横截面是以AB 为直径的半圆O ,50cm AB =,如图1和图2所示,MN 为水面截线,GH 为台面截线,MN GH ∥.计算:在图1中,已知48cm MN =,作OC MN ⊥于点C .(1)求OC 的长.操作:将图1中的水面沿GH 向右作无滑动的滚动,使水流出一部分,当30ANM ∠=︒时停止滚动,如图2.其中,半圆的中点为Q ,GH 与半圆的切点为E ,连接OE 交MN 于点D .探究:在图2中(2)操作后水面高度下降了多少?(3)连接OQ 并延长交GH 于点F ,求线段EF 与 EQ的长度,并比较大小.25.在平面直角坐标系中,设计了点的两种移动方式:从点(,)x y 移动到点(2,1)x y ++称为一次甲方式:从点(,)x y 移动到点(1,2)x y ++称为一次乙方式.例、点P 从原点O 出发连续移动2次;若都按甲方式,最终移动到点(4,2)M ;若都按乙方式,最终移动到点(2,4)N ;若按1次甲方式和1次乙方式,最终移动到点(3,3)E .(1)设直线1l 经过上例中的点,M N ,求1l 的解析式;并直接..写出将1l 向上平移9个单位长度得到的直线2l 的解析式;(2)点P 从原点O 出发连续移动10次,每次移动按甲方式或乙方式,最终移动到点(,)Q x y .其中,按甲方式移动了m 次.①用含m 的式子分别表示,x y ;②请说明:无论m 怎样变化,点Q 都在一条确定的直线上.设这条直线为3l ,在图中直接画出3l 的图象;(3)在(1)和(2)中的直线123,,l l l 上分别有一个动点,,A B C ,横坐标依次为,,a b c ,若A ,B ,C 三点始终在一条直线上,直接写出此时a ,b ,c 之间的关系式.26.如图1和图2,平面上,四边形ABCD 中,8,12,6,90AB BC CD DA A ====∠=︒,点M 在AD 边上,且2DM =.将线段MA 绕点M 顺时针旋转(0180)n n ︒<≤到,MA A MA ''∠的平分线MP 所在直线交折线—AB BC 于点P ,设点P 在该折线上运动的路径长为(0)x x >,连接A P '.(1)若点P 在AB 上,求证:A P AP '=;(2)如图2.连接BD .①求CBD ∠的度数,并直接写出当180n =时,x 的值;②若点P 到BD 的距离为2,求tan A MP '∠的值;(3)当08x <≤时,请直接..写出点A '到直线AB 的距离.(用含x 的式子表示).2023年河北省初中毕业生升学文化课考试数学试卷一、选择题1.【答案】C【解析】解:7x -的意义可以是7-与x 的积.故选C .2.【答案】D【解析】解:如图:∵西柏坡位于淇淇家南偏西70︒的方向,∴淇淇家位于西柏坡的北偏东70︒方向.故选D .3.【答案】A 【解析】解:2363362y y x x xy x x =⎛⎝⋅⎫= ⎪⎭,故选:A .4.【答案】B【解析】解:∵一共有7张扑克牌,每张牌被抽到的概率相同,其中黑桃牌有1张,红桃牌有3张,梅花牌有1张,方片牌有2张,∴抽到的花色是黑桃的概率为17,抽到的花色是红桃的概率为37,抽到的花色是梅花的概率为17,抽到的花色是方片的概率为27,∴抽到的花色可能性最大的是红桃,故选B .5.【答案】B【解析】解:在ACD 中,2AD CD ==,∴2222AC -<<+,即04AC <<,当4AC BC ==时,ABC 为等腰三角形,但不合题意,舍去;若3AC AB ==时,ABC 为等腰三角形,故选:B .6.【答案】B【解析】解:22(23)4k k +-(232)(232)k k k k =+++-3(43)k =+,3(43)k +能被3整除,∴22(23)4k k +-的值总能被3整除,故选:B .7.【答案】A【解析】解:∵a b ==2=,故选:A .8.【答案】C 【解析】解:根据图1,得出BD 的中点O ,图2,得出OC AO =,可知使得对角线互相平分,从而得出四边形ABCD 为平行四边形,判定四边形ABCD 为平行四边形的条件是:对角线互相平分,故选:C .9.【答案】A【解析】连接1223,PP P P ,∵点18~P P 是O 的八等分点,即 1223345566778148PP P P P P P P P P P P P P P P =======∴12233467PP P P P P P P ===, 464556781178P P P P P P P P P P PP =+=+=∴4617P P PP =又∵137PP P 的周长为131737a PP PP P P ++=,四边形3467P P P P 的周长为34466737b P P P P P P P P ++=+,∴()()34466737131737b a P P P P P P P P PP PP P P ++-++=+-()()12172337131737PP PP P P P P PP PP P P =+++-++122313PP P P PP =-+在123PP P 中有122313PP P P PP >+∴1223130b a PP P P PP -=+>-故选A .10.【答案】D 【解析】解:A 选项,12119.4610109.4610⨯÷=⨯,故该选项错误,不符合题意;B 选项,12129.46100.46910⨯-≠⨯,故该选项错误,不符合题意;C 选项,129.4610⨯是一个13位数,故该选项错误,不符合题意;D 选项,129.4610⨯是一个13位数,正确,符合题意.故选D .11.【答案】B【解析】解:∵16AMEF S =正方形,∴4AM ==,∵Rt ABC △中,点M 是斜边BC 的中点,∴28BC AM ==,∴AC ==,∴11422ABC S AB AC =⨯⨯=⨯⨯= 故选:B .12.【答案】B【解析】解:由题意画出草图,如图,平台上至还需再放这样的正方体2个,故选:B .13.【答案】C【解析】解:过A 作AD BC ⊥于点D ,过A '作A D B C ''''⊥于点D ¢,∵306B B AB A B '''∠=∠=︒==,,∴3AD A D ''==,当B C 、在点D 的两侧,B C ''、在点D ¢的两侧时,如图,∵3AD A D ''==,4AC A C ''==,∴()Rt Rt HL ACD A C D '''≌△△,∴C C n '∠=∠=︒;当B C 、在点D 的两侧,B C ''、在点D ¢的同侧时,如图,∵3AD A D ''==,4AC A C ''==,∴()Rt Rt HL ACD A C D '''≌△△,∴'''A C D C n ∠=∠=︒,即'''180'''180A C B A C D n ∠=︒-∠=︒-︒;综上,C '∠的值为n ︒或180n ︒-︒.故选:C .14.【答案】D【解析】解:由题意可得:机器人(看成点)分别从M ,N 两点同时出发,设圆的半径为R ,∴两个机器人最初的距离是AM CN R ++,∵两个人机器人速度相同,∴同时到达点A ,C ,∴两个机器人之间的距离y 越来越小,故排除A ,C ;当两个机器人分别沿A D C →→和C B A →→移动时,此时两个机器人之间的距离是半径R ,保持不变,当机器人分别沿C N →和A M →移动时,此时两个机器人之间的距离越来越大,故排除C ,故选:D .15.【答案】C【解析】如图,∵146ADE ∠=︒∴18034ADB ADE Ð=°-Ð=°∵ADB AHDαÐ=Ð+Ð∴503416AHD ADB αÐ=Ð-Ð=°-°=°∵12l l ∥∴16GIF AHD Ð=Ð=°∵EGF GIFβÐ=Ð+Ð∴601644EGF GIF βÐ=Ð-Ð=°-°=°故选:C .16.【答案】A【解析】解:含0y =,则220x m x -+=和220x m -=,解得0x =或2x m =或x m =-或x m =,∵抛物线22y x m =-的对称轴为0x =,抛物线22y x m x =-+的对称轴为222m x ==,∴这两个函数图象对称轴之间的距离为2,故选:A .二、填空题17.【答案】4(答案不唯一,满足39k <<均可)【解析】解:当反比例函数(0)k y k x=≠图像过(3,3)A 时,339k =⨯=;当反比例函数(0)k y k x =≠图像过(3,1)B 时,313k =⨯=;∴k 的取值范围为39k <<∴k 可以取4.故答案为4(答案不唯一,满足39k <<均可).18.【答案】①.52②.2-【解析】解:当x n =时,31x b +=,即31n b +=,当2x =时,21x a x +=,即221522a ⨯+==,当x n =时,211x x +=,即211n n +=,解得1n =-,经检验,1n =-是分式方程的解,∴()3112b =⨯-+=-,故答案为:52;2-19.【答案】①.30②.【解析】解:(1)作图如下:根据中间正六边形的一边与直线l 平行及多边形外角和,得60ABC ∠=︒,906030A α∠=∠=︒-︒=︒,故答案为:30;(2)取中间正六边形的中心为O ,作如下图形,由题意得:AG BF ∥,AB GF ∥,BF AB ⊥,∴四边形ABFG 为矩形,AB GF ∴=,,90BAC FGH ABC GFH ∠=∠∠=∠=︒ ,()Rt Rt SAS ABC GFH ≌,BC FH ∴=,在Rt PDE △中,1,3DE PE ==,由图1知23AG BF PE ===,由正六边形的结构特征知:1332OM =⨯=()1312BC BF CH =-= ,3133tan 33BC AB BAC ∴==-∠,231BD AB ∴=-=,又1212DE =⨯= ,3BE BD DE ∴=+=,3ON OM BE ∴=+=故答案为:3三、解答题20.【答案】(1)珍珍第一局的得分为6分;(2)6k =.【解析】(1)解:由题意得()4321426⨯+⨯+⨯-=(分),答:珍珍第一局的得分为6分;(2)解:由题意得()()3311032613k k +⨯+--⨯-=+,解得:6k =.21.【答案】(1)2132S a a =++,251S a =+,当2a =时,1223S S +=(2)12S S >,理由见解析【解析】(1)解:依题意得,三种矩形卡片的面积分别为:21S a S a S ===甲乙丙,,,∴213232S S S S a a =++=++甲乙丙,2551S S S a =+=+乙丙,∴()()2212325183S S a a a a a +=++++=++,∴当2a =时,212282323S S +=+⨯+=;(2)12S S >,理由如下:∵2132S a a =++,251S a =+∴()()()222123251211S S a a a a a a -=++-+=-+=-∵1a >,∴()21210S S a -=->,∴12S S >.22.【答案】(1)中位数为3.5分,平均数为3.5分,不需要整改(2)监督人员抽取的问卷所评分数为5分,中位数发生了变化,由3.5分变成4分【解析】(1)解:由条形统计图可知,客户所评分数按从小到大排列后,第10个数据是3分,第11个数据是4分;∴客户所评分数的中位数为:34 3.52+=(分)由统计图可知,客户所评分数的平均数为:1123364555 3.520⨯+⨯+⨯+⨯+⨯=(分)∴客户所评分数的平均数或中位数都不低于3.5分,∴该部门不需要整改.(2)设监督人员抽取的问卷所评分数为x 分,则有:3.520 3.55201x ⨯+>+解得: 4.55x >∵调意度从低到高为1分,2分,3分,4分,5分,共5档,∴监督人员抽取的问卷所评分数为5分,∵45<,∴加入这个数据,客户所评分数按从小到大排列之后,第11个数据不变依然是4分,即加入这个数据之后,中位数是4分.∴与(1)相比,中位数发生了变化,由3.5分变成4分.23.【答案】(1)1C 的最高点坐标为()32,,19a =-,1c =;(2)符合条件的n 的整数值为4和5.【解析】(1)解:∵抛物线21:(3)2C y a x =-+,∴1C 的最高点坐标为()32,,∵点(6,1)A 在抛物线21:(3)2C y a x =-+上,∴21(63)2a =-+,解得:19a =-,∴抛物线1C 的解析式为21(3)29y x =--+,令0x =,则21(03)219c =--+=;(2)解:∵到点A 水平距离不超过1m 的范围内可以接到沙包,∴点A 的坐标范围为()()5171 ,,,当经过()51,时,211551188n =-⨯+⨯++,解得175n =;当经过()71,时,211771188n =-⨯+⨯++,解得417n =;∴174157n ≤≤∴符合条件的n 的整数值为4和5.24.【答案】(1)7cm ;(2)11cm 2;(3)253cm 3EF =, 25π=cm 6EQ , EF EQ >.【解析】解:(1)连接OM ,∵O 为圆心,OC MN ⊥于点C ,48cm MN =,∴124cm 2MC MN ==,∵50cm AB =,∴125cm 2OM AB ==,∴在Rt OMC 中,7cm OC ==.(2)∵GH 与半圆的切点为E ,∴OE GH⊥∵MN GH∥∴OE MN ⊥于点D ,∵30ANM ∠=︒,25cm ON =,∴125cm 22OD ON ==,∴操作后水面高度下降高度为:25117cm 22-=.(3)∵OE MN ⊥于点D ,30ANM ∠=︒∴60DOB ∠=︒,∵半圆的中点为Q ,∴ AQ QB=,∴90QOB ∠=︒,∴30QOE ∠=︒,∴253tan 3EF QOE OE =∠⋅=,30π2525π==cm 1806EQ ⨯⨯,∵()25π25325π50325π03666-==>,∴ EF EQ>.25.【答案】(1)1l 的解析式为6y x =-+;2l 的解析式为15y x =-+;(2)①10,20x m y m =+=-;②3l 的解析式为30y x =-+,图象见解析;(3)538a c b+=【解析】(1)设1l 的解析式为y kx b =+,把(4,2)M 、(2,4)N 代入,得4224k b k b +=⎧⎨+=⎩,解得:16k b =-⎧⎨=⎩,∴1l 的解析式为6y x =-+;将1l 向上平移9个单位长度得到的直线2l 的解析式为15y x =-+;(2)①∵点P 按照甲方式移动了m 次,点P 从原点O 出发连续移动10次,∴点P 按照乙方式移动了()10m -次,∴点P 按照甲方式移动m 次后得到的点的坐标为()2,m m ;∴点()2,m m 按照乙方式移动()10m -次后得到的点的横坐标为21010m m m +-=+,纵坐标为()21020m m m +-=-,∴10,20x m y m =+=-;②由于102030x y m m +=++-=,∴直线3l 的解析式为30y x =-+;函数图象如图所示:(3)∵点,,A B C 的横坐标依次为,,a b c ,且分别在直线123,,l l l 上,∴()()(),6,,15,,30A a a B b b C c c -+-+-+,设直线AB 的解析式为y mx n =+,把A 、B 两点坐标代入,得615ma n a mb n b +=-+⎧⎨+=-+⎩,解得:9196m b a a n b a ⎧=-+⎪⎪-⎨⎪=-⎪-⎩,∴直线AB 的解析式为9916a y x b a b a⎛⎫=-++- ⎪--⎝⎭,∵A ,B ,C 三点始终在一条直线上,∴991630a c c b a b a⎛⎫-++-=-+ ⎪--⎝⎭,整理得:538a c b +=;即a ,b ,c 之间的关系式为:538a c b +=.26.【答案】(1)见解析(2)①90CBD ∠=︒,13x =;②76或236(3)22816x x +【解析】(1)∵将线段MA 绕点M 顺时针旋转()0180n n ︒<≤到MA ',∴A M AM'=∵A MA '∠的平分线MP 所在直线交折线AB BC -于点P ,∴A MP AMP'∠=∠又∵PM PM=∴()SAS A MP AMP 'V V ≌∴A P AP '=;(2)①∵8AB =,6DA =,90A ∠=︒∴10BD ==∵=BC ,12CD =∴(222210144BC BD +=+=,2212144CD ==∴222BC BD CD +=∴90CBD ∠=︒;如图所示,当180n =时,∵PM 平分A MA'∠∴90PMA ∠=︒∴PM AB∥∴DNM DBAV V ∽∴DN DM MN DB DA BA==∵2DM =,6DA =∴21068DN MN ==∴103DN =,83MN =∴203BN BD DN =-=∵90PBN NMD ∠=∠=︒,PNB DNM∠=∠∴PBN DMNV V ∽∴PB BN DM MN =,即203823PB =∴解得5PB =∴8513x AB PB =+=+=.②如图所示,当P 点在AB 上时,2PQ =,A MP AMP '∠=∠∵8,6,90AB DA A ==∠=︒,∴22226810BD AB AD =+=+=,63sin 105AD DBA BD ∠===,∴2103sin 35BQ BP DBA ===∠,∴1014833AP AB BP =-=-=∴1473tan tan 46AP A MP AMP AM '∠=∠===;如图所示,当P 在BC 上时,则2PB =,过点P 作PQ AB ⊥交AB 的延长线于点Q ,延长MP 交AB 的延长线于点H ,∵90PQB CBD DAB ∠=∠=∠=︒,∴90QPB PBQ DBA ∠=︒-∠=∠,∴PQB BAD∽∴PQ QB PB BA AD BD ==即8610PQ QB PB ==∴4855PQ PB ==,3655BQ PB ==,∴465AQ AB BQ =+=∵,PQ AB DA AB⊥⊥∴PQ AD ∥,∴HPQ HMA ∽,∴HQ PQ HA AM =∴854645HQ HQ =+解得:9215HQ =∴922315tan tan tan 865HQ A MP AMP QPH PQ '∠=∠=∠===,综上所述,tan A MP '∠的值为76或236;(3)解:∵当08x <≤时,∴P 在AB 上,如图所示,过点A '作A E AB '⊥交AB 于点E ,过点M 作MF A E '⊥于点F ,则四边形AMFE 是矩形,∴AE FM =,4EF AM ==,∵A MP AMP ' ≌,∴90PA M A '∠=∠=︒,∴90PA E FA M ''∠+∠=︒,又90A MF FA M ''∠+∠=︒,∴PA E A MF ''∠=∠,又∵90A EP MFA ''∠=∠=︒,∴A PE MA F '' ∽,∴A P PE A E MA A F FM''==''∵A P AP x '==,4MA MA '==,设FM AE y ==,A E h '=即44x x y h h y-==-∴4h y x=,()()44x y x h -=-∴()444h x x h x ⎛⎫-=- ⎪⎝⎭整理得22816x h x =+即点A '到直线AB 的距离为22816x x +.。
2023河北中考数综试题及答案

2023河北中考数综试题及答案第一部分数学试题1. 计算:2 × 4 + 3 × 5 = 262. 简化下列代数式:(3x + 4y) + (5x - 2y) = 8x + 2y3. 某图形的面积是48平方厘米,它的长度是8厘米,求它的宽度:宽度为6厘米4. 某女生考试成绩为90分,比及格线多8分,求及格线:及格线为82分5. 已知正方形边长为2x,求其周长:周长为8x...第二部分综合试题1. 在一群学生中,60%的学生喜欢听音乐,其中一半的学生还喜欢画画,画画和听音乐都不喜欢的学生共占学生总数的20%,问喜欢画画的学生占总人数的百分之几:喜欢画画的学生占总人数的30%2. 某班级共有40名男生和50名女生,男生的人数比女生多10人,求男生的百分比:男生的百分比为44%3. 王涛和李明两人一起骑自行车去书店,王涛骑车的速度是每小时18千米,李明骑车的速度是王涛速度的80%,问李明骑车到书店所需的时间是王涛的百分之几:李明骑车到书店所需的时间是王涛的百分之90%4. 某商场举办打折促销活动,原价为100元的商品打85折,原价为200元的商品打9折,原价为300元的商品打8.5折,小明购买了一件原价300元的商品,他实际支付了多少钱:小明实际支付了255元5. ...第三部分解答题1. 一曲线与x轴相交于点A(-1, 0),与y轴相交于点B(0, 2),求该曲线上任意一点P的坐标:曲线上任意一点P的坐标为(x, y)2. 已知两个正方形的面积之和为68平方厘米,另一个正方形的边长是已知正方形的边长的一半,求已知正方形的面积:已知正方形的面积为36平方厘米3. 三角形ABC的周长是30厘米,边AB的长度是10厘米,边AC的长度是6厘米,求三角形ABC的面积:三角形ABC的面积为14平方厘米4. 已知矩形的周长是20厘米,长是宽的3倍,求这个矩形的长和宽:矩形的长为12厘米,宽为4厘米5. ...以上是2023河北中考数综试题及答案的部分内容,希望对您有所帮助。
河北省唐山市路北区2023年中考数学测评试卷(3月份)(含解析)

河北省唐山市路北区2023年中考数学测评试卷(3月份)(解析版)一、选择题(本大题共16个小题。
1~10小题每题3分,11~16小题每题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,数轴上被遮挡住的整数的相反数是( )A.1B.﹣3C.﹣1D.02.如图,有一个破损的扇形零件,小明利用图中的量角器量出这个扇形零件的圆心角度数为50°,你认为小明测量的依据是( )A.垂线段最短B.对顶角相等C.圆的定义D.三角形内角和等于180°3.实数a,b在数轴上表示的位置如图所示,则( )A.a>0B.a>b C.a<b D.|a|<|b|4.在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是( )A.(a+b)(a﹣b)=a2﹣b2B.a2﹣b2=(a+b)(a﹣b)C.a2+b2=(a+b)2D.(a﹣b)2=a2﹣2ab+b25.如图,直线l1∥l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )A.10°B.15°C.20°D.30°6.《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿曰兆.”说明了大数之间的关系:1亿=1万×1万,1兆=1万×1万×1亿.则1兆等于( )A.108B.1012C.1016D.10247.从图1的正方体上截去一个三棱锥后,得到如图2所示的几何体,则这个几何体的主视图是( )A.B.C.D.8.过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )A.B.C.D.9.试卷上一个正确的式子(+)÷★=被小颖同学不小心滴上墨汁.被墨汁遮住部分的代数式为( )A.B.C.D.10.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是( )A.13.44πB.12πC.11.52πD.7.2π11.小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,接着活动学具成为图2所示,并测得∠ABC=90°,若图2对角线BD=40cm,则图1中对角线BD的长为( )A .20cmB .20cmC .20cmD .20cm12.为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格y 1(元/件)随时间t (天)的变化如图所示,设y 2(元/件)表示从第1天到第t 天该商品的平均价格,则y 2随t 变化的图象大致是( )A .B .C .D .13.以下有关勾股定理证明的图形中,不是中心对称图形的是( )A.B.C.D.14.甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:甲乙丙丁9899S2 1.60.830.8根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )A.甲B.乙C.丙D.丁15.某工厂生产A、B两种型号的扫地机器人.B型机器人比A型机器人每小时的清扫面积多50%;清扫100m2所用的时间A型机器人比B型机器人多用40分钟.两种型号扫地机器人每小时分别清扫多少面积?若设A型扫地机器人每小时清扫xm2,根据题意可列方程为( )A.=+B.+=C.+=D.=+16.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )A.+1B.+C.2+1D.2﹣二、填空题(本大题共3个小题,每小题0分,共9分.其中18小题第一空2分,第二空1分,19小题每空1分)17.某班按课外阅读时间将学生分为3组,第1、2组的频率分别为0.2、0.5,则第3组的频率是 .18.综合实践活动课上,小亮将一张面积为24cm2,其中一边BC为8cm的锐角三角形纸片(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形BCDE(如图2),则矩形的周长为 cm.19.根据图中给出的信息.(1)若在左边水桶中放入一个小球和一个大球,则水桶中的水位高度是 .(2)若在左边水桶中放入10个球,水桶中的水位升高到50cm,则放入大球的数量是 .三、解答题(本大题共7个小题,共69分。
2023年河北中考数学试题

2023年河北省初中学业水平考试时间:120分钟 满分:120分一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)1. 代数式-7x 的意义可以是( )A. -7与x 的和 B. -7与x 的差 C. -7与x 的积 D. -7与x 的商2. 淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西70°的方向,则淇淇家位于西柏坡的( )第2题图A. 南偏西70°方向B. 南偏东20°方向C. 北偏西20°方向D. 北偏东70°方向3. 化简x 3(y 3x)2的结果是( )A. xy 6B. xy 5C. x 2y 5D .x 2y 64. 有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上.若从中随机抽取一张,则抽到的花色可能性最大的是( )A.(黑桃) B.(红心) C.(梅花) D.(方块)第4题图5. 四边形ABCD 的边长如图所示,对角线AC 的长度随四边形形状的改变而变化.当△ABC 为等腰三角形时,对角线AC 的长为( )A. 2 B. 3 C. 4 D. 5第5题图6. 若k为任意整数,则(2k+3)2-4k2的值总能( )A. 被2整除B. 被3整除C. 被5整除D. 被7整除7. 若a=2,b=7,则14a2b2=( )A. 2B. 4C. 7D. 28. 综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.图①~图③是其作图过程.(1)作BD的垂直平分线交BD于点O;图①(2)连接AO,在AO的延长线上截取OC=AO;图②(3)连接DC,BC,则四边形ABCD即为所求.图③第8题图在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )A. 两组对边分别平行B. 两组对边分别相等C. 对角线互相平分D. 一组对边平行且相等9. 如图,点P1~P8是⊙O的八等分点.若△P1P3P7,四边形P3P4P6P7的周长分别为a,b,则下列正确的是( )第9题图A. a<bB. a=bC. a>bD. a,b大小无法比较10. 光年是天文学上的一种距离单位,一光年是指光在一年内走过的路程,约等于9.46×1012 km.下列正确的是( )A. 9.46×1012-10=9.46×1011B. 9.46×1012-0.46=9×1012C. 9.46×1012是一个12位数D. 9.46×1012是一个13位数11. 如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( )A. 43B. 83C. 12D. 16第11题图12. 如图①,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图②,平台上至少还需再放这样的正方体( )A. 1个B. 2个C. 3个D. 4个图①图②第12题图13. 在△ABC 和△A ′B ′C ′中,∠B =∠B ′=30°,AB =A ′B ′=6,AC =A ′C ′=4.已知∠C =n °,则∠C ′=( )A. 30°B. n °C. n °或180°-n °D. 30°或150°14. 下图是一种轨道示意图,其中ADC ︵ 和ABC ︵均为半圆,点M ,A ,C ,N 依次在同一直线上,且 AM =CN .现有两个机器人(看成点)分别从M ,N 两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M →A →D →C →N 和N →C →B →A →M .若移动时间为x ,两个机器人之间距离为y ,则y 与x 关系的图象大致是( )第14题图15. 如图,直线l 1∥l 2,菱形ABCD 和等边△EFG 在l 1,l 2之间,点A ,F 分别在l 1,l 2上,点B ,D ,E ,G 在同一直线上.若∠α=50°,∠ADE =146°,则∠β=( )第15题图A. 42°B. 43°C. 44°D. 45°16. 已知二次函数y =-x 2+m 2x 和y =x 2-m 2(m 是常数)的图象与x 轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )A. 2 B. m 2 C. 4 D. 2m 2二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)17. 如图,已知点A (3,3),B (3,1),反比例函数y =kx (k ≠0)图象的一支与线段AB 有交点,写出一个符合条件的k 的整数值:________.第17题图18. 根据表中的数据,写出a 的值为________,b 的值为________. 代数式 结果x 2n3x +17b 2x +1xa119. 将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图①,正六边形边长为2且各有一个顶点在直线l 上,两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图②,其中,中间正六边形的一边与直线l 平行,有两边分别经过两侧正六边形的一个顶点.则图②中(1)∠α=________度;(2)中间正六边形的中心到直线l 的距离为________(结果保留根号).第19题图三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)20. (本小题满分9分)某磁性飞镖游戏的靶盘如图.珍珍玩了两局,每局投10次飞镖,若投到边界则不计入次数,需重新投.计分规则如下:投中位置A区B区脱靶一次计分(分)31-2第20题图在第一局中,珍珍投中A区4次,B区2次,脱靶4次.(1)求珍珍第一局的得分;(2)第二局,珍珍投中A区k次,B区3次,其余全部脱靶.若本局得分比第一局提高了13分,求k的值.21. (本小题满分9分)现有甲、乙、丙三种矩形卡片各若干张,卡片的边长如图①所示(a>1).某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图②和图③,其面积分别为S1,S2.图①图②图③第21题图(1)请用含a的式子分别表示S1,S2;当a=2时,求S1+S2的值;(2)比较S1与S2的大小,并说明理由.22. (本小题满分9分)某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现.满意度从低到高依次分为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,下图是根据这20份问卷中的客户所评分数绘制的统计图.(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改;(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评分数为几分?与(1)相比,中位数是否发生变化?第22题图23. (本小题满分10分)嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.如图,在平面直角坐标系中,一个单位长度代表1 m 长.嘉嘉在点A (6,1)处将沙包(看成点)抛出,其运动路线为抛物线C 1:y =a (x -3)2+2的一部分,淇淇恰在点B (0,c )处接住,然后跳起将沙包回传,其运动路线为抛物线C 2:y =-18x 2+n8x +c +1的一部分.(1)写出C 1的最高点坐标,并求a ,c 的值;(2)若嘉嘉在x 轴上方1 m 的高度上,且到点A 水平距离不超过1 m 的范围内可以接到沙包,求符合条件的n 的整数值.第23题图24. (新考法 真实问题情境)(本小题满分10分)装有水的水槽放置在水平台面上,其横截面是以AB 为直径的半圆O ,AB =50 cm ,如图①和图②所示,MN 为水面截线,GH 为台面截线,MN ∥GH .计算 在图①中,已知 MN =48 cm ,作 OC ⊥MN 于点C.(1)求OC 的长.操作 将图①中的水槽沿GH 向右作无滑动的滚动,使水流出一部分,当∠ANM =30°时停止滚动,如图②.其中,半圆的中点为Q ,GH 与半圆的切点为E ,连接OE 交MN 于点D.探究 在图②中.(2)操作后水面高度下降了多少?(3)连接OQ 并延长交GH 于点F ,求线段EF 与EQ ︵的长度,并比较大小.第24题图25. (本小题满分12分)在平面直角坐标系中,设计了点的两种移动方式:从点(x,y)移动到点(x+2,y+1)称为一次甲方式;从点(x,y)移动到点(x+1,y+2)称为一次乙方式.例点P从原点O出发连续移动2次:若都按甲方式,最终移动到点M(4,2);若都按乙方式,最终移动到点N(2,4);若按1次甲方式和1次乙方式,最终移动到点E(3,3).(1)设直线l1经过上例中的点M,N,求l1的解析式;并直接写出将l1向上平移9个单位长度得到的直线l2的解析式;(2)点P从原点O出发连续移动10次,每次移动按甲方式或乙方式,最终移动到点Q(x,y).其中,按甲方式移动了m次.①用含m的式子分别表示x,y;②请说明:无论m怎样变化,点Q都在一条确定的直线上.设这条直线为l3,在图中直接画出l3的图象;(3)在(1)和(2)中的直线l1,l2,l3上分别有一个动点A,B,C,横坐标依次为a,b,c,若A,B,C三点始终在一条直线上,直接写出此时a,b,c之间的关系式.第25题图26. (新考法 线段旋转结合分类讨论考查图形变化))(本小题满分13分)如图①和图②,平面上,四边形ABCD中,AB=8,BC=211,CD=12,DA=6,∠A=90°,点M在AD 边上,且DM=2.将线段MA绕点M顺时针旋转n°(0<n≤180)到MA′,∠A′MA的平分线MP所在直线交折线AB-BC于点P,设点P在该折线上运动的路径长为x(x>0),连接A′P.(1)若点P在AB上,求证:A′P=AP;(2)如图②,连接B D.①求∠CBD的度数,并直接写出当n=180时,x的值;②若点P到BD的距离为2,求tan∠A′MP的值;(3)当0<x≤8时,请直接写出点A′到直线AB的距离(用含x的式子表示).第26题图2023年河北省初中学业水平考试解析快速对答案一、选择题(1~6小题,每小题3分,7~16小题,每小题2分)1-5 CDABB 6-10 BACAD 11-15 BBCDC 16 A二、填空题(17小题2分,18~19小题各4分,每空2分)17. 4(答案不唯一) 18. 52,-2 19. (1)30;(2)23三、解答题标准答案及评分标准:20~26 题见详解详析详解详析一、选择题1. C 【解析】-7x表示-7与x的积.2. D 【解析】∵分别以淇淇家和西柏坡为中心的南北方向是平行的,∴淇淇家位于西柏坡的北偏东70°方向.3. A 【解析】原式=x3·y6x2=xy6.4. B 【解析】∵这几张扑克牌中黑桃有1张,红心有3张,梅花有1张,方块有2张,∴随机抽取一张,抽到红心的可能性最大,故选项B符合题意.(新考法) 定性的考查可能性大小,渗透对简单概率问题的理解.5. B 【解析】当△ABC为等腰三角形时,AC可能为3或4,在△ADC中,0<AC<4,则AC只能为3.6. B 【解析】(2k+3)2-4k2=(2k+3+2k)(2k+3-2k)=3(4k+3),∵k为任意整数,∴原式的值总能被3整除.(命题立意)通过因式分解对代数式变形,考查代数推理.7. A 【解析】原式=14×(2)2(7)2=14×27=4=2.8. C 【解析】根据尺规作图痕迹可得OD=OB,OC=OA,∴可根据对角线互相平分的四边形是平行四边形判定四边形ABCD为平行四边形.9. A 【解析】如解图,连接P1P8,P7P8,∵P1~P8是⊙O的八等分点,∴P1P3=P4P6=P1P7,P3P4=P6P7=P7P8=P 1P 8,∵P 1P 8+P 7P 8>P 1P 7,∴P 3P 4+P 6P 7>P 1P 7,∴a <b .第9题解图10. D 【解析】9.46×1012复原后的数有12+1=13位数,故选项D 符合题意.11. B 【解析】∵S 正方形AMEF =16,∴AM =4,∵M 是斜边BC 的中点,∴AM 是Rt △ABC 斜边上的中线,∴BC =2AM =8,在Rt △ABC 中,由勾股定理,得AC =BC 2-AB 2=43,∴S △ABC =12AB ·AC =12×4×43=83.12. B 【解析】如解图,满足主视图和左视图的要求,只需在原图的①②位置各放一个小正方体即可,∴平台上至少还需再放这样的正方体2个.第12题解图 13. C 【解析】如解图,当点C 在C 1位置,∠B ′C 1A ′=∠C =n °,当点C 在C ′位置,∵A ′C ′=A ′C 1,∴∠C ′=∠1,∵∠C =n °,∴∠1=180-n °,∴∠C ′=180-n °,综上所述,∠C ′=n °或180°-n °.第13题解图14. D 【解析】设这两个机器人分别为甲、乙,当两个机器人同时出发,甲在MA 段时,乙在NC 段,此时甲、乙之间的距离y 随x 的增大而减小;∵AM =CN ,ADC ︵ =ABC ︵,∴当甲在CN 段,乙在AM 段,甲、乙之间的距离y 随x 的增大而增大,故选项D 符合题意.15. C 【解析】如解图,过点D 作l 3∥l 1,延长DE 交l 2于点M ,则l 2∥l 3,∵∠α=50°,∴∠1=180°-50°=130°,∵∠ADE =146°,∴∠2=146°-130°=16°,则∠M =∠2=16°,∵△EFG 为等边三角形,∴∠EGF =60°,∴∠β=∠EGF -∠M =60°-16°=44°.第15题解图(命题立意) 考查平行线的性质,三角形内角和,等边三角形的性质,综合性较强,需构造平行线,要求学生熟悉教材中的几何模型.16. A 【解析】如解图,令-x 2+m 2x =0,解得x =0或x =m 2,∴设y =-x 2+m 2x 的图象与x 轴交点为O (0,0),C (m 2,0),令x 2-m 2=0,解得x =m 或x =-m ,∴设y =x 2-m 2的图象与x 轴交点为A (-m ,0),B (m ,0),又∵四个交点中每相邻两点间的距离都相等,∴OA =OB =BC ,∴|m|=m 2-|m|,由题意,得m ≠0,①当m >0时,m =m 2-m ,解得m 1=0(不合题意,舍去),m 2=2; ②当m <0时, -m =m 2+m ,解得m 1=0(不合题意,舍去),m 2=-2;∵y =-x 2+m 2x图象的对称轴为直线x =m 22,y =x 2-m 2图象的对称轴为直线x =0,∴这两个函数图象对称轴之间的距离为m 22=2.第16题解图二、填空题17. 4(答案不唯一,符合条件即可) 【解析】当y =k x (k ≠0)的图象经过点A (3,3)时,则3=k3,解得k =9,当y =k x (k ≠0)的图象经过点B (3,1)时,则1=k3,解得k =3,∴反比例函数图象的一支与线段AB 有交点时,k 的取值范围为3≤k ≤9,∴符合条件的k 的整数值可以为3,4,5,6,7,8,9.(任选其一,答案不唯一,符合条件即可)18. 52,-2 【解析】根据表格可知,当x =2时,2x +1x =2×2+12=52=a ,当x =n 时,2n +1n =1,解得n =-1(使分母不为0,符合题意),当x =n 时,3n +1=b ,将n =-1 代入,得3n +1=b ,解得b =-2.(新考法) 代数式的值以表格信息为依托,考查学生阅读能力,理解分析问题的能力,综合性较强,又不失基础性.19. (1)30 【解析】如解图,延长AB 交直线l 于点E ,延长HC 交AE 于点B ,∵多边形是正六边形,∴∠ACB =60°,∠PDE =60°,易得∠DPE =30°,∴∠DEP =90°,∵BC ∥直线l ,∴∠ABC =90°,∴α=30°.(2)23 【解析】如解图,取中间正六边形的中心为O ,过点O 作ON ⊥直线l 于点N ,连接AG ,延长CH 交右侧的正六边形于点F ,由题意得,AG ∥BF ,AB ∥GF ,则BF ⊥AB ,四边形ABFG 为矩形,∴AB =GF ,∵∠BAC =∠FGH ,∠ABC =∠GFH =90°,∴△ABC ≅△GFH (SAS),∴BC =FH ,∵在Rt △PDE 中,DP =2,∴DE =1,PE =3,由正六边形的性质易得AG =BF =2PE =23,OM =PE =3,∵BC =12(BF -CH )=3-1,∴AB =BC tan ∠BAC =3-133=3-3,∴BD =2-AB =3-1,∵DE =12×2=1,∴BE =BD +DE =3,∴ON =OM +BE =23,∴中间正六边形的中心到直线l 的距离为23.第19题解图(命题立意) 正多边形中有关角与线段的计算,以及学生基本运算能力,以及对教材中的基本几何模型的理解,构造基本辅助线解直角三角形.三、解答题20. 解:(1)3×4+1×2+(-2)×4(2分)=12+2+(-8)=6,(4分)答:珍珍第一局的得分为6分;(5分)(2)根据题意,得3k +1×3-2(10-k -3)=6+13,…(7分)解得k =6,∴k 的值为6.(9分)21. 解:(1)S 1=a 2+a ×1×3+2×12=a 2+3a +2,S 2=a ×1×5+12=5a +1,(2分)∴S 1+S 2=a 2+3a +2+5a +1=a 2+8a +3,(3分)将a =2代入,得S 1+S 2=22+8×2+3=23;(4分)(2)S 1>S 2.(5分)理由:S 1-S 2=(a 2+3a +2)-(5a +1)=a 2-2a +1=(a -1)2,(7分)∵a >1,∴(a -1)2>0,∴S 1>S 2. (9分)22. 解:(1)在20个数据中,有1个1分,3个2分,6个3分,5个4分,5个5分,最中间的两个数据是第10个数据和第11个数据,这两个数据分别是3分和4分,∴中位数为12(3+4)=3.5(分),(2分)这20个数据的平均数为120(1+3×2+6×3+5×4+5×5)=120×70=3.5(分),(4分)∵中位数和平均数都不低于3.5,∴该部门不需要整改;(5分)(2)设监督人员抽取的问卷所评分数为x 分,根据题意,得121(20×3.5+x )>3.55,解得x >4.55,∴抽取的问卷所评分数为5分,(7分)在21个数据中,有1个1分,3个2分,6个3分,5个4分,6个5分,最中间的数据是第11个数据,这个数据是4分,∴中位数是4分,∴中位数发生了变化.(9分)23. 解:(1)∵抛物线y =a (x -3)2+2的顶点坐标为(3,2),∴C 1的最高点坐标为(3,2),(2分)将A (6,1)代入抛物线y =a (x -3)2+2中,得1=a (6-3)2+2,解得a =-19,(4分)∴抛物线C 1:y =-19(x -3)2+2.将B (0,c )代入抛物线y =-19(x -3)2+2中,得c =-19(0-3)2+2=1;(6分)(2)将c =1代入抛物线y =-18x 2+n8x +c +1中,得y =-18x 2+n8x +2.根据题意,可知嘉嘉恰好在(5,1)和(7,1)两个点间能接到沙包.将(5,1)代入抛物线y =-18x 2+n8x +2中,得1=-18×52+n 8×5+2,解得n =175;将(7,1)代入抛物线y =-18x 2+n8x +2中,得1=-18×72+n 8×7+2,解得n =417,(8分)∴175≤n ≤417,∴符合条件的n 的整数值为4和5.(10分)24. 解:(1)如解图,连接OM .∵OC ⊥MN ,MN =48 cm ,∴MC =12×48=24(cm).∵AB =50 cm ,∴OM =12×50=25(cm).在Rt △OMC 中,根据勾股定理,得OC =252-242=7 cm ;(3分)第24题解图(2)∵GH 与半圆相切于点E ,∴OE ⊥GH .∵MN ∥GH ,∴OE ⊥MN .在Rt △ODB 中,OB =25 cm ,∠ANM =30°,∴OD =12×25=12.5(cm).∴操作后水面高度为25-12.5=12.5(cm),∵操作前水面高度为25-7=18(cm),∴操作后水面高度下降了18-12.5=5.5 cm ; (6分)(3)∵Q 为半圆的中点,∴∠QOB =12×180°=90°.∵∠ANM =30°,∴∠BOD =60°,∴∠FOE =90°-∠BOD =30°.∴EQ ︵的长=30π×25180=25π6(cm).在Rt △OFE 中,tan ∠FOE =EF OE,∴EF =OE ·tan ∠FOE =25×33=2533(cm). ∵25π6=256×π,2533=256×23,π<23,∴EQ ︵的长<EF .(10分)25. 解:(1)设直线l 1的解析式为y =kx +b (k ≠0),将M (4,2),N (2,4)代入y =kx +b ,得{4k +b =22k +b =4,解得{k =-1b =6.∴直线l 1的解析式为y =-x +6,(2分)将l 1向上平移9个单位长度得到得直线l 2,∴直线l 2的解析式为y =-x +6+9=-x +15;(4分)(2)①∵按甲方式移动了m 次,∴按乙方式移动了(10-m )次.根据题意可知,x =2m +(10-m )=m +10,y =m +2(10-m )=-m +20;(6分)②∵x +y =(m +10)+(-m +20)=30,∴y =-x +30,∴无论m 怎样变化,点Q 都在直线y =-x +30上. (9分)直线l 3的图象如解图;(10分)第25题解图(3)5a +3c =8b .(12分)(解法提示) ∵点A ,B ,C 分别在y =-x +6,y =-x +15,y =-x +30的图象上,点A ,B ,C 的横坐标分别为a ,b ,c ,∴A (a ,-a +6),B (b ,-b +15),A (c ,-c +30),∵点A ,B ,C 在同一条直线上,∴直线AB 与直线BC 的k 值相等,即(-b +15)-(-a +6)b -a =(-c +30)-(-b +15)c -b ,化简得5a +3c =8b .26. (1)证明:∵A ′M 是由AM 旋转得到,∴A ′M =AM ,∵MP 平分∠A ′MA ,∴∠AMP =∠A ′MP ,在△A ′MP 和△AMP 中,{MA ′=MA∠A ′MP =∠AMP MP =MP,∴△A ′MP ≌△AMP (SAS),∴A ′P =AP ;(4分)(2)解:①在Rt △ABD 中,AB =8,DA =6,∴BD =82+62=10,在△CBD 中,∵BD 2+BC 2=102+(211)2=144,CD 2=122=144,∴BD 2+BC 2=CD 2,∴∠CBD =90°,(7分)如解图①,当n =180时,∠A ′MP =∠AMP =90°,设BD 与PM 相交于点N ,∵∠A =∠A ′MP ,∴PM ∥AB ,∴△DNM ∽△DBA ,∴DN DB =DM DA =MN AB ,即DN 10=26=MN 8,解得DN =103,MN =83.∵∠CBD =∠DMP ,∠PNB =∠DNM ,∴△PNB ∽△DNM ,∴PB DM =BN MN ,即PB 2=10-10383,解得PB =5.∴x =PB +AB =5+8=13;(9分)图① 图②第26题解图②分两种情况讨论:如解图②,当点P 在AB 上且到BD 的距离为2时,过点P 作PQ ⊥BD 于点Q ,则PQ =2,∴∠BQP =∠BAD ,又∵∠PBQ =∠DBA ,∴△BQP ∽△BAD ,∴PBDB =PQ DA ,即PB 10=26,解得PB =103,在Rt △APM 中,AP =8-103=143,AM =4,∴tan ∠AMP =AP AM =1434=76,即tan ∠A ′MP =76;如解图③,当点P 在BC 上且到BD 的距离为2时,则PB =2,过点P 作PG ⊥AB 交AB 的延长线于点G ,PH ⊥DA 于点H .第26题解图③∵∠CBD =90°,∴∠PBG +∠ABD =90°.又∵∠PBG +∠GPB =90°,∴∠GPB =∠AB D.又∵∠PGB =∠A =90°,∴△PBG ∽△BDA ,∴PGBA =BGDA =PB BD ,即PG 8=BG 6=210,解得PG =85,BG =65.∴PH =65+8=465,MH =4-85=125.∴tan ∠AMP =PH MH =465125=236,即tan ∠A ′MP =236;综上所述,tan ∠A ′MP 的值为76或236;(11分)(3)解:8x 2x 2+16.(13分)(解法提示) 分两种情况讨论:①如解图④,过点A ′作A ′I ⊥AB 于点I ,过点M 作MJ ⊥A ′I 于点J .易证△A ′JM ∽△PIA ′,∴A ′J PI =MA ′A ′P .设A ′I =d ,则A ′J =4-d ,IP =x 2-d 2,即4-d x 2-d 2=4x,解得d =8x 2x 2+16.②如解图⑤,过点A ′作A ′I ⊥AB 于点I ,过点M 作MK ⊥A ′I 于点K ,易证△A ′IP ∽△MKA ′,∴A ′I MK =IP KA ′=A ′PMA ′,设A ′I=y,则KA′=y-4,即yx-IP=IPy-4=x4,∴IP=x4(y-4)=xy4-x,∴yx-(xy4-x)=x4,即y=8x2x2+16,综上所述,点A′到直线AB的距离为8x2 x2+16图④图⑤第26题解图。
河北中考数学试卷真题2023

河北中考数学试卷真题2023一、选择题1. 下列各式中,等式恒成立的是()A. x + 2 = 5B. 4x = 12C. 3x = 2 + xD. 2(x - 3) = 2x - 62. 已知等差数列的第1项是2,公差是4,那么该等差数列的第10项是()A. 16B. 36C. 20D. 103. 地形图上,1厘米表示实际距离5千米,其中两点直线距离为7.2厘米,则这两点的实际距离是()A. 2.4千米B. 3.6千米C. 14千米D. 36千米4. 边长为3厘米的正方形ABC∠B为顶点,与边BC相交于点D,连接AD,若AD=2.5cm,则图中阴影部分的面积为()A. 1.25cm²B. 2.5cm²C. 3.75cm²D. 5cm²5. 已知函数y = ax² + bx + c的图像经过点(1, 7),(2, 12)和(3, 17),则函数的解析式为()A. y = 2x² + 3x + 2B. y = 2x² + 3x + 1C. y = x² + 4x + 2D. y = x² + 2x + 3二、填空题1. 若x - 5 = 2,则x = _________。
2. 将半径为5cm的圆铁丝围成一个圆环,该圆环的面积为_________。
3. 一种混合饲料A的价格是每袋30元,其中含有A种颗粒,B种颗粒,和C种颗粒三种,按质量比例,A:B:C=3:4:5,若购买100袋饲料A,则其中A种颗粒的质量是__________。
4. 设函数y = f(x)的图像关于x轴对称,且y = f(2),则y = f(-2)的值为__________。
5. 甲、乙、丙三个整数,甲与丙的和比乙多9,乙与丙的和比甲多19,则甲、乙、丙的和是__________。
三、解答题1. 若直线y = kx - 2与坐标轴的交点的x坐标是2,则k的值为多少?2. 一对兔子出生后第3个月开始生育,从第3个月生产开始,每月都能生一对兔子,新生的兔子也同样满3个月后才开始生育。
2023届中考数学考向信息卷 河北专版(含解析)

2023届中考数学考向信息卷河北专版【满分:120】一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.从百年前的“奥运三问”到今天的“双奥之城”,2022年中国与奥运再次牵手,2022年注定是不平凡的一年.数字2022的倒数是( )A.2022B.-2022C.D.2.一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( )A. B. C. D.3.如图, 将直角三角板中角的顶点放在直线l上, 若, 则( )A. B. C. D.4.下列各式的运算结果中, 与单项式次数不同的是( )A. B. C. D.5.有一道题: “某工程队铺设一条长 8000 米的管道, 实际施工时, . 求原计划每天铺设管道多少米. ”若设原计划每天铺设x 米,则可得方程, 则题目中 “____”上的条件应是( )A.每天比原计划多铺设 10 米,结果延期 20 天完成B.每天比原计划少铺设 10 米,结果延期 20 天完成C.每天比原计划多铺设 10 米, 结果提前 20 天完成D.每天比原计划少铺设 10 米, 结果提前 20 天完成6.有两个正多边形, 边数分别为m,n, 且有一个外角的度数分别为,, 若, 则( )A. B. C. D.7.已知, 且, 则代数式的值为( )A.3B. -3C.D.8.华为Mate21手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米,数据0.000000007用科学记数法表示为( ).A. B. C. D.9.甲、乙两人同时各接受了 600 个同种零件的加工任务, 甲比乙每分钟加工的数量多, 两人同时开始加工, 加工过程中, 甲因故障停止一段时间后又继续按原速加工, 直到两人完成任务. 甲比乙多加工的零件数量y (个) 与加工时间x (分钟) 之间的函数关系如图所示, 点A 的横坐标为 12 , 点B的坐标为, 点C的横坐标为 128 , 则下列说法中不正确的是( )A.甲每分钟加工的零件数量是 5 个B.在 60 分钟时, 甲比乙多加工了 120 个零件C.点D的横坐标是 200D. y的最大值是21610.在四边形ABCD中, , 添加条件①可得到四边形 ABCD是平行四边形, 再添加条件②可得到四边形ABCD是菱形,则( )A.①可以是 “”,②可以是“”B.①可以是 “,②可以是 “”C.①可以是“”,②可以是“”D.①可以是 “”,②可以是 “”11.如图, 在平面直角坐标系中, 过点作轴于点B, 连接OA. 将绕点A逆时针旋转, 点O,B的对应点分别为点C,D. 当双曲线与有公共点时, k的取值范围是( )A. B. C. D.12.如图,在中,,,半径为1的与OB交于点C,且AB与相切,过点C作交AB于点D,点M是边OA上动点.则周长最小值为( )A. B. C. D.13.尺规作图: 如图 (1), 在中, ,, 在AC边上求作一点P, 使. 如图 (2) 是四名同学的作法, 其中正确的有( )A.1 种B.2 种C.3 种D.4 种14.如图, 点P,Q对应的数分别为p,q, 则下列说法正确的是( )A.点P向右平移 3 个单位长度与点Q重合B.C.的相反数的整数部分为 2D.15.如图, EF是的中位线. 在图 (1) 中, 将沿EF所在直线折叠, 点A的对应点D落在BC边上; 在图(2) 中, 将沿中线AM平移, 得到, 已知点A 的对应点为, 点E,F的对应点,在边BC上. 某数学小组成员总结了以下 4 个结论: ①是等腰三角形;②四边形是平行四边形;③图(1) 中阴影部分的周长与图 (2) 中阴影部分的周长相等;④图 (1) 中阴影部分的面积与图 (2) 中阴影部分的面积相等. 其中正确的结论是( )A.③④B.①②C.②③④D.①②③④16.如图,已知正方形 ABCD和正方形EFGH是以点O为位似中心的位似图形, 且点B,C,F,G共线,结论结论 II : 的面积为 2 或.下列判断正确的是( )A. I 和 II 都对B. I 和 II 都不对C. I 对 II 不对D. I 不对 II 对二、填空题(本大题有3个小题,每小题3分,共9分.其中18,19小题第一空1分,第二空2分)17.已知一组数据2,3,a,5,b,6,7:. 从分别写有4,5,6,7的四张卡片(背面完全相同) 中抽取两张作为a,b的值, 则使得该组数据的众数不唯一的概率为________18.如图, 在由边长为 1 的小正方形组成的网格中, 点A,B,C,D都在这些小正方形的顶点上, AB,CD相交于点O, 则(1) AB与CD长度的大小关系是____________(2)的值为____________19.已知抛物线为常数, 且经过点,.(1)该抛物线与x 轴的交点的坐标为____________.(2)若当时, y随x的增大而增大, 且当,时, , 则m的取值范围是________.三、解答题(本大题有7个小题,共69分.解答应写出文字说明、证明过程或演算步骤)20.(9分)已知的三条边长分别为,.(1)用含x,y的代数式表示的周长L.(2)从以下三组数据中选择合适的一组, 计算的周长L的值. 第一组:,;第二组:,;第三组:,.21.(9分)2022 年 3 月 23 日下午, “天宫课堂” 第二课开讲, “太空教师” 翟志刚、王亚平、叶光富在中国空间站再次为广大青少年带来一堂精彩的太空科普课. 三位航天员相互配合, 生动演示了太空 “冰雪” 实验、液桥演示实验、水油分离实验、太空抛物实验 (依次记为 A, B, C, D). 某校九 (1) 班在教室观看了这堂科普课, 为了解同学们对这四个实验的喜爱情况, 课外兴趣小组对全班同学进行了调查, 并根据调查结果绘制出如下统计图表 (不完整). 赵老师查看后指出, 条形统计图中男生人数有一处错误.(1)喜欢哪个实验的男生人数有误? 并直接写出正确的人数.(2)喜欢实验A的女生人数为________ , ________.(3)兰兰想用扇形统计图反映喜欢各个实验的人数占全班总人数的百分比, 是否可行? 若可行, 求出 C对应扇形圆心角的度数; 若不可行, 请说明理由.22.(9分)定义如果一个正整数等于两个连续偶数的平方差, 那么称这个正整数为 “奇巧数”.发现数28,32,36 中, 是 “奇巧数” 的是探究已知正奇数的 4 倍一定是 “奇巧数”, 设一个正奇数为 (n为正整数), 请你论证这个结论.23.(10分)如图, 已知直线与y 轴交于点A, 与x轴交于点C, 且, 将直线 l绕点A旋转得到直线, 直线与双曲线的一个交点为B.(1)求直线 l的解析式;(2)连接BC, 当, 且恰好是直角时, 求直线与双曲线的交点情况;(3)在(2)的情形下, 若点是点A 关于 x轴的对称点, 求线段 AB,BC,与y 轴围成的封闭区域的面积.24.(10分)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C 处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度米,,且B、C、D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.25.(10分)如图, 在平面直角坐标系中, 有一个正方形ABCD, 点N,M,E,F分别是AB,CD,AD,BC的中点, MN , EF将正方形ABCD分成四个小正方形, MN 与EF 交于点P. 抛物线G的解析式为.(1)若抛物线G的顶点为M, 求抛物线的解析式, 并判断九个格点 (小正方形的顶点) 中哪些点在抛物线G上.(2)若抛物线G经过点F, 且与y轴交于一点, 直线与抛物线G的两个交点关于原点对称.①求抛物线G的解析式.②当时, y的最大值是 2 , 求t的值.26.(12分)在边长为 12 的等边三角形ABC中, AD是 BC边上的高, P为边AC上一动点(不与点A,C重合), 连接PD, 将PD绕点 P顺时针旋转得到PQ, 连接AQ,DQ.(1) 如图 (1), 当点Q落在线段AD上时, 求证:.(2) 点E 为AC边的中点, 连接EQ.①试猜想线段EQ,CP 之间的数量关系, 并就图(2) 所示的情形给出证明;②求AQ长的最小值.(3)在点P 运动的过程中, 当的面积为 9 时, 请直接写出线段CP的长.答案以及解析1.答案:D解析:2022的倒数是.故选:D.2.答案:C解析:俯视图是一个正方形内有一个内切圆,且内切圆是看得见的,为实线,故选C.3.答案:D解析:. 故选D.4.答案:C解析:单项式的次数为 3,,,,.其中单项式,,的次数均为 3 , 单项式的次数为2. 故选C.5.答案:B解析:原计划每天铺设管道x米,那么由可知实际每天比原计划少铺设 10 米, 结合, 可知完成此项工程实际用的时间比原计划多 20 天,故题目中“_____”上的条件应是“每天比原计划少铺设 10 米, 结果延期 20 天完成”.6.答案:B解析:由题意得,,,. 故选 B.7.答案:A解析:,,8.答案:C解析:.故选:C.9.答案:B解析:观察题中图象, 甲的加工总时间为(分钟), 甲每分钟加工的零件数量是 (个), 故 A 正确. 设乙每分钟加工的零件数量是a个, 则有, 解得,乙每分钟加工的零件数量是 3 个. 在 60 分钟时, 甲比乙多加工了(个) 零件, 故 B 错误. 由题意知, 点D 的横坐标为乙的加工总时间, (分钟), 点D 的横坐标为 200 , 故 C 正确. 由图象知, 在C 点时y值最大, 此时 , 故 D 正确. 故选 B.10.答案:D解析:选项A中, 若②是 “”, 不能得到四边形ABCD是菱形; 选项B 中, 若①是“”, 不能得到四边形ABCD是平行四边形; 选项C 中, 若①是“”, 可得到, 不能得到四边形ABCD是平行四边形; 根据 “两组对边分别相等的四边形是平行四边形” “一组邻边相等的平行四边形是菱形”, 易知选项 D 符合题意.11.答案:C解析:由旋转的性质可知点,,当双曲线分别经过点A,C,D时, k值分别为 2,3 ,6 ,故当该双曲线与有公共点时, k 的取值范围为.12.答案:A解析:如图,延长CO交于点E,连接ED,交AO于点M,此时周长最小.设AB于相切于点F,连接OF,则....且OC为的半径.CD是的切线....即:.解得:..的周长最小值为:.故选:A.13.答案:D解析:①中, , 故;②中, 由尺规作图知;③中, 根据线段的垂直平分线的性质得, 故;④中, 根据直径所对的圆周角是, 可知, 故.故正确的作法有 4 种.14.答案:C解析:由题图可知,,,,点P 向右平移 3 个单位长度不与点Q重合, , 故选项 A,B 中的说法都不正确;, ,的相反数的整数部分为 2 , 故选项 C 中的说法正确;,,, 故选项D 中的说法错误. 故选C.15.答案:D解析:由折叠可知,是等腰三角形, 故结论①正确. 易知点在EF 上, 故. 又由平移可知, 故四边形是平行四边形, 故结论②正确. 题图(1) 中阴影部分的周长. 题图 (2) 中阴影部分的周长, 故题图 (1) 和题图(2)中的阴影部分周长相等, 故结论③正确. 题图 (1) 中阴影面积, 题图(2) 中阴影面积, 故题图 (1) 和题图 (2) 中的阴影部分面积相等, 故结论④正确.16.答案:D解析:由题意可知, 正方形ABCD和正方形EFGH的相似比为, 边长分别为 1,2 .当点 O的位置如图 (1) 所示时,. 易得,,,,,. 当点O的位置如图 (2) 所示时,. 过点 O作于点P, 则,,,. 故 I 不对 II 对.17.答案:解析:画树状图如下由树状图可知共有 12 种等可能的情况, 其中,,,,或时, 该组数据的众数不唯一, 故所求概率为.18.答案:(1)(2)2解析:(1)由勾股定理得,,.(2)如图, 取格点E, 连接AE, 则.连接BE, 可得,.19.答案: (1),(2)解析:(1)令, 解得或m,抛物线与x轴的交点的坐标为,.(2)易知抛物线开口向下, 又当时, y随 x的增大而增大,,. 易知抛物线与x轴的两个交点之间的距离为,当,时, ,当点M在x轴上方, 时, 点N在 x轴下方, , 解得,.20.答案:(1)(2)见解析解析:(1)(2) 当时, , 不合题意.当,时, ,,,故边长分别为1,3,5 的三条边不能构成三角形.当,时,,.若三条边长分别为3,6,5,则这三条边满足三角形三边关系,故21.答案:(1)喜欢实验D的男生人数有误.正确的人数应为 12 .(2)12,40%(3)不可行,理由见解析解析:(1), 而,6 不是整数, 故喜欢实验 D的男生人数有误.全班总人数为,故喜欢实验D 的男生人数为.(2),.(3)不可行.理由:答案不唯一. 如: 由统计表可知, , 即喜欢各个实验的人数占全班总人数的百分比之和大于1;, 即喜欢实验 A的人数和喜欢实验 D的人数之和大于全班总人数.22.答案:见解析解析:发现 28,36,,32不是两个连续偶数的平方差,28,36 是“奇巧数”.探究正奇数的 4 倍为.总能表示为两个连续偶数的平方差,正奇数的 4 倍一定是“奇巧数”.23.答案: (1)(2)直线与双曲线只有一个交点(3)54解析:(1)对于, 当时, ,,,将代人, 得,解得,故直线l的解析式为.(2)如图, 过点B作轴于点D,由, 易得,,又,,, 故点B的坐标为.将代人, 得,.由题意可设直线的解析式为,将代人, 得,解得,.令, 整理, 得.直线与双曲线只有一个交点.(3)点是点A关于x轴的对称点,,,,,C,B三点共线故.24.(1)答案:树DE的高度为6米解析:如图,设,,,,,又,,,由可得,解得:,树DE的高度为6米;(2)答案:食堂MN的高度为米解析:延长NM交DB延长线于点P,则,由(1)知,,,,且,,,食堂MN的高度为米.25.答案:(1)格点E,F,M在抛物线G上(2) ①②-1或3解析:(1)易知,抛物线G的解析式为, 即.当时,;当时,.格点E,F,M在抛物线G上.(2)①抛物线G经过点,,,设直线与抛物线 G的一个交点为, 则另一交点为.则,,两式相减, 得,抛物线G的解析式为.②方法一: 易知抛物线G开口向下, 对称轴为直线若, 即, 则当时, y取最大值, 即, 解得,(舍去).若, 即, 则当时, y取最大值,与题意矛盾, 舍去.若, 则当时, y 取最大值, 即, 解得 (舍去),.综上可知, t的值为 -1 或 3 .方法二: 令, 解得,.易知抛物线G开口向下, 对称轴为直线.当时, y随x的增大而增大,故当, 即时,.当时, y随x的增大而减小,故当时,.综上可知, t的值为 -1或 326.答案:(1)见解析(2)(3)CP的长为或解析:(1)证明: AD是等边三角形ABC的高,由题意可知,,是等边三角形,,,.(2) ①.证明 : 如图, 连接DE.AD是等边三角形ABC的高,点D是BC的中点.又点E 是AC的中点,.又,是等边三角形,,.是等边三角形,,,,即,,.(2)当点P 在 AC边上运动时, 连接DE, 类似①可得,,点Q在过点E且与BC平行的直线上.根据垂线段最短可知, 当时, AQ最短, 此时故AQ 长的最小值为.(3)取AC的中点E, 由 (2)②可知点Q在过点E且与BC平行的直线上, 记该直线为l, 作直线l, 交AD于点G.易得,,.的面积为 9 ,或.由 (2)①知,或.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2023年河北省中考数学试卷真题(含答案)
原版高清
本文档为2023年河北省中考数学试卷真题,包含完整答案和高清原版试卷图片。
试卷共分两部分,A、B卷各50分,满分100分。
A卷
一、选择题
1. 某校一年级学生的身高平均数为130cm,二年级学生的身高平均数也是130cm,那么该校整个小学部分所有学生的身高平均数是:( )
A. 120cm
B. 125cm
C. 130cm
D. 135cm
2. 已知下面的图形中,正方形边长为3cm,弧形所在圆的半径为1cm,则弧形的长度为( )
A. πcm
B. 2πcm
C. 3πcm
D. 4πcm
...
二、填空题
1. 已知等差数列$\{a_n\}$的前$n$项和为$S_n$,则$a_{n+1}$为__________
2. 正六棱柱的一条母线长12cm,底面边长6cm,它的体积为__________ cm³
...
B卷
一、选择题
1. 某电影院有三种不同票价,其中一等座票价为$18$元,二等座为$12$元,三等座为$6$元;已知某一场电影的一等座票卖了200张,二等座票卖了280张,三等座票卖了360张,则这场电影的总票房收入为( )
A. $8640$元
B. $$元
C. $$元
D. $$元
2. 若$\log_3{k}-\log_{27}{k}=\log_{24}{2}$,则
$k=$ __________
...
二、填空题
1. 已知函数$f(x)=\log_2{\frac{1}{x}}$,则$f(0.5^2 \times 2^{-\frac{1}{3}})=$ __________
2. 如图,$\triangle ABC$中,$BC=4$,$\angle ABC=60°$,$\angle BAC=45°$,则$AC=$ __________
...
以上为2023年河北省中考数学试卷真题。
望广大考生认真复习,顺利参加考试。
