补充例题
补充例题-企业合并

企业合并【例2.1】A公司取得B公司100% 的股权比例,形成同一控制下的控股合并。
合并日B公司的资产、负债以及所有者权益情况如下表所示:【例】A、B公司分别为P公司控制下的两家子公司。
A公司于20×6年3月10日自母公司P处取得B公司l00%的股权,合并后B公司仍维持其独立法人资格继续经营。
为进行该项企业合并,A公司发行了1 500万股本公司普通股〔每股面值l元〕作为对价。
假定A、B公司采用的会计政策相同。
合并日,A公司及B公司的所有者权益构成如下:表1 单位:万元A公司在合并日应进行的会计处理为:【拓展】①在合并工作底稿中,应编制以下调整分录:借:资本公积30 000 000贷:盈余公积l0 000 000未分配利润20 000 000②在编制合并日合并资产负债表时编制的抵销分录:借:股本 1 500资本公积500盈余公积 1 000未分配利润 2 000贷:长期股权投资 5 000【例2.3】20X7年6月30日,P公司向S公司的股东定向增发1 000万股普通股〔每股面值为1元,市价为10.85元〕对S公司进行吸收合并,并于当日取得S公司净资产。
当日,P公司、S公司资产、负债情况如表2-1所示。
表2-1 资产负债表〔简表〕【例2.4】A公司取得B公司100% 的股权比例,形成非同一控制下的控股合并。
购买日B【例2.5】20X7年1月1日,P公司收购了S公司的全部资产,并承担S公司的全部负债。
假定P公司和S公司的合并属于非同一控制下的企业合并。
S公司20X7年1月1日的资产和负债的账面价值和公允价值见下表。
S公司的资产和负债的账面价值和公允价值〔1〕假定P公司以支付现金800 000元、发行普通股100 000股的方式换取S公司的净资产,P公司普通股每股账面价值为10元,每股市价为20元。
P公司以现金支付发行股票发生的手续费、佣金100 000元,合并过程中发生审计费用100 000元,法律服务费50 000元。
电学—补充例题
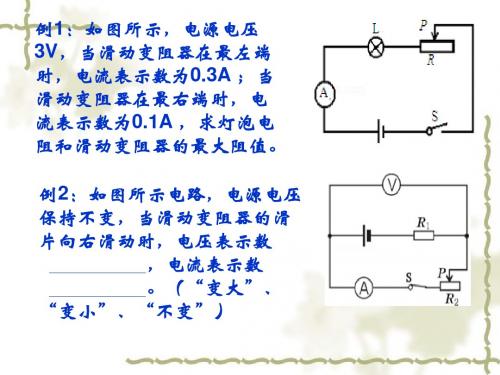
例3:如图所示电路,电源电压 保持不变,当滑动变阻器的滑 片向右滑动时,电压表V1示数 ,电压表V2示数 ,电流表示数 。(“变大”、 “变小”、“不变”) 例4:如图所示电路,电源电压 保持不变,当滑动变阻器的滑 片向左滑动时,电压表示数 ,电流表示数 。(“变大”、 “变小”、“不变”)
例5:如下图是甲、乙两个电阻的电流 I与电压U的关系图象,将它们并连接 入电路,下列说法正确的是( ) A.通过甲的电流大于通过乙的电流 B.通过甲的电流小于通过乙的电流 C.甲、乙并联的总电阻随它们两端 电压的升高而减小 D.甲、乙并联的总电阻随它们两端 电压的升高而增大 例6:常温下,两条长度相等.横截面积不同的同 种材料制成的电阻丝,粗电阻丝的电阻 细电 阻丝的电阻;把它们并联在电路中,通过粗电阻 丝的电流 通过细电阻丝的电流.(选填“大 于”、“等于”或“小于”)
例9:在图3 所示的电路中,电源电压为 12V,滑动变阻器R1的滑片在滑动变阻器 中间。闭合开关后,电流表的示数为 0.4A,电压表的示数为8V,则电阻R2的 阻值是。将滑动变阻器R1的滑 片向左移动,电压表的示数将变, 电压表的示数为。 例10:如图是利用滑动变阻器控制电流的 电路,其中电阻R为100欧姆,它与滑动变 阻器串联在电路中,通过电阻R的电流可 在10毫安~100毫安范围内调节。 (1)、选用电源的电压应为多大? (2)、变阻器的总电阻为多大?额定电流 至少要多大? (3)、上述电路能否使电阻R两端的电压 调为零?请说明理由。
例1:如图所示,电源电压 3V,当滑动变阻器在最左端 时,电流表示数为0.3A ;当 滑动变阻器在最右端时,电 流表示数为0.1A ,求灯泡电 阻和滑动变阻器的最大阻值。
例2:如图所示电路,电源电压 保持不变,当滑动变阻器的滑 片向右滑动时,电压表示数 ,电流表示数 。(“变大”、 “变小”、“不变”)
将竖式补充完整例题

选择题在竖式计算中,如果个位上的数相加满十,应该如何处理?A. 向十位进一B. 向百位进一C. 个位直接写结果,不考虑进位D. 放弃计算,重新列竖式A(正确答案)下列哪个竖式中的计算是错误的?A. 4523————68B. 7819————87(正确答案)C. 6721————88D. 5432————86在竖式减法中,如果被减数的个位小于减数的个位,应该如何处理?A. 从十位退一,个位加十再减B. 直接用个位减,不管结果是否为负C. 放弃计算,重新列竖式D. 个位直接写0,十位照减A(正确答案)下列哪个竖式中的计算是正确的?A. 9247————55(正确答案)B. 8329————64C. 7634————32D. 6128————43在进行竖式乘法时,乘数的哪一位与被乘数相乘,积的末位就应该与哪一位对齐?A. 乘数的个位B. 乘数的十位C. 乘数的当前位(正确答案)D. 乘数的最高位下列哪个竖式中的乘法计算是错误的?A. 12x 3————36B. 24x 2————48C. 43x 5————205(正确答案)D. 11x 9————99在进行竖式除法时,如果除到被除数的某一位不够除,应该如何处理?A. 在这一位上写0,然后继续除下一位B. 放弃计算,说明不能整除C. 在这一位上商1,然后余数与被除数的下一位合成新的被除数继续除D. 在这一位上直接写余数,然后继续除下一位A(正确答案)下列哪个竖式中的除法计算是正确的?A. 48 ÷ 6 = 8(正确答案)B. 55 ÷ 7 = 8C. 32 ÷ 4 = 7D. 72 ÷ 9 = 7在竖式计算中,如果需要借位,通常是从哪一位借?A. 从个位向十位借B. 从十位向百位借C. 从高位向低位借(正确答案,通常是从十位向个位借)D. 从低位向高位借。
《统计学》-第五章-时间数列(补充例题)

第五章动态数列例1、“九五”时期我国国内生产总值资料如下:单位:亿元解:【分析】这是时期数列资料,可按简单算术平均数(n a)计算平均发展水平。
计算结果如下:国内生产总值平均发展水平78432.7亿元33711 83AF 莯+)31116 798C 禌22548 5814 堔23888 5D50 嵐35943 8C67 豧其中:第一产业平均发展水平14258.3亿元;第二产业平均发展水平39100.1亿元;第三产业平均发展水平25074.2亿元。
例2、我国人口自然增长情况见下表:试计算我国在“七五”时期年平均增加人口数量。
解:【分析】新增长人口是时期指标,故平均增加人口数量仍用na a ∑=计算。
年平均增加4.1696516291678172617931656=++++==∑na a (万人)例3、某商店2010年商品库存资料如下:30139 75BB 疻\22102 5656 噖36028 8CBC 貼j20316 4F5C 作$试计算第一季度、第二季度、上半年、下半年和全年的平均库存额。
解:这是一个等间隔时点数列,用“首末折半法”计算:试计算2002年该企业平均工人数。
解:【分析】这是不等间隔时点数列,用间隔月数进行加权的公式计算平均工人数:12111232121)(21)(21)(21---+++++++++=n n n n f f f f a a f a a f a a a 133221124124123241241432414408224083352233533012330326+++++⨯++⨯++⨯++⨯++⨯++⨯+==385(人) 例5、某企业2002年各季度计划利润和利润计划完成程度的资料如下:试计算该企业年度利润计划平均完成百分比。
解:【分析】应该按两个时期数列对比组成的相对指标动态数列计算序时平均数的算式计算: 该企业利润年平均计划完成百分比(%)%132898875887860%125898%138875%135887%130860=+++⨯+⨯+⨯+⨯=例6、1995-2000年各年底某企业职工工人数和工程技术人员数资料如下:解:【分析】这是由两个时点数列对比所组成的相对指标动态数列计算序时平均数的问题。
补充例题
第五节特殊交易在合并财务报表中的会计处理【补充例题】【2016·综合题】甲公司为境内上市公司,专门从事能源生产业务。
2×15年,甲公司发生的企业合并及相关交易或事项如下:(1)2×15年2月20日,甲公司召开董事会,审议通过了以换股方式购买专门从事新能源开发业务的乙公司80%股权的议案。
2×15年3月10日,甲公司、乙公司及其控股股东丙公司各自内部决策机构批准了该项交易方案。
2×15年6月18日,证券监管机构核准了甲公司以换股方式购买乙公司80%股权的方案。
2×15年6月30日,甲公司以3:1的比例向丙公司发行6 000万股普通股,取得乙公司80%股权,有关股份登记和股东变更手续当日完成;同日,甲公司、乙公司的董事会进行了改选,丙公司开始控制甲公司,甲公司开始控制乙公司。
甲公司、乙公司普通股每股面值均为1元,2×15年6月30日,甲公司普通股的公允价值为每股3元,乙公司普通股的公允价值为每股9元。
2×15年7月16日,甲公司支付为实施上述换股合并而发生的会计师、律师、评估师等费用350万元,支付财务顾问费1 200万元。
【手写板】(2)甲公司、乙公司资产、负债等情况如下:2×15年6月30日,甲公司账面资产总额17 200万元,其中固定资产账面价值4 500万元,无形资产账面价值1 500万元;账面负债总额9 000万元;账面所有者权益(股东权益)合计8 200万元,其中:股本5 000万元(每股面值1元),资本公积1200万元,盈余公积600万元,未分配利润1 400万元。
2×15年6月30日,甲公司除一项无形资产外,其他资产、负债的公允价值与其账面价值相同,该无形资产为一项商标权,账面价值1 000万元,公允价值3 000万元,按直线法摊销,预计尚可使用5年,预计净残值为零。
2×15年6月30日,乙公司账面资产总额34 400万元,其中固定资产账面价值8 000万元,无形资产账面价值3 500万元;账面负债总额13 400万元;账面所有者权益(股东权益)合计21 000万元,其中,股本2 500万元(每股面值1元),资本公积500万元,盈余公积1 800万元,未分配利润16 200万元。
补充例题_运算符重载

}
赋值前:b = (3+2i)
6.3 典型运算符的重载
13
例6-14:为Student类重载基于深 层复制的赋值运算符 =
//Student.h #include<iostream> #include<sstream> using namespace std; class Student{ char *name; //姓名 char the_class[12]; //班号 public: Student():name(NULL){ the_class[0]=„\0‟; } Student(char *name, char the_class[]); ~Student(){ delete []name; } const char *getName()const{ return name; } const char *getClass()const{ return the_class; } void toUpper(){ strupr(name); } string toString()const; Student& operator =(const Student &st); };
6.3 典型运算符的重载
20
例6-16(续)
DoubleArray::DoubleArray(int max) { min_index = 0; max_index = max; data=new double[max_index+1]; } double & DoubleArray::operator [](int index) { if(index<min_index || index>max_index) { cout<<“Index out of range”; exit(1); } return data[index-min_index]; }
统计学统计综合指标补充例题

第四章统计综合指标(五)计算题例1、某集团公司所属各拖拉机厂某月生产情况如下表所示:厂别类型每台马力数产量(台)第1厂履带式36 75履带式18 105轮式28 400 第2厂履带式75 85轮式15 94轮式12 150 第3厂履带式45 40履带式75 25轮式24 50 要求按产品类型和功率核算有关总量指标。
解:【分析】通常总量指标中首选核算实物量。
这里可以核算自然实物量、双重单位实物量和标志单位实物量。
从下面两表看出核算的过程及结果:(1)按自然单位和双重单位核算:产品类型产量(台)产量(台/马力)履带式330 330/14640轮式694 694/15610合计1024 1024/30250 (2)按标准单位核算(以15马力拖拉机为标准单位):产品类型与功率产量(台)换算系数标准台数(1)(2)(3)=(1)÷15 (4)=(2)×(3)履带式18马力105 12636马力75 18045马力40 12075马力110 550小计330 —976轮式12马力150 12015马力94 9424马力50 8028马力400 747小计694 —1041合计1024 —2017例2、下面是某市年末户籍人口和土地面积的资料:单位:人户籍人口数2001年 2002年 人口总数男 女1343599 682524 6610751371588 695762 675826已知该土地面积1565平方公里,试计算全部可能计算的相对指标,并指出它们属于哪一种相对数。
解:计算结果列表如下:2001年 2002年 人口总数男 女(1)男性人口占总人口比重(%) (2)女性人口占总人口比重(%) (3)性别比例(%)男:女 (4)人口密度(人/平方公里)(5)人口增长速度(%) 1343599 682524 661075103 858 —1371588 695762 675826102 876在所计算的相对指标中:(1)、(2)为结构相对数,(3)为比例相对数,(4)为强度相对数,(5)为动态相对数。
8.6 补充例题
2 补充2的 拟合检验计算表
Ai
A1 : x 129.5 A2 : 129.5 x 134.5
fi
1 4 10 33 24 9 3
ˆi p
0.0087 0.0519 0.1752 0.3120 0.2811 0.1336 0.0375
ˆi np
ˆi fi 2 / np
4.91
6.79 41.55 24.40 10.02 =87.67
A3 : 134.5 x 139.5
A4 : 139.5 x 144.5
A5 : 144.5 x 149.5 A6 : 149.5 x 154.5 A7 : 154.5 x
0.73 5.09 4.36 14.72 26.21 23.61 11.22 14.37 3.15
所以拒绝 H0, 认为这颗பைடு நூலகம்子的六个面不是匀称的.
补充2 下面列出了84个依特拉斯坎人男子的头 颅的最大宽度(mm), 试验证这些数据是否来自 ( 0.1) 正态总体? 141 148 132 138 154 142 150 146 155 158 150 140 147 148 144 150 149 145 149 158 143 141 144 144 126 140 144 142 141 140 145 135 147 146 141 136 140 146 142 137 148 154 137 139 143 140 131 143 141 149 148 135 148 152 143 144 141 143 147 146 150 132 142 142 143 153 149 146 149 138 142 149 142 137 134 144 146 147 140 142 140 137 152 145
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ii =
(5)ab两点间的电势差 ) 两点间的电势差
ε总
R
(方向如图)
(6)bc两点间的电势差 ) 两点间的电势差
1 Vab = Va −Vb = −Ii ⋅ R(b点点位高) 4
1 Vbc = εbc − Ii ⋅ R(b点电位高) 4
3.如图所示,一半径为r的非常小的圆环,在初始时 刻与一半径为r´( r´>>r)的很大的圆环共面而且 同心,今在大环中通以恒定电流I´,而小环则以 匀角速度ω绕着一条直径转动。设小环的电阻为R。 试求(1)小环中产生的感生电流;(2)使小环 作匀角速度转动须作用在其上的力矩;(3)大环 中的感生电动势。
φ大小 = Bs cosθ =
大环对小环的互感为
µ0 I ′
2r′
πr 2 cosωt
M=
φ大小
I′
=
µ0πr 2
2r′
cosωt
小环上的电流I所产生的磁场对大环的互感磁通为 小环上的电流 所产生的磁场对大环的互感磁通为
φ小大 = MI
所以小环在大环上所产生的互感电动势为
dφ小大 d dI dM = − (MI ) = −M − I ε小大 = − dt dt dt dt
解:
(1) 由于 ) 由于d>>a ,通过两导线间的单位长度上的磁通量为
r r d −a µ0 I µ0 I µ0 I d − a µ0 I d φ = ∫ B ⋅ ds = ∫ + dr = π ln a ≈ π ln a a 2πr 2π (d − r)
单位长度上的自感系数为
= 5.55×10−5 J > 0
(3)单位长度上磁能的改变为 )
1 2 1 2 µ0 I 2 d′ ∆w = L′I − LI = ln = 5.55×10−5 J > 0 2 2 2π d
磁场力作正功和磁能的增加,这两部分的能量都来自电源。 磁场力作正功和磁能的增加,这两部分的能量都来自电源。 导线在分开的过程中,自感系数增加,因此回路中出现负的自感电动势, 导线在分开的过程中,自感系数增加,因此回路中出现负的自感电动势,而 电源必须克服自感电动势作功, 电源必须克服自感电动势作功,这样就把电能转变为磁场能和移动导线时所消耗 的能量。 的能量。
补充例题
1.如图所示,载流长直导线与矩形回路ABCD共面,且导线平行于 AB。求下列情况下ABCD中的感应电动势: r (1)长直导线中电流恒定,ABCD以垂直于导线的恒定速度 v 从图示初始位置远离导线平移到任意位置时。
(2)长直导线中的电流为
I = I 0 sin ωt
,ABCD不动。
(3)长直导线中的电流为 I = I 0 sin ωt ,ABCD以垂直于导线 r 的速度 v 从图示初始位置远离导线平移到任意位置时。
解: (1)电流恒定,线框运动
r r x+b µ0 I µ0 Il x + b φ = ∫ B ⋅ ds = ∫ ⋅ ldr = ln x 2πr 2π x
a A b D l
B v
C
x A x+b
B v
D
µ0 Il x dφ b dx µ0 Il bv εi = − = − ⋅ ⋅ (− 2 ) ⋅ = ⋅ dt 2π x + b x dt 2π x(x + b)
=−
2 µ0π 2r 4ω2 I ′
4r′ R
2
cos 2ωt
4.两根足够长的平行中心距离d为20cm,在导线中 维持一强度为20A而方向相反的恒定电流。(1) 若导线半径为10mm,求两导线间每单位长度的 自感系数;(2)若将导线分开到距离d´=40cm, 磁场对导线单位长度所作的功;(3)位移时,单 位长度的磁能改变了多少?是增加还是减少?说 明能量的来源。(忽略导线内部磁通量)
l
C
其中x = a + vt
(2)
I = I0 sin ωt, 线框不动
µ0l ln
a +b a +b µ0 I0lω ln cosωt dI a ⋅ =− a 2π dt 2π
dφ εi = − = − dt
(3)
I = I0 sin ωt, 线框运动
x +b µ0 Il d x + b µ0l ln x dI dφ ⋅ ln − ⋅ εi = − = − dt 2π dt x 2π dt
解: 已知 (1)
dB = −0.1T / s dt
Ea = 0 l dB Eb = = 10−2 V/m 2 dt l 2 dB Ec = = 0.71×10−2 V/m 2 2l dt Ed = Eb
方向如图
εab = ∫ (2) a bc段的电动势由法拉第电磁感应定律求得: 段的电动势由法拉第电磁感应定律求得: 段的电动势由法拉第电磁感应定律求得 构建回路abca, 因为εab=0, εca=0
解: 小环上产生的电流
由于小环很小, 由于小环很小,可以认为其处在匀强 磁场中。 磁场中。 其上感应电动势为 dφ d µ I′ ε = − = − (Bs cosωt) = 0 πr 2ω sin ωt dt dt 2r′ 感应电流为
I=
ε
R
=
µ0πr 2ωI ′
2r′R
sin ωt
使小环作匀速转动的外力矩
小环受到的力矩为: 小环受到的力矩为:外力矩和电磁力矩
M外 + M磁 = 0
r r ω µ0πr 2ωI ′ Q M磁 = pm × B = IsB sin θ = ( sin ωt)2 4R r′ ω µ0πr 2ωI ′ ∴ M外 = ( sin ωt)2 4R r′
大环上的电流产生的磁场穿过小环的磁通为
b
r r r r Ei ⋅ dl = 0(QEi与dl 垂直)
ε bc = εi回路abc
方向c 同理求得
ε总
dφ dB dB 1 2 = = ⋅ S扇形abe = ⋅ πl dt dt dt 8
b
(3)
dB dB 1 2 = ⋅ S扇形abd = ⋅ πl dt dt 4
方向a d
c b
a
(4) 回路中的电流
L=
φ
I
=
µ0 d ln = 1.2×10−6 H π a
分开至d (2)将导线间的距离由 分开至 ´时,磁场对单位长度导线所作的功 )将导线间的距离由d分开至
2 r r d′ d′ µ I µ0 I 2 d′ ln w = ∫ F ⋅ dr = ∫ IBldr = ∫ 0 dr = d d 2π 2π d
µ0 I0l bv sin ωt x + b = x(x + b) −ω cosωt ln x 2π
2.边长为l=20cm的正方形导体回路,置于半径为l的 圆柱形空间的均匀磁场中,B为0.5T,方向垂直于 导体回路,且以0.1T/s的变化率减小,图中a点为 圆心,ab、ad沿直径,求(1)a、b、c、d各点感 应电场的方向和大小(用矢量在图上标明方向); (2)ab、bc段的电动势;(3)回路内的感应电动势 有多大?(4)如果回路的电阻为R=2Ω,回路中的 电流有多大?(5)a和b两点间的电势差为多少? 哪一点的电势高一些?(6)b和c两点间的电势差 为多少?哪一点的电势高?
