递延年金终值和现值
延期(递延)年金的计算
例:ABC公司面临两个投资机会可供选择,A 项目是一个高科技项目,该领域市场竞争激烈, 如果经济发展迅速并且项目研制开发搞得好, 则能够取得较大的市场份额,获得较高的利润; 反之,将会获得较少的利润甚至亏损。B项目 是一个成熟的产品,市场发展稳定,销售前景 可以根据市场调研资料进行可靠的预测。经预 测发现未来的市场行情可能有三种情况:繁荣、 一般、衰退,每种情况发生的可能概率以及各 种情况下的预期报酬率资料见表:
i
例
例:某企业要建立一项永久性的奖励基金,计 划每年发放500000元,在年利率为8%的情况 下,该企业现在应该存入银行多少元? P=A÷i=500000÷8%=6 250 000(元) 例:某企业在第一年年初向银行借入100万元, 银行规定从第一年到第五年每年年末应等额偿 还25.6万元,试计算利率? i=A/P=25.6÷100=25.6%
(二)递延期m的确定: (1)首先搞清楚该递延年金的第一次收付发生在第几期末(假设为第W 期末); (2)然后根据(W-1)的数值即可确定递延期m的数值; 注意:在确定“该递延年金的第一次收付发生在第几期末”时,应该记住 “本期的期初和上期的期末”是同一个时间点。 〔例1〕 某递延年金从第4年开始,每年年末支付A元。 〔解答〕由于第一次发生在第4期末,所以,递延期m=4-1=3 〔例2〕 某递延年金从第4年开始,每年年初支付A元。 〔解答〕由于第一次发生在第4期初(即第3期末),所以,递延期m=31=2 (三)下面把上述的内容综合在一起,计算一下各自的现值: 〔例1〕 某递延年金从第4年起,每年年末支付A元,直至第8年年末为止。 〔解答〕由于n=5,m=3,所以,该递延年金的现值为: A[(PVAi,8)-(PVAi,3)]或A(PVAi,5)×(PVi,3) 〔例2〕 某递延年金从第4年起,每年年初支付A元,直至第8年年初为止。 〔解答〕由于n=5,m=2,所以,该递延年金的现值为: A[(PVAi,7)-(PVAi,2)]或 A(PVAi,5)×(PVi,2)
各类年金终值、现值计算公式对比表

FVAn
= A
* FVIFAi,n
年金现值系数之差法:
文 字
V0 = A × ( PVIFAi,n+m - PVIFAi,m )
永久年金
永久年金没有终值
永久年金现值 = 年金 / 折现率 = A / i
复利终值系数与复利现值系数之间互为倒数
FVn
= PV * FVIFi,n
FVIF
i,n=复利终值系数
年金终值 = 年金 * 年金终值系数利率,期数 FVIFAi,n=年金的复利终值系数
年金现值 = 年金 * 年金现值系数 PVIFAi,n=年金的复利现值系数 PVAn = A * PVIFAi,n
后付年金
(普通年金)
FVAn
= A
* FVIFAi,n
文 字
年金终值 = 年金 * (年金终值系数利率,期数+1 -1) 年金终值 = 年金 * 年金终值系数利率,期数 *(1+利率) 方法一:期数加一,系数减一
年金现值 = 年金 * (年金现值系数利率,期数+1-1) 年金现值 = 年金 * 年金现值系数利率,期数 *(1+利率) 方法一: 期数加一,系数减一 方法二: 普通年金公式*(1+利率)
先付年金
方法一: 字 母
方法二:普通年金公式*(1+利率) Vn = A *(FVIFAi,n+1-1)
方法一:
V0 = A *(PVIFAi,n+1-1)
方法二:
方法二:
Vn = A * FVIFAi,n *(1+i)
V0 =
两次折现法:ห้องสมุดไป่ตู้
A * PVIFAi,n *(1+i)
财务管理基础知识

1. 不等额现金流量的终值 为求得不等额系列收付款终值之和,可先计算每次
收付款的复利终值,然后加总。
F= A0(1+i)n+A1(1+i)n-1+……+ An-1(1+I)1 +An (1+i)0
n
=ΣAt (1+i)t
t=0
20
2 不等额现金流量的现值 为求不等额系列收付款现值之和,可先计算每次收付
13
0
1
2
3 ...
n-1 n
A
A
A ...
A
A
普通年金的收付示意图
0
1
2
3
…
A
A
A
A
...
n-1 n A
预付年金的收付示意图
预付年金与普通年金相比,收付款次数是一样的,只是收付款的时
点不一样,预付年金的终值比普通年金的终值多计一年的利息,而预
付年金的现值比普通年金的现值少折现一年,因此,在普通年金终值
第二章 财务管理基础知识
第一节 资金时间价值
1
第一节 资金时间价值
一、资金时间价值的概述 1、资金时间价值的含义
是指一定量资金在不同时点上具有不同的价值而 产生的差额。
2
2、现值与终值
(1)现值的含义 现值又称本金,未
来某一时点上的一定 量资金折算到现在的 价值,用P表示。
(2)终值的含义
终值又称未来值, 现在一定量的资金在 未来某一时用点上的 价值,俗称本利和, 用 F表示。
4
4、复利现值和终值的计算
(1)复利终值 F=P×(1+i)n =P(F/P,i,n)
(2) 复利现值 P=F÷(1+i)n=F×(1+i)-n =F(P/F,i,n)
年金终值和现值得计算

1.4 资本回收额
[例题]:某企业想投资100万元购买设备, 预计可使用3年,社会平均利润率8%。 则该设备每年至少带来多少收益是可行 的?
A= P/ (P/A, 8%, 3)=100/2.577=38.88万元
1.4 资本回收额
[例题]:某公司借入2000万元,约定8内, 按i=12%均匀偿还,则每年还本付息多 少?
年金的终值及现值的计算
年金
定义:年金是指一定时期内每期相等金 额的收付款项。
按付款时间分类: 普通年金(或称后付年金) 先付年金(或称即付年金、预付年金) 延期年金(或称递延年金) 永续年金
1. 普通年金(0rdinary Annuity)
普通年金,即后付年金,是指在一定时期 内,每期期末有等额收付款项的年金。
定义:普通年金现值是指一定时期内每期期末等 额的系列收付款项的现值之和. 令P——年金现 值
公式:P=A﹡ [(1+i)n-1]/i(1+i) n=A ﹡ [1-(1+i)-n ]/i [1−(1+i)-n]/ i被称做年金现值系数或年金贴现系数 记作(P/A, i, n)
普通年金现值,通常借助于“年金现值系数表”计算。 P=A ﹡(P/A,i, n)
1.1 普通年金终值
定义:普通年金终值是一定时期内每期 期末等额收付款项的复利终值之和。
令:A——年金数额 i ——利息率 n ——计息期数 F——年金终值
1.1 普通年金终值
计算公式: F=A﹡ [(1+i)n −1]/i 其中[(1+i)n −1]/i被称作年金终值系数, 记作(F/A, i, n) 普通年金终值,通常借助于“年金终值系 数表”计算。 F=A ﹡(F/A, i, n)
递延年金终值与现值的计算

m+n
06
P=50 000×(P/A,10%,10)×(P/F,10%,5) =50 000×6.1446×0.6209 =190 759.11(元)
按第二种方法计算:
P=50 000×(P/A,10%,15)-50 000×(P/A,10%,5) =50 000×7.6061-50 000×3.7908 =190 765(元)
03
m+2 …
04
Hale Waihona Puke m+n05
先求递延年金终值,再折现为现值,即:
【例2-14】农庄的累计投资限额为多少?
接例2-13,假设江南公司决定投资开发该农庄,根据其收益情况,该农庄的累计投资限额为多少? 递延期m为5年,发生递延年金收付期数n为10年。
0
按第一种方法计算:
1
01
…
02
m
03
m+1
04
m+2 …
2.
把递延期每期期末都当作有等额的年金收付A,把递延期和以后各期看成是一个普通年金,计算出这个普通年金的现值,再把递延期虚增的年金现值减掉即可。 即:
假设递延期内每期都有A收付
2 …
单击此处添加正文。
m+1
单击此处添加正文。
m+n
单击此处添加正文。
m
m+2 …
单击此处添加正文。
3.
…
01
m
02
m+1
m+1
单击此处添加正文。
2 …
递延期
m
递延年金发生的期数
01
02
03
04
m+n
单击此处添加正文。
年金的公式总结

关于年金的总结1.单利现值P=F/(1+n*i) , 单利现值系数1/(1+n*i)。
2.单利终值F=P*(1+n*i) , 单利终值系数(1+n*i)。
3.复利现值P=F/ (1+i )n =F*(P/F ,i ,n) ,复利现值系数1/(1+i )n ,记作(P/F ,i ,n)。
4.复利终值F=P*(1+i )n =P*(F/P ,i ,n ),复利终值系数(1+i )n , 记作(F/P ,i ,n )。
结论(一)复利终值与复利现值互为逆运算。
(二)复利终值系数 1/(1+i )n 与复利现值系数 (1+i )n 互为倒数。
即 复利终值系数(F/P ,i ,n )与 复利现值系数(P/F ,i ,n)互为倒数。
可查“复利终值系数表”与“复利现值系数表”!5.普通年金终值F=A*(1)1n i i +-=A*(F/A ,i ,n) ,年金终值系数(1)1n i i+-,记作(F/A ,i ,n)。
可查“年金终值系数表”(1)在普通年金终值公式中解出A ,这个A 就是“偿债基金”。
偿债基金A=F*(1)1n i i +-=F*( A/F ,i ,n),偿债基金系数(1)1n i i +-,记作( A/F ,i ,n)。
结论(一)偿债基金 与 普通年金终值 互为逆运算。
(二)偿债基金系数(1)1n i i +-与 普通年金系数(1)1n i i +- 互为倒数。
即 偿债基金系数( A/F ,i ,n) 与 普通年金系数(F/A ,i ,n)互为倒数。
6.普通年金现值P=A*1(1)n i i --+=A*(P/A ,i ,n) , 年金现值系数1(1)n i i--+,记作(P/A ,i ,n )。
可查“年金现值系数表”(1).在普通年金现值公式中解出A ,这个A 就是“年资本回收额”。
年资本回收额A=P* 1(1)n i i --+=P*(A/P ,i ,n) , 资本回收系数1(1)ni i --+,记作(A/P ,i ,n)。
有关年金_复利_现值_终值的计算

例如:本金为50000元,利率或者投资回报率为3%,投资年限为30年,那么,30年后所获得的利息收入,按复利计算公式来计算就是:50000×(1+3%)30由于,通胀率和利率密切关联,就像是一个硬币的正反两面,所以,复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。
只需将公式中的利率换成通胀率即可。
这均是时间价值问题,简单来讲,今天的100元不等于5年后的100元,那5年后的100元相当于今天的多少呢?这就需要贴现,即用100乘以期限为5,相应利率的复利现值系数,而如果要知道今天的100元相当于5年后的多少呢?则用100乘以复利终值系数,也就是求本利和。
这里的复利终值系数和复利现值系数都是在复利计算下推出的。
(一次性收付款)年金是每隔相同时间就发生相等金额的收付款,比如房租,如果发生时间在每期期末,则称为普通年金,如果以后5年中每年末可以得到100元,相当于今天能得多少(从时间价值考虑,肯定不是500元)就要用100乘以普通年金现值系数 ,反之,比如每年末存银行100元,在复利下5年能得到多少?则用100乘以年金终值系数复利终值系数、复利现值系数是针对一次性收付款,而年金终值系数和年金现值系数是系列收付款,而且是特殊的系列收付款不知道明白没有,最好能看看财务管理中时间价值章节终值的计算终值是指货币资金未来的价值,即一定量的资金在将来某一时点的价值,表现为本利和。
单利终值的计算公式:f=p(1+r×n)n复利终值的计算公式:f = p(1+r)式中f表示终值;p表示本金;r表示年利率;n表示计息年数其中,(1+r)n称为复利终值系数,记为fvr,n,可通过复利终值系数表查得。
现值的计算现值是指货币资金的现在价值,即将来某一时点的一定资金折合成现在的价值。
单利现值的计算公式:复利现值的计算公式:式中p表示现值;f表示未来某一时点发生金额;r表示年利率;n表示计息年数其中称为复利现值系数,记为pvr,n,可通过复利现值系数表查得。
各类年金终值 现值计算公式对比表
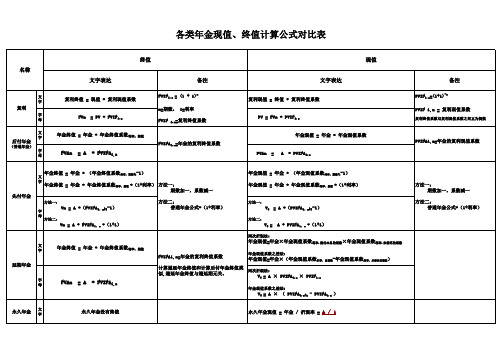
两次折现法:
年金现值=年金×年金现值系数利率,偿付本息的期数×年金现值系数利率,未偿还的期数
FVIFAi,n=年金的复利终值系数
计算递延年金终值和计算后付年金终值类 似,递延年金终值与递延期无关。
年金现值系数之差法:
年金现值=年金×(年金现值系数利率,总期数-年金现值系数利率,未偿还的期数)
方法二: 普通年金公式*(1+利率)
年金现值 = 年金 * (年金现值系数利率,期数+1-1) 年金现值 = 年金 * 年金现值系数利率,期数 *(1+利率)
方法一:
V0 = A *(PVIFAi,n+1-1)
方法二:
V0 = A * PVIFAi,n *(1+i)
文 字
延期年金
字 母
年金终值 = 年金 * 年金终值系数利率,期数
各类年金现值、终值计算公式对比表
名称
文 字
复利
字 母
文 字
后付年金
(普通年金) 字 母
终值
文字表达
复利终值 = 现值 * 复利现值系数 FVn = PV * FVIFi,n
年金终值 = 年金 * 年金终值系数利率,期数
FVAn = A * FVIFAi,n
备注
FVIFi,n = (1 + i)n n=期数, i=利率 FVIF i,n=复利终值系数
PVIFAi,n=年金的复利现值系数
先付年金
文 年金终值 = 年金 * (年金终值系数利率,期数+1-1)
字
年金终值 = 年金 * 年金终值系数利率,期数 *(1+利率) 方法一: 期数加一,系数减一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
财务管理》第二章重难点讲解及例题:递延年金终值和现值
递延年金终值和现值
(1)递延年金终值(已知从第二期或第二期以后等额收付的普通年金A,求FA)递延年金是指第-次等额收付发生在第二期或第二期以后的普通年金。
图示如下:
求递延年金的终值与求普通年金的终值没有差别(要注意期数),递延年金终值与递延期无关。
如上图中,递延年金的终值为:FA=AX(F/A,i,n),其中,“n,,表示的是A的个数,与递延期无关。
(2)递延年金现值(已知从第二期或第二期以后等额收付的普通年金A,求PA)方法-:把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第-次等额收付前-期的数值,再往前推递延期期数就得出递延年金的现值。
图示如下:
PA=AX(P/A,i,n)×(P/F,i,m)
方法二:把递延期每期期末都当作有等额的收付,把递延期和以后各期看成是-个普通年金,计算这个普通年金的现值,再把递延期多算的年金现值减去即可。
图示如下:
PA=AX(P/A,i,m+n)-A×(P/A,i,m)
【提示】方法-、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题,再求递延年金现值。
方法三:先求递延年金的终值,再将终值换算成现值,图示如下:
PA=A×(F/A,i,n)×(P/F,i,m+n)
【提示】递延年金现值计算公式中的“n”指的是等额收付的次数,即A的个数;递延期“m”的含义是,把普通年金(第-次等额收付发生在第1期期末)递延m期之后,就变成了递延年金(第-次等额收付发生在第W期期末,W>1)。
因此,可以按照下面的简便方法确定递延期m的数值:
(1)确定该递延年金的第-次收付发生在第几期末(假设为第W期末)(此时应该注意“下-期的期初相当于上-期的期末”);
(2)根据(W-1)的数值确定递延期m的数值。
【例题7.单选题】下列关于递延年金的说法中,错误的是()。
A.递延年金是指隔若干期以后才开始发生的系列等额收付款项
B.递延年金没有终值
C.递延年金现值的大小与递延期有关,递延期越长,现值越小
D.递延年金终值与递延期无关
【答案】B
【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项;递延年金存在终值,其终值的计算与普通年金是相同的;终值的大小与递延期无关;但是递延年金的现值与递延期是有关的,递延期越长,递延年金的现值越小,所以选项B的说法是错误的。
【例题8.计算题】张先生准备购买-套新房,开发商提供了三种付款方案让张先生选择:
(1)A方案,从第4年年末开始支付,每年年末支付20万元,-共支付8年;
(2)B方案,按揭买房,每年年初支付15万元,-共支付10年;
(3)C方案,从第4年年初开始支付,每年年末支付19万元,-共支付8年。
假设银行利率为5%,请问张先生应该选择哪种方案。
【答案】
A方案是递延年金的形式,由于第-次支付发生在第4年年末,所以,W=4,递延期m=4—1=3.
A方案付款的现值=20×(P/A,5%,8)×(P/F,5%,3)=20×6.4632×0.8638=111.66(万元)
B方案是预付年金的方式,由于-共支付10次,所以,n=10.
B方案付款的现值=15×[(P/A,5%,10—1)+1]=15×(7.1078+1)=121.62(万元)
C方案是递延年金形式,由于第-次支付发生在第4年年初(相当于第3年年末),所以,W=3,递延期m=3-1=2.
C方案付款的现值=19×(P/A,5%,8)×(P/F,5%,2)=19×6.4632×0.9070=111.38(万元)
由于C方案付款的现值最小,所以张先生应该选择C方案。
4.永续年金终值和现值
(1)永续年金终值
永续年金没有到期日,因此没有终值。
(2)永续年金现值(已知无限期等额收付的普通年金A,求PA)
永续年金的现值是普通年金现值的极限形式(n→∞):PA=A/i
【例题9.判断题】王先生打算在某高校建立-项永久性奖学金,款项-次性存入银行,-年后开始提款,每年提款-次,每次提款2万元用于奖励学生,假设银行存款年利率为4%,那么王先生应该存入银行50万元。
()
【答案】√
【解析】由于是永久性奖学金,并且每次发放的数额相同,所以,这是永续年金现值计算问题。
王先生应该-次性存入银行的款项=2/4%=50(万元)。
递延年金现值计算公式P=A×(P/A,i,n)×(P/F,i,m):
在递延期为m期的递延年金中,从第m+1期开始,属于典型的普通年金,n表示的是该普通年金中A的个数,所以,A×(P/A,i,n)表示的是折现到第(m+1)期期初(即第m期期末)的数值,而我们想求的递延年金现值是指第1期期初的数值,并且第(m+1)期期初距离第1期期初的间隔为m期,所以,应该对A×(P/A,i,n)进行复利折现m期,即P=A×(P/A,i,n)×(P/F,i,m)。
递延年金现值的计算公式P=A×(F/A,i,n)×(P/F,i,n+m):
使用这个公式计算递延年金现值实际上就是先求终值然后折现。
A×(F/A,i,n)计算的是等额收付n次的年金在第(m+n)期期末的终值,由于我们需要计算的是第1期期初的现值,所以需要在此基础上乘以(m+n)期的复利现值系数,即P=A×(F/A,i,n)×(P/F,i,n+m)。
递延年金现值的计算公式P=A×(P/A,i,n)×(P/F,i,m):
把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第一个等额收付前一期的数值,再往前推递延期期数就得出递延年金的现值。
Welcome To Download !!!
欢迎您的下载,资料仅供参考!。
