应力疲劳SN曲线课件
合集下载
应力疲劳s-n曲线
建立方法
疲劳试验
通过在给定的应力水平下进行疲劳试 验，记录材料的疲劳寿命，从而获得 S-N曲线数据。
数据分析
将试验数据进行分析和整理，绘制出 S-N曲线，并确定各个应力水平下的 疲劳寿命。
影响因素
1 2 3
材料性质
不同材料的S-N曲线存在差异，材料的力学性能、 微观结构和成分等因素都会影响其疲劳性能。
比较不同材料的疲劳强度
通过比较不同材料的S-N曲线，可以评估各种材料的疲劳强度，从 而选择适合特定应用场景的材料。
优化材料加工工艺
了解材料的S-N曲线有助于优化材料的加工工艺，提高材料的疲劳 性能。
在寿命预测中的应用
预测疲劳寿命
根据S-N曲线，结合实际工况条 件，可以预测材料的疲劳寿命，
为产品设计提供依据。
如温度、湿度、介质等环境因 素对材料的疲劳性能产生影响 。
材料性质
材料的化学成分、微观组织结 构、热处理状态等对疲劳性能
产生影响。
02 S-N曲线原理
CHAPTER
定义
S-N曲线是指描述材料在循环应力作 用下的疲劳寿命与应力幅值之间的关 系曲线。
该曲线以应力幅值S为横坐标，以对应 的疲劳寿命N为纵坐标，反映了材料 在不同应力水平下的疲劳性能。
01
确定安全系数
结合S-N曲线和安全系数方法，可以确 定产品的安全系数，确保产品在承受疲 劳载荷时仍能保持安全性能。
02
03
疲劳载荷分析
通过S-N曲线可以分析产品的疲劳载荷 分布情况，为优化产品结构提供依据。
04 S-N曲线实验
CHAPTER
实验设备
疲劳试验机
用于施加循环应力并检测材料或结构的疲劳 性能。
应力疲劳S-N曲线.
a m
u 1090MPa 0 1010MPa e 510MPa
Sa ( 1)
Su
第二章 应力疲劳
平均应力的影响(R-1)
船舶与海洋工程学院
Sa Smax Smin / 2 (759 69) 345MPa Sm Smax Smin / 2 (759 69) 414MPa R Smin / Smax 0.091
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船洋工程学院
第二章 应力疲劳
CH6疲劳裂纹扩展 :
船舶与海洋工程学院
2 2
Goodman linear
Sm Su
1
第二章 应力疲劳
平均应力的影响(R-1)
船舶与海洋工程学院
例题
构件受拉压循环应力作用。已知 (1) Smax=800 MPa, Smin=80 MPa。 (2) 材料的极限强度为 Su=1200 MPa。 (3) 基本S-N曲线可用幂函数式 Sm N=C 表达，其中 C=1.5361025；m=7.314。 试估算其疲劳寿命。
指数式
ems N=C S=A+BLgN A=LgC/mLge B=-1/mLge 单对数 S
三参数式
(S-Sf)m N=C
A=LgC/m B=-1/m
双对数 lgS
lgS lgN lgN
lgN
第二章 应力疲劳
张亚军，S-N疲劳曲线的数学表达式处理方法探讨，理化检验-物理分册，2007年43卷11期，563-565
u 1090MPa 0 1010MPa e 510MPa
Sa ( 1)
Su
第二章 应力疲劳
平均应力的影响(R-1)
船舶与海洋工程学院
Sa Smax Smin / 2 (759 69) 345MPa Sm Smax Smin / 2 (759 69) 414MPa R Smin / Smax 0.091
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船舶与海洋工程学院
第二章 应力疲劳
船洋工程学院
第二章 应力疲劳
CH6疲劳裂纹扩展 :
船舶与海洋工程学院
2 2
Goodman linear
Sm Su
1
第二章 应力疲劳
平均应力的影响(R-1)
船舶与海洋工程学院
例题
构件受拉压循环应力作用。已知 (1) Smax=800 MPa, Smin=80 MPa。 (2) 材料的极限强度为 Su=1200 MPa。 (3) 基本S-N曲线可用幂函数式 Sm N=C 表达，其中 C=1.5361025；m=7.314。 试估算其疲劳寿命。
指数式
ems N=C S=A+BLgN A=LgC/mLge B=-1/mLge 单对数 S
三参数式
(S-Sf)m N=C
A=LgC/m B=-1/m
双对数 lgS
lgS lgN lgN
lgN
第二章 应力疲劳
张亚军，S-N疲劳曲线的数学表达式处理方法探讨，理化检验-物理分册，2007年43卷11期，563-565
疲劳曲线计算PPT课件
5. 用图解法求安全系数
2019/11/24
10
例题3.2 一杆件如图所示，受脉动循环拉力F=0N~3×105 N，r=常数，材料为 40Mn钢，调质处理，200HB~230HB，σ B =735MPa, σS =471MPa,圆角精铣加工 （相当于精车），要求应力循环次数不低于5×105 ，求圆角处危险截面的安全 系数Sσ 。
解： 2. 求σ-1 和σ0
3.求寿命系数KN
2019/11/24
8
例题3.2 一杆件如图所示，受脉动循环拉力F=0N~3×105 N，r=常数，材料为 40Mn钢，调质处理，200HB~230HB，σ B =735MPa, σS =471MPa,圆角精铣加工 （相当于精车），要求应力循环次数不低于5×105 ，求圆角处危险截面的安全 系数Sσ 。
过B做斜率等于-1/9的直线，即为所求
2019/11/24
2
知识点：疲劳极限应力图
σa : 应力幅 σ-1：对称循环疲劳极限 σs: 屈服极限
σm: 平均应力 σ0： 脉动循环疲劳极限 σB:强度极限
2019/11/24
3
许用疲劳极限应力图
KN ：寿命系数
（Kσ）D ： 综合影响系数 Kσ ：应力集中系数 βσ：表面状态系数
知识点：疲劳曲线
疲劳曲线：表示循环次数N与疲劳极限间的关系的曲线。
有限寿命区内：
N
2019/11/24
循环次数N0、疲劳极限σr 则N次循环时疲劳极限
1
例题3.1
已知 45钢的σ-1 =300MPa，N0 =107 ，m=9，用对数坐标绘出该材料的疲劳 曲线图。
解： 在对数坐标上取一点B，其坐标为： lgN0 =lg107 lg σ-1 =lg300
2019/11/24
10
例题3.2 一杆件如图所示，受脉动循环拉力F=0N~3×105 N，r=常数，材料为 40Mn钢，调质处理，200HB~230HB，σ B =735MPa, σS =471MPa,圆角精铣加工 （相当于精车），要求应力循环次数不低于5×105 ，求圆角处危险截面的安全 系数Sσ 。
解： 2. 求σ-1 和σ0
3.求寿命系数KN
2019/11/24
8
例题3.2 一杆件如图所示，受脉动循环拉力F=0N~3×105 N，r=常数，材料为 40Mn钢，调质处理，200HB~230HB，σ B =735MPa, σS =471MPa,圆角精铣加工 （相当于精车），要求应力循环次数不低于5×105 ，求圆角处危险截面的安全 系数Sσ 。
过B做斜率等于-1/9的直线，即为所求
2019/11/24
2
知识点：疲劳极限应力图
σa : 应力幅 σ-1：对称循环疲劳极限 σs: 屈服极限
σm: 平均应力 σ0： 脉动循环疲劳极限 σB:强度极限
2019/11/24
3
许用疲劳极限应力图
KN ：寿命系数
（Kσ）D ： 综合影响系数 Kσ ：应力集中系数 βσ：表面状态系数
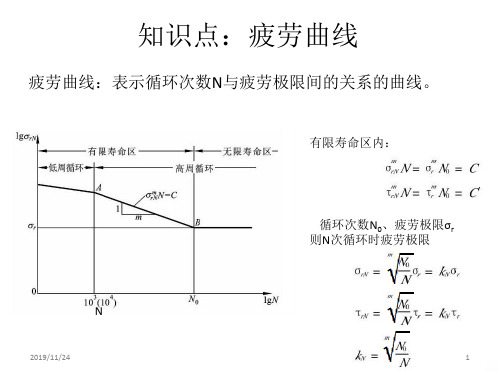
知识点：疲劳曲线
疲劳曲线：表示循环次数N与疲劳极限间的关系的曲线。
有限寿命区内：
N
2019/11/24
循环次数N0、疲劳极限σr 则N次循环时疲劳极限
1
例题3.1
已知 45钢的σ-1 =300MPa，N0 =107 ，m=9，用对数坐标绘出该材料的疲劳 曲线图。
解： 在对数坐标上取一点B，其坐标为： lgN0 =lg107 lg σ-1 =lg300
20 S-N曲线
S-N曲线☐精确估算疲劳寿命保证不发生疲劳失效；☐采用科学的技术和措施延长疲劳寿命。
循环应力有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）特征参数循环应力应力幅：平均应力：应力范围：应力比：Δσ= σmax-σminσa=Δσ/2=(σmax-σmin)/2 σm＝(σmax+σmin)／2R=σmin/σmax典型循环应力根据应力幅和平均应力，典型循环应力情况：交变对称循环交变不对称循环σm =0R ＝-10＜σm ＜σa-1＜R ＜0有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）典型循环应力根据应力幅和平均应力，典型循环应力情况：脉动循环波动循环σm =σa R ＝0 σm >σa 0＜R ＜1S-N 曲线最古老的疲劳试验：旋转弯曲疲劳1☐仿火车轮轴工作环境；☐纯弯曲、完全对称循环；有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）S-N曲线记录在应力幅σa 作用下的循环数Nf，获得系列(σa, Nf)2以循环数为横坐标，应力为纵坐标绘图获得S-N曲线。
3非对称循环应力，除σa 外，要给出σm或R。
典型S-N 曲线高应力下，很少的循环次数后（小于104或105）断裂——短寿命疲劳。
循环应力低于弹性极限，Nf ＞105次循环——长寿命疲劳。
低于某一临界应力幅σac ，经受无数次应力循环而不断裂。
有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）谢谢观赏！Thanks!。
第五讲 p-s-n曲线,疲劳统计学_secret
第五讲 p-S-N曲线，疲劳统计学前节回顾影响疲劳性能的若干因素荷载形式、尺寸效应、表面光洁度的影响、温度和环境的影响应力集中的影响，缺口系数：理论弹性应力集中系数、疲劳缺口系数、缺口敏感系数1．疲劳数据的分散性S-N曲线为中值曲线，一般对同一应力水平实验点有分散性，其分散性与材料、应力水平、环境等相关。
某铝合金构件的疲劳实验应力水平（MPa）件数寿命±207 57 2⨯106～1⨯108±240 29 7⨯105～4⨯106±275 34 1⨯105～8⨯105±310 29 4⨯104～1⨯105±430 25 1.5⨯104～2⨯104应力水平低则寿命长，分散性也大，在同样应力水平下，疲劳寿命可以相差几十到几百倍。
2．P-S-N曲线lgN Sp-S-N曲线是组成不同成活率p下的S-N曲线集，这一曲线集给出了：1）在给定应力水平下失效循环次数N的分布数据；2）在给定的有限寿命下疲劳强度S的分布数据；3）无限寿命或N > N L 的疲劳强度－疲劳极限的分布数据。
p-S-N曲线由成组实验获得。
p-S-N曲线在有限寿命段（103< N <106）在双对数坐表系上近似为直线。
3．疲劳寿命与疲劳强度概率分布之间的关系疲劳破坏是疲劳损伤逐渐累积的结果，材料中宏观或微观的不可逆变形是疲劳损伤的主要形式。
疲劳寿命概率分布：在给定疲劳强度下构件的疲劳寿命概率分布形式。
一般可由疲劳实验获得。
疲劳强度概率分布：在给定疲劳寿命下构件的疲劳强度概率分布形式。
设在一疲劳荷载作用下，构件在给定疲劳强度S*下的疲劳寿命N的概率分布密度为f(n|S*)，而在给定疲劳寿命N*下的疲劳强度S 的概率分布密度为g(s|N*)，则可以证明lgNSp = 0.99 p = 0.5ds N s g dn S n f S N )()(***0*⎰⎰=即在给定的疲劳强度S*下 疲劳寿命N 小于或等于N*的 概率与在给定的疲劳寿命N* 下疲劳强度S 小于或等于S* 的概率相等。
应力疲劳SN曲线PPT课件
C=1.5361025；m=7.314。 试估算其疲劳寿命。
[注意]S-N曲线主要针对R=-1得到的，对于应力比不等于1的应力循环，当我们计算
其疲劳寿命时，需要采用Goodman 公式进行转换
[解答] 步骤1
Sa Sm 1.0 Sa(1) Su
Sa Smax Smin / 2 360MPa Sm Smax Smin / 2 440MPa
R Smin / Smax 0.1
第10页/共33页
平均应力的影响(R-1)
步骤2 Goodman linear
equation
Sa(1)
Sa
1
Sm Su
360
1
1424000
5 6 8.4MP a
Sa Sm 1.0 Sa(1) Su
Sa 360MPa Sm 440MP5 / 568.47.314
第3页/共33页
基本S-N曲线(R=-1)
幂函数
SmN=C LgS=A+BLgN
A=LgC/m
S-N曲线的数学表达式
指数式
S=C Nn
ems N=C
S=A+BLgN A=LgC/mLge
三参数式
(S-Sf)m N=C
B=-1/m 双对数 lgS
B=-1/mLge
单对数
S
lgS
lgN
lgN
lgN
P n
第17页/共33页
Miner线性累计损伤理论
第18页/共33页
Miner线性累计损伤理论
S
0.8S 0.6S 0.4S
2.5104/S S2/2.51040.05
2
2.5104/0.64 S2/2.51040.10.6
[注意]S-N曲线主要针对R=-1得到的，对于应力比不等于1的应力循环，当我们计算
其疲劳寿命时，需要采用Goodman 公式进行转换
[解答] 步骤1
Sa Sm 1.0 Sa(1) Su
Sa Smax Smin / 2 360MPa Sm Smax Smin / 2 440MPa
R Smin / Smax 0.1
第10页/共33页
平均应力的影响(R-1)
步骤2 Goodman linear
equation
Sa(1)
Sa
1
Sm Su
360
1
1424000
5 6 8.4MP a
Sa Sm 1.0 Sa(1) Su
Sa 360MPa Sm 440MP5 / 568.47.314
第3页/共33页
基本S-N曲线(R=-1)
幂函数
SmN=C LgS=A+BLgN
A=LgC/m
S-N曲线的数学表达式
指数式
S=C Nn
ems N=C
S=A+BLgN A=LgC/mLge
三参数式
(S-Sf)m N=C
B=-1/m 双对数 lgS
B=-1/mLge
单对数
S
lgS
lgN
lgN
lgN
P n
第17页/共33页
Miner线性累计损伤理论
第18页/共33页
Miner线性累计损伤理论
S
0.8S 0.6S 0.4S
2.5104/S S2/2.51040.05
2
2.5104/0.64 S2/2.51040.10.6
应力疲劳SN曲线
Sf(R=-1)或S-1
基本S-N曲线(R=-1)
S-N曲线的一般形状及若干特性值
基本S-N曲线(R=-1)
幂函数
SmN=C
LgS=A+BLgN A=LgC/m
S-N曲线的数学表达式
指数式
S=C Nn
ems N=C
S=A+BLgN A=LgC/mLge
三参数式
(S-Sf)m N=C
B=-1/m 双对数 lgS
平均应力的影响(R-1)
Sa
S 1
1
Gerber
paraboSlaic
S a ( 1)
Sm Su
2
1.0
Kececioglu, Chester and
Dodge Bagci
Sa Sa(1)
a
Sm Su
2
1.0
4
Sa Sa(1)
Determine the bar diameter to give infinite fatigue life based on a safety
factor of 2.5
u 1090MPa 0 1010MPa e 510MPa
Cylindrical cross section of the bar =A, the variation of stress will be
Miner累计损伤，是与载荷Si的作用先后次序无关的。
Ni
a
( i )m
D
1 a
Nblock
ni ( i )m
i 1
Miner线性累计损伤理论
对于承受变幅疲劳载荷的构件，应用Miner累积损伤理论，可解决下述 二类问题，即：1) 已知设计寿命期间的应力谱型，确定应力水平。
基本S-N曲线(R=-1)
S-N曲线的一般形状及若干特性值
基本S-N曲线(R=-1)
幂函数
SmN=C
LgS=A+BLgN A=LgC/m
S-N曲线的数学表达式
指数式
S=C Nn
ems N=C
S=A+BLgN A=LgC/mLge
三参数式
(S-Sf)m N=C
B=-1/m 双对数 lgS
平均应力的影响(R-1)
Sa
S 1
1
Gerber
paraboSlaic
S a ( 1)
Sm Su
2
1.0
Kececioglu, Chester and
Dodge Bagci
Sa Sa(1)
a
Sm Su
2
1.0
4
Sa Sa(1)
Determine the bar diameter to give infinite fatigue life based on a safety
factor of 2.5
u 1090MPa 0 1010MPa e 510MPa
Cylindrical cross section of the bar =A, the variation of stress will be
Miner累计损伤，是与载荷Si的作用先后次序无关的。
Ni
a
( i )m
D
1 a
Nblock
ni ( i )m
i 1
Miner线性累计损伤理论
对于承受变幅疲劳载荷的构件，应用Miner累积损伤理论，可解决下述 二类问题，即：1) 已知设计寿命期间的应力谱型，确定应力水平。
疲劳与断裂第二章应力疲劳1ppt课件
在应力寿命法中，缺口的影响是用疲劳缺口系数 Kf 表示的， Kf 是在给定寿命下，无缺口构件疲 劳强度与相应的缺口件疲劳强度之比。一般地说， 疲劳缺口系数Kf 小于理论弹性应力集中系数Kt 。
:
3
2.5 变幅载荷谱下的疲劳寿命
variable amplitude
Ulopatdoinngow, the discussion about fatigue
实际零构件 缺口 应力集中 疲劳性能下降。
:
2
In the stress-life approach the effect of notches is accounted for by the fatigue notch factor, Kf , which is the ratio between the unnotched fatigue strength of a member and the corresponding notched fatigue strength at a given life. In general, the fatigue notch factor, Kf , is smaller then Kt .
:
7
线性累积损伤理论与载荷的作用次序无关。
D = ni Ni = 1
D
1
A
B
D
1
A
B
n
D2
1 n2
D 1
D
n
1
1
n2
D2
0
N1
Nn
2
D = n1 + n2 =1
N1 N2
:
0
N1
Nn
2
D = n2 + n1 =1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平均应力的影响(R-1)
船舶与海洋工程学院
步骤2 Goodman linear equation
Sa Sm 1.0
Sa(1) Su
Sa(1)
Sa 360 56.48MPa
1SSm u
1440 1200
Sa Sm
360MPa 440MPa
步骤3
NCS/m1.531 62 05/56.48 7.314
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 10
船舶与海洋工程学院
Sa S 1
1
平均应力的影响(R-1)
Gerber parabolic
Sa Sa(1)
Sm Su
2
1.0
Kececioglu, Chester and Dodge
Bagci
Sa Sa(1)
a
Sm Su
Sm= 0 Sa可调整
R=1 Sa= 0 静载荷
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 9
船舶与海洋工程学院
平均应力的影响(R-1)
根据三角形相似
a(1)
a
a(1)
m
u
Goodman公式
a m 1.0
a(1)
u
Goodman formula present the relationship between the R≠-1 with R=-1.
1.09 15 0(次)
Sa(1) 56.48MPa
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 13
船舶与海洋工程学院
Example: A 4340 steel bar is subjected to a fluctuating axial load that varies from a maximum of 330kN tension to a minimum of 110kN compression the mechanical properties of the steel are:
船舶与海洋工程学院
例题
构件受拉压循环应力作用。已知
(1) Smax=800 MPa, Smin=80 MPa。 (2) 材料的极限强度为 Su=1200 MPa。 (3) 基本S-N曲线可用幂函数式 Sm N=C 表达，其中
C=1.5361025；m=7.314。 试估算其疲劳寿命。
[注意]S-N曲线主要针对R=-1得到的，对于应力比不等于1的应力循环，当我们计算
平均应力的影响(R-1)
船舶与海洋工程学院
R=-1，对称循环时的S-N曲线，是基本S-N曲线
R-1
？
1 R Sm 1RSa
证明上式
第二章 应力疲劳
讨论应力比R的影响，实际上是讨论均应力Sm的影响。
《工程结构疲劳与断裂力学》解德 版权所有2011© 7
船舶与海洋工程学院
平均应力的影响(R-1)
基本S-N曲线
S=A+BLgN
A=LgC/m
A=LgC/mLge
B=-1/m 双对数 lgS
B=-1/mLge
单对数
S
lgS
lgN
lgN
lgN
张亚军，S-N疲劳曲线的数学表达式处理方法探讨，理化检验-物理分册，2007年43卷11期，563-565
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 6
Sm
1 1
R R
Sa
R<-1 R=-1 R>-1
在实践中，用喷丸、冷挤压和预应变等方法，在高应力细节处引入压缩 残余压应力，是提高疲劳寿命的有效措施。
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 8
平均应力的影响(R-1)
船舶与海洋工程学院
Sm
1 1
R R
Sa
R=-1
(1-R)Sm= (1+R)Sa
船舶与海洋工程学院
按照作用循环应力的大小，疲劳可分成为应力疲劳 (Stress Fatigue)和应变疲劳(Strain Fatigue)。
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 1
船舶与海洋工程学院
载荷谱特征描述
What are the important parameters to characterize a given cyclic loading history?
寿命N定义为到破坏的循环次数
《工程结构疲劳与断裂力学》解德 版权所有2011© 3
船舶与海洋工程学院
基本S-N曲线(R=-1)
S-N曲线的一般形状及若干特性值
寿命为N循环的疲劳强度
疲劳极限
Sf(R=-1)或S-1
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 4
船舶与海洋工程学院
其疲劳寿命时，需要采用Goodman 公式进行转换
[解答] 步骤1
Sa Sm 1.0 Sa(1) Su
S a S m aS x m/i2 n 3M 60Pa S m S m aS x m/i2 n 4M 40Pa
RSmi/nSma x0.1
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 12
Stress Range
Mean Stress
Stress amplitude
Stress Ratio
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 2
船舶与海洋工程学院
载荷谱特征描述
特例
第二章 应力疲劳
恒幅循环载：R=-1 Sa=Smax=S
S-N曲线 是材料的基本疲劳性能曲线
u 1 0 9 0 M P a 0 1 0 1 0 M P a e 5 1 0 M P a
Determine the bar diameter to give infinite fatigue life based on a safety factor of 2.5
2
1.0
Sa Sa(1)
Sm Sy
4
1.0
Sa Sm 1.0 Sa(1) Su
Goodman linear
第二章 应力疲劳
Marin quadratic/elliptic
Sa Sa(1)
2
Sm Su
2
1.0
Sm Su
1
《工程结构疲劳与断裂力学》解德 版权所有2011© 11
平均应力的影响(R-1)
基本S-N曲线(R=-1)
S-N曲线的一般形状及若干特性值
第二章 应力疲劳
《工程结构疲劳与断裂力学》解德 版权所有2011© 5
船舶与海洋工程学院
幂函数
基本S-N曲线(R=-1)
S-N曲线的数学表达式 指数式
三参数式
SmN=C S=C Nn
ems N=C
(S-Sf)m N=C
LgS=A+BLgN