R×C列联表资料的统计分析
定性资料常用的统计学方法
定性资料常用的统计学方法一、χ2检验χ2检验（chi-square test）是一种主要用于分析分类变量数据的假设检验方法，该方法主要目的是推断两个或多个总体率或构成比之间有无差别。
（一）四格表资料的χ2检验例17：为了解吲达帕胺片治疗原发性高血压的疗效，将70名高血压患者随机分为两组，试验组用吲达帕胺片加辅助治疗，对照组用安慰剂加辅助治疗，观察结果见表4 -5-1，试分析吲达帕胺片治疗原发性高血压的有效性。
表4 -5-1 两种疗法治疗原发性高血压的疗效1.四格表χ2检验的原理：对于四格表资料，χ2检验的基本公式为：式中，A为实际频数（actual frequency），T为理论频数（theoreticalfrequency）。
理论频数T根据检验假设H0：π1=π2确定，其中π1和π2分别为两组的总体率。
计算理论频数T的公式为：式中Tij 为第i行第j列的理论频数，ni+和n+j分别为相应行与列的周边合计数，n为总例数。
现以例17为例说明χ2检验的步骤：（1）建立检验假设并确定检验水准。
H0：π1=π2，即试验组与对照组的总体有效率相等H1：π1≠π2，即试验组与对照组的总体有效率不等α=0.05（2）计算检验统计量。
按式（4 -5-2）计算T11，然后利用四格表的各行列的合计数计算T12、T21和T22，即T11=（44×41）／70=25.77，T12=44-25.77=18.23T21=41-25.77=15.23，T22=26-15.23=10.77按式（4 -5-3）计算χ2值（3）确定P值，作出推断结论。
以ν=1查χ2分布界值表，得P＜0.005。
按α=0.05水准，拒绝H，接受H1，可以认为两组治疗原发性高血压的总体有效率不等，即可以认为吲达帕胺片治疗原发性高血压优于对照组。
2.四格表资料χ2检验的专用公式：在对两样本率比较时，当总例数n≥40且所有格子的T≥5时，可用χ2检验的通用公式（4 -5-1）。
实验4——列联表分析(R×C)
3）直方图
500
400
300
200
Count
100
0
1
2
转移情况
组织分类
1 2 3 4 5 3
第二站
3.9 -2.5 -1.6
组织学类型 低分化腺癌 粘液细胞癌
-1.7
-2.5
1.6
2.1
-0.2
0.3
粘液腺癌 -2.3 0.8 1.8
未分化癌 1.2
-1.5 0.6
2） 残差分析 将残差值与 u /2 1.96进行比较
固定列
△由于d11= 3.9 > 1.96 ,
说明 P( 1| 1) P( 1)
df 8
Asymp. Sig. (2-sided)
.001
Likelihood Ratio
26.240
8
1
Linear-by-Linear Association
7.187
1
.007
N of Valid Cases
2063
a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 27.31.
将“转移情况”添加到行变量中，“组织分类” 添加到列变量中。
点击Statistics
此处提供了多种检验方法，我们选择 2检验
点击Cell（交叉格），选择格中的值为观 测值 、残差……
4. 主要结果：
Chi-Square Tests
Pearson Chi-Square
Value 26.090a
【宝典】R×C列联表（分类数据）的统计分析方法选择与SPSS实现
【宝典】R×C列联表（分类数据）的统计分析方法选择与SPSS实现分类资料在医学统计中很常见，有些统计学书上称为计数资料，比如（有效、无效），（发病、不发病），（男、女），血型（A、B、O、AB）等等。
分类资料一般根据频数整理成列联表的形式，一般的列联表多是二维的（也称行列表，或R×C列联表，高维列联表下次讨论），列联表根据变量是否有序可以分为双向无序、单项有序、双向有序列联表，统计方法是不同的，分析如下：一、双向无序列联表（一）成组四格表是指行、列变量均为无序的列联表，例如要研究吸烟和肺癌之间的关系，行变量为是否吸烟：吸烟、不吸烟，列变量为肺癌发病：发病，不发病，如下表：发生肺癌未发生肺癌吸烟a b不吸烟 c d对于这种数据，我们的统计目的是分析行列变量的独立性，即：肺癌发病是否与吸烟有关，可选用的方法有以下两种：1、Pearson卡方检验：基于卡方分布，H0为行、列变量相互独立，SPSS中“分析->描述性统计->交叉表”可实现。
四格表使用条件：专用公式①样本总数大于40；②各个单元格理论值均大于5。
校正公式：①样本总数大于40；②理论值1<T<5;Fisher确切概率法：①样本总数小于40，或T<1，无需选择，软件自动计算成组四格表Fisher。
2、Fisher精确概率：基于超几何分布，当数据不满足Pearson卡方检验时使用。
SPSS 中“分析->描述性统计->交叉表”可实现。
注意SPSS仅提供了2×2表的精确概率，需要计算R×C列联表的精确概率，可以选择精确按钮中的蒙特卡罗近似法实现。
（一）成组R×C表(双向无序)A型B型O型AB型A地区 a b c dB地区 e f j hC地区i j k l1.Pearson卡方检验条件：不能有任何一个格子的理论频数T<1,同时1<T<5的格子数不能超过总格子数的1/5.如若不符合：可以增加研究样本量（通常少用）；对理论频数较小的行或者列进行合并或者删除；采用R×C表的Fisher确切概率法（通常采用蒙特卡洛近似法）2.R×C表Fisher确切概率法操作：分析—描述—交叉表—设置好行列变量—点击精确—选择蒙特卡洛。
如何在SAS中实现R×C列联表的两两比较
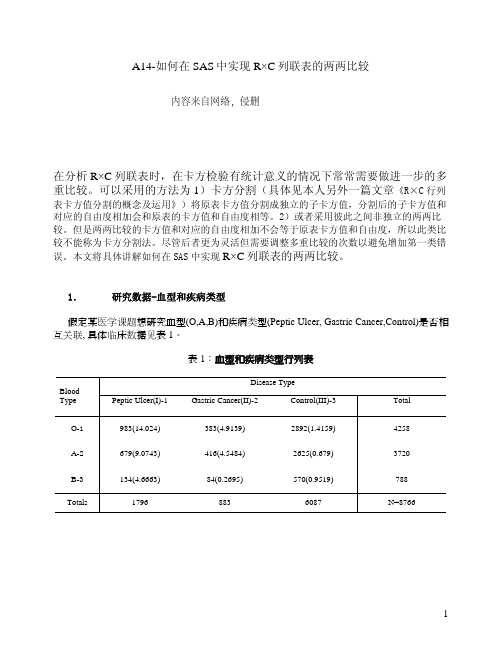
A14-如何在SAS中实现R×C列联表的两两比较内容来自网络，侵删在分析R×C列联表时，在卡方检验有统计意义的情况下常常需要做进一步的多重比较。
可以采用的方法为1）卡方分割（具体见本人另外一篇文章《R×C行列表卡方值分割的概念及运用》）将原表卡方值分割成独立的子卡方值，分割后的子卡方值和对应的自由度相加会和原表的卡方值和自由度相等。
2）或者采用彼此之间非独立的两两比较。
但是两两比较的卡方值和对应的自由度相加不会等于原表卡方值和自由度，所以此类比较不能称为卡方分割法。
尽管后者更为灵活但需要调整多重比较的次数以避免增加第一类错误。
本文将具体讲解如何在SAS中实现R×C列联表的两两比较。
1．研究数据-血型和疾病类型假定某医学课题想研究血型(O,A,B)和疾病类型(Peptic Ulcer, Gastric Cancer,Control)是否相互关联, 具体临床数据见表1。
表1：血型和疾病类型行列表Disease TypeBloodType Peptic Ulcer(I)-1 Gastric Cancer(II)-2 Control(III)-3 Total O-1983(14.024)383(4.9139)2892(1.4159)4258A-2679(9.0743)416(4.5484)2625(0.679)3720B-3134(4.6663)84(0.2695)570(0.9519)788Totals17968836087N=87662．初步分析我们先用SAS/PROC FREQ 和PROC CORRESP 先对数据做初步的分析，来判断行列变量之间的关系。
CELLCHI2 选项是计算按公式2-1计算每个单元格在总体值的组成。
2χij ijijji E OE C 2,)(-=（2-1）proc freq data=paper14;weight count;table r*c/chisq cellchi2nopercent;run;proc corresp data=paper14;weight count;les r, c;tabrun;表2 – 卡方检验结果Table of r by cr cFrequencyCell Chi-SquareRow PctCol Pct 123Total198314.02423.0954.733834.91398.9943.3728921.415967.9247.51425826799.074318.2537.814164.548411.1847.1126250.67970.5643.12372031344.666317.017.46840.269510.669.515700.951972.349.36788Total 179688360878766 Statistics for Table of r by cStatistic DF Value Prob ------------------------------------------------------ Chi-Square 4 40.5434 <.0001 Likelihood Ratio Chi-Square 4 40.6401 <.0001 Mantel-Haenszel Chi-Square 1 21.0035 <.0001 Sample Size = 8766从表２中可以看出第１行（血型Ｏ）的卡方检验分值在所有行中所占比重最高（(14.024+4.9139+1.4159)/40.5434≈50％）;第１列（Peptic Ulcer(I)）的卡方检验分值在所有列中所占比重最高（(14.024+9.0743+4.6663)/40.5434≈68.5%）。
R×C列联表资料的统计分析PPT课件
二、双向无序RC表的统计分析
c2检验的计算公式
RC
2 i1 j1
2
Aij Tij Tij
v R 1C 1
二、双向无序RC表的统计分析
实例分析
专业
表10 不同专业学生的气质类型分布 例数
气质类型： 多血质 胆汁质 抑郁质
粘液质
计算机 金融 传媒
16
13
7
14
12
15
10
13
18
表 4 不同药物组中患者的疗效情况
药物
患者例数
类型 疗效： 痊愈
显效
好转
无效
A
5
10
8
7
B
4
9
10
7
C
10
12
13
5
在二维列联表中，仅结果变量的取值为有序的， 而原因变量是无序的，由此排列成的RC表称之 为结果变量为有序变量的单向有序RC表
结果变量为有序变量的单向有序RC表
表5 284例受试对象的冠状动脉造影结果
双向有序且属性不同RC表的统计方法
第四个分析目的，希望考察各行上的频数分布是 否相同，此时，将此资料视为双向无序的RC列 联表资料，可根据资料具备的前提条件，选用一
般 检验或Fish2 er精确检验。若P＜0.05，不能
认为两有序变量之间有相关关系，而只能认为各 行上的频数分布不同
双向有序且属性相同的RC表
双向有序且属性不同的RC表
表 6 不同年龄组中患者的疗效情况
年龄
患者例数
疗效： 痊愈 显效
好转
无效
<40
5
6
3
1
40~49
8985来自50~5969
生物统计学考试复习题库17182
生物统计学各章题目一填空1．变量按其性质可以分为(连续）变量和（非连续）变量。
2．样本统计数是总体（参数）的估计值。
3．生物统计学是研究生命过程中以样本来推断(总体)的一门学科。
4．生物统计学的基本内容包括（试验设计)和(统计分析）两大部分.5．生物统计学的发展过程经历了（古典记录统计学）、（近代描述统计学)和（现代推断统计学）3个阶段。
6．生物学研究中，一般将样本容量（n ≥30)称为大样本。
7．试验误差可以分为（随机误差）和（系统误差）两类。
判断1．对于有限总体不必用统计推断方法。
（×)2．资料的精确性高，其准确性也一定高。
（×）3．在试验设计中，随机误差只能减小,而不能完全消除。
（∨）4．统计学上的试验误差，通常指随机误差。
（∨）二填空1．资料按生物的性状特征可分为（数量性状资料）变量和（质量性状资料)变量.2。
直方图适合于表示（连续变量）资料的次数分布。
3．变量的分布具有两个明显基本特征，即(集中性）和（离散性）。
4．反映变量集中性的特征数是（平均数），反映变量离散性的特征数是(变异数）。
5．样本标准差的计算公式s=（ ）。
判断题1。
计数资料也称连续性变量资料,计量资料也称非连续性变量资料。
（×）2。
条形图和多边形图均适合于表示计数资料的次数分布。
(×）3. 离均差平方和为最小。
(∨)4。
资料中出现最多的那个观测值或最多一组的中点值,称为众数。
（∨）5. 变异系数是样本变量的绝对变异量。
（×）单项选择1. 下列变量中属于非连续性变量的是( C ）。
A.身高 B.体重 C.血型 D.血压 2. 对某鱼塘不同年龄鱼的尾数进行统计分析，可做成( A )图来表示。
A.条形 B 。
直方 C 。
多边形 D 。
折线 3。
关于平均数,下列说法正确的是( B ）.A. 正态分布的算术平均数和几何平均数相等. 122--∑∑n n x x )(B.正态分布的算术平均数和中位数相等。
SPSS超详细操作：卡方检验（R×C列联表）
SPSS超详细操作：卡⽅检验（R×C列联表）医咖会之前推送过⼀些卡⽅检验相关的⽂章，包括：卡⽅检验(2x2)、卡⽅检验(2xC)、配对卡⽅检验、分层卡⽅检验等。
今天我们再和⼤家分享⼀下，如何⽤SPSS来做RxC列联表的卡⽅检验。
⼀、问题与数据研究者拟分析购房⼈与购房类型的关系，共招募了在过去12个⽉中有过购房记录的333位受试者，收集了购房⼈类型（buyer_type）和房屋类型（property_type）的变量信息。
其中研究对象类型按照单⾝男性（single male）、单⾝⼥性（single female）、已婚两⼈（married couple）和多⼈家庭（family）分类；房屋类型按照楼房（flat）、平房（bungalow）、独栋别墅（detached house）和联排别墅（terrace）分类，部分数据如下图。
其中，Individual scores for each paticipant（左图）列出了每⼀个研究对象的情况，⽽Total count data (frequencies)（右图）则是对相同情况研究对象的数据进⾏了汇总。
⼆、对问题的分析研究者想分析多种购房⼈类型与多种房屋类型的关系，建议使⽤卡⽅检验（R×C），但需要先满⾜3项假设：假设1：存在两个⽆序多分类变量，如本研究中购房⼈类型和房屋类型均为⽆序分类变量。
假设2：具有相互独⽴的观测值，如本研究中各位研究对象的信息都是独⽴的，不会相互⼲扰。
假设3：样本量⾜够⼤，最⼩的样本量要求为分析中的任⼀期望频数⼤于5。
本研究数据符合假设1和假设2，那么应该如何检验假设3，并进⾏卡⽅检验（R×C）呢？三、SPSS操作1. 数据加权如果数据是汇总格式（如上图中的Total count data），则在进⾏卡⽅检验之前，需要先对数据加权。
如果数据是个案格式（如上图中的Individual scores for each paticipant），则可以跳过“数据加权”步骤，直接进⾏卡⽅检验的SPSS操作。
R×C表卡方检验
2 =9.60< 2 0.1，6=10.64，P>0.1， 按α=0.0病5水人准中，医不各拒型绝的H构0成，比即不不同能.认为三组
Q Technology limited
1.建立数据文件
Q Tech
在SPSS数据编辑窗，建立数据文件Li8-4.sav。
行变量：“疗法”，Values为：1＝“生胃宁素 片”，2＝“中药组” ，3＝“西药组” ；
Q Technology limited
Q Tech
（3） 2检验
从菜单选择 Analyze→Descriptive
Statistics→Crosstable 指定 Row(s)：疗法 Columns(s)：疗效 击Statistics按钮选择Chi-square。
Q Technology limited
血压病效果不同。
Q Technology limited
1.建立数据文件
Q Tech
在SPSS数据编辑窗，建立数据文件题18.sav 。
行变量：“组别”，Values为：1＝“新复方 ”，2＝“降压片” ，3＝“安慰剂” ；
列变量：“疗效”，Values为：1＝“有效” ，2＝“无效；
频数变量：“频数”。
Q Technology limited
2. spss操作过程
Q Tech
（1）在spss中调出数据文件题18.sav （2）频数变量加权。 从菜单选择
Data→Weight Cases 弹出Weight Cases对话框，选择
Weight Cases by框，框内选入“频 数”，即指定该变量为频数变量
Data→Weight Cases 弹出Weight Cases对话框，选择
(完整)R×C列联表资料的统计分析ppt
缓慢心律
患者例数
失常种类 部位： 下壁 前壁 真后壁 心内膜下 合计
窦性过缓
8
7
2
1 18
被动心律
1
1
0
0
2
房室阻滞
6
3
1
1 11
束支阻滞
1
16
1
0 18
合计
16
27
4
2 49
双向无序RC表的统计方法 2 检验
Fisher精确概率法：有1/5以上的格子的 理论频数小于5
结果变量为有序变量的单向有序RC表
四、双向有序且属性不同RC表的统计分析
Spearman秩相关 Spearman 秩相关是一种非参数的度量
相关性的分析方法，它对数据进行秩变换， 然后计算直线相关系数
四、双向有序且属性不同RC表的统计分析
实例分析
表16 某地地方性甲状腺肿病分年龄组的疗效
年龄 疗效： 治愈
例数 显效
好转
无效
11~
35
双向有序且属性不同RC表的统计方法
第四个分析目的，希望考察各行上的频数分布是 否相同，此时，将此资料视为双向无序的RC列 联表资料，可根据资料具备的前提条件，选用一
般 检验或Fish2 er精确检验。若P＜，不能认为
两有序变量之间有相关关系，而只能认为各行上 的频数分布不同
双向有序且属性相同的RC表
➢ 第一个分析目的，只关心各组结果变量取值之间的差别是 否具有统计学意义，此时，原因变量的有序性就变得无关 紧要了，可将此时的“双向有序RC列联表资料”视为 “结果变量为有序变量的单向有序RC列联表资料”，可 以选用的统计分析方法有秩和检验、Ridit分析和有序变量 的logistic回归分析
SPSS列联表分析
例3： 以下是胃癌真菌病因研究中3种食物样品的真菌检出率,比较3种食物真菌检出率有无差异.
本例中SPSS提示没有理论频数小于5,且最小的理论频数为8.00,故直接选择Pearson 卡方结果,即χ2=22.841,P<0.001,提示三种食物中真菌检出率不同.此时还需要进一步考虑三种食物真菌检出率到底谁与谁之间的差异存在统计学意义,这里就需要用到卡方分割,通俗讲就是把RC列联表拆分成若干个四个表分别进行χ2检验,进而判断不同组两两比较差异是否用统计学意义,但是因为多组比较可能会增加犯I类错误概率,所以还需要对χ2检验的P值进行校正.常用Bonferroni法进行校正,本例中需要进行3次两两比较,校正的检验水准α=0.05/比较次数=0.05/3=0.0167,即当两两比较P<0.0167才能认为差异有统计学意义.
Kappa一致性检验
1、Kappa检验旨在评价两种方法是否存在一致性，或者是同一个研究者先后两次的诊断结果 2、Kappa检验会利用列联表的全部数据 3、Kappa检验可计算Kappa值用于评价一致性大小
配对χ2检验(McNemar检验)
1、配对χ2检验主要确定两种方法诊断结果是否有差别 2、配对χ2检验只利用“不一致“数据，如表中b和c 3、配对χ2检验只能给出两种方法差别是否具有统计学意义的判断
无效 疗效=1
好转 疗效=2
显效 疗效=3
治愈 疗效=4
合计
有效率%
甲法
24
26ห้องสมุดไป่ตู้
72
186
308
92.2
乙法
20
16
24
32
92
78.3
丙法
20
22
14
22
(仅供参考)如何在SAS中实现R×C列联表的两两比较
A14-如何在SAS中实现R×C列联表的两两比较内容来自网络，侵删在分析R×C列联表时，在卡方检验有统计意义的情况下常常需要做进一步的多重比较。
可以采用的方法为1）卡方分割（具体见本人另外一篇文章《R×C行列表卡方值分割的概念及运用》）将原表卡方值分割成独立的子卡方值，分割后的子卡方值和对应的自由度相加会和原表的卡方值和自由度相等。
2）或者采用彼此之间非独立的两两比较。
但是两两比较的卡方值和对应的自由度相加不会等于原表卡方值和自由度，所以此类比较不能称为卡方分割法。
尽管后者更为灵活但需要调整多重比较的次数以避免增加第一类错误。
本文将具体讲解如何在SAS中实现R×C列联表的两两比较。
1．研究数据-血型和疾病类型假定某医学课题想研究血型(O,A,B)和疾病类型(Peptic Ulcer, Gastric Cancer,Control)是否相互关联, 具体临床数据见表1。
表1：血型和疾病类型行列表Disease TypeBloodType Peptic Ulcer(I)-1 Gastric Cancer(II)-2 Control(III)-3 Total O-1983(14.024)383(4.9139)2892(1.4159)4258A-2679(9.0743)416(4.5484)2625(0.679)3720B-3134(4.6663)84(0.2695)570(0.9519)788Totals17968836087N=87662．初步分析我们先用SAS/PROC FREQ 和PROC CORRESP 先对数据做初步的分析，来判断行列变量之间的关系。
CELLCHI2 选项是计算按公式2-1计算每个单元格在总体值的组成。
2χij ijijji E OE C 2,)(-=（2-1）proc freq data=paper14;weight count;table r*c/chisq cellchi2nopercent;run;proc corresp data=paper14;weight count;les r, c;tabrun;表2 – 卡方检验结果Table of r by cr cFrequencyCell Chi-SquareRow PctCol Pct 123Total198314.02423.0954.733834.91398.9943.3728921.415967.9247.51425826799.074318.2537.814164.548411.1847.1126250.67970.5643.12372031344.666317.017.46840.269510.669.515700.951972.349.36788Total 179688360878766 Statistics for Table of r by cStatistic DF Value Prob ------------------------------------------------------ Chi-Square 4 40.5434 <.0001 Likelihood Ratio Chi-Square 4 40.6401 <.0001 Mantel-Haenszel Chi-Square 1 21.0035 <.0001 Sample Size = 8766从表２中可以看出第１行（血型Ｏ）的卡方检验分值在所有行中所占比重最高（(14.024+4.9139+1.4159)/40.5434≈50％）;第１列（Peptic Ulcer(I)）的卡方检验分值在所有列中所占比重最高（(14.024+9.0743+4.6663)/40.5434≈68.5%）。
生物统计学习题集参考答案
生物统计学习题集参考答案生物统计学习题集参考答案第一章概论一、填空1 变量按其性质可以分为连续变量和非连续变量。
2 样本统计数是总体参数的估计量。
3 生物统计学是研究生命过程中以样本来推断总体的一门学科。
4 生物统计学的基本内容包括_试验设置、统计分析_两大部分。
5 统计学的发展过程经历了古典记录统计学、近代描述统计学现代推断统计学3个阶段。
6 生物学研究中，一般将样本容量n大于等于30称为大样本。
7 试验误差可以分为__随机误差、系统误差两类。
二、判断（-）1 对于有限总体不必用统计推断方法。
（-）2 资料的精确性高，其准确性也一定高。
(+) 3 在试验设计中，随机误差只能减少，而不可能完全消除。
（+）4 统计学上的试验误差，通常指随机误差。
三、名词解释样本：从总体中抽出的若干个体所构成的集合称为样本。
总体：具有相同的个体所构成的集合称为总体。
连续变量：是指在变量范围内可抽出某一范围的所有值。
非连续变量：也称离散型变量，表示变量数列中仅能取得固定数值并且通常是整数。
准确性：也称准确度指在调查或试验中某一试验指标或性状的观测值与真实值接近的程度。
精确性：也称精确度指在调查或试验中同一试验指标或性状的重复观测值彼此接近程度的大小。
第二章试验资料的整理与特征数的计算一、填空1 资料按生物的性状特征可分为___数量性状资料_变量和__变量性状资料_变量。
2 直方图适合于表示__计量、连续变量_资料的次数分布。
3 变量的分布具有两个明显基本特征，即_集中性_和__离散性_。
4 反映变量集中性的特征数是__平均数__，反映变量离散性的特征数是__变异数（标准差）_。
5 样本标准差的计算公式s= √∑（x-x横杆）平方/(n-1)。
二、判断( - ) 1 计数资料也称连续性变量资料，计量资料也称非连续性变量资料。
( - ) 2 条形图和多边形图均适合于表示计数资料的次数分布。
（ +）3 离均差平方和为最小。
卫生统计学 卡方检验
者未住院原因构成比是否不同？
表4
甲、乙两县应住院者未住院原因构成比(%)
① 建立假设 H0：甲、乙两县应住院者未住院原因总体构成比相同同 H1：甲、乙两县应住院者未住院原因总体构成比不同 ② 确定检验水准 α=0.05
2 ③ 计算统计量 值
2 A 2 n( 1) nR nC
2932 102 62 639 ( ... 1) 4.170 333 575 333 19 306 19
2
1. 当n≥40，且T≥5时，不须校正，直接用基本公式 (8-2)或专用公式(8-3)计算。 2. 任一格子的1≤T<5，且n≥40时，需计算校正 值，
2
或使用四格表的确切概率法。
2
2
( A T 0.5)2 T
2
( ad - bc - n / 2) n (a b)(c d)(a c)(b d)
v k 1 s ( R 1)(C 1)
式中，k为格子数，s为估计的参数个数，R为行数， C为列数。 如本例中，4个格子，估计甲乙两药的有效率，则k=4， s=2，v=4-1-2=(2-1)(2-1)=1。
2分布是一种连续型随机变量的概率分布。
如果Z服从标准正态分布，那么Z2服从自由度为1的 小值的可能性较大，取较大值的可能性较小。 设有v 个相互独立的标准正态分布随机变量Z1, Z2, Zv，
④ 确定P值 2 υ＝(3－1)(2－1)＝2，查 界值表得P<0.01。
⑤ 下结论 因为P<0.01，按α=0.05的水准，拒绝H0，接受 H1，差异有统计学意义。即可认为三个地区的出
生婴儿的致畸率有差别。
例 为研究某镇痛药的不同剂量镇痛效果是否有差别，研 究人员在自愿的原则下，将条件相似的53名产妇随机分成 三组，分别按三种不同剂量服用该药，镇痛效果如下表。 试分析该药不同剂量的镇痛效果有无差别？ 表 某药不同剂量的镇痛效果
R×C表卡方检验
2020年月27日
（1） 新复方与安慰剂比较：列出表A，
2=30.50，P=0.000，按α’=0.025水准
拒绝H0，可以认为新复方治疗高血压有效。
表A 新复方与安慰剂比较
药物
有效
无效
新复方
35
5
安慰剂
7
25
合计
42
30
合计 40 32 72
2020年4月27日
（2）降压药与安慰剂比较：列出表B，
2020年4月27日
R×C表2 检验应注意的问题
❖2.多组比较时，若效应有强弱的等级，如+，++
，+++，最好采用后面的非参数检验方法。 2检
验只能反映其构成比有无差异，不能比较效应的 平均水平。 ❖3.行列两种属性皆有序时，可考虑趋势检验或 等级相关分析。
❖4.多个率比较的2检验，结论为拒绝H0时、需
2020年4月27日
相关性分析
结果分析： Spearman等级相关系数＝0.214，近似概率P
＝0.001<0.05，可认为行和列两等级变量之间的总体相关系 数不等于0，两变量之间有一定的相关关系。
2020年4月27日
线性趋势检验
结果分析： MH 2 ＝10.281，近似概率P＝0.001<0.05，
拒绝H0，可以认为三种疗法效果不同。
2020年4月27日
三、两组或多组构成比的比较
例8-5 用三种治疗方法治疗199例消化性 溃疡住院病人资料如表8-6，试分析三组 病人按4种中医分型的构成比有无差别。
2020年4月27日
表8-6 三种消化性溃疡住院病人四种证型的构成
中医分型 疗法 肝胃不和 胃阴不和 脾胃虚寒 寒热夹杂 合计
R×C表资料的分类及其检验方法的选择
R×C表资料的分类及其检验方法的选择R×C表资料可以分为双向无序、单项有序、双向有序属性相同和双向有序属性不同4类。
1.双向无序R×C表资料R×C表资料中两个分类变量（X和Y）皆为无序分类变量，如表7-8、表7-9和表7-10（X、Y均为名义变量）。
对于该类资料，①若研究目的为多个样本率（或构成比）的比较，可用行×列表资料的x2检验；②若研究目的为分析两个分类变量之间有无关联性以及关系的密切程度时，可用行×列表资料的x2检验以及Pearson列联表系数进行分析。
2.单向有序R×C表资料有两种形式。
一种R×C表资料中的分组变量（如年龄）是有序的，而指标变量（如传染病的类型）是无序的。
其研究目的通常是分析不同年龄组各种传染病的构成情况，此种单向有序R×C表资料可用行×列表资料的x2检验进行分析。
另一种情况是R×C表资料中的分组变量（如疗法）为无序的，而指标变量（如疗法按等级分组）是有序的。
其研究目的为比较不同疗法的疗效，此种单向有序R×C表资料宜用秩转换的非参数检验进行分析（见第八章）。
3.双向有序属性相同的R×C表资料R×C表资料中的两个分类变量皆为有序且属性相同。
实际上是为配对四格表资料的扩展，即水平数≥3的配伍资料，如用两种检测方法同时对同一批样品的测定结果。
其研究目的通常是分析两种检测方法的一致性，此时宜用一致性检验或称Kappa检验（见第三十三章）；也可用特殊模型分析方法（SAS软件）。
4.双向有序属性不同的R×C表资料R×C表资料中两个分类变量皆为有序的，但属性不同，如表7-13（X、Y均为等级资料、等距资料）。
对于该类资料，①若研究目的为分析不同年龄组患者疗效之间有无差别时，可把它视为单向有序R×C表资料，选用秩转换的非参数检验；②若研究目的为分析两个有序分类变量间是否存在相关关系，宜用等级相关分析或Pearson积差相关分析（见第九章）；③若研究目的为分析两个有序分类变量间是否存在线性变化趋势，宜用有序分组资料的线性趋势检验（test for linear trend）。
R×C表卡方检验
❖ （3） 2检验
从菜单选择
Analyze→Descriptive Statistics→Crosstable
指定 Row(s)：疗法 Columns(s)：疗效 击Statistics按钮选择Chi-square。
输出结果
结果分析：Pearson 2 =32.736，双侧P＝0.000<0.05，
9.60
df (3 1) (4 1) 6
2 =9.60< 2 0.1，6=10.64，P>0.1，
按α=0.05水准，不拒绝H0，即不能认为三组病 人中医各型的构成比不同.
1.建立数据文件
❖ 在SPSS数据编辑窗，建立数据文件Li8-4.sav。
❖ 行变量：“疗法”，Values为：1＝“生胃宁素 片”，2＝“中药组” ，3＝“西药组” ；
T
nR nC
❖ 自由度= (R1)(C1)
二、多个样本率的比较
❖ 例8-4 （ P419题18）研究新复方治疗高血压病 效果的临床试验，并与标准对照药物降压片和 安慰剂作对照，结果如表8-5，比较三组效果。
表8-5 三种药物治疗高血压病的有效率
组别
疗效
有效
无效
合计
有效率 （%）
新复方
35
5
40
87.50
拒绝H0，可以认为三种疗法效果不同。
三、两组或多组构成比的比较
❖ 例8-5 用三种治疗方法治疗199例消化性溃疡 住院病人资料如表8-6，试分析三组病人按4 种中医分型的构成比有无差别。
表8-6 三种消化性溃疡住院病人四种证型的构成
中医分型 疗法 肝胃不和 胃阴不和 脾胃虚寒 寒热夹杂 合计
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、 RC列联表资料的认识与分析方法选择
定量变量：年龄、红细胞
二值变量：性别（男、女）
多值名义变量：药物类型（A、B、C）、血型 （A、B、AB、O）
多值有序变量：疗效（痊愈、显效、好转、无 效）、临床诊断（Ⅰ级、Ⅱ级、Ⅲ级）、CT诊断 （Ⅰ级、Ⅱ级、Ⅲ级）
双向无序的RC表
药物 类型 A B C 血型： A 8 7 10
二、双向无序RC表的统计分析
原因变量为多值有序变量R2表除了可以应用 线性趋势检验外，其他分析方法与双向无序的 RC表相同
表 14 化合物剂量 100mg 200mg 300mg 400mg 合计 60 只大鼠肿瘤发生情况 例数 肿瘤发生情况： 未发生 12 10 9 5 36 发生 3 5 6 10 24 合计 15 15 15 15 60
三、单向有序RC表的统计分析
秩和检验 原因变量为二值变量：Wilcoxon秩和检验
u
3 (tk tk ) 1 n1n2 ( N 1)(1 ) 3 12 N N
T n1 ( N 1) / 2
原因变量为多值名义变量：Kruskal-Wallis H检验
Ri2 12 H ( ) 3( N 1) H c N ( N 1) ni
双向有序且属性不同RC表的统计方法
第二个分析目的，希望考察原因变量与结
果变量之间是否存在相关关系，此时，需 要选用处理定性资料的相关分析方法，通 常采用Spearman秩相关分析方法
双向有序且属性不同RC表的统计方法
第三个分析目的，若两个有序变量之间存
在的相关关系有统计学意义，研究者希望 进一步了解这两个有序变量之间的变化关 系是呈直线关系还是呈某种曲线关系，此 时宜选用线性趋势检验
所以，3个专业学生的气质类型构成没有统
计学差异
24
二、双向无序RC表的统计分析
原因变量为多值有序变量，结果变量为多值名 义变量的RC表，将其视为双向无序RC表进 行分析
表 11 不同年龄成人获取健康知识途径情况 年龄 20~35 36~50 51~ 例数 途径： 大众媒体 20 42 27 网络 35 17 10 社区教育 26 26 57
双向有序且属性不同RC表的统计方法
对于双向有序且属性不同的RC表资料应根据具 体的分析目来确定分析方法：
第一个分析目的，只关心各组结果变量取值之间的差别是
否具有统计学意义，此时，原因变量的有序性就变得无关 紧要了，可将此时的“双向有序RC列联表资料”视为 “结果变量为有序变量的单向有序RC列联表资料”，可 以选用的统计分析方法有秩和检验、Ridit分析和有序变 量的logistic回归分析
三、单向有序RC表的统计分析
第三步，计算检验统计量。
90272 137702 137882 12 H 3 271 53.29 270 271 100 85 85
Hc 1
53.29 61.09 3 3 3 3 20 20 73 73 126 126 51 51 2703 270
表 2 不同药物组中患者的血型分布情况 患者例数 B 9 10 12 AB 4 2 5 O 9 11 13
在二维列联表中，两个定性变量都是名义变量， 并且这两个名义变量分别有R个与C个可能的取 值，由此排列成的RC表称之为双向无序的RC 表
双向无序的RC表
表3 缓慢心律 失常种类 窦性过缓 被动心律 房室阻滞 束支阻滞 合 计 部位： 心律失常种类与心肌梗塞部位关系的调查结果 患者例数 下壁 8 1 6 1 16 前壁 7 1 3 16 27 真后壁 2 0 1 1 4 心内膜下 合计 1 0 1 0 2 18 2 11 18 49
双向有序且属性不同RC表的统计方法
第四个分析目的，希望考察各行上的频数分布 是否相同，此时，将此资料视为双向无序的 RC列联表资料，可根据资料具备的前提条件， 2 选用一般 检验或Fisher精确检验。若P＜0.05， 不能认为两有序变量之间有相关关系，而只能 认为各行上的频数分布不同
双向有序且属性相同的RC表
胆汁质
13 15 9
抑郁质
7 10 8
粘液质
14 13 15
二、双向无序RC表的统计分析
第一步，建立检验假设。
H0： 3个专业学生的气质类型构成（频数分布） 相同 H1： 3个专业学生的气质类型构成（频数分布） 不全相同 a0.05。
二、双向无序RC表的统计分析
第二步，计算检验统计量。
2
二、双向无序RC表的统计分析
原因变量为二值变量，结果变量为多值 名义变量的2C表
表 12 满族与回族居民血型的频数分布 民族 满族 回族 合计 例数 血型：A 442 369 811 B 483 384 867 O 416 487 903 AB 172 115 287 合计 1513 1355 2868
双向无序RC表的统计方法
2
检验
Fisher精确概率法：有1/5以上的格子的 理论频数小于5
结果变量为有序变量的单向有序RC表
表 4 不同药物组中患者的疗效情况 药物 类型 A B C 患者例数 疗效： 痊愈 5 4 10 显效 10 9 12 好转 8 10 13 无效 7 7 5
在二维列联表中，仅结果变量的取值为有序的， 而原因变量是无序的，由此排列成的RC表称之 为结果变量为有序变量的单向有序RC表
结果变量为有序变量的单向有序RC表的统计方法
秩和检验
Ridit分析 有序变量的Logistic回归分析
双向有序且属性不同的RC表
表 6 不同年龄组中患者的疗效情况 年龄 <40 40~49 50~59 60~ 患者例数 疗效： 痊愈 5 8 6 4 显效 6 9 9 6 好转 3 8 8 7 无效 1 5 7 8
v R 1 3 1 2
三、单向有序RC表的统计分析
第四步，确定P值，给出结论。
查2界值表可知， 20.02,2 =9.21，而本例 中检验统计量的值61.09>9.21，故P<0.01。
所以，3种药物疗效之间的差别有统计学意
义
四、双向有序且属性不同RC表的统计分析
Spearman秩相关
表9 甲、乙两名医生对200例棉屑沉着病可疑患者的诊断结果 甲医生的 诊断结果 正常 Ⅰ期 Ⅱ期 合计 病例数 乙医生的诊断结果： 正常 78 6 0 84 Ⅰ期 5 56 10 71 Ⅱ期 0 13 32 45 合计 83 75 42 200
双向有序且属性相同RC表的统计方法
双向有序且属性相同的RC表是一个“方 形”列联表，它实际上是配对设计22列联 表资料的“扩大”。其主要目的是希望回 答行变量与列变量的检测结果是否一致的 问题，常用的统计分析方法叫做一致性检 验或称为Kappa检验
22
24 51
85
85 270
三、单向有序RC表的统计分析
第一步，建立检验假设。
H0： 3种药物的疗效总体分布位置相同 H1： 3种药物的疗效总体分布位置不全相同 a0.05。
三、单向有序RC表的统计分析
第二步，对原始数据编秩， 遇数据相等者取 平均秩 秩和检验法分析 3 种药物疗效所需数据
RC列联表资料的统计分析
主要内容
RC列联表资料的认识与分析方法选择
四种不同类型RC列联表资料的统计分析 与SAS实现 RC列联表资料统计分析中的错误辨析与 释疑
一、 RC列联表资料的认识与分析方法选择
表 1 某临床研究中 100 例患者的资料 编号 1 2 3 4 „ 年龄 60 53 49 66 „ 性别 女 男 女 男 „ 药物 类型 A C B B „ 红细 胞 3.78 4.26 3.53 4.71 „ 血型 O A AB B „ 临床 诊断 Ⅱ级 Ⅰ级 Ⅲ级 Ⅰ级 „ CT 诊断 Ⅲ级 Ⅰ级 Ⅲ级 Ⅱ级 „ 疗效 好转 痊愈 显效 无效 „
H 1 (t 3 t p ) /( N 3 N ) p
p 1 m
三、单向有序RC表的统计分析
实例分析
表15 3种药物治疗某病患者疗效的观察结果 药物 种类 疗效： 治愈 A 15 例数 显效 49 好转 31 无效 5 合计 100
B
C 合计
4
1 20
9
15 73
50
45 126
二、双向无序RC表的统计分析
2检验的计算公式
2 i 1 j 1
R
C
A
ij
Tij Tij
2
v R 1 C 1
二、双向无序RC表的统计分析
实例分析
表10 不同专业学生的气质类型分布 例数 专业 计算机 金融 传媒
气质类型： 多血质
16 12 18
16 15.33
15.33 3.43
13 12.33
12.33
2
15 14
14
2
v R 1 C 1 3 1 4 1 6
二、双向无序RC表的统计分析
第三步，确定P值，给出结论。
查2界值表可知， 20.05,6 =12.59，而本 例中检验统计量的值3.43<12.59，故P>0.05。
表 8 100 例患者的临床诊断与 CT 诊断结果 临床诊断 Ⅰ级 Ⅱ级 Ⅲ级 患者例数 CT 诊断： Ⅰ级 60 4 3 Ⅱ级 4 12 3 Ⅲ级 2 3 9
当行变量与列变量的性质相同且取值的水平数及 含义也相同时，称这样的RC表为双向有序且属 性相同的RC列联表
双向有序且属性相同的RC表
二、双向无序RC表的统计分析
原因变量为多值名义变量，结果变量为二值变 量的R2表
表 13 药物种类 安慰剂 A药 B药 C药 D药 E药 合计 5 种药物治疗精神抑郁症的疗效 例数 疗效：改善 8 12 21 15 14 19 89 未改善 22 18 9 15 16 11 91 合计 30 30 30 30 30 30 180