分类资料统计分析
分类资料的统计分析
分类资料的统计分析一、概念分类资料是指观测对象按照其中一种特征进行分类或分组的数据。
常见的分类资料有性别（男、女）、学历（小学、初中、高中、大学）、职业（医生、教师、律师等）。
分类资料中每个分类称为一类或一组，根据组别统计频数或百分比可以揭示不同分类间的差异和关系。
二、方法1.频数与频率分析：通过统计每个类别的个数，得到各类别的频数和频率（频次比），并绘制柱状图、饼图等图表，直观地展示不同类别的占比情况。
2.极差分析：对于有序分类资料，比如学历，可以计算最高和最低值的差距，该差距称为极差。
极差分析衡量了不同类别之间的距离，有助于比较不同类别在一些变量上的差异。
3.交叉分析：用于分析两个或多个分类资料之间的关系。
通过交叉表格（列联表）和卡方检验，可以计算出各类别之间的关联度，判断不同分类是否相互关联。
4.分类资料的描述性统计分析：主要包括计算百分比、计算平均数、计算方差等统计指标。
通过这些指标，可以对不同类别的分布情况进行综合分析。
三、实践应用1.人口统计学：年龄、性别、婚姻状况等是人口统计学中常见的分类资料。
通过对这些资料的统计分析，可以了解人口结构、人口变动趋势等，为制定人口政策提供参考。
2.市场调研：对于市场调研中收集到的消费者分类资料，可以通过频数分析和交叉分析揭示不同人群的消费偏好和购买行为，帮助企业制定更加精准的销售策略。
3.教育评估：对学生的学历、家庭背景等进行统计分析，可以了解学生群体的整体素质水平、教育资源配置情况等，为教育政策制定和学校招生计划提供依据。
4.健康管理：对医疗数据中患者的病种、治疗效果等分类资料进行统计分析，可以评估不同病种的流行趋势、治疗效果、药物副作用等，为医疗决策提供参考。
总之，分类资料的统计分析是统计学中的重要内容，通过对分类资料的频数、频率、交叉分析等方法进行利用，可以揭示分类之间的差异、关系和趋势，为各个领域的决策者和研究者提供参考依据。
分类变量资料的统计分析.I
详细描述
市场调查中，分类变量常用于描述消费者的偏好、态度 和行为。例如，消费者对于某产品的品牌偏好、购买频 率、使用体验等都可以用分类变量来表示。对这些分类 变量进行分析，可以帮助企业了解市场需求、消费者行 为模式和产品优缺点，从而制定更有效的营销策略。
案例二：医学研究中的分类变量分析
总结词
医学研究中，分类变量常用于描述患者的疾病类型、治疗方式等。
比例与百分比
比例
某一类别的观察值数量与另一类别观察值数量的比值，用于比较不同类别的相对 大小。
百分比
某一类别的观察值数量与总观察值数量的比值乘以100，用于了解各类别的相对比 例。
集中趋势的度量
众数
出现次数最多的数值，反映数据的集 中趋势。
中位数
将数据从小到大排列后，位于中间位 置的数值，反映数据的集中趋势。
案例四：市场细分中的分类变量分析
要点一
总结词
要点二
详细描述
市场细分是市场营销中的重要概念，分类变量是市场细分 的重要依据。
市场细分是根据消费者的需求、行为和特征等因素将市场 划分为若干个具有相似性的子市场。分类变量是市场细分 的重要依据，例如消费者的年龄、性别、收入、职业等因 素都可以作为分类变量用于市场细分。通过对这些分类变 量的分析，企业可以更好地了解不同市场的需求特点，从 而制定更有针对性的营销策略，提高市场占有率和竞争力 。
总结词
社交网络分析中，分类变量常用于描述用户的行为、 关系和属性。
详细描述
在社交网络分析中，分类变量被广泛用于描述用户的 行为、关系和属性。例如，用户的行为可以分为发帖 、评论、点赞等类型；关系可以分为好友、关注、粉 丝等类型；属性可以包括用户的性别、年龄、职业等 。对这些分类变量进行分析，可以帮助研究者了解社 交网络的结构、用户行为模式和信息传播规律等，从 而更好地理解社交网络中的各种现象。
第十七章分类资料的统计推断
H0 ：1=2，… H1 ：12，… =0.05
（2）求检验统计量值
c2
a
ad bc n /
bc da
22 n
cb
d
251 7 27 60 / 22 60
32 28528
2.89 (2 1)(2 1) 1
(3) 确定P 值，作出推断结论
2 0.05,1
3.84
P>0.05….
• n ≥ 40，且Tmin ≥ 5时，用2检验基本公式和专用公式
• n≥ 40，但1≤Tmin<5时，用2检验校正公式 • n<40，或Tmin<1时，或P≈α用四格表Fisher确切概率法
校正公式：
2 c
( A T 0.5)2 T
( ad bc n)2 n
2 c
(a
b)(c
d )(a
阴性
b d
b+d
合计
a+b
c+d a+b + c+d
2
(ad bc)2 n
, 1
(a b)(c d )(a c)(b d )
为了不计算理论频数T, 可由基本公式推导出，直接由各 格子的实际频数（a、b、c、d）计算卡方值的公式：
基本公式abc
❖(3) 确定P 值，作出推断结论
查2界值表：
2 0.05,1
3.84
2 0.025,1
5.02
2 0.01,1
6.63
故P < 0.01，按=0.05的检验水准，拒绝 H0，接受H1，差别有统计学意义，可认为 女生的患病率高于男性。
二、四格表资料2检验的专用公式
组别 A组 B组
分类资料组间比较的统计方法选择与应用
分类资料组间比较的统计方法选择与应用在统计学中，分类资料组间比较是指对不同分类资料组之间的差异进行统计分析。
分类资料是指将个体按其中一种特征分组，而分类资料组是指这些不同特征组成的组。
此时，为了确定不同组之间的差异，我们需要选择适当的统计方法进行比较。
下面介绍几种常用的分类资料组间比较的统计方法选择与应用。
1.基本原则：在选择分类资料组间比较的统计方法时，需要根据变量的测定水平来确定，通常可以根据资料的测定水平来进行分类资料分析的方法选择。
对于分类资料，我们可以采用卡方检验分析，对于有序分类资料，我们可以采用秩和检验分析。
2.卡方检验：卡方检验适用于分类资料的比较，其基本思想是比较实际观测频数与理论频数之间的差异。
卡方检验有两种形式：独立性检验和拟合优度检验。
独立性检验用于检验两个或多个分类变量之间是否存在关联；拟合优度检验用于检验观测频数与理论频数之间的差异是否显著。
3.秩和检验：对于有序分类资料，我们可以采用秩和检验进行比较。
秩和检验的基本思想是将不同组之间的观测值按顺序排列，并将其转化为秩次，然后将秩次相加得到秩和，通过比较秩和的大小来判断不同组之间的差异是否显著。
4.t检验：当分类资料分为两个组进行比较时，可以采用t检验。
t检验的基本思想是通过比较两个组的均值差异来判断两个组之间的差异是否显著。
但是需要注意的是，t检验要求数据满足正态分布的假设，所以在进行t检验之前需要进行正态分布检验。
5.方差分析：当分类资料包含多个组时，可以使用方差分析进行比较。
方差分析的基本思想是比较组间方差与组内方差之间的差异，通过计算F值来判断不同组之间的差异是否显著。
方差分析也需要满足正态分布的假设。
6.非参数检验：如果数据不满足正态分布假设，或者样本量较小，可以使用非参数检验。
非参数检验不依赖于总体分布形式的假设，比如Mann-Whitney U检验适用于两个独立样本的比较，Kruskal-Wallis H检验适用于多个独立样本的比较。
医学统计方法—分类变量资料的统计分析
常用类型： ➢率（rate） ➢构成比（constituent ratio） ➢相对比（relative ratio），等
概念：又称频率指标或强度指标，是指某一现象在一定条件 下实际发生的例数与可能发生该现象的总例数之比，用以说 明某现象发生的频率或强度。
2
91 1 4.90
bc
9 1
（3）确定P值：
查
x
2界
值表，来自得x 2 0.05,1
3.84
x2 0.01,1
6.63。
现 x2 =4.90，x2> x20.05, 故 P＜0.05 （4） 做出推断结论：
按α＝0.05水准，拒绝H0 ，接受H1，差异有统计学 意义，可以认为两种培养方法的效果不同, A培养基 效果优于B培养基。
计算相对数时应有足够的样本含量； 资料分析时不能以构成比代替率； 资料的对比应注意其可比性； 样本率（或构成比）的比较应考虑抽样误差。
表 某年某医院两种疗法治疗某传染病各型的治愈率（%）
病型
新疗法
传统疗法
治疗例数 治愈例数 治愈率 治疗例数 治愈例数 治愈率
普通型 350
重型
150
217
药物 甲药 乙药 合计
表1 两药物疗效的比较
有效
无效
合计
65 (57.4) 17(24.6)
82
40 (47.6) 28 (20.4)
68
105
45
150
表内蓝体数字为实际頻数，括号里数字为 理论頻数，是假设两药物疗效无差别算得
若假设H0:π1=π2成立，四个格子的实际频数 A 与理论 频数 T 相差不应该很大，即统计量x2值不应该很大。如 果x2值很大，则反过来推断A 与T 相差太大，超出了抽样 误差允许的范围，从而怀疑H0的正确性，继而拒绝H0， 接受其对立假设 H1，即π1≠π2 。
12无序分类资料的统计分析
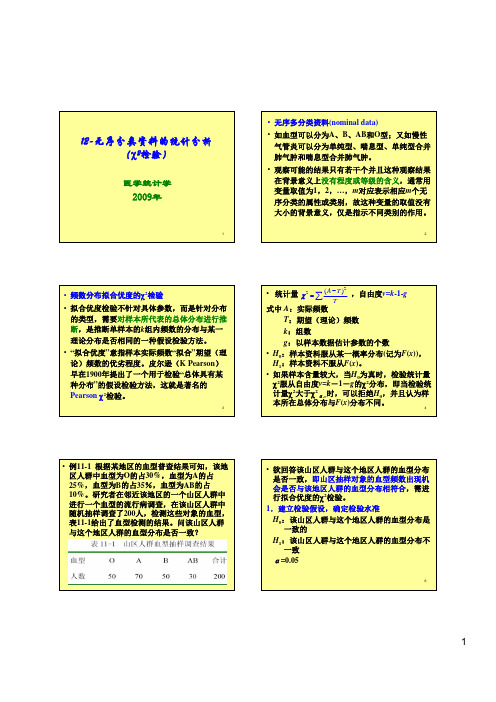
与这个地区人群的血型分布是否一致？53．计算χ统计量及自由度22()20.38A T Tχ−==∑10与消咳喘治疗慢性支气管炎的疗效是否相同？11数据，其余数据均由此派生。
13•一般地，R 行C 列的理论频数n ：总频数n R ：第R 行频数合计n C ：第C 列频数合计•两个独立样本率的比较可用基本公式•亦可用上述基本公式的展开式n n n T CR =∑−=TT A 22)(χ)1(22−=∑CR n n A n χ14•四格表专用公式•在此，式（11-1）、（11-3）及（11-4）等价。
•由于受到“行频数合计等于n ，且列频数合计等于n ”条件的约束，自由度为•对于两独立样本四格表资料，自由度22()()()()()ad bc na b c d a c b d χ−=++++）（列数）行数11(−×−=ν11212(=−×−=）（）ν151．建立检验假设，确定检验水准H 0：π1=π2，即两种药物治疗慢性支气管炎的疗效相同H 1：π1≠π2，即两种药物治疗慢性支气管炎的疗效不同α=0.05162．求检验统计量χ2值和自由度v•首先，计算a 、b 、c 、d 对应的理论频数。
•当然，在计算T 11基础上，其余三个理论数也可以按以下方式计算。
253.100237/19812011=×=T 747.19237/3912012=×=T 747.97237/19811721=×=T 253.19237/3911722=×=T 747.19253.10012012=−=T 747.97253.10019821=−=T 253.19747.9711722=−=T 17然后，计算检验统计量χ2值和自由度v•四个表专用公式：45.30 253.19)253.1935(747.97)747.9782(747.19)747.194(253.100)253.100116( )(222222=−+−+−+−=−=∑TT A χ1ν=×（2-1）（2-1)=222()()()()()(11635482)23730.44631(1164)(8235)(11682)(435)ad bc na b c d a c b d −=++++×−××==+×+×+×+χ183．确定P 值，下结论•查附表8，χ20.05,1=3.84，χ2=30.45>χ20.05,1，P<0.05，按α=0.05水准拒绝H 0，差别有统计学意义，可认为慢支口服液II 号治疗慢性支气管炎有效率高于消咳喘。
分类变量资料的统计分析 详细讲解
分类变量资料的统计分析详细讲解资料的统计分析通常包括描述统计和推断统计两个方面。
描述统计主要是对变量的单个特征进行分析，常用的统计指标包括频数、比例、均值、中位数、众数、标准差等；推断统计则是在样本数据的基础上推断总体数据的特征，常用的方法包括假设检验、方差分析、回归分析等。
本文将以分类变量为例，详细介绍分类变量资料的统计分析方法和步骤。
首先，分类变量是一种相互独立、不可顺序比较的变量，常见的示例包括性别、职业、学历等。
对于分类变量资料的统计分析，首先需要进行数据的整理和描述。
数据整理包括去除缺失值、异常值和重复值等处理。
应根据实际情况选择合适的处理方法，常用的方法有均值填充、删除等。
同时，需要将数据进行编码或离散化处理，便于后续的分析。
数据描述主要包括频数及比例的统计，可以用来描述分类变量的分布情况。
通过计算每个类别的频数和比例，可以获得分类变量的基本特征。
同时，可以使用图表来展示分类变量的分布情况，如饼图、柱状图等。
接下来，可以对分类变量与其他变量之间的关系进行分析。
常用的方法有卡方检验和列联表分析。
卡方检验适用于两个分类变量之间的关系检验，可以用来判断两个分类变量是否相关；列联表分析则可以用来描述两个分类变量之间的关系程度。
通过分析发现两个或多个分类变量之间的关联关系，可以更好地理解数据。
此外，对于分类变量的统计分析还可以进行组内和组间的比较。
组内比较主要是对同一分类变量的不同类别进行比较，常用的方法有t检验和方差分析；组间比较则是对不同分类变量之间的差异进行比较，可以使用相关分析和回归分析等方法。
最后，需要进行结果的解释和报告。
对分类变量资料的统计分析得出的结果进行解读，并进行相关性讨论。
通过各种统计方法对变量进行分析，报告结果可以提供决策者一个更全面的了解。
总结起来，分类变量资料的统计分析主要包括数据整理和描述、关联分析、比较分析和结果解释等步骤。
通过这些步骤可以更好地分析分类变量的特征、关系和差异，为实际问题的解决提供有力的支持和参考。
医学统计学课件：分类资料的统计描述
交叉表是一种更为复杂的表格形式 ，可以展示两个或多个分类变量之 间的关系，进一步分析变量之间的 关联。
分层资料的统计描述
分层平均数
对于分层资料，可以使用分层平 均数来描述各层内数据的平均水 平，通过比较不同层的平均数，
可以了解各层之间的差异。
层间方差
层间方差是用来衡量不同层次间 的变异程度，通过计算和比较层 间方差，可以了解各层次之间的
辅助决策制定
准确的分类资料统计描述 能够为决策制定提供有力 支持，帮助决策者了解情 况、制定合理方案。
分类资料统计描述的应用场景
临床研究
在临床研究中，分类资料 统计描述常用于分析患者 的疾病分布、治疗反应等 。
流行病学
流行病学中，分类资料统 计描述用于分析疾病的地 区分布、人群特征等。
公共卫生
公共卫生领域中，分类资 料统计描述用于监测和评 估公共卫生状况、健康问 题分布等。
动态数的计算与解读
动态数的计算
动态数是用来描述某一指标在不同时间点上的变化情况，通常通过将某一指标在 不同时间点的数值进行对比来计算。例如，某医院某年的治愈率与前一年的治愈 率之比。
动态数的解读
动态数的值越大，说明该指标的变化趋势越明显；反之，则越小。动态数可以用 来预测未来的发展趋势，以及评估政策或措施的效果。
相对数与动态数的应用场景
相对数在医学研究中应用广泛，如比较不同地区、不同时间 、不同人群的发病率、患病率、死亡率等指标，以了解疾病 在特定人群中的分布和发生情况。
动态数在医学监测和流行病学研究中应用较多，如监测某种 疾病的发病率、死亡率等指标的变化趋势，以及评估干预措 施的效果等。
04
统计图表在分类资料中的应用
在制作箱线图时，应将数据按照数值 大小进行排序，并使用合适的横轴和 纵轴尺度。
STATA软件操作(四)分类与等级资料的统计分析
STATA软件操作(四)分类与等级资料的统计分析STATA软件操作（四）分类与等级资料的统计分析在统计学中，数据可分为分类数据和等级数据。
分类数据是指事物被划分为不同的类别或类型，每个类别之间没有顺序或大小的关系。
而等级数据则是指事物按照某种特定的顺序或大小排列。
STATA是一款功能强大的统计分析软件，它提供了丰富的工具和函数，可以进行分类数据和等级数据的统计分析。
本文将介绍如何使用STATA软件进行分类与等级资料的统计分析。
一、分类数据的统计分析分类数据的统计分析主要包括频数和比例统计、列联表分析和卡方检验等。
下面以一个简单的示例说明如何用STATA软件进行分类数据的分析。
假设我们有一份调查问卷数据，其中包含了100个受访者的性别（男、女）和喜好的水果（苹果、香蕉、橙子）信息。
我们想要了解男女受访者喜好的水果分布是否存在差异。
首先，我们需要将数据导入STATA软件。
在STATA命令窗口中输入以下命令：```use "文件路径/文件名.dta"```接着，我们可以使用`tab`命令来计算频数和比例。
输入以下命令：```tab sex fruit```这样，STATA会输出一个包含性别和水果的频数表和比例表。
通过观察这些表，我们可以得到男女受访者对不同水果的喜好情况。
如果我们还想了解性别和喜好水果的关系是否显著，可以进行列联表分析和卡方检验。
输入以下命令：```tab sex fruit, chi2```STATA会输出一个包含列联表和卡方检验结果的表格。
通过观察卡方检验的p值，我们可以判断性别和喜好水果之间是否存在显著差异。
二、等级数据的统计分析等级数据的统计分析主要包括描述统计分析和推断统计分析。
下面以一个实例介绍如何使用STATA软件进行等级数据的分析。
假设我们有一份学生数学考试成绩数据，其中包含了100个学生的分数信息。
我们想要了解这些学生成绩的分布情况。
首先，我们需要将数据导入STATA软件。
分类变量资料的统计分析
分类变量资料的统计分析分类变量是一种在研究或分析中常见的类型数据，它描述了被观察个体或对象之间的不同特征，可以将其分为不同的类别或组。
在统计学中，对分类变量的分析可以帮助我们了解不同类别的分布情况、比较不同类别之间的差异、探索不同类别与其他变量之间的关系等。
本文将介绍分类变量资料统计分析的一些常用方法。
首先，我们可以通过计算频数和频率来描述分类变量的分布情况。
频数是指每个类别中观察到的个体或对象的数量，频率则是频数除以总数后的比例。
通过绘制条形图或饼图，可以直观地展示分类变量不同类别的频数或频率分布，帮助我们了解变量的整体情况。
其次，我们可以对不同类别之间的差异进行比较。
其中一种常用的方法是卡方检验，它用于检验两个或多个分类变量之间是否存在显著性差异。
卡方检验的原理是通过比较观察到的频数与期望频数之间的差异来判断差异是否显著。
比如，我们可以用卡方检验来确定两个不同群体之间的分布是否存在显著差异。
此外，分类变量的统计分析还可以探索其与其他变量之间的关系。
当我们有一个分类变量和一个或多个连续变量时，可以使用方差分析（ANOVA）来检验分类变量对连续变量的影响是否显著。
方差分析通过比较不同类别下的连续变量的均值来判断差异是否显著。
另外，我们还可以使用列联表分析来研究两个或多个分类变量之间的关联关系，例如，我们可以通过计算卡方值来确定两个分类变量之间的关联程度。
此外，还有一些其他常用的分类变量分析方法。
比如，在研究中，我们经常遇到多个分类变量之间的关联关系，可以使用多项Logistic回归模型来分析这些多分类变量之间的依赖关系。
另外，如果我们想预测或分类新的个体或对象所属的类别，可以使用分类树或逻辑回归等方法进行建模和预测。
综上所述，分类变量的统计分析是一种有价值的工具，可以帮助我们理解和揭示数据背后的模式和关联关系。
通过对分类变量的分布和差异进行描述分析，我们可以更好地理解数据，并从中提取有用的信息。
有序多分类数据的统计分析
有序多分类数据的统计分析有序多分类数据是指数据集中的变量具有多个有序类别的情况。
在统计分析中，对于这种类型的数据，我们需要采取相应的方法来进行分析和解释。
本文将介绍有序多分类数据的统计分析方法，包括描述性统计、推断统计和可视化分析等内容，帮助读者更好地理解和处理这类数据。
一、描述性统计分析描述性统计是对数据进行总体描述和概括的统计方法，可以帮助我们了解数据的基本特征。
对于有序多分类数据，我们可以通过计算频数、频率、众数、中位数、四分位数等指标来描述数据的分布情况。
此外，还可以计算累积频数和累积频率，以便更直观地展示数据的分布情况。
例如，假设我们有一组有序多分类数据，包括“低”、“中”、“高”三个类别，我们可以计算每个类别的频数和频率，然后绘制频数分布直方图或频率分布柱状图，以便直观地展示数据的分布情况。
二、推断统计分析推断统计是通过样本数据对总体进行推断的统计方法，可以帮助我们从样本数据中获取总体的信息。
对于有序多分类数据，我们可以进行卡方检验、秩和检验等方法来检验不同类别之间的关联性和差异性。
以卡方检验为例，假设我们想要检验两个有序多分类变量之间是否存在相关性，可以利用卡方检验来进行检验。
首先建立原假设和备择假设，然后计算卡方统计量，并根据显著性水平进行假设检验，从而判断两个变量之间是否存在显著相关性。
三、可视化分析可视化分析是通过图表、图形等可视化手段来展示数据的分布和关系，可以帮助我们更直观地理解数据。
对于有序多分类数据，我们可以利用条形图、箱线图、热力图等图表来展示数据的分布和关系。
例如，我们可以通过绘制箱线图来比较不同类别之间的中位数和四分位数，从而直观地展示数据的差异性。
此外，还可以利用热力图来展示不同类别之间的相关性，帮助我们发现变量之间的潜在关系。
综上所述，有序多分类数据的统计分析涉及描述性统计、推断统计和可视化分析等多个方面，通过综合运用这些方法，可以更全面地理解和解释这类数据。
分类变量资料统计分析
2、发展速度和增长速度 ①定基比发展速度 ②环比发展速度 ③定基比增长速度 ④ 环比增长速度
2020/7/10
11
常用相对数指标：
发病率＝某同时时期期内平某均病人新口病数例k数 患病率观 ＝察同期时间期患平某均病人 病 的口 例 新数 数 旧 k
第四章 分类变量资料的统计分析
统计分析统 统计 计推 描断 述
2020/7/10
1
第一节 分类变量资料的统计描述
一、常用的相对数指标 （一）构成比（proportion）
构成比即一事物内部各组成部分所占的比重 或分布。常用百分数表示。又称构成指标。
构成比 同＝ 某 一一 事组 物成 各部 组观 分 成位 察 的 部数 单 观 分位 察 1的0数 ％ 单 0
（1）研究对象是否同质 （2）其它影响因素在各组的内部构成是否相同 （3）同一地区不同时期资料的对比应注意客观
条件有无变化 5、样本率或构成比的比较应做假设检验
2020/7/10
16
三、率的标准化法
例4.4（ P54） 某省疾病控制中心欲进行甲、 乙两地某病总死亡率的比较，收集资料见表4-5。
2020/7/10
感染率＝感染受某检病人原数体人数 k 死亡率＝ 同 某年 年平 死均 亡人 总口 人k数 数
某病死(亡 疾率 病别死 )＝ 亡 某同 率 年年因平某均病人死 口 k亡数
某年龄组(年 死龄 亡别 率死 )＝同 亡 某年 率 年同 某年 年龄 龄组 数 组平 k死
某死因构成因比某 总 ＝类 死死 亡因 人死 数亡 10人 ％ 0 数
术前中性白细胞构成比是71.66％。
构成比的特点： ①各组成部分的构成比之和为100 ％或1。 ②事物内部某一部分的构成比发生变化，其它
分类数据处理的统计评析
否相 同。
表 的统计方法 当属 检验 ，９ ６
检验中的统计量是 ，而 是一种与 自由度有关的统 计量 ，它等于若干个标准正态分布变量的平方和Ⅲ ，但
验方 法不仅功能上有很 大差别，而且结果 的统计解释也存在比较大的差异。 关键词 ：分类数据 ；顺序数据 ； 检验 ；秩和检 验 正确认识 ｘ 检验的功能
一
、
对 的 。最 常见 的例 子是采 用 检验 进行两 组或 多组 有序分类资料 （ 也称为等级资料 ）的比较 ，而其 结论
时要谨 慎外 ，通常采用 Ｐ ａｓｎ 检验解决 上述 问题 ｅｒｏ 。 都 是可行 的 ，所 以在 计数资 料 的统计 处理 中 检验
际不符 。就上 面的例子把痊愈 、显效 、有效合并成 总 有效与无效分类 比较 ， 合并后 的数据如表 ３ ．
表 ３ 两种不 同疗法的总有效 率比较
应用 的比较广泛 。但也有人产生误 解 ，以为一切分类 计数资料的统计检验都可采用 。 检验 ，这显然是不
显然和实 际对疗效量化评价的等级不符 ，致 使从数据 获得的信息不仅粗糙 ，更主要 的是大多数情况下和实
正是基于上述理论基础 ， 在实际的分类计数资料作 两组或 多组样本率 的比较 、构成 比比较的统计检验都
采 用 Ｐ ａ ｏ 检验 。仅 当 自由度 为 １ ｅｒ ｎ ｓ ，且样 本量小
有差别 ，这和 检验所作的结果恰恰相反 。还有一些 类 似的问题 ，如有 的作者将疗效 的等级评价标准 中的 痊愈 （ 或控 制） 、显效 、有效合并 为总有效率来分析 ， 这 实际是把疗效视为两分类 ，变成 了有效与无效 ，这
有序分类资料的统计分析课件
推动不同数据源之间的融合与共享，以增 加有序分类资料的数据量。
建立统一的分类标准和方法，提高不同数 据源之间的可比性。
发展高级统计方法
研究和发展针对有序分类资料的高级统计 分析方法，以满足更复杂的数据分析需求 。
提高数据分析的透明度和可重复 性
通过制定标准操作程序和使用开源软件， 提高有序分类资料分析的透明度和可重复 性。
有序分类资料的统计分析课 件
目 录
• 有序分类资料的概述 • 有序分类资料的统计分析方法 • 有序分类资料的实际应用 • 有序分类资料的局限性及未来发展方向 • 案例分析
01
有序分类资料的概述
有序分类资料的概念
有序分类资料
有序分类资料是有等级差异的分 类资料，例如疾病程度、教育程 度等，每个类别之间存在顺序关 系。
特点
有序分类资料具有等级性和有序 性，各类别之间存在明确的顺序 关系，可以用于描述和比较不同 类别的优劣或程度差异。
有序分类资料的类型
等级资料
等级资料是有序分类资料的一种，按 照优劣或程度的不同分为不同的等级 ，例如疗效等级、病情严重程度等级 等。
计数资料
顺序资料
顺序资料是有序分类资料的一种，通 过将观察单位按照优劣或程度的不同 排序来描述数据，例如收入水平的排 序。
案例三：有序分类资料在社会学研究中的应用
总结词
社会学研究的有序分类资料分析
详细描述
在社会学研究中，有序分类资料常用于研究社会阶层、教育程度、职业类型等社会结构 变量。例如，将受访者的教育程度分为“小学及以下”、“初中”、“高中”、“大学 及以上”等类别，可以分析不同教育程度人群的就业、收入、消费等方面的差异，为社
谱系聚类
通过谱系聚类，将有序分类资料按照树状图的形 式进行分类。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
四格表资料的x2检验
100000
3
1.2
0.3
30~
96667
29
11.2
3.0
40~
63000
82
31.8
13.0
50~
24000
96
37.2
40.0
60 ~
6000
58
18.6
80.0
合计
289667 258
100.0
8.9
率的标准化
标准化法：为了消除相比较组间因构 成不同对所比较指标的影响，采用 统一的标准构成，使相比较的各组 在相同构成条件下进行比较。
相对数的概念
相对数（relative number）： 是描述分类变量资料的统计指标 用于分析比较
绝对数（absolute number）： 分类变量资料整理后所得到的数据 表示绝对水平
常用的相对数
1.率（rate） 又称频率指标或强度指标，说明某现象发生 的频率或强度。常以百分率（%）、千分率 （‰）、万分率（1⁄万）、十万分率（1⁄10 万）等表示
500 225 45.0
标准化率的计算
①选定标准：
标准组应根据研究目的选择有代表性的、稳 定的、数量较大的人群
一般可将相互比较的两组合并作为标准
②计算 已知标准组年龄别人口数时： P’
∑Nipi
已知标准组年龄别人口构成比时= ： N
③比较得出结论
Ni
P’=∑ （
N ）pi
表7-14某市甲、乙两医院某传染病标准化治愈率
医护人员 病床数
=
1436 875
=1.64
即每名医护人员平均负责1.64张病床
计划完成指标举例： 某县原计划在一个伤寒疫区对1500名 居民接种伤寒疫苗，而实际上接种了 1958人
1958 计划完成指标=
×100%=130.5%
1500
即完成了计划的130.5%或1.305倍
应用相对数应注意的问题
表7-13某市甲、乙两医院某传染病各型治愈率的比较
类型
甲医院
乙医院
病人数 治愈数 治愈率(%) 病人数 治愈数 治愈率（%）
普通型 300 180
60.0
100 65 65.0
重型 100 40
40.0
300 135 45.0
爆发型 100 20
20.0
100 25 25.0
合计 500 240
48.0
s u p1 p2 p1 p2
s p1 p2
11
pc
(1
pc
)( n1
n2
)
pc
X1 n1
X2 n2
卡方检验
x2检验：用来判断2个或2个以上的率之 间 差异是否具有显著性的统 计学方法
表7-16吸烟者与不吸者慢性支气管炎患病率比较 分组 患病人数 未患人数 合计 患病率（%）
表7-10某正常人的白细胞分类计数构成比
白细胞分类 分类计数
构成比（%）
中性粒细胞
140
70.0
淋巴细胞
50
25.0
单核细胞
5
2.5
嗜酸粒细胞
4
2.0
嗜碱粒细胞
1
0.5
合计
200
100.0
3.相对比（relative ratio） 表示两个有关指标之比，常以倍数或百分 比表示
甲指标
相对比=
（或×100%）
类型 标准
甲医院
乙医院
病人数 原治愈率 预期治愈人数 原治愈率 预期治愈人数
普通型 400 60.0
240
65.0
260
重型 400 40 .0
160
45.0
180
爆发型 200 20 .0
40
25.0
50
合计 1000 —
440
—
490
表7-15某市甲、乙两医院某传染病标准化治愈率
类型 标准
甲医院
1.计算相对数时分母不宜过小 2.分析时不能以构成比代替率 3.观察单位不等的几个率，不能直接相加求
其总率 4.比较相对数时应注意资料的可比性 5.对样本率的比较应随机抽样，并作假设检
验
表7-11某地各年龄组妇女宫颈癌患病情况统计
年龄（岁）检查人数 患者数 患者构成比 （%） 患病率(1/万)
<30
总体率95%CI： p 1.96 s p
总体率99%CI： p 2.58 s p
2.查表法
当样本含量n较小（ n ≤50）；样本 率 p≥0.01时查百分率的可信区间表， 直接得出总体率的可信区间
率的u检验
1.样本率与总体率比较的u检验
p p
u
p (1 )
n
2.两样本率比较的u检验
★选定的标准构成不同，所得标化 率也不同，因此仅限于采用共同 标准构成的组间比较。
率的抽样误差与标准误
理论值 估计值
p
(1 )
n
sp
p(1 p) n
总体率的可信区间
1.正态近似法 当样本含量n（ n >50）足够大；样本率p、 1－p均不小（np、n（1－p）均≥5）时， 样本率的分布近似正态分布
5.09
乙 75135
264
3.51
丙 118730
466
3.92
合计 292605
1233
4.21
2.构成比（constituent ratio）
又称构成指标，说明某一事物内部各组成 部分的比重或分布。常以百分数表示
某一组成部分的观察单位数
构成比=
×100%
同一事物各组成部分的观察单位总数
注意：各组成部分构成比之和为100%
乙医院
病人构成 原治愈率 分配治愈率 原治愈率 分配治愈率
普通型 0.4
60.0
24.0
65.0
26.0
重型 0.4
40 .0
16.0
45.0
18.0
爆发型 0.2
20 .0
4.0
25.0
5.0
合计 1.0
—
44.0
—
49.0
注意：★标准化率不能反映率的实际水平， 只能表明相互比较资料间的相对 水平。
乙指标
注意： ★甲乙两指标可以性质相同，也可 以性质不同，如RR、CV。
★两指标可以是绝对数、相对数或 平均数
★习惯上，若甲>乙，用倍数表示； 若甲<乙，用百分数表示
常用： ●对比指标：两同类事物某种指标 的比
●关系指标：两非同类但相关的事 物数量的比
●计划完成指标：说明计划完成的 程度
关系指标举例： 某医院1995年医护人员为875人 同年平均开病床1436张
发生某现象的观察单位数
率=
×100%（或…）
可能发生某现象的观察单位总数
注意：★据医学习惯用法 ★一般至少保留一、二位整数
常用：●出生率、死亡率、发病率、患病率 （习惯上用‰）
●病死率、治愈率（习惯上用%）
表7-9 某年某市三个区的肠道传染病发病率
区 人口数 发病数 发病率(%)
甲 98740
503