物理化学 计算题
物理化学习题-含答案
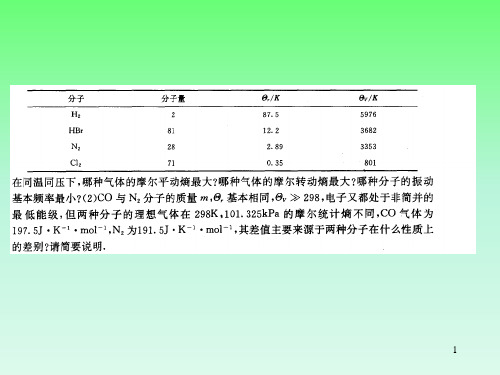
基态是单态。计算在298K、1atm下一氧化碳气体的 摩尔熵值。
7
解:由于CO气体为非定位体系,其熵公式为:
ln Q Q NkT S k ln N! T
N
ln Q Nk ln Q k ln N! NkT T
可将其看成是体系的平动熵、转动熵、振动熵及电子熵等之 和。可先分别求出各运动形式的熵、再求和而得体系的总熵 。上式的-k lnN! 项归入平动熵计算。
32
将题中给出的数据直接代入上式得:
Q转
2 8 1.1461045 1.381023 298 (3.1416 )
2 (6.62610
34 2
)
424
5
(3)如果将分子看成是谐振子,则有
Q振 1 1 e h kT 1 1 e h c kT
由题意知,
565cm1 565102 m1
~
1 代入上式得: Q振 6.6261034 565102 2.998108 1 exp[ ] 23 1.3810 298
1
1 e
2.73
1.07
6
计算题
2.已知一氧化碳分子的转动惯量是
I 1.451046 kg m2 ~ 1 基本振动波数 2170cm ,分子量为 28.0,其电子
2170cm1 217000 m1
ln Q h c e h c kT T kT2 1 e h c kT
12
将数据代入得
ln Q振 T
计算题
10.5 e10.5 0 10.5 298 (1 e )
S振 R ln Q振 RT T 8.314 ln 1 8.314 298 0 0
物理化学试卷及答案3套

物理化学试卷及答案3套三、计算题( 共5题60分)21. 10 分(0824)计算1mol He(理想⽓体) 在下列状态变化过程中的ΔH和ΔG。
He (101.325 kPa,473 K)??→He (101.325 kPa,673 K)已知:C p, m [He(g)] = (5/2)R,473K 时S m$[He(g)] = 135.1 J·K-1·mol-1。
22. 15 分(1104)某⽓体状态⽅程为pV = n(RT + Bp),始态为p1T1,该⽓体经绝热真空膨胀后终态压⼒为p2,试求该过程的Q,W及⽓体的ΔU,ΔH,ΔF,ΔG,ΔS。
23. 10 分(1809)两液体A, B形成理想液体混合物。
在320 K,溶液I含3 mol A和1 mol B,总蒸⽓压为:5.33×104 Pa。
再加⼊2 mol B 形成理想液体混合物II,总蒸⽓压为6.13×104 Pa。
(1) 计算纯液体的蒸⽓压p A*,p B*;(2) 理想液体混合物I的平衡⽓相组成y B;(3) 理想液体混合物I的混合过程⾃由能变化Δmix G m;(4) 若在理想液体混合物II中加⼊3 mol B形成理想液体混合物Ⅲ,总蒸⽓压为多少?24. 15 分(2419)固体CO2的蒸⽓压与温度间的经验式为:ln(p/Pa)=-3116 K/T + 27.537已知熔化焓?fus H m= 8326 J·mol-1,三相点的温度为217 K。
试求出液体CO2的蒸⽓压与温度的经验关系式。
25. 10 分(2965)3H2+ N2= 2NH3在350℃的K p= 6.818×10-8(kPa)-2,并设与压⼒⽆关,从3:1的H2,N2混合物出发,在350℃下要获得物质的量分数为0.08 的NH3,压⼒⾄少要多⼤?26. 13 分(0957)4 g Ar(可视为理想⽓体,其摩尔质量M(Ar)=39.95 g·mol-1)在300 K时,压⼒为506.6 kPa,今在等温下反抗202.6 kPa的恒定外压进⾏膨胀。
物理化学习题

物理化学习题题目一某物质的熔点为100°C,沸点为200°C。
若将36g的该物质从液态加热到气态,需要吸收多少热量?已知该物质的熔化热为40 cal/g,汽化热为80 cal/g。
解答:首先计算熔化过程需要的热量。
根据熔化热的定义,熔化过程需要的热量可以通过以下公式计算:Q = m * ΔHf其中,Q为热量,m为物质的质量,ΔHf为熔化热。
将已知数据代入公式计算:Q1 = 36g * 40 cal/g = 1440 cal接下来计算汽化过程需要的热量。
根据汽化热的定义,汽化过程需要的热量可以通过以下公式计算:Q = m * ΔHv其中,Q为热量,m为物质的质量,ΔHv为汽化热。
将已知数据代入公式计算:Q2 = 36g * 80 cal/g = 2880 cal所以,将36g的该物质从液态加热到气态需要吸收的总热量为:Q总 = Q1 + Q2 = 1440 cal + 2880 cal = 4320 cal题目二某有机物A的摩尔热容为25 J/(mol·K),某有机物B的摩尔热容为40J/(mol·K)。
已知在一定温度下,物质A和物质B的摩尔比为1:2,试求混合物的摩尔热容。
解答:首先计算物质A和物质B在混合物中所占的摩尔数。
根据题目中给出的摩尔比,我们可以设物质A的摩尔数为x,物质B的摩尔数为2x。
根据摩尔热容的定义,摩尔热容可以通过以下公式计算:C = Q / (n * ΔT)其中,C为摩尔热容,Q为热量,n为物质的摩尔数,ΔT为温度变化。
将物质A和物质B的摩尔热容代入公式计算:C_A = 25 J/(mol·K) C_B = 40 J/(mol·K)混合物的总摩尔数为x + 2x = 3x。
根据题目中给出的温度变化,假设为ΔT,混合物的热量可以通过以下公式计算:Q = C_A * n_A * ΔT + C_B * n_B * ΔT将已知的摩尔热容和摩尔数代入公式计算:Q = 25 J/(mol·K) * x * ΔT + 40 J/(mol·K) * 2x * ΔT = 25x ΔT + 80x ΔT = 105x ΔT所以混合物的摩尔热容为:C_混合物 = Q / (n_混合物* ΔT) = (105x ΔT) / (3x * ΔT) = 35 J/(mol·K)题目三某物质的密度为2.5 g/mL,摩尔质量为40 g/mol。
物理化学计算题(2003版本)

第一、二章:热力学1. 2mol 单原子理想气体在298.2K 时,分别按下列三种方式从15.00dm 3膨胀到40.00dm 3:1)等温可逆膨胀;2)等温对抗100kPa 外压;3)在气体压力与外压力相等并保持恒定下加热。
求三种过程的Q\W\ΔU 和ΔH 。
解:1) 因为理想气体的热力学能和焓都只是温度的函数,所以等温过程ΔU=ΔH=0W=-nRTln =-2*8.314*298.2ln =-4863 JQ=-W=4863 J2) 同理,ΔU=ΔH=0W=-p e (V 2-V 1)=-100*103*(40.00-15.00)*10-3=-2500 JQ=-W=2500 J3) 气体压力为:P= = =330.56kPaW=-330560*(40.00-15.00) *10-3=-8264JT 2= = =795.2KΔH=Qp=nC p,m (T2-T1)=n* R(T2-T1)= 2* *8.314*(795.2-298.2)=20660 JΔU=nC v,m (T2-T1)= 2* *8.314*(795.2-298.2)=12396 J或 ΔU=Q+W=20660-8264=12396 J2. 3mol 单原子理想气体从300K ,400kPa 膨胀到最终压力为200kPa.若分别经1)绝热可逆膨胀;2)绝人等外压200kPa 膨胀至终态。
试计算两种过程的W/E/ΔU/ΔH.解:1) 此过程的始、终态如下:绝热可逆膨胀对于单原子理想气体,则:r=C p,m /C v,m =(5/2R)/(3/2R)=5/3=1.67据理想气体的绝热可逆过程方程求T2T 1r p 11- r = T 2r p 21- r 代入T 1\p 1\p 2求得:3001.67*4001-1.67=T 21.67*2001-1.67T 2=227K因为绝热过程,Q=0,则:W= ΔU=nC v,m (T 2-T 1)=3*3/2*8.314*(227-300)=-2731JΔH=nC p,m (T 2-T 1)=3*5/2*8.314*(227-300)=-4.552J2) 此过程为绝热不可逆过程,始、终态如下:绝热等膨胀因为绝热过程,Q=0,则:W= ΔU=nC v,m (T 2-T 1)W=-p e (V2-V1)=-p2(V2-V1)V2= V1=所以W= ΔU=nC v,m (T 2-T 1)=-p 2( )3*3/2*8.314*(T 2-300)=-3*8.314*T 2+200/400*3*8.314*300T2=240KW= ΔU=nC v,m (T 2-T 1)=3*3/2*8.314*(240-300)=-2245JΔH=nC p,m (T 2-T 1)=3*5/2*8.314*(240-300)=-3741J3. 试求100kPa 、1mol 的286K 过冷液体苯变为固体苯的ΔS ,并判断此凝固过程是否可能发生。
03 物理化学练习题计算题new(4)

物理化学练习-计算题一计算题1. (13分)已知水在100℃及标准压力下蒸发焓为2259 J/g,求1mol100 ℃及标准压力的水变为100 ℃、5*104Pa的水蒸气之△U、△H、△A、△G。
2. 10 分H2,N2与100 g水在313 K时处于平衡态,平衡总压为105 378 Pa,平衡蒸气经干燥后,含H2 40%(体积分数),假设溶液上方水的蒸气压等于纯水的蒸气压,即313 K时为7376.5Pa。
计算313 K时溶解的H2,N2的质量。
已知313 K时,H2和N2的亨利常数分别为7.61×109 Pa和1.054×1010 Pa。
3. 10 分NaCl-H2O所组成的二组分体系。
在 -21℃时有一个低共熔点。
此时,冰、NaCl·2H2O(s)和浓度为22.3% (质量分数) 的NaCl水溶液平衡共存。
在 -9℃时不稳定化合物(NaCl·2H2O)分解,生成无水NaCl和27%的NaCl水溶液。
已知无水NaCl在水中的溶解度受温度的影响不大 (当温度升高时,溶解度略有增加)。
(1) 试绘出相图,并指出各部分存在的相态;(2) 若有1000g28%的NaCl 溶液,由160℃冷到 -10℃,问此过程中能析出多少纯NaCl?(3) 以海水(含2.5% NaCl ) 制取淡水,问冷到何温度时析出淡水最多?4. 10 分1 mol 单原子分子理想气体经过一个绝热不可逆过程到达终态,该终态的温度为273(273K) = 188.3 J·K-1·m ol-1。
K,压力为p ,熵值为Sm已知该过程的S m= 20.92 J·K-1·m ol-1,W = 1255 J。
(1) 求始态的p1,V1,T1;(2) 求气体的ΔU, ΔH, ΔG。
5. 10 分假定温度是80.1℃(即苯的沸点),并设蒸气为理想气体。
求下列各过程中,苯的ΔF和ΔG(设为1mol)。
物理化学期末考题(四,计算题参考答案)

仅供参考,请勿外传计算题参考答案1.1mol 单原子理想气体的始态为300K ,500kPa 。
(1)在等温条件下向真空膨胀至100kPa ,求此过程的Q 、W 、U ∆、H ∆、S ∆、A ∆、G ∆。
(2)在恒压条件下,体积增至原来的两倍(V 2=2V 1), 求此过程的Q 、W 、U ∆、H ∆、S ∆。
解:(1) 因为向真空膨胀,等温过程,故:01=Q ,01=W ,01=∆U ,01=∆HJ 4014kPa500kPa100ln K 300K mol J 8.314mol 1ln111211-=⨯⨯⋅⋅⨯==∆=∆--p p nRT G A 111211K J 38.13kPa100kPa 500ln K mol J 8.314mol 1ln---⋅=⨯⋅⋅⨯==∆p p nR S (2) 因为12212,V V p p ==,所以,由111222T V p T V p =,得K 600212==T T J 6236K 300)(600K m o l J 8.31425m o l 1)(1112m ,22=-⨯⋅⋅⨯⨯=-==∆--T T nC Q H p J 3741K 300)(600K m o l J 8.31423m o l 1)(1112m ,2=-⨯⋅⋅⨯⨯=-=∆--T T nC U V J 2495J 6236J 3741222-=-=-∆=Q U W1K600K300m,m ,2K J 4.14K300K600ln 8.314251d 1d 21-⋅=⨯⨯=⨯==∆⎰⎰T TC T TnC S p T T p2.1mol 理想气体,始态压力202650Pa ,体积为22.4dm 3,连续经历下列三个过程达到终态。
(1) 从始态可逆膨胀至B ,其压力为101325Pa ;(2)从B 再等容加热至C ,其温度为1091.9K ; (3)从C 再在等压条件下冷却至终态D ,其温度为545.9K 。
物理化学试题集计算题
在298.15K 及p θ下,过冷水蒸气变为同温同压下的水,求此过程的⊿G 。
已知298.15K 时水的饱和蒸气压为3167Pa 。
解:⊿G=⊿G 1+⊿G 2+⊿G 3=J85901013253167ln15.298314.81ln021122112-=⨯⨯⨯==≈++⎰⎰⎰p p g p p l p p g p p nRT dp V dpV dp V或J23.8588)3167101325(110018.01013253167ln15.298314.81)(ln032112211221-=-⨯++⨯⨯⨯=-+=∆+=++-⎰⎰⎰p p l l g p p l p p g p p V p p nRT P V dp V dp V dp V在298.15K 及p θ下,过冷水蒸气变为同温同压下的水,求此过程的⊿G 。
已知298.15K 时水的饱和蒸气压为3167Pa 。
1.已知反应C(石墨)+CO 2(g)=2CO(g)r m G θ∆(1000K) =-3.4 k J ·mol -1,计算(1) 1000K 时该反应的平衡常数。
(2)当p (CO)=200kPa, p (CO 2)=800kPa 时,判断该反应方向。
解:(1)410775.11000314.8303.24.3)1000(lg -⨯=⨯⨯--=K K θK θ=1.00(2)方法一2.303lg r m G RT Kθθ∆=-∵⊿r G m(1000K)<0,∴反应正向自发进行方法二Q=(200/100)2/(800/100)=4/8=0.5Kθ=1.00∵Q<Kθ∴反应正向自发进行某抗菌素在人体内的代谢反应为一级反应,若服药后每24小时药物代谢一半,而药物代谢20%则必须补充该药,问第二次服药时间?解:t1/2=0.693/kk=0.693/24=0.028875(小时)-1ln(C0/CA)=ktt=7.73(小时)Zn-Hg(含Zn10%)∣ZnSO4·7H2O(s)饱和溶液‖Hg2SO4(s)(饱和溶液)∣Hg(l)。
物理化学考研题库计算题及答案
物理化学考研题库计算题及答案物理化学考研题库计算题及答案在物理化学的考研中,计算题占据了很大的比重。
掌握好计算题的解题方法和技巧,对于提高分数至关重要。
本文将介绍一些常见的物理化学考研计算题及其解答方法,希望对考生有所帮助。
一、热力学计算题1. 根据给定的反应热和反应物的摩尔数,计算反应物的标准摩尔焓变。
解答方法:根据反应热的定义,可以得到反应物的标准摩尔焓变公式为ΔH = ΔH反应/反应物的摩尔数。
根据题目给出的数据,代入公式中即可计算出反应物的标准摩尔焓变。
2. 根据给定的物质的热容和温度变化,计算物质的热量变化。
解答方法:根据热容的定义,可以得到物质的热量变化公式为Q = mCΔT,其中Q为热量变化,m为物质的质量,C为物质的热容,ΔT为温度变化。
根据题目给出的数据,代入公式中即可计算出物质的热量变化。
二、量子化学计算题1. 根据给定的波长和速度,计算光的频率。
解答方法:根据光的速度公式v = λf,其中v为光的速度,λ为光的波长,f为光的频率。
根据题目给出的数据,代入公式中即可计算出光的频率。
2. 根据给定的电子的能级差和普朗克常数,计算电子的能量。
解答方法:根据能量和频率的关系E = hf,其中E为能量,h为普朗克常数,f 为频率。
根据题目给出的数据,代入公式中即可计算出电子的能量。
三、动力学计算题1. 根据给定的反应速率常数和反应物的浓度,计算反应速率。
解答方法:根据反应速率的定义v = k[A],其中v为反应速率,k为反应速率常数,[A]为反应物的浓度。
根据题目给出的数据,代入公式中即可计算出反应速率。
2. 根据给定的反应速率和反应物的浓度,计算反应速率常数。
解答方法:根据反应速率的定义v = k[A],可以得到反应速率常数公式为k = v/[A]。
根据题目给出的数据,代入公式中即可计算出反应速率常数。
以上是物理化学考研中常见的计算题及其解答方法。
在解题过程中,注意理清思路,将题目所给的数据代入相应的公式中,正确计算出结果。
物理化学试题及答案
物理化学试题之一一、选择题(每题2分,共50分,将唯一的答案填进括号内)1。
下列公式中只适用于理想气体的是1. BA。
ΔU=Q V B. W=nRTln(p2/p1)(用到了pv=nRT) C。
ΔU= D. ΔH=ΔU+pΔV2。
ΔH是体系的什么 2. CA。
反应热 B。
吸收的热量C。
焓的变化 D。
生成热3.2000K时反应CO(g)+1/2O2(g)=CO2(g)的K p为6.443,则在同温度下反应为2CO2(g)=2CO(g)+O2(g)的K p应为3。
CA. 1/6。
443 B。
(6.443)1/2 C. (1/6.443)2 D. 1/(6.443)1/24。
固态的NH4HS放入一抽空的容器中,并达到化学平衡,其组分数、独立组分数、相数及自由度分别是A。
1,1,1,2 B. 1,1,3,0 C. 3,1,2,1D。
3,2,2,25。
下列各量称做化学势的是A。
B。
C. D。
6. A和B能形成理想溶液。
已知在100℃时纯液体A的饱和蒸汽压为133.3kPa, 纯液体B的饱和蒸汽压为66.7 kPa,当A和B的二元溶液中A的摩尔分数为0.5时,与溶液平衡的蒸气中A的摩尔分数是A。
1 B. 0.75 C。
0.667 D. 0.57。
理想气体的真空自由膨胀,哪个函数不变?A.ΔS=0B. V=0 C。
ΔG=0 D.ΔH=07。
D( ) 8. A、B两组分的气液平衡T—x图上,有一最低恒沸点,恒沸物组成为x A=0。
7。
现有一组成为x A=0.5的AB液体混合物,将其精馏可得到A. 纯A和恒沸混合物B。
纯B和恒沸混合物 C. 只得恒沸混合物 D. 得纯A和纯B8. B( )9。
实验测得浓度为0。
200mol·dm-3的HAc溶液的电导率为0。
07138S·m-1,该溶液的摩尔电导率Λm(HAc)为9。
BA. 0。
3569S·m2·mol—1B。
0.0003569S·m2·mol—1C。
物理化学计算题及问题详解
第一章例4 在100℃,p ψ下,1mol 水(1)可逆蒸发, (2)向真空蒸发为蒸气。
已知 ∆vap H m ψ = 40.7 kJ ⋅mol-1, 假设蒸气为理想气体,液体水的体积可忽略不计,求Q, W, ∆U, ∆H 。
解:(1) ∆H = Qp = 40.7kJW = -p ψ ∆V = -p ψV g =- RT = -3.1kJ∆U = Q-W =(40.7-3.1)kJ = 37.6kJ(2) 始终态同(1) 故∆H = 40.7kJ ∆U = 37.6kJ向真空蒸发W = 0Q = ∆U = 37.6kJ例5 将100g,40℃水和100g, 0℃的冰在杜瓦瓶中(恒压,绝热)混合,求平衡后的状态,及此过程的∆H 。
已知冰的熔化热 =335J ⋅g-1 ,Cp (水)= 4.18 J ⋅K-1⋅g-1解:设水和冰为系统。
因恒压,绝热所以∆H = Qp = 0又 ∆H =∆H (水) + ∆H (冰) = 0设终态温度为T∆H =∆H (水) + ∆H (冰)=100⨯4.18⨯(T – 313)+ 100⨯335=0T = 253K ???该结果是不可能的!100g 水全部降温至0℃,放热:∆H (水)= – 100⨯4.18⨯40 = –16.7kJ100g 冰全部融化吸热:∆H (冰)=33.5kJ说明冰不能全部融化,终态应是0℃的冰水混合物。
设 m 克冰融化,∆H =∆H (冰)+∆H (水)= m ⨯0.335-16.7=0m = 50g平衡后的状态为50g 冰和150g 水的0℃的冰水混合物。
例6 已知某气体的状态方程为: pV m = RT + bp (b >0常数) 请依据推导结果判断(1)在绝热自由膨胀过程中,该气体的温度如何变化?(2)在绝热节流膨胀过程中,该气体的温度如何变化? 解:(1) 绝热自由膨胀过程是等内能过程,∆U =0,则 所以本题要解的是μJ 的正负? 令U =f (T, V ),根据循环关系式:现在只要判断[ ]是>0, =0, 还是<0?其中的偏微商 与气体的状态方程有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理化学 计算题1.1mol 单原子理想气体,由298K 、5p 的始态膨胀到压力为p 的终态,经过下列途径:⑴等温可逆膨胀;⑵外压恒为p 的等温膨胀;⑶绝热可逆膨胀;⑷外压恒为p 的绝热膨胀。
计算各途经的Q 、W 、∆U 、∆H 、∆S 、∆A 与∆G 。
巳知m S (298K) = 126 J·K -1·mol -1 。
解:(1)等温过程:ΔU = ΔH = 0,J5.3987K J 38.132985.3987J 5.3987J 5.39875ln 298314.81ln 1-R 21-=∆=∆⋅===∆-==⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=-=G A T Q S W p p nRT W Q ,;(2) ΔU = ΔH = 0,()()221118.31429810.21982J p Q W p V V RT p ⎛⎫=-=-=-=⨯⨯-= ⎪⎝⎭J 5.3987KJ 38.13ln 1-21-=∆=∆⋅=⎪⎪⎭⎫ ⎝⎛=∆A G p p nR S , (3) K 8.1565298355212112=⨯=⎪⎪⎭⎫ ⎝⎛==--γγγp p T T , ()()()()()()()J129652988.1566.1122934J143182988.1566.1121761K J 6.1125ln 126ln 2980J1761J 29342988.15625J 17612988.1562312121-2121m ,m ,=-⨯--=--∆=∆=-⨯--=--∆=∆⋅=-=⎪⎪⎭⎫ ⎝⎛-===∆-=∆=-=-⨯=∆=∆=-=-⨯=∆=∆T T S H G T T S U A R p p R K S S S S U W R T nC H Q R T nC U p V ,,,(4) ()()12212230V V p T T R W U Q --=-=∆=,,()()()()()()()()()J76612986.1126.2021181983J84542986.1126.2021181190K J 11836.56.112K J 6.112K J 36.5ln ln J19832986.20225J 19902986.20223K 6.2025129829823112211221-121-11-2112m ,12m ,12m ,222=⨯-⨯--=--∆=∆=⨯-⨯--=--∆=∆⋅=+=∆+=⋅=⋅=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∆-=-⨯=-=∆=-=-⨯=-=∆=⎪⎭⎫ ⎝⎛⨯--=-T S T S H G T S T S U A S S S S p p nR T T nC S R T T nC H WR T T nC U T T R T R p p V ,,2.10mol H 2(理想气体),C V ,m = 5/2R J·K -1·mol -1,在298K 、p ө时绝热可逆地压缩到10p ө,计算该过程的Q 、W 、∆U 、∆H 、∆S 、∆F 和∆G 。
巳知 m S (298K) = 130.59 J·K -1·mol -1 。
解:3.银可能受到的腐蚀而发生下列反应:H 2S(g)+2Ag(s) = Ag 2S(s)+H 2(g)今在298K 和标准压力Pθ下,将银放在等体积的氢和H 2S 组成的混合气中。
已知:298K 时,Ag 2S(s)和H 2S(g)的标准生成吉布斯自由能分别为-40.26和-33.02kJ.mol -1。
试问是否可能发生腐蚀而生成硫化银。
在混合气中,硫化氢的百分数低于多少,才不致发生腐蚀? ⑴ 判断Ag 能否被腐蚀而生成Ag 2S,就是判断在给定的条件下,所给的反应能否自发进行。
可以计算ΔG 值,由ΔG 的正、负来判断,也可以计算反应的平衡常数K ,再比较K与Qa 的大小来判断。
用ΔG 判断:ΔG=ΔG+RTlnQa该复相反应Qa=Qp ,Qp 为指定条件下的压力商,其值为其中摩尔分数之比等于体积百分数之比。
此时 ΔG=ΔG=ΔGf ,Ag 2S(S)-ΔG f ,H 2S(g) =-40.25+32.93 =-7.32KJ/molΔG<0,故在该条件下,Ag 能被腐蚀而生成Ag 2S ⑵ 若使Ag 不致被腐蚀,应使ΔG≥0,即Qa≥K 设此时H 2S 的体积百分数为X,则H 2的百分数为1-X 。
则Q a =(1-X )/X Q a ≥K,即(1-X )/X>=19.15 解得 X≤4.96%即在混合气体中,H 2S 的百分数低于4.96%时,才不致发生腐蚀。
4.在Hittorf 迁移管中,用Cu 电极电解已知浓度的CuSO 4溶液。
通电一定时间后,串联在电路中的银库仑计阴极上有0.0405 g Ag(s) 析出。
阴极区溶液质量为36.434 g ,据分析知,在通电前其中含CuSO 4 1.1276 g ,通电后含CuSO 4 1.109 g 。
试求2+Cu 和 24SO -的离子迁移数。
解法1:先求2+Cu 的迁移数,以2+Cu 为基本粒子,已知:14(CuSO )159.62 g mol M -=⋅14()0.0405 g/(2107.88 g mol ) 1.877110 mol n --=⨯⋅=⨯电 13() 1.1276 g/159.62 g mol 7.064310 mol n --=⋅=⨯始 13() 1.109 g/159.62 g mol 6.947610 mol n --=⋅=⨯终阴极上2+Cu 还原,使2+Cu 浓度下降 2+Cu2e Cu(s)-+→()()()()n n n n =+-终始迁电 5()7.1010 mol n -=⨯迁2+()(Cu )0.38()n t n ==迁电 24(SO )10.62t t -+=-= 解法2:先求2-4SO 的迁移数,以2-41SO 2为基本粒子。
阴极上2-4SO 不发生反应,电解不会使阴极区2-4SO 离子的浓度改变。
电解时2-4SO 迁向阳极,迁移使阴极区2-4SO 减少。
((n n n =-终)(始)迁)(mol n ⨯-4求得迁)=2.33102-4((SO )0.62()n t n ==迁)电 10.38t t +-=-= 解法3:如果分析的是阳极区的溶液,基本计算都相同,只是离子浓度变化的计算式不同。
(1)阳极区先计算2+Cu 的迁移数,阳极区Cu 氧化成2+Cu ,另外2+Cu 是迁出的,()()()()n n n n =+-终始电迁(2)阳极区先计算24SO -迁移数,阳极区24SO -不发生反应,24SO -迁入。
()()()n n n =+终始迁5.用银电极电解 KCl 水溶液。
电解前每 100g 溶液中含 KCl 0.7422g 。
阳极溶解下来的银与溶液中的 Cl - 反应生成 AgCl(S),其反应可表示为 Ag→Ag ++e -,Ag ++Cl -→AgCl(S),总反应为 Ag +Cl -→AgCl(S)+e -。
通电一定时间后,测得银电量计中沉积了 0.6136g Ag ,并测知阳极区溶液重 117.51g ,其中含 KCl 0.6659g 。
试计算 t (K +) 和 t (Cl -)。
解: 对于只含一种正离子和一种负离子的电解质溶液,只需求出其中任一种离子的迁移数即可。
由 Ag 电量计上析出的 Ag 计算通过电解池电荷的物质的量n =0.6136g/107.87g·mol -1=5.688x10-3mol设阳极区水的量在电解前后不变。
W 水(阳极区)=(117.51-0.6659)g =116.844g电解前后 Cl - 的物质的量为6.电池Pt,H2( pө)|HBr(a = 1)|AgBr(s),Ag 的Eө与温度T的关系式为:Eө = 0.07150 - 4.186 × 10-7T(T- 298) 。
(1) 写出电极反应与电池反应;(2) 求T = 298K时正极φө与AgBr的K sp,巳知φө(Ag+/Ag) = 0.7991 V ;(3) 求T = 298K电池反应的平衡常数(可逆放电2F);(4) 此电池在298K下可逆放电2F时,放热还是吸热?热是多少?解:(1) 负极:H2(g)-2e →2H+;正极:2AgBr(s) + 2e →2Ag(s) + 2Br-电池反应:H2(g) + 2AgBr(s) = 2Ag(s) + 2HBr(a = 1)(2) T = 298K ,Eθ= 0.07150 Vφθ(正) =φθ(AgBr/Ag) = Eθ-φθ(H+/H2) = Eθ= 0.07150 V∵φθ(AgBr/Ag) =φθ(Ag+/Ag) + 0.05915lg K sp即0.07150 = 0.7991 + 0.05915lg K sp∴K sp = 5.0 × 10-13(3) Δr Gθm=-RT ln Kθ=-nFEθln Kө= nFEө/RT = 2 × 96500 × 0.07150/(8.314 × 298) = 5.5640,所以Kө= 2.62 × 102(4) (∂E/∂T)p=-4.186×10-7×2T + 4.186×10-7×298=-9.372×10-7T + 124.76×10-6T= 298K (∂E/∂T)p =-124.76×10-6 < 0,放热Q r = nFT(∂E/∂T)p = 2×96500×298×(-124.76×10-6) =-7175 J7.298K,pH = 5时,蔗糖转化反应有一个常数的半衰期为500分钟(即半衰期与糖的起始浓度无关),在同一温度下,当pH = 4时,常数半衰期为50分钟,试问蔗糖转化反应:A(蔗糖) + H+-→P的速率方程中,a、b值为多少?8.对峙反应D-R1R2R3CBr L-R1R2R3CBr若正逆向反应为一级反应且半衰期均为10min。
今从1.000molD-溴化物开始,试问10min后可得到L-溴化物若干?解:k1= ㏑2/t1/2=0.693/10=0.0693,因题意k1=k-1 故有㏑[a(a-(k1+k-1)/k1)x]=(k1+k-1)t代入a=1 k1=k-1=0.0693 x=0.375mol证明题。
