中南大学电路理论基础电路
合集下载
中南大学电路理论第10章一阶电路分析
第10章 10.1
§10-1电路中的过渡过程及换路定律
一. 动态电路及方程 描述含有储能元件(电容或电感)时电路的方程
为微分方程. ------动态方程 含有电容或电感元件的电路, 称为动态电路.
二. 一阶电路
能用一阶微分方程描述的电路称为一阶电路. 按储能元件的性质,一阶电路可分为:
RC电路 R L电路
放电过程。
一. RC放电电路
上图中，若开关S合于a，电容上电压充电到U0时， 将S由a合向b， 即 uC(0–)= U0 ，
根据KVL uR + uC=0
RC
—d —uC
dt
+ uC =0
15
2020年10月1日
S t=0
a
+
U-
uR
R
bi
U0
uC
o
i
U0
uR
R
–U0 变化曲线
16
RC
—d —uC
)
1 L
t
t 0
u(
)d
令t0 0 , t 0
iL (0
)
iL (0
)
1 L
0
u(
0
)d
由于u(t)为有限值, 则
iL(0 ) iL(0 ) ------电感里的电流不会发生突变
当iL(0 ) iL(0 ) 0时, 电感在换路的瞬间电感相当于开路
11
2020年10月1日
三. 其他非独立初始条件的计算
dt
+ uC =0
第10章 10.2
上式的通解为指数函数，即
uc uC = Ae pt
C
由特征方程 RCp +1=0
中南大学电工学第2章正弦交流电路_02
例3 电路如图所示，图中各仪表均为交流电流表，其读数是 电路如图所示，图中各仪表均为交流电流表， 电流表的有效值。已知A 的读数为8A 8A， 的读数为60A 60A， 电流表的有效值。已知A1的读数为8A，A2的读数为60A，A3的 读数为66A 求电流表A 66A。 的读数，并画出相量图。 读数为66A。求电流表A和A4的读数，并画出相量图。 I4 I 解：由于电路为并联电 A A4 A3 路，则可设 I3 + A1 A2 US= US 0 V 1 US I1 I j L ω R j L 2 ω 则由已知条件得 I1= 8 0 A， 2= 60 -90 A，I3= 66 90 A ， I ， 根据KCL有 有 根据 I4= I2+I3= 60 -90 +66 90 =6 90 A I= I1+I4= 8 0 +6 90 =10 36.9 A 故表A的读数为 的读数为6A。 故表 的读数为10A，表A4的读数为 。 的读数为 ， 的读数为 相量图如图。 相量图如图。 I2 I2 I4 I I1 US I3
▲额定视在功率 额定视在功率 SN = UN IN —— 额定容量 ▲有功功率守恒 有功功率守恒: 有功功率守恒 P = ∑Pi =∑ Ui Ii cosϕ i ▲无功功率守恒 无功功率守恒: 无功功率守恒 Q = ∑Q i = ∑ Ui Ii sinϕ i ▲视在功率不守恒 视在功率不守恒: 视在功率不守恒 S ≠∑S i =∑ Ui Ii
& I 1 = 10 90 ° A = j10 A & & & I = I 1 + I 2 = 10 0 ° A
& & U L = I ( j10 )V = j100 V
中南大学 电路理论基础 电路第9章1PPT课件
2、根据相量模型列出相量方程式或画相量图
3、用复数运算或相量图求解 4、将结果变换成要求的时域形式
各种方
法
11
例1
i2 i1
i3 + _u
R 1 10 ,R 0 2 1 0 0 ,L 5m 0,0 C H 1F 0 ,
U 1V 0 , 0 3r 1a /s 4 ,求d :各支路电流。
说明：Z 是一个复数，但并不是正弦交流量，上面不能加点。
Z在方程式中只是一个运算工具。
4
二. 复导纳 正弦激励下
I +
U -
无源 线性
I
+
U
Y
-
复导 Yd e Z 1f 纳 U I U I i uY Y
单 纯电阻 YR G
个 元 件
纯电感
YL1jLjBL
感纳
BL
1
L
时 纯电容 YCjCjBC 容纳 BC C
I
ZZ3
11 1
•
IS 1.13/82oA
Z1 Z2 ZZ3
16
例3. 列写电路的回路电流方程 _ U S +
I1
jL R1
I 2
R4
R2
I 3
R3
1 j c
I S
?
解：
( R 1 R 2 jL ) I 1 ( R 1 jL ) I 2 R 2 I 3 U S
第9章正弦稳态电路分析
要求 ： 1. 复阻抗、复导纳 2.定性分析：相量图 3.定量计算：相量形式的各种分析计算方法 4. 功率计算：P、Q、S、cos ф 、复功率 5. 谐振分析
1
9. 1 复阻抗和复导纳
一. 复阻抗 正弦激励下
中南大学电路理论基础作业
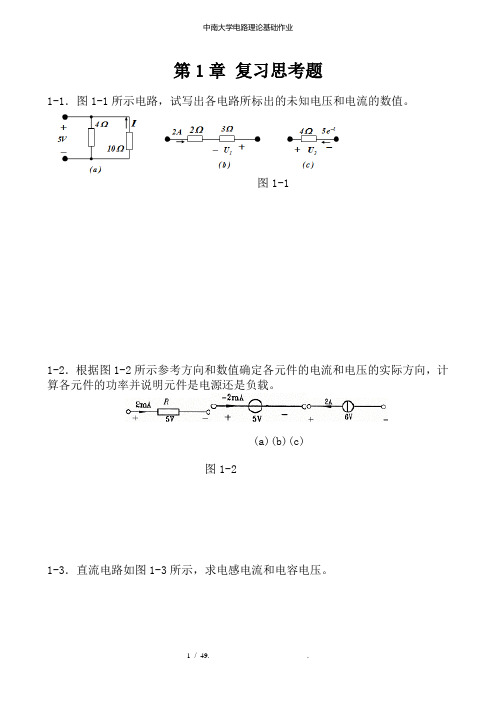
第1章复习思考题1-1．图1-1所示电路，试写出各电路所标出的未知电压和电流的数值。
图1-11-2．根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向，计算各元件的功率并说明元件是电源还是负载。
(a)(b)(c)图1-21-3．直流电路如图1-3所示，求电感电流和电容电压。
图1-31-4．如图1-4所示，电路中包含的各个元件的电压和电流参考方向如图所示，其中100P 1=W ，10P 2-=W ，50P 3=W ，20P 4=W ，求5P ，元件5是电源还是负载？图1-41-5．求图1-5所示电路中的电压1u 和1i 。
图1-51-6．求图1-6所示电路中的电压u 。
3Ω2Ω4Ωi10 V图1-61-7．求图1-7所示电路中的电压U 。
2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8．图1-8所示电路中，已知5u ab -=V ，求电压源电压s u 。
图1-81-9．电路如图1-9所示，试求电压U X。
图1-91-10．如图1-10所示的图，如果选1、2、3、4、8支路为树，则其基本回路组是什么？如果选择自然网孔为基本回路组，则其对应的树由哪些支路组成？②⑤123 4 6 10 ④ 8 9 ⑥57 ③图1-10第2章 复习思考题2-1．写出题21图所示各电路的端口电压电流的伏安特性方程。
(a) (b)图2-12-2．电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示，试计算a 、b 两端的电阻，其中电阻R =8。
(a) (b)(c)(d)(e) (f)图2-22-3．利用电源等效变换，化简图2-3(a)和(b)的一端口网络。
(a) (b)图2-32-4．利用电源的等效变换求图示2-4电路中的电流I 。
图2-42-5．求图2-5电路中的受控电流源的功率。
2Ω6V+I2Ω 2A7Ω6A2Ω图2-52-6．求图2-6各电路的输入电阻R in。
图2-6第3章复习思考题3-1．用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。
中南大学电路第10章
返 回 上 页 下 页
解 ①先求 iL (0 ) 1 4
小结 求初始值的步骤:
1.由换路前电路（稳定状态）求uC(0－)和iL(0－)。 2.由换路定律得 uC(0+) 和 iL(0+)。
3.画0+等效电路。
(1)换路后的电路; (2)电容（电感）用电压源（电流源）替代。 （取0+时刻值，方向与原假定的电容电压、电 感电流方向相同）。 4.由0+电路求所需各变量的0+值。
返 回
上 页
下 页
uC (0+) = uC (0－)
q =C uC
结论
q (0+) = q (0－)
电荷 守恒
换路瞬间，若电容电流保持为有限值， 则电容电压（电荷）换路前、后保持不变。
返 回
上 页
下 页
③电感的初始条件
iL
+
1 t iL (t ) u L ( )d L ∞ 1 0 1 t uL ( )d uL ( )d L ∞ L 0
代入初始值
uC (0+)=uC(0－)=U0
A=U0
返 回 上 页 下 页
uC U 0e
uC U 0 i e R R
或
t RC
t 0
t RC
t RC
I 0e
t 0
t t duC 1 U 0 RC i C CU 0e RC ( ) e dt RC R
f (0 ) f (0 )
0－ O 0＋ t
注意 初始条件为 t = 0＋时，u 、i 及其各阶导
数的值。
返 回 上 页 下 页
△例1-1 图示为电容放电电路，电容原先带有电压Uo， 求开关闭合后电容电压随时间的变化。 (t=0) Ri uC 0 (t 0) 解 + C uC duC R RC uC 0 i －
解 ①先求 iL (0 ) 1 4
小结 求初始值的步骤:
1.由换路前电路（稳定状态）求uC(0－)和iL(0－)。 2.由换路定律得 uC(0+) 和 iL(0+)。
3.画0+等效电路。
(1)换路后的电路; (2)电容（电感）用电压源（电流源）替代。 （取0+时刻值，方向与原假定的电容电压、电 感电流方向相同）。 4.由0+电路求所需各变量的0+值。
返 回
上 页
下 页
uC (0+) = uC (0－)
q =C uC
结论
q (0+) = q (0－)
电荷 守恒
换路瞬间，若电容电流保持为有限值， 则电容电压（电荷）换路前、后保持不变。
返 回
上 页
下 页
③电感的初始条件
iL
+
1 t iL (t ) u L ( )d L ∞ 1 0 1 t uL ( )d uL ( )d L ∞ L 0
代入初始值
uC (0+)=uC(0－)=U0
A=U0
返 回 上 页 下 页
uC U 0e
uC U 0 i e R R
或
t RC
t 0
t RC
t RC
I 0e
t 0
t t duC 1 U 0 RC i C CU 0e RC ( ) e dt RC R
f (0 ) f (0 )
0－ O 0＋ t
注意 初始条件为 t = 0＋时，u 、i 及其各阶导
数的值。
返 回 上 页 下 页
△例1-1 图示为电容放电电路，电容原先带有电压Uo， 求开关闭合后电容电压随时间的变化。 (t=0) Ri uC 0 (t 0) 解 + C uC duC R RC uC 0 i －
中南大学电路理论基础课件电路第章
–us2
R3
+
–us3
us11
ia
us 22 R11
R21
R11ia+R12ib=us11 R21ia+R22ib=us22
R12
us1-us2
us2-us3
R22 R12
R22 Δ
us11
R12 Δ
us 22
R22
R22 Δ
us1
R12 Δ
R22
us 2
R12 Δ
us 3
证得
ia = ia1 + ia2 + ia3
A
A
A
1A
++
1V -
_1V
1A
+
1A +
1V 1
?
-
-
1A
B
满足
B
不满足
B
2) 被替代的支路和电路其它部分应无耦合关系。 （控制量或受控源）
20
第20页，共58页。
§4-3. 戴维南定理 和 诺顿定理
在有些情况下，只需计算电路中某一支路中的电流， 如计算右图中电流 I3，若用前面的方法需列方程组， 必然出现一些不需要的变量。
源去掉，使电路开路。
13
第13页，共58页。
例3 求电压Us 。
注意受控源
I1 6
+ 10 I1 –
+ 10V
–
+
4
Us 4A
–
解: (1) 10V电压源单独作用：
I1' 6
+ 10 I1'–
+
10V –
+
+
R3
+
–us3
us11
ia
us 22 R11
R21
R11ia+R12ib=us11 R21ia+R22ib=us22
R12
us1-us2
us2-us3
R22 R12
R22 Δ
us11
R12 Δ
us 22
R22
R22 Δ
us1
R12 Δ
R22
us 2
R12 Δ
us 3
证得
ia = ia1 + ia2 + ia3
A
A
A
1A
++
1V -
_1V
1A
+
1A +
1V 1
?
-
-
1A
B
满足
B
不满足
B
2) 被替代的支路和电路其它部分应无耦合关系。 （控制量或受控源）
20
第20页，共58页。
§4-3. 戴维南定理 和 诺顿定理
在有些情况下，只需计算电路中某一支路中的电流， 如计算右图中电流 I3，若用前面的方法需列方程组， 必然出现一些不需要的变量。
源去掉，使电路开路。
13
第13页，共58页。
例3 求电压Us 。
注意受控源
I1 6
+ 10 I1 –
+ 10V
–
+
4
Us 4A
–
解: (1) 10V电压源单独作用：
I1' 6
+ 10 I1'–
+
10V –
+
+
中南大学电工学第2章正弦交流电路_03
三、线电压与相电压的关系 1、Y接法
A +
IA
A
UA
– Y X Z
C UC
UA B UCA
设 U AN U A U0o UBN UB U 120o UCN UC U120o
B
IB I C U BC
N B C
UB
U AB U AN U BN U0o U 120 o 3U30 o U BC U BN U CN U 120 o U120 o 3U 90 o U CA U CN U AN U120 o U0o 3U150 o
(2) 三相负载不对称（RA=5 、RB=10 、RC=20 ） 分别计算各线电流 U 220 0 A IA A 44 0A RA 5
U 220 120 B IB A 22 120 A RB 10
U 220 120 C IC A 11 120 A RC 20
Δ 接 : U l U p , I l 3I p 1 P 3U l I l cosφ 3U l I l cosφ 3
注意： (1) 为相电压与相电流的相位差角(阻抗角)，不要误以为 是线电压与线电流的相位差。
(2) cos为每相的功率因数，在对称三相制中即三相功率因数： cos A= cos B = cos C = cos 。
U A U0 U B U 120o U C U120o Z | Z | φ
UA UC
中南大学 电路理论基础课件 电路第6章3
(t-t0)
（1） 0 t0
9
t
3. 函数的筛分性（或采样特性）
f ( t ) ( t ) d t f ( 0 ) ( t ) d t f ( 0 )
f(0)(t)
(1)
(t)
f(0)
0
f(t)
t
* f(t)在 t0 处连续 同理有：
f ( t ) ( t t 0 ) d t f ( t 0 )
（1）加4ε的阶跃输入时：
iL (t )
4 2 .4
(1 e
24 t
) ( t )
（2）加4δ的冲激输入时： i ( t ) 40 e 24 t ( t ) L
u L (t ) L di L dt
22
96 e
24 t
(t )
1 RC
t RC
e
(t )
uC
R 阶跃响应 0
1 C
iC
1 t 0 t iC (1) t t
1 RC
21
uC
冲激响应 0
例6-7：求冲激响应 uL(t)和 iL(t)
R1 6 Req iL + uL – 等效 R2 4 4δ
2.4
+
10δ L –
0.1H
+
L –
0.1H
iL + uL –
iL ( 0
) 0
L
iL不可能是冲激
dt
0 0
Ri L dt
0
0 0
L
di L dt
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R6
1 R2
R1 i1
+
US1
_
i2 2 i3 i4
R4 3
i5
IS5
R3 4
R5
(2) 标注节点，列独立KCL方程 节点 1： – i1 +i2 + i6 =0
对n个节点的电路， 可以证明：独立的 KCL方程只有n-1个 。
节点 2：– i2 + i3 + i4 =0 (1) 节点 3：– i4 + i5 – i6 =0
#1
+
#2
R3 R4
#1
+
uS5 _
uS5 _
_ uS1
R6 #2 R3
平面电路：可以画在平面上,不出现支路交叉的电路。
非平面电路：在平面上无论将电路怎样画，总有支 路相互交叉。
02:05:07
∴ 是平面电路
总有支路相互交叉 ∴是非平面电路
9
独立回路的选取：
可以证明: 用KVL只能列出b–n+1个独立回路电压方程， 对平面电路，b–n+1个网孔即是一组独立回路。
i6
R6
平面电路
1 R2
i2 2 3
R4 3
R1 i1
i3 i4
i5
IS5
+
US1
_ 1 R3
4 2 R5
i5 +
R5 +
R5IS5_
—
(3) 选定b-n+1个独立回路，列写独立KVL电压方程。
要弄清支路电压与电流关系 u5 = R5（ i5 + is5）
回路1：R1 i1 + R2 i2 + R3 i3 = uS1
目的：找出求解线性电路的一般分析方法 。
对象：含独立源、受控源的电阻网络的直流稳态解。
(可推广应用于其他类型电路的稳态分析中）
应用：主要用于复杂的线性电路的求解。
基础： 电路的连接关系—KCL，KVL定律
元件特性(约束)(对电阻电路，即欧姆定律)
相互独立
复杂电路的分析法就是根据KCL、KVL及元件VCR 列方程、 解方程。根据列方程时所选变量的不同可分为支路电流法、 网孔电流法、回路电流法、节点电压法。
2
n=8，
1 4 3 b=12
5
对非平面电路，要使用树的概念来找到独立回路
02:05:07
10
3.3 支路电流法 (branch current method )
支路电流法：以各支路电流为未知量列写电路方程分析电 路的方法。支路电流法是最基本的方法，在 方程数目不多的情况下可以使用
支路电流法的一般步骤：
有 向 图3
1. 连通图 图分：连通图与不连通图。 图G的任意两节点间至少有一条路经时称G为连通图。
+
抽象
-
不连通图
+
抽象
-
连通图
2. 路经
从图G的一个节点出发沿着一些支路连续移动到达 另一节点所经过的支路构成路经。
3. 回路
回路L是连通图G的一个子图。 具有下述性质 (1)连通； (2)每个节点关联支路数恰好为2。
123 75 6 84
02:05:06
23 5
回路
12 5
7 84
不是回路
5
4 . 树 (Tree)
树T是连通图G的一个子图，具有下述性质：
(1)连通； (2)包含G的所有节点； (3)不包含回路。
16个
树支：属于树T 的支路
树不唯一
连支：属于G而不属于T的支路
02:05:06
6
显然，有n结点和b条支路的连通图，任取一个树 则：树支数 bt= n-1、连支数 bl=b-(n-1)
2i1 0i2 4i2 5
0i1 3i2 7i3 9
02:05:06
2
§3-1/2 电路的图
+
抽象
-
支路
i1 i2 i3
抽象 i1
i2 i3
电路图
抽象图
பைடு நூலகம்
i1 i2 i3
一. 图的基本概念 G={支路，节点}
L
uS
R2
+
R1
R3
抽象 C
抽象
无 箭头为支路电压 向 和电流的参考方 图 向（关联）
02:05:07
14
例1. US1=130V, US2=117V, R1=1, R2=0.6, R3=24.
a
I1
I2
R1
R2
+ 1+ 2
US1
US2
–
–
I3
求各支路电流及电压源 各自发出的功率。
KCL
R1 i1 + R2 i2 + R3 i3 = +uS1 –R3 i3 + R4 i4 + R5 i5 = – R5 iS5 – R2 i2 – R4 i4 + R6 i6 = 0
i1,i2….i6
KVL
对一般形式：1、等式左边为电阻压降的代数和；2、等 式右边是回路经过的所有电压源及电流源（电流源与电 阻的并→电压源与电阻的串）；3、在等式右边时，电压 源极性与回路绕行方向一致，取—，反之取 + 。
一、先确定树：树T是连通图G的一个子图，具有下述性质： (1)连通； (2)包含G的所有节点； (3)不包含回路。
二、每加一条连支，得到一个单连支回路，共一组b-n+1 个单连支回路，就是一组基本独立回路（？）
图中，粗红线即被选为树支，细线即为连支
R1
+
_
R1
+
R2 #3
uS1
#3
R2
R5
R6
R5
R4
02:05:06
1
关于多变量线性代数方程的标准形式
a11x1 a12x2 a1n xn b1
a21x1
a22x2
a2n xn
b2
an1x1 an2x2 ann xn bn
例如： i1 i2 i3 0
(1) 标定各支路电流（电压）的参考方向； (2) 选定(n–1)个节点，列写其KCL方程； (3) 选定b–(n–1)个独立回路，列写其KVL方程；
(元件特性代入)
(4) 求解上述方程，得到b个支路电流；
(5) 进一步计算支路电压和进行其它任何分析。
02:05:07
11
举例说明原理：b=6， n=4 ： （ R5、 IS5为一条支路） (1) 标定各支路电流的参考方向 i6
回路2：–R3 i3 + R4 i4 + R5 i5 = – R5 iS5
（2）
回路3：– R2 i2 – R4 i4 + R6 i6 = 0
02:05:07
在此：元件特性已直接代入
13
（4）联立求解，求出各支路电流，进一步求出各支路电压。
– i1 +i2 + i6 =0 – i2 + i3 + i4 =0 – i4 + i5 – i6 =0
4 1
3 56 2
7
树支数 4：
（2、3、6、7）
树
连支数 3：
（1、4、5）
单连支回路（在树的基础上，每加一连支，即得一回路。 共b-(n-1)个单连支回路，必为一组独立基本回路）
4
1 5
特点：1、所有的支路 都出现了；2、两两之
间必有不同的支路。
02:05:07
7
归纳：列KVL方程时，如何得基本独立回路组？
1 R2
R1 i1
+
US1
_
i2 2 i3 i4
R4 3
i5
IS5
R3 4
R5
(2) 标注节点，列独立KCL方程 节点 1： – i1 +i2 + i6 =0
对n个节点的电路， 可以证明：独立的 KCL方程只有n-1个 。
节点 2：– i2 + i3 + i4 =0 (1) 节点 3：– i4 + i5 – i6 =0
#1
+
#2
R3 R4
#1
+
uS5 _
uS5 _
_ uS1
R6 #2 R3
平面电路：可以画在平面上,不出现支路交叉的电路。
非平面电路：在平面上无论将电路怎样画，总有支 路相互交叉。
02:05:07
∴ 是平面电路
总有支路相互交叉 ∴是非平面电路
9
独立回路的选取：
可以证明: 用KVL只能列出b–n+1个独立回路电压方程， 对平面电路，b–n+1个网孔即是一组独立回路。
i6
R6
平面电路
1 R2
i2 2 3
R4 3
R1 i1
i3 i4
i5
IS5
+
US1
_ 1 R3
4 2 R5
i5 +
R5 +
R5IS5_
—
(3) 选定b-n+1个独立回路，列写独立KVL电压方程。
要弄清支路电压与电流关系 u5 = R5（ i5 + is5）
回路1：R1 i1 + R2 i2 + R3 i3 = uS1
目的：找出求解线性电路的一般分析方法 。
对象：含独立源、受控源的电阻网络的直流稳态解。
(可推广应用于其他类型电路的稳态分析中）
应用：主要用于复杂的线性电路的求解。
基础： 电路的连接关系—KCL，KVL定律
元件特性(约束)(对电阻电路，即欧姆定律)
相互独立
复杂电路的分析法就是根据KCL、KVL及元件VCR 列方程、 解方程。根据列方程时所选变量的不同可分为支路电流法、 网孔电流法、回路电流法、节点电压法。
2
n=8，
1 4 3 b=12
5
对非平面电路，要使用树的概念来找到独立回路
02:05:07
10
3.3 支路电流法 (branch current method )
支路电流法：以各支路电流为未知量列写电路方程分析电 路的方法。支路电流法是最基本的方法，在 方程数目不多的情况下可以使用
支路电流法的一般步骤：
有 向 图3
1. 连通图 图分：连通图与不连通图。 图G的任意两节点间至少有一条路经时称G为连通图。
+
抽象
-
不连通图
+
抽象
-
连通图
2. 路经
从图G的一个节点出发沿着一些支路连续移动到达 另一节点所经过的支路构成路经。
3. 回路
回路L是连通图G的一个子图。 具有下述性质 (1)连通； (2)每个节点关联支路数恰好为2。
123 75 6 84
02:05:06
23 5
回路
12 5
7 84
不是回路
5
4 . 树 (Tree)
树T是连通图G的一个子图，具有下述性质：
(1)连通； (2)包含G的所有节点； (3)不包含回路。
16个
树支：属于树T 的支路
树不唯一
连支：属于G而不属于T的支路
02:05:06
6
显然，有n结点和b条支路的连通图，任取一个树 则：树支数 bt= n-1、连支数 bl=b-(n-1)
2i1 0i2 4i2 5
0i1 3i2 7i3 9
02:05:06
2
§3-1/2 电路的图
+
抽象
-
支路
i1 i2 i3
抽象 i1
i2 i3
电路图
抽象图
பைடு நூலகம்
i1 i2 i3
一. 图的基本概念 G={支路，节点}
L
uS
R2
+
R1
R3
抽象 C
抽象
无 箭头为支路电压 向 和电流的参考方 图 向（关联）
02:05:07
14
例1. US1=130V, US2=117V, R1=1, R2=0.6, R3=24.
a
I1
I2
R1
R2
+ 1+ 2
US1
US2
–
–
I3
求各支路电流及电压源 各自发出的功率。
KCL
R1 i1 + R2 i2 + R3 i3 = +uS1 –R3 i3 + R4 i4 + R5 i5 = – R5 iS5 – R2 i2 – R4 i4 + R6 i6 = 0
i1,i2….i6
KVL
对一般形式：1、等式左边为电阻压降的代数和；2、等 式右边是回路经过的所有电压源及电流源（电流源与电 阻的并→电压源与电阻的串）；3、在等式右边时，电压 源极性与回路绕行方向一致，取—，反之取 + 。
一、先确定树：树T是连通图G的一个子图，具有下述性质： (1)连通； (2)包含G的所有节点； (3)不包含回路。
二、每加一条连支，得到一个单连支回路，共一组b-n+1 个单连支回路，就是一组基本独立回路（？）
图中，粗红线即被选为树支，细线即为连支
R1
+
_
R1
+
R2 #3
uS1
#3
R2
R5
R6
R5
R4
02:05:06
1
关于多变量线性代数方程的标准形式
a11x1 a12x2 a1n xn b1
a21x1
a22x2
a2n xn
b2
an1x1 an2x2 ann xn bn
例如： i1 i2 i3 0
(1) 标定各支路电流（电压）的参考方向； (2) 选定(n–1)个节点，列写其KCL方程； (3) 选定b–(n–1)个独立回路，列写其KVL方程；
(元件特性代入)
(4) 求解上述方程，得到b个支路电流；
(5) 进一步计算支路电压和进行其它任何分析。
02:05:07
11
举例说明原理：b=6， n=4 ： （ R5、 IS5为一条支路） (1) 标定各支路电流的参考方向 i6
回路2：–R3 i3 + R4 i4 + R5 i5 = – R5 iS5
（2）
回路3：– R2 i2 – R4 i4 + R6 i6 = 0
02:05:07
在此：元件特性已直接代入
13
（4）联立求解，求出各支路电流，进一步求出各支路电压。
– i1 +i2 + i6 =0 – i2 + i3 + i4 =0 – i4 + i5 – i6 =0
4 1
3 56 2
7
树支数 4：
（2、3、6、7）
树
连支数 3：
（1、4、5）
单连支回路（在树的基础上，每加一连支，即得一回路。 共b-(n-1)个单连支回路，必为一组独立基本回路）
4
1 5
特点：1、所有的支路 都出现了；2、两两之
间必有不同的支路。
02:05:07
7
归纳：列KVL方程时，如何得基本独立回路组？