高中数学 章末检测卷(二)苏教版选修2-2
苏教版高中数学选修2-2第1章章末检测(A).docx

第1章导数及其应用(A)(时间:120分钟满分:160分) 一、填空题(本大题共14小题,每小题5分,共70分)1.物体自由落体运动方程为s(t)=12gt2,g=9.8 m/s2,若当Δt无限趋近于0时,s(1+Δt)-s(1)Δt无限趋近于9.8 m/s,那么下面说法正确的是__________.(填序号)①9.8 m/s是0~1 s这段时间内的平均速度;②9.8 m/s是从1 s到(1+Δt) s这段时间内的速度;③9.8 m/s是物体在t=1这一时刻的速度;④9.8 m/s是物体从1 s到(1+Δt) s这段时间内的平均速度.2.曲线y=x+ln x在点(e2,e2+2)处的切线在y轴上的截距为________.3.若f(x0)存在且f′(x0)=0,下列结论中正确的是________.(填序号)①f(x0)一定是极值点;②如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值;③如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极小值;④如果在x0附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x0)是极大值.4.下列有关导数的说法正确的是________.(填序号)①f′(x0)就是曲线f(x)在点(x0,f(x0))的切线的斜率;②f′(x0)与(f(x0))′意义是一样的;③设s=s(t)是位移函数,则s′(t0)表示物体在t=t0时刻的瞬时速度;④设v=v(t)是速度函数,则v′(t0)表示物体在t=t0时刻的加速度.5.如图为y=f(x)的导函数的图象,则下列判断正确的是________.(填序号)①f(x)在(-3,1)内是增函数;②x=-1是f(x)的极小值点;③f(x)在(2,4)内是减函数,在(-1,2)内是增函数;④x=1是f(x)的极大值点.6.某汽车启动阶段的路程函数为s(t)=2t3-5t2+2,则t=2时,汽车的加速度是________.7.函数f(x)=4x-x4在[-1,2]上的最大值、最小值分别为__________.8.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是下图中的________.(填序号)9.一批物资用13辆汽车从A 地运到300 km 以外的B 地,若车速为v km/h ,则两车的距离不能小于⎝⎛⎭⎫v102 km 时,这批物资全部从A 地运到B 地至少要花________h.10.函数y =x +cos x 在区间[0,π2]上的最大值是________.11.若两曲线y =x 2与y =cx 3 (c >0)围成图形的面积是23,则c =________.12.已知函数f (x )=-x 3+ax 在区间(-1,1)上是增函数,则实数a 的取值范围是________.13.f ′(x )是f (x )=13x 3+2x +1的导函数,则f ′(-1)的值是________.14.若ʃa 1⎝⎛⎭⎫2x +1x d x =3+ln 2,则a 的值是______. 二、解答题(本大题共6小题,共90分)15.(14分)求过点(1,-1)的曲线y =x 3-2x 的切线方程.16.(14分)某物流公司购买了一块长AM =30米,宽AN =20米的矩形地块AMPN ,规划建设占地如图中矩形ABCD 的仓库,其余地方为道路和停车场,要求顶点C 在地块对角线MN 上,B 、D 分别在边AM 、AN 上,假设AB 长度为x 米.若规划建设的仓库是高度与AB 的长相同的长方体建筑,问AB 长为多少时仓库的库容最大?(墙体及楼板所占空间忽略不计)17.(14分)已知直线l 1为曲线y =f (x )=x 2+x -2在点(1,0)处的切线,l 2为该曲线的另外一条切线,且l 1⊥l 2.(1)求直线l 2的方程;(2)求由直线l 1、l 2及x 轴所围成的三角形的面积. 18.(16分)要设计一容积为V 的有盖圆柱形储油罐,已知侧面的单位面积造价是底面造价的一半,盖的单位面积造价又是侧面造价的一半.问储油罐的半径r 和高h 之比为何值时造价最省?19.(16分)若函数f (x )=ax 3-bx +4,当x =2时,函数f (x )有极值-43.(1)求函数的解析式;(2)若方程f (x )=k 有3个不同的根,求实数k 的取值范围.20.(16分)已知函数f (x )=ax 3-32x 2+1(x ∈R ),其中a >0.(1)若a =1,求曲线y =f (x )在点(2,f (2))处的切线方程;(2)若在区间[-12,12]上,f (x )>0恒成立,求a 的取值范围.答案 1.③ 2.1解析 因为y ′=1+1x ,所以曲线在点(e 2,e 2+2)处的切线的斜率为k =1+1e2,切线方程为y -e 2-2=⎝⎛⎭⎫1+1e 2(x -e 2). 即y =⎝⎛⎭⎫1+1e 2x +1,令x =0,得y =1. 3.②解析 由题意x 0附近的左侧f ′(x)>0,即x 0附近的左侧函数单调递增,同理x 0附近右侧函数单调递减,故f (x 0)为极大值.4.①③④解析 因f ′(x 0)表示在x =x 0处的导数, 而[f (x 0)]′表示对函数值f (x 0)求导. 因f (x 0)为常数,所以[f (x 0)]′=0.5.②③解析 ①错,因在(-3,-1)上f ′(x )<0, 在(-1,1)上f ′(x )>0,故f (x )在(-3,-1)内是减函数,在(-1,1)内是增函数; ②正确,因f ′(x )在(-3,-1)上为负, f ′(-1)=0,f ′(x )在(-1,2)上为正;③正确,因在(2,4)内f ′(x )<0,故f (x )在(2,4)内是减函数; 在(-1,2)内f ′(x )>0,故f (x )在(-1,2)内为增函数, ④错,在(-1,1)内f ′(x )>0,在(1,2)内f ′(x )>0, 且f ′(1)≠0,故x =1不是极值点. 6.14解析 v (t )=s ′(t )=6t 2-10t ,a (t )=v ′(t)=12t -10. ∴当t =2时,a (2)=24-10=14. 7.3、-8解析 f ′(x )=4-4x 3,由f ′(x )=0得x =1,易知x =1为极值点,又f(1)=3,f(-1)=-5,f(2)=-8.所以f(x )在[-1,2]上的最大值为3,最小值为-8. 8.③解析 由已知图象可知,当x ∈(-∞,0)时,f ′(x )>0,所以函数f (x )在(-∞,0)上递增;当x ∈(0,2)时,f ′(x )<0,所以函数f (x )在(0,2)上递减;当x ∈(2,+∞)时,f ′(x )>0,所以函数f (x )在(2,+∞)上递增.注意观察导函数f ′(x )的图象的特点,根据图象划分好区间.9.12解析 最后一辆汽车从A 地到B 地所用的时间为t =300+12×⎝⎛⎭⎫v 102v =300v +3v25,v ∈(0,+∞),则t ′=-300v 2+325.令t ′=0,得-300v 2+325=0,∴v =50.又∵函数t =300v +3v25在(0,+∞)内只有一个极值点v =50,且这是极小值点.∴当v =50时,所花费的时间最短为12 h .10.π2解析 y ′=1-sin x ,令y ′=0,得sin x =1,∴x =π2,又因f (0)=0+cos 0=1,f (π2)=π2+cos π2=π2, 所以y =x +cos x 在[0,π2]上的最大值为π2.11.12解析 由⎩⎪⎨⎪⎧y =x 2y =cx 3得x 2=cx 3, 解之得x =0或x =1c,∴S =123()c c dx x x -⎰取F (x )=13x 3-14cx 4,则F ′(x )=x 2-cx 3.∴S =123()c c dx x x -⎰=1'0c F dx ⎰=F ⎝⎛⎭⎫1c -F(0)=112·1c 3=23, ∴c 3=18,即c =12.12.a ≥3解析 由题意应有f ′(x )=-3x 2+a ≥0,在区间(-1,1)上恒成立,则a ≥3x 2,x ∈(-1,1)恒成立,故a ≥3.13.3解析 ∵f ′(x )=x 2+2,∴f ′(-1)=3. 14.2解析 取F (x )=x 2+ln x ,则F ′(x )=2x +1x,∴ʃa 1⎝⎛⎭⎫2x +1x d x =ʃa 1F ′(x )=F (a )-F (1) =a 2+ln a -1=3+ln 2,∴a =2.15.解 设P (x 0,y 0)为切点,则切线的斜率为 f ′(x 0)=3x 20-2.故切线方程为y -y 0=(3x 20-2)(x -x 0),即y -(x 30-2x 0)=(3x 20-2)(x -x 0),又知切线过点(1,-1),代入上述方程,得-1-(x 30-2x 0)=(3x 20-2)(1-x 0),解得x 0=1或x 0=-12,故所求的切线方程为y +1=x -1或y +1=-54(x -1).即x -y -2=0或5x +4y -1=0.16.解 因为DC AM =NDAN ,且AM =30,AN =20.所以ND =AB AM ·AN =2x3,得AD =AN -ND =20-2x3.仓库的库容V (x )=(20-2x3)·x ·x=-2x 33+20x 2(0<x <30),令V ′(x )=-2x 2+40x =-2x (x -20)=0, 得x =20或x =0(舍去). 当x ∈(0,20)时,V ′(x )>0; 当x ∈(20,30)时,V ′(x )<0.所以当x =20时,V (x )有极大值也是最大值. 即AB 的长度为20米时仓库的库容最大.17.解 (1)因为f ′(x )=2x +1,所以f ′(1)=3, 所以直线l 1的方程为y =3(x -1), 即y =3x -3.设直线l 2过曲线上点B (b ,b 2+b -2), 因为f ′(b )=2b +1,所以直线l 2的方程为y -(b 2+b -2)=(2b +1)(x -b ), 即y =(2b +1)x -b 2-2.又l 1⊥l 2,所以3(2b +1)=-1,所以b =-23,所以直线l 2的方程为y =-13x -229.即3x +9y +22=0.(2)解方程组⎩⎪⎨⎪⎧y =3x -3y =-13x -229,可得⎩⎨⎧x =16y =-52. 因为直线l 1、l 2与x 轴的交点坐标分别为(1,0)、⎝⎛⎭⎫-223,0, 所以所求三角形的面积为S =12×⎪⎪⎪⎪-52×⎪⎪⎪⎪1+223=12512. 18.解 由V =πr 2h ,得h =Vπr2.设盖的单位面积造价为a ,则储油罐的造价M =a πr 2+2a ·2πrh +4a ·πr 2=5a πr 2+4aVr,M ′=10a πr -4aVr 2,令M ′=0,解得r =32V 5π,经验证,当r =32V 5π时,函数取得极小值,也是最小值,此时,h =Vπr 2=325V 4π. ∴当rh =32V 5π325V 4π=25时,储油罐的造价最省. 19.解 f ′(x )=3ax 2-b .(1)由题意得⎩⎪⎨⎪⎧f ′(2)=12a -b =0f (2)=8a -2b +4=-43,解得⎩⎪⎨⎪⎧a =13b =4,故所求函数的解析式为f (x )=13x 3-4x +4.(2)由(1)可得f ′(x )=x 2-4=(x -2)(x +2), 令f ′(x )=0,得x =2或x =-2.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,-2) -2 (-2,2)2 (2,+∞) f ′(x ) + 0 - 0 + f (x ) 283-43因此,当x =-2时,f (x )有极大值283,当x =2时,f (x )有极小值-43,所以函数f (x )=13x 3-4x +4的图象大致如右图所示.若f (x )=k 有3个不同的根,则直线y =k 与函数f (x )的图象有3个交点,所以-43<k <283.20.解 (1)当a =1时,f (x )=x 3-32x 2+1,f (2)=3.f ′(x )=3x 2-3x ,f ′(2)=6,所以曲线y =f (x )在点(2,f (2))处的切线方程为y -3=6(x -2),即6x -y -9=0.(2)f ′(x )=3ax 2-3x =3x (ax -1).令f ′(x )=0,解得x =0或x =1a.以下分两种情况讨论:①若0<a ≤2,则1a ≥12.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-12,0) 0 (0,12)f ′(x ) + 0 -f (x ) 极大值当x ∈[-12,12]时,f (x )>0等价于⎩⎨⎧f (-12)>0,f (12)>0,即⎩⎨⎧5-a8>0,5+a 8>0.解不等式组得-5<a <5.因此0<a ≤2.②若a >2,则0<1a <12.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-12,0) 0 (0,1a )1a (1a ,12) f ′(x ) + 0 - 0 +f (x )极大值极小值当x ∈[-12,12]时,f (x )>0等价于⎩⎨⎧f (-12)>0,f (1a )>0,即⎩⎨⎧5-a8>0,1-12a 2>0.解不等式组得22<a <5或a <-22. 因此2<a <5.综合①②,可知a 的取值范围为0<a <5.。
苏教版高中数学选修2-2:3.2《复数的运算》综合测试2(选修2—2).docx

高中新课标数学选修(2-2)第三章测试题一、选择题1.0a =是复数()z a bi a b =+∈R ,为纯虚数的( )A.充分条件但不是必要条件B.必要条件但不是充分条件C.充要条件D.既不是充分也不必要条件答案:B2.若12z i =+,23()z ai a =+∈R ,12z z +的和所对应的点在实轴上,则a 为( ) A.3B.2 C.1 D.1-答案:D3.复数22(2)(2)z a a a a i =-+--对应的点在虚轴上,则( )A.2a ≠或1a ≠ B.2a ≠且1a ≠ C.0a =D.2a =或0a =答案:D4.设1z ,2z 为复数,则下列四个结论中正确的是( )A.若22120z z +>,则2212z z >- B.2121212()4z z z z z z -=+-C.22121200z z z z +=⇔== D.11z z -是纯虚数或零答案:D5.设22(253)(22)z t t t t i =+-++-+,t ∈R ,则下列命题中正确的是( ) A.z 的对应点Z 在第一象限B.z 的对应点Z 在第四象限C.z 不是纯虚数D.z 是虚数答案:D6.若1i +是实系数方程20x bx c ++=的一个根,则方程的另一个根为( ) A.1i - B.1i -+ C.1i -- D.i答案:A7.已知复数1cos z i θ=-,2sin z i θ=+,则12z z ·的最大值为( ) A.32 B.2 C.62 D.3答案:A8.已知m ∈R ,若6()64m mi i +=-,则m 等于( )A.2- B.2± C.2- D.4答案:B9.在复平面内,复数1322i ω=-+对应的向量为OA ,复数2ω对应的向量为OB .那么向量AB 对应的复数是( )A.1 B.1- C.3i D.3i -答案:D10.在下列命题中,正确命题的个数为( )①两个复数不能比较大小;②123z z z ∈C ,,,若221221()()0z z z z -+-=,则13z z =;③若22(1)(32)x x x i -+++是纯虚数,则实数1x =±;④z 是虚数的一个充要条件是z z +∈R ;⑤若a b ,是两个相等的实数,则()()a b a b i -++是纯虚数;⑥z ∈R 的一个充要条件是z z =.A.0B.1 C.2 D.3答案:B11.复数()a bi a b +∈R ,等于它共轭复数的倒数的充要条件是( )A.2()1a b +=B.221a b += C.221a b -= D.2()1a b -=答案:B12.复数z 满足条件:21z z i +=-,那么z 对应的点的轨迹是( )A.圆B.椭圆 C.双曲线 D.抛物线答案:A二、填空题13.若复数cos sin z i θθ=-·所对应的点在第四象限,则θ为第 象限角.答案:一14.复数3z i =+与它的共轭复数z 对应的两个向量的夹角为 .答案:60°15.已知2z i =-,则32452z z z -++= .答案:216.定义运算a b ad bc c c =-,则符合条件2132i z zi -=+的复数z = .答案:7455i -三、解答题17.已知复数(2)()x yi x y -+∈R ,的模为3,求y x的最大值. 解:23x yi -+=∵,22(2)3x y -+=∴,故()x y ,在以(20)C ,为圆心, 3为半径的圆上,y x表示圆上的点()x y ,与原点连线的斜率. 如图,由平面几何知识,易知y x 的最大值为3.18.已知1z i a b =+,,为实数.(1)若234z z ω=+-,求ω;(2)若2211z az b i z z ++=--+,求a ,b 的值.解:(1)2(1)3(1)41i i i ω=++--=--,2ω=∴;(2)由条件,得()(2)1a b a i i i+++=-, ()(2)1a b a i i +++=+∴,121a b a +=⎧⎨+=⎩,,∴解得12a b =-⎧⎨=⎩,.19.已知2211z x x i =++,22()z x a i =+,对于任意x ∈R ,均有12z z >成立,试求实数a 的取值范围.解:12z z >∵,42221()x x x a ++>+∴,22(12)(1)0a x a -+->∴对x ∈R 恒成立.当120a -=,即12a =时,不等式成立; 当120a -≠时,21201124(12)(1)0a a a a ->⎧⇒-<<⎨---<⎩, 综上,112a ⎛⎤∈- ⎥⎝⎦,.20.已知()z i z ω=+∈C ,22z z -+是纯虚数,又221116ωω++-=,求ω.解:设()z a bi a b =+∈R , 2(2)2(2)z a bi z a bi--+=+++∴2222(4)4(2)a b bi a b +-+=++. 22z z -+∵为纯虚数, 22400a b b ⎧+-=⎨≠⎩,.∴ 222211(1)(1)(1)(1)a b i a b i ωω++-=++++-++∴ 2222(1)(1)(1)(1)a b a b =++++-++222()44a b b =+++844b =++124b =+.12416b +=∴.1b =∴.把1b =代入224a b +=,解得3a =±.3z i =±+∴.32i ω=±+∴.21.复数3(1)()1i a bi z i++=-且4z =,z 对应的点在第一象限内,若复数0z z ,,对应的点是正三角形的三个顶点,求实数a ,b 的值.解:2(1)(1)()2()221i i z a bi i i a bi a bi i++=+=+=---···, 由4z =,得224a b +=. ①∵复数0,z ,z 对应的点是正三角形的三个顶点,z z z =-∴,把22z a bi =--代入化简,得1b =. ②又Z ∵点在第一象限内,0a <∴,0b <. 由①②,得31a b ⎧=-⎪⎨=-⎪⎩,. 故所求3a =-,1b =-.22.设z 是虚数1z zω=+是实数,且12ω-<<. (1)求z 的值及z 的实部的取值范围.(2)设11z zμ-=+,求证:μ为纯虚数; (3)求2ωμ-的最小值.(1)解:设0z a bi a b b =+∈≠R ,,,, 则1a bi a bi ω=+++2222a b a b i a b a b ⎛⎫⎛⎫=++- ⎪ ⎪++⎝⎭⎝⎭. 因为ω是实数,0b ≠,所以221a b +=,即1z =.于是2a ω=,即122a -<<,112a -<<. 所以z 的实部的取值范围是112⎛⎫- ⎪⎝⎭,; (2)证明:2222111211(1)1z a bi a b bi b i z a bi a b a μ------====-++++++. 因为112a ⎛⎫∈- ⎪⎝⎭,,0b ≠,所以μ为纯虚数; (3)解:22222122(1)(1)b a a a a a ωμ--=+=+++1222111a a a a a -=-=-+++12(1)31a a ⎡⎤=++-⎢⎥+⎣⎦因为112a ⎛⎫∈- ⎪⎝⎭,,所以10a +>,故2122(1)31a a ωμ-+-+··≥431-=. 当111a a +=+,即0a =时,2ωμ-取得最小值1.高中新课标数学选修(2-2)第三章测试题一、选择题1.实数x ,y 满足(1)(1)2i x i y ++-=,则xy 的值是( ) A.1B.2 C.2- D.1-答案:A2.复数cos z i θ=,[)02πθ∈,的几何表示是( ) A.虚轴B.虚轴除去原点C.线段PQ ,点P ,Q 的坐标分别为(01)(01)-,,,D.(C)中线段PQ ,但应除去原点答案:C3.z ∈C ,若{}22(1)1M z z z =-=-|,则( ) A.{}M =实数B.{}M =虚数 C.{}{}M实数复数苘D.{}M ϕ=答案:A4.已知复数1z a bi =+,21()z ai a b =-+∈R ,,若12z z <,则( ) A.1b <-或1b > B.11b -<<C.1b >D.0b >答案:B5.已知复数z 满足2230z z --=的复数z 的对应点的轨迹是( ) A.1个圆B.线段 C.2个点 D.2个圆答案:A6.设复数()z z ∈C 在映射f 下的象是z i ·,则12i -+的原象为( ) A.2i -B.2i + C.2i -+ D.13i +-答案:A7.设A ,B 为锐角三角形的两个内角,则复数(cot tan )(tan cot )z B A B A i =-+-对应的点位于复平面的( )A.第一象限 B.第二象限 C.第三象限 D.第四象限答案:B8.已知()22f z i z z i +=++,则(32)f i +=( ) A.9iB.93i + C.9i - D.93i --答案:B9.复数2()12mi A Bi m A B i-=+∈+R ,,,且0A B +=,则m =( ) A.2 B.23 C.23- D.2答案:C10.(32)(1)i i +-+表示( )A.点(32),与点(11),之间的距离 B.点(32),与点(11)--,之间的距离 C.点(32),与原点的距离D.点(31),与点(21),之间的距离答案:A11.已知z ∈C ,21z -=,则25z i ++的最大值和最小值分别是( ) A.411+和411-B.3和1 C.52和34D.39和3答案:A12.已知1z ,2z ∈C ,1222z z +=,13z =,22z =,则12z z -=( ) A.1B.12 C.2 D.2答案:D二、填空题13.若()1()f z z z =-∈C ,已知123z i =+,25z i =-,则12z f z ⎛⎫= ⎪ ⎪⎝⎭ .答案:19172626i -14.“复数z ∈R ”是“11z z =”的 .答案:必要条件,但不是充分条件15.A ,B 分别是复数1z ,2z 在复平面上对应的两点,O 为原点,若1212z z z z +=-,则AOB △为 .答案:直角16.若n 是整数,则6(1)(1)nn i i -+-=· .答案:8±或8i ±三、解答题17.已知复数3z z -对应的点落在射线(0)y x x =-≤上,12z +=,求复数z .解:设()z a bi a b =+∈R ,,则33324z z a bi a bi a bi -=+-+=+, 由题意得4120b a b ⎧=-⎪⎨⎪>⎩,,① 又由12z +=,得22(1)2a b ++=, ②由①,②解得21a b =-⎧⎨=⎩,,2z i =-+∴.18.实数m 为何值时,复数216(815)55m z m i m i m m -⎛⎫=++++ ⎪++⎝⎭. (1)为实数;(2)为虚数;(3)为纯虚数;(4)对应点在第二象限.解:226(815)5m m z m m i m +-=++++. (1)z 为实数28150m m ⇔++=且50m +≠,解得3m =-;(2)z 为虚数2815050m m m ⎧++≠⇔⎨+≠⎩,, 解得3m ≠-且5m ≠-;(3)z 为纯虚数226058150m m m m m ⎧+-=⎪⇔+⎨⎪++≠⎩,,解得2m =;(4)z 对应的点在第二象限226058150m m m m m ⎧+-<⎪⇔+⎨⎪++>⎩,,解得5m <-或32m -<<.19.设O 为坐标原点,已知向量1OZ ,2OZ 分别对应复数12z z ,,且213(10)5z a i a =+-+,22(25)1z a i a=+--,a ∈R .若12z z +可以与任意实数比较大小,求1OZ ,2OZ 的值. 解:213(10)5z a i a =--+,则31232[(10)(25)]51z z a a i a a +=++-+-+-的虚部为0,22150a a +-=∴.解得5a =-或3a =.又50a +≠∵,3a =∴. 则138z i =+,21z i =-+,1318OZ ⎛⎫= ⎪⎝⎭,,2(11)OZ =-,. 1258OZ OZ =∴·. 20.已知z 是复数,2z i +与2z i-均为实数,且复数2()z ai +在复平面上对应的点在第一象限,求实数a 的取值范围.解:设()z x yi x y =+∈R ,,2(2)z i x y i +=++为实数,2y =-∴.211(22)(4)2255z x i x x i i i -==++---为实数, 4x =∴,则42z i =-.22()(124)8(2)z ai a a a i +=+-+-∵在第一象限,212408(2)0a a a ⎧+->⎨->⎩,,∴解得26a <<.21.已知关于x 的方程2(6)90()x i x ai a -+++=∈R 有实数根b .(1)求实数a ,b 的值;(2)若复数z 满足2z a bi z --=,求z 为何值时,z 有最小值并求出最小值.解:(1)将b 代入题设方程,整理得2(69)()0b b a b i -++-=, 则2690b b -+=且0a b -=,解得3a b ==;(2)设()z x yi x y =+∈R ,,则2222(3)(3)4()x y x y -++=+, 即22(1)(1)8x y ++-=.∴点Z 在以(11)-,为圆心,22为半径的圆上, 画图可知,1z i =-时,min 2z =.。
高中数学 第2章 推理与证明单元检测 苏教版选修2-2(2021年整理)

高中数学第2章推理与证明单元检测苏教版选修2-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第2章推理与证明单元检测苏教版选修2-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第2章推理与证明单元检测苏教版选修2-2的全部内容。
第2章 推理与证明单元检测一、填空题1.用反证法证明命题“若a 2+b 2=0,则a ,b 全为0(a ,b ∈R )",其反设是__________. 2.周长一定的平面图形中圆的面积最大,将这个结论类比到空间,可以得到的结论是________.3.用数学归纳法证恒等式111111111234212122n n n n n-+-++-=+++-++,由n =k 到n=k +1时,两边应同时加上________.4.对于等差数列{a n }有如下命题:“若{a n }是等差数列,a 1=0,s ,t 是互不相等的正整数,则有(s -1)a t -(t -1)a s =0".类比此命题,给出等比数列{b n }相应的一个正确命题:“__________________________________________”.5.若P =Q =(a ≥0),则P ,Q 的大小关系是__________. 6.补充下列证明过程:要证a 2+b 2+c 2≥ab +bc +ac ,即证______________,即证________________________________________________________________________.7.下列四个图形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为__________.8.已知x ,y 为正数,当x 2+y 2=________时,有1=.9.一个等差数列{a n },其中a 10=0,则有a 1+a 2+…+a n =a 1+a 2+…+a 19-n (1≤n <19,n ∈N *).一个等比数列{b n },其中b 15=1。
苏教版选修2-2高中数学第2章《推理与证明》word章末测试

章末质量评估(二)(时间:120分钟 满分:160分)一、填空题(本大题共14小题,每小题5分,共70分,请把答案填写在题中的横线上) 1.若数列{a n }(n ∈N *)是等差数列,则有b n =a 1+a 2+…+a nn (n ∈N *)也为等差数列.类比上述性质,相应地,若数列{c n }是等比数列,且c n >0(n ∈N *).则数列d n =________(n ∈N *)也是等比数列.解析 通常正数的算术平均数,类比其几何平均数. 答案n c 1c 2…c n2.用反证法证明方程F (x )=0至少有两个实根,其反证假设为____________________.解析 方程F (x )=0至少有两个实根,意指方程F (x )=0有两个或两个以上实根,其反面是方程F (x )=0至多只有一个实根. 答案 方程F (x )=0至多只有一个实根 3.观察下列数表规律则从数2 007到2 008的箭头方向是________.解析 因上行奇数是首项为3,公差为4的等差数列.若2 007在上行,则2 007=3+(n -1)×4⇒n ∈N *,故2 007在上行,又因为上行奇数的箭头为→a n ↓.答案 ↓4.用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:①∠A +∠B +∠C =90°+90°+∠C >180°,这与三角形内角和为180°相矛盾,∠A =∠B =90°不成立;②所以一个三角形中不能有两个直角;③假设∠A 、∠B 、∠C 中有两个角是直角,不妨设∠A =∠B =90°. 正确顺序的序号排列为________. 答案 ③①②5.用数学归纳法证明(n +1)(n +2)…(n +n )=2n ×1×3×…×(2n -1)时,从“k ”到“k +1”左边需增乘的代数式是________. 解析 若n =k 时等式成立,此时有(k +1)(k +2)…(k +k )=2k ×1×3×…×(2k -1)若n =k +1时,左边变为(k +2)(k +3)…(k +k )(k +k +1)(k +1+k +1). 与上式相比增的代数式应为(k +k +1)(k +1+k +1)k +1=2(2k +1).答案 2(k +1)6.由代数式的乘法法则类比推导向量的数量积的运算法则:①“mn =nm ”类比得到“a ·b =b·a ”;②“(m +n )t =mt +nt ”类比得到“(a +b )·c =a ·c +b·c ”; ③“(m ·n )t =m (n ·t )”类比得到“(a ·b )·c =a ·(b ·c )”;④“t ≠0,mt =xt ⇒m =x ”类比得到“p ≠0,a ·p =x ·p ⇒a =x ”; ⑤“|m ·n |=|m |·|n |”类比得到“|a·b|=|a |·|b |”; ⑥“ac bc =a b ”类比得到“a·c b·c =ab”.以上的式子中,类比得到的结论正确的个数是________. 解析 只有①②对,其余错误. 答案 27.凡自然数是整数,4是自然数,所以4是整数.对以上三段论推理下列说法正确的是________(请填写相应的序号). ①正确;②推理形式不正确;③两个“自然数”概念不一致; ④“两个整数”概念不一致.解析 三段论中的大前提、小前提及推理形式都是正确的. 答案 ①8.若数列{a n }中,a 1=1,a 2=3+5,a 3=7+9+11,a 4=13+15+17+19,…,则a 8=________.解析 由a 1,a 2,a 3,a 4的形式可归纳, ∵1+2+3+4+…+7=7×(1+7)2=28,∴a 8的首项应为第29个正奇数,即2×29-1=57. ∴a 8=57+59+61+63+65+67+69+71 =8×(57+71)2=512.答案 5129.在数列{a n }中,a 1=1,且S n 、S n +1、2S 1成等差数列(S n 表示数列{a n }的前n 项和),则S 2、S 3、S 4分别为______________,猜想S n =________.解析 由S n ,S n +1,2S 1成等差数列,得2S n +1=S n +2S 1,因为S 1=a 1=1,所以2S n+1=S n +2.令n =1,则2S 2=S 1+2=1+2=3⇒S 2=32,同理,分别令n =2,n =3,可求得S 3=74,S 4=158.由S 1=1=21-120,S 2=32=22-121,S 3=74=23-122,S 4=158=24-123,猜想S n =2n -12n -1.答案 32、74、158 2n-12n -1(n ∈N *)10.观察下列等式:13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第五个等式为________.解析 由前三个式子可以得出如下规律:每个式子等号的左边是从1开始的连续正整数的立方和,且个数依次多1,等号的右边是一个正整数的平方,后一个正整数依次比前一个大3,4,…,因此,第五个等式为13+23+33+43+53+63=212. 答案 13+23+33+43+53+63=21211.对于等差数列{a n }有如下命题:“若{a n }是等差数列,a 1=0,s 、t 是互不相等的正整数,则有(s -1)a t =(t -1)a s ”.类比此命题,给出等比数列{b n }相应的一个正确命题是:“__________________________________”. 解析 由类比推理可得.答案 若{b n }是等比数列,b 1=1,s ,t 是互不相等的正整数,则有b s -1t =b t -1s12.已知f (1,1)=1,f (m ,n )∈N *(m ,n ∈N *),且对任意m ,n ∈N *都有:①f (m ,n +1)=f (m ,n )+2;②f (m +1,1)=2f (m,1).给出以下三个结论:(1)f (1,5)=9;(2)f (5,1)=16;(3)f (5,6)=26.其中正确的个数为________.解析 f (1,5)=f (1,4)+2=f (1,3)+4=f (1,2)+6=f (1,1)+8=9; f (5,1)=2f (4,1)=4f (3,1)=8f (2,1)=16f (1,1)=16;f (5,6)=f (5,5)+2=f (5,4)+4=f (5,3)+6=f (5,2)+8=f (5,1)+10=26. 所以这3个结论都正确. 答案 313.凸函数的性质定理为:如果函数f (x )在区间D 上是凸函数,则对于区间D 内的任意x 1,x 2,…,x n ,有f (x 1)+f (x 2)+…+f (x n )n ≤f⎝⎛⎭⎫x 1+x 2+…+x n n ,若函数y =sin x 在区间(0,π)上是凸函数,则在△ABC 中,sin A +sin B +sin C 的最大值为________. 解析 根据凸函数的性质定理,可得sin A +sin B +sin C ≤3sin ⎝⎛⎭⎫A +B +C 3=332,即sin A +sin B +sin C 的最大值为332.答案33214.(2011·陕西高考)观察下列各式:1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……照此规律,第n 个等式为________.解析 由前4个等式可知,第n 个等式的左边第一个数为n ,且连续2n -1个整数相加,右边为(2n -1)2,故第n 个等式为n +(n +1)+(n +2)+…+(3n -2)=(2n -1)2.答案 n +(n +1)+(n +2)+…+(3n -2)=(2n -1)2二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)已知a 、b 、c 为正数,且a +b +c =1,求证:a +b +c ≤ 3.证明 ∵a ·13≤a +132, b ·13≤b +132, c ·13≤c +132, 三式相加得a 3+b 3+c 3≤12(a +b +c )+12=1.∴a +b +c ≤ 3.16.(本小题满分14分)设a ,b ,c 均为奇数,求证:方程ax 2+bx +c =0无整数根.证明 假设方程有整数根x =x 0,∴ax 20+bx 0+c =0,∴c =-(ax 20+bx 0). 若x 0是偶数,则ax 20,bx 0是偶数, ax 20+bx 0是偶数,从而c 是偶数,与题设矛盾; 若x 0是奇数,则ax 20,bx 0是奇数, ax 20+bx 0是偶数,从而c 是偶数,与题设矛盾.综上所述,方程ax 2+bx +c =0没有整数根.17.(本小题满分14分)在数列{a n }中,a 1=-23,a n =S n +1S n+2(n ≥2,n ∈N *).(1)求S 1,S 2,S 3;(2)猜想S n 的表达式,并用数学归纳法证明你的猜想. 解 (1)∵n ≥2时,a n =S n -S n -1=S n +1S n +2,∴S n -1+1S n +2=0(n ≥2),S n =-1S n -1+2(n ≥2),S 1=a 1=-23,S 2=-1S 1+2=-34,S 3=-1S 2+2=-45.(2)猜想S n =-n +1n +2(n ∈N *),下面用数学归纳法证明:①当n =1时,S 1=-23=-1+11+2,猜想正确.②假设当n =k (k ∈N *)时猜想正确,即S k =-k +1k +2,那么S k +1=-1S k +2=-1-k +1k +2+2=-(k +1)+1(k +1)+2,这表明当n =k +1时猜想也正确.根据①,②可知对任意n ∈N *,S n =-n +1n +2.18.(本小题满分16分)由下列各个不等式:1>12,1+12+13>1,1+12+13+14+…+17>32,1+12+13+14+…+115>2,…,你能得到一个怎样的一般不等式?并加以证明.解 根据给出的几个不等式可以猜测第n 个不等式,即一般不等式为1+12+13+14+…+12n -1>n2(n ∈N *).用数学归纳法证明如下: (1)当n =1时,1>12,猜想成立.(2)假设当n =k (k ∈N *)时,猜想成立,即1+12+13+14+…+12k -1>k2,则当n =k +1时,1+12+13+14+…+12k -1+12k +12k +1+…+12k +1-1>k 2+12k +12k +1+…+12k 1-1>k 2+12k 1+12k 1+…+12k 1=k 2+2k 2k 1=k +12,即当n =k +1时,猜想也正确.由(1)(2)知,不等式对一切n ∈N *都成立.19.(本小题满分16分)在Rt △ABC 中,AB ⊥AC ,AD ⊥BC 于D ,求证:1AD 2=1AB 2+1A C 2,那么在四面体A -BCD 中,类比上述结论,你能得到怎样的猜想,并说明理由.解 如图①所示,由射影定理知 AD 2=BD ·DC , AB 2=BD ·BC ,AC 2=BC ·DC , 图①∴1AD 2=1BD ·DC=BC 2BD ·BC ·DC ·BC =BC 2AB 2·AC 2. 又BC 2=AB 2+AC 2,∴1AD 2=AB 2+AC 2AB 2·AC 2=1AB 2+1AC 2. 所以1AD 2=1AB 2+1AC2.类比AB ⊥AC ,AD ⊥BC 猜想:四面体A -BCD 中,AB 、AC 、AD 两两垂直,AE ⊥平面BCD ,则1AE 2=1AB 2+1AC 2+1AD 2.如图②,连接BE 并延长交CD 于F , 连接AF .∵AB ⊥AC ,AB ⊥AD , 图② ∴AB ⊥平面ACD .而AF ⊂平面ACD ,∴AB ⊥AF . 在Rt △ABF 中,AE ⊥BF , ∴1AE 2=1AB 2+1AF2. 在Rt △ACD 中,AF ⊥CD ,∴1AF 2=1AC 2+1AD 2.∴1AE 2=1AB 2+1AC 2+1AD2,故猜想正确. 20.(本小题满分16分)已知等差数列{a n }的公差d 大于0,且a 2,a 5是方程x 2-12x +27=0的两根,数列{b n }的前n 项和为T n ,且T n =1-12b n .(1)求数列{a n }、{b n }的通项公式;(2)设数列{a n }的前n 项和为S n ,试比较1b n与S n +1的大小,并说明理由.解 (1)由已知得⎩⎪⎨⎪⎧a 2+a 5=12,a 2a 5=27.因为{a n }的公差大于0,所以a 5>a 2,所以a 2=3,a 5=9. 所以d =a 5-a 23=9-33=2,a 1=1,即a n =2n -1.因为T n =1-12b n ,所以b 1=23.当n ≥2时,T n -1=1-12b n -1,所以b n =T n -T n -1=1-12b n -1-12b n -1,化简得b n =13b n -1,所以{b n }是首项为23,公比为13的等比数列,即b n =23·13n -1=23n .所以a n =2n -1,b n =23n .(2) 因为S n =1+(2n -1)2×n =n 2,所以S n +1=(n +1)2,1b n =3n2.下面比较1b n与S n +1的大小:当n =1时,1b 1=32,S 2=4,所以1b 1<S 2,当n =2时,1b 2=92,S 3=9,所以1b 2<S 3,当n =3时,1b 3=272,S 4=16,所以1b 3<S 4,当n =4时,1b 4=812,S 5=25,所以1b 4>S 5.猜想:n ≥4时,1b n >S n +1.下面用数学归纳法证明: ①当n =4时,已证.②假设当n =k (k ∈N *,k ≥4)时,1b k >S k +1,即3k2>(k +1)2,那么,1b k+1=3k+12=3·3k2>3(k+1)2=3k2+6k+3=(k2+4k+4)+2k2+2k-1>[(k+1)+1]2=S(k+1)+1,所以当n=k+1时,1b n>S n+1也成立.由①②可知,对任何n∈N*,n≥4,1b n>S n+1都成立.综上所述,当n=1,2,3时,1b n<S n+1,当n≥4时,1b n>S n+1.。
高中数学苏教版选修2-2同步训练:第二章 章末检测 PDF版含答案

第二章 章末检测1、观察下列各式:22334455134711a b a b a b a b a b +=,+=,+=,+=,+=,…,则1010a b +=( )A. 28B. 76C. 123D. 1992、用反证法证明命题:“若,N,a b ab ∈能被3整除,那么,a b 中至少有一个能被3整除”时,假设应为( )A.,a b 都能被3整除B.,a b 都不能被3整除C.,a b 不都能被3整除D.a 不能被3整除3、《论语·子路》篇中说:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足”,所以,名不正,则民无所措手足.上述推理用的是( )A.类比推理B.归纳推理C.演绎推理D.—次三段论4、下面是一段“三段论”推理过程:若函数()f x 在(),a b 内可导且单调递增,则在(),a b 内, ()'0f x >恒成立.因为()3f x x =在()1,1-内可导且单调递增,所以在()1,1-内,()230f x x ='>恒成立,以上推理中( )A.大前提错误B.小前提错误C.结论正确D.推理形式错误5、证明命题:“()1x xf x e e =+在()0,+∞上是增函数”,现给出的证法如下:因为()1x x f x e e =+,所以()1'x x f x e e=-, 因为0x >,所以1x e >,101x e <<,所以10x x e e ->,即()0f x '>,所以()f x 在()0,+∞上是增函数,使用的证明方法是( )A.综合法B.分析法C.反证法D.以上都不是6、用数学归纳法证明“111111111234212122n n n n n-+-++-=+++-++”时,由n k =的假设证明1n k =+时,如果从等式左边证明右边,则必须证得右边为( )A. 1111221k k k +++++B. 1111122122k k k k +++++++ C. 1112221k k k +++++ D. 11122122k k k ++++++ 7、在证明命题"对于任意角θ,44cos sin cos 2θθθ-="的过程"44cos sin θθ+()()2222cos sin cos sin θθθθ=+-22cos sin θθ=-cos2θ="中,应用了( )A.分析法B.综合法C.分析法和综合法综合使用D.间接证明法8、如图所示的三角形数阵叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n 行有n 个数且两端的数均为()12n n≥,每个数是它下一行左右相邻两数的和,如111122=+,111236=+,1113412=+,则第10行第4个数(从左往右数)为( )A.1360B. 1504C. 1840D. 11260 9、若数列{}n a 是等比数列,则数列{}1n n a a ++ ( )A.一定是等比数列B.一定是等差数列C.可能是等比数列也可能是等差数列D.一定不是等比数列10、求证:>证明:,>,只需证明22>,展开得55+>,即0>,此式显然成立,>.上述证明过程应用了( )A.综合法B.分析法C.综合法、分析法配合使用D.间接证法11、用数学归纳法证明: 422123,2n n n ++++⋯+=其初始值为______,当1n k =+时,其式子的左端应在n k =时的左端再加上_________.12、已知1131,,23n n n a a a a +==+则234,,a a a 的值分别为_______,由此猜想n a =________. 13、已知,,x y R ∈且2,x y +<则,x y 中至多有一个大于1,在用反证法证明时,假设应为__________.14、若三角形的周长为L ,面积为S ,内切圆半径为r ,则有2s r L=,类比此结论,在四面体中,设其表面积为S ,体积为V ,内切球半径为R ,则有__________.15、已知21()(1)bx f x ax +=+(1x a≠-,0a >),且16(1)log 2f =,(2)1f -=. 1.求函数()f x 的表达式;2.已知数列{}n x 的项满足[][][]1(1)1(2)1()n x f f f n =-⋅-⋅⋅-,试求1x 、2x 、3x 、4x ;3.猜想{}n x 的通项.答案以及解析1答案及解析:答案:C解析:2答案及解析:答案:B解析:反证法证明命题时,应假设命题的反面成立.而",a b 中至少有一个能被3整除"的反面是;",a b 都不能被3整除",故应假设,a b 都不能被3整除,故选B .3答案及解析:答案:C解析:这是一个复合三段论,从“名不正”推出“民无所措手足”,连续运用五次三段论,属演绎推理形式.4答案及解析:答案:A解析:()f x 在(),a b 内可导且单调递增,则在(),a b 内, ()'0f x ≥恒成立,故大前提错误.故选A.5答案及解析:答案:A解析:题中命题的证明方法是由所给的条件,利用所学的定理、定义、公式证得要证的结论,故此题的证明方法属于综合法,6答案及解析:答案:D解析:当1n k =+时,右边应为111(1)1(1)2(1)(1)k k k k ++⋯+++++++ 11111.2222122k k k k k =++⋯+++++++ 故D 正确.7答案及解析:答案:B解析:因为证明过程是“从左往右”,即由条件⇒结论.8答案及解析:答案:C解析:设第n 行第 m 个数为(),a n m ,由题意知()17,17a =,()18,18a =,()19,19a =,()110,110a =, ∴()()()11110,29,110,191090a a a =-=-=, ()()()1118,27,18,17856a a a =-=-=, ()()()1119,28,19,18972a a a =-=-=, ∴()()()110,39,210,2360a a a =-=,()()()19,38,29,2252a a a =-=, ∴()()()110,49,310,3840a a a =-=, 则第10行第4个数为1840,故选C.9答案及解析:答案:C解析:设等比数列{}n a 的公比为q ,则1(1)n n n a a a q ++=+.∴当1q ≠-时, {}1n n a a ++一定是等比数列;当1q =-时, 10,n n a a ++=此时为等差数列.10答案及解析:答案:B解析:证明过程中的“为了证明……”,“只需证明……”这样的语句是分析法所特有的,是分析法的证明模式.11答案及解析:答案:1;()()()k k k +++++⋯+222121解析:代入验证可知n 的初始值为1. n k =时的左端为2123,1k n k +++⋯+=+时的左端为()()()2222123121.k k k k +++⋯++++++⋯++ 故增加的式子为()()()222121.k k k ++++⋯++12答案及解析: 答案:3333,,;7895n + 解析:121133332,1372532a a a ⨯====+++ 同理, 232333,3835a a a ===++ 433,945a ==+ 533,1055a ==+ 猜想3.5n a n =+13答案及解析:答案:x ,y 都大于1解析:“至多有一个大于1”包括“都不大于1和有且仅有一个大于1”,故其对立面为“,x y 都大于1”.14答案及解析: 答案:3V R S= 解析:三角形可分解为三个以内切圆圆心为顶点的三角形,于是有12L r S ⋅=,即2S r L=,四面体可分解为四个以四面体各面为底面,内切球球心为顶点的三棱锥.于是13S R V ⋅⋅=,即3V R S =.15答案及解析:答案:1.由16(1)log 2f =,(2)1f -=解得1a =,0b =,所以21()(1)(1)f x x x =≠-+. 2. 134x =,223x =,358x =,435x =. 3.猜想: 22(1)n n x n +=+*()n N ∈. 数学归纳法证明22(1)n n x n +=+. ①当1n =时,因为134x =,而()1232114+=⨯+, 所以猜想成立. ②假设当()*1,n k k k N =≥∈时,猜想成立,即()221k k x k +=+, 当1n k =+时, ()111k k x x f k +=-+⎡⎤⎣⎦()()22112111k k k ⎡⎤+=-⎢⎥+++⎢⎥⎣⎦()()()()221212212k k k k k +++-+=⋅++ ()()121322211k k k k +++=⋅=+++⎡⎤⎣⎦. 所以当1n k =+时,猜想也成立.所以{}n x 的通项为22(1)n n x n +=+. 解析:1.实际上是用待定系数法求()f x 的解析式.2.体现的则是“归纳-猜想-证明”的思想方法.3.点评:这是一道函数、数列与数学归纳法相结合的综合题,重点是培养我们分析问题和解决问题的能力.由Ruize收集整理。
高中数学(苏教版 选修2-2)章末分层突破2 Word版含答案
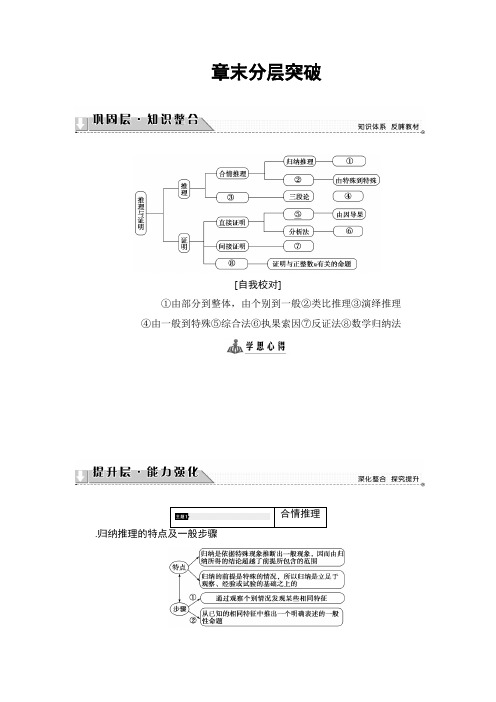
章末分层突破
[自我校对]
①由部分到整体,由个别到一般②类比推理③演绎推理
④由一般到特殊⑤综合法⑥执果索因⑦反证法⑧数学归纳法
.
.类比推理的特点及一般步骤
(·温州月
考)下面四个图案都是由小正三角形构成的,设第个图形中有个正三角形,且所
有小正三角形边上黑点的总数为().
图-
()求(),(),(),();
()找出()与(+)的关系,并求出()的表达式.【精彩点拨】()根据图案推导计算(),(),(),()及它们之间的关系.()利用()推
导出的关系归纳出()与(+)的关系,然后再求()的表达式.【规范解答】()由题意有()=,()=()++×=,()=()++×=,()=()++×
=,()=()++×=.
()由题意及()知,(+)=()++×=()++,
即(+)-()=+,所以()-()=×+,
()-()=×+,()-()=×+,…,
()-(-)=×(-)+,
将上面-个式子相加,得
()-()=[+++…+(-)]+(-)
=×+(-)=-,
又()=,所以()=.
[再练一题]
.已知函数=+(∈)的值域是,则
()函数=+(∈)的值域是;
()类比上述结论,函数=+(∈*)的值域是.。
高中数学(苏教版选修2-2)综合检测卷 Word版含解析
综合检测卷(时间:分钟满分:分)一、填空题(本大题共小题,每小题分,共分).已知是虚数单位,则(-+)(-)=.答案-+解析(-+)(-)=-+-=-+..演绎推理“因为对数函数=(>且≠)是增函数,而函数=是对数函数,所以=是增函数”所得结论错误的原因是.答案大前提错误解析对数函数=(>,且≠),当>时是增函数,当<<时是减函数,故大前提错误..用反证法证明命题:“若,∈,能被整除,那么,中至少有一个能被整除”时,假设应为.答案,都不能被整除解析“至少有一个”的否定为“一个也没有”..为虚数单位,复平面内表示复数=的点在第象限.答案三解析因为===--,所以复平面内表示复数=的点在第三象限..若=+,=+(≥),则,的大小关系为.答案<解析要比较与的大小,只需比较与的大小,只需比较++与++的大小,只需比较+与++的大小,即比较与的大小,而<,故<..函数()在定义域内可导,若()=(-),且(-)′()>,=(),=(),=(),则,,的大小关系是.答案>>解析因为(-)′()>,所以当>,′()>,即函数=()在(,+∞)上是增函数.又()=(-),所以=()=(),=()=(),所以>>..设()=--,则()的单调递增区间为.答案(,+∞)解析()定义域为(,+∞),又由′()=--=>,解得-<<或>,所以′()>的解集为(,+∞)..设,,都是正数,则三个数+,+,+的值说法正确的是.①都小于②至少有一个不大于③至少有一个不小于④都大于答案③解析假设这三个数都小于,即+<,+<,+<,则(+)+(+)+(+)<,又由基本不等式>,>,>时,(+)+(+)+(+)≥++=,与假设矛盾.故选③..曲线()=+-在点处的切线平行于直线=-,则点的坐标为.答案()或(-,-)解析设点的坐标为(,),因为′()=+,所以点处的切线的斜率为′()=+,又切线平行于直线=-,所以+=,解得=±.当=时,由(,)为曲线()=+-上的点,得=;当=-时,同理可得=-,所以点的坐标为()或(-,-)..设△的三边长分别为,,,△的面积为,内切圆半径为,则=,类比这个结论可知:四面体—的四个面的面积分别为,,,,内切球半径为,四面体—的体积为,则=.答案解析设四面体的内切球的球心为,则球心到四个面的距离都是,所以四面体的体积等于以为顶点,分别以四个面为底面的个三棱锥体积的和.则四面体的体积为四面体—=(+++),∴=..若复数=θ-θ所对应的点在第四象限,则θ为第象限角.答案一。
高中数学(苏教版选修2-2)章末检测卷(二) Word版含解析
章末检测卷(二)(时间:分钟满分:分)一、填空题(本大题共小题,每小题分,共分).由=+=++=+++=,…,得到++…+(-)=用的是推理.答案归纳.在△中,、分别为、的中点,则有∥,这个问题的大前提为.答案三角形的中位线平行于第三边解析这个三段论推理的形式为:大前提:三角形的中位线平行于第三边;小前提:为△的中位线;结论:∥..用反证法证明命题“三角形的内角至多有一个钝角”时,反设为.答案假设至少有两个钝角.用数学归纳法证明:+++…+=时,由=到=+左边需要添加的项是.答案解析由=到=+时,左边需要添加的项是=..已知(+)=,()=(∈*),猜想()的表达式为.答案()=解析当=时,()===,当=时,()===;当=时,()===,故可猜想()=..下列四个图形中,着色三角形的个数依次构成一个数列的前页,则这个数列的一个通项公式为.答案=-(∈*,≥)解析==,==,==,==,…,由此猜想=-(∈*,≥)..对“,,是不全相等的正数”,给出下列判断:①(-)+(-)+(-)≠;②=与=及=中至少有一个成立;③≠,≠,≠不能同时成立.其中判断正确的个数为.答案解析若(-)+(-)+(-)=,则==,与“,,是不全相等的正数”矛盾,故①正确.=与=及=中最多只能有一个成立,故②不正确.由于“,,是不全相等的正数”,有两种情形:至多有两个数相等或三个数都互不相等,故③不正确..我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有个.①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱椎.答案解析类比相似形中的对应边成比例知,①③属于相似体..数列{}满足=,+=-,则=.答案解析∵=,+=-,∴=-=-,=-=,=-=,=-=-,=-=,。
高二数学苏教版选修2-2阶段质量检测(二)推理与证明
3 _______ () 8 9 4AC BD ABCD AC BD51 21 21 46 ( )F V E8 x y R x 2 y 2 __________ 甘y X 1.91 2 22 2n 1 2n 1(n N *) n 1121 1 1[ 120 160 ](14)5 70ABCB②假设当n = k(k € N *)时,等式成立,即 1+ 2 + 22+…+ 2k 「1 = 2k — 1; 高中数学14 .(湖北高考)古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数 1,3,6,10,…,第n 个三角形数为 中+1 = *n 2+切.记第n 个k 边形数为N(n , k)(k >3),以下列出了部分k 边形数中第n 个数的表达式:三角形数 1 2 1N(n ,3) = ?n +尹 正方形数 N(n,4) = n 2, 五边形数3 2 1 N(n,5) = ?n 2—1n ,六边形数N( n,6) = 2n 2— n ,可以推测N(n , k)的表达式,由此计算 N(10,24) = _________、解答题(本大题共6个小题,共90分.解答应写出文字说明、 证明过程或演算步骤)③则当n = k + 1时,k + 11+ 2+尸+…十2k —1 + 2k=等—T =2k +1 -1则当n = k + 1时等式* »成立•由此可知,对任何 n € N ,等式都成立.上述证明步骤中错误的是 _________ •2 2 210.如图,在平面直角坐标系 xOy 中,圆x + y = r (r > 0)内切于正 方形 ABCD ,任取圆上一点 P ,若 OP = m OA + n OB (m , n € R ), 则和2 2m 2, n 2的等差中项;现有一椭圆 X 2+ y ^= 1(a >b > 0)内切于矩形 ABCD ,a b任取椭圆上一点 P ,若OP = m OA + n OB (m , n € R ),贝U m 2, n 2的等差中项为 ____________11.(安徽高考)如图,在等腰直角三角形 ABC 中,斜边BC = 2 . 2. 过点A 作BC 的垂线,垂足为A 1 ;过点A 1作AC 的垂线,垂足为A 2; 过点A 2作A 1C 的垂线,垂足为 A 3 ;…,依此类推.设 BA = a 1 , AA 1 =a 2 , A 1A 2= a 3,…, A 5A 6= a 7,贝a 7=___________________________________________ .1 4 27 a12 .已知 x>0,不等式 x +-> 2, x + -2 >3, x + r > 4,…,可推广为 x + n + 1,则x x x xa 的值为 _________ .13.如图,第n 个图形是由正n + 2边形“扩展”而来(n = 1,2,3,…),则第n 个图形中 共有 ________ 个顶点.15 ( 14 ) a>0 b>0 a b 1 1 1 1 a b ab16 (14 ) {a n}a1 a3 52a n 5n 3 b n 6T n 5n a n{b n}1 a n a n 1 g"n N *)T n a1 a2 5n17 ( 14 ) sin210 2cos 40 sin 10 cos 402 si n262cos 36 sin 6 cos 3634.18 ( 16 ) a b c 0<a b c<2 (2 a)b (2 b)c1.(2 c)a19. (本小题满分16分)数列{a n}满足S n= 2n-a n(n € N ).(1)计算a i, a2, a3, a4,并由此猜想通项a n的表达式;⑵用数学归纳法证明(1)中的猜想.1 320. (本小题满分16分)已知函数f(x) = 3X -x,数列{a n}满足条件:a1> 1, a n+1>f' (a n+ 1),(1) 证明:a n> 2n- 1(n€ N ).1 1 1(2) 试比较一 + -一+…+ —与1的大小,并说明理由.1 + a1 1 + a2 1 + a n答案1. 解析:由甲、丙的回答易知甲去过A城市和C城市,乙去过A城市或C城市,结合乙的回答可得乙去过A城市.答案:A2. 解析:平面图形中的图类比空间几何体中的球,周长类比表面积,面积类比体积.故可以得到的结论是:表面积一定的空间几何体中,球的体积最大.答案:表面积一定的空间几何体中,球的体积最大3. 解析:如果演绎推理的大前提和小前提都正确,则结论一定正确.大前提和小前提中,只要有一项不正确,则结论一定也不正确•故②错误.答案:①③④4. 形对角线互相垂直且平分V1_竺_包也」1_ 15.解析:V2 1 S2 h2 4 2 8'1站2答案:1 : 8高中数学12x6 6 10 26 8 12 2F V E 2.8x y 4x 2 122222x (1 y ) 1 y (1 x ) 2yp1 x 2y x 2 1 x 2 y 2.y)2 0 yx 2 y 2 1.1944 2 XT XT x xa n n n n10P(x y) 227 p 2 1 A(a b) B( a b)m OA n OBn 2(m n a (m n p22 , m n 1 ~~24m 2 n 21 4.11 ABCBC 2^2 ABAC a 1AA 1 a 2 V 2 A 1A 2a 3 1 ABCAn 1A nan 12 /(m n) (m A 5A 6 a 7 a 11 4.2 , 2A 2a7a 1 2 AA 13 27 3 P x4 x xn n -n n x13 a n a1 3 3 3 a2 4 4 4高中数学12 xa n -2 = n + n •,22a n = (n + 2) + n + 2 = n + 5n + 6. 答案:n 5+ 5n + 614. 解析:N(n , k) = a k n 2 + b k n(k 》3),其中数列{a k }是以舟为首项,2为公差的等差数列; 数列{b k }是以*为首项,一1为公差的等差数列;所以N(n,24) = 11n 2- 10n,当n = 10时,N(10,24)=11 x 102- 10 x 10= 1 ooo.答案:1 00015. 证明:•/ a>0, b>0, a + b = 1.1 11 = a + b >2 ab , ab <㊁,ab <4, •-存4当a = 2, b = 2时等号成立 又 a +6=(a +b) 1+b当a =1,b =2■时等号成立 1 1 1 •1+ b +新 8. 16. 解:因为 T n = a 1 + a2 5+ a3 52+ …+ an 5nS ① 所以 5T n = a 1 5+ a 2 5 + a 3 5 + …+ a n -1 5 1+a n 5,② 由①+②得:6T n = a 1+ (a 1 + a ?) 5+ @+ 83) 52 + …+ (a n -1+ a *) 5n 1+ a * 5n=1 + 5x 5+ 1 2x 52+-+n -1x 5n -1 + a n 5n=n+ an 5 ,所以 6T n — 5n a n = n ,所以数列{ b n }的通项公式为b n = n.17•解:观察 40。
高中数学苏教版选修2-2章末综合测评2含解析
章末综合测评(二)(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分,请把答案填在题中的横线上)1.有一段“三段论”推理是这样的:对于可导函数f(x),若f(x)=0,则x=x是函数f(x)的极值点.因为f(x)=x3在x=0处的导数值f′(0)=0,所以x =0是f(x)=x3的极值点.以上推理中________错误.【解析】大前提是错误的,若f′(x0)=0,x=x不一定是函数f(x)的极值点.【答案】大前提2.下列四个图形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为________.图1【解析】由图形可知,着色三角形的个数依次为:1,3,9,27,…,故an =3n-1.【答案】3n-13.(2016·日照联考)已知f(n)=1+12+13+…+1n(n∈N*),计算得f(22)>2,f(23)>52,f(24)>3,f(25)>72,由此推测,当n≥2时,有________.【解析】因为f(22)>42,f(23)>52,f(24)>62,f(25)>72,所以推测,当n≥2时,f(2n)>n+2 2.【答案】f(2n)>n+2 24.已知圆x2+y2=r2(r>0)的面积为S=πr2,由此类比椭圆x2a2+y2b2=1(a>b>0)的面积最有可能是________.【解析】将圆看作椭圆的极端情况,即a=b情形. ∴类比S圆=πr2,得椭圆面积S=πab.【答案】πab5.已知a>0,b>0,m=lg a+b2,n=lga+b2,则m与n的大小关系为________.【解析】∵(a+b)2=a+b+2ab>a+b>0,∴a+b>a+b>0,则a+b2>a+b2.∴lg a+b2>lga+b2,则m>n.【答案】m>n6.已知数列{an }为等差数列,数列{bn}是各项均为正数的等比数列,且公比q>1,若a1=b1,a2 013=b2 013,则a1 007与b1 007的大小关系是________.【解析】由2a1 007=a1+a2 013,得a1 007=a1+a2 0132.又b21 007=b1·b2 013,得b1 007=b1·b2 013,∵a1=b1>0,a2 013=b2 013>0,且a1≠a2 013,∴a1 007>b1 007.【答案】a1 007>b1 0077.利用数学归纳法证明不等式1n+1+1n+2+…+1n+n>12(n>1,n∈N*)的过程中,第一步的代数式为____________________.【解析】第一步:n=2时,左边为12+1+12+2,故代数式为12+1+12+2>1 2 .【答案】12+1+12+2>128.(2016·江西一模)观察下列等式:(1+x+x2)1=1+x+x2,(1+x+x2)2=1+2x+3x2+2x3+x4,(1+x +x 2)3=1+3x +6x 2+7x 3+6x 4+3x 5+x 6,(1+x +x 2)4=1+4x +10x 2+16x 3+19x 4+16x 5+10x 6+4x 7+x 8,由以上等式推测:对于n ∈N *,若(1+x +x 2)n =a 0+a 1x +a 2x 2+…+a 2n x 2n ,则a 2=________.【解析】 观察知,a 2为数列1,3,6,10,…中的第n 项,而1=22=1×22,3=62=2×32,6=122=3×42,10=202=4×52,…,归纳得a 2=n (n +1)2. 【答案】n (n +1)29.将全体正整数排成一个三角形数阵:图2根据以上排列规律,数阵中第n(n ≥3)行从左到右的第三个数是________. 【解析】 前n -1行共有正整数1+2+3+…+(n -1)=n 2-n2个,∴第n 行第3个数是n 2-n 2+3=n 2-n +62.【答案】 n 2-n +6210.(2016·东北三校二模)观察下列等式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第n 个等式为________.【解析】 由题知13=12; 13+23=⎝⎛⎭⎪⎫2×322; 13+23+33=⎝⎛⎭⎪⎫3×422; 13+23+33+43=⎝⎛⎭⎪⎫4×522; …。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末检测卷(二)(时间:120分钟 满分:160分)一、填空题(本大题共14小题,每小题5分,共70分)1.由1=12,1+3=22,1+3+5=32,1+3+5+7=42,…,得到1+3+…+(2n -1)=n 2用的是________推理. 答案 归纳2.在△ABC 中,E 、F 分别为AB 、AC 的中点,则有EF ∥BC ,这个问题的大前提为__________________.答案 三角形的中位线平行于第三边解析 这个三段论推理的形式为:大前提:三角形的中位线平行于第三边;小前提:EF 为△ABC 的中位线;结论:EF ∥BC .3.用反证法证明命题“三角形的内角至多有一个钝角”时,反设为__________________. 答案 假设至少有两个钝角 4.用数学归纳法证明:1+11+2+11+2+3+…+11+2+3+…+n =2nn +1时,由n =k 到n =k +1左边需要添加的项是________. 答案2k +1k +2解析 由n =k 到n =k +1时,左边需要添加的项是11+2+3+…+k +1=2k +1k +2. 5.已知f (x +1)=2fxfx +2,f (1)=1(x ∈N *),猜想f (x )的表达式为________. 答案 f (x )=2x +1解析 当x =1时,f (2)=2f 1f 1+2=23=22+1,当x =2时,f (3)=2f 2f 2+2=24=23+1; 当x =3时,f (4)=2f3f3+2=25=24+1, 故可猜想f (x )=2x +1. 6.下列四个图形中,着色三角形的个数依次构成一个数列的前4页,则这个数列的一个通项公式为________.答案 a n =3n -1(n ∈N *,n ≥1)解析 a 1=1=30,a 2=3=31,a 3=9=32,a 4=27=33,…, 由此猜想a n =3n -1(n ∈N *,n ≥1).7.对“a ,b ,c 是不全相等的正数”,给出下列判断: ①(a -b )2+(b -c )2+(c -a )2≠0; ②a =b 与b =c 及a =c 中至少有一个成立; ③a ≠c ,b ≠c ,a ≠b 不能同时成立. 其中判断正确的个数为________. 答案 1解析 若(a -b )2+(b -c )2+(c -a )2=0,则a =b =c ,与“a ,b ,c 是不全相等的正数”矛盾,故①正确.a =b 与b =c 及a =c 中最多只能有一个成立,故②不正确.由于“a ,b ,c 是不全相等的正数”,有两种情形:至多有两个数相等或三个数都互不相等,故③不正确. 8.我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有________个. ①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱椎. 答案 2解析 类比相似形中的对应边成比例知,①③属于相似体. 9.数列{a n }满足a 1=12,a n +1=1-1a n ,则a 2 013=________.答案 2解析 ∵a 1=12,a n +1=1-1a n,∴a 2=1-1a 1=-1,a 3=1-1a 2=2,a 4=1-1a 3=12,a 5=1-1a 4=-1,a 6=1-1a 5=2, ∴a n +3k =a n (n ∈N *,k ∈N *) ∴a 2 013=a 3+3×670=a 3=2.10.用数学归纳法证明n 3+5n (n ∈N *)能被6整除时,当n =k +1时,(k +1)3+5(k +1)应变形为________.答案 k 3+5k +3k (k +1)+6 11.观察下列等式:(1+1)=2×1(2+1)(2+2)=22×1×3(3+1)(3+2)(3+3)=23×1×3×5 …照此规律,第n 个等式可为______________.答案 (n +1)(n +2)…(n +n )=2n×1×3×…×(2n -1)解析 由已知的三个等式左边的变化规律,得第n 个等式左边为(n +1)(n +2)…(n +n ),由已知的三个等式右边的变化规律,得第n 个等式右边为2n与n 个奇数之积,即2n×1×3×…×(2n -1).12.已知对于任意实数α,我们有正弦恒等式sin αsin(π3-α)·sin(π3+α)=14sin 3α,也有余弦恒等式cos αcos(π3-α)·cos(π3+α)=14cos 3α,类比以上结论对于使正切有意义的α,可以推理得正切恒等式为________________. 答案 tan αtan(π3-α)tan(π3+α)=tan 3α13.已知S k =1k+2k+3k+…+n k,当k =1,2,3,…时,观察下列等式:S 1=12n 2+12n , S 2=13n 3+12n 2+16n , S 3=14n 4+12n 3+14n 2, S 4=15n 5+12n 4+13n 3-130n , S 5=An 6+12n 5+512n 4+Bn 2,…可以推测,A -B =________. 答案 14解析 由S 1,S 2,S 3,S 4,S 5的特征,推测A =16.又各项的系数和为1,∴A +12+512+B =1,则B =-112.因此推测A -B =16+112=14.14.在平面几何中,△ABC 的内角平分线CE 分AB 所成线段的比为AE EB =AC BC,把这个结论类比到空间:在三棱锥A —BCD 中(如图所示),面DEC 平分二面角A —CD —B 且与AB 相交于E ,则得到的类比的结论是________.答案AE EB =S △ACDS △BCD解析 CE 平分∠ACB ,而面CDE 平分二面角A —CD —B . ∴AC BC 可类比成S △ACDS △BCD, 故结论为AE EB =S △ACDS △BCD.二、解答题(本大题共6小题,共90分)15.(14分)1,3,2能否为同一等差数列中的三项?说明理由.解 假设1,3,2能为同一等差数列中的三项,但不一定是连续的三项,设公差为d ,则 1=3-md,2=3+nd ,m ,n 为两个正整数,消去d 得m =(3+1)n .∵m 为有理数,(3+1)n 为无理数, ∴m ≠(3+1)n . ∴假设不成立.即1,3,2不可能为同一等差数列中的三项. 16.(14分)设a ,b 为实数,求证:a 2+b 2≥22(a +b ). 证明 当a +b ≤0时,∵a 2+b 2≥0, ∴a 2+b 2≥22(a +b )成立. 当a +b >0时,用分析法证明如下: 要证a 2+b 2≥22(a +b ), 只需证(a 2+b 2)2≥⎣⎢⎡⎦⎥⎤22a +b 2, 即证a 2+b 2≥12(a 2+b 2+2ab ),即证a 2+b 2≥2ab .∵a 2+b 2≥2ab 对一切实数恒成立,∴a 2+b 2≥22(a +b )成立. 综上所述,对任意实数a ,b 不等式都成立.17.(14分)已知a 、b 、c 是互不相等的非零实数.求证三个方程ax 2+2bx +c =0,bx 2+2cx +a =0,cx 2+2ax +b =0至少有一个方程有两个相异实根. 证明 反证法:假设三个方程中都没有两个相异实根,则Δ1=4b 2-4ac ≤0,Δ2=4c 2-4ab ≤0,Δ3=4a 2-4bc ≤0. 相加有a 2-2ab +b 2+b 2-2bc +c 2+c 2-2ac +a 2≤0, (a -b )2+(b -c )2+(c -a )2≤0.①由题意a 、b 、c 互不相等,∴①式不能成立.∴假设不成立,即三个方程中至少有一个方程有两个相异实根.18.(16分)设a ,b ,c 为一个三角形的三条边,s =12(a +b +c ),且s 2=2ab ,试证:s <2a .证明 要证s <2a ,由于s 2=2ab ,所以只需证s <s 2b,即证b <s .因为s =12(a +b +c ),所以只需证2b <a +b +c ,即证b <a +c .由于a ,b ,c 为一个三角形的三条边,所以上式成立.于是原命题成立. 19.(16分)数列{a n }满足a 1=16,前n 项和S n =nn +12·a n .(1)写出a 2,a 3,a 4;(2)猜出a n 的表达式,并用数学归纳法证明. 解 (1)令n =2,∵a 1=16,∴S 2=2×2+12a 2,即a 1+a 2=3a 2.∴a 2=112.令n =3,得S 3=3×3+12a 3, 即a 1+a 2+a 3=6a 3,∴a 3=120.令n =4,得S 4=4×4+12a 4, 即a 1+a 2+a 3+a 4=10a 4,∴a 4=130.(2)猜想a n =1n +1n +2,下面用数学归纳法给出证明.①当n =1时,a 1=16=11+11+2,结论成立.②假设当n =k 时,结论成立,即a k =1k +1k +2, 则当n =k +1时,S k =k k +12a k =k k +12·1k +1k +2=k2k +2, S k +1=k +1k +22a k +1, 即S k +a k +1=k +1k +22a k +1.∴k 2k +2+a k +1=k +1k +22a k +1.∴a k +1=k2k +2k +1k +22-1=kk k +3k +2=1k +2k +3.当n =k +1时结论成立.由①②可知,对一切n ∈N *都有a n =1n +1n +2.20.(16分)设f (n )=1+12+13+…+1n ,是否存在关于自然数n 的函数g (n ),使等式f (1)+f (2)+…+f (n -1)=g (n )·[f (n )-1]对于n ≥2的一切自然数都成立?并证明你的结论. 解 当n =2时,由f (1)=g (2)·[f (2)-1], 得g (2)=f 1f2-1=11+12-1=2, 当n =3时,由f (1)+f (2)=g (3)·[f (3)-1], 得g (3)=f 1+f 2f 3-1=1+1+121+12+13-1=3,猜想g (n )=n (n ≥2). 下面用数学归纳法证明:当n ≥2时,等式f (1)+f (2)+…+f (n -1)=n [f (n )-1]恒成立. ①当n =2时,由上面计算可知,等式成立.②假设n =k (k ∈N *且k ≥2)时,等式成立,即f (1)+f (2)+…+f (k -1)=k [f (k )-1](k ≥2)成立,那么当n=k+1时,f(1)+f(2)+…+f(k-1)+f(k)=k[f(k)-1]+f(k)=(k+1)f(k)-k=(k+1)[f(k+1)-1k+1]-k=(k+1)[f(k+1)-1],∴当n=k+1时,等式也成立.由①②知,对一切n≥2的自然数n,等式都成立,故存在函数g(n)=n,使等式成立.。
