理论力学课件—摩擦.
合集下载
理论力学课件——摩 擦

全tan约束f 力F和FmNax法线f间Fs FN的N 夹f角s 的
正切等于静滑动摩擦系数。
摩擦锥(角) 0 f
2 自锁现象
3 测定摩擦系数的一种简易方法,斜面与螺纹自锁条件
tan tan f fs
斜面自锁条件
螺纹自锁条件 f
§4-3 考虑滑动摩擦时物体的平衡问题
仍为平衡问题,平衡方程照用,求解步骤与 前面基本相同。 几个新特点 1 画受力图时,必须考虑摩擦力; 2 严格区分物体处于临界、非临界状态; 3 因 0 Fs Fmax ,问题的解有时在一个范围内。
第四章 摩擦
摩擦
滑动摩擦 滚动摩擦
静滑动摩擦 动滑动摩擦
静滚动摩擦 动滚动摩擦
干摩擦 摩擦
湿摩擦
《摩擦学》
§ 4-1滑动摩擦
Fx 0
FT Fs 0
Fs FT
静滑动摩擦力的特点
1 方向:沿接触处的公切线,
与相对滑动趋势反向;
2 大小:
3
(库仑摩擦定律)
§ 4-1滑动摩擦
静F滑x 动0摩擦FT力的Fs特点0 Fs FT
例4-1 已知:P 1500N fs 0.2 fd 0.1 F 400N
求: 物块是否静止,摩擦力的大小和方向。 解: 取物块,设物块平衡
Fx 0, F cos 300 P sin 300 Fs 0
Fy 0,F sin 300 P cos 300 FN 0
解得: Fs 403.6N FN 1499N
0 Fs Fmax
0 M M max
Fmax fs FN M max FN 最大滚动摩阻(擦)力偶
滚动摩阻(擦)系数,长度量纲 的物理意义
使圆轮滚动比滑动省力的原因
处于临界滚动状态,轮心拉力为 F1
正切等于静滑动摩擦系数。
摩擦锥(角) 0 f
2 自锁现象
3 测定摩擦系数的一种简易方法,斜面与螺纹自锁条件
tan tan f fs
斜面自锁条件
螺纹自锁条件 f
§4-3 考虑滑动摩擦时物体的平衡问题
仍为平衡问题,平衡方程照用,求解步骤与 前面基本相同。 几个新特点 1 画受力图时,必须考虑摩擦力; 2 严格区分物体处于临界、非临界状态; 3 因 0 Fs Fmax ,问题的解有时在一个范围内。
第四章 摩擦
摩擦
滑动摩擦 滚动摩擦
静滑动摩擦 动滑动摩擦
静滚动摩擦 动滚动摩擦
干摩擦 摩擦
湿摩擦
《摩擦学》
§ 4-1滑动摩擦
Fx 0
FT Fs 0
Fs FT
静滑动摩擦力的特点
1 方向:沿接触处的公切线,
与相对滑动趋势反向;
2 大小:
3
(库仑摩擦定律)
§ 4-1滑动摩擦
静F滑x 动0摩擦FT力的Fs特点0 Fs FT
例4-1 已知:P 1500N fs 0.2 fd 0.1 F 400N
求: 物块是否静止,摩擦力的大小和方向。 解: 取物块,设物块平衡
Fx 0, F cos 300 P sin 300 Fs 0
Fy 0,F sin 300 P cos 300 FN 0
解得: Fs 403.6N FN 1499N
0 Fs Fmax
0 M M max
Fmax fs FN M max FN 最大滚动摩阻(擦)力偶
滚动摩阻(擦)系数,长度量纲 的物理意义
使圆轮滚动比滑动省力的原因
处于临界滚动状态,轮心拉力为 F1
第四章 摩擦(赵) 理论力学课件

F max FN
2、FP = FPm,物体 处 于临界平衡状态。 Fmax ——极限摩擦力, 也称最大静摩擦力
(maximum static friction
force)。
Fmax ≈ fs ·FN ——库仑静摩擦定律 (Coulomb law of friction)
FN ——法向压力, f s——fric静tion摩fa擦cto因r)。数(static
FPmax
FN2 - FPmax sin - FQ cos = 0
补充 FL2 = f ·FN2
sinα+ f cosα
FPmax = cosα- f sinα
FQ
= FQ tan(α+φm )
2020/10/3
FQ FL1
FN1
∵ F Pmin = FQ tan(α-φm )
FQ FP
F Pmax = FQ tan(α+φm )
∴ 圆柱绕B点处于只滚不滑状态。
2020/10/3
例4 讨 论 条件:FP = 20 kN , fA = fB=0.3 ,FW = 10 kN ,
轮半径为R。求能使轮运动的拉力FR。
4m
FP
2m
O
R/2 R/2
A FW C
B
C
FR
2020/10/3
二、滚动摩擦
FQ
FT r mI
F FN
FN = -FQ, FT = -F
补充 FL1 = f ·FN1
sinα- f cosα
FPmin = cosα+f sinα FQ = FQ tan(α-φm )
2020/10/3
FQ FP
FPmin
FQ FL1
2、FP = FPm,物体 处 于临界平衡状态。 Fmax ——极限摩擦力, 也称最大静摩擦力
(maximum static friction
force)。
Fmax ≈ fs ·FN ——库仑静摩擦定律 (Coulomb law of friction)
FN ——法向压力, f s——fric静tion摩fa擦cto因r)。数(static
FPmax
FN2 - FPmax sin - FQ cos = 0
补充 FL2 = f ·FN2
sinα+ f cosα
FPmax = cosα- f sinα
FQ
= FQ tan(α+φm )
2020/10/3
FQ FL1
FN1
∵ F Pmin = FQ tan(α-φm )
FQ FP
F Pmax = FQ tan(α+φm )
∴ 圆柱绕B点处于只滚不滑状态。
2020/10/3
例4 讨 论 条件:FP = 20 kN , fA = fB=0.3 ,FW = 10 kN ,
轮半径为R。求能使轮运动的拉力FR。
4m
FP
2m
O
R/2 R/2
A FW C
B
C
FR
2020/10/3
二、滚动摩擦
FQ
FT r mI
F FN
FN = -FQ, FT = -F
补充 FL1 = f ·FN1
sinα- f cosα
FPmin = cosα+f sinα FQ = FQ tan(α-φm )
2020/10/3
FQ FP
FPmin
FQ FL1
理论力学第七章摩擦课件

>>摩擦力与摩擦角
当物体A保持静止并且临界状态为先滑动时,只要保证所有主动
外力的合力与公法线的夹角小于等于摩擦角m,则无论外力多大,
全约束反力总可以与其形成平衡,而不会滑动。这种现象称为自锁 现象。如果主动力合力的作用线位于摩擦锥以外,则无论力多小, 物体都不能保持平衡。
7.2 考虑摩擦时物体系统的平衡
F
F4
b cos h sin a cos
W 2
1m cos20 2m sin20 200 kN
1.8m cos30
2
104 .2kN
综合以上四个结果,可得系统保持平衡时,拉力F的取值范围为
40.2 kN F1 F F4 104 .2 kN
>> 考虑摩擦时物体系统的平衡
例7-4 等厚均质矩形体A和B,如图7.14 所示。A重20kN,A与铅垂墙间是光 滑的,A与B和B与水平固定面间的摩 擦系数均为fs。试求系统平衡时fs至 少应为多大?B的重量W2至少应为多 少?
(2) 当物体处于向上滑动的临界状态时,摩擦力方向与图(b)所示的 摩擦力方向相反。
F
F2
sin cos
f f
cos sin
W
sin 20 0.2 cos 20 200 kN cos30 0.2 sin 30
109 .7 kN
(3) 当物体处于绕O点翻倒的临界状态时,此时有:x=0
Fy 0 FNB W 0 (c)
求解可得:
FNB
W cos 2 s in
Fs
W cos 2 s in
>> 考虑摩擦时物体系统的平衡
(2)这属于平衡的临界状态。首先
求角度的最小值,此时梯子的受力
理论力学电子教程摩擦34页PPT

理论力学电子教程摩擦
1、 舟 遥 遥 以 轻飏, 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色,裛 露掇其 英。 3、 日 月 掷 人 去,有 志不获 骋。 4、 未 言 心 相 醉,不 再接杯 酒。 5、 黄 发 垂 髫 ,并怡 然自乐 。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
ห้องสมุดไป่ตู้
1、 舟 遥 遥 以 轻飏, 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色,裛 露掇其 英。 3、 日 月 掷 人 去,有 志不获 骋。 4、 未 言 心 相 醉,不 再接杯 酒。 5、 黄 发 垂 髫 ,并怡 然自乐 。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
ห้องสมุดไป่ตู้
理论力学教学PPT摩擦教学课件PPT

4
(2)临界平衡状态:
FS
Fmax
Fmax :最大静摩擦力
静摩 擦力有一个范围:0 Fs Fmax
Fmax
有限约束力
实验表明:Fm
的大小与接触面上法向反力
ax
FN
的大小成正比,方向与物体相对滑动趋势的方向相反.
P
Fmax
A
FN
Fmax = fs FN f s ----- 静摩擦系数
静滑动摩擦定律 T
49.61N m MC 70.39 N m
40
例5-14 已知: 力 P 角 ,不计自重的 A , B 块间的
静摩擦系数为 f s ,其它接触处光滑;
求:使系统保持平衡的力 F的值.
41
解: 取整体 Fy 0 FNA P 0 FNA P
设力 F小于 F1时,楔块 A 向右运动, 取楔块 A ,F1 FNA tan( ) P tan( )
解得 Fs 866 N FN 4500 N d 0.171m
而 Fmax fs FN 1800 N
因 Fs Fmax , 木箱不会滑动;
又 d 0 , 木箱无翻倒趋势.
木箱平衡
(2)设木箱将要滑动时拉力为 F1 Fx 0 Fs F1 cos 0 Fy 0 FN P F1 sin 0
画两杆受力图.
(a)
(b)
38
对图 (a) , M A 0 FN1 AB M A 0
对图 (b) , M C 0 M C1 FN1 l sin 60o Fs1 l cos 60o 0 又 Fs1 Fs1 fs FN1 fs FN1
解得 MC1 70.39N m
设 M C M C2 时,系统有顺时针方向转动趋势,
理论力学(第7版)第四章 摩擦PPT课件

系数f=0.1,求能自锁的倾斜角a 。
解:研究楔块,受力如图
X 0 , R c o ) R s 1 c( o 0
由二力平衡:条 R件 R1
, 2
又 tg 0 .1 f, t g 1 0 .1 5 0 4'
211026' (极 限 状 ) 态
[思考题:P125 4-1 、4-4,4-5]
fs
全约束力和法线间的夹角的正切等于静
滑动摩擦系数.
0f
摩擦锥
(顶角为 2)f
13
14
4-2 摩擦角和自锁现象 二、自锁: ①定义:当物体依靠接触面间的相互作用的摩擦力与正压力
(即组成的全反力)自己把自己卡紧,不会松开(无论外力 多大),这种现象称为自锁。
②自锁条件:
当0时f,永远平衡(即自锁)
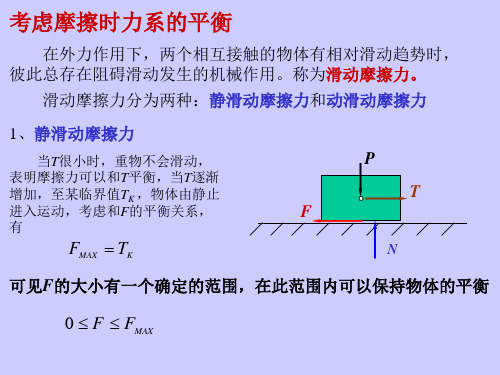
1、静滑动摩擦力: 当物体上作用一大小可变化的水平拉
力P时,当拉力P由零值逐渐增加但不很 大时,物体仅有相对滑动趋势,但仍保 持静止。即,如图支承面对物体除有法 向约束力FN外,还有一个阻碍物体沿水 平面向右滑动的切向约束力,此力即静 滑动摩擦力,简称静摩擦力。
6
4-1 滑动摩擦
2、状态:①静止: Fs P,(PFS ,FS为不固)定
全约束力必在摩擦角之内 15
16
4-2 摩擦角和自锁现象
结论: (1)如果作用于物块的全部 主动力的合力F R的作用线在摩
擦角 之 f内,则无论这个力怎
样大,物块必保持静止—— 自锁现象。
[注]:此时还有个方向问题,主动力 合力的方向应与全约束反力方向相 反,否则,则不会平衡,也不会自 锁。
(实际中常应用该原理的机构:圆锥销、压榨机)
解得:Fs 40.63 N(向上)
解:研究楔块,受力如图
X 0 , R c o ) R s 1 c( o 0
由二力平衡:条 R件 R1
, 2
又 tg 0 .1 f, t g 1 0 .1 5 0 4'
211026' (极 限 状 ) 态
[思考题:P125 4-1 、4-4,4-5]
fs
全约束力和法线间的夹角的正切等于静
滑动摩擦系数.
0f
摩擦锥
(顶角为 2)f
13
14
4-2 摩擦角和自锁现象 二、自锁: ①定义:当物体依靠接触面间的相互作用的摩擦力与正压力
(即组成的全反力)自己把自己卡紧,不会松开(无论外力 多大),这种现象称为自锁。
②自锁条件:
当0时f,永远平衡(即自锁)
1、静滑动摩擦力: 当物体上作用一大小可变化的水平拉
力P时,当拉力P由零值逐渐增加但不很 大时,物体仅有相对滑动趋势,但仍保 持静止。即,如图支承面对物体除有法 向约束力FN外,还有一个阻碍物体沿水 平面向右滑动的切向约束力,此力即静 滑动摩擦力,简称静摩擦力。
6
4-1 滑动摩擦
2、状态:①静止: Fs P,(PFS ,FS为不固)定
全约束力必在摩擦角之内 15
16
4-2 摩擦角和自锁现象
结论: (1)如果作用于物块的全部 主动力的合力F R的作用线在摩
擦角 之 f内,则无论这个力怎
样大,物块必保持静止—— 自锁现象。
[注]:此时还有个方向问题,主动力 合力的方向应与全约束反力方向相 反,否则,则不会平衡,也不会自 锁。
(实际中常应用该原理的机构:圆锥销、压榨机)
解得:Fs 40.63 N(向上)
理论力学课件 摩擦

5
如果改变水平力QK的作用 线方向, 则Fm及FRm的方向 也将随之作相应的改变; 若 QK在水平面转过一圈, 则全 约束力FRm的作用线将在空 间画出一个锥面,称为摩擦 锥.
O
f
全约束力与接触面法线所形成的夹角不会大 于f ,即FR作用线不可能超出摩擦锥.即: 静止时, ‹ f
6
如果物体所受的 主动力合力 S (G,Q S 的合力)的作用线 在摩擦锥之外,即 > f时,则全约束力FR 就不可能与S共线. 此时两力不符合二 力平衡条件,物体将 发生滑动.
f
FR
7
如果物体所受的主动力合 力 S 的作用线在摩擦锥之内, 即 < f时,则无论主动力多 大,它总是与FR相平衡,因而 物体将保持不动.
主动力合力的作用线在 摩擦锥的范围内,物体依靠 摩擦总能静止而与主动力 大小无关的现象,称为自锁.
S
f
FR
8
S
如果物体所受的主
动力合力 S 的作用线
N
2sin
W f
cos
17
取OA板为研究对象画受力图.此时的 水平力有极小值Pmin
mO(Fi) = 0
A
F1 P1 N1
C
N1 r ctg Pmind ctg
Pm in
2dsin
Wr f
cos
Fx O
Fy
(2)求P的极大值
当P达到极大值时,圆柱处于上滑临界状态.只要改变
W P
a
b
25
假定方块处于滑动临界平衡状 态画受力图.
Fy = 0 N - W = 0
Fx = 0 P - Fm = 0 Fm=f N
理论力学摩擦.ppt
列平衡方程
F
C
G
A
FA
FB x
B
FNA
FNB
MB 0,
G
a 2
F
h
FNA
a
0
柜不绕 B 翻倒条件:
FNA≥0
a
解得
F ≤ Ga
2h
F
当h=b时,使柜翻倒的最小推力为
C b
G
h
F
Fmin2
Ga 2b
柜体保持滑动而不翻到时,应满足
Fmin2 F Fmin1
即
Ga 2b
F
Gfs
a
F
C b
G
h
在坑道施工中,广泛采用各种利用摩擦锁紧装置—楔联结。 坑道支柱中的联结结构装置如图所示。它包括顶梁I,楔块II,用 于调节高度的螺旋III及底座IV。螺旋杆给楔块以向上的推力FN1。 已知楔块与上下支柱间的静摩擦因数均为fs(或摩擦角φf )。求楔 块不致滑出所需顶角的大小。
Fx 0, FNC sin 60 FC cos 60 F FD 0 (c)
Fy 0, FNC cos 60 G FC sin 60 FND 0 (d)
MO F 0, FCr FDr 0
(e)
由式(e)可得 FD FC
将 FNC FNC 100 N, FD FC FC 40 N
B
FB
C r
F
O
G Aα
D
解: 此题在C,D两处都有摩擦,两个摩擦力之 中只要有一个达到最大值,系统即处于临 界状态。
B
FB
C r
F
O
G Aα
D
先假设C处的摩擦 达到最大值,当力F为 最小时,轮有沿水平 向右滚动的趋势。
