光学第一章
《现代光学》课件第1章

29
第1章 现代光学的数学物理基础
可将r0、r1和r的表达式作泰勒展开,取旁轴近似为 (1.1-29)
30
第1章 现代光学的数学物理基础
由于振幅随r的变化比较缓慢,故振幅因子中的r可作 近似: r≈d,于是得到旁轴近似条件下轴外点光源发出的 球面波在(x,y,z1)面上的复振幅分布的表达式为
(1.1-22)
21
第1章 现代光学的数学物理基础
3. 柱面波 均匀无限长同步辐射的线光源发出的光波为柱面波。 柱面波的特征是: 相位间隔为2π的等相面是一组等间距同 轴柱面,光波场中各点的振幅与该点到轴线的距离的平方 根成反比。
22
第1章 现代光学的数学物理基础
图1.1-3 柱面波示意图
23
第1章 现代光学的数学物理基础
复振幅为
令 (1.1-24)
25
第1章 现代光学的数学物理基础
对于给定的观察面,z1为常量,则U0也是与x、y无关 的常量。显然U0不影响该面上复振幅的相对分布。于是该 观察面上的复振幅可简写为
(1.1-25)
26
第1章 现代光学的数学物理基础
2. 球面光波场中任意平面上的复振幅 这里以发散球面波为例讨论。如图1.1-4所示,点光源 Q(x0,y0)在(x0,y0,z0)面内,观察点P(x,y)在(x,y,z1)面内,两平 面间距离为d=z1-z0。Q到P的矢径为r,z0到P的矢径为r0, Q到z1的矢径为r1,这些矢径的长度分别为
由式(1.1-4)与式(1.1-2),可以给出相应的光学拉格朗 日函数定义:
(1.1-5) 此处,z可假定起着与拉格朗日力学中的时间相同的作用。 与经典力学中的情况类似,我们同样能够引入哈密顿量。 根据经典力学中广义动量p和q的定义:
光学教程答案(第一章)

1. 波长为nm 500的绿光投射在间距d 为cm 022.0的双缝上,在距离cm 180处的光屏上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为nm 700的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离.解:由条纹间距公式λd r y y y j j 01=-=∆+ 得cm 328.0818.0146.1cm146.1573.02cm818.0409.02cm573.010700022.0180cm 409.010500022.018021222202221022172027101=-=-=∆=⨯===⨯===⨯⨯==∆=⨯⨯==∆--y y y drj y d rj y d r y d r y j λλλλ2.在杨氏实验装置中,光源波长为nm 640,两狭缝间距为mm 4.0,光屏离狭缝的距离为cm 50.试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若p 点离中央亮条纹为mm 1.0,问两束光在p 点的相位差是多少?(3)求p 点的光强度和中央点的强度之比.解:(1)由公式λd r y 0=∆得λd r y 0=∆ =cm 100.8104.64.05025--⨯=⨯⨯(2)由课本第20页图1-2的几何关系可知52100.01sin tan 0.040.810cm 50y r r d d dr θθ--≈≈===⨯521522()0.8106.4104r r πππϕλ--∆=-=⨯⨯=⨯(3) 由公式2222121212cos 4cos 2I A A A A A ϕϕ∆=++∆= 得8536.042224cos 18cos 0cos 421cos 2cos42cos 422202212212020=+=+==︒⋅=∆∆==πππϕϕA A A A I I pp3. 把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m .解:未加玻璃片时,1S 、2S 到P 点的光程差,由公式2rϕπλ∆∆=可知为 Δr =215252r r λπλπ-=⨯⨯=现在1S 发出的光束途中插入玻璃片时,P 点的光程差为()210022r r h nh λλϕππ'--+=∆=⨯=⎡⎤⎣⎦所以玻璃片的厚度为421510610cm 10.5r r h n λλ--====⨯-4. 波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解:6050050010 1.250.2r y d λ-∆==⨯⨯=mm122I I = 22122A A =12A A =()()122122/0.94270.94121/A A V A A ∴===≈++5. 波长为700nm 的光源与菲涅耳双镜的相交棱之间距离为20cm ,棱到光屏间的距离L 为180cm ,若所得干涉条纹中相邻亮条纹的间隔为1mm ,求双镜平面之间的夹角θ。
光学第一章总结

第一章 光和光的传播§1光和光学一、光的本性光是一种波长极短、频率极高的电磁波,具有波粒二象性: 光在传播过程中,表现出波动性;光在与物质相互作用过程中表现出光的粒子性(量子性)。
二、 光源与光谱(1)热(辐射)光源 热能转变为辐射的光源。
任何温度下,任何固体或液体中原子、分子热运动能量改变时辐射出各种波长的电磁波(光波)。
光波为连续谱。
如太阳,白炽灯等。
由于物体辐射总能量及能量按波长分布都决定于温度,所以称为热辐射。
注意:1.物体由大量原子组成,热运动引起原子碰撞使原子激发而辐射电磁波。
原子的动能越大,通过碰撞引起原子激发的能量就越高,从而辐射电磁波的波长就越短。
2.任何物体在任何温度下都有热辐射,波长自远红外区连续延伸到紫外区(连续谱)。
(2)非热光源A 气体放电光源B 金属蒸气电弧光源C 固态发光体 —红宝石 蓝宝石 YAG 激光器D 同步辐射光源:高强度,宽波谱,高准直性,脉冲性,偏振性 三、热光源与非热光源的区别(1)本质上 在热光源中是原子、分子的热运动能量转化为光辐射;而非热光源是电子跃迁产生辐射。
(2)光谱上 热光源为连续谱;而非热光源是各原子独立发光,为分立的线光谱。
(3)温度上 热光源辐射的光谱与物质无关,强度与物质的表面温度有关;而非热光源与温度无关。
四、光强A.能流:单位时间内垂直通过某一面积 S 的能量.B.平均能流:能流也是周期性变化的,其在一个周期内的平均值称为平均能流。
能流(功率)单位:瓦特WC.能流密度 ( 光的强度 ) 单位时间,垂直通过单位面积的平均能量。
注意:在波动光学中常把振幅的平方所表征的光照度叫光强度。
五、 光谱W wSu =W wSu =WI S=u A 2221ωρ=2A I =光谱:非单色光的光强按波长的分布 i ~ λ.有连续光谱,线状光谱,带状光谱谱线宽度 Δλ:单位波长区间的光强,又称为谱密度。
六、光是电磁波的一部分(1)长波段表现出显著的波动性。
大学物理光学第一章答案
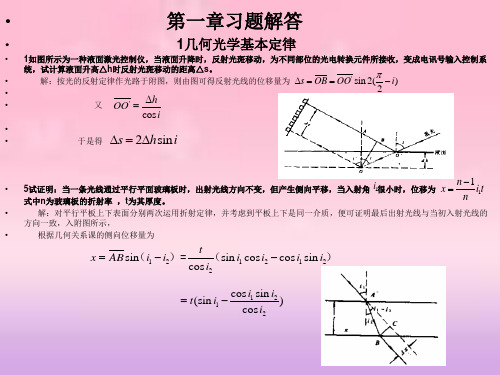
i1《1的条件下,取小角近似
于是有
sin i1 i1 ,cos i1 cos i2 1
x n 1 i1t n
•
12如图所示,在水中有两条平行线1和2,光线2射到水和平行平板玻璃的分界面上。
• •
(1)两光线射到空气中是否还平行? (2)如果光线1发生全反射,光线2能否进入空气? 解: 我们先推到一下光线经过几个平行界面的多层媒质时出射光线的方向。 因为界面都是平行的,所以光线在同一媒质中上界面的的折射角与下界面的入射角相等,如下图所示:
• • • • •
解得
S0 R
sin i sin u
S0 ' R
sin i ' sin u '
u u ' (i ' i)
又根据折射定律 进一步得到 由此可见,只在
n sin i n 'sin u
S0 n ' sin i ' R n sin u
以及角度关系
S0 '
f 如设该透镜在空气中和在水中的焦距分别为 f1 ,2 ,按上式有 f2 n 1 L f1 ( nL 1) n0 1.50 1 ( f1 10.0) f1 则 f2 3 1.50 1 4
4 f1 40cm
•
• •
• •
3用一曲率半径为20cm的球面玻璃和一平玻璃粘合成空气透镜,将其浸入水中(见图),设玻璃壁厚可忽略,水和空气的折射 率分别为4/3和1,求此透镜的焦距f。此透镜是会聚的还是发散的? 1 n 4 r 解:以 nL 1 ,0 3 , 20cm , r2 代入薄透镜焦距公式 f 1 n 1 1 ( L 1)( ) n0 r1 r2 算出该空气薄透镜(置于水中)的焦距为 f= - 80cm ,它是发散透镜。
《光学教程第一章》课件

光学教程第一章PPT课件
章节概述
光学基础知识
从光学的起源和发展,介绍光学的基本概念 和原理。
光的本质和特性
探索光的波粒二象性,频率和波长,速度以 及偏振。
光的传播和衍射
解读光的传播方式,直线传播,散射和吸收, 以及衍射现象。
光的折射和反射
揭示光的折射规律,全反射,反射规律,并 介绍实验。
3
光的速度
探索光在不同介质中传播时的速度变化。
4
光的偏振
讲解光的偏振现象及其在实际应用的意义。
光的传播和衍射
光的传播方式
详细介绍光是如何在空间中传播的。
光的散射和吸收
探讨光在遇到粗糙和杂乱表面时的散射和吸 收现象。
光的直线传播
解析光在均匀介质中直线传播的规律。
光的衍射现象
阐述光通过孔隙或障碍物时发生的衍射现象。
光的折射和反射
光的折射规律 光的全反射
光的反射规律 光的反射实验
介绍光在两个介质交界面发生折射时的规律。 探索光从光密介质射向光疏介质时发生的全反 射。 解析光在平面镜和曲面镜上的反射规律。 介绍一些简单的光的反射实验,如镜子实验。
光的干涉和衍射
光的干涉现象
阐述不同光波相互作用导致的干涉现象。
干涉的类型
光学基础知识
光的定义
详细讲解光的定义和相关概念。
光的属性
解析光的属性,如波动性和微粒性。
光的来源和产生
探索光的来源和产生,如自然光和人工光源。
光学实验
介绍一些基本的光学实验,如折射、反射和干涉。
光的本质和特性
1
光的波粒二象性
阐述光的波动性和微粒性的双重特性。
《光学》全套课件 PPT

τ
cosΔ
dt =0
τ0
I = I1 +I2
叠加后光强等与两光束单独照射时的光强之和,
无干涉现象
2、相干叠加 满足相干条件的两束光叠加后
I =I1 +I2 +2 I1I2 cosΔ 位相差恒定,有干涉现象
若 I1 I2
I =2I1(1+cosΔ
)
=4I 1cos2
Δ 2
Δ =±2kπ I =4I1
r2
§1-7 薄膜干涉
利用薄膜上、下两个表面对入射光的反射和 折射,可在反射方向(或透射方向)获得相干光束。
一、薄膜干涉 扩展光源照射下的薄膜干涉
在一均匀透明介质n1中
放入上下表面平行,厚度
为e 的均匀介质 n2(>n1),
用扩展光源照射薄膜,其
反射和透射光如图所示
a
n1
i
a1 D
B
n2
A
n1 C
2、E和H相互垂直,并且都与传播方向垂直,E、H、u三者满 足右螺旋关系,E、H各在自己的振动面内振动,具有偏振性.
3、在空间任一点处
εE = μH
4、电磁波的传播速度决定于介质的介电常量和磁导率,
为
u= 1 εμ
在真空中u= c =
1 ≈3×108[m ε0μ0
s 1]
5、电磁波的能量
S
=E
×H ,
只对光有些初步认识,得出一些零碎结论,没有形
成系统理论。
二、几何光学时期
•这一时期建立了反射定律和折射定律,奠定了几何光学基础。
•李普塞(1587~1619)在1608年发明了第一架望远镜。
•延森(1588~1632)和冯特纳(1580~1656)最早制作了复 合显微镜。 •1610年,伽利略用自己制造的望远镜观察星体,发现了木星 的卫星。 • 斯涅耳和迪卡尔提出了折射定律
应用光学第一章

光的直线传播图例
当两束或多束光在空间相遇时,各光线的传播不会受其它光线的影响。
例如:光束相交处的光强是一种简单的叠加,探照灯。
2.的独立传播定律
3.光的折射定律和反射定律
当一束光线由折射率为n的介质射向折射率为n′的介质时,在分界面上,一部分光线将被反射,另一部分光线将被折射,反射光线和折射光线的传播方向将遵循反射定律和折射定律。
全反射现象
TEXT
TEXT
TEXT
返 回
全反射的应用举例
全反射棱镜
全反射的应用举例
(2)光纤的全反射传光
全反射光纤
返 回
费马原理与几何光学的基本定律一样,也是描述光线传播规律的基本理论。
它以光程的观点描述光传播的规律,涵盖了光的直线传播和光的折、反射规律,具有更普遍的意义。
根据物理学,光在介质中走过的几何路程与该介质折射率的乘积定义为光程。设介质的折射率为n,光在介质中走过的几何路程为l,则光程s表示为
返 回
几何光学的基本定律决定了光线在一般情况下的传播方式,也是我们研究光学系统成像规律以及进行光学系统设计的理论依据。
几何光学的基本定律有三大定律:
二、几何光学的基本定律
的直线传播定律
各向同性的均匀介质中,光沿着直线传播。 用光的直线传播定律可以解释日蚀、月蚀等自然现象,也可以解释光照射物体时为什么会出现影子等类似问题,小孔成像就是利用了光的直线传播定律。
虚物和虚像
物方光线延长线交点
像方光线反像延长线交点
B’
A
返 回
物空间:即物体所在的空间;实物所在的空间为实物空间,虚物所在空间为虚物空间,无论实物空间还是虚物空间都使用实物空间介质的折射率。
像空间:即像所在的空间;实像所在的空间为实像空间,虚像所在空间为虚像空间,无论实像空间还是虚像空间都使用实像空间介质的折射率。
大学光学教案第一章

教学目标:1. 了解光学的基本概念和发展历程。
2. 掌握光的传播规律,包括光的直线传播、反射和折射。
3. 理解光的波动性和粒子性。
4. 能够运用光学原理解决简单的实际问题。
教学重点:1. 光的传播规律。
2. 光的波动性和粒子性。
教学难点:1. 光的波动性和粒子性的统一理解。
2. 复杂光学现象的解释。
教学时间:2课时教学内容:第一课时一、导入1. 通过展示生活中常见的光学现象(如镜子的反射、透镜的成像等),引导学生思考光的基本性质。
2. 提问:什么是光?光有哪些基本特性?二、光学基本概念1. 光的定义:光是一种电磁波,具有波粒二象性。
2. 光的传播速度:光在真空中的传播速度为3×10^8 m/s。
3. 光的波长和频率:光的波长和频率是描述光波动特性的重要参数。
三、光的直线传播1. 光的直线传播原理:光在同一种均匀介质中沿直线传播。
2. 光的直线传播现象:影子、小孔成像等。
3. 光的直线传播应用:激光、光纤通信等。
四、光的反射1. 反射定律:入射角等于反射角。
2. 反射现象:平面镜成像、凹面镜成像等。
3. 反射应用:太阳能电池、光纤通信等。
五、光的折射1. 折射定律:折射角与入射角之间存在一定的关系。
2. 折射现象:透镜成像、彩虹等。
3. 折射应用:眼镜、望远镜等。
第二课时一、光的波动性和粒子性1. 光的波动性:光的干涉、衍射等现象表明光具有波动性。
2. 光的粒子性:光电效应等现象表明光具有粒子性。
3. 波粒二象性:光既具有波动性,又具有粒子性。
二、光的干涉1. 干涉现象:两束或多束光相遇时,相互叠加产生干涉条纹。
2. 干涉条件:相干光源、相同的介质等。
3. 干涉应用:激光干涉仪、全息照相等。
三、光的衍射1. 衍射现象:光通过狭缝或障碍物时,会发生弯曲和扩散。
2. 衍射条件:波长与障碍物尺寸相当或更大。
3. 衍射应用:衍射光栅、全息照相等。
四、总结1. 光学的基本概念和发展历程。
2. 光的传播规律:直线传播、反射、折射。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谓白光,经常指具有和太阳连续光谱相近的多色混合光。
式中 P 为电极化强度矢量; e 为电极化率;
E*
为电源化学力等非静电力场强度。
若电磁波在介质中传播时,上述波动方程的微分形式应为
2 E B 2 E ( B) 0 0 2 ( ) 0 0 2 t t t t
光的微粒说能很好的解释光在均匀介质中的直线传播,光在 界面上的反射;但不能用来解释光在两种介质界面上引起的折 射现象,因为用牛顿的更应解释时,理论与结果相反;同时, 光的微粒说无法解释光的绕射、干涉和偏振现象。 (2)波动说 1679年,荷兰物理学家惠更斯(Huygens)提出光的波动说 (wave theory),他认为光是在充满整个空间的特殊介质“以 太”(ether)中传播的某种弹性波。用波动说解释光在介质中传 播比在空气中或真空中要慢,与实验事实相符合;用波动说还 能推出反射定律和折射定律,并解释方解石晶体中发现的双折 射现象。尽管如此,由于当时实验条件及牛顿的权威性,直到 18世纪以前,微粒说一直占上风。 到了19世纪初,“光的波动说”才开始打破“光的微粒说” 的优势:
紫
蓝
青
绿
黄
橙
红
3、光波的基本性质 (1)光波的速度 麦克斯韦方程组的积分形式及微分形式
A
D dA 0 dV q
V
积分形式
微分形式
D 0
B L E dl A t d A
D L H dl A ( j 0 t ) d A
二、光源与光谱
1、光源 任何发光的物体都可以叫做光源。如:太阳、腊烛的火焰、 日光灯等。 光是一种电磁辐射,按照能量补给方式不同,大致可分为 两大类: (1)热辐射 不断给物体加热来维持一定的温度,物体就会持续地发射 光,包括红外线、紫外线等不可见光。 在一定温度下处于热平衡状态下物体的辐射叫做热辐射或 温度辐射。
*1801年,英国物理学家托马斯˙杨(Young)做了著名的 “杨氏双孔干涉实验”。杨氏让一束狭窄的光束穿过两个 十分相近的小孔,然后投射到一张白屏幕上,通过两个小 孔的两束光在屏上重叠处出现一组明暗相间的条纹。光的 微粒说无法解释暗条纹处的光微粒跑到哪去了?但是用光 的波动说观点却可以圆满地解释上述现象:两列同频率的 波相遇,产生干涉现象。 *1819年,法国物理学家菲涅耳(Fresnel)做了著名的“光 的绕射实验”。他的实验证明,若障碍物足够小,以至可 以与光波长相比拟时,则光波在传播中可以绕过障碍物并 在其后面的屏上形成明暗相间的图形,叫做绕射花样或衍 射花样。
式中 0 为自由电荷体密度。
AB d A 0
B E t B 0
D H j0 t
当电磁波在各向同性介质中传播时
D 0 E P 0 E 0e E 0 E
B 0 H
j 0 ( E E*)
(4)波动说的确立 1905年,爱因斯坦(Einstein)提出狭义相对论,否定了以太 的存在。他认为光在真空中传播并不需要任何媒体。而且假 设光在真空中传播时永远以确定的速度c传播,与光源或观察 者的运动状态无关。明确光是什么的答案:光是电磁波,能 够通过自由空间传播,光波本身是一种实体(即物质)。
*1861年~1862年,英国物理学家麦克斯韦(Maxwell)总结了 一系列电学和磁学实验,推出了著名的麦克斯韦方程组,并 预言了电磁波,而且推出电磁波在真空中的传播速度与当时 测得的光速数据极相近。于是大胆地预言:光是一种以波的 形式通过以太传播的电磁扰动。这一预言直到他去世后8年才 由赫兹(Hertz)实验所证实。 (3)波动说中的问题 证实光波传播介质“以太”存在 著名的迈克尔逊(Michelson)——莫雷(Moley)实验,用精密 的迈克尔逊干涉仪观察地球相对于“以太”的运动,结果通 过实验没有观察到任何实验现象。于是人们认识到,“以太” 根本不存在。
一般在描述光波强度时,并不直接表示出具体光强的大小, 而是只关心其分布,因此常忽略式中的常数因子。故通常光 强表示为光场 复数的模的平方。即
I U (r )U * (r )
④ 光谱的性质
或
I U (r )U * (r ) U (r )
2
单一波长的光称为单色光,否则是非单色光。
如果用棱镜或其它分光仪器对各种普通光源发出的光进行分 析,发现绝在部分都不是单色光。 令dIλ表示波长在λ ~ λ + dλ间光的强度,则
dI i ( ) d
代表单位波长区间的光强,非单色光的i(λ)按波长 的分布,叫做光谱。i(λ)称为谱密度,总光强I与谱密度 的关系为:I Nhomakorabea
0
dI i( )d
0
不同的光源有不同的光谱,光强在很大波长范围内连续 分布,称为连续光谱;光强集中在一些离散的波长值附近而 形成一条条谱线,称为线光谱。 对于线光谱,每条谱线只是近似的单色光,它们的光强分 布有一定的波长范围Δλ,这个Δλ称为谱线宽度。Δλ愈小,表示 单色性愈好。如激光器的谱线宽度比普通光源小得多。 太阳光谱除了一些暗线外,基本上是连续光谱,它所发出 的各种波长的可见光混合起来,给人的感觉是白色。光学中所
E h
h 6.626 10
34
J s
被称为普朗克常数
近代量子理论的发展表明,微观粒子都具有波粒二重性, 光子也具有波粒二重性。
光的传播速度:c≈3×108m/s;
光子的能量:E = hν;
光子的动量:P = hν/c = h/λ; 光子的静止质量:m0 = 0; 光子的质量:m = hν/c2;
D、E
O B、H
k (S)
B 0
D D H j0 t t
S EH
kE 0
kD0
k E B 0 H
kB0
kH 0
k H D 0 E
由此可见,电磁波中矢量D、H、k是两两正交的,S为 玻印亭矢量,与传播方向(k)一致,因此说明电磁波是横 波。证明是横波的另一个性质是偏振。
② 玻印亭矢量
S EH
玻印亭矢量即为能流密度矢量,它表示电磁场能量的传播, 大小等于垂直通过单位面积的功率,代表了电磁波的波强, 也称为光强I。
0 2 0 2 2 H u 0 H 2 I S EH E u 0 E 0 0
2、光谱 电磁波谱的波长(或频率) 大约范围: γ射线:小于10-3 nm 大于 3 10 20 Hz X射线:0.1~5 nm
18 (0.03~300) 10
Hz
紫外线:5~400 nm
可见光:400~760 nm
14 (7.5~3000) 10 Hz 14 (3.9~7.5) 10 Hz 12 (0.4~390) 10 Hz
(3)电磁波能量传播——坡印亭矢量 光强 ① 电磁波的能量 电磁波的强弱描述与机械波一样,是由电磁波的能流密度来 表示的,即表示在单位时间内通过单位面积上的能量多少。 对于非导体介质
0
没有热损耗,电磁波的能量守恒表现为单位时间内流出 (入)闭合体积的电磁波能量等于单位时间内闭合体积 内能量减少(增加),其数学表达式为:
d VwdV A ( E H ) d A dt
其中A表示截面面积;w为电磁场的能量密度。
1 1 w we wm D E B H 2 2 1 1 2 0 E 0 H 2 0 E 2 0 H 2 2 2
微分方程为
1 2 E E 2 u t 2
2
1 2 H 2 H 2 u t 2
(2)电磁波的横波性 将电磁波的方程解代入麦克斯韦的微分形式中,由于在电磁 波传播到的空间里,没有传导电流和自由电荷,故
j0 0
D 0 0
B E t
0 0
式中u为光波在介质中的传播速度。
③ 光强 由光强的表达式可见,光强与光场的平方成正比。并且 对于光信号,无论是探测器还是人眼,一般只对电场强度 有感应,因此在表达电磁波强度时都用电场强度;另外, 由于光的频率极高(约1015Hz),探测元件只能测得其检
测时间内的平均值。如对于真空中的标量单色平面波,光 强对时间的平均值为
波粒二重性
*1887年,赫兹用实验证明麦克斯韦预言——电磁波的存在。 然而在气体放电实验中发现,如果用紫外光照射在相对放臵 的两电极的一个电极上,将加速两电极之间的放电。雷纳德 (Lenard)用紫外光照射阴极表面时,引起了电子辐射,这就 是光电效应(photoelectric effect)。
*1922年康普顿 (Compton)用一束单色X射线(X--ray)照 射在石墨样品上,研究被石墨散射的X射线。这就是康普 顿效应(Compton effect)。 *1922年普朗克(Planck)提出新的理论——量子理论,辐 射是不连续的。 *1905年,爱因斯坦提出“光子”的概念,能很好地解释 光电效应。他认为每个光子的能量E与光子频率成正比,即
红外光:760~105 nm
无线电波:大于105 nm
小于10-12 Hz
光波是电磁波中的一个很小的范围。一般情况下认为能被人 眼所感受到的电磁波段为400nm~760nm的狭小范围,这个波 段内的电磁波称为可见光。 可见光的波长与颜色对应关系:
400
430
450
500
570
600
630
760nm
(2)光的非热辐射
① 电致发光 各种气体放电管(如日光灯、水银灯)管内的发光过程是靠电 场来补给能量的,这样发光的过程称为电致发光。 ② 荧光 某些物质在放射线、X射线、紫外线、可见光或电子束的照射 或轰击下,可以发出可见光来,这样发出的光称为荧光。
