高中数学必修二第二章解析几何初步
高中数学必修2第2章212第二课时两点式课件(_1

1.直线的两点式方程
(1)条件:P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2). (2)方程:_y_y2-_-_yy_11_=__xx2_--_x_x1_1 __ 2.直线的截距式方程 (1)条件:A(a,0),B(0,b)且___a_b_≠__0_______ (2)方程:__xa_+__by_=__1______
1.在例1的条件下,求过点B且平行于AC的直线方程. 解:设所求的直线为 l,由于 l 与直线 AC 平行,则这两条直线 的倾斜角相等,所以 kl=kAC=3-0--22=-25, 故直线 l 的方程为 y-2=-25(x-3).
直线的截距式方程 求过定点P(2,3)且在两轴上截距相等的直线方程.
(本题满分 12 分)求过点 A(4,2),且在两坐标轴上的 截距的绝对值相等的直线 l 的方程.
[解] 当直线过原点时 ,它在 x 轴、y 轴上的截距都是 0, 满足题意,此时,直线的斜率为12,所以直线方程为 y=12x.2 分 当直线不过原点时 ,由题意可设直线方程为xa+by=1,又过 点 A,所以4a+2b=1①,4 分 因为直线在两坐标轴上的截距的绝对值相等,所以|a|=|b| ②,
[错因与防范] (1)方程xa+by=1 中的 a 与 b 是直线在 x 轴与 y 轴上的截距,而不是距离,所以由三角形面积为 4,应该有12|a||b| =4. (2)直线的截距是指直线在坐标轴上对应的坐标,因此可为正、 可为负、可为零;而距离是线段的长度,是非负的.截距不是 距离,解题中应注意准确把握两者的区别.
2.求过点 A(3,4),且在坐标轴上截距互为相反数的直线 l 的 方程. 解:(1)当直线 l 在坐标轴上截距互为相反数且不为 0 时,可 设直线 l 的方程为xa+-ya=1.又 l 过点 A(3,4), 所以3a+-4a=1,解得 a=-1.
北师大版必修2高中数学第2章《解析几何初步》1两条直线的交点导学案

高中数学 第2章《解析几何初步》1两条直线的交点导学案
北师大版必修2
【学习目标】
1.学会判断两条直线相交的方法,会求两条直线的交点坐标;
2.体会判断两条直线相交中的数形结合思想.
【重点难点】 重点:熟练求出两条直线的交点坐标. 难点:对方程组系数的分类讨论与两直线位置关系对应情况的理解.
【自主学习】
3.判断下列各对直线的位置关系.如果相交,求出交点坐标.
(1)1l :0y x 3=-与2l :0y 3x 6=-;
(2)1l :01y 4x 3=++与2l :03y 8x 6=-+;
(3)1l :0y x =-与2l :010y 3x 3=-+.
【合作探究】 1.求经过两直线03y 3x 2=--和01y x =-+的交点且与直线02y x 3=-+垂直 的直线方程.
2.已知两直线1l :01y mx =+-与2l :0m 2y 3x 6=+-,当m 为何值时两直线:
(1)相交;(2)平行;(3)垂直.
【课堂检测】
1.求经过两直线04y x 2=--和03y 2x =++的交点且与直线02y x 5=+- 平行的直线方程.
【课堂小结】。
高中数学 第二章 解析几何初步 1.2.2 直线方程的两点式和一般式练习(含解析)北师大版必修2-北
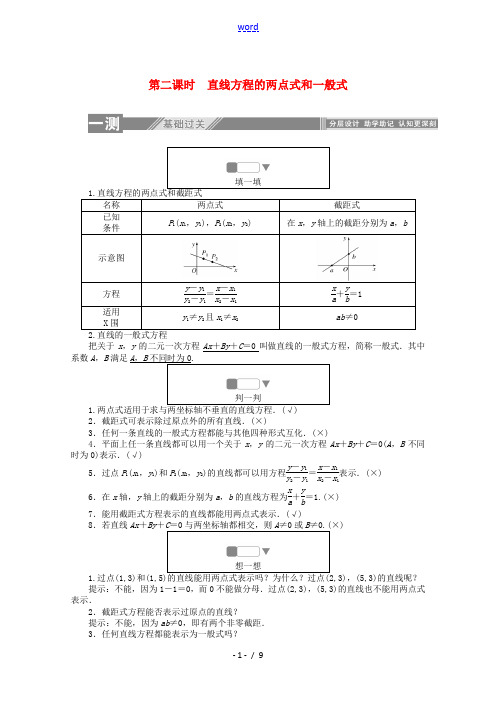
第二课时 直线方程的两点式和一般式填一填1.直线方程的两点式和截距式名称 两点式 截距式已知条件 P 1(x 1,y 1),P 2(x 2,y 2)在x ,y 轴上的截距分别为a ,b示意图方程y -y 1y 2-y 1=x -x 1x 2-x 1 x a +y b=1 适用X 围y 1≠y 2且x 1≠x 2 ab ≠02.直线的一般式方程把关于x ,y 的二元一次方程Ax +By +C =0叫做直线的一般式方程,简称一般式.其中系数A ,B 满足A ,B 不同时为0.判一判1.两点式适用于求与两坐标轴不垂直的直线方程.(√) 2.截距式可表示除过原点外的所有直线.(×)3.任何一条直线的一般式方程都能与其他四种形式互化.(×)4.平面上任一条直线都可以用一个关于x ,y 的二元一次方程Ax +By +C =0(A ,B 不同时为0)表示.(√)5.过点P 1(x 1,y 1)和P 2(x 2,y 2)的直线都可以用方程y -y 1y 2-y 1=x -x 1x 2-x 1表示.(×)6.在x 轴,y 轴上的截距分别为a ,b 的直线方程为x a +y b=1.(×) 7.能用截距式方程表示的直线都能用两点式表示.(√)8.若直线Ax +By +想一想1.过点(1,3)和,(5,3)的直线呢? 提示:不能,因为1-1=0,而0不能做分母.过点(2,3),(5,3)的直线也不能用两点式表示.2.截距式方程能否表示过原点的直线?提示:不能,因为ab ≠0,即有两个非零截距. 3.任何直线方程都能表示为一般式吗?提示:能.因为平面上任意一条直线都可以用一个关于x ,y 的二元一次方程表示. 4.当A ,B 同时为零时,方程Ax +By +C =0表示什么?提示:当C =0时,方程对任意的x ,y 都成立,故方程表示整个坐标平面; 当C ≠0时,方程无解,方程不表示任何图像.故方程Ax +By +C =0,不一定代表直线,只有当A ,B 不同时为零时,即A 2+B 2≠0时才代表直线.思考感悟:练一练1.直线x a +y b=1(ab <0)的图像可能是( )答案:C2.过两点(2018,2019),(2018,2020)的直线方程是( ) A .x =2018 B .x =2019 C .y =2018 D .x +y =2020 答案:A3.直线x -y +5=0的倾斜角为( ) A .45° B.60° C .120° D.135° 答案:A4.在x 轴、y 轴上的截距分别是5,-3的直线的截距式方程为( ) A.x 5+y 3=1 B.x 5-y 3=1 C.y 3-x5=1 D.x 5+y3=0 答案:B5.直线2x +3y -6=0与坐标轴围成的三角形面积为________. 答案:3知识点一 直线的两点式方程1.已知直线l 经过点A (1,-2),B (-3,2),则直线l 的方程为( ) A .x +y +1=0 B .x -y +1=0 C .x +2y +1=0 D .x +2y -1=0解析:由两点式得直线l 的方程为y +22--2=x -1-3-1,即y +2=-(x -1).故选A.答案:A2.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( )A .-32B .-23C.25D .2 解析:由直线的两点式方程可得直线方程为y -19-1=x +13+1,即2x -y +3=0,令y =0得x=-32.故选A.答案:A知识点二 直线的截距式方程3.过点A (4,1)且在两坐标轴上截距相等的直线方程为( ) A .x +y =5 B .x -y =5C .x +y =5或x -4y =0D .x -y =5或x -4y =0解析:当直线过点(0,0)时,直线方程为y =14x ,即x -4y =0;当直线不过点(0,0)时,可设直线方程为x a +y a=1(a ≠0),把(4,1)代入,解得a =5,∴直线方程为x +y =5.综上可知,直线方程为x +y =5或x -4y =0.选C. 答案:C4.两条直线l 1:x a -y b =1和l 2:x b -y a=1在同一平面直角坐标系中的图像可以是( )解析:将两直线方程化成截距式为l 1:x a +y -b =1,l 2:x b +y-a=1,则l 1与x 轴交于(a,0),与y 轴交于(0,-b ),l 2与x 轴交于(b,0),与y 轴交于(0,-a ).结合各选项,先假定l 1的位置,判断出a ,b 的正负,然后确定l 2的位置,知A 项符合.选A.答案:A知识点三直线的一般式方程5.已知直线l 的方程为x -3y +2=0,则直线l 的倾斜角为( ) A .30° B.45° C .60° D .150°解析:设直线l 的倾斜角为θ,则tan θ=13,则θ=30°.答案:A6.设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ),若l 不经过第二象限,则实数a 的取值X 围是________.解析:将直线l 的方程化为y =-(a +1)x +a -2. 则⎩⎪⎨⎪⎧ -a +1>0,a -2≤0或⎩⎪⎨⎪⎧-a +1=0,a -2≤0,∴a ≤-1. 答案:(知识点四 直线方程的应用7.(1)求证:不论a 为何值,直线l 总经过第一象限; (2)为使直线不经过第二象限,求a 的取值X 围.解析:(1)证明:方法一 将直线l 的方程整理为 y -35=a ⎝ ⎛⎭⎪⎫x -15, ∴l 的斜率为a ,且过定点A ⎝ ⎛⎭⎪⎫15,35,而点A ⎝ ⎛⎭⎪⎫15,35在第一象限,故不论a 为何值,l 恒过第一象限.方法二 直线l 的方程可化为(5x -1)a +(3-5y )=0. 当定点为(x ,y )时,上式对任意的a 总成立,必有⎩⎪⎨⎪⎧5x -1=0,3-5y =0,即⎩⎪⎨⎪⎧x =15,y =35,即l 过定点A ⎝ ⎛⎭⎪⎫15,35.以下同方法一.(2)如图,直线OA 的斜率为 k =35-015-0=3. 要使l 不经过第二象限,需它在y 轴上的截距不大于零,即令x =0时,y =-a -35≤0,∴a ≥3.8.已知直线l :y =kx +2k +1.(1)求证:对于任意的实数k ,直线l 恒过一个定点;(2)当-3<x <3时,直线l 上的点都在x 轴的上方,某某数k 的取值X 围. 解析:(1)由y =kx +2k +1, 得y -1=k (x +2).由直线的点斜式方程,可知直线l 恒过定点(-2,1). (2)设函数f (x )=kx +2k +1.若-3<x <3时,直线l 上的点都在x 轴的上方,则⎩⎪⎨⎪⎧f -3≥0,f 3≥0,即⎩⎪⎨⎪⎧-3k +2k +1≥0,3k +2k +1≥0,解得-15≤k ≤1.所以实数k 的取值X 围是⎣⎢⎡⎦⎥⎤-1,1. 综合知识 直线的方程9.(1)经过点(-1,3),且斜率为-3; (2)经过两点A (0,4)和B (4,0);(3)经过点(2,-4)且与直线3x -4y +5=0平行; (4)经过点(3,2),且垂直于直线6x -8y +3=0.解析:(1)根据条件,写出该直线的点斜式方程为 y -3=-3(x +1),即y -3=-3x -3, 整理得其一般式为3x +y =0.(2)根据条件,写出该直线的截距式为x 4+y4=1,整理得其一般式为x +y -4=0.(3)设与直线3x -4y +5=0平行的直线为3x -4y +c =0,将点 (2,-4)代入得6+16+c =0,所以c =-22.故所求直线的一般式为3x -4y -22=0.(4)设与直线6x -8y +3=0垂直的直线为8x +6y +c =0,代入点(3,2)得24+12+c =0,c =-36.从而得8x +6y -36=0,即所求直线的一般式为4x +3y -18=0.10.已知△ABC 的三个顶点为A (0,3),B (1,5),C (3,-5). (1)求边AB 所在的直线方程; (2)求中线AD 所在直线的方程.解析:(1)设边AB 所在的直线的斜率为k ,则k =5-31-0=2.它在y 轴上的截距为3.所以,由斜截式得边AB 所在的直线的方程为y =2x +3.(2)B (1,5)、C (3,-5),1+32=2,5+-52=0,所以BC 的中点D (2,0).由截距式得中线AD 所在的直线的方程为x 2+y3=1.基础达标一、选择题1.下列四个命题中的真命题是( )A .经过定点P 0(x 0,y 0)的直线都可以用方程y -y 0=k (x -x 0)表示B .经过任意两个不同点P 1(x 1,y 1)、P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示C .不经过原点的直线都可以用方程x a +yb=1表示D .经过定点A (0,b )的直线都可以用方程y =kx +b 表示解析:当直线与y 轴平行或重合时,斜率不存在,直线方程不能用点斜式、斜截式,选项A 、D 不正确;当直线垂直于x 轴或y 轴时,直线方程不能用截距式表示,选项C 不正确;选项B 正确.故选B.答案:B2.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则a 的值是( ) A .1 B .-1 C .-2或-1 D .-2或1解析:①当a =0时,y =2不合题意.②当a ≠0时,令x =0,得y =2+a ,令y =0,得x =a +2a ,则a +2a=a +2,得a =1或a =-2.故选D.答案:D3.直线l 过点P (1,3),且与x ,y 轴正半轴围成的三角形的面积等于6的直线方程是( ) A .3x +y -6=0 B .x +3y -10=0 C .3x -y =0 D .x -3y +8=0 解析:设所求的直线方程为x a +yb=1. 所以⎩⎪⎨⎪⎧1a +3b =1,12|ab |=6,解得a =2,b =6.故所求的直线方程为3x +y -6=0.故选A.答案:A4.如果AB <0,且BC <0,那么直线Ax +By +C =0不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限解析:因为直线Ax +By +C =0可化为y =-A B x -C B ,又AB <0,BC <0,所以-A B >0,-C B>0,所以直线过第一、二、三象限,不过第四象限.故选D. 答案:D5.已知m ≠0,则过点(1,-1)的直线ax +3my +2a =0的斜率为( ) A .3 B .-3 C.13 D .-13解析:由题意,得a -3m +2a =0,所以a =m ,又因为m ≠0,所以直线ax +3my +2a =0的斜率k =-a 3m =-13.故选D.答案:D6.已知两条直线的方程分别为l 1:x +ay +b =0,l 2:x +cy +d =0,它们在坐标系中的位置如图所示,则( )A .b >0,d <0,a <cB .b >0,d <0,a >cC .b <0,d >0,a >cD .b <0,d >0,a <c解析:由题图可知,直线l 1的斜率-1a >0,在y 轴上的截距-ba<0,因此a <0,b <0;直线l 2的斜率-1c >0,在y 轴上的截距-d c >0,因此c <0,d >0.且l 1的斜率大于l 2的斜率,即-1a >-1c,因此a >c ,故选C.答案:C7.若方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则实数m 满足( )A .m ≠0 B.m ≠-32C .m ≠1 D.m ≠1且m ≠-32且m ≠0解析:∵当2m 2+m -3=0时,m =1或m =-32;当m 2-m =0时,m =0或m =1,要使方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则2m 2+m -3,m 2-m 不能同时为0,∴m ≠1,故选C.答案:C 二、填空题 8.经过A (1,3)和B (a,4)的直线方程为________________________________________________________________________.解析:当a =1时,直线AB 的斜率不存在,所求直线的方程为x =1;当a ≠1时,由两点式,得y -34-3=x -1a -1,即x -(a -1)y +3a -4=0.这个方程中,对a =1时方程为x =1也满足. 所以,所求的直线方程为x -(a -1)y +3a -4=0. 答案:x -(a -1)y +3a -4=09.过点(5,2),且在x 轴上的截距是在y 轴上的截距的2倍的直线方程是________________。
高中数学第二章解析几何初步优化总结北师大版必修2

[解] 原方程可化为(x-2)2+y2=3,表示以点(2,0)为圆心,
3为半径的圆.
(1)设xy=k,即 y=kx,当直线 y=kx 与圆相切时,斜率 k 取得
最大值和最小值,
此时有 |2k-0| = k2+1
3,解得 k=± 3,
故xy的最大值是 3,最小值是- 3.
(2)设 y-x=b,即 y=x+b,当直线 y=x+b 与圆相切时 b 取
得最大值和最小值,此时|2-0+b|= 3, 2
解得 b=-2± 6,
故 y-x 的最大值为-2+ 6,最小值为-2- 6.
(3)x2+y2 表示圆上的点与原点距离的平方,由平面几何的知 识知,其在原点和圆心的连线与圆的两个交点处分别取得最 大值和最小值,又知圆心到原点的距离为 2,故 x2+y2 的最大 值为(2+ 3)2=7+4 3,最小值为(2- 3)2=7-4 3.
2.求过圆外一点的圆的切线过程 求过圆外一点的圆的切线方程,一般设为点斜式,运用待定
系数法或判别式法求出斜率k,但用点斜式表示直线方程的前
提是斜率必须存在.过圆外一点可以作圆的两条切线,如果 只有一解,那么一定有一条切线斜率不存在,这时可用数形 结合的方法把“丢掉”的切线方程找回来. 3.已知斜率求圆的切线
如图所示,在平面直角坐标系 xOy 中,已知圆 C1:(x +3)2+(y-1)2=4 和圆 C2:(x-4)2+(y-5)2=4. (1)若直线 l 过点 A(4,0), 且被圆 C1 截得的弦长为 2 3,求直线 l 的方程;
(2)设 P 为平面上的点,满足:存在过点 P 的无穷多对互相垂直
的直线 l1 和 l2,它们分别与圆 C1 和圆 C2 相交,且直线 l1 被圆 C1 截得的弦长与直线 l2 被圆 C2 截得的弦长相等,试求所有满 足条件的点 P 的坐标.
「精品」高中数学 第二章 解析几何初步 2.2 圆与圆的方程 2.2.2 圆的一般方程课件 北师大版必修2-精品资料

规范解答
圆的一般方程的应用
(本题满分12分)已知方程x2+y2+ax+2ay+2a2+a- 1=0. (1)若此方程表示圆,求实数a的取值范围; (2)求此方程表示的圆的面积最大时a的值及此时圆的方程.
[解] (1)由条件知 a2+(2a)2-4(2a2+a-1)>0. 2 分
2.圆x2+y2-4x+6y=0的圆心坐标是( D )
A.(2,3)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
解析:化成标准方程为(x-2)2+(y+3)2=13,
所以圆心为(2,-3).
3.如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)表示的曲 线关于y=x对称,那么必有( A ) A.D=E B.D=F C.E=F D.D=E=F 解析:由题得该方程表示圆,且圆心在y=x上,再结合一般 方程的意义,可得D=E.
第二章 解析几何初步
2.2 圆的一般方程
1.问题导航 (1)当 m 为何值时,方程 x2+y2+mxy-2x=0 表示圆? (2)任何圆的方程都可以写成二元二次方程的形成吗? (3)如何选择圆的方程形式?
2.例题导读 P80例4.通过本例学习,学会利用待定系数法求圆的一般方程 的方法,解答本例时要注意,利用待定系数法求圆的方程时, 如何选择圆的方程形式要视题目中所给条件而定.
综合应用
已知△ABC的边AB长为2a,若BC的中线为定长m,求
顶点C的轨迹方程.(轨迹方程是动点坐标所满足的方程)
[解] 如图,以直线 AB 为 x 轴,线段 AB 的中垂线为 y 轴建 立坐标系,则 A(-a,0),B(a,0),设 C(x,y),BC 中点为 D(x0,y0), 则 x0=x+2 a,y0=2y,① 因为|AD|=m,所以(x0+a)2+y20=m2.② 将①式代入②式整理得 (x+3a)2+y2=4m2. 因为 C 不能在 x 轴上, 所以 y≠0,故所求轨迹方程为(x+3a)2+y2=4m2(y≠0).
北师大版必修2高中数学第2章《解析几何初步》2直线与圆、圆与圆的位置关系(2)导学案

高中数学 第2章《解析几何初步》2直线与圆、圆与圆的位置关系(2)
导学案 北师大版必修2
使用说明
1.课前根据学习目标,认真阅读课本第83页到第84页内容,完成预习引导的内容.
2.课堂上(最好在课前完成讨论)发挥学习小组作用,积极讨论,大胆展示,完成合作探究部分.
学习目标
1、能根据两个圆的方程,判断两个圆的位置关系;
2、能根据两个圆的位置关系,求有关直线或圆的方程;
学习重点 用两点间距离公式判断计算连心线长并判断两圆的位置关系.
学习难点 判断两圆的位置关系.
一、自主学习
【预习导引】
【基础演练】
1. 判断下列各题中两圆的位置关系:
(1)4)1y (1x 22=-+-)(和8)3y (x 2
2=-+;
(2)9)3y (2x 22=-++)(和06y 4x 4y x 22=++-+;
(3)08y 8x 2y x 22=-+++和02y 4x 4y x 22=--++
2. 已知两圆9y )3x (22=+-与m 4)2y (x 22+=-+,问m 为何值时,两圆外切.
二、合作探究
1.在直角坐标系中画出圆1)1y (1x 22=-+-)(与9)2y (x 22=-+的图形,并说明它们的位
置关系.
2. 已知两圆0x 6y x 22=-+与k y 4y x 2
2=-+,问k 为何值时,两圆相切.
3. 已知两圆10y x 22=+和20)3y (1x 22=-+-)(交于B ,A 两点,求直线AB 的方程.
四.收获及疑问
【小结】
1.圆与圆的位置关系:
2.圆与圆的位置关系的判定:
【疑问】。
数学北师大版高中必修2北师大版高中数学必修2第二章解析几何初步2.1.3两条直线的位置关系PPT课件

1 所求直线的斜率k 2 2
x 2 y 0.
例7 求证以A(-2,-3)、B(6,3)、C(-5,1) 为顶点的三角形是直角三角形. 证明:直线AB的斜率
k AB k AC
3 (3) 3 6 (2) 4 1 (3) 4 5 (2) 3
直线AC的斜率
1 4 l1 : y x 2 7
1 1 k1 , k 2 , k1 k 2 . ∴两直线不相交. 2 2
1 5 l2 : y x 2 2
7 5 b1 , b2 4 2
b1 b2 ∴两直线不重合,
∴
l1 // l 2
如果直线L1,L2的方程为
L1:A1x+B1y+C1=0, L2:A2x+B2y+C2=0
2 (D) 3
-1=0互相垂直,则( C )
A.a=2 B.a=-2 C.a=2或a=-2 D.a=2,0,-2
3.直线2x+y+m=0和x+2y+n=0的位置关系是( C )
(A)平行 (B)垂直 (C)相交但不垂直
(D)不能确定,与m,n取值有关
4.求与直线3x-2y+2=0垂直,纵截距为-2的直 线方程. 5.直线ax+4y-2=0垂直于2x-5y+b=0且交点为 M(1,c), 求a、b、c. 6.证明以A(3,1)、B(6,4)、C(5,8)、D(2,5) 为顶 点的四边形ABCD是平行四边形.
那么 l1 // l2 A1B2-A2 B1=0且B1C2-B2C1 0或A1C2-A2C1 0 A1 B1 C1 (A 2 B2C2 0) A2 B2 C2
l1与l2重合
2020年高中数学第二章解析几何初步11.1直线的倾斜角和斜率课件北师大版必修2

【解析】 当 0°≤α<135°时,l1 的倾斜角为 α+45°;当 135°≤α<180°时,如图.此时 l1 的倾斜角为 β,则
β=α+45°-180°=α-135°. 【答案】 当 0°≤α<135°时,倾斜角为 α+45°,当 135°≤α <180°时,为 α-135°
【规律总结】 求倾斜角时,主要根据定义,画出图形,找 准倾斜角.有时需分类讨论,把角分为四类:①0°角;②锐角; ③直角;④90°<α<180°.
【错因分析】 (2)中求斜率 k 的取值范围时,未结合图形分 析 k 的变化趋势.
【正解】 (1)kPM=-23--11=-4,kPN=- -23- -11=34.
(2)如图所示,l′是经过点 P 且与 x 轴垂直 的直线,当直线 l 由 PN 位置绕点 P 向 l′位置 旋转时,直线的倾斜角在锐角范围内逐渐增 大,斜率也逐渐增大,此时 k≥kPN=34;当直 线 l 由 l′位置绕点 P 向直线 PM 位置旋转时,直线的倾斜角在钝角 范围内逐渐变大,斜率也逐渐增大,此时,k≤kPM=-4.
5.已知 a>0,若平面上三点 A(1,-a),B(2,a2),C(3,a3) 共线,求 a 的值.
解:∵kAB=a2-2--1 a=a2+a 存在, 又 A,B,C 三点共线,∴kAC=a3-3--1 a=a3+2 a也存在,且 kAB=kAC,即 a2+a=a3+2 a,整理得 a(a2-2a-1)=0. 解得 a=0 或 a=1± 2.又∵a>0,∴a=1+ 2.
已知三点 A(a,2),B(5,1),C(-4,2a)在同一
直线上,求 a 的值. 解:∵kBC=-2a4--15=-2a- 9 1存在, 又 A,B,C 三点共线, ∴kAB 也存在,且 kAB=kBC. 即-2a- 9 1=15- -2a(a≠5), ∴2a2-11a+14=0, 解得 a=72或 a=2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学必修二第二章解析几何初步
一、选择题:
1.x 轴上任一点到定点(0,2)、(1,1)距离之和最小值是( ) A .2 B .22+ C .10 D .15+
2.点(4,0)关于直线5x+4y+21=0对称的点是( )
A .(-6,8)
B .(-6,-8)
C .(-8,-6)
D .(6,8)
3.直线 032=+-y x l :
关于x y -=,对称的直线方程是( ) A .032=+-y x B .032=-+x y C .032=--y x D .032=--y x
4.过点P (2,1),且倾斜角是直线l :01=--y x 的倾斜角的两倍的直线方程为() A .012=--y x B .2=x C .)2(21-=-x y D .012=--y x
5.以点A (-5,4)为圆心,且与x 轴相切的圆的方程是()
A .25)4()5(22=-++y x
B .16)4()5(2
2=++-y x C .16)4()5(22=-++y x D .
25)4()5(22=++-y x 6.一条直线过点P (-3,
23
-
),且圆2522=+y x 的圆心到该直线的距离为3,则该直线的方程为() A .3-=x B .
23
3-
=-=y x 或 C .015433=++-=y x x 或 D .01543=++y x
7.过点A (1,-1),B (-1,1),且圆心在直线02=-+y x 上的圆的方程是()
A .4)1()3(22=++-y x
B .4)1()1(2
2=-+-y x C .4)1()3(22=-++y x D .
4)1()1(22=+++y x 8.已知圆C :4)2()(2
2=-+-y a x (0 a ),有直线l :03=+-y x ,当直线l 被圆C 截得弦长为32时,a 等于()
A .12-
B .2-2
C .2
D .12+ 9.直线)(0)11()3()12(R k k y k x k ∈==--+--,所经过的定点是() A .(5,2) B .(2,3)
C .(-21
,3) D .(5,9)
10.若直线12++=k kx y 与直线2
21
+-=x y 的交点位于第一象限,则实数k 的取值范围是() A .26-- k B .0
61
k -
C .0
61
k -
D .
21 k 11.三条直线0155,02,0321=--=-+=-ky x l y x l y x l :
::构成一个三角形,则k 的范围是() A .R k ∈
B .R k ∈且0,1≠±≠k k
C .R k ∈且10,5-≠±≠k k
D .R k ∈且1,15≠±≠k k
12.若点(2,k )到直线06125=+-y x 的距离是4,则k 的值是()
A .1
B .-3
C .1或35
D .-3或317
13.已知点P (y x ,)在直线l :01043=-+y x 上,O 为原点,则当
OP
最小时,点P 的坐标是( )
A .⎪⎭⎫ ⎝⎛58,56
B .)4,2(
C .⎪⎭⎫ ⎝
⎛-45,5 D .⎪
⎭⎫
⎝⎛-53,51 14.若点(2,k )到直线06125=+-y x 的距离是4,则k 的值是( )
A .-3或317
B .-3
C .1或35
D .1
二、填空题
15.已知点A (2,5)、B (4,-1),若在y 轴上存在一点P ,使||||PB PA +最小,则点P 的坐标为____.
16.直线0632=-+y x 关于点(1,-1)对称的直线方程为 _.
17.若直线l 经过点(-1,3),且斜率为-2,则直线l 的方程为_ .
18.已知一条直线经过点P(1,2),且斜率与直线y= 2x +3的斜率相同,则该直线的方程是_ .
19.在x 轴上的截距是5,倾斜角为
4
3π
的直线方程为 。
20.过010531=--y x l :和012=++y x l :的交点,且平行于0523=-+y x l :的直线方程为_ . 21.点P 在直线04=-+y x 上,O 是坐标原点,则||OP 的最小值是 .
22. 已知圆C :
()
2
2
19
x y -+=内有一点P (2,2),过点P 作直线l 交圆C 于A 、B 两点.
(Ⅰ)当l 经过圆心C 时,求直线l 的方程; (Ⅱ)当弦AB 被点P 平分时,写出直线l 的方程; (Ⅲ)当直线l 的倾斜角为45º时,求弦AB 的长.
23. 已知圆
22
:()(2)4(0)C x a y a -+-=>及直线:30l x y -+=. 当直线l 被圆C 截得的弦长为22时, 求
(Ⅰ)a 的值;
(Ⅱ)求过点)5,3(并与圆C 相切的切线方程.
24. 已知方程
04222=+--+m y x y x . (Ⅰ)若此方程表示圆,求m 的取值范围;
(Ⅱ)若(Ⅰ)中的圆与直线042=-+y x 相交于M ,N 两点,且OM ⊥ON (O 为坐标原点)求m 的
值;
(Ⅲ)在(Ⅱ)的条件下,求以MN 为直径的圆的方程.
25.已知P 是3x+4y+8=0上的点,PA,PB 是圆x 2+y 2-2x-2y+1=0的两条直线,A,B 是切点,C 是圆心,那么四边形PACB 面积是多少?。
