高二数学 实系数一元二次方程2
实系数一元二次方程

实系数一元二次方程
实系数一元二次方程
一元二次方程(又称“二次多项式方程”)是指一个等式的次数较高,且只包含一个未知数的方程。
在一元二次方程中,自变量有且只有一个,称为一元二次函数,即 y=ax2+bx+c(a≠ 0)。
解一元二次方程的方法主要有三种:
1、因式分解法
因式分解法是一种常用方法,只要把方程改为一种可以分解的形式,便可以得到解。
步骤:
(1)首先,将一元二次方程化为相当于 0 的形式。
(2)把一元二次方程转换为包含两个未知数的多项式形式:
ax2+bx+c=d。
(3)用因数分解的方法把 d 分解成两个实数的乘积:d=e·f。
(4)将 ae 和 bf 分别作为新的因式,并同时入方程,即:
ax2+bx+c=ae+bf,再把此多项式撤分,可得 x 的解。
2、求根公式法
求根公式法是通过特定的公式来求解方程的一种方法,只有在一元二次方程系数为实数时才适用,其求根公式为:
x1= -b+√(b2-4ac) /2a
x2= -b-√(b2-4ac) /2a
3、图解法
图解法也是一个求一元二次方程解的方法,也是利用函数图像来分析一元二次方程解的方法,即将方程图像化,通过图像中的拐点、凹点及相关函数曲线的性质来分析、计算方程的解。
一元二次方程讲解

一元二次方程讲解
一元二次方程是数学中常见的一种方程形式,它由变量的二次项、一次项和常数项构成。
一元二次方程的一般形式为ax^2 + bx + c = 0,其中a、b、c为实数,且a不等于零。
解一元二次方程的方法主要有两种:公式法和配方法。
公式法是指根据一元二次方程的解的公式,求出方程的根。
一元
二次方程的解公式为x = (-b ± √(b^2 - 4ac))/(2a)。
其中,
√(b^2 - 4ac) 表示开方,若其结果为实数,则方程有两个不相等的
实根;若结果为零,则方程有一个实根;若结果为负数,则方程没有
实数解。
配方法是指通过对一元二次方程进行变形和整理,使其变为可以
进行因式分解的形式,从而求解方程的根。
例如,对于形如ax^2 + bx + c = 0的方程,我们可以尝试将其变形为(a1x + b1)(a2x + b2) = 0的形式。
通过展开式相乘,并与原方程进行比较,可以得到一组关于
a1、b1、a2、b2的方程。
解这组方程后,将所得的值带入原方程中,
即可求得方程的解。
在解一元二次方程时,我们还可以观察方程的系数之间的关系来
判断方程的解的性质。
例如,当方程的判别式b^2 - 4ac为负数时,
方程没有实数解;当判别式为零时,方程有一个实数解;当判别式为
正数时,方程有两个不相等的实数解。
总之,一元二次方程是数学中常见的方程形式,可以通过公式法
或配方法求解。
在解方程时,需要了解公式和判别式的含义,并根据
方程的特点选择适合的解法。
沪教版高中数学高二下册第十三章13.6 实系数一元二次方程 课件 (共10张PPT)

二、新课
1、实系数一元二次方程在复数集C中解的情况:
设一元二次方程 a x 2 b x c 0 ( a 、 b 、 c R 且 a 0 )
原方程可变形为
x2
b x c aa
即
(xb)2 2a
b24a42ac
(1)当b24ቤተ መጻሕፍቲ ባይዱ c0时,原方程有两个不相等的实数根
xb b24ac 2a 2a
(2)当b24a c0时,原方程有两个相等的实数根
为你制造一些困难和障碍的人未必是你的敌人,把你从困境里拉出来的人未必是你的朋友。不要用眼前的利益得失看人,要看长远,所谓路 遥知马力,日久见人心! 没有哪一个聪明人会否定痛苦与忧愁的锻炼价值。 我在奋斗在坚持在拼搏在努力你要等。 人的一生,可以有所作为的时机只有一次,那就是现在。
奋斗的路上,时间总是过得很快,目前的困难和麻烦是很多,但是只要不忘初心,脚踏实地一步一步的朝着目标前进,最后的结局交给时间 来定夺。 再好的种子,不播种下去,也结不出丰硕的果实。 战士的意志要象礁石一样坚定,战士的性格要象和风一样温柔。 如果上帝没有帮助你那他一定相信你可以。 在灾难面前不屈服,而应更加勇敢地去正视它。
x b 2a
(3)当b24ac0时,原方程有两个不相等的虚数根
xb 4acb2i 为一对共轭虚数根
2a 2a
例1、在复数集中解方程
(1) 4x2+9=0
(2) 2x2-4x+5=0
例2、在复数集中分解因式
(1)x2+8 (2)a4-b4 (3)3x2-6x+4
例3、
例4、
不能强迫别人来爱自己,只能努力让自己成为值得爱的人。
一定不要把别人都当傻子,事实上,所有你能遇到的人都比你聪明。如果你能抱着这样的心态为人处世,那么你的人脉会越来越宽,财富越 来越多,人生也就越来越好! 凡过于把幸运之事归功于自我的聪明和智谋的人多半是结局很不幸的。 当你飞黄腾达的时候,你的朋友知道你是谁;当你穷困潦倒的时候,你才知道你的朋友是谁。 眼要看远,脚要近迈。 志在峰巅的攀登者,不会陶醉在沿途的某个脚印之中。 没有人能预知未来的命运,但我们可以用愉悦的表情面对命运。 相信自己,你能作茧自缚,就能破茧成蝶。 别拿自己的无知说成是别人的愚昧! 不要抱怨自己所处的环境,如果改变不了环境,那么就改变自己的心态。 人总是在失去了才知道珍惜!
一元二次方程2(PPT)2-2

试一试
解方程:(1) x2+2x=5 (2)x2-4x+2=0
提 小示 结:: 能 观否 察经 以过 上适两当题变的形变, 形将 ,它 可们 以转 发化 现为 它的(a左x+边b)是2=一c的 形 个式 含, 有然 未后知用数直的接完开 全平方法 式? ,右边是一个非负 常数.这样,就能应用直接开平方的方法求解.
程两边同 时添加的
x2
5x
______
(x
_____)2
常数项等
于一次项 系数一半 的平方。
x2 x2
3 2
bx
x _____ _____)2
华东师范大学出版社 ;微信红包群 微信红包群
复习回顾 只含有一个未知数,并且未知数的最高次数 是2,这样的方程叫做一元二次方程. 特点: (1) 都是整式方程 (2) 只含有一个未知数 (3) 未知数的最高次数是2 通常可写成如下的一般形式:ax2+bx+c=0 (a≠0)
其中a、b、c分别叫做二次项系数、一次项系数和常数项.
一元一次方程的解法: 直接开平方法
这种解一元二次方程的方法叫做配方法.
例:用配方法解方程:
(1) x2-6x=7
(2) x2+3x+1=0
关于x的完全平方公式:
试一试:对下列各式进行配方:
配方的关 x 2 8x _+_1_6__ (x __4___)2
键是在方 x2 10x _+_2_5__ (x __5___)2
数学
更多证据有关始祖鸟与恐龙的关系,例如长有羽毛的恐龙。始祖鸟较接近现今鸟类的祖先,因它有著很多鸟类的特征;因它与当时鸟类的分歧程度仍有疑义。同许多古代生物的名字一样,始祖鸟的名字——Archaeopteryx也来源于希腊文,“archaeo”的意思是“古代的”,而“pteryx” 则是“翅膀”的意思。所以“Archaeopteryx”直译为“古代的翅膀”,当然,应当翻译为“长着古代翅膀的生物”更合适。但始祖鸟并不是现代鸟类的始祖。化石在空中飞翔的鸟类要保存为化石很困难,这是因为鸟类为了飞上蓝天,在身体结构上发育了轻而中空的骨骼。当远古时期的 一只鸟寿终正寝,长眠于地上时,它的纤细的骨骼在风吹、雨淋和日晒的打击下,会逐渐破碎解体,最后变成尘埃;即便落在阴暗的地方,也会有其它食腐动物光顾,在它们饱餐之后,原地将只余下一堆破碎的骨头。只有宁静的湖泊和沼泽,才是鸟类永久安息的理想坟墓。在古代湖边或 沼泽地栖息的鸟类,在死亡之后如果恰好坠落在细腻的淤泥中,而且此后的漫长岁月中淤泥缓慢地压实,变成石头,没有被温度、压力摧毁,才最终会保留下那只鸟儿的骨骼,幸运的话,还能在岩石中留下羽毛的印痕。如此苛刻的形成条件使鸟类的完整保存成为奇迹,保存下来的每件远 古鸟类化石都价值连城。而且越是古老,化石的价值就越大,始祖鸟从年代上看,确实是人们发现的最古老的鸟类,它生活在侏罗纪。因此人们在教科书中记录了这样一句话:始祖鸟是最早的鸟类。把始祖鸟划到鸟类家族中,主要是因为它的羽毛。我们用肉眼观察一根羽毛时,看到的是 一条中空的茎的两边伸展出排列整齐的“毛发”,似乎结构很简单。只有当我们把羽毛拿到显微镜下观察时,我们才发现,每一条细小的“毛发”上面,还有许多复杂的结构,枝杈纵横,并且有钩状物相连。这是鸟类的羽毛才有的特征。所以,确定一块化石是否属于鸟类的,要从显微结 构上看化石上是否有鸟类羽毛独特的细微结构。始祖鸟的羽毛展现出了这些细微的特征,因此理所当然地成为鸟类家族的成员,甚至有人说它就是现代所有鸟类的老祖宗。但是可以从其骨骼里辨认爬行类具有的特征。例如:结构轻巧的头颅在颚上的凹窝里有真正的齿;胸骨很小,没有龙 骨,前肢骨骼仍保留个有作用的指,而没有其它鸟类所有的退化和融合。已演化的后肢带还具有明显的恐龙特点,具有长的骨质尾。其它非特片化的鸟类特征有扁平的脊椎,腹肋条,以及下腿骨的不完全融合。与块已知骨骼相连接的羽毛印模表明这个生物是鸟。世界上只发现8例始祖鸟 的化石。这8例始祖鸟化石都是在德国的巴伐利亚州的石灰岩层中发现的,已有.亿年了,这些化石被证明为始祖鸟。这些化石上有清晰的羽毛印痕,而且分为初级和次级飞羽,还有尾羽。它的前肢特化成飞行的翅膀,后足有个趾,三前一后;锁骨愈合成叉骨,耻骨向后伸长。这些特征都 与现代鸟类相似。但奇怪的是,它的嘴里长着牙齿,翅膀尖上长着三个指爪;掌骨和跖骨都是分离的,还有一条由许多节分离的尾椎骨构成的长尾巴,这些特点又和爬行类极为相似。经研究证明,它是爬行类向鸟类过渡的中间阶段的代表,所以被称为“始祖鸟”。始祖鸟肯定能够飞行, 但可能在内陆海岸边的地上追逐和捕捉昆虫和爬行动物。据测定,始祖鸟最小飞行速度是每秒7.米,它可以鼓翼飞行,但不能持久。始祖鸟是怎样从地栖生活转变为飞翔生活的呢?关于这个问题,有两种说法。一种认为,原始鸟类在树上攀缘,逐渐过渡到短距离滑翔,进一步变为飞翔。另 一种认为,原始鸟类是双足奔跑动物,靠前肢网捕小型动物为食,前肢在助跑过程中发展成翅膀。始祖鸟虽然仅仅发现在化石里,但它为鸟类的起源于恐龙提供了证据。随着热河生物群的发现,始祖鸟的分类地位遇到了挑战。在热河生物群,许多有真羽毛甚至有完整羽翼的动物都被归入 了恐龙类,而其中的某些种类比始祖鸟更接近鸟类另一些则比始祖鸟更原始。但是因为古生物种类是不许改名字的,所以始祖鸟这个名称没有被触动,而它的
复数集内实系数一元二次方程的根的问题PPT课件

在实数集内,若实系数一元二次方程ax2 bx c 0
有根x1、x2 ,则ax2 bx c可因式分解为a(x x1)(x x2 )
在复数集内,若实系数一元二次方程ax2 bx c 0
有根x1,x2 ,则ax2 bx c可因式分解为a(x x1)(x x2 )
第5页/共11页
0 0
x1,2 x1 x2
b b2 4ac
2a b
2a 两个
相等实根
2a
(3) 当b2 4ac 0 x b 2a
4ac b2 2a
i
一对 共轭虚根
第1页/共11页
2、共轭虚根定理:(虚根成对出现)
若实系数一元二次方程有一虚根为a bi
(a、b R),则可知另一虚根为a bi.
欧拉在《微分公式》(1777年)一文中第一次
用i来表示-1的平方根,首创了用符号i作为虚数 的单位
第4页/共11页
例1、在复数集中解方程:
2x2 4x 5 0 x1,2 1
6i 2
变式1、2x在2 复4数x集 5中因 2式(x分 1解:26 i)( x 1
6 i) 2
x1,x2为实系数一元二次方程ax2 bx c 0的两个根
二、实系数一元二次方程的解
方程ax 2 bx c 0(a, b, c R, a 0)
称为实系数一元二次方程.
1、讨论实系数一元二次方程ax2 bx c 0的根
ax2 bx c 0
配方得: x
b
2
2a
b2两个4ac 不等4a实2根
(1) (2)
当b 2 当b 2
4ac 4ac
(2) x 2 x 1 0
(3) x 2 2ix 2 0
沪教版高中数学高二下册第十三章13.6.1实系数一元二次方程 教案

活动一的小 结
小结:1、以上结论的使用条件--------实系数一元二次方程。
1/2
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
2、实系数一元二次方程的根在复数集中共有三种不同情况:两 个不等实根、两个相等实根和一对共轭虚根。
3、代数基本定理:在复数域里,任何一元 n 次方程至少严格证 明。有一个根。据此退出,在复数范围里一元 n 次方程有且仅有 n 个根(k 重根作 k 个根计)。1797 年高斯首先给出。
知识像烛光,能照亮一个人,也能照亮无数的人。--培程 1、 通过用比较的方法讨论在复数集内解实系数一元二次方
程的问题,完整掌握实系数一元二次方程的解,完善实 系数一元二次方程的基本理论。 2、 会在复数集内对二次及简单的三次、四次多项式进行分 解因式。
教学重点与难点: 1、 理解在复数范围内,实系数一元二次方程总有两个根, 并掌握根的求法。
1、若关于 x 的一元二次方程 x2 − 2kx − k = 0 有虚根,则实数 k 的取值范围是____________。 2、判断下列命题的真假: (1)在复数范围内,方程 ax2 + bx + c = 0(a、b、c R,且a 0) 总 有两个根。
(2)若 2i −1 是方程 x2 + px + q = 0( p、q R) 的一个根,则 2i +1 是方程的另一个根。
(3)若1+ 2i 是方程 x2 + px + q = 0 的一个根,则这个方程的另 一个根是 1− 2i 。
活动二 测一测,你掌 握了吗?
例 1:在复数集中解下列一元二次方程: (1)2(x2 + 4) = 5x (2)x3 −1 = 0 (3)x2 − ax + 4 = 0(a R)
上海高二数学下册--02—复数的方根与实系数一元二次方程
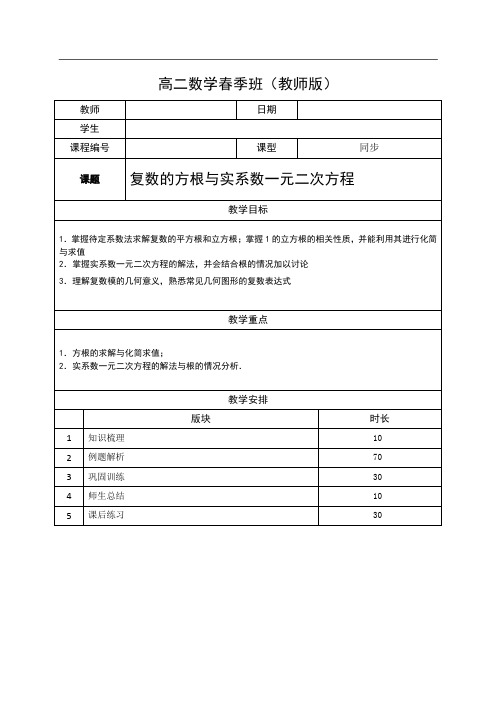
高二数学春季班(教师版)一、复数的平方根与立方根 1.复数的平方根的定义若复数1z ,2z 满足212z z =,则称1z 是2z 的平方根.2.复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等,把复数平方根问题转化为实数方程组来求. 3.复数的平方根的性质复数(0)z z ≠总有两个平方根1z ,2z ,且120z z +=(见图1). 4.复数的立方根的定义类似的,若复数1z ,2z 满足312z z =,则称1z 是2z 的立方根.5.1的立方根设复数12ω=-+,则21,,ωω都是1的立方根. 6.ω的性质 ①210ωω++=, ②31ω=,③212ωω==-. 可运用这些性质化简相关问题(见图2). 7.其他有用结论2(1)2i i -=-,2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式,那么(1)0∆>⇔方程有两个不相等的实根2b a-±;复数的方根与实系数一元二次方程知识梳理(2)0∆=⇔方程有两个相等的实根2b a-; (3)0∆<⇔,在(3)的情况下,方程的根与系数关系(韦达定理)仍然成立. 求解复数集上的方程的方法:(1)设(,)z x yi x y =+∈R 化归为实数方程来解决(化归思想).(2)把z 看成一个未知数(而不是实部和虚部两个未知数),用复数的性质来变形(整体思想). (3)对二次方程,直接用一元二次方程的求根公式(公式法).三、常见几何图形的复数表达式复数1z ,2z 为定值,且12z z ≠.(1)线段12Z Z 的中垂线方程:12||||z z z z -=-; (2)以1Z 为圆心,半径为r 的圆方程:1||z z r -=; (3)以1Z 、2Z 为焦点,长轴长为2(0)a a >的椭圆方程:12||||2z z z z a -+-=(其中12||2z z a -<); (4)以1Z 、2Z 为焦点,实轴长为2(0)a a >的双曲线方程:12||||||2z z z z a ---=(其中12||2z z a ->).1、复数的平方根与立方根 【例1】求4-及86i -的平方根.【难度】★【答案】4-的平方根为2i 或2i -;86i -的平方根为3i -或3i -+ 【例2】计算:(112112(1)22i i i ⎛⎫-+ ⎪⎝⎭;(2)50820028)i +-++⎝⎭. 【难度】★★【答案】(1)513;(2)247+【例3】记12ω=-,求1ωω+,221ωω+. 【难度】★★ 【答案】11ωω+=-,2211ωω+=-【例4】已知等比数列123,,,,n z z z z ,其中11z =,2z x yi =+,3z y xi =+(,,0x y x ∈>R ).(1)求,x y 的值; (2)试求使1230n z z z z ++++=的最小正整数n ;(3)对(2)中的正整数n ,求123n z z z z 的值.【难度】★★【答案】(1)12x y ⎧=⎪⎪⎨⎪=⎪⎩;(2)12n =;(3)1-.【巩固训练】1.复数34i +的平方根是 .例题解析【难度】★ 【答案】(2)i ±+2.计算:(11996= . (2)151512(1)(1)(1)i -+=-+ .【难度】★ 【答案】(1)12-;(2)03.已知ω满足等式210ωω++=.(1)计算4(1)ωω++;304050ωωω++;224(1)(1)ωωωω-+-+;(2)求证:对任意复数u ,有恒等式33233(1)()()3(1)u u u u ωω+++++=+; (3)计算:21n n ωω++,*n ∈N . 【难度】★★【答案】(1)1-;0;4;(2)略;(3)*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式:2223x x ++ 【难度】★【答案】22232x x x x ⎛++=-⎝⎭⎝⎭11222x x ⎛⎫⎛⎫-+=+- ⎪⎪ ⎪⎪⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=,求()41z z ++的值 【难度】★★【答案】由210z z ++=得,21102z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1.若虚数z 满足327z =,则32315z z z +++的值为 . 【难度】★★ 【答案】332.,,求的值.【难度】★★【答案】12ω=-时,原式=15-;12ω=-时,原式;3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ,求方程的解. 【难度】★【答案】920m ∆=- 当0∆>时,即920m <时,32x ±=;当0∆=时,即920m =时,32x =; 当0∆<时,即920m >时,32i x =.【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根,且2αβ∈R ,求βα的值.【难度】★★【答案】∵2αβ∈R ,∴2222ααβαββαβ=⇒=,即330αβ-=∴12αβ=-± 1≠ω13=ω32302ωωω+++【例9】已知12,x x 是实系数方程20x x p ++=的两个根,且满足12||3x x -=,求实数p 的值. 【难度】★★ 【答案】14p ∆=-, (1)当0∆≥时,即14p ≤时,12,x x 是实根,∴12||3x x -==,即32p =⇒=-; (2)当0∆<时,即14p >时,12,x x 是共轭虚根,设1(,)x a bi a b =+∈R ,则2x a bi =-, ∴123|||2|2||32x x bi b b -===⇒=±,由1221x x a +==-,得12a =-.从而21215||2p x x x ===.综上,2p =-或52.【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根,求||||αβ+的值. 【难度】★★【答案】212m ∆=-,(1)当0∆≥时,即m ≥m ≤-30αβ=>,∴||||||||m αβαβ+=+=; (2)当0∆<时,即m -<<||||2||αβα+===.【例11】已知复数12,z z 满足1||2z =,2||1z =,12||2z z -=,求12z z . 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=, ∴12121z z z z ⋅+⋅=, ∴122211211z zz z z z z z ⋅⋅+⋅⋅=, ∴122141z zz z +=. 令12z t z =,则141t t+=,∴240t t -+=,∴122t =±,即12122z i z =±.【例12】(1)方程20()x px k p -+=∈R 有一个根为12i +,求实数k 的值; (2)方程240x x k -+=有一个根为12i +,求k 的值. 【难度】★【答案】(1)由题意:另一个根为12i -,∴(12)(12)5k i i =+-=; (2)由题意2(12)4(12)074i i k k i +-++=⇒=+.【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根,且一个根的模是2,求实数a 、b 的值. 【难度】★★【答案】设()t t ∈R 是方程的一实根,则2(2)()i 0t at a bt b -++-=.则220,0t at a bt b ⎧-+=⎨-=⎩.(1)当0b =时,此方程为220x ax a -+=. ①有实根,0∆≥即1a ≥或0a ≤.当根为2时,440a a -+=.得43a =. 当根为2-时,440a a ++=.得45a =-.②有一对共轭虚根即01a <<.模为2,即有4a =(舍).(2)当0b ≠时,则1t =,此时1a =.又因为模为2,所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1.下列命题在复数集中是否正确?为什么?(1)若,,a b c ∈R ,0a ≠,且240b ac -≥,则方程20ax bx c ++=有两个实数根;(2)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则12b x x a +=-,12cx x a=; (3)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则221212||()x x x x -=-;(4)若,,a b c ∈R ,0a ≠,且α是方程20ax bx c ++=的根,则α也是方程的根. 【难度】★★ 【答案】(1)、(2)、(4)正确,(3)不正确2.若12,x x 为方程270x x -+=的两个根,则212||x x -= .【难度】★★ 【答案】273.已知,0x y ≠且,求20092009()(x y x y x y+++的值. 【难度】★★【答案】14.关于x 的方程222(31)10x m x m --++=的两根为αβ、,且||||3αβ+=,求实数m 的值. 【难度】★★【答案】53m =-或2m =5.设αβ、为方程220x x t ++=,(t ∈R )的两个根,()||||f t αβ=+, (1)求()f t 的解析式;(2)证明关于t 的方程()f t m =,当2m >时恰有两个不等的根,且两根之和为定值. 【难度】★★【答案】(1)0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩...(2)证明:函数()y f t =的图像关于直线12t =对称(证略) 当(1,)t ∈+∞时,()f t 为增函数,且()(2,)f t ∈+∞;022=++y xy x当(,0)t ∈-∞时,()f t 为减函数,且()(2,)f t ∈+∞.所以当2m >,方程()f t m =在区间(1,)+∞上有唯一解1t ,在区间(,0)-∞上也有唯一解2t , 则121212t t +=⨯=.4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中,1z ,2z ,m 都是复数,且21241620z z i -=+,设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值. 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=.∴2121|(4)|74m z z --=,即|(45)|7m i -+=, 这表明复数m 在以(4,5)C 为圆心,7为半径的圆周上,∴max ||7m =min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<.【例14】已知22016220160122016(1)x x a a x a x a x ++=++++,试求0362016a a a a ++++的值。
一元二次方程中的知识点

一元二次方程中的知识点
一元二次方程是代数学中的一种常见方程,其一般形式为:
ax^2+bx+c=0,其中a、b、c为实数且a不为0。
一元二次方程的知识点如下:
1. 方程的解:一元二次方程的解是使方程等号成立的数值。
方
程可能有两个实数解、一个实数解或者没有实数解。
2. 判别式:一元二次方程的判别式Δ=b^2-4ac用于判断方程的
根的情况。
若Δ>0,则方程有两个不相等的实数解;若Δ=0,则方程
有两个相等的实数解;若Δ<0,则方程没有实数解,但仍有复数解。
3. 顶点坐标:一元二次方程的图像是一个抛物线,其顶点坐标
为(-b/2a, -Δ/4a)。
顶点坐标可以用来确定抛物线的最值以及对称轴。
4. 因式分解:当一元二次方程有两个实数解时,可以根据已知
的解因式分解方程。
因式分解后的方程可以表示为(x-x1)(x-x2)=0,
其中x1和x2为方程的解。
5. 求解方法:一元二次方程的求解方法包括因式分解法、配方法、公式法和图像法等。
不同的方法适用于不同的方程形式和解的情况。
6. 实际应用:一元二次方程在现实生活中有广泛的应用。
例如,用于计算抛物线的轨迹、物体运动的模拟、工程建模等。
以上是一元二次方程的一些基本知识点,有助于理解和解决与一
元二次方程相关的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
—
x2 x1
∴ x1 x2 | x1 |2 x1 x2 2 Re x1
(二)巩固练习
1.已知1-i是实系数一元二次方程x2 px q 0
的一个根,则 p q= .
2.若两个数之和为2,两个数之积为3,则这两个数
分别为
.
3.在复数集中分解因式:3x2 2x 1=
.
4.若方程 x2 ax 2 0(a R)有虚数根z,则|z|= .
(四)课堂练习
1.若、是方程 x2 x 7 0的两个根,则
2 =
.
2.见课本P93练习13.6(2)T4.
(五)课堂小结
(六)课后作业 1.书面作业:练习册P55 习题13.6
P57 习题13.6 2.思考题:(补充题及备选题)
A组 T6.8. B组 T4.5.
(1)若方程 2x2 8x a 1 0(a R)有一个虚根的模为
5,则实数a的值为
.
(2)已知关于x的方程 x2 2x m 0(m R)的两根为
、 ,求 .
(3)已知关于x的方程 x2 (k 2i)x 2 ki 0(k R) 有实根,求实数k的值,并解方程.
(三)例题
例1、已知方程x2 px 1 0( p R) 的两根为
x1 、x2 ,若 x1 x2 1 ,求实数p的值.
例2、已知关于x的方程 x2 2ax a2 4a 4 0(a R)
的两根为 、,且 3,求实数a的值.
例3、已知关于x的方程ax2 (1 2i)x 2a(1 i) 0(a R) 有实数根,求实数a的值.
x b 4ac b2 i 2内分解因式:
ax2 bx c a(x x1)(x x2 )
3、实系数一元二次方程ax2 bx c 0 的韦达定理:
b x1 x2 a
特别地,
x1
x2
c a
当 b2 4ac 0时,x1和x2 为一对共轭虚根,即
13.6(2)实系数一元二次方程
(一)复习
1、设一元二次方程 ax2 bx c 0(a、b、c R且a 0)
(1)当 b2 4ac 0 时,原方程有两个不相等的实数根
x b b2 4ac
2a
2a
(2)当 b2 4ac 0时,原方程有两个相等的实数根
x b 2a
(3)当 b2 4ac 0时,原方程有一对共轭虚数根
