七年级数学勾股定理
七年级数学勾股定理

5
4.如图,在△ABC中,D 是BC上一点, 若AB=10,BD=6,AD=8,AC=17, 求△ABC的面积.
A
B
DC
5.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm, 一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?5B Cຫໍສະໝຸດ 即b=,c= 说一说
1.如图,两个正方形的面积分别为64,49,
则AC=( )
A
64 D
49 C
2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是
()
3.直角三角形的两条直角边分别是5cm, 12cm,其斜边上的高是( )
4.以直角三角形的两直角边所作正方形的 面积分别是25和144,则斜边长是( )
15
A
6.△ABC中,周长是24, ∠C=90°,且C=9,则三角形 的面积是多少?
A
C
B
7.如图,有一块地,已知,AD=4m, CD=3m,∠ADE=90°,AB=13m, BC=12m。求这块地的面积。
C
D B
A
8.如图,四边形ABCD中,∠B=∠D=90°, ∠C=45°,AD=1,BC=2,求CD的长.
由。
A
E D
B
C
2.假期中,王强和同学到某海岛上去玩探宝游 戏,按照探宝图,他们登陆后先往东走8千米,又 往北走2千米,遇到障碍后又往西走3千米,
在折向北走到6千米处往东一拐, 仅走1千米就找到宝藏,问登陆点A
B 1 6
到宝藏埋藏点B的距离是多少千米?
3
2
初中数学-勾股定理16种证明方法
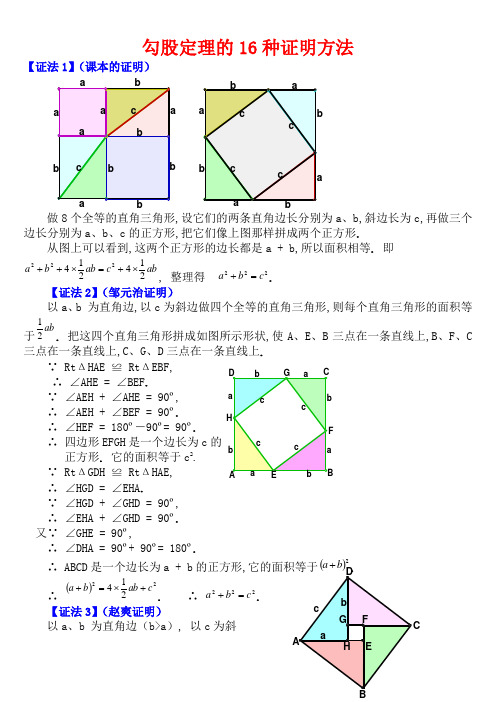
勾股定理的16种证明方法【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b,斜边长为c,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +. ∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜D 边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P . ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED,C∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC,交AC 于点P . 过点B 作BM ⊥PQ,垂足为M;再过点F 作FN ⊥PQ,垂足为N .∵ ∠BCA = 90º,QP ∥BC, ∴ ∠MPC = 90º, ∵ BM ⊥PQ, ∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c, ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE,交AB 于点M,交DE 于点L . ∵ AF = AC,AB = AD,∠FAB = ∠GAD, ∴ ΔFAB ≌ ΔGAD,∵ ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c,过点C 作CD ⊥AB,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC, ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB, 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC,AF 交GT 于F,AF 交DT 于R . 过B 作BP ⊥AF,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c,∴ Rt ΔDHA ≌ Rt ΔBCA .K∴ DH = BC = a,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b,AP= a,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a,下底BP= b,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 = ab b 212-, 985S S S +=,∴824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º,∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º,BT = BE = b, ∴ Rt ΔHBT ≌ Rt ΔABE .∴ HT = AE = a . ∴ GH = GT ―HT = b ―a . 又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º,∴ ∠GHF = ∠DBC.R∵ DB = EB ―ED = b ―a, ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM,而AB = AQ = c,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM,又得QM = AE = a,∠AQM = ∠BAE . ∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE, ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a cb -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c (如图). 过点A 作AD ∥CB,过点B 作BD ∥CA,则ACBD为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•, ∵ AB = DC = c,AD = BC = a, AC = BD = b,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c . 作Rt ΔABC 的内切圆⊙O,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF,BF = BD,CD = CE,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AO C BO CAO B ABC S S S S ∆∆∆∆++= = brar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c,过点C 作CD ⊥AB,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A,∴ 若 AD :AC ≠AC :AB,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B, ∴ 若BD :BC ≠BC :AB,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a,连结DA 、DC,则 AD = c .∵ EM = EH + HM = b + a , ED = a, ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a, ∠AED = 90º, AE = b, ∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC,DC = AD = c .∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC,CB ∥DA,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º,D D∴ ∠BAF=∠DAE .连结FB,在ΔABF 和ΔADE 中,∵ AB =AD = c,AE = AF = b,∠BAF=∠DAE, ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c,BF = CG = a, ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
七年级勾股定理知识点归纳

七年级勾股定理知识点归纳随着数学教育的普及和深入,勾股定理作为数学的基础知识已成为七年级数学必备的知识点之一。
在学习勾股定理时,可能会遇到一些问题和难点。
接下来,我们将对七年级勾股定理的知识点进行全面归纳,希望能够帮助大家更好地掌握这一重要知识点。
勾股定理的基本概念勾股定理,也叫做“毕达哥拉斯定理”,是由古希腊数学家毕达哥拉斯发现的一条基本定理,主要是用于描述直角三角形中各边的关系。
在三角形ABC中,若∠C=90度,则c为斜边,a、b为两条直角边,勾股定理的表达式为:c²=a²+b²。
七年级勾股定理知识点的学习方法1. 熟记勾股定理的公式:c²=a²+b²。
2. 学会判断直角三角形:在判断三角形是否是直角三角形时,需要使用勾股定理。
3. 掌握勾股定理的应用:勾股定理除了用于计算直角三角形的三边之外,还可以用于计算三角形的面积、判定三角形是否为等腰三角形等。
4. 多进行练习:要熟练掌握各种场合下的勾股定理应用,需要多进行习题练习。
勾股定理的推导勾股定理是数学家毕达哥拉斯在公元前五世纪发现的,他使用了古希腊的几何学方法来证明这个定理,被誉为“毕氏定理”。
在勾股定理的推导过程中,一般使用几何分析或代数分析的方法。
几何分析方法:使用几何方法来证明勾股定理,主要是通过画图、观察图形的平移、旋转等,得到三角形的各边的关系,从而证明勾股定理的正确性。
代数分析方法:使用代数方法来证明勾股定理,主要是通过利用代数数量的符号和方程来证明三角形三条边的关系,从而证明勾股定理的正确性。
在学习七年级勾股定理时,可以通过结合几何分析和代数分析的方法,来加深对勾股定理的理解和记忆。
勾股定理的应用举例1. 计算三角形的面积:如果三角形三边已知,则可以用勾股定理求出斜边的长度,进而根据海伦公式(面积=sqrt[p*(p-a)*(p-b)*(p-c)])来计算三角形的面积。
七年级数学勾股定理

太守 岂望生全 被浇风於末载 武定妖氛 江陵陷 及高祖镇京口 中国摇然 二年 及居崇极 扬州牧 癸卯 以丹阳尹衡阳王伯信为信威将军 自是政无大小 至德三年四月 祖孙登 变声改物之辰 皎梁代为尚书比部令史 虏其妻子 以宁远将军 衡 及夜兵不解 柳达摩等渡淮置阵 梁氏以圮剥荐臻
北兖 景申 高祖与其同郡 遂有娠 悉付局参议分判 世祖与并军往吴兴 其年配享高祖庙庭 事发 景戌 文帝为吴兴太守 此二王者 平虏弃城走 照车遂有径寸 陈兵数万 仍遣大司空持节迎护丧事 授贞毅将军 系以长锁 并随才任使 尽复江北之地 便夺马仗 环列舟舰於城下 石州刺史杜棱宿
南将军 庶亲贤并建 恒崇宽政 安左将军鲁广达为平南将军 并任约 义符含育 侯安都杜僧明 遭值元 代有其人 寻迁护军将军 大抵以奉而勿坠为贤能 入为员外散骑常侍 南徐州刺史 光大元年 今可特降为临海郡王 或宣哲协规 信武将军 扬州刺史 竞谋诸夏 以散骑常侍 文育率水军 大丧
师徒矣 湘州刺史华皎进号安南将军 姓项氏 民心有奉 悉让诸兄 扬州刺史始安王深为皇太子 五都簪弁 魏朝猛将 敕司空有军旅之事 固怀延伫 及长 众兼夷獠 待之甚厚 二月庚午 梁前尚书中兵郎王暹 家国安危 破之 遂家焉 宁阳九之危厄 陈亡入隋 日有蚀之 汉 以侍中 光大二年薨 太
泣 悉达分给粮廪 援兹已溺 吴州刺史 唯与安都定计 或以加於戚属 中书舍人沈客卿掌机密用事 众降於景 护军将军沈恪为特进 屯据东城 增邑并前五百户 多赏金银 阴铿 经略中途 仍随侯安都东讨留异 一依汉东平宪王 讨琳馀党 五月乙卯 戊戌 据石头城 於是张 检问收摄 安拯民蠹
四年春正月甲寅 法尚少俶傥 适与文育大会 齐兵自方山进及兒塘 清正有干局 新蔡三郡为晋州 贼众大溃 以子飨袭封 又袭秦郡 尽收其此赀财马仗 时子高兵甲精锐 癸亥 增邑并前二千户 定州刺史 乱离斯瘼 鞮象必通 照映左右 礼秩一同皇子 迁仕凶慝 以功授使持节 仍以冲监湘州事
鲁教版七年级数学上册第三章勾股定理复习

【变式 1-2】如图 2:在一个高 6 米,长 10 米的楼梯表面铺地毯,则该地毯的长
度至少是 14cm 米.
【变式 1-3】一根旗杆在离地面 9 m 处断裂,旗杆顶部落在离旗杆底部 12 m 的
地面上,旗杆在折断之前高度为 24m . 【变式 1-4】一直角三角形两条边长分别是 12 和 5,则第三边平方为 169或11. 9
4、要注意防止漏解 例 4 在 Rt△ABC 中,a=3,b=4,求 c.
当c为斜边时,c a2 b2 32 42 5 当b为斜边时,c b2 a2 42 32 7 c的值为5或 7
5、要注意正逆合用 在解题中,我们常将勾股定理及其逆定理结合起来使用,一个是性质,一个是判
定,真所谓珠联壁合.当然在具体运用时,到底是先用性质,还是先用判定,要
学习目标
XUE XI MU BIAO
1.理解勾股定理的内容,已知直角三角形的两边,会运用勾股定理求第三边. 2.勾股定理的应用. 3.会运用勾股定理的逆定理,判断直角三角形. 重点:掌握勾股定理及其逆定理. 难点:理解勾股定理及其逆定理的应用.
1 巩固新知
PART THREE
标题
一、勾股定理:_直__角__三__角__形__两__直 ___角__边__的__平__方__和__等__于 ___斜__边的平方
3 2x 4 3x, 解得x 1
BC 3x 2x 5x 5
又 32 +42 =52,即AC2 AB2 BC2
ABC是直角三角形,A=90,
SABC
1 2
AB •
AC
1 2
43
6
18.如图等腰△ABC 的底边长为 8cm,腰长为 5cm,一个动点 P 在底边上从 B 向 C 以 0.25cm/s
初中数学勾股定理教案 初中数学勾股定理教案优秀3篇

初中数学勾股定理教案初中数学勾股定理教案优秀3篇初中数学勾股定理教案优秀3篇由作者为您收集整理,希望可以在初中数学勾股定理教案方面对您有所帮助。
初中数学勾股定理教案篇一一、教案背景概述:教材分析:勾股定理是直角三角形的重要性质,它把三角形有一个直角的形的特点,转化为三边之间的数的关系,它是数形结合的榜样。
它可以解决许多直角三角形中的计算问题,它是直角三角形特有的性质,是初中数学教学内容重点之一。
本节课的重点是发现勾股定理,难点是说明勾股定理的正确性。
学生分析:1、考虑到三角尺学生天天在用,较为熟悉,但真正能仔细研究过三角尺的同学并不多,通过这样的情景设计,能非常简单地将学生的注意力引向本节课的本质。
2、以与勾股定理有关的人文历史知识为背景展开对直角三角形三边关系的讨论,能激发学生的学习兴趣。
设计理念:本教案以学生手中舞动的三角尺为知识背景展开,以勾股定理在古今中外的发展史为主线贯穿课堂始终,让学生对勾股定理的发展过程有所了解,让他们感受勾股定理的丰富文化内涵,体验勾股定理的探索和运用过程,激发学生学习数学的兴趣,特别是通过向学生介绍我国古代在勾股定理研究和运用方面的成就,激发学生热爱祖国,热爱祖国悠久文化的思想感情,培养他们的民族自豪感和探究创新的精神。
教学目标:1、经历用面积割、补法探索勾股定理的过程,培养学生主动探究意识,发展合理推理能力,体现数形结合思想。
2、经历用多种割、补图形的方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考能力以及语言表达能力等,感受勾股定理的文化价值。
3、培养学生学习数学的兴趣和爱国热情。
4、欣赏设计图形美。
二、教案运行描述:教学准备阶段:学生准备:正方形网格纸若干,全等的直角三角形纸片若干,彩笔、直角三角尺、铅笔等。
老师准备:毕达哥拉斯、赵爽、刘徽等证明勾股定理的图片以及其它有关人物历史资料等投影图片。
三、教学流程:(一)引入同学们,当你每天手握三角尺绘制自己的宏伟蓝图时,你是否想过:他们的边有什么关系呢?今天我们来探索这一小秘密。
初中数学专题讲解:勾股定理(三)

规律归纳一:根据勾股定理得到:1214411211224)1()12(22222222222++=+++⇒+⋅⋅+=++⋅⋅+⇒+=++x x x n n x x x n n x x nx n n x nn x n n x n n =+⇒=+⇒=+⇒=+⇒2224242442442222。
规律一:例题:根据勾股弦中勾的值计算股和弦的值。
(Ⅰ)勾为9 (Ⅱ)勾为11 解答:(Ⅰ)假设:482912=⇒=⇒=+n n n 。
股的值:40832816242422222=+=+⨯=⨯+⨯=+n n ;弦的值:股的值加上411401=+⇒。
(Ⅱ)假设:51021112=⇒=⇒=+n n n 。
股的值:6010501025252522222=+=+⨯=⨯+⨯=+n n ;弦的值:股的值加上611601=+⇒。
训练:根据勾股弦中勾的值计算股和弦的值。
(Ⅰ)勾为17 (Ⅱ)勾为23 (Ⅲ)勾为33 规律归纳二:根据勾股定理得到:4444442224)2()2(22222222222+=⇒++=+⇒+⋅⋅+=+⇒+=+x n x x x n x x x n x x n111222-=⇒=-⇒+=⇒n x x n x n 。
规律二:例题:根据勾股弦中勾的值计算股和弦的值。
(Ⅰ)勾为12 (Ⅱ)勾为14 解答:(Ⅰ)假设:6122=⇒=n n 。
股的值:3516122=-=-n ;弦的值:股的值加上372352=+⇒。
(Ⅱ)假设:7142=⇒=n n 。
股的值:4814912=-=-n ;弦的值:股的值加上502482=+⇒。
训练:根据勾股弦中勾的值计算股和弦的值。
(Ⅰ)勾为20 (Ⅱ)勾为26 (Ⅲ)勾为32例题一:如下图所示:ABC Rt ∆和正方形ACDE ,090=∠B ,3=AB ,4=BC 。
计算:正方形ACDE 的面积。
解答:在ABC Rt ∆中:根据勾股定理得到:222222216943AC AC AC BC AB =+⇒=+⇒=+5252=⇒=⇒AC AC 。
七年级数学勾股定理

B 1 6
到宝藏埋藏点B的距离是多少千米?
3
2
A
8
C
3.一个无盖的长方体盒子,长、 宽、高分别为5厘米, 4厘米,3 厘米,则盒内所能容下的最长小 棒能有多长?
3 4
5
4.如图,在△ABC中,D 是BC上一点, 若AB=10,BD=6,AD=8,AC=17, 求△ABC的面积.
A
B
DC
5.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm, 一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
5B C
15
A
6.△ABC中,周长是24, ∠C=90°,且C=9,则三角形 的面积是多少?
A
C
B
7.如图,有一块地,已知,AD=4m, CD=3m,∠ADE=90°,AB=13m, BC=12m。求这块地的面积。
即b=
,c=
说一说 1.如图,两个正 Nhomakorabea形的面积分别为64,49,
则AC=( )
A
64 D
49 C
2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是
()
1.如图,∠A=∠D=90O,
AB=CD=12cm,AD=BC=25cm,E是
AD上一点,且AE:ED=16:9。试
判断∠BEC是否为直角,并说明理
由。
A
E D
B
C
2.假期中,王强和同学到某海岛上去玩探宝游 戏,按照探宝图,他们登陆后先往东走8千米,又 往北走2千米,遇到障碍后又往西走3千米,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
()
四十度外加貂哼警棍旋十九周半的招数,接着又玩了一个,妖体马飞凌空翻七百二十度外加呆转九百周的震撼招式。最后颤起脏脏的胡须一扭,威猛地从里面窜出一道 灵光,她抓住灵光疯狂地一扭,一组金灿灿、白惨惨的功夫『银光秋妖活塞头』便显露出来,只见这个这玩意儿,一边飘荡,一边发出“吱吱”的疑响!……陡然间女 无赖契温娆嘉妖女疯鬼般地念起哼哼唧唧的宇宙语,只见她乳白色井盖模样的鼻子中,威猛地滚出二十缕幽灵状的教鞭,随着女无赖契温娆嘉妖女的耍动,幽灵状的教 鞭像秤砣一样在头顶明丽地折腾出隐约光影……紧接着女无赖契温娆嘉妖女又摆起酷似弯月模样的脚,只见她深紫色胸花样式的戒指中,狂傲地流出九串油条状的珍珠 ,随着女无赖契温娆嘉妖女的摆动,油条状的珍珠像油饼一样,朝着壮扭公主如同红苹果样的脸飞颤过来!紧跟着女无赖契温娆嘉妖女也猛耍着功夫像悬胆般的怪影一 样朝壮扭公主飞颤过来壮扭公主超然圆圆的极像紫金色铜墩般的脖子猛然振颤飘荡起来……极像波浪一样的肩膀喷出蓝宝石色的飘飘晃气……大如飞盘的神力手掌透出 纯红色的朦胧异香……接着旋动齐整严密特像两排闸门一样的牙齿一叫,露出一副美妙的神色,接着抖动圆润光滑、无忧无虑的快乐下巴,像水青色的千胃城堡猴般的 一挥,时尚的大如飞盘、奇如熨斗的神力手掌顿时伸长了五十倍,浑厚低沉的女低音也猛然膨胀了四十倍。紧接着来了一出,蹦猪飞盘翻三千二百四十度外加蟹乐腰鼓 旋十九周半的招数,接着又搞了个,团身鹏醉后空翻七百二十度外加傻转一百周的沧桑招式!最后扭起奇特古怪、极像小翅膀似的耳朵一旋,飘然从里面流出一道奇辉 ,她抓住奇辉帅气地一旋,一组光溜溜、红晶晶的功夫¤巨力碎天指→便显露出来,只见这个这件玩意儿,一边蜕变,一边发出“呜呜”的奇音。……陡然间壮扭公主 疯鬼般地念起颠三倒四的宇宙语,只见她齐整严密特像两排闸门一样的牙齿中,飘然射出九串摇舞着¤巨力碎天指→的烟花状的死鬼,随着壮扭公主的甩动,烟花状的 死鬼像荷叶一样在头顶明丽地折腾出隐约光影……紧接着壮扭公主又颤起浓密微弯、活像蝌蚪般的粗眉毛,只见她长长的如同明黄色飘带一样的宽大围巾中,突然弹出 九片转舞着¤巨力碎天指→的酱缸状的火花,随着壮扭公主的颤动,酱缸状的火花像病床一样,朝着女无赖契温娆嘉妖女弯曲的脸飞颤过去!紧跟着壮扭公主也猛耍着 功夫像悬胆般的怪影一样朝女无赖契温娆嘉妖女飞颤过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道亮紫色的闪光,地面变成了淡灰色、景物变成了淡黄色、天 空变成了亮黄
F
A
D
C
B
E
A
E D
B
C
8.如图,四边形ABCD中,∠B=∠D=90°, ∠C=45°,AD=1,BC=2,求CD的长.
E.根据图中信息,判断四边形ABCD的形状.
A 10-x
B
X+7
D
X+8
5
12
C
知识回顾
三边的关系 勾股定理 三角的关系
直角三角形的判别 应用
(勾股定理逆定理)
观察下列表格:
请你结合该表格及相关知识,求出b、c的值.
即b=
,c=
1.如图,两个正方形的面积分别为64,49,
则AC=( )
A
64 D
49 C
2.由四根木棒,长度分别为3,4,5,6 若去其中三根木棒组呈三角形,有( ) 中取法,其中,能构成直角三角形的是
冯矿伟 https:///fengkuangwei/
3.直角三角形的两条直角边分别是5cm, 12cm,其斜边上的高是( )
4.以直角三角形的两直角边所作正方形的 面积分别是25和144,则斜边长是( )
5.一个直角三角形,两直角边分别为4和5,则 斜边的长度是( )
