聚合物流变学
第四章-聚合物流体的流变性

(4)聚合物链结构中的侧基 当侧基体积较大时,自由体积增
大,流体黏度对压力和温度敏感性增 加. 如PMMA和PS可以提高T或者改 变P来改善流动性
顺丁胶的黏度与相对分子质量的关系 1-直链,2—三支链,3—四支链
2. 相对分子质量的影响
(1)相对分子质量对0 的影响
丙烯腈共聚物在NaSCN-H2O 中浓溶液的零切黏度对分子量的依赖性
0 A exp E RT
ln0 ln A E RT
lg 0
lg
A
E 2.303 RT
当T>Tg+100℃时, 由Arrhenius方程式:
0 A exp E RT
ln0 ln A E RT
lg 0
lg
A
E 2.303 RT
须知
➢ 黏流活化能的大小显著受剪切应力或剪切速率的 影响,因此,测定黏流活化能必须说明具体的实 验条件。
C =45.4%,Mc=1.3103; C = 15%时, Mc=6.03104
(2)分子量对流动曲线的影响(P71)
聚合物流体流动曲线对分 子量的依赖性
M ↑ 流动曲线上移 , 0 ↑
相cr同向低值移下动的a ↑
cr
3.相对分子质量分布的影响
(二) 聚合物溶液浓度对黏度的影响
1.聚合物溶液浓度对0 (或)的影响
不稳定流动
• 凡流体在输送通道中流动 时,其流动状况及影响流 动的各种因素都随时间而 变化,此种流动称为不稳 定流动。如在注射成型的 充模过程中,在模腔内的 流动速率、温度和压力等 各种影响流动的因素均随 时间而变化。
等温流动和非等温流动
等温流动
• 流体各处的温度保持不变 情况下的流动。在等温流 动情况下,流体与外界可 以进行热量传递,但传入 和输出的热量保持相等, 达到平衡。
聚合物流变学

1
a`a b`b c`c 1 a b c 1 V / V (abc abc) / abc abc / abc 1
V / V 3 1 (1 )3 1 3 3 2 3
1
-tyx -txy 在y面施加一个剪切力tyx时,必须在x面作用一个大 小相等的剪应力txy才能使试样保持平衡。
在简单剪切实验中,应力张量为:
0 t t yx 0
t xy 0 0
0 0 0
返回
1.6 接触力(内力)
接触力是物体内的一部分通过假想的分隔 面作用在相邻部分上的力,也即外力向物 体内传递。
y B A C f D x
A
-f z
t yx f / A
txy
dz
tyx
y
x dx dy
-tyx
-txy 顺时针方向总力矩为: 必须有作用力
z
t x 0, t xy ,0
dL t yx dxdydz t xy dxdydz
txy
tyx
总力矩为dL=0,即:
t xy t yx
返回
1.5 简单实验中的应力张量
1.5.1 单向拉伸实验
y c b` f l` b A c` z l x f
t xx f / A
f t x t xx , t xy , t xz ,0,0 A t y t yx , t yy , t yz 0,0,0 t z t zx , t zy , t zz 0,0,0
V / V 3
1.2.2 单向拉伸和压缩
y
c b` f z l`
l ` l b` b c` c
聚合物的粘性流动-聚合物流变学基础课件
9.1.2 聚合物熔体流动特点
(1)粘度大,流动性差: 这是因为高分子链的流动 是通过链段的相继位移来实现分子链的整体迁移, 类似蚯蚓的蠕动。 (2)不符合牛顿流动规律:在流动过程中粘度随 切变速率的增加而下降(剪切变稀)。
(3)熔体流动时伴随高弹形变:因为在外力作用 下,高分子链沿外力方向发生伸展,当外力消失后, 分子链又由伸展变为卷曲,使形变部分恢复,表现 出弹性行为。
M > Mc 0 =KMw3~3.4
logMc logM
23
不同用途对分子量有不同的要求: 合成橡胶一般控制在20万; 塑料居橡胶和与纤维之间, 合成纤维一般控制在1.5万~10万;
不同加工方法对分子量有不同要求: 挤出成型要求分子量较高; 注射成型要求分子量较低; 吹塑成型在挤出和注射两者之间。
When T >Tg+100
a AeE/RT
E - 粘流活化能 viscous flow energy
高分子流动时的运动单元: 链段(的协同运动)
E 由链段的运动能力决定, 与分子链的
柔顺性有关, 而与分子量无关!!
29
a AeE/RT
刚性链 E大 粘度对温度敏感
柔性链
E小
粘度对温度不敏感 对剪切速率敏感
工业上常用MI值作为衡量聚合物分子量大小的一种相对指标,分 子量越大,MI值越小。
15
锥板式旋转粘度计
锥板粘度计是用于测定聚合物熔体粘度的常用仪器。
门尼粘度计
在一定温度下(通常 100C)和一定的转子速 度下,测定未硫化的橡 胶对转子转动的阻力
Mooney Index
100C
M
I100 34
预热3min
熔融指数(Melt index ——简MI ):指在一定的温度下和规定
聚合物流变学(绪论)课件

除了在高分子材料加工和性能研究中的应用外,聚合物流变学还广泛应用于其他领域,如生物医学、食品科学、石油化工等。
05
聚合物流变学的未来发展
1
2
3
流变学与材料科学、物理学、化学等学科的交叉融合将进一步加强,为流变学理论的发展提供更多思路和方法。
跨学科融合
实验和计算模拟的相互补充和验证将成为流变学研究的重要手段,有助于更深入地揭示流体的复杂行为。
实验与计算模拟相结合
人工智能、大数据和云计算等技术在流变学中的应用将逐渐普及,提高流变学研究的效率和精度。
智能化技术的应用
聚合物流变学研究面临实验难度大、理论模型复杂、多尺度效应等问题,需要不断探索和创新。
随着科技的发展,聚合物流变学在材料制备、加工、性能优化等方面具有广阔的应用前景,为相关领域的发展提供有力支持。
机遇
挑战
THANK YOU
聚合物流变学(绪论)课件
目录
contents
聚合物流变学简介聚合物流变学基础知识聚合物流变学研究方法聚合物流变学应用聚合物流变学的未来发展
01
聚合物流变学简介
01
02
它涉及到高分子材料的流变性质、流动行为、结构变化以及与加工工艺之间的关系等多个方面。
聚合物流变学是一门研究高分子材料在流动和变形过程中所表现出来的各种物理和化学行为的科学。
将连续的流体离散为有限个单元,如有限差分法、有限元法等。
离散化方法
根据物理定律和边界条件,建立描述流体运动的偏微分方程或积分方程。
建立模型方程
聚合物流变学(绪论)

❖ 加工流变学:属于宏观流变学,主要研究
与高分子材料加工工程有关的理论与技术 问题。
❖ 比如说,研究加工条件变化与材料流 动性质(主要指粘度、弹性)及产品力学 性质之间的关系,异常的流变现象如挤出 胀大、熔体破裂现象发生的规律、原因及 克服办法;高分子材料典型加工成型操作 单元(如挤出、吹塑、注射等过程的流变 学分析;多相高分子体系的流变性规律, 以及模具与机械设计中遇到的种种与材料 流动性质有关的问题等。)
32
主要内容:
挤出流变学 密炼流变学 塑炼流变学 压延流变学 注模流变学 吹塑流变学 熔体纺丝流变学
33
研究和学习流变学的意义
1)对高分子材料合成而言,流变学与高分子化学结合在一 起,流变性质通过与分子结构参数的联系成为控制合成产 物品质的重要参数。
2)对高分子材料成型加工而言,流变学与高分子物理学和 高分子材料成型工艺原理结合在一起,成为设计和控制材 料配方及加工工艺条件,以获取制品最佳的外观和内在质 量的重要手段。
图 1-8 孔压误差 21
牛顿型流体不存在孔压误差,无论压力传 感器端面安装得与流道壁面是否相平,测得 的压力值相等。高分子液体有孔压误差现象。
22
2 原因:在凹槽附近,流线发生弯曲,但法向应
力差效应有使流线伸直的作用,于是产生背向凹 槽的力,使凹置的压力传感器测得的液体内压力 值小于平置时测得的值。在实施流变测量时,应 当注意这一效应。同样地,当高分子液体流经一 个弯形流道时,液体对流道内侧壁和外侧壁的压 力,也会因法向应力差效应而产生差异。通常内 侧壁所受的压力较大。
10
11
二、Weussebberg效应
12
三、Barus效应
13
四、不稳定流动与熔体破裂
聚合物流变学研究意义

聚合物流变学研究意义聚合物流变学是研究聚合物在外力作用下的流变特性的学科。
聚合物是一类大分子化合物,具有高分子量、高分子链的柔韧性和长期的耐久性等特点。
聚合物在外力作用下会产生不同的变形和流动行为,而聚合物流变学正是研究这些变形和流动行为的学科。
聚合物流变学的研究意义主要体现在以下几个方面:1. 工程应用:聚合物流变学的研究可以为聚合物工程应用提供重要的理论基础。
比如,聚合物在塑料加工中的流动行为和变形特性对于塑料工程的设计和制造至关重要。
另外,在航空、汽车、电子等领域,聚合物的流变特性也对产品的性能和可靠性有着重要的影响。
2. 医学应用:聚合物在生物医学领域中有着广泛的应用,比如注射用聚合物、生物材料、组织工程等。
聚合物流变学的研究可以为这些应用提供重要的理论支持和技术指导。
3. 环境保护:聚合物在环境领域中也有着重要的应用,比如塑料袋、塑料瓶等。
聚合物流变学的研究可以为这些应用提供技术支持,使其更加环保和可持续。
聚合物流变学的研究主要涉及到以下几个方面:1. 本构关系:聚合物的流变特性与其分子结构有关,通过研究聚合物的分子结构和流变行为,可以建立聚合物的本构模型,从而预测其力学性能。
2. 流变行为:聚合物的流变行为包括弹性、塑性、粘弹性等,通过研究聚合物的流变行为,可以了解其在复杂工况下的行为规律,从而为工程应用提供理论指导。
3. 流变测试:聚合物的流变测试是研究聚合物流变行为的重要手段,包括剪切测试、拉伸测试、压缩测试等。
通过流变测试,可以获得聚合物的粘度、弹性模量、屈服点等流变参数,为聚合物工程应用提供重要的数据支持。
聚合物流变学的研究对于聚合物工程应用、生物医学、环境保护等领域都具有重要的意义。
在未来,随着聚合物材料的广泛应用,聚合物流变学的研究也将变得越来越重要。
聚合物流变学第一章

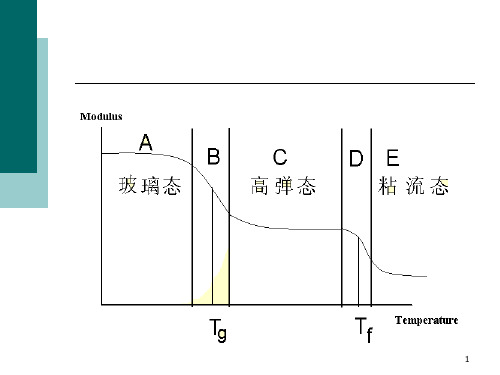
第一章 绪 论1. 流变学概念流变学——研究材料流动及变形规律的科学。
高分子材料流变学——研究高分子液体,主要指高分子熔体、高分子溶液,在流动状态下的非线性粘弹行为,以及这种行为与材料结构及其它物理、化学性质的关系。
图1-1 液体流动与固体变形的一般性对比Newton’s 流动定律 γησ 0= 牛顿流体 H ooke’s 弹性定律 εσE = 虎克弹性体实际材料往往表现出远为复杂的力学性质。
如沥青、粘土、橡胶、石油、蛋清、血浆、食品、化工原材料、泥石流、地壳,尤其是形形色色高分子材料和制品,它们既能流动,又能变形;既有粘性,又有弹性;变形中会发生粘性损耗,流动时又有弹性记忆效应,粘弹性结合,流变性并存。
对于这类材料,仅用牛顿流动定律或虎克弹性定律已无法全面描述其复杂力学响应规律,必须发展一门新学科——流变学对其进行研究。
流变性实质——“固-液两相性”,“粘弹性”并存。
这种粘弹性不是小变形下的线性粘弹性,而是材料在大变形、长时间应力作用下呈现的非线性粘弹行为。
流动与变形又是两个紧密相关的概念。
在时间长河中,万物皆流,万物皆变。
流动可视为广义的变形,而变形也可视为广义的流动。
两者的差别主要在于外力作用时间的长短及观察者观察时间的不同。
按地质年代计算,坚硬的地壳也在流动,地质学中著名的“板块理论”揭示了亿万年来地球大陆板块的变化和运动。
另一方面,如果以极快的速度瞬间打击某种液体时,甚至连水都表现了一定的“反弹性”。
1928年,美国物理化学家E.C.Bingham正式命名“流变学(rheology)”,字头取古希腊哲学家Heraclitus所说的“ ”,意即万物皆流。
1929年成立流变学会,创办流变学报(Journal of Rheology),一般将此认为流变学诞生日。
流变学是一门涉及多学科交叉的边缘科学。
高分子材料流变学的研究内容与高分子物理学、高分子化学、高分子材料加工原理、高分子材料工程、连续体力学、非线性传热理论等联系密切;其研究对象的力学、热学性质相当复杂。
聚合物的流变学性质

为何具有“剪切增稠”特性?
多分散体系; 高含量,高硬度微粒为分散相,分散介质在其间起润滑作用。
增大 ,粒子相互碰撞,导致润滑不足,流动阻力增加,粘度上升。
2
1
特征:τ较小不流动,呈现凝胶状态,只发生弹性变形;
该液体在静止时内部存有凝胶结构,当外加应力大于 τy时,凝胶崩溃,流动行为与牛顿流体相似。
05
提高熔体的流动性。
1.3 聚合物的流变学性质
温度及压力对聚合物熔体粘度的影响
——聚合物大分子的热运动有赖于温度。
与分子热运动有关的熔体流动必然与温度有关。
——在聚合物注射成型过程中,温度对熔体粘
度的影响与剪切速率同等重要。
温度升高——
大分子间的自由空间随之增大,分子间作用力
减小,分子运动变得容易,从而有利于大分子的
01
这时,大分子链段的运动相对减少,分子间的
02
相互作用力(范德华力)逐渐减弱,熔体内的自由
03
空间增加,从而导致相对运动加大,宏观上体现
04
为表观粘度相对降低。
05
——注射成型中,多数聚合物的表观粘度对熔
06
体内部的剪切速率具有敏感性,可以通过调整剪
07
切速率来控制聚合物的熔体粘度。
08
在注射成型中,聚合物熔体发生剪切稀化效应
率区域时,流体变形和流动所需的切应力随剪切
速率而变化,并呈指数规律增大;
流体的表观粘度也随剪切速率而变化,呈指数
规律减小。
假塑性液体的“剪切稀化”的原因:
聚合物具有大分子结构,当熔体进行假塑性流
动时,剪切速率的增大,使熔体所受的切应力加
大,从而导致聚合物大分子结构伸长、解缠和滑
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
聚合物流变学的学习与心得体会通过一学期的聚合物流变学的学习,使我对其有了初步的了解。
现在针对平时学习笔记和课后浏览相关书籍所获知识进行总结。
一、聚合物流变学学习内容1. 流变学中的基本概念流变学是研究材料的流动和变形规律的科学,是一门介于力学、化学、物理与工程科学之间的新兴交叉学科。
聚合物随其分子结构、分子量的不同,以及所处温度的不同,可以是流体或固体,它们的流动和变形规律各不相同,也即有不同的流变性能。
聚合物流变学是研究聚合物及其熔体的变形和流动特性。
1.1 粘弹性流体特性及材料流变学分类粘性流体的流动是:变形的时间依赖性;变形不可恢复(外力作的功转化为热能);变形大,力与变形速率成正比,符合Newton's流动定律。
根据经典流体力学理论,不可压缩理想流体的流动为纯粘性流动,在很小的剪切应力作用下流动立即发生,外力释去后,流动立即停止,但粘性形变不可恢复。
切变速率不大时,切应力与切边速率呈线性关系,遵循牛顿粘性定律,且应力与应变本身无关。
流体→流动→粘性→耗散能量→产生永久变形→无记忆效应根据经典固体力学理论,在极限应力范围内,各向同性的理想弹性固体的形变为瞬时间发生的可逆形变。
应力与应变呈线性关系,服从胡克弹性定律,且应力与应变速率无关。
固体→变形→弹性→储存能量→变形可以恢复聚合物流动时所表现的粘弹性,即有粘性流动又有弹性变形,与通常所说的理想固体的弹性和理想液体的粘性大不相同,也不是二者的简单组合。
材料流变学分类⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧==⎩⎨⎧⋅=⋅=⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧==∞=⎩⎨⎧⋅=⋅=)),,(()),,((.3.2())((.1)),,(.30,(.2))((.1t f t f t f G G G G E γγσγγσγησγγησγγσγγγσγσ&&&&&非线性线性粘弹性流体无粘性牛顿流体)线性非线性粘性流体流体非线性线性(粘弹性固体)刚体非线性)为常数、线性(弹性固体固体 其中非牛顿流体⎩⎨⎧粘弹性流体广义牛顿流体非牛顿流体 基本变形方式:拉伸(压缩)、剪切、膨胀。
1.2 高分子流体的粘弹性(1)即有粘性流动又有弹性变形,粘弹性流体的流动是一种有可恢复形变的流动,具有流体和固体的双重性质。
(2)应力(应变)取决于应变(应力)历史,而不是应变(应力)的瞬时值。
即应力(应变)相应具有时间依赖性。
(3)流动过程中表现出的粘弹性偏离胡克定律和牛顿定律,模量和粘度强烈的依赖于应变(应变速率),应力与应变(速率)之间呈现非线性关系。
1.3 流变学力学基础聚合物流动时,其内部的应力状态十分复杂,既存在剪切应力,还存在法向应力,各个不同方向上的应力值不等。
为了正确的研究聚合物的非线性粘弹性行为,借助于线性理论的概念进行讨论,定义流变学研究中的基本物理量:应力张量、偏应力张量、形变张量、形变率张量、速度梯度张量,以及基本流变学函数:剪切粘度,第一、二法向应力差函数,拉伸粘度等。
(1)应力和应力张量物体在外力或外力矩作用下会产生流动或形变,同时为抵抗流动或形变,物体内部产生相应的应力。
牛顿流体的应力状态比较简单,但是聚合物流动过程中既有粘性形变,又有弹性形变,其内部应力状态相当复杂,要全面描述非牛顿流体内部的粘弹性应力及其形变,则需要引入应力张量。
剪切应力的物理实质是粘滞力或内摩擦力,法向力的物理实质是弹性力(拉力或压力),于是应力张量可以完整的描述粘弹性物体在流变过程中的复杂内应力状态。
应力张量一般表达式:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=zz zy zx yz yy yx xz xy xx ij σσσσσσσσσσ(2)偏应力张量根据力的性质不同,应力张量可以分解表示。
其中最常见的一种分解形式如下:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-+-+-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=)](2[31)](2[31)](2[31100010001yy xx zz zy zx yz zz xx yy yx xz xy zz yy xx m ij σσσσσσσσσσσσσσσσσ =ij ij ij ij m p τδτδσ+-=+式中:ij τ称偏应力张量,P 为各向同性压力。
处在任何状态下的流体内部都具有各向同性压力。
由此表明,应力张量可以分解为各向同性压力和偏应力张量两部分。
偏应力张量是应力张量中最重要的部分,直接关系到物体流动和形变。
与应力张量相似,偏应力张量σ也是对称张量,只有六个独立分量。
三个为法向应力分量:ii σ(i =1,2,3),三个为剪切应力分量:1221σσ=,1331σσ= ,2332σσ= 。
偏应力张量中法向分量ii σ的绝对值并无很大意义,重要的是沿不同方向的法向应力分量的差值,它们对于描述非牛顿流体的弹性行为十分重要。
定义两个法向应力差函数来描写材料弹性形变行为:第一法向应力差: 11122N σσ=-第二法向应力差: 22233N σσ=-N 1、N 2加上粘度函数,用此三个函数就可以完整描写简单剪切流场中高分子流体的应力状态和粘弹性。
(3)形变和形变张量形变是物体在平衡外力或外力矩作用下发生形状和尺寸的变化。
实际物体的形变往往是这些简单形变的复杂组合。
高分子液体流动中发生的主要形变方式有剪切、拉伸、压缩及其组合。
设在t 1, t 2时刻物体分别占有空间位形1、位形2。
在t 1时刻物体内的任一线元dX ,在t 2时刻占据的空间位置变为dx ,则定义t 1, t 2时刻间,物体内发生的形变梯度为:x F X∂=∂ F 称形变梯度张量,这是一个二阶张量。
用分量式展开来写,记为:111123222123333123,(,1,2,3)i ij j x x x X X X x x x x F i j X X X X x x x X X X ⎡⎤∂∂∂⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂∂===⎢⎥∂∂∂∂⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎣⎦ 从应力张量的性质看,应力张量和偏应力张量都是对称张量,由此可见与其相对应的形变度量也应该是对称张量。
形变张量分为Cauchy-Green 形变张量和Finger 形变张量。
Cauchy-Green 形变张量,定义为 T C F F =⋅,式中T F 为F 的转置张量 ,()T ij ji F F =。
Finger 形变张量,定义为 11111()()T T C F F F F -----=⋅=⋅式中1F -为F 的逆张量。
当x F X ∂=∂,有11,X F F F I x--∂==∂g 。
另外上式中还利用了张量的性质:11()()T T F F --=。
(4)速度梯度,形变率张量流动过程中,与流体应力状态相关的更重要物理量是形变进行的速率,它与流动场中的速度梯度密切相关。
设在某瞬时位形,流体内的流动速度场为v ,则定义速度梯度张量如下:v L x∂=∂ 速度梯度张量L 可以分解成一个对称张量与一个反对称张量之和。
1()2T d L L =+, 1()2T L L ω=-, 其中d 为对称张量,称为形变率张量,表征材料形变的速率。
ω为反对称张量,称为旋转速率张量,与材料形变无关。
(4)表观剪切粘度Newton 流体流动时所受的剪切应力与剪切速率呈简单线性关系。
但是聚合物流体的流动行为比较复杂。
剪切应力与剪切速率不能始终成线性比例。
定义()()a σγηγγ=&&&为聚合物流体的表观剪切粘度。
在一定温度下,若剪应力没有时间依赖性,a η主要是剪切速率γ&的函数。
(5)第一、第二法向应力差函数高分子液体在剪切流场中,除表现有粘性外,还表现出奇异的弹性行为,存在法向应力差效应。
在简单剪切流场中,当规定流速方向为第一坐标轴方向,速度梯度方向为第二坐标轴方向,中性方向为第三坐标轴方向,则根据第一、第二法向应力差函数N 1、N 2 。
定义 ()211122122N σσψγγγ-==&&& ,()222332222N σσψγγγ-==&&&为第一、第二法向应力差系数。
聚合物第一法向应力差系数1ψ随剪切速率的变化规律与表观粘度曲线相似。
剪切速率很小时,1ψ也趋向一恒定值;当剪切速率增大时,第一法向应力差系数1ψ随剪切速率增大而减小。
2. 聚合物流变学中的本构方程本构方程又称状态方程是描述一大类材料所遵循的与材料结构属性相关的力学响应规律的方程。
从形式上分,非线性粘弹流体的本构方程主要分为两大类:微商型本构方程和积分型本构方程。
(1)经典的线性粘弹性模型—Maxwell 模型Maxwell 模型由一个虎克型弹簧和一个牛顿型粘壶串联而成,描述流体的线性粘弹性质。
图1 弹簧粘壶串联模型,/,/021ησγσγ==G ;21γγγ+=,//021ησσγγγ+=+=G &&&& ,0γησλσ&&=+其中 松弛时间)(/0G ηλ= t∂∂=σσ& 蠕变过程 0)()(0==t t σσσ& 000000000///)0()(ησσησγγγησγησt G t t d dt +=+==⋅=& 蠕变柔量 00//1/)()(ησγt G t t J +==松弛过程 λσσσλσγγγ/00)(00)()(t e t t t -==+==&& 松弛模量 λλγσγσ//000/)()(t t Ge e t t G -===(2)V oigt(kelvin)模型 V oigt 模型由一个虎克型弹簧和一个牛顿型粘壶并联而成,描述固体的线性粘弹性质。
图2 弹簧粘壶并联模型202112121γησγσγγγσσσ⋅=⋅=+=+=G)(/00推弛时间G G ητσγηγ==+&000)(σγηγσσ=+=dtd G t 从t=0时,0=γ积分, )1)(()1()(//0ττγσγt te e G t ---∞=-=蠕变柔量 )1()1(1/)()(/0/0ττσγt t e J e Gt t J ---=-== (3)Boltzmann 叠加原理 Boltzmann 叠加原理是对于时间序列中一系列阶跃应变(或应力)的输入。
应变(应力)史是各个独立的应力(应变)史产生的应变(应力)史线性加和。
⎪⎩⎪⎨⎧+=2110σσσσt 1100θθ≥≤≤<t t t)()()()()()()()(1212121θσσγγγσσσ-+=+=+=t J t J t t t t t t 3. 输运过程的基本方程及基本流动形式(1)连续性方程—质量守恒定律:()0v tρρ∂+∇=∂g 此公式称连续性方程的微分型式。
对于任何一种稳定流动,有0tρ∂=∂,得到 ()0v ρ∇=g 对于不可压缩流体的稳定流动,进一步有:0v ∇=g在直角座标系中,0v ∇=g 式的显式表示为:0y x z x y zυυυ∂∂∂++=∂∂∂ 这是不可压缩流体稳定流动的连续性方程。
