四年级奥数 第7讲 最有问题
7-8.四年级奥数 年龄问题

四年级秋季尖子班第七讲年龄问题(一)年龄问题,就是知道两人的年龄关系,求两人的年龄,或知道两人的年龄,求两人年龄之间的关系。
年龄问题有自己独特的解题思路和方法,同学们在思考和解答这类题目时可以从以下几个方面去考虑:1.两人的岁数无论怎样变化,其年龄差始终不变(定差)。
2.定差的两量,随着年份的变化,倍数关系也发生变化。
3.解题时,依据年龄之间的倍数关系,参照年龄差(和),画出线段图,可以更好地帮助我们理解题中的数量关系。
典例精讲例1 奶奶今年57岁,孙子今年5岁,再过多少年,奶奶的年龄是孙子的5倍?【思路点拨】不管是今年还是几年后,奶奶的年龄始终比孙子大57-5=52(岁)。
几年后奶奶的年龄是孙子的5倍,也就是奶奶的年龄比孙子5倍,如下图:【详细解答】例2 父亲今年比儿子大32岁,2年后父亲的年龄是儿子的5倍。
今年儿子多少岁?【思路点拨】画图分析:2年后,父子之间的年龄差没有变化。
如果将2年后儿子的年龄看作1份的量,则父亲的年龄比儿子多(5-1)份的量,是32岁,由此可求出2年后儿子的年龄,进而求出今年儿子的年龄。
【详细解答】例3 王亮5年前的年龄等于小丽7年后的年龄,王亮4年后与小丽3年前的年龄和是45岁。
问:王亮、小丽两人今年各多少岁?【思路点拨】根据题意可知,王亮比小丽大5+7=12(岁),今年他们两人的年龄和是45+3-4=44(岁)。
由和差问题的解法,可求出王亮今年的年龄,再求小丽今年的年龄。
【详细解答】达标练习1.今年叔叔40岁,丽丽12岁,再过多少年,叔叔的年龄是丽丽的3倍?2.兰兰今年10岁,奶奶比兰兰大60岁,再过多少年,奶奶的年龄是兰兰的5倍?3.今年强强12岁,叔叔的年龄是强强的3倍,再过多少年,叔叔的年龄是强强的2倍?4.母亲今年比儿子大28岁,4年后母亲的年龄是儿子的5倍。
今年儿子多少岁?5.今年妈妈比儿子大30岁,3年后妈妈的年龄是儿子的3倍。
今年妈妈多少岁?6.强强今年10岁,2年后爷爷的年龄是强强的6倍。
四年级奥数之最值问题

【课前小练习】
本讲主线 1. 最值中的三个常用方法 2. 两数和一定,差小积大
数字和是6的无重复数字 的多位数中,最大的是 多少?
1. 整体思想:比如,比较大小先看位数,再由高到底比较位置. 2. 局部调整思想 3. 平均分配思想 【例1】(★★) 电视台要播放一部30集的电视连续剧,如果要求每天播放的集数互不 相等 该电视剧最多可以播放几天? 相等,该电视剧最多可以播放几天?
1
4. 两数和一定,差越小乘积越大. 例如,a+b=10,那么,a×b最大等于____. 例如,一根绳子长度是20米,那么这根绳子围城的 , ,那 长方形,长和宽分别是多少的时候,长方形的面积 最大?
知识要点屋
a b
【例5】(★★★★) 如图,一个长方形被分成 4 个小长方形,其中长方形A、B、大 是___平方厘米.
【例4】(★★★) 牧羊人用15段,每段长2米的篱笆,一面靠墙围成一个长方形羊圈,则 羊圈 最 羊圈的最大面积是多少平方米? 多少平 米
最值问题 1. 整体方法,局部调整方法,平均数方法. 2. 两数和一定,差越小乘积越大. (1) 固定长度的绳子,围成正方形面积最大; (2) ( ) 当和不确定时,凑算式,使和变为一个定值. 和 确 时, 算式,使和变 个 值 【今日讲题】 例2 例3 例4 例2,例3,例4 【讲题心得】
知识大总结
a b
答案
墙
【课前小练习】①531, 47 ② 222 【例1】 7 【例2】 19, 517 【例3】 55, 15, 1, 5 【例4】 112 【例5】16
_____________________________________________________________。
学而思奥数2016秋季班提高班第7讲讲义

6 6 7 7 7 7 86436; (2)多拆 3,少拆 2,不拆 1: 20 3 6 2,3 3 3 3 3 3 2 1458 .
四年级秋季尖子班第 7 讲 最值问题初步
例1 电视台要播放一部 30 集电视连续剧. 如果要求每天安排播出的集数互不相 等,不能不播,该电视连续剧最多可 以播几天? 【答案】7 【分析】由于 1 2 3 4 5 6 7 28 30 , 1 2 3 4 5 6 7 8 36 30,所以 至多播 7 天.
形(小棍不能折断),这个长方形的面
积最大是多少?如果用 98 根呢?
【答案】169;600
【分析】 (1)长与宽的和一定,和为52 2 26 厘米,26 13 13,所以面积最大为 13 13 169平方厘米; (2)长与宽的和一定,和为98 2 49 厘米,49 24 25,所以面积最大为 24 25 600平方厘米.
次,分别组成两个三位数,这两个三 位数的乘积最小是多少? 【答案】54243 【分析】使乘积最小,首位 1、3,十 位 4、6,个位 7、9,和一定差大积小, 所以乘积最小为147 369 54243.
作业 5 (1)把 31 拆成三个互不相同的自然 数的和,使这些自然数的乘积最大, 最大乘积是多少? (2)把 31 拆成若干个可重复自然数 的和,使这些自然数的乘积最大,最
4.5123 4876 247 首先千位要接近,而千位大的数后边 的三位数尽量小,千位小的数后边的 三位数尽量大,才能减出最小的差, 所以后三位最好分别为 876 和 123, 5123 4876 247.
5.82
其余 4 人共得 334 分, 334 4 83 2 .所以得分依次为 85, 84,83,82.
小学奥数:第7讲四年级数学火车过桥问题教案
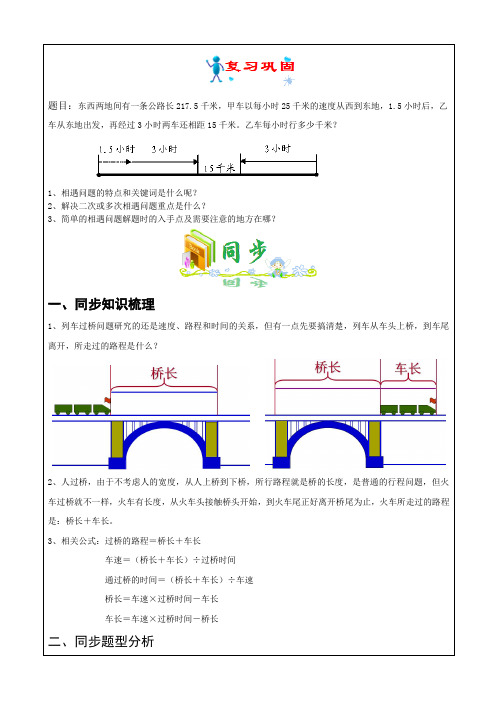
题目:东西两地间有一条公路长217.5千米,甲车以每小时25千米的速度从西到东地,1.5小时后,乙车从东地出发,再经过3小时两车还相距15千米。
乙车每小时行多少千米?1、相遇问题的特点和关键词是什么呢?2、解决二次或多次相遇问题重点是什么?3、简单的相遇问题解题时的入手点及需要注意的地方在哪?一、同步知识梳理1、列车过桥问题研究的还是速度、路程和时间的关系,但有一点先要搞清楚,列车从车头上桥,到车尾离开,所走过的路程是什么?2、人过桥,由于不考虑人的宽度,从人上桥到下桥,所行路程就是桥的长度,是普通的行程问题,但火车过桥就不一样,火车有长度,从火车头接触桥头开始,到火车尾正好离开桥尾为止,火车所走过的路程是:桥长+车长。
3、相关公式:过桥的路程=桥长+车长车速=(桥长+车长)÷过桥时间通过桥的时间=(桥长+车长)÷车速桥长=车速×过桥时间-车长车长=车速×过桥时间-桥长二、同步题型分析题型1、求时间例:一列火车长180米,每秒行20米,这列火车通过320米长的大桥需要多长时间?分析:根据路程÷速度=时间,可以求出列车通过桥梁时用的时间。
列车完全通过桥梁一共走的路程是桥长+车长:180+320=500(米),列车通过这座桥梁要500÷20=25(秒)。
题型2、求速度例1:一列长300米的列车,完全通过一座长450米的桥梁,一共用了2分钟。
这列火车过桥时每分钟行多少米?分析:列车完全通过一座桥梁,行的路程是桥长+车长。
火车完全通过桥梁一共走的路程是300+450=750(米),这列火车过桥时每分钟行750÷2=375(米)。
例2:一列火车通过一座长500米的桥梁用了40秒,用同样的速度通过另一座600米的桥梁用了45秒。
这列火车过桥时每秒钟行多少米?列车通过第一座桥梁:行的路程是500米+车长 40秒列车通过第二座桥梁:行的路程是600米+车长 45秒这列火车(45-40)秒钟行的路程是(600-500)米。
四年级下册数学试题-奥数专题讲练:第七讲 应用问题综合强化 竞赛篇(解析版)全国通用

第七讲应用问题综合强化编写说明本讲将要分成:和差倍分问题、年龄问题和盈亏问题三个方面进行讲解.这三个方面按照小学奥数的一般进度,都在四年级上半期的前半期进行系统学习,我们在此讲解的目的主要是帮助孩子“温故”,防止他们遗忘,同时帮助之前没有学习过奥数的同学把这部分知识补习上!教师根据本班孩子学习接受的情况,进行适当的基础知识讲解.内容概述从三年级到最后的小升初、分班考试中,很多学生都会问学了那么多专题(行程问题、年龄问题,植树问题,鸡兔同笼,盈亏问题,牛吃草问题等等),到底应该怎么去记忆和具体解答呢,这也是许多听课的家长所迷惑的问题.其实这所有的专题都不是平行的,也就是划分标准不同,一般是按照三类来划分:第一:按照题目内容,行程问题、年龄问题、时钟问题等;第二:按照题目本质,和差倍分问题、盈亏问题、鸡兔同笼等,涉及的是思想,可以变成第一类的任何一种问题;第三:按照解题思想,从反面考虑问题、还原问题等.本讲是对原来学过和差倍分、年龄、盈亏问题进行总结强化,同时帮助你不断回顾已有知识,更加深刻体会做题的思路方法!和差倍分问题【例1】有5堆苹果.较小的3堆平均有18个苹果.较大的2堆,苹果数之差为5个.又较大的3堆平均有26个苹果,较小的2堆苹果数之差为7个.最大堆与最小堆平均有22个苹果.问:每堆各有多少个苹果?分析:最大堆与最小堆共22×2=44个苹果.较大的2堆与较小的2堆共44×2+7-5=90个苹果.所以中间的一堆有:(18×3+26×3—90)÷2=21个苹果;较大的2堆有:26×3—21=57个苹果;最大的一堆有:(57十5)÷2=31个苹果;次大的2堆有:57—31=26个苹果;较小的2堆有:18×3—21=33个苹果;次小的一堆有:(33+7)÷2=20个苹果;最小的一堆有:20—7=13个苹果.【前铺】小明、小红、小玲共有73块糖.如果小玲吃掉3块,那么小红与小玲的糖就一样多;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍.问小红有多少块糖?分析:如果小玲吃掉3块,那么小红与小玲的糖就一样多,说明小玲比小红多3块;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍,即小明加2是小红减2后的2倍,说明小明是小红的2倍少6(2×2+2).小红的颗数=(73-3+6)÷(1+1+2)=19块.【例2】某项竞赛分一等奖、二等奖和三等奖,每个一等奖的奖金是每个二等奖奖金的2倍,每个二等奖的奖金是每个三等奖奖金的2倍. 如果评出一、二、三等奖各2人,那么每个一等奖的奖金是308元.如果评出1个一等奖,2个二等奖,3个三等奖,那么一等奖的奖金是多少元?分析:我们把每个三等奖奖金看作1份,那么每个二等奖奖金是2份,每个一等奖奖金则是4份.当一、二、三等奖各评2人时,2个一等奖的奖金是(308×2)元,2个二等奖的奖金等于1个一等奖的奖金308元,2个三等奖的奖金等于1个二等奖奖金(308÷2)元.所以奖金总数是:(308×2+308+308÷2)元.当评1个一等奖,2个二等奖,3个三等奖时,1个一等奖奖金看做4份,2个二等奖奖金2×2=4(份),3个三等奖奖金的份数是1×3=3(份),总份数就是:4+4+3=1l(份).这样,可以求出1份数为98元,一等奖的奖金:98×4=392(元).【例3】有8只盒子,每只盒内放有同一种笔.8只盒子所装笔的支数分别为17支、23支、33支、36支、38支、42支、49支、51支.在这些笔中,圆珠笔的支数是钢笔支数的2倍,钢笔支数是铅笔支数的13,只有一只盒里放的是水彩笔.这盒水彩笔共有多少支?分析:铅笔数是钢笔的3倍,圆珠笔数是钢笔的2倍,因此这三种笔支数的和是钢笔数的6(=l+3+2)倍.17+23+33+36+38+42+49+5l 除以6余l,所以水彩笔的支数除以6余l,在上述8盒的支数中,只有49除以6余1,因此水彩笔共有49支.【前铺】盒中有黄、红、蓝三种颜色的棋子共66粒,其中黄色棋子数是红色棋子数的4倍,蓝色棋子数的2倍等于黄色棋子数的3倍.这个盒中三种颜色的棋子各有多少粒?分析:把红棋子数看作1份,则黄棋子为4份,蓝棋子为6份,红、黄、蓝棋子数分别为:6、24、36粒.【例4】有长短两支蜡烛(两支蜡烛同样时间燃烧的长度相同),它们的长度之和为56厘米.将它们同时点燃一段时间后,长蜡烛同短蜡烛点燃之前一样长,这时短蜡烛的长度又恰好是长蜡烛的23.点燃前,长蜡烛有多长?分析:我们要注意发掘题目中真正的不变量,实际上这个题目中两根蜡烛的长度差是不变的.(为什么?由于两根蜡烛燃烧的速度一样).把原来短蜡烛的长度看作3份,那么后来长蜡烛的长度也为3份,后来短蜡烛的长度为2份,差值为1份,那么原来长蜡烛长度为4份,所以1份为56÷(4+3)=8(厘米),原来长蜡烛为4×8=32(厘米).【前铺】某日停电,房间里燃起了长短两根蜡烛,它们燃烧速度是—样的.开始时长蜡烛是短蜡烛长度的2倍,当送电后吹灭蜡烛,发现此时长蜡烛是短蜡烛长度的3倍.短蜡烛燃烧掉的长度是5厘米.问原来两根蜡烛各有多长?分析:我们要注意发掘题目中真正的不变量,实际上这个题目中两根蜡烛的长度差是不变的.(为什么?由于两根蜡烛燃烧的速度一样).那么我们根据题意可知:原长蜡烛长度=2倍原短蜡烛长度,差为1倍原短蜡烛长度;后长蜡烛长度=3倍后短蜡烛长度,差为2倍后短蜡烛长度;所以原短蜡烛长度=2倍后短蜡烛长度,也就是说短蜡烛燃烧了1倍后短蜡烛长度,为5厘米,所以原短蜡烛长10厘米,原长蜡烛长20厘米.【巩固】某日停电,房间里同时点燃了两支同样长的蜡烛.这两支蜡烛的质量不同,一支可以维持3小时,另一支可以维持5小时,当送电时吹灭蜡烛,发现其中一支剩下的长度是另一支剩下长度的3倍.这次停电时间是多少小时?分析:设停电x小时,可得:1113(1)53x x-=⨯-,解得:x=2.5(小时).【例5】有三堆棋子每堆棋子一样多并且都只有黑白两色棋子.已知第一堆里的黑子和第二堆里的白子一样多,第三堆里的黑子占到三堆棋子里黑子总数的25,如果把三堆棋子集中到一起,那么白子占全部棋子的几分之几?分析:第一堆里的黑子和第二堆里的白子一样多,那么我们不妨把第一堆里的黑子与第二堆里的白子调换一下,那么第一堆全白子,第二堆全黑子,且每堆总数不变.因为第三堆里的黑子占到三堆棋子里黑子总数的25,我们不妨把第三堆里的黑棋子看作2份,那么剩下的3份都是第二堆的黑子,所以每堆都是三份,白子共(1+3)份,白子占全部棋子的9分之4.【例6】有一个分数,如果分子减1,那么这个分数就变成13;如果分母减少1,那么这个分数变成12.那么这个分数是多少?分析:把分母看成一个3倍量,那么分子就是1倍量+1,根据:如果分母减少1,那么这个分数变成12,那么分母就是:(2倍量+2)+1=2倍量+3,所以1倍量代表3,所以分数为:4 9 .【例7】一批工人到甲乙两个工地进行清理工作,甲工地的工作量是乙工地的工作量的3 2 .每天分成上午和下午两段,每人在上午和下午所完成的工作量相等,上午去甲工地的人数是去乙工地人数的3倍;下午这批工人中有712的人去甲工地,其他的人到乙工地.到晚上时,甲工地的工作已完成,乙工地的工作还需要4名工人再做1天.那么这批工人有多少名?分析: 我们定义一个单位量:一个单位工人工作半天所完成的工作量称作1个单位量.假设一共有12单位个工人,那么上午分成4份,每一份有3个.去甲工地的工人是3份9个,完成的工作量是9个单位;去乙工地的工人是1份,3个单位.因此乙工地完成的工作量是3个.下午是这样子的:712的人去甲工地,其他的人到乙工地.所以去甲工地的人有12×712=7个单位,完成了7个单位工作量,乙工地完成的工作量是(12—7)=5个.这样一天和起来:甲工地完成了(9+7)=16个工作量,乙工地完成了(5+3)=8个工作量.甲工地的工作量全部完成了,所以甲工地的任务工作量是16个.甲工地的工作量是乙工地的工作量的32,所以乙工地的任务工作量是16÷3×2=323个.乙工地完成了8个工作量,这样乙工地剩下的工作量是(323-8)=83个工作量,这83个工作量需要4个人工作1天也就是需要8个人工作半天.而83是83个单位的工人作半天完成的工作量,因此83个单位的工人有8个.所以1个单位的工人有8÷83=3(个).这批工人一共是12个单位,所以一共有工人:3×12=36(个).年龄问题年龄问题是小学数学中常见的一类问题.例如:已知两个人或若干个人的年龄,求他们年龄之间的某种数量关系等等.年龄问题又往往是和倍、差倍、和差等问题的综合.它有一定的难度,因此解题时需抓住其特点.年龄问题变化关系的三个基本规律:1、两人年龄的差是不变的量;2、两人年龄的倍数关系是变化的量;3、每个人的年龄随着时间的增加都增加相等的量.年龄问题的解题要点是:1、入手:分析题意从表示年龄间倍数关系的条件入手理解数量关系.2、关键:抓住“年龄差”不变.3、解法:应用“差倍”、“和倍”或“和差”问题数量关系式.年龄问题的解题正确率保证:验算!【例8】女儿今年(2007年)12岁,妈妈对女儿说:“当你有我这么大岁数时,我已经60岁喽!”问:妈妈12岁时,是哪一年?分析:画线段图分析.母女年龄的差是(60-12)÷2=24,2007-24=1983(年).【巩固】(第一届祖冲之杯数学邀请赛) 甲对乙说:“当我的岁数是你现在的岁数时,你才5岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将50岁.”那么,甲现在( )岁,乙现在( )岁.分析:画图分析.年龄差=(50-5)÷3=15,乙现在的岁数为:15+5=20(岁),甲现在的岁数为:20+15=35(岁).【前铺】兄弟二人的年龄相差5岁,兄3年后的年龄为弟4年前的3倍.问:兄、弟二人今年各多少岁?分析:根据题意,作示意图如右:由上图可以看出,兄3年后的年龄比弟4年前的年龄大5+3+4=12(岁),由“差倍问题”解得,弟4年前的年龄为(5+3+4)÷(3-1)=6(岁). 由此得到,弟今年6+4=10(岁),兄今年10+5=15(岁).【前铺】今年爷爷78岁,三个孙子的年龄分别为27、23、16岁.经过多少年后爷爷的年龄等于三个孙子年龄和?分析:三个孙子的年龄和是:27+23+16=66(岁),跟爷爷年龄差等于12岁,过一年两者的年龄差减少2岁,所以6年后爷爷的年龄等于三个孙子年龄和.【拓展】已知祖孙三人,祖父和父亲年龄的差与父亲和孙子年龄的差相同,祖父和孙子年龄之和为82岁,明年祖父年龄恰好等于孙子年龄的5倍.求祖孙三人各多少岁?分析:“祖父和父亲年龄差与父亲和孙子年龄的差相同”这一条件较难理解,可作出示意图,从图中容易看出,祖父和孙子年龄之和恰为父亲年龄的2倍.父亲的年龄:82÷2=41(岁) ,孙子的年龄:(82+1×2)÷(1+5)-1=13(岁),祖父的年龄:82-13=69(岁).【例9】五位老人的年龄互不相同,其中年龄最大的比年龄最小的大6岁,已知他们的平均年龄为85岁,其中年龄最大的一位老人是谁?分析:如果最小的比85只小一岁,那么由于这时其他人的年龄均不小于85,而最大的比85大5(=6-1)岁,这样平均年龄必超过85;如果最小的比85小2,那么可能还有一人比85小1,但最大的比85大4(=6-2)岁,而4>1+2,从而是年龄仍超过85;如果最小的比85小3,那么最大的比85大3(=6-3),两人的平均年龄正好是85,其他三人如果年龄是84、85、86(或83、85、87)那么五人平均年龄正好是85;如果最小的比85小4或小5,这时平均年龄必小于85(与开始两种情况的推理类似,只是将大、小互易)因此,最大的年龄一定是88(=85+3)岁. 【例10】梁老师问陈老师有多少子女,她说:“现在我和爱人的年龄和是子女年龄和的6倍;两年前,我们的年龄和是子女年龄和的10倍;六年后,我们的年龄和是子女年龄和的3倍。
高思奥数导引小学四年级含详解答案第7讲 直线形计算.

第7讲直线形计算一兴趣篇1、如图,由十六个同样大小的正方形组成一个“5”字。
如果这个图形的周长是102厘米,那么它的面积是多少平方厘米?2、如图,用两块长方形纸片和一块小正方形纸片拼成了一个大正方形纸片,其中小正方形纸片面积是49平方厘米,其中一个长方形纸片的面积为28平方厘米,那么最后拼成的大正方形纸片面积是多少平方厘米?3、如图,小、中、大三个正方形从左到右依次紧挨着摆放,边长分别是3、7、9。
图中两个阴影平行四边形的面积分别是多少?4、如图,从梯形ABCD中分出两个平行四边形ABEF和CDFG。
其中ABEF的面积等于60平方米,且AF的长度为10米,FD的长度为4米。
平行四边形CDFG的面积等于多少平方米?5、如图,把大、小两个正方形拼在一起,它们的边长分别是8厘米和6厘米,那么左图和右图中阴影部分的面积分别是多少平方厘米?6、如图,在正方形ABCD中,对角线AC的长度为8厘米,那么正方形的面积是多少平方厘米?7、如图,平行四边形ABCD中,AD的长度为20厘米,高CH的长度为9厘米;E是底边BC上的一点,且BE长6厘米,那么两个阴影三角形的面积之和是多少平方厘米?8、图中,平行四边形ABCD的面积是32平方厘米,三角形CED是一个直角三角形。
已知AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?9、如图,在平行四边形ABCD中,三角形BCE的面积是42平方厘米,BC的长度为14厘米,AE的长度为9厘米,那么平行四边形ABCD的面积是多少平方厘米?三角形BCE的面积又是多少平方厘米?10、如图,小正方形ABCD放在大正方形EFGH的上面。
已知小正方形的边长为4厘米,且梯形AEHD的面积是28平方厘米,那么梯形AFGD的面积多少平方厘米?拓展篇1、如图,有一块长方形田地被分成了五小块,分别栽种了茄子、黄瓜、豆角、莴笋和苦瓜。
其中栽种茄子的面积是16平方米,栽种黄瓜的面积是28平方米,栽种豆角的面积是32平方米,栽种莴笋的面积是72平方米,而且左上角栽种茄子的田地恰好是一个正方形。
四年级奥数教程

小学奥数基础教程(四年级)第1讲速算及巧算(一)第2讲速算及巧算(二)第3讲高斯求和第4讲 4,8,9整除的数的特征第5讲弃九法第6讲数的整除性(二)第7讲找规律(一)第8讲找规律(二)第9讲数字谜(一)第10讲数字谜(二)第11讲归一问题及归总问题第12讲年龄问题第13讲鸡兔同笼问题及假设法第14讲盈亏问题及比较法(一)第15讲盈亏问题及比较法(二)第16讲数阵图(一)第17讲数阵图(二)第18讲数阵图(三)第19将乘法原理第20讲加法原理(一)第21讲加法原理(二)第22讲还原问题(一)第23讲还原问题(二)第24讲页码问题第25讲智取火柴第26讲逻辑问题(一)第27讲逻辑问题(二)第28讲最不利原则第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲速算及巧算(一)计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率、节省计算时间,更可以锻炼记忆力,提高分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算及巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同及同补速算法。
例1 四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86,78,77,83,91,74,92,69,84,75。
求这10名同学的总分。
分析及解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数及80的差如下:6,-2,-3,3,11,-6,12,-11,4,-5,其中“-”号表示这个数比80小。
于是得到总和=80×10+(6-2-3+3+11-=800+9=809。
实际计算时只需口算,将这些数及80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80×10,就可口算出结果为809。
四年级奥数专题第7讲 上楼梯问题

四年级奥数专题第7讲上楼梯问题有这样一道题目:如果每上一层楼梯需要1分钟,那么从一层上到四层需要多少分钟?如果你的答案是4分钟,那么你就错了.正确的答案应该是3分钟。
为什么是3分钟而不是4分钟呢?原来从一层上到四层,只要上三层楼梯,而不是四层楼梯。
下面我们来看几个类似的问题。
例1 裁缝有一段16米长的呢子,每天剪去2米,第几天剪去最后一段?例2 一根木料在24秒内被切成了4段,用同样的速度切成5段,需要多少秒?例3 三年级同学120人排成4路纵队,也就是4个人一排,排成了许多排,现在知道每相邻两排之间相隔1米,这支队伍长多少米?例4 时钟4点钟敲4下,12秒钟敲完,那么6点钟敲6下,几秒钟敲完?例5.某人要到一座高层楼的第8层办事,不巧停电,电梯停开,如从1层走到4层需要48秒,请问以同样的速度走到八层,还需要多少秒?例6 晶晶上楼,从1楼走到3楼需要走36级台阶,如果各层楼之间的台阶数相同,那么晶晶从第1层走到第6层需要走多少级台阶?习题1.一根木料截成3段要6分钟,如果每截一次的时间相等,那么截7段要几分钟?2.有一幢楼房高17层,相邻两层之间都有17级台阶,某人从1层走到11层,一共要登多少级台阶?3.从1楼走到4楼共要走48级台阶,如果每上一层楼的台阶数都相同,那么从1楼到6楼共要走多少级台阶?4.一座楼房每上1层要走16级台阶,到小英家要走64级台阶,小英家住在几楼?5.一列火车共20节,每节长5米,每两节之间相距1米,这列火车以每分钟20米的速度通过81米长的隧道,需要几分钟?6.时钟3点钟敲3下,6秒钟敲完,12点钟敲12下,几秒钟敲完?7.某人到高层建筑的10层去,他从1层走到5层用了100秒,如果用同样的速度走到10层,还需要多少秒?8.A、B二人比赛爬楼梯,A跑到4层楼时,B恰好跑到3层楼,照这样计算,A跑到16层楼时,B跑到几层楼?9.铁路旁每隔50米有一根电线杆,某旅客为了计算火车的速度,测量出从第一根电线杆起到经过第37根电线杆共用了2分钟,火车的速度是每秒多少米?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7周最优问题
专题简析:在日常生活中,我们经常会遇到下面类似的问题:完成一件事情怎样合理安排才能做到用时最少、效果最佳。
这类问题在数学中称为统筹问题。
解决此类问题时,必须树立统筹思想,能同时做的事,尽量同时做。
有时,我们还会遇到“费用最省”“面积最大”“损耗最小”等问题。
这些问题往往可以从极端情况去探讨它的最大(小)值。
这些问题在数学中称为极值问题。
统筹问题和极值问题实际上都属于最优问题。
例1:用一只平底锅煎鸡蛋,每次只能放两个,煎一个需2分钟(规定正反面各需要1分钟)。
问煎三个至少需要多少分钟?
练习一:1、烤面包时,第一面要烤2分钟,第二面只要烤1分钟,即烤一片面面包需要3分钟。
小丽用的烤面包机一次只能放两片面包,她每天早上吃三片面包,最少需要烤多少分钟?
2、用一只平底锅烙大饼,锅里只能同时放两张大饼,烙熟大饼的一面需要3分钟,现在要烙三张大饼,最少需要几分钟?
3、小华用平底锅烙饼,这只锅同时能放四张大饼,烙一张要4分钟(每面各需要2分钟),可小华烙六张饼只用了6分钟,他是怎样做的?
例2:妈妈让小明给客人烧水沏茶。
洗水壶需要1分钟,烧开水需要15分钟,洗茶壶需要1分钟,洗茶杯需要1分钟,拿茶叶需要2分钟。
为了使客人早点喝上茶,按照最合理的安排,多少分钟后就能沏茶了?
练习二:1、小虎早晨要完成这样几件事:烧一壶开水需要10分钟,把开水灌进热水瓶需要2分钟,取奶需要5分钟,整理书包需要4分钟。
为了尽快做完这些事情,最少需要几分钟?
2、小强给客人沏茶,烧开水要12分钟,洗茶杯要2分钟,买茶叶要8分钟,放茶叶要1分钟。
为了使客人能早点喝上茶,按照最合理的安排,多少分钟就能沏茶了?
3、在早晨起床后的1小时之内,小欣需要完成以下事情:叠被子3分钟,刷牙洗脸8分钟,读外语30分钟,吃早餐10分钟,收碗擦桌子5分钟,收听广播30分钟。
为了尽快做完这些事,应怎样安排才能使所用的时间最少?最少需要多少分钟?
例3:五(1)班赵明、孙勇、李佳三位同学同时到校卫室等候校医治病,赵明打针需要5分钟,孙勇包纱布需要3分钟上,李佳点眼药水只需要1分钟,卫生室只有一位校医。
问校医如何安排三位同学的治病次序,才能使三位同学留在卫生室的时间总和最短?请你算出这个时间?
练习三:1、甲、乙、丙三人分别拿着2个、3个、1个热水瓶同时到开水供应点打热水。
热水龙头只有一个,怎样安排他们打水的次序,可以使他们打热水所花的总时间(包括等候时间)最少?(假如打满1瓶水需要1分钟)
2、甲、乙、丙三人到商场批发部洽谈业务,甲10分钟就能洽谈完,乙16分钟能洽谈完,丙8分钟能洽谈完。
怎样安排三人谈话的先后次序,使三人所花的总时间最少?最少时间是多少?
3、甲、乙、丙、丁四人同时到1个水龙头处用水,甲洗拖把需要3分钟,乙洗抹布需要2分钟,丙洗衣服需要10分钟,丁用桶接水需要1分钟。
怎样安排四人用水的次序,使他们所花的总时间最少?最少时间是多少?
例4:用长18厘米的铁丝围成各种长方形,要求长和宽的长度都是整数,并比较它们面积的大少。
练习四:1、用长26厘米的铁丝围成各种长方向形,要求长和宽的长度都是整数,那么围成的长方形的面积最大是多少?
2、一个长方形的周长是20分米,它的面种最大是多少?
3、一个长方形的面积是36平方厘米,并且长和宽的长度都是整数。
这个长方形的周长最长是多少厘米?
例5:用3~6这四个数字分别组成两个两位数,使这两个两位数的乘积最大。
练习五:1、用1~4这四个数字分别组成两个两位数,使这两个两位数的乘积最大。
2、用5~8这四个数字分别组成两个两位数,使这两个两位数的乘积最小。
3、用3~8这六个数字分别组成两个三位数,使这两个三位数的乘积最大。
课后练习
1、用一只平底锅做煎饼,每次能同时放两块饼,如果一块饼需要4分钟(正反两面各需2分钟),问前2004块饼至少需要几分钟?
2、妞妞每天早晨要完成这样几件事,烧一壶开水要8分钟,灌开水要1分钟,取牛奶和报纸要5分钟,整理书包要6分钟,为了尽快做完这些事,怎样安排才能使所用的时间最少?最少需要几分钟?
3、家里来了客人,妈妈要给客人沏茶,洗水壶要1分钟,烧开水要10分钟,洗茶杯要2分钟,取茶叶要1分钟,泡茶要2分钟。
为了让客人早点喝上茶,你来设计,如何安排所需时间最少?
4、玲玲帮奶奶下碗面:买面条5分钟,切葱花2分钟,洗锅4分钟,烧开水9分钟,把面条煮熟3分钟。
为了让奶奶尽快吃到面条,你帮玲玲算算最少要多少时间。
5、老师分别要和甲、乙、丙三个人谈话,和甲要谈8分钟,和乙要谈5分钟,和丙要谈6分钟。
甲、乙、丙三位同学同时到办公室,老师应如何安排和他们谈话的次序,使他们三人所花的总时同最少?总时间是多少分钟?
6、丽丽、小红、嘉嘉三人同时到后台准备表演节目,丽丽表演唱歌要7分钟,小红表演小品要12分钟,嘉嘉表演魔术要10分钟。
这时主持人应如何安排他们三人的表演顺序,可以使他们用的总时间最少(包括在后台等候的时间)?共花了多少时间?
提优练习
1、牛牛要赶黑、白、灰、棕色的四匹马过河,黑马过河要4分钟,白马过河要6分钟,灰马过河要3分钟,棕马过河要9分钟,牛牛每次只能赶两匹马过河,再骑其中一匹马返回。
要把四匹马赶到河对岸,应怎样赶时间最少?
2、用34厘米的钢丝围成一个长方形,长和宽的长度都是整厘米数,围成的长方形的面积最大是多少?
3、用一根长14分米的铁丝围成一个长方形,长和宽的长度都是整分米数,围成的长方形的面积最小是多少?
4、若干千个长方形的面积都为48平方厘米,而且长和宽的长度都是整厘米数,周长最短的那个长方形的周长是多少厘米?
5、用1,3,5,7这四个数字分别组成两个两位数,使这两个两位数的乘积最小。
6、用4~9这六个数字分别组成两个三位数,使这两个三位数的乘积最大。
