重庆八中初2017级初三(上)入学考试
重庆八中初2017级1617学年一模考试英语试题

重庆八中2016—2017学年度(下)初三年级第一次全真模拟考试英语试题(本卷共九大题,满分150分,考试时间120分钟)第I卷(共98分)II. 单项选择。
(每小题1分,共18分)从A、B、C、D四个选项中选出可以填入空白处的最佳答案,并把答题卡上对应题目的答案标号涂黑。
21. There will be __________ sports competition between Class 4 and Class 5 tomorrow .A. aB. anC. theD. /22. My best friend and I were born __________ July , and we both like swimming .A. inB. onC. atD. from23. Her son can look after __________ though he is only 7 years old .A. yourselfB. myselfC. himselfD. herself24. --- I didn’t see you at the meeting yesterday . What happened ?--- I __________ a doctor at that time .A. seeB. sawC. am seeingD. was seeing25. On March 8 , all the __________ teachers in this school can have half a day off .A. womanB. womenC. woman’sD. man’s26. I meant __________ in the UK after middle school , but my father would not allow me toA. to studyB. studyingC. studiedD. was studying27. --- Mom , can I stay out a little later ?--- __________ . You have a test tomorrow and you should go to bed early .A. Yes , you canB. Yes , you mustC. No , you can’tD. No , you needn’t28. If everything goes well , the sports meeting __________ next week .A. holdsB. heldC. is heldD. will be held29. You’d better go to bed early next time , __________ you’ll be late again .A. andB. orC. butD. so30. The government is going to set up the Xiongan New Area . __________ great plan it is !A. WhatB. What aC. HowD. How an31. --- Which do you like to drink , tea or coffee ?--- __________ . I just want some water .A. EitherB. NeitherC. EachD. None32. In Japan , you should __________ your shoes before entering one’s room .A. take offB. turn offC. turn upD. put up33. Among all the programs on TV , I think Readers is __________ . I enjoy watching it a lot .A. less interestingB. more interestingC. the least interestingD. the most interesting34. --- You speak Chinese so well . __________ have you been in Chongqing ?-- Since 2006 .A. How oftenB. how longC. how soonD. How far35. When your coat __________ dirty , you should wash it was soon as possible .A. staysB. keepsC. getsD. smells36. Don’t talk so loudly . Both Lisa and her sister __________ sleeping in the room .A. isB. areC. will beD. were37. --- Jack , I am sorry that I can’t go to the cinema with you tonight .--- __________ . We may go there next time .A. Sounds interestingB. You’re welcomeC. With pleasureD. It doesn’t matter38. --- I’d like to know __________ .--- I’m not sure . Maybe on Monday .A. if there will be an art showB. if will there be an art showC. when there will be an art showD. when will there be an art showIII. 完形填空。
重庆市九年级数学上学期入学试卷(含解析) 新人教版

2016-2017学年重庆市九年级(上)入学数学试卷一、选择题(4X10)1.下列是关于x的一元二次方程的是()A.B.(x﹣1)(x﹣5)=x2﹣5 C.x2=0 D.x2﹣2xy=12.画出如图中物体的俯视图,正确的是()A.B.C.D.3.若分式的值为0,则x的值为()A.1 B.﹣1 C.±1 D.04.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD5.若x=3是关于x的方程x2﹣bx﹣3a=0的一个根,则a+b的值为()A.3 B.﹣3 C.9 D.﹣96.一个密闭不透明盒子中有若干个白球,现又放入8个黑球,摇匀后从中随机摸出一个球记下颜色,再放回盒中,像这样共摸200次,其中40次摸到黑球,估计盒中大约有白球()A.28个B.30个C.32个D.34个7.如图,在▱ABCD中,AB=3,BC=5,对角线AC、BD相交于点O.过点O作OE⊥AC,交AD 于点E.连接CE,则△CDE的周长为()A.3 B.5 C.8 D.118.如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=9厘米,EF=12厘米,则边AD的长是()A.12厘米B.15厘米C.20厘米D.21厘米9.从﹣3,﹣1,,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组无解,且使关于x的分式方程﹣=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是()A.﹣3 B.﹣2 C.﹣ D.10.如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为()A.y=﹣x B.y=﹣C.y=﹣D.y=﹣x二、填空题(4X10)11.方程x2﹣4=0的解是.12.关于x的一元二次方程2x2+kx+1=0有两个相等的实根,则k= ;方程的解为.13.如图,已知△ACP∽△ABC,AC=4,AP=2,则AB的长为.14.如图:M为反比例函数图象上一点,MA⊥y轴于A,S△MAO=2时,k= .15.在分别写有﹣2,﹣1,0,1,2的五张卡片中随机抽取两张,所抽取的两个数差的绝对值大于1的概率为.16.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是.17.若关于x的分式方程+=1有增根,则m= .18.如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC 的最小值是.19.如图,已知M是平行四边形ABCD中AB边的三等分点,BD与CM交于E,阴影部分面积为7,则平行四边形ABCD的面积为.20.在正方形ABCD中,点E为BC边上一点且CE=2BE,点F为对角线BD上一点且BF=2DF,连接AE交BD于点G,过点F作FH⊥AE于点H,连结CH、CF,若HG=2cm,则△CHF的面积是cm2.三、解答题(共70分)21.解方程:(1)x2﹣4x+1=0(2)﹣=.22.先化简,再求值:,其中a满足方程a2+4a+1=0.23.如图,已知直线y=mx+b(m≠0)与双曲线y=(k≠0)交于A(﹣3,﹣1)与B(n,6)两点,连接OA、OB.(1)求直线与双曲线的表达式;(2)求△AOB的面积.24.今年前两个月,全国商品住宅市场销售出现销售量和销售价格齐跌态势.数据显示,2016年前两个月,鲁能地产开发公司开发的鲁能星城13街区的销售面积一共8000平方米,其中1月份的销售面积不多于总面积的40%.(1)求鲁能地产开发公司开发的鲁能星城13街区2016年2月份最少销售了多少平方米?(2)鲁能地产前两月每平方米的售价为8000元,为了解资金链问题,公司决定从3月份开始,以降价促销的方式回笼资金.根据数据调查显示,每平方米销售单价下调a%,3月份销售面积将会在2月份最少销售面积的基础上增加(a+10)%,结果3月份总销售额为3456万元,求a的值.25.任意写一个个位数字不为零的四位正整数A,将该正整数A的各位数字顺序颠倒过来,得到四位正整数B,则称A和B为一对四位回文数.例如A=2016,B=6102,则A和B就是一对四位回文数,现将A的回文数B从左往右,依次顺取三个数字组成一个新数,最后不足三个数字时,将开头的一个数字或两个数字顺次接到末尾,在组成三位新数时,如遇最高位数字为零,则去掉最高位数字,由剩下的两个或一个数字组成新数,将得到的所有新数求和,把这个和称为A的回文数B作三位数的和.例如将6102依次顺取三个数字组成的新数分别为:610,102,26,261,它们的和为:610+102+26+261=999,把999称为2016的回文数作三位数的和.(1)请直接写出一对四位回文数:猜想一个四位正整数和回文数作三位数的和能否被111整除?并说明理由;(2)已知一个四位正整数1x1y(千位数字为1,百位数字为x且0≤x≤9,十位数字为1,个位数字为y且0≤y≤9)的回文数作三位数的和能被27整除,请求出x与y的数量关系.26.已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.(1)如图1,连接AF,若AB=4,BE=1,求AF的长;(2)如图2,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:GO平分∠AGF;(3)如图3,在第(2)问的条件下,连接CG,若CG⊥GO,请直接写出的值.27.如图1,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH:AC=2:3.(1)延长HF交AB于G,求△AHG的面积.(2)操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停止,设运动的时间为t秒,运动后的直角梯形为DEFH′(如图2).探究1:在运动中,四边形CDH′H能否为正方形?若能,请求出此时t的值;若不能,请说明理由.探究2:在运动过程中,延长HF交AB于G,三角形GEB能否为等腰三角形?若能,求出此时的t值;若不能,请说明理由.2016-2017学年重庆市巴蜀中学九年级(上)入学数学试卷参考答案与试题解析一、选择题(4X10)1.下列是关于x的一元二次方程的是()A.B.(x﹣1)(x﹣5)=x2﹣5 C.x2=0 D.x2﹣2xy=1【考点】一元二次方程的定义.【分析】根据一元二次方程的定义进行判断.【解答】解:A、该方程属于分式方程,故本选项错误;B、由已知方程得到﹣6x﹣10=0,属于一元一次方程,故本选项错误;C、该方程符合一元二次方程的定义,故本选项正确;D、该方程中含有2个未知数,属于二元一二次方程,故本选项错误;故选:C2.画出如图中物体的俯视图,正确的是()A.B.C.D.【考点】简单组合体的三视图.【分析】俯视图是从上面看所得到的图形,因此找到从上面看所得到的图形即可.【解答】解:从上面看可得;故选D.3.若分式的值为0,则x的值为()A.1 B.﹣1 C.±1 D.0【考点】分式的值为零的条件.【分析】直接利用分式的值为零,则其分母不为零,分子为零,进而得出答案.【解答】解:∵分式的值为0,∴x2﹣1=0,﹣x﹣1≠0,∴x=1,故选:A.4.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD【考点】矩形的判定.【分析】由四边形ABCD的对角线互相平分,可得四边形ABCD是平行四边形,再添加AC=BD,可根据对角线相等的平行四边形是矩形证明四边形ABCD是矩形.【解答】解:可添加AC=BD,∵四边形ABCD的对角线互相平分,∴四边形ABCD是平行四边形,∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,∴四边形ABCD是矩形,故选:D.5.若x=3是关于x的方程x2﹣bx﹣3a=0的一个根,则a+b的值为()A.3 B.﹣3 C.9 D.﹣9【考点】一元二次方程的解.【分析】将x=3代入方程,得出32﹣3b﹣3a=0,然后利用等式的性质变形即可得到答案.【解答】解:∵x=3是关于x的方程x2﹣bx﹣3a=0的一个根,∴32﹣3b﹣3a=0,∴3a+3b=9,∴a+b=3,故选A.6.一个密闭不透明盒子中有若干个白球,现又放入8个黑球,摇匀后从中随机摸出一个球记下颜色,再放回盒中,像这样共摸200次,其中40次摸到黑球,估计盒中大约有白球()A.28个B.30个C.32个D.34个【考点】用样本估计总体.【分析】设盒中大约有白球x个,根据题意列出方程,求出方程的解即可得到结果.【解答】解:设盒中大约有白球x个,根据题意得: =,解得:x=32,则盒中大约有白球32个,故选C7.如图,在▱ABCD中,AB=3,BC=5,对角线AC、BD相交于点O.过点O作OE⊥AC,交AD 于点E.连接CE,则△CDE的周长为()A.3 B.5 C.8 D.11【考点】平行四边形的性质.【分析】由平行四边形ABCD的对角线相交于点O,OE⊥AC,根据线段垂直平分线的性质,可得AE=CE,又由平行四边形ABCD的AB+BC=AD+CD=8,继而可得△CDE的周长等于AD+CD.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC,∵AB=3,BC=5,∴AD+CD=8,∵OE⊥AC,∴AE=CE,∴△CDE的周长为:CD+CE+DE=CD+CE+AE=AD+CD=8.故选:C.8.如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=9厘米,EF=12厘米,则边AD的长是()A.12厘米B.15厘米C.20厘米D.21厘米【考点】翻折变换(折叠问题).【分析】利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF 的长即为边AD的长.【解答】解:∵∠HEM=∠AEH,∠BEF=∠FEM,∴∠HEF=∠HEM+∠FEM=×180°=90°,同理可得:∠EHG=∠HGF=∠EFG=90°,∴四边形EFGH为矩形.∵AD=AH+HD=HM+MF=HF,HF===15,∴AD=15厘米.故选:B.9.从﹣3,﹣1,,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组无解,且使关于x的分式方程﹣=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是()A.﹣3 B.﹣2 C.﹣ D.【考点】解分式方程;解一元一次不等式组.【分析】根据不等式组无解,求得a≤1,解方程得x=,于是得到a=﹣3或1,即可得到结论.【解答】解:解得,∵不等式组无解,∴a≤1,解方程﹣=﹣1得x=,∵x=为整数,a≤1,∴a=﹣3或1或﹣1,∵a=﹣1时,原分式方程无解,故将a=﹣1舍去,∴所有满足条件的a的值之和是﹣2,故选B.10.如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为()A.y=﹣x B.y=﹣C.y=﹣D.y=﹣x【考点】一次函数图象与几何变换;菱形的性质.【分析】连接AC,求出△BAC是等边三角形,推出AC=AB,求出△DC′B′是等边三角形,推出C′D=B′D,得出CB=BD=B′C′,推出A和D重合,连接BB′交x轴于E,求出AB′=AB=2,∠B′AE=60°,求出B′的坐标即可求得正比例函数的解析式.【解答】解:连接AC,∵四边形OABC是菱形,∴CB=AB,∠CBA=∠AOC=60°,∴△BAC是等边三角形,∴AC=AB,∵将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,∴BD=B′D,CD=C′D,∠DB′C′=∠ABC=60°,∵∠B′DC′=60°,∴∠DC′B′=60°,∴△DC′B′是等边三角形,∴C′D=B′D,∴CB=BD=B′C′,即A和D重合,连接BB′交x轴于E,则AB′=AB=2,∠B′AE=180°﹣=60°,在Rt△AB′E中,∠B′AE=60°,AB′=2,∴AE=1,B′E=,OE=2+1=3,即B′的坐标是(3,﹣),设正比例函数的解析式为y=kx,∵正比例函数图象经过B′,∴﹣=3k,∴k=﹣.故选B.二、填空题(4X10)11.方程x2﹣4=0的解是±2 .【考点】解一元二次方程-直接开平方法.【分析】首先把4移项,再利用直接开平方法解方程即可.【解答】解:x2﹣4=0,移项得:x2=4,两边直接开平方得:x=±2,故答案为:±2.12.关于x的一元二次方程2x2+kx+1=0有两个相等的实根,则k= ;方程的解为x1=x2=.【考点】根的判别式.【分析】根据一元二次方程的根的判别式,建立关于k的等式,求出k的取值.【解答】解:∵a=2,b=k,c=1,方程有两个相等的实数根,∴△=b2﹣4ac=k2﹣8=0∴k=±2.把k=±2代入原方程,得2x2±2x+1=0,解得x1=x2=.13.如图,已知△ACP∽△ABC,AC=4,AP=2,则AB的长为8 .【考点】相似三角形的性质.【分析】根据相似三角形对应边的比相等即可求解.【解答】解:∵△ACP∽△ABC,∴AC:AB=AP:AC,∴4:AB=2:4,∴AB=8.故答案为:8.14.如图:M为反比例函数图象上一点,MA⊥y轴于A,S△MAO=2时,k= ﹣4 .【考点】反比例函数系数k的几何意义.【分析】根据反比例函数y=(k≠0)系数k的几何意义得到S△AOM=|k|=2,然后根据k <0去绝对值得到k的值.【解答】解:∵AB⊥x轴,∴S△AOM=|k|=2,∵k<0,∴k=﹣4.故答案为﹣4.15.在分别写有﹣2,﹣1,0,1,2的五张卡片中随机抽取两张,所抽取的两个数差的绝对值大于1的概率为0.6 .【考点】列表法与树状图法;绝对值.【分析】本具体以可以写出所有的可能性,求出相应的两数差的绝对值,从而可以解答本题.【解答】解:任意抽取两张的所有可能性是:(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣1,0),(﹣1,1),(﹣1,2),(0,1)(0,2),(1,2),它们的差的绝对值分别是:1,2,3,4,1,2,3,1,2,1,∴所抽取的两个数差的绝对值大于1的概率为: =0.6,故答案为:0.6.16.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是24cm2.【考点】菱形的性质;勾股定理.【分析】先求出菱形的边长,然后设菱形的两对角线分别为8x,6x,根据菱形的对角线垂直平分求出两对角线的一半,再利用勾股定理列式求出x,从而得到对角线的长,然后根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.【解答】解:∵菱形的周长是20cm,∴边长为20÷4=5cm,∵两条对角线的比是4:3,∴设菱形的两对角线分别为8x,6x,则对角线的一半分别为4x,3x,根据勾股定理得,(4x)2+(3x)2=52,解得x=1,所以,两对角线分别为8cm,6cm,所以,这个菱形的面积=×8×6=24cm2.故答案为:24cm2.17.若关于x的分式方程+=1有增根,则m= 2 .【考点】分式方程的增根.【分析】根据方程有增根求出x=1,把原方程去分母得出整式方程,把x=1代入整式方程,即可求出m.【解答】解:∵关于x的分式方程+=1有增根,∴x﹣1=0,解得:x=1,方程+=1去分母得:3x﹣1﹣m=x﹣1①,把x=1代入方程①得:3﹣1﹣m=1﹣1,解得:m=2,故答案为:2.18.如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是.【考点】轴对称-最短路线问题;正方形的性质.【分析】要求PE+PC的最小值,PE,PC不能直接求,可考虑通过作辅助线转化PE,PC的值,从而找出其最小值求解.【解答】解:如图,连接AE,∵点C关于BD的对称点为点A,∴PE+PC=PE+AP,根据两点之间线段最短可得AE就是AP+PE的最小值,∵正方形ABCD的边长为2,E是BC边的中点,∴BE=1,∴AE==,故答案为:.19.如图,已知M是平行四边形ABCD中AB边的三等分点,BD与CM交于E,阴影部分面积为7,则平行四边形ABCD的面积为24 .【考点】平行四边形的性质.【分析】由M是平行四边形ABCD中AB边的三等分点,易求得S△BEM:S△CDE=1:9,S△BEM:S△DEM=S:S△BCE=1:3,然后由阴影部分面积为7,求得各三角形的面积,继而求得答案.△BEM【解答】解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴△BEM∽△DEC,∵M是平行四边形ABCD中AB边的三等分点,∴BM:CD=BE:DE=EM:CE,∴S△BEM:S△CDE=1:9,S△BEM:S△DEM=S△BEM:S△BCE=1:3,∵阴影部分面积为7,∴S△BEM=1,∴S△BCE=3,S△CDE=9,∴S△BCD=S△BCE+S△CDE12,∴S▱ABCD=2S△BCD=24.故答案为:24.20.在正方形ABCD中,点E为BC边上一点且CE=2BE,点F为对角线BD上一点且BF=2DF,连接AE交BD于点G,过点F作FH⊥AE于点H,连结CH、CF,若HG=2cm,则△CHF的面积是cm2.【考点】相似三角形的判定与性质;正方形的性质.【分析】如图,过F作FI⊥BC于I,连接FE,FA,得到FI∥CD,设BE=EI=IC=a,CE=FI=2a,AB=3a,由勾股定理得到FE=FC=FA=a,推出HE=AE=,根据正方形的性得到BG平分∠ABC,由三角形角平分线定理得到=,求得HG=AE=a=2,于是得到结论.【解答】解:如图,过F作FI⊥BC于I,连接FE,FA,∴FI∥CD,∵CE=2BE,BF=2DF,∴设BE=EI=IC=a,CE=FI=2a,AB=3a,∴则FE=FC=FA=a,∴H为AE的中点,∴HE=AE=,∵四边形ABCD是正方形,∴BG平分∠ABC,∴=,∴HG=AE=a=2,∴a=,∴S△CHF=S△HEF+S△CEF﹣S△CEH=(a)2+•2a•2a﹣•2a•a=a2=,故答案为:.三、解答题(共70分)21.解方程:(1)x2﹣4x+1=0(2)﹣=.【考点】解一元二次方程-配方法;解分式方程.【分析】(1)在本题中,把常数项1移项后,应该在左右两边同时加上一次项系数﹣4的一半的平方;(2)先把分式方程整理成整式方程,再按照解整式方程的步骤进行计算,最后再进行检验,即可得出答案.【解答】解:(1)x2﹣4x+1=0,x2﹣4x=﹣1,x2﹣4x+4=﹣1+4,(x﹣2)2=3,x﹣2=±,解得x1=2﹣,x2=2+;(2)﹣=,x+5﹣3(x﹣1)=6x,x+5﹣3x+3=6x,﹣8x=﹣8,x=1,经检验x=1是增根,故原方程无解.22.先化简,再求值:,其中a满足方程a2+4a+1=0.【考点】分式的化简求值.【分析】把原式括号里的第二项提取﹣1,然后把原式的各项分子分母都分解因式,找出括号里两项分母的最简公分母,利用分式的基本性质对括号里两项进行通分,然后利用同分母分式的减法运算法则:分母不变,只把分子相减,计算出结果,然后利用分式的除法法则:除以一个数等于乘以这个数的倒数,变形为乘法运算,约分后即可把原式化为最简分式,把a满足的方程变形后,代入原式化简后的式子中即可求出值.【解答】解:原式=====,∵a2+4a+1=0,∴a2+4a=﹣1,∴原式=.23.如图,已知直线y=mx+b(m≠0)与双曲线y=(k≠0)交于A(﹣3,﹣1)与B(n,6)两点,连接OA、OB.(1)求直线与双曲线的表达式;(2)求△AOB的面积.【考点】反比例函数与一次函数的交点问题.【分析】(1)把A的坐标代入反比例函数的解析式求得k的值,然后代入B的坐标求得n 的值,利用待定系数法求得一次函数的解析式;(2)首先求得AB与y轴的交点坐标,根据三角形的面积公式即可求解.【解答】解:(1)把(﹣3,﹣1)代入y=得k=3,则反比例函数的解析式是y=;把(n,6)代入y=得n=.根据题意得:,解得:,则一次函数的解析式是y=2x+5;(2)在y=2x+5中,令x=0,解得y=5,则S△AOB=×5×(+3)=.24.今年前两个月,全国商品住宅市场销售出现销售量和销售价格齐跌态势.数据显示,2016年前两个月,鲁能地产开发公司开发的鲁能星城13街区的销售面积一共8000平方米,其中1月份的销售面积不多于总面积的40%.(1)求鲁能地产开发公司开发的鲁能星城13街区2016年2月份最少销售了多少平方米?(2)鲁能地产前两月每平方米的售价为8000元,为了解资金链问题,公司决定从3月份开始,以降价促销的方式回笼资金.根据数据调查显示,每平方米销售单价下调a%,3月份销售面积将会在2月份最少销售面积的基础上增加(a+10)%,结果3月份总销售额为3456万元,求a的值.【考点】一元二次方程的应用;一元一次不等式的应用.【分析】(1)设1月份的销售面积为xm2,根据“1月份的销售面积不多于总面积的40%”列出不等式求解;(2)根据“与2月份相比较,每平方米销售单价下调a%,则销售面积将增加(a+10)%,结果3月份总销售额为3456万元”找到等量关系列出方程即可.【解答】解:(1)设2月份的销售面积为xm2,则8000﹣x≤8000×40%,解得:x≥4800,答:鲁能地产开发公司开发的鲁能星城13街区2016年2月份最少销售了4800m2.(2)由题意可得:8000(1﹣a%)×4000[1+(a+10)%]=34560000令t=a%,则整理为:50t2+5t﹣1=0,解得:t=0.1或t=﹣0.2故a=10或a=﹣20(不符合题意,舍去)答:a的值为10.25.任意写一个个位数字不为零的四位正整数A,将该正整数A的各位数字顺序颠倒过来,得到四位正整数B,则称A和B为一对四位回文数.例如A=2016,B=6102,则A和B就是一对四位回文数,现将A的回文数B从左往右,依次顺取三个数字组成一个新数,最后不足三个数字时,将开头的一个数字或两个数字顺次接到末尾,在组成三位新数时,如遇最高位数字为零,则去掉最高位数字,由剩下的两个或一个数字组成新数,将得到的所有新数求和,把这个和称为A的回文数B作三位数的和.例如将6102依次顺取三个数字组成的新数分别为:610,102,26,261,它们的和为:610+102+26+261=999,把999称为2016的回文数作三位数的和.(1)请直接写出一对四位回文数:猜想一个四位正整数和回文数作三位数的和能否被111整除?并说明理由;(2)已知一个四位正整数1x1y(千位数字为1,百位数字为x且0≤x≤9,十位数字为1,个位数字为y且0≤y≤9)的回文数作三位数的和能被27整除,请求出x与y的数量关系.【考点】整式的加减.【分析】根据回文数的概念、根据整式的混合运算法则解答即可.【解答】解:(1)一个四位正整数和回文数作三位数的和能否被111整除.例如A=1234和B=4321是一对四位回文数,将4321依次顺取三个数字组成的新数分别为:432,321,214,143,它们的和为432+321+214+143=1110,1110能被111整除;(2)正整数1x1y的回文数是y1x1,则回文数作三位数的和为:100y+10+x+100+10x+1+100x+10+y+100+10y+1=100x+100y+222=111(x+y+2),由题意得,x+y+2=27,则x+y=25.26.已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.(1)如图1,连接AF,若AB=4,BE=1,求AF的长;(2)如图2,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:GO平分∠AGF;(3)如图3,在第(2)问的条件下,连接CG,若CG⊥GO,请直接写出的值.【考点】四边形综合题.【分析】(1)由正方形的性质得出BC=CD=AD=AB=4,∠ABE=∠C=∠D=90°,AC⊥BD,∠ABO=45°,证出∠BAE=∠CBF,由ASA证明△BCF≌△ABE,得出CF=BE=1,因此DF=CD﹣CF=3,由勾股定理求出AF即可;(2)证明A、B、G、O四点共圆,由圆周角定理得出∠AGO=∠ABO=45°,求出∠FGO=453,即可得出结论;(3)连接EF,证明C、E、G、F四点共圆,由圆周角定理得出∠EFC=∠EGC=45°,证出△CEF是等腰直角三角形,CE=CF,同(1)得:△BCF≌△ABE,得出CF=BE,因此CE=BE=BC,得出OA=AC=CE,由(1)得:A、B、G、O四点共圆,由圆周角定理得出∠BOG=∠BAE,证出∠GOA=∠GEC,得出△AOG∽△CEG,由相似三角形的对应边成比例得出=.【解答】(1)解:∵四边形ABCD是正方形,∴BC=CD=AD=AB=4,∠ABE=∠C=∠D=90°,AC⊥BD,∠ABO=45°,∴∠ABG+∠CBF=90°,∵BF⊥AE,∴∠ABG+∠BAE=90°,∴∠BAE=∠CBF,在△BCF和△ABE中,,∴△BCF≌△ABE(ASA),∴CF=BE=1,∴DF=CD=CF=3,∴AF==5;(2)证明:∵AC⊥BD,BF⊥AE,∴∠AOB=∠AGB=∠AGF=90°,∴A、B、G、O四点共圆,∴∠AGO=∠ABO=45°,∴∠FGO=90°﹣45°=45°=∠AGO,∴GO平分∠AGF;(3)证明:连接EF,如图所示:∵CG⊥GO,∴∠OGC=90°,∵∠EGF=∠BCD=90°,∴∠EGF+∠BCD=180°,∴C、E、G、F四点共圆,∴∠EFC=∠EGC=180°﹣90°﹣45°=45°,∴△CEF是等腰直角三角形,∴CE=CF,同(1)得:△BCF≌△ABE,∴CF=BE,∴CE=BE=BC,∴OA=AC=BC=CE,由(1)得:A、B、G、O四点共圆,∴∠BOG=∠BAE,∵∠GEC=90°+∠BAE,∠GOA=90°+∠BOG,∴∠GOA=∠GEC,又∵∠EGC=∠AGO=45°,∴△AOG∽△CEG,∴.27.如图1,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH:AC=2:3.(1)延长HF交AB于G,求△AHG的面积.(2)操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停止,设运动的时间为t秒,运动后的直角梯形为DEFH′(如图2).探究1:在运动中,四边形CDH′H能否为正方形?若能,请求出此时t的值;若不能,请说明理由.探究2:在运动过程中,延长HF交AB于G,三角形GEB能否为等腰三角形?若能,求出此时的t值;若不能,请说明理由.【考点】三角形综合题.【分析】(1)由于三角形AHG和ACB相似,可通过相似比求出HG的值,然后根据三角形的面积计算公式即可求出三角形AHG的面积.(2)①首先四边形CDH′H是个矩形,如果使四边形CDH′H成为正方形,那么需满足的条件是CD=DH′,可先根据AH:AC的值,求出HC的长即H′D的长,然后除以梯形的速度即可求出t的值.②要分三种情况进行讨论:(Ⅰ)当E在三角形ABC内部时,即当0≤t≤4时,重合部分是整个直角梯形,因此可通过计算直角梯形的面积得出重合部分的面积.(Ⅱ)当E在三角形ABC外部,且H′在G点左侧或G点上时,即当4<t≤5时,重合部分是直角梯形,其面积可用:四边形CBGH的面积一矩形CDH′H的面积来求得.(Ⅲ)当H′在G点右侧一直到D与B重合的过程中,即当5<t≤8时,重合部分是个直角三角形.可通过计算这个直角三角形的面积来得出关于S,t的函数关系式.【解答】解:(1)∵AH:AC=2:3,AC=6∴AH=AC=×6=4又∵HF∥DE,∴HG∥CB,∴△AHG∽△ACB∴=,即=,∴HG=,∴S△AHG=AH•HG=×4×=.(2)①能为正方形∵HH′∥CD,HC∥H′D,∴四边形CDH′H为平行四边形,又∠C=90°,∴四边形CDH′H为矩形,又CH=AC﹣AH=6﹣4=2∴当CD=CH=2时,四边形CDH′H为正方形此时可得t=2秒时,四边形CDH′H为正方形.②(Ⅰ)∵∠DEF=∠ABC,∴EF∥AB∴当t=4秒时,直角梯形的腰EF与BA重合.当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积.过F作FM⊥DE于M,∴=tan∠DEF=tan∠ABC===,∴ME=FM=×2=,HF=DM=DE﹣ME=4﹣=,∴直角梯形DEFH′的面积为(4+)×2=,∴y=.(Ⅱ)∵当4<t≤5时,重叠部分的面积为四边形CBGH的面积一矩形CDH′H的面积.而S边形CBGH=S△ABC﹣S△AHG=×8×6﹣=,S矩形CDH′H,∴y=﹣2t.(Ⅲ)当5<t≤8时,如图,设H′D交AB于P,BD=8﹣t,又=tan∠ABC=,∴PD=DB=(8﹣t),∴重叠部分的面积y=S,△PDB=PD•DB=•(8﹣t)(8﹣t)=(8﹣t)2=t2﹣6t+24.∴重叠部分面积y与t的函数关系式:y=.。
重庆八中2016—2017学年度(上)期末考试初三年级数学试题(Word版)含答案

重庆八中2016—2017学年度(上)期末考试初三年级数 学 试 题一、选择题:(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上对应题目的正确答案标号涂黑。
1.在-41、0、-2、5这四个数中,最大的数是( )A. -41 B.0 C.-2 D.52.下列图形是中心对称图形的是( )3.重庆八中新校区占地约为220000平米,将数220000用科学记数法表示是( )A.220×103B.22×104C.2.2×105D.0.22×1064.计算(2a)2·a 4的结果是( )A.2a 6B.2a 5C.4a 6D.4a 55.如图,已知直线AB 、CD 被直线EF 所截,且AB ∥CD ,若∠1=50°,则∠2的度数是( ) A.120° B.130° C.140° D.150°6.为了参加“畅想太空”为主题的趣味运动会入场式,某班级需要统一购买鞋子,小岚统计了全班女同学的鞋子码数,调查结果如下表,A.37B.37.5C.38D.38.5 7.在函数y=223x 中,x 的取值范围是( )A.x ﹥1 B. .x ﹥-1 C.x ≠1 D. x ≠-18.若|a-b-1|+|m+3+n|=0,则代数式a 2+b 2-2ab+m+n 的值是( )A.-4 B.-2 C.2 D.49.下列图形是按一定规律组成的图形,第①个图形中对顶角的对数与三角形的个数和是3,第②个图形中对顶角的对数与三角形的个数和是9,第③个图形中对顶角的对数与三角形的个数和是18,第④个图形中对顶角的对数与三角形的个数和是30,…,第⑧个图形中对顶角的对数与三角形的个数和是( )A.45 B.72 C.92 D.108第①个图 第②个图 第③个图 第④个图10.如图,在△ABC 中,∠BAC=90°,BC=2AB=6,以点A 为圆心AB 作半径作弧,分别交BC 、AC 于点D 、E ,则图中阴影部份的面积是( ) A.23439π- B.23429π- C.43439π- D.43429π-第10题 第11题11.如图,小周站在A 处,他的对面有一斜坡BC (坡度i=12:5),现测得小周所站A 处到斜坡底端B 的距离,AB=15米,坡面BC 长为13米,在斜坡顶端C 不远处D 有一颗树,测得CD=10米,小周看树的顶部E 的仰角为30°,此时小周眼睛到地面的高度为1.8米,则小树的高度DE 约为( )(精确到1米,3=1.73,5=2.24)A.5B.7C.12D.1712.从-2、-1、21、1、2这五个数中,随机抽取一个数,记为a ,若数a 使关于x 的不等式⎩⎨⎧<-≥+0972a x x 无解,且使分式方程132232-=--+-x a x a 的解为正确分数,那么这五个数中所有满足条件的a 的什的和是( )A.-3B.-25C.-2D.二、填空题:(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡(卷)......中对应的横线上。
重庆八中初2017级九年级下周考(一)数学试题(Word版)

重庆八中初2017级九年级下周考(一)数 学 试 题(满分150分 考试时间120分钟)一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的框涂黑. 1.下列各数中最大的数是( )A .- 2B . 2C .0D .12.在下列“循环再生”、“QS 食品认证”、“绿色食品”、“节约用水”这四个标志中,属于轴对称图形的是( )3.计算(-2a)2²a 3正确的是( )A .2a 5B .-4a 5C .4a 5D .4a 64.下列调查中,最适合采用抽样调查方式的是( )A .对重庆八中初2017级全体学生体育入学考试成绩的B .对初二某班学生的身高情况进行调查C .对今年元宵节重庆市市场上彩色汤圆质量情况的调查D .对用于发射卫星的运载火箭主要零部件的检查5.如图,直线AB∥CD,∠E =40°,∠A=110°,则∠C 的度数为( ) A .60°B .80°C .75°D .70° 第5题图ED CB A1第8题图DCBA6.若△ABC∽△DEF,且相似比为2:1,△ABC 面积为8,则△DEF 的面积为( )A .2 B .4 C .8D .16 7.若分式x 2-9x +3的值为0,则x 的值为( )A .±3B .3C .-3D .9 8.如图,A 、B 、C 、D 是圆上四点,∠1=68°,∠A =40°,则∠D 的度数为( )A .28°B .38°C .22°D .32°9.如图,每一个图形都是由正方形按一定规律组成的,其中第①个图形中一共有9个正方形,第②个图形中一共有17个正方形,第③个图形中一共有25个正方形,…,按此规律排列,则第⑧个图形中正方形的个数为( )A .38B .44C .65D .7310.已知实数a 是方程x 2-3x -2=0的其中一个根,则-2a 2+6a +7等于( )A .11 B .9C .7D .311.如图,某人在山坡坡脚C 处测得一座建筑物顶点A 的仰角为63.4°,沿山坡向上走到P 处再测得该建筑物顶点A 的仰角为53°。
重庆八中初2017级初三(上)第一次月考数学试题及答案

重庆八中初2017级初三(上)第一次月考数 学 试 题(满分150分 考试时间120分钟)一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的框涂黑.1.15-的相反数是( )A .15B .15- C .5 D .5-2.随着人民生活水平的提高,我国拥有汽车的家庭也越来越多,下列汽车标志中,是中.心对称图形.....的是( )A .B .C .D .3.计算232x x ⋅的结果是( ) A .x 2 B .52xC .62xD .5x4.若分式12x +有意义,则x 的取值范围是( )A .2x >-B .2x <-C .2x ≠-D .2x ≥-5.已知ABC DEF △∽△,其相似比为4:9,则ABC △与DEF △的面积比是( )A . 2:3B . 3:2C .16:81D .81:166.下列调查中,最适宜采用全面调查(普查)的是( ) A .了解重庆市市民家庭月平均支出情况 B .了解一批导弹的杀伤半径C .了解某校九年级某班学生月考体育成绩D .了解重庆市民生活垃圾分类情况7.九年级某同学7天进行自主复习时间(单位:分钟)如下: 50, 60, 80,90,60,70,60.这组数据的众数是( ) A .90B .80C .70D . 608.如图,已知ABCD 中,AC ,BD 相交于点O ,8AD BD ==,12AC =,则ADO ∆的周长是( ) A .20B .18C .16D .129.已知1=-b a ,则代数式201622+-b a 的值是( )A .2018B .2017C .2016D .201510.如图,下列图形是一组按照某种规律摆放而成的图案,则图⑧中圆点的个数是( )A .64B .65C .66D .6711.小明去爬山,在山脚B 处看山顶A 的仰角为30°,小明在坡度为512i =的山坡BD 上走1300米到达D 处,此时小明看山顶A 的仰角为60°,则山高AC 约为( )米1.73≈) A .167.5 B .788 C .955.5D .86512.已知关于x 的分式方程2332=-++-x ax x 有增根,且关于x 的不等式组⎩⎨⎧≤>bx a x 只有4个整数解,那么b 的取值范围是( ) A .31≤<-b B .32≤<b C .98<≤bD .43<≤bODC BA…图① 图② 图③ 图④ ABCD二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.13.在2016年8月21日进行的里约奥运会女排决赛中,中国队战胜塞尔维亚队,勇夺金牌.据报道,这场比赛吸引了全中国大约94849万人通过电视直播收看.将数94849用科学计数法表示为______________. 14212sin 60()-+=______________.17.甲、乙两人分别从两个地点同时出发登山,甲、乙两人距山脚的竖直高度y (米)与登山时间x (分)之间的图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速登山,且乙在加速后的速度是甲速度的4倍,那么他们出发______________分钟时,乙追上了甲.乙甲18.如图,在正方形ABCD 中2AB =,点E 是CD 的中点,连接AE .将ADE ∆沿AE折叠至AFE ∆,连接BF .延长AE 、BF 交于点G ,则AFG ∆的面积为_________.DEABCFG三、解答题:(本大题共2小题,每小题7分,共14分)解答时每小题必须给出必要的演算过程或推理步骤. 19.如图,点,,,A B C D 在同一条直线上,CE ∥DF ,,AC DF CE BD ==.求证:=A F ∠∠.A B C DEF20.2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查.规定每人只能从A 类(立刻去抢购)、B 类(降价后再去买)、C 类(犹豫中)、D 类(肯定不买)这四类中选择一类,并制成了以下两幅不完整的统计图.由图中所给出的信息解答下列问题: (1)扇形统计图中B 类对应的百分比为_______%,请补全条形统计图;(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机?各类型购买意向人数的条形统计图各类型购买意向人数占调查总人数的百分比扇形统计图16%CB DA406080100120140类型人数0A B C D 140四、解答题:(本大题共4小题,每题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤.21.计算:(1)2(2)(43)a b a a b --- (2)212(3)11x x x x -+-÷--22.某体育用品制造公司通过互联网销售某品牌排球,第一周的总销售额为3000元,第二周的总销售额为3520元,第二周比第一周多售出13个排球. (1)求每个排球的售价;(2)该公司在第三周将每个排球的售价降低了1%2a ,并预计第三周能售出120个排球.恰逢中国女排勇夺里约奥运会冠军,极大地激发了广大青少年积极参与排球运动的热情,该款排球在第三周的销量比预计的120个还多了4%a .已知每个排球的成本为16元,该公司第三周销售排球的总利润为4320元,求a 的值(其中50a ≤).23.如图,抛物线223y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),交y 轴于点C ,连接BC .抛物线的顶点为点D . (1)求AB 的长度和点D 的坐标;(2)在抛物线的对称轴上有一动点M ,连接MB 、MC ,当MBC ∆的周长最小时,求点M 的坐标和MBC ∆周长的最小值.24.若一个正整数,它的各位数字是左右对称的,则称这个数是对称数,如22,797,12021都是对称数.最小的对称数是11,没有最大的对称数,因为数位是无穷的. (1)若将任意一个各位数字均不为零的四位对称数分解为前两位数所表示的数和后两位数所表示的数,请你证明这两个数的差一定能被9整除;(2)若将一个三位对称数aba 减去其各位数字之和(其中02a <≤,90≤≤b ),所得的结果能被11整除,求所有满足条件的三位对称数.五、解答题:(本大题2个小题,每题12分,共24分)解答时每小题必须给出必要的演算过程或推理步骤.25.如图1,在ABC ∆中BD AC ⊥于点D ,在线段DA 上取点E 使得ED CD =,DF 平分ADB ∠交AB 于点F ,连接EF .(1)若AB =BC =8AD =,求CD 的长; (2)若+BD ED ,求证:FB FE =且FB FE ⊥; (3)如图2,在(2)的情况下,若=90ABC ∠,求ABBC的值. 图1 图2A BC D E FABCDE F26.如图,在平面直角坐标系中四边形ABCD 为菱形,边AD 在y 轴上,其中()1,0A ,()0,3-B ,双曲线my x=经过点C . (1)求反比例函数的解析式;(2)连接CO 并延长交双曲线于点E ,连接DE ,P 是双曲线在第一象限上的一个动点,满足CDE BDP S S ∆∆=2,求点P 的坐标;(3)将直线..BD 沿x 轴向右平移,交x 轴于点K ,交射线BA 于点H ,问是否存在某一时刻,使得KOH ∆为等腰三角形,若存在求出线段OK 的值,若不存在,请说明理由.答案 选择题1-5 AABCC 6-10 CDBAB 11-12BD 填空题13. 49.484910⨯14.4 15. -10 16.12 17. 103 18. 65解答题19. 证明:∵CD ∥DF∴∠ACE =∠D ……………………………………………………3分 在△ACE 和△FDBAC DF ACE D CE BD =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△FDB ……………………………………………………6分 ∴∠A =∠F …………………………………………………………7分 20. (1)20 ………………………………………………………2分补图略……………………………………………………4分 (2)204000320250⨯=(人) 答:统计该小区大约有320人立刻去抢购该款手机……………7分 21. (1)解:原式=2224443a ab b a ab -+-+ …………………2分 =2b ab - ……4分(2)解:原式=()()2131112x x x x x+---⋅-- …………………………2分 =()()()221112x x x x x-+-⋅-- …………………………4分=()()21m x --+=22x x -++ ………………………………………6分22. 解:(1)设每个排球售价为x 元,则3000352013x x+=………………………………………………1分 解得40x = ……2分经检验,40x =是原方程的解…………………………………3分 答:每个排球的售价为40元…………………………………4分 (2)()1401%1612014%43202a a ⎡⎤⎛⎫--⋅+= ⎪⎢⎥⎝⎭⎣⎦令%a m =,则()1401161201443202m m ⎡⎤⎛⎫--⋅+= ⎪⎢⎥⎝⎭⎣⎦……………………………7分∴2201930m m -+=()()51430m m --=∴115m =,234m =∴120a =,275a =∵50a ≤∴20a = ……9分答:a 的值为20………………………………………………10分 23. 解:(1)由2230x x --+=的解 13x =-,21x = ∴()3,0A -,()1,0B∴4AB = ………………………………………………………2分 ∵223y m x =--+ ∴对称轴为直线1x =- 当1x =-时,4y =∴()1,4D -………………………………………………………5分 (2)连接AC 交对称轴于点M :3AC y x =+∴()1,2M - ………………………………………………………7分 MBCCAC BC =+=分24. 解:设这个四位数为abba(1)∵()1010999ab ba a b b a a b a b -=+--=-=-……………3分 ∵a 、b 均为整数……4分 ∴ab ba -能被9整除……5分(2)()10010999aba a b a a b a a b a a b -++=++---=-………7分 ∵结果能被11整除 ∴99911a b k -= ()911911a b k -=……………………………………………………8分∵02a <≤,097b ≤≤ ∴10a b =⎧⎨=⎩,20a b =⎧⎨=⎩………………………………………………9分∴这样的对称数为101或202…………………………………10分25. (1)4BD =1CD == ……3分(2)过点F 作FM ⊥FD 交AC 于点M……………………4分 △MFE ≌△DFB∴FB =FE ,∠MFE =∠DFB ∵∠DFM =90°∴∠EFM =90° ∴EF ⊥BF∴FB ⊥FE 且FB ⊥FE ……………………………………………………7分(3)延长BD 、FE 交于点N ,连接BE△BDC ≌△EDN△BFN ≌△EF A ……10分设BF =x ,则BE ,BC =∴FE =x ,EN =∴)1FN x =∴)1AF x =∴)2AB x =∴21x AB BC ==………………………………………………12分26. 解(1)∵()0,1A ,()B∴1OA =,OB =在Rt △ABO 中AB =2又∵四边形为菱形∴BC =AB =2∴()2C -∴双曲线解析式:y =………………………………………………2分 (2)∵112CDE S ∆=⨯⨯=∴BDP S ∆=∵:1BO y x =- ………………………………………………3分 M A B C D E F A B C D E F N设P m ⎛ ⎝⎭,,1Q m ⎛⎫- ⎪ ⎪⎝⎭112⎫⋅+⎪⎪⎝⎭30=230m -+=941∆=-=∴m =∴1m =2m =∴)P,()………………………………………………6分 (3)每个答案2分OK =OK =OK =……………………………………………………………12分。
重庆八中九年级(下)入学数学试卷

2016-2017学年重庆八中九年级(下)入学数学试卷一、选择题(共12小题)1.下列实数中是无理数的是()A.B.πC.0.38D.2.下列图形选自历届世博会会徽,其中是轴对称图形的是()A.B.C.D.3.下列运算中,正确的是()A.m2•m3=m6B.(﹣m2)3=m6C.﹣m2﹣2m2=﹣3m2D.﹣3m﹣2=﹣4.如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF 交CD于点G.若∠1=36°,则∠2的大小是()A.72°B.67°C.70°D.68°5.如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为()A.2B.2C.4D.6.下列调查中,最适合采用普查方式的是()A.调查2017年春节晚会的收视率B.调查重庆全市市民春节期间外出旅游人数C.调查全国初三学生的视力情况D.调查某航班的旅客是否携带了违禁物品7.函数y=中,自变量x的取值范围是()A.x>4B.x≥2C.x≥2且x≠﹣4D.x≠﹣48.已知,且3x﹣2y=10,a的值为()A.2B.3C.4D.59.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于()A.5:8B.3:8C.3:5D.2:510.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有1个空心小圆圈,第②个图形中一共有6个空心小圆圈,第③个图形中一共有13个空心小圆圈,…,按此规律排列,则第⑦个图形中空心圆圈的个数为()A.61B.63C.76D.7811.游客上歌乐山山有两种方式:一种是如图,先从A沿登山步道走到B,再沿索道乘座缆车到C,另一种是沿着盘山公路开车上山到C,已知在A处观铡到C,得仰角∠CAD=3l°,且A、B的水平距离AE=430米,A、B的竖直距离BE=210米,索道BC的坡度i=1:1.5,CD⊥AD于D,BF⊥CD于F,则山篙CD为()米;(参考数据:tan31°≈0.6.cos3l°≈0.9)A.680B.690C.686D.69312.若关于x的方程=﹣的解为整数,且不等式组无解,则这样的非负整数a有()A.2个B.3个C.4个D.5个二、填空题:13.据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数用科学记数法表示为元.14.计算:﹣(﹣)﹣2+|4﹣2|=.15.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是.16.从﹣3,﹣1,﹣,1,2这五个数中,随机抽取一个数,作为抛物线y=x2+2mx+m 中m的值,恰好使所得抛物线的顶点在第四象限概率为.17.甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y 甲(千米),乙与学校相离y 乙(千米),甲离开学校的时间为t (分钟).y 甲、y 乙与x 之间的函数图象如图所示,则乙返回到学校时,甲与学校相距 千米.18.在正方形ABCD 中,点E 、F 分别是BC 、DC 边上一点,且BE=CE ,DF=2FC ,连接DE ,BF 交于点G ,连接∠DAG 的平分线交DC 于M ,若BG=,则四边形AGFM 的面积是 .三、解答题:19.如图,在▱ABCD 中,对角线AC ,BD 相交于点O ,点E 、F 分别在边AD ,BC上,且DE=BF ,连接OE ,OF .求证:OE=OF .20.为了解某住宅区的家庭用水量情况,从该住宅区中随机抽样调查了50户家庭去年每个月的用水量,统计得到的数据绘制了下面的两幅统计图.图1是去年这50户家庭月总用水量的折线统计图,图2是去年这50户家庭月总用水量的不完整的频数分布直方图.(1)根据图1提供的信息,补全图2中的频数分布直方图;(2)在抽查的50户家庭去年月总用水量这12个数据中,极差是米3,众数是米3,中位数是米3;(3)请你根据上述提供的统计数据,估计该住宅区今年每户家庭平均每月的用水量是多少米3?21.化简下列各式:(1)(2a﹣1)(1+2a)﹣(a﹣2)(a+3)﹣(a﹣1)2;(2)÷(﹣)﹣.22.如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=.(1)一次函数的解析式和反比例函数的解析式;(2)求△POQ的面积.23.每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.(1)求该商场两次共购进多少瓶葡萄酒.(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).24.一个多位数整数,a代表这个整数分出来的左边数,b代表这个整数分出来的右边数,其中a,b两部分数位相同,若正好为剩下的中间数,则这个多位数就叫平衡数,例如:357满足=5,233241满足=32.(1)写出一个三位平衡数和一个六位平衡数,并证明任意一个六位平衡数一定能被3整除;(2)若一个三位平衡数后两位数减去百位数字之差为3的倍数,且这个平衡数为偶数,求这个三位数.五、解答题:25.在Rt△ABC中,∠ABC=90°,∠BAC的平分线AD交BC于点D(l)如图1,过点B作BE⊥AC于点E,BE与AD相交于点F,当AD=6,BF=2时,求线段AB的长度;(2)如图2.过点B作BE⊥AC于点E,BE与AD相交于点F,在线段AF上取点G,使FG=DF,连接BG.过点F作FH⊥AD交BG于点H,连接DH交BE于点I,求证:BD=2IF.(3)如图3,若∠BCA=60°,作∠BCA=∠MCB交AD的延长线于M,过M作MN ⊥MA交AB的延长线上于N点,猜想线段ND与线段AB之间有怎样的数量关系,请直接写出结论(不需证明)26.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,)((1)求抛物线解析式及D点坐标;(2)如图1,P为线段OB上(不与O、B重舍)一动点,过点P作y轴的平行线交线段AB于点M,交抛物线于点N,点N作NK⊥BA交BA于点K,当△MNK与△MPB的面积相等时,在X轴上找一动点Q,使得CQ+QN最小时,求点Q的坐标及CQ+QN最小值;(3)如图2,在(2)的条件下,将△ODN沿射线DN平移,平移后的对应三角形为△O′D′N′,将△AOC绕点O逆时针旋转到A1OC1的位置,且点C1恰好落在AC上,△A1D′N′是否能为等腰三角形,若能求出N′的坐标,若不能,请说明理由.2016-2017学年重庆八中九年级(下)入学数学试卷参考答案与试题解析一、选择题(共12小题)1.下列实数中是无理数的是()A.B.πC.0.38D.【分析】根据无理数的三种形式,结合选项找出无理数的选项.【解答】解:A、=2,是有理数,故本选项错误;B、π是无理数,故本选项正确;C、0.38是有理数,故本选项错误;D、﹣是有理数,故本选项错误.故选:B.【点评】本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.2.下列图形选自历届世博会会徽,其中是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A、不是轴对称图形,故此选项错误;B、是轴对称图形,故此选项正确;C、不是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项错误;故选:B.【点评】此题主要考查了轴对称图形,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.3.下列运算中,正确的是()A.m2•m3=m6B.(﹣m2)3=m6C.﹣m2﹣2m2=﹣3m2D.﹣3m﹣2=﹣【分析】根据同底数幂的乘法、幂的乘方、合并同类项、负整数指数幂,即可解答.【解答】解:A、m2•m3=m5,故错误;B、(﹣m2)3=﹣m6,故错误;C、﹣m2﹣2m2=﹣3m2,正确;D、,故错误;故选:C.【点评】本题考查了同底数幂的乘法、幂的乘方、合并同类项、负整数指数幂,解决本题的关键是熟记同底数幂的乘法、幂的乘方、合并同类项、负整数指数幂.4.如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF 交CD于点G.若∠1=36°,则∠2的大小是()A.72°B.67°C.70°D.68°【分析】根据角平分线的性质可以求得∠3的度数,然后根据平行线的性质来求∠2的大小.【解答】解:如图,∵∠1=36°,∠1+∠AEF=180°,∴∠AEF=144°.又∵EG平分∠AEF,∴∠3=∠AEF=72°.∵AB∥CD,∴∠2=∠3=72°.故选:A.【点评】本题考查了平行线的性质.根据邻补角和角平分线的定义求得∠3的度数是解题的关键.5.如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为()A.2B.2C.4D.【分析】连接OC,由圆周角定理得出∠BOC=2∠A=60°,由垂径定理得出CE=DE=CD=3,再由三角函数求出OC即可.【解答】解:连接OC,如图所示:则∠BOC=2∠A=60°,∵AB⊥CD,∴CE=DE=CD=3,∵sin∠BOC=,∴OC===2.故选:A.【点评】本题考查了垂径定理、圆周角定理以及三角函数;熟练掌握圆周角定理,由垂径定理求出CE是解决问题的关键.6.下列调查中,最适合采用普查方式的是()A.调查2017年春节晚会的收视率B.调查重庆全市市民春节期间外出旅游人数C.调查全国初三学生的视力情况D.调查某航班的旅客是否携带了违禁物品【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果不准确.【解答】解:A、人数众多,不容易调查,因而适合抽样调查,故选项不符合题意;B、人数众多,不容易调查,因而适合抽样调查,故选项不符合题意;C、人数众多,不容易调查,因而适合抽样调查,故选项不符合题意;D、事关重大,必须进行普查,故选项正确.故选:D.【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.7.函数y=中,自变量x的取值范围是()A.x>4B.x≥2C.x≥2且x≠﹣4D.x≠﹣4【分析】根据分式和二次根式有意义的条件进行选择即可.【解答】解:由题意得,解得x≥2,x≠﹣4,∴自变量x的取值范围是x≥2,故选:B.【点评】本题考查了函数自变量的取值范围问题,掌握分式和二次根式有意义的条件是解题的关键.8.已知,且3x﹣2y=10,a的值为()A.2B.3C.4D.5【分析】直接将两式相加进而结合已知条件3x﹣2y=10,得出答案.【解答】解:∵,∴3x﹣2y=1+3a,∵3x﹣2y=10,∴1+3a=10,解得:a=3.故选:B.【点评】此题主要考查了解二元一次方程组,正确得出3x﹣2y=1+3a是解题关键.9.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于()A.5:8B.3:8C.3:5D.2:5【分析】先由AD:DB=3:5,求得BD:AB的比,再由DE∥BC,根据平行线分线段成比例定理,可得CE:AC=BD:AB,然后由EF∥AB,根据平行线分线段成比例定理,可得CF:CB=CE:AC,则可求得答案.【解答】解:∵AD:DB=3:5,∴BD:AB=5:8,∵DE∥BC,∴CE:AC=BD:AB=5:8,∵EF∥AB,∴CF:CB=CE:AC=5:8.故选:A.【点评】此题考查了平行线分线段成比例定理.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.10.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有1个空心小圆圈,第②个图形中一共有6个空心小圆圈,第③个图形中一共有13个空心小圆圈,…,按此规律排列,则第⑦个图形中空心圆圈的个数为()A.61B.63C.76D.78【分析】由已知图形中空心小圆圈个数,知第n个图形中空心小圆圈个数为4n ﹣(n+2)+n(n﹣1),据此可得答案.【解答】解:∵第①个图形中空心小圆圈个数为:4×1﹣3+1×0=1个;第②个图形中空心小圆圈个数为:4×2﹣4+2×1=6个;第③个图形中空心小圆圈个数为:4×3﹣5+3×2=13个;…∴第⑦个图形中空心圆圈的个数为:4×7﹣9+7×6=61个;故选:A.【点评】本题考查了规律型﹣图形变化类:先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.11.游客上歌乐山山有两种方式:一种是如图,先从A沿登山步道走到B,再沿索道乘座缆车到C,另一种是沿着盘山公路开车上山到C,已知在A处观铡到C,得仰角∠CAD=3l°,且A、B的水平距离AE=430米,A、B的竖直距离BE=210米,索道BC的坡度i=1:1.5,CD⊥AD于D,BF⊥CD于F,则山篙CD为()米;(参考数据:tan31°≈0.6.cos3l°≈0.9)A.680B.690C.686D.693【分析】根据题目中的数据和锐角三角函数可以求得CD的长,从而可以解答本题.【解答】解:∵索道BC的坡度i=1:1.5,∴CF:BF=1:1.5,设CF=x,则BF=1.5x,∵∠CAD=3l°,且A、B的水平距离AE=430米,A、B的竖直距离BE=210米,∴tan∠CAD=,∵tan31°≈0.6,∴,解得,x=480,∴CD=CF+DF=480+210=690,故选:B.【点评】本题考查解直角三角形的应用,解答此类问题的关键是明确题意,利用锐角三角函数解答.12.若关于x的方程=﹣的解为整数,且不等式组无解,则这样的非负整数a有()A.2个B.3个C.4个D.5个【分析】先把a当常数解分式方程,x=,再将a当常数解不等式组,根据不等式组无解得:a≤6,找出当a为非负整数时,x也是整数的值时,a有几个即可.【解答】解:=﹣,去分母,方程两边同时乘以x﹣2,ax=3+a+x,x=,且x≠2,,由①得:x>6,由②得:x<a,∵不等式组无解,∴a≤6,当a=0时,x==﹣3,当a=1时,x=无意义,当a=2时,x===5,当a=3时,x===3,当a=4时,x===,当a=5时,x===2,分式方程无解,不符合题意,当a=6时,x===,∵x是整数,a是非负整数,∴a=0,2,3;故选:B.【点评】此题考查了解分式方程、一元一次不等式组的解的情况,求出分式方程和不等式组的解是解本题的关键,要注意分式方程有意义,即分母不为0.二、填空题:13.据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数用科学记数法表示为 6.8×108元.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将680000000用科学记数法表示为6.8×108.故答案为:6.8×108.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.14.计算:﹣(﹣)﹣2+|4﹣2|=.【分析】原式利用二次根式性质,负整数指数幂法则,以及绝对值的代数意义化简,即可得到结果.【解答】解:原式=3﹣4+4﹣2=,故答案为:【点评】此题考查了实数的运算,绝对值,以及负整数指数幂,熟练掌握运算法则及绝对值的代数意义是解本题的关键.15.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8﹣π.【分析】作DH⊥AE于H,根据勾股定理求出AB,根据阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积、利用扇形面积公式计算即可.【解答】解:作DH⊥AE于H,∵∠AOB=90°,OA=3,OB=2,∴AB==,由旋转的性质可知,OE=OB=2,DE=EF=AB=,△DHE≌△BOA,∴DH=OB=2,阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=×5×2+×2×3+﹣=8﹣π,故答案为:8﹣π.【点评】本题考查的是扇形面积的计算、旋转的性质、全等三角形的性质,掌握扇形的面积公式S=和旋转的性质是解题的关键.16.从﹣3,﹣1,﹣,1,2这五个数中,随机抽取一个数,作为抛物线y=x 2+2mx +m中m 的值,恰好使所得抛物线的顶点在第四象限概率为 .【分析】确定使函数的图象顶点在第四象限的m 的值,找到同时满足两个条件的m 的值即可.【解答】解:因为抛物线y=x 2+2mx +m 的顶点在第四象限, 可得:,解得:m <0, 所以恰好使所得抛物线的顶点在第四象限概率为, 故答案为:【点评】此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.17.甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y 甲(千米),乙与学校相离y 乙(千米),甲离开学校的时间为t (分钟).y甲、y乙与x之间的函数图象如图所示,则乙返回到学校时,甲与学校相距20千米.【分析】先求出乙追上甲所用的时间,再加上乙返回学校所用的时间就是甲步行所用的时间,再求出甲步行的速度,就可以求出乙回到学校时,甲与学校的距离.【解答】解:由题意,电动车的速度为18÷20=0.9千米/分钟,乙从学校追上甲所用的时间为:(36﹣13.5)÷0.9=25分钟,∴甲步行所用的时间为:20+25=45分钟.∴甲步行的速度为:(36﹣13.5﹣18)÷45=0.1.∵乙返回到学校时,甲与学校的距离为:18+0.1×20=20.∴乙返回到学校时,甲与学校相距20km.故答案为20.【点评】本题考查一次函数的应用、速度=路程÷时间的运用、追击问题的运用等知识,解答本题时认真分析函数图象反应的数量关系是关键.18.在正方形ABCD中,点E、F分别是BC、DC边上一点,且BE=CE,DF=2FC,连接DE,BF交于点G,连接∠DAG的平分线交DC于M,若BG=,则四边形AGFM的面积是.【分析】如图,作AK ⊥BF 于H 交BC 于K ,延长CB 到P ,使得BP=DM ,连接AP 、KM ,延长DE 交AB 的延长线于N .则△ADM ≌△ABP ,△DCE ≌△NBE .首先求出正方形ABCD 的边长,再证明∠KAM=45°,KM=BK +DM ,设DM=x ,在Rt △KMC 中,利用勾股定理列出方程即可切线x ,根据S 四边形AEFM =S 正方形ABCD ﹣S △ADM ﹣S △ABE ﹣S △EFC 计算即可解决问题.【解答】解:如图,作AK ⊥BF 于H 交BC 于K ,延长CB 到P ,使得BP=DM ,连接AP 、KM ,延长DE 交AB 的延长线于N .则△ADM ≌△ABP ,△DCE ≌△NBE . ∵四边形ABCD 是正方形,AK ⊥BF ,∴AB=BC ,∠ABK=∠BCF=∠AHB=90°,∴∠BAK +∠ABH=90°,∠ABH +∠CBF=90°,∴∠BAK=∠CBF ,∴△ABK ≌△BCF ,∴BK=CF ,∵BN ∥DF ,∴==,∴FG=,BF=, 设CF=a ,则BC=3a ,∵a 2+(3a )2=()2, ∴a=,∴AB=5,BK=,AK==,∵BH===BG ,∴BH=HG ,AH=5, ∵AH ⊥BG ,∴AB=AG ,∴∠KAB=∠KAG∵∠MAD=∠MAG ,AG=AD ,AM=AM ,∴△AMG ≌△AMD ,∠MAK=45°,∴∠AGM=∠ADM=90°,∠DAM+∠BAK=∠BAK+∠PAB=45°,∴K、G、M共线,∠KAM=∠KAP=45°,∵KA=KA,AP=AM,∴△KAM≌△KAP,∴MK=PK,∴MK=PB+BK=DM+BK=DM+,设DM=x,则MK=x+,在Rt△KMC中,(5﹣x)2+()2=(x+)2,∴x=,∴AM=,=S正方形ABCD﹣S△ADM﹣S△ABG﹣S△BFC=25﹣﹣••﹣∴S四边形AGFM•5•=.故答案为.【点评】本题考查正方形的性质、平行线分线段成比例定理、勾股定理、全等三角形的判定和性质、线段的垂直平分线的性质、角平分线定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.三、解答题:19.如图,在▱ABCD中,对角线AC,BD相交于点O,点E、F分别在边AD,BC 上,且DE=BF,连接OE,OF.求证:OE=OF.【分析】根据平行四边形的性质得出DO=BO,AD∥BC,推出∠EDO=∠FBO,证出△DEO≌△BFO即可.【解答】证明:∵四边形ABCD是平行四边形,∴OD=OB,AD∥BC,∴∠EDO=∠FBO,在△DEO和△BFO中,,∴△DEO≌△BFO(SAS),∴OE=OF.【点评】本题考查了平行四边形的性质,平行线的性质,全等三角形的性质和判定的应用,关键是推出△DEO≌△BFO.20.为了解某住宅区的家庭用水量情况,从该住宅区中随机抽样调查了50户家庭去年每个月的用水量,统计得到的数据绘制了下面的两幅统计图.图1是去年这50户家庭月总用水量的折线统计图,图2是去年这50户家庭月总用水量的不完整的频数分布直方图.(1)根据图1提供的信息,补全图2中的频数分布直方图;(2)在抽查的50户家庭去年月总用水量这12个数据中,极差是250米3,众数是750米3,中位数是725米3;(3)请你根据上述提供的统计数据,估计该住宅区今年每户家庭平均每月的用水量是多少米3?【分析】(1)根据折线统计图的数据可以将频数直方图补充完整;(2)极差是一组数据中最大值与最小值之间的差值;众数是一组数据中出现次数最多的数据;中位数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数;(3)现计算出去年50户家庭年总用水量,再用去年50户家庭年总用水量除以户数再除以月数即可求得该住宅区今年每户家庭平均每月的用水量.【解答】解:(1)补全的频数分布图如下图所示:(2)极差=800﹣550=250(米3);众数为750(米3);中位数为第6个数与第7个数的平均数(700+750)÷2=725(米3);(3)∵去年50户家庭年总用水量为:550+600×2+650+700×2+750×4+800×2=8400(米3)8400÷50÷12=14(米3)∴估计该住宅区今年每户家庭平均每月的用水量是14米3.【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数、众数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据量的数.给定一组数据,出现次数最多的那个数,称为这组数据的众数.21.化简下列各式:(1)(2a﹣1)(1+2a)﹣(a﹣2)(a+3)﹣(a﹣1)2;(2)÷(﹣)﹣.【分析】(1)根据平方差公式、多项式乘多项式及完全平方公式展开,再去括号、合并同类项即可得;(2)先将分子分母因式分解,再依次计算括号内的和除法、减法即可.【解答】解:(1)原式=(2a)2﹣1﹣(a2+3a﹣2a﹣6)﹣(a2﹣2a+1)=4a2﹣1﹣a2﹣3a+2a+6﹣a2+2a﹣1=2a2+a+4;(2)原式=÷﹣=•﹣=﹣=﹣==.【点评】本题主要考查整式的混合运算和分式的混合运算,熟练掌握整式的混合运算和分式的混合运算的顺序和法则是解题的关键.22.如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=.(1)一次函数的解析式和反比例函数的解析式;(2)求△POQ的面积.【分析】(1)作PM⊥x轴于点M.则∠POM=90°﹣∠BOP=45°,△OPM是等腰直角三角形.首先求得B的坐标,然后根据三角函数的定义求得OB的长,在直角△PAM中利用三角函数求得P的坐标,然后利用待定系数法求得一次函数以及反比例函数的解析式;(2)解两个函数解析式组成的方程组求得Q的坐标,然后利用三角形面积公式求得三角形的面积.【解答】解:(1)作PM⊥x轴于点M.则∠POM=90°﹣∠BOP=45°,△OPM是等腰直角三角形.在y=kx+1中令x=0,则y=1,即B的坐标是(0,1),OB=1.∵tan∠BAO==,∴OA=2.即设PM=m,则OM=PM=x.在直角△APM中,AM=2+x,tan∠PAM==,解得x=2,则P的坐标是(2,2).把(2,2)代入y=kx+1得2=2k+1,解得k=,则一次函数的解析式是y=x+1.设反比例函数的解析式是y=,把(2,2)代入得n=4,则反比例函数的解析式是y=;(2)根据题意得,解得或,则Q的坐标是(﹣4,﹣1).则S=×1×(2+4)=3.△POQ【点评】本题考查了待定系数法求函数解析式,以及三角函数的定义,求得P 的坐标是解决本题的关键.23.每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.(1)求该商场两次共购进多少瓶葡萄酒.(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).【分析】(1)根据题意可以列出相应的分式方程,从而可以解答本题;(2)根据题意可以列出相应的关于a的方程,从而可以求得a的值.【解答】解:(1)设第一批购买了x瓶葡萄酒,,解得,x=50,经检验x=50是原分式方程的解,∴x(1﹣20%)=50(1﹣20%)=40,∴该商场两次共购进多少瓶葡萄酒是:50+40=90,即该商场两次共购进多少瓶葡萄酒90瓶;(2)由题意可得,(200﹣)×50+[200(1+2a%)﹣]×50(1﹣a%)=3200,解得,a1=92.5,a2=20(舍去),即a的值是92.5.【点评】本题考查分式方程的应用,解答此类问题的关键是明确题意,列出相应的方程,注意分式方程要检验、(2)中注意a>25.24.一个多位数整数,a代表这个整数分出来的左边数,b代表这个整数分出来的右边数,其中a,b两部分数位相同,若正好为剩下的中间数,则这个多位数就叫平衡数,例如:357满足=5,233241满足=32.(1)写出一个三位平衡数和一个六位平衡数,并证明任意一个六位平衡数一定能被3整除;(2)若一个三位平衡数后两位数减去百位数字之差为3的倍数,且这个平衡数为偶数,求这个三位数.【分析】(1)根据题意举例得到三位平衡数及六位平衡数,并根据题意设出六位平衡数,分解后验证即可;(2)根据题意表示出这个三位数即可.【解答】解:(1)三位平衡数:例如321,六位平衡数:例如183654.若有一个六位平衡数,由于a代表这个整数分出来的左边数,b代表这个整数分出来的右边数,其中a,b两部分数位相同,若正好为剩下的中间数.设六位平衡数为1000a+×100+b=10000a+50a+50b+b=1050a+51b=3(350a+17b),∵a、b都是两位整数,∴六位数一定能被3整除;(2)设这个三位数百位上的数为a.十位上的数为b.个位上的数为c.由题意a+c=2b ①,10b+c﹣a=3n(n为整数)②,①+②得到4a+6c=3n,∴4a是3的倍数,∵c是偶数,a+c=2b,∴a是偶数,∴a=6,∴c=0时,b=3,c=2时,b=4,c=4时,b=5,c=6时,b=6,c=8时,b=7,∴三位数为630,642,654,666,678.【点评】此题考查了因式分解的应用,熟练掌握因式分解的方法是解本题的关键.五、解答题:25.在Rt△ABC中,∠ABC=90°,∠BAC的平分线AD交BC于点D(l)如图1,过点B作BE⊥AC于点E,BE与AD相交于点F,当AD=6,BF=2时,求线段AB的长度;(2)如图2.过点B作BE⊥AC于点E,BE与AD相交于点F,在线段AF上取点G,使FG=DF,连接BG.过点F作FH⊥AD交BG于点H,连接DH交BE于点I,求证:BD=2IF.(3)如图3,若∠BCA=60°,作∠BCA=∠MCB交AD的延长线于M,过M作MN ⊥MA交AB的延长线上于N点,猜想线段ND与线段AB之间有怎样的数量关系,请直接写出结论(不需证明)【分析】(1)首先证明BD=BF,在Rt△在Rt△ABD中,根据AB=计算即可.(2)如图2中,作BK∥DG交DH的延长线于K,连接KG.首先证明四边形BFGK。
2017年重庆八中中考数学一模试卷及解析答案word版

2017年重庆八中中考数学一模试卷一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的框涂黑.1.(4分)有四个数﹣6,﹣4,﹣3,﹣1,其中比﹣2大的数是()A.﹣6 B.﹣4 C.﹣3 D.﹣12.(4分)下列图形中,是轴对称图形的是()A.B. C. D.3.(4分)下列计算正确的是()A.a3+a3=a6 B.3a﹣a=3 C.(a3)2=a5D.a•a2=a34.(4分)若一个多边形的内角和为720°,则该多边形为()边形.A.四B.五C.六D.七5.(4分)函数y=+2中,自变量x的取值范围是()A.x≥1 B.x>1 C.x<1 D.x≤16.(4分)下列实数,介于5和6之间的是()A. B. C. D.7.(4分)已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为()A.3:4 B.2:3 C.9:16 D.3:28.(4分)如果是方程ax+(a﹣2)y=0的一组解,则a的值()A.1 B.2 C.﹣1 D.﹣29.(4分)如图,扇形AOB的圆心角为124°,C是上一点,则∠ACB=()A.114°B.116°C.118° D.120°10.(4分)下列图形都是由同样大小的矩形按一定的规律组成,其中,第①个图形中一共有6个矩形,第②个图形中一共有11个矩形,第③个图形中一共有16个矩形,…,按此规律,第⑧个图形中矩形的个数为()A.30 B.36 C.41 D.4511.(4分)在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为()米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73)A.10.61 B.10.52 C.9.87 D.9.3712.(4分)从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m 使得关于x,y的二元一次方程组有解,且使关于x的分式方程﹣1=有正数解,那么这五个数中所有满足条件的m的值之和是()A.1 B.2 C.﹣1 D.﹣2二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.13.(4分)2017年第一季度,我市在改善环境绿化方面投入资金达到4080000元,4080000用科学记数法表示为.14.(4分)2sin60°﹣()﹣2+(π﹣)0=.15.(4分)某数学小组进行数学速算,比赛成绩如下:得100分的有2人,96分的有4人,90分的2人,那么这个数学小组速算比赛是平均成绩为分.16.(4分)从﹣3、﹣1、、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为.17.(4分)小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距米.18.(4分)如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD 于点M.若DG=6,AG=7,则EF的长为.三、解答题:(本大题共两小题,每小题8分,共16分)19.(8分)如图,C、E、F、D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.20.(8分)最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为度;请补全条形统计图;(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.四、解答题:(本大题共六个小题,21-25题每小题10分,26题12分,共62分)21.(10分)化简:(1)(2x+1)(2x﹣1)﹣(x+1)(3x﹣2)(2)(﹣x+1)÷.22.(10分)一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.(1)求一次函数和反比例函数的解析式;(2)求△ABH面积.23.(10分)某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.24.(10分)如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.(1)若∠AMB=30°,且DM=3,求BE的长;(2)证明:AM=CF+DM.25.(10分)一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M 的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.(1)求证:M与其“友谊数”的差能被15整除;(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值.26.(12分)如图,抛物线y=﹣x2﹣x+与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,已知点D(0,﹣).(1)求直线AC的解析式;(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD面积最大时,过P 作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM,NQ,求PM+MN+NQ的最小值;(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△BPQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E.则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.2017年重庆八中中考数学一模试卷参考答案与试题解析一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的框涂黑.1.(4分)有四个数﹣6,﹣4,﹣3,﹣1,其中比﹣2大的数是()A.﹣6 B.﹣4 C.﹣3 D.﹣1【解答】解:|﹣6|>|﹣4|>|﹣3|>|﹣2|>|﹣1|,∴﹣6<﹣4<﹣3<<﹣2<﹣1,故选:D.2.(4分)下列图形中,是轴对称图形的是()A.B. C. D.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选A.3.(4分)下列计算正确的是()A.a3+a3=a6 B.3a﹣a=3 C.(a3)2=a5D.a•a2=a3【解答】解:A、a3+a3=2a3,错误;B、3a﹣a=2a,错误;C、(a3)2=a6,错误;D、a•a2=a3,正确;故选D.4.(4分)若一个多边形的内角和为720°,则该多边形为()边形.A.四B.五C.六D.七【解答】解:设多边形为n边形,由题意,得(n﹣2)•180°=720°,解得n=6,故选:C.5.(4分)函数y=+2中,自变量x的取值范围是()A.x≥1 B.x>1 C.x<1 D.x≤1【解答】解:由题意得,x﹣1≥0,解得x≥1.故选A.6.(4分)下列实数,介于5和6之间的是()A. B. C. D.【解答】解:A、∵4<<5,∴本选项错误;B、∵5<<6,∴本选项正确;C、∵6<<7,∴本选项错误;D、∵=4,∴本选项错误;故选:B.7.(4分)已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为()A.3:4 B.2:3 C.9:16 D.3:2【解答】解:∵△ABC∽△DEF,面积比为9:4,∴△ABC与△DEF的对应边之比3:2.故选D.8.(4分)如果是方程ax+(a﹣2)y=0的一组解,则a的值()A.1 B.2 C.﹣1 D.﹣2【解答】解:将代入方程ax+(a﹣2)y=0得:﹣3a+a﹣2=0.解得:a=﹣1.故选:C.9.(4分)如图,扇形AOB的圆心角为124°,C是上一点,则∠ACB=()A.114°B.116°C.118° D.120°【解答】解:如图所示,在⊙O上取点D,连接AD,BD,∵∠AOB=124°,∴∠ADB=∠AOB=×124°=62°.∵四边形ADBC是圆内接四边形,∴∠ACB=180°﹣62°=118°.故选C.10.(4分)下列图形都是由同样大小的矩形按一定的规律组成,其中,第①个图形中一共有6个矩形,第②个图形中一共有11个矩形,第③个图形中一共有16个矩形,…,按此规律,第⑧个图形中矩形的个数为()A.30 B.36 C.41 D.45【解答】解:∵图①有矩形有6个=5×1+1,图②矩形有11个=5×2+1,图③矩形有16=5×3+1,∴第n个图形矩形的个数是5n+1当n=8时,5×8+1=41个.故选C.11.(4分)在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为()米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73)A.10.61 B.10.52 C.9.87 D.9.37【解答】解:如图,过点C作CG⊥EF于点G,延长GH交AD于点H,过点H作HP⊥AB于点P,则四边形BCHP为矩形,∴BC=PH=6,BP=CH,∠CHD=∠A=37°,∴AP===8,过点D作DQ⊥GH于点Q,∴∠CDQ=∠CEG=30°,∴CQ=CD=2,DQ=CDcos∠CDQ=4×=2,∵QH===,∴CH=QH﹣CQ=﹣2,则AB=AP+PB=AP+CH=8+﹣2≈10.61,故选:A.12.(4分)从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m 使得关于x,y的二元一次方程组有解,且使关于x的分式方程﹣1=有正数解,那么这五个数中所有满足条件的m的值之和是()A.1 B.2 C.﹣1 D.﹣2【解答】解:∵有解,∴直线y=﹣2x+2与直线y=x+不平行,∴≠﹣2,∴m≠﹣4,解﹣1=得,x=4﹣m,∵x=4﹣m是正数,∴m=﹣3,1,3,当m=3时,原方式方程无意义,故m=﹣3,1,∴﹣3+1=﹣2,故选:D.二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.13.(4分)2017年第一季度,我市在改善环境绿化方面投入资金达到4080000元,4080000用科学记数法表示为 4.08×106.【解答】解:4080000=4.08×106.故答案为:4.08×106.14.(4分)2sin60°﹣()﹣2+(π﹣)0=﹣3.【解答】解:原式=2×﹣4+1=﹣3.故答案为:﹣3.15.(4分)某数学小组进行数学速算,比赛成绩如下:得100分的有2人,96分的有4人,90分的2人,那么这个数学小组速算比赛是平均成绩为95.5分.【解答】解:(100×2+96×4+90×2)÷(2+4+2)=(200+384+180)÷8=764÷8=95.5(分).答:这个数学小组速算比赛的平均成绩为95.5分.故答案为:95.5.16.(4分)从﹣3、﹣1、、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为.【解答】解:当a=﹣3,则y=﹣x﹣3,此时图象与x轴交点为:(﹣3,0),与y 轴交点为:(0,﹣3),故一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为4.5,不合题意;当a=3,则y=﹣x+3,此时图象与x轴交点为:(3,0),与y轴交点为:(0,3),故一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为4.5,不合题意;当a=﹣1、、1时,一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为:,,符合题意,故关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为:.故答案为:.17.(4分)小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.【解答】解:观察图象可知小兵爸爸的速度为=90米/分,设小兵的速度为x米/分,由图象可知10(90+x)=1500,解得x=60米/分,60×4=240,1500+240=1740米.故答案为1740.18.(4分)如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7,则EF的长为.【解答】解:如图作AH⊥BG于H交BC于T,AN⊥GD于N,取BD的中点O,连接OA、OG.∴∠BAD=∠BGD=90°,∴OA=OD=OB=OG,∴A、B、G、D四点共圆,∴∠AGB=∠ADB=45°,∠AGD=∠ABD=45°,∴AH=GH,AN=NG,∵∠N=∠AHG=∠HGN=90°,∴四边形ANGH是矩形,∵AH=HG,∴四边形ANGH是正方形,∵AG=7,∴AH=HG=GN=AN=7,易证△AND≌△AHB,∴DN=BH,∴GD+GB=GN﹣DN+GH+BH=2GN=AG,∴6+GB=14,∴GB=8,BD==10,∴BH=1,∵△BHT∽△AHB,∴BH2=AH•HT,∴HT=,∴AT=AH+TH=,易证△ABT≌△BCF,∴AT=BF=,∵△BEF∽△BGD,∴=,∴=,∴EF=,故答案为.三、解答题:(本大题共两小题,每小题8分,共16分)19.(8分)如图,C、E、F、D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.【解答】证明:∵AB∥FD,BG∥FH,∴∠B=∠BEF,∠BEF=∠DFH,∴∠B=∠DFH,在△ABG和△DHF中,,∴△ABG≌△DHF(SAS),∴∠A=∠D.20.(8分)最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为120度;请补全条形统计图;(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.【解答】解:(1)由题意可得,本次调查的学生有:15÷50%=30(人),扇形统计图中“基本了解”部分所对应扇形的圆心角为:360°×=120°,了解的有:30﹣10﹣15﹣2=3(人),补全的条形统计图如右图所示;(2)设了解的学生为(A男,A女,A女),不了解的为(B男,B女),则出现的所有可能性为:(A男,B男)、(A男、B女)、(A女,B男)、(A女,B 女)、(A女,B男)、(A女,B女)、(A女,B男)、(A女,B女),∴恰好抽到1名男生和1名女生的概率是:,即恰好抽到1名男生和1名女生的概率是.四、解答题:(本大题共六个小题,21-25题每小题10分,26题12分,共62分)21.(10分)化简:(1)(2x+1)(2x﹣1)﹣(x+1)(3x﹣2)(2)(﹣x+1)÷.【解答】解:(1)原式=4x2﹣1﹣3x2﹣x+2=x2﹣x+1;(2)原式=•=﹣•=﹣.22.(10分)一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.(1)求一次函数和反比例函数的解析式;(2)求△ABH面积.【解答】解:(1)∵点D的坐标为(﹣1,0),tan∠CDO=2,∴CO=2,即C(0,2),把C(0,2),D(﹣1,0)代入y=ax+b可得,,解得,∴一次函数解析式为y=2x+2,∵点A的横坐标是1,∴当x=1时,y=4,即A(1,4),把A(1,4)代入反比例函数y=,可得k=4,∴反比例函数解析式为y=;(2)解方程组,可得或,∴B(﹣2,﹣2),又∵A(1,4),BH⊥y轴,∴△ABH面积=×2×(4+2)=6.23.(10分)某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.【解答】解:(1)设售价应为x元,依题意得:2290﹣15(x﹣11)÷0.5≥2200,解得x≤14.答:2月份售价应不高于14元;(2)[14(1﹣m%)﹣10(1+10%)]×2200(1+m%)=6600,令m%=t,原式为(3﹣2t)(1+t)=3.t1=0(不合题意,舍去),t2=0.5,∴m=50.答:m的值是50.24.(10分)如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.(1)若∠AMB=30°,且DM=3,求BE的长;(2)证明:AM=CF+DM.【解答】(1)解:如图1中,∵四边形ABCD是菱形,∠BAD=60°,∴△ABD,△BCD的是等边三角形,∴∠ABD=∠CBD=∠ADB=∠BAD=60°,BA=BC,∵∠AMB=30°,∠ADB=∠AMB+∠DAM,∴∠DAM=∠DMA=30°,∴∠BAM=90°,DA=DM=AB=BC=CE=3,在△BMA和△BMC中,,∴△BMA≌△BMC,∴∠BCM=∠BAM=90°,在Rt△BCE中,BE==3.(2)如图2中,在BD上取一点G,使得BG=DF,连接CG交BE于O.∵BG=DF,∠CBG=∠BDF,BD=BC,∴△GBC≌△FDB,∴∠BGC=∠BFD,∠DBF=∠BCG,∴∠MGC=∠BFC,∵∠COF=∠CBO+∠OCB=∠CBO+∠DBF=60°在△COE中,∠ECO+∠EOC+∠CEO=180°,在△BCF中,∠BFC+∠CBF+∠BCF=180°,∵CB=CE,∴∠CBE=∠CEO,∵∠BCF=∠COE=60°,∴∠ECO=∠BFC=∠MGC,∴MC=MG,由(1)可知△BMA≌△BMC,∴AM=MC=MG,∵MG=DG+DM,∵BD=CD,BG=DF,∴DG=CF,∴AM=CF+DM25.(10分)一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M 的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.(1)求证:M与其“友谊数”的差能被15整除;(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值.【解答】解:(1)由题意可得,设M为100a+10b+c,则它的友谊数为:100b+10a+c,(100a+10b+c)﹣(100b+10a+c)=100a+10b+c﹣100b﹣10a﹣c=100(a﹣b)+10(b﹣a)=90(a﹣b),∵,∴M与其“友谊数”的差能被15整除;(2)由题意可得,N=2×100+10a+b=200+10a+b,N的团结数是:10×2+a+10a+2+10×2+b+10×b+2+10a+b+10b+a=22a+22b+44,∴22a+22b+44﹣(200+10a+b)=24,解得,或,即N是284或218.26.(12分)如图,抛物线y=﹣x2﹣x+与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,已知点D(0,﹣).(1)求直线AC的解析式;(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD面积最大时,过P 作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM,NQ,求PM+MN+NQ的最小值;(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△BPQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E.则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.【解答】解:(1)∵抛物线y=﹣x2﹣x+与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,∴A(﹣4,0),B(1,0),C(0,),设直线AC的解析式为y=kx+b,则有,∴k=,b=,∴直线AC的解析式为y=x+.(2)如图1中,分别过D、B作x轴,y轴的平行线交于点K,连接PK.设P(m,﹣m2﹣m+).S△PDB=S△PDK+S△PBK﹣S△DKB=•1•(﹣m2﹣m++)+••(1﹣m)﹣•1=﹣(m+3)2+,∵﹣<0,∴m=﹣3时,△PBD的面积最大,此时P(﹣3,),Q(﹣3,0).如图2中,作Q关于y轴的对称点Q′,将Q′向左平移个单位得到Q″,连接PQ″交抛物线对称轴于M,此时PM+MN+NQ最短.易证四边形MNQ′Q″是平行四边形,∴NQ=NQ′=Q″M,∴PM+MN+NQ=PM+MQ″+MN=PQ″+MN,∵Q″(,0),∴PQ″==,∴PM+MN+NQ的最小值为+.(3)如图3中,由(2)可知直线PB的解析式为y=﹣x+,直线BD的解析式为y=x﹣,易证∠PBQ=30°,∠DBO=60°,PB⊥BD.①当点Q″与Q重合时,∵∠B′EQ=∠QB′E=30°,∴EQ=B′Q″=4,∴OE=QE+OQ=7.②如图4中,当B′E=B′Q″时作B′N⊥x轴于N.∵B′E=B′Q″=4,∠B′EN=30°,∴B′N=B′E=2,EN=2,∴B′(,﹣2),∴OE=2+=﹣1.③如图5中,当EQ″=EB′时,作B′N⊥x轴于N.易知EP′=EQ″=EB′=,B′N=,EN=2,∴B′(,﹣),∴EO=.④如图6中,当B′E=B′Q″时,易知B′E=B′Q″=4,在Rt△BEB′中,BE=EB′÷cos30°=,∴OE=OB+BE=+1,综上所述,满足条件的OE的值为7或﹣1或或+1.赠送:初中数学几何模型【模型一】半角型:图形特征:FAB正方形ABCD中,∠EAF=45°∠1=12∠BAD推导说明:1.1在正方形ABCD中,点E、F分别在BC、CD上,且∠FAE=45°,求证:EF=BE+DFE-aa B E1.2在正方形ABCD中,点E、F分别在BC、CD上,且EF=BE+DF,求证:∠FAE=45°E-a aBE挖掘图形特征:x-aa-a运用举例:1.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM(2)当AE=1时,求EF的长.E3.如图,梯形ABCD中,AD∥BC,∠C=90°,BC=CD=2AD=4,E为线段CD上一点,∠ABE=45°.(1)求线段AB的长;(2)动点P从B出发,沿射线..BE运动,速度为1单位/秒,设运动时间为t,则t为何值时,△ABP为等腰三角形;(3)求AE-CE的值.。
重庆八中 2017-2018学年 九年级上 半期测试卷(含答案)
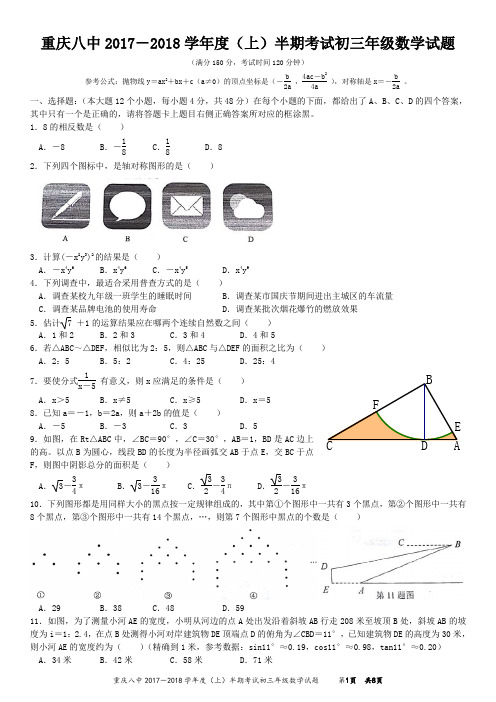
重庆八中2017-2018学年度(上)半期考试初三年级数学试题(满分150分,考试时间120分钟)参考公式:抛物线y =ax 2+bx +c (a≠0)的顶点坐标是(-b 2a ,4ac -b 24a ),对称轴是x =-b2a。
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题目右侧正确答案所对应的框涂黑。
1.8的相反数是( ) A .-8B .-18C .18D .82.下列四个图标中,是轴对称图形的是( )3.计算(-x 2y 3)2的结果是( )A .-x 4y 6B .x 4y 6C .-x 4y 5D .x 4y 94.下列调查中,最适合采用普查方式的是( )A .调查某校九年级一班学生的睡眠时间B .调查某市国庆节期间进出主城区的车流量C .调查某品牌电池的使用寿命D .调查某批次烟花爆竹的燃放效果5.估计7 +1的运算结果应在哪两个连续自然数之间( ) A .1和2 B .2和3 C .3和4 D .4和56.若△ABC~△DEF ,相似比为2:5,则△ABC 与△DEF 的面积之比为( ) A .2:5 B .5:2 C .4:25 D .25:4 7.要使分式1x -5有意义,则x 应满足的条件是( )A .x >5B .x ≠5C .x ≥5D .x =5 8.已知a =-1,b =2a ,则a +2b 的值是( )A .-5B .-3C .3D .59.如图,在Rt△ABC 中,∠BC=90°,∠C=30°,AB =1,BD 是AC 边上的高。
以点B 为圆心,线段BD 的长度为半径画弧交AB 于点E ,交BC 于点F ,则图中阴影总分的面积是( )A .3-34πB .3-316πC .32-34πD .32-316π10.下列图形都是用同样大小的黑点按一定规律组成的,其中第①个图形中一共有3个黑点,第②个图形中一共有8个黑点,第③个图形中一共有14个黑点,…,则第7个图形中黑点的个数是()A .29B .38C .48D .5911.如图,为了测量小河AE 的宽度,小明从河边的点A 处出发沿着斜坡AB 行走208米至坡顶B 处,斜坡AB 的坡度为i =1:2.4,在点B 处测得小河对岸建筑物DE 顶端点D 的俯角为∠CBD=11°,已知建筑物DE 的高度为30米,则小河AE 的宽度约为( )(精确到1米,参考数据:sin11°≈0.19,cos11°≈0.98,tan11°≈0.20) A .34米 B .42米 C .58米 D .71米12.使得关于x 的分式方程ax -14-x +34-x =-2的解为正数,且关于x 的不等式组x >0a +x 2≥x -32有解的所有整数a的和为( )A .-2B .-3C .-5D .-6 二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八中初2017级初三(上)入学考试
数 学 试 题
(满分150分 考试时间120分钟)
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的框涂黑.
1.﹣2017的倒数是( ) A .2017
B .﹣2017
C .
20171
D .2017
1
-
2.下列图标既是轴对称图形又是中心对称图形的是( )
A .
B .
C .
D .
3.函数2
1
--=
x x y 中自变量x 的取值围是( ) A .1≥x B .2>x
C .1≥x 且2≠x
D .2≠x 4.下列运算正确的是( )
A .651a a -=
B .5
3
2
a a a =⋅
C .23
5
()a a =
D .632a a a ÷=
5.市主城区2016年8月10日至8月19日连续10天的最高气温统计如下表:
最高气温(℃) 38 39 40 41 天 数 3 2 1 4
则这组数据的中位数和平均数分别为( )
A .39.5,39.6
B .40,41
C .41,40
D .39,41
6.分式方程
x
x x -=--23
252的解是( ) A .2-=x
B .2=x
C .1=x
D .1=x 或2=x
7.若反比例函数x
y 1
=的图象上有两点P 1(1,1y )和P 2(2,2y ),那么( ) A .021>>y y
B .012>>y y
C .021<<y y
D .012<<y y
8.三角形的两边长分别是3和6,第三边是方程0
8
6
2=
+
-x
x的解,则这个三角形的周长是()
A.11 B.13 C.11或13 D.以上答案都不对9.如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为()
A.10 B.12 C.14 D.16
(9题图)
10.某星期六的早晨,晓林从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示晓林离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中
错误
..的是().
A.晓林在公园休息了5分钟B.晓林乘出租车用了17分钟
C.出租车的平均速度是900米/分钟D.晓林跑步的速度为180米/分钟11.如图,用菱形纸片按规律依次拼成下列图案.由图知,第1个图案中有5个菱形纸片;第2个图案中有9个菱形纸片;第3个图形中有13个菱形纸片.按此规律,第6个图案中有()个菱形纸片.
A.21 B.23 C.25 D.29
12.在– 3、– 2、– 1、0、1、2这六个数中,随机取出一个数记为a,那么使得关于x的一元二次方程2250
x ax
-+=无解,且使得关于x的方程
1
3
11
x a
x x
+
-=
--
有整数解的所有a的值之和为().
A.1
-B.0C.1D.2
(10题图)
1800
y (米)
17
15
10(分)
O
A C
D 二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上. 13.不等式组⎩⎨
⎧-><-2
1
32x x 的解集是 .
14.如图,菱形ABCD 中,两条对角线长610==BD AC ,
,则菱形ABCD 的面积为 .
(14题图) (17题图) (18题图)
15.△ABC 与△DEF 相似,且它们的面积比为1:4,则△ABC 与△DEF 对应高的比为 .
16.在一个口袋中有3个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球然后放回..,再随机摸出一个小球,则两次取出的小球标号相同的概率为_______. 17.如图,△AOB 和△ACD 均为正三角形,顶点B 、D 在双曲线)0(8
>=x x
y 上,线段BC 、AD 交于点P ,则=∆OBP S .
18.如图,点E 是边长为52的正方形ABCD 外一点,∠BED = 90°,DE = 8,连接AE ,
则AE 的长为
三、解答题(本大题2个小题,每小题 7分,共14分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡中对应的位置上.
19.已知:如图,CD = BE ,CD ∥BE ,∠D =∠E .
求证:点C 是线段AB 的中点.
20.如图,在边长为1的正方形网格中,△ABC 的顶点均在格点上,点A 、B 的坐标分别是A (4,3)、B (4,1),把△ABC 绕点C 逆时针旋转90°后得到△A 1B 1C . (1)画出△A 1B 1C ,直接写出点A 1、B 1的坐标; (2)求在旋转过程中,△ABC 所扫过的面积.
四、解答题:(本大题4个小题,每小题10分,共40分)解答时每个小题必须给出必要的演算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡中对应的位置上.
21.计算:
(1)236x x x ++-()() (2)232
2(+1)121
x x x x x x x x ++-÷--+
22.八中宏帆中学某年级为了选拔参加“全国汉字听写大赛”赛区比赛的队员,特在年
级举行全体学生的“汉字听写”比赛,首轮每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如下的图表.
根据以上信息完成下列问题:
(1)统计表中的m = ,n = ,并补全条形统计图;
(2)已知该年级共有1500名学生,如果听写正确的字的个数不少于24个则进入第二轮的比赛,请你估计本次听写比赛顺利进入第二轮的学生人数;
(3)第二轮比赛过后,为了更有针对性地应对本次大赛,该年级决定从没有担任班主任的5个语文老师(其中3个男老师2个女老师)中随机抽取两个老师对胜出的学生进行培训、辅导.请用树状图或列表法求出抽取的两个老师恰好都是男老师的概率.
23.如图,已知一次函数b ax y +=的图象与反比例函数x
k
y =
的图象相交于点A (﹣2,m )和点B (4,﹣2),与x 轴交于点C .
(1)求一次函数与反比例函数的解析式; (2)求△AOB 的面积.
24.某轻轨工程指挥部,要对某轻轨路段工程进行招标,接到了甲、乙两个工程队的投标书.根据投标书所知,甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的;若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为9.2万元,乙队每天的施工费用为6.8万元.工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,那么预算的施工费用是否够用?若不够用,需追加预算多少万元?
五、解答题:(本大题2个小题,每小题12分,共24分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡中对应的位置上. 25.在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分。
而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密
码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:222
3--+x x x 因式分解的结果为)2)(1)(1(++-x x x ,当18=x 时,202,191,171=+=+=-x x x ,此时可以得到数字密码171920.
(1)根据上述方法,当7,21==y x 时,对于多项式2
3xy x -分解因式后可以形成哪些
数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为y x 、,求出一个由多项式3
3
xy y x +分解因式后得到的密码(只需一个即可);
(3)若多项式21)3(2
3
---+nx x n m x 因式分解后,利用本题的方法,当27=x 时可以得到其中一个密码为242834,求n m 、的值.
26.如图1,在Rt ABC ∆中,90ACB ∠=,D 为直线CB 上一点,且满足CD CA =,连接AD .过点C 作CE AB ⊥于点E .
(1) 若10=AB ,6==CA CD ,则______________==CE BD ,
;
(2) 如图2,若点F 是线段CE 延长线上一点,连接FD ,若45F ∠=,求证:
AE FE =;
(3) 如图3,设直线CE 与直线AD 交于点G ,在线段CD 的延长线上取一点H ,使
得DH CB =,连接HG 交直线AB 于点I ,若CGH B ∠=∠,请直接写出....
线段AC 和AI 之间的数量关系(不需证明).
图1 图2 图3
A C D
B
A
C B。
